Mathematical Model for Economic Growth, Corruption and Unemployment: Analysis of the Effects of a Time Delay in the Economic Growth
Abstract
1. Introduction
2. Mathematical Model
Proposed Mathematical Model with Delay
3. Stability Analysis of Equilibria
3.1. Equilibrium Points
- The trivial equilibrium point .
- The axial equilibrium point .
- The axial equilibrium point .
- Economic-specific equilibrium point .
- Unemployment-free equilibrium .
- Positive interior equilibrium .
3.2. Computing the Jacobian Matrix of the System
3.3. Stability Analysis and Possible Hopf Bifurcation Arising from
3.4. Stability Analysis and Existence of Hopf Bifurcation Arising from
3.5. Stability Analysis and Existence of Hopf Bifurcation Arising from
- If , the equilibrium point is locally asymptotically stable.
- If , a Hopf bifurcation occurs for system (2) at the equilibrium point .
- If , the equilibrium point is unstable.
3.6. Stability Analysis and Existence of Hopf Bifurcation Arising from
- If , the equilibrium point is locally asymptotically stable.
- If , a Hopf bifurcation occurs for system (2) at the equilibrium point .
- If , the equilibrium point is unstable.
3.7. Stability Analysis and Existence of Hopf Bifurcation Arising from
3.8. Stability Analysis and Existence of Hopf Bifurcation Arising from
3.9. Summary of Stability Analysis
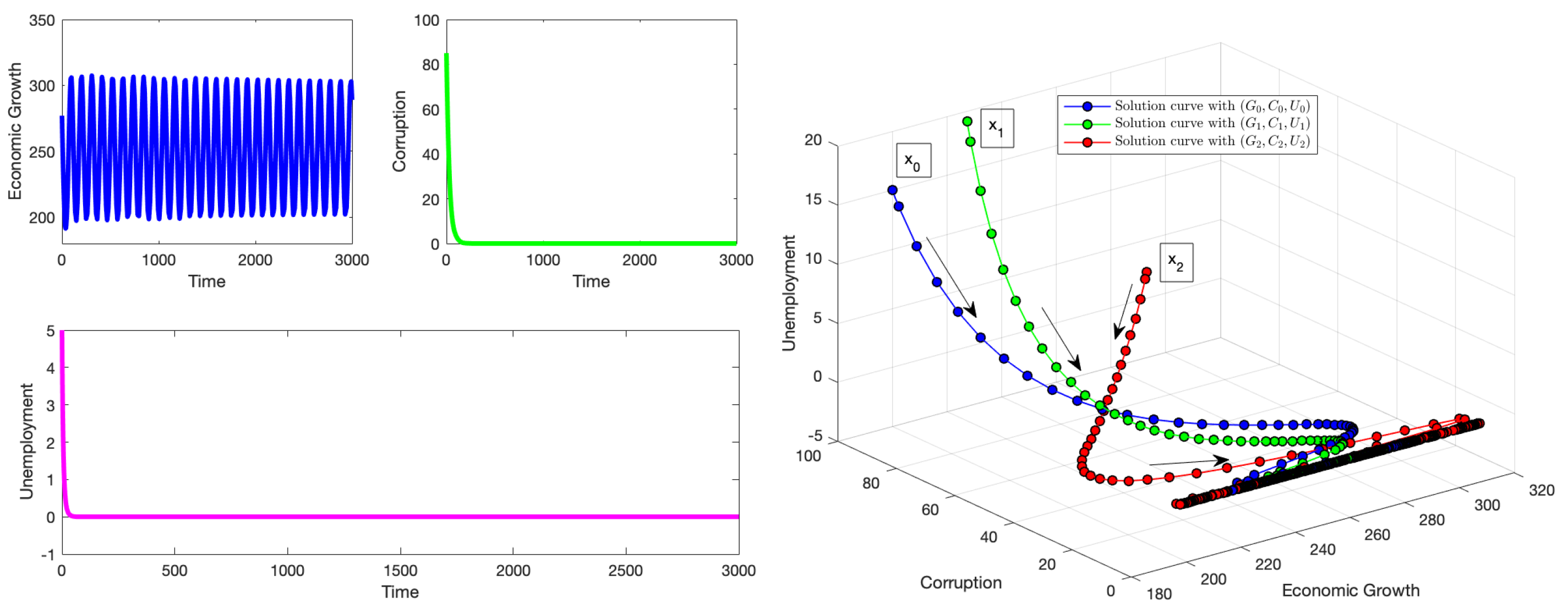
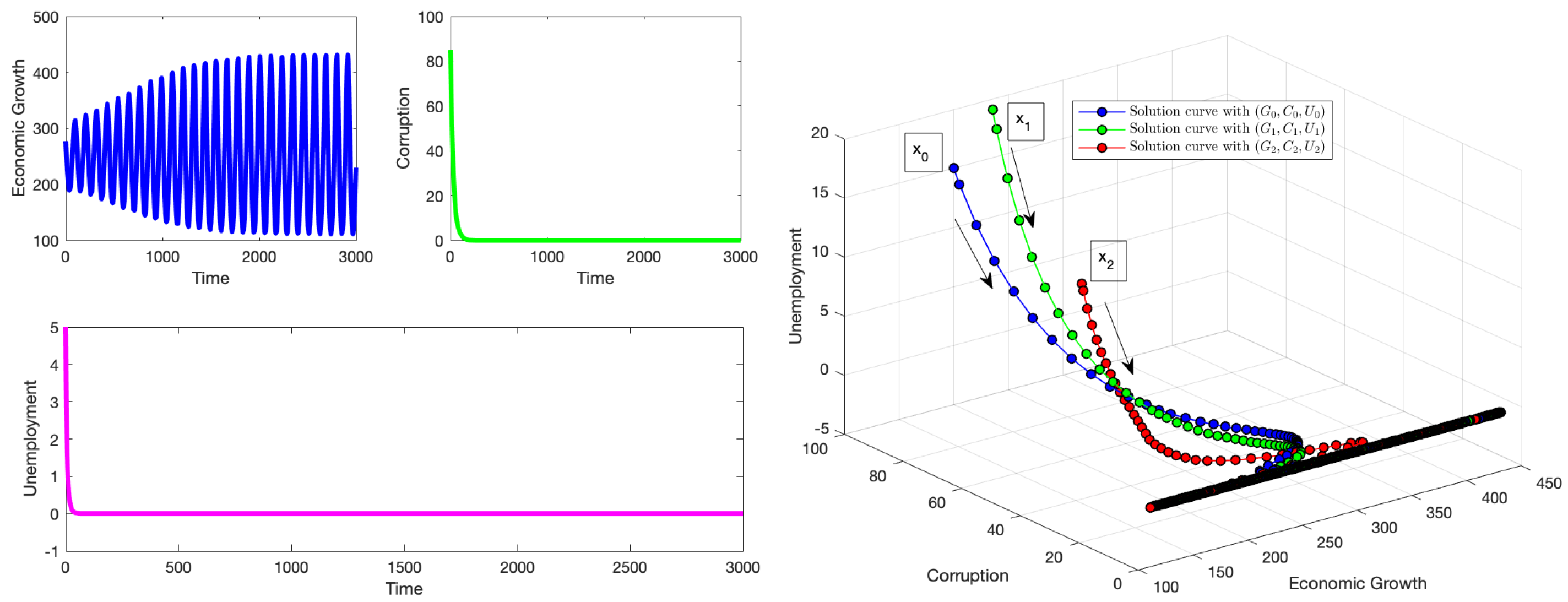
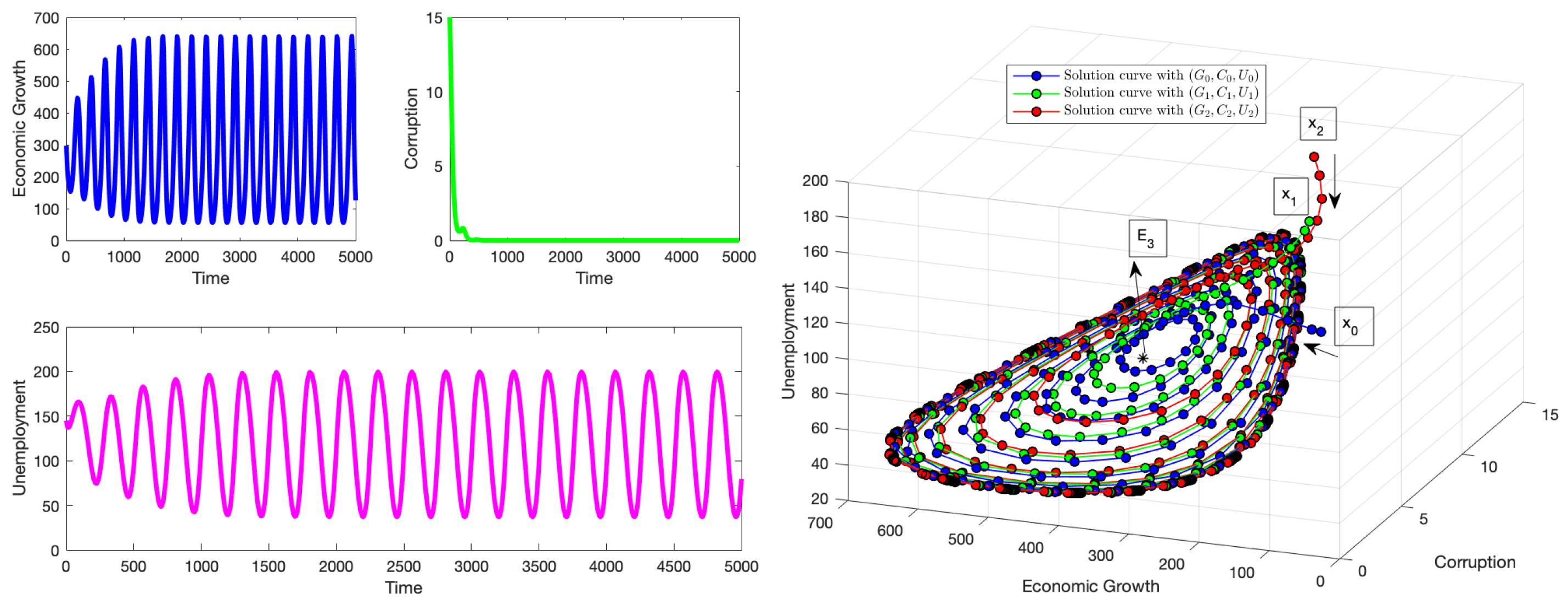
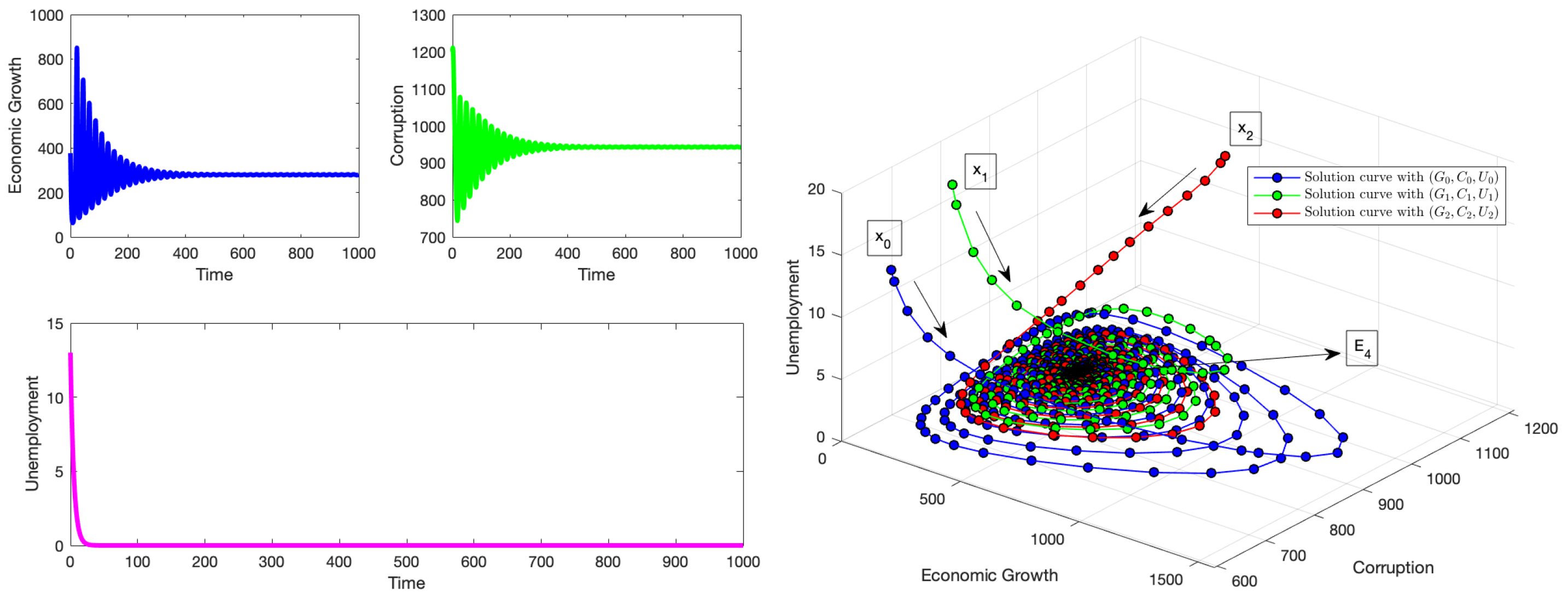
4. Numerical Simulations
4.1. Simulations for the Equilibrium Point
4.2. Simulations for the Equilibrium Point
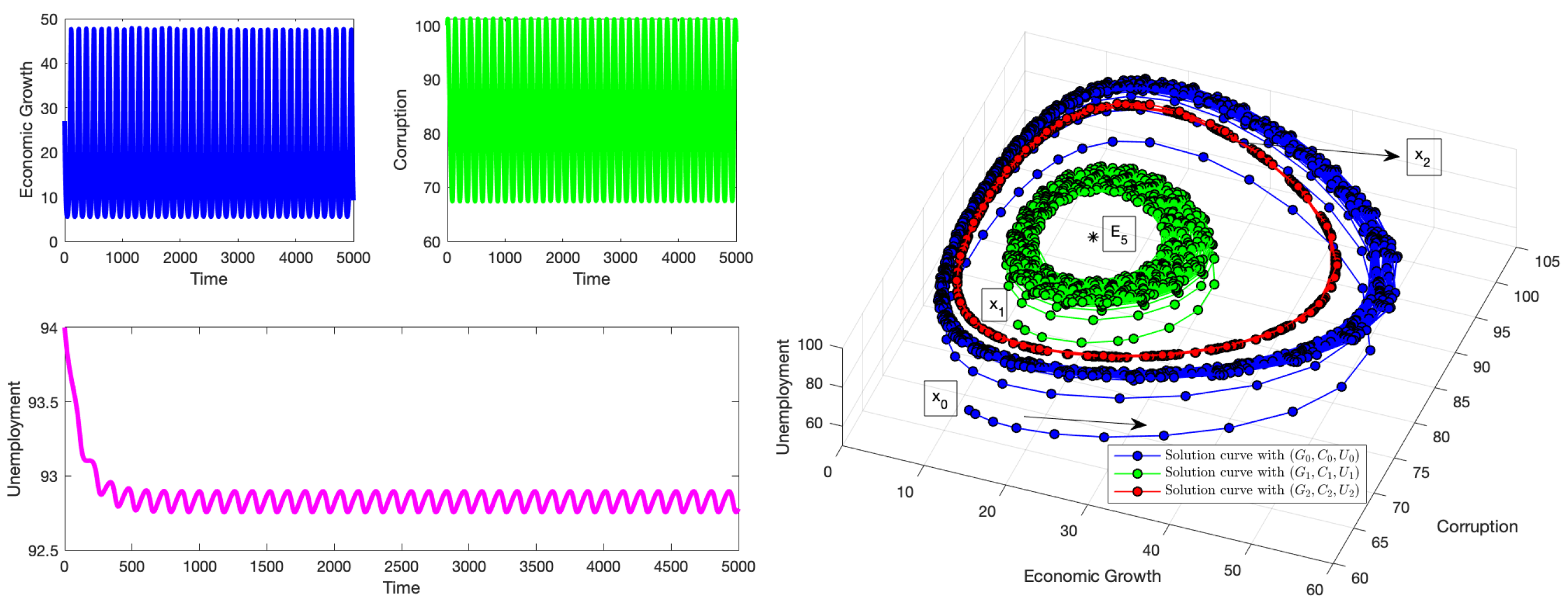
4.3. Simulations for the Equilibrium Point
4.4. Simulations for the Equilibrium Point
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De la Fuente, A.; De La Fuente, A. Mathematical Methods and Models for Economists; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Morgan, M.S.; Knuuttila, T. Models and modelling in economics. Philos. Econ. 2012, 13, 49–87. [Google Scholar]
- Radzicki, M.J. System dynamics and its contribution to economics and economic modeling. In System Dynamics: Theory and Applications; Springer: New York, NY, USA, 2020; pp. 401–415. [Google Scholar]
- Zhang, W.B. Differential Equations, Bifurcations and Chaos in Economics; World Scientific Publishing Company: Singapore, 2005; Volume 68. [Google Scholar]
- Feldstein, M.; Horioka, C.; Savings, D. The Solow growth model. Q. J. Econ. 1992, 107, 407–437. [Google Scholar]
- Nonneman, W.; Vanhoudt, P. A further augmentation of the Solow model and the empirics of economic growth for OECD countries. Q. J. Econ. 1996, 111, 943–953. [Google Scholar] [CrossRef]
- Solow, R.M. Technical progress, capital formation, and economic growth. Am. Econ. Rev. 1962, 52, 76–86. [Google Scholar]
- Aniţa, S.; Arnăutu, V.; Capasso, V. An Introduction to Optimal Control Problems in Life Sciences and Economics: From Mathematical Models to Numerical Simulation with MATLAB; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bosi, S.; Desmarchelier, D. Local bifurcations of three and four-dimensional systems: A tractable characterization with economic applications. Math. Soc. Sci. 2019, 97, 38–50. [Google Scholar] [CrossRef]
- González-Parra, G.; Chen-Charpentier, B.; Arenas, A.J.; Díaz-Rodríguez, M. Mathematical modeling of physical capital diffusion using a spatial Solow model: Application to smuggling in Venezuela. Economies 2022, 10, 164. [Google Scholar] [CrossRef]
- Ashi, H.; Al-Maalwi, R.M.; Al-Sheikh, S. Study of the unemployment problem by mathematical modeling: Predictions and controls. J. Math. Sociol. 2022, 46, 301–313. [Google Scholar] [CrossRef]
- Roslan, U.A.M.; Zakaria, S.; Alias, A.; Malik, S. A mathematical model on the dynamics of poverty, poor and crime in West Malaysia. Far. East J. Math. Sci. 2018, 107, 309–319. [Google Scholar] [CrossRef]
- Buedo-Fernández, S.; Liz, E. On the stability properties of a delay differential neoclassical model of economic growth. Electron. J. Qual. Theory Differ. Equ. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Erman, S. Stability Analysis of Some Dynamic Economic Systems Modeled by State-Dependent Delay Differential Equations. In Global Approaches in Financial Economics, Banking, and Finance; Dincer, H., Hacioglu, Ü., Yüksel, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 227–240. [Google Scholar]
- Matsumoto, A.; Szidarovszky, F. Delay differential nonlinear economic models. In Nonlinear Dynamics in Economics, Finance and Social Sciences: Essays in Honour of John Barkley Rosser Jr; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–214. [Google Scholar]
- Ruzgas, T.; Jankauskienė, I.; Zajančkauskas, A.; Lukauskas, M.; Bazilevičius, M.; Kaluževičiūtė, R.; Arnastauskaitė, J. Solving Linear and Nonlinear Delayed Differential Equations Using the Lambert W Function for Economic and Biological Problems. Mathematics 2024, 12, 2760. [Google Scholar] [CrossRef]
- Segura, J.; Franco, D.; Perán, J. Long-run economic growth in the delay spatial Solow model. Spat. Econ. Anal. 2023, 18, 158–172. [Google Scholar] [CrossRef]
- Rajpal, A.; Bhatia, S.K.; Goel, S.; Kumar, P. Time delays in skill development and vacancy creation: Effects on unemployment through mathematical modelling. Commun. Nonlinear Sci. Numer. Simul. 2024, 130, 107758. [Google Scholar] [CrossRef]
- Çalış, Y.; Demirci, A.; Özemir, C. Hopf bifurcation of a financial dynamical system with delay. Math. Comput. Simul. 2022, 201, 343–361. [Google Scholar] [CrossRef]
- Özbay, H.; Sağlam, H.Ç.; Yüksel, M.K. Hopf cycles in one-sector optimal growth models with time delay. Macroecon. Dyn. 2017, 21, 1887–1901. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 42. [Google Scholar]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Marsden, J.E.; McCracken, M. The Hopf Bifurcation and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 19. [Google Scholar]
- Al-Hdaibat, B. Computational Dynamical Systems Analysis: Bogdanov-Takens Points and an Economic Model. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2015. [Google Scholar]
- Krawiec, A.; Szydłowski, M. Economic growth cycles driven by investment delay. Econ. Model. 2017, 67, 175–183. [Google Scholar] [CrossRef]
- Manfredi, P.; Fanti, L. Cycles in dynamic economic modelling. Econ. Model. 2004, 21, 573–594. [Google Scholar] [CrossRef]
- Pribylova, L. Bifurcation routes to chaos in an extended Van der Pol’s equation applied to economic models. Electron. J. Differ. Equ. (EJDE) 2009, 2009, 1–21. [Google Scholar]
- Dockner, E.J.; Feichtinger, G. On the optimality of limit cycles in dynamic economic systems. J. Econ. 1991, 53, 31–50. [Google Scholar] [CrossRef]
- Feichtinger, G. Limit cycles in dynamic economic systems. Ann. Oper. Res. 1992, 37, 313–344. [Google Scholar] [CrossRef]
- Feichtinger, G.; Novak, A.; Wirl, F. Limit cycles in intertemporal adjustment models: Theory and applications. J. Econ. Dyn. Control 1994, 18, 353–380. [Google Scholar] [CrossRef]
- Kryuchkov, V.; Solomonovich, M.; Anton, C. Moving limit cycles model of an economic system. In Proceedings of the Numerical Analysis and Its Applications: 6th International Conference, NAA 2016, Lozenetz, Bulgaria, 15–22 June 2016; Revised Selected Papers 6. Springer: Berlin/Heidelberg, Germany, 2017; pp. 456–463. [Google Scholar]
- Markakis, M.; Douris, P. Stability and analytical approximation of limit cycles in Hopf bifurcations of four-dimensional economic models. Appl. Math. Sci. 2014, 8, 3697–3990. [Google Scholar] [CrossRef]
- Araujo, R.A.; Flaschel, P.; Moreira, H.N. Limit cycles in a model of supply-side liquidity/profit-rate in the presence of a Phillips curve. Economia 2020, 21, 145–159. [Google Scholar] [CrossRef]
- Asada, T.; Demetrian, M.; Zimka, R. The stability of normal equilibrium point and the existence of limit cycles in a simple Keynesian macrodynamic model of monetary policy. In Essays in Economic Dynamics: Theory, Simulation Analysis, and Methodological Study; Springer: Singapore, 2016; pp. 145–162. [Google Scholar]
- Bazán Navarro, C.E.; Benazic Tomé, R.M. Structural Stability Analysis in a Dynamic IS-LM-AS Macroeconomic Model with Inflation Expectations. Int. J. Differ. Equ. 2022, 2022, 5026061. [Google Scholar] [CrossRef]
- Ifeacho, O.; González-Parra, G. Hopf Bifurcations in a Mathematical Model for Economic Growth, Corruption, and Unemployment: Computation of Economic Limit Cycles. Axioms 2025, 14, 173. [Google Scholar] [CrossRef]
- Anderson, R.M.; Jackson, H.C.; May, R.M.; Smith, A.M. Population dynamics of fox rabies in Europe. Nature 1981, 289, 765–771. [Google Scholar] [CrossRef]
- Greenhalgh, D. Hopf bifurcation in epidemic models with a latent period and nonpermanent immunity. Math. Comput. Model. 1997, 25, 85–107. [Google Scholar] [CrossRef]
- Sepulveda, G.; Arenas, A.J.; González-Parra, G. Mathematical modeling of COVID-19 dynamics under two vaccination doses and delay effects. Mathematics 2023, 11, 369. [Google Scholar] [CrossRef]
- Baráková, L. Asymptotic Behaviour and Hopf Bifurcation of a Three-Dimensional Nonlinear Autonomous System. Georgian Math. J. 2002, 9, 207–226. [Google Scholar] [CrossRef]
- Ifeacho, O.; González-Parra, G. Mathematical Modeling of Economic Growth, Corruption, Employment and Inflation. Mathematics 2025, 13, 1102. [Google Scholar] [CrossRef]
- Callen, T. Gross Domestic Product: An Economy’s All; International Monetary Fund: Washington, DC, USA, 2012. [Google Scholar]
- McCusker, J.J. Estimating early American gross domestic product. Hist. Methods J. Quant. Interdiscip. Hist. 2000, 33, 155–162. [Google Scholar] [CrossRef]
- Belda Mullor, G. Citizens’ Attitude Towards Political Corruption and the Impact of Social Media. Ph.D. Thesis, Universitat Jaume I, Castellón de la Plana, Spain, 2018. [Google Scholar]
- Dritsaki, C.; Dritsaki, M. Phillips curve inflation and unemployment: An empirical research for Greece. Int. J. Comput. Econ. Econom. 2013, 3, 27–42. [Google Scholar] [CrossRef]
- Flaschel, P.; Landesmann, M. Mathematical Economics and the Dynamics of Capitalism: Goodwin’s Legacy Continued; Routledge: London, UK, 2016. [Google Scholar]
- Ho, S.Y.; Iyke, B.N. Unemployment and inflation: Evidence of a nonlinear Phillips curve in the Eurozone. J. Dev. Areas 2019, 53, 151–163. [Google Scholar] [CrossRef]
- Ormerod, P.; Rosewell, B.; Phelps, P. Inflation/unemployment regimes and the instability of the Phillips curve. Appl. Econ. 2013, 45, 1519–1531. [Google Scholar] [CrossRef]
- Ravenna, F.; Walsh, C.E. Vacancies, unemployment, and the Phillips curve. Eur. Econ. Rev. 2008, 52, 1494–1521. [Google Scholar] [CrossRef]
- Calmfors, L.; Holmlund, B. Unemployment and economic growth: A partial survey. Swed. Econ. Policy Rev. 2000, 7, 107–154. [Google Scholar]
- Jibir, A.; Bappayaya, B.; Babayo, H. Re-examination of the impact of unemployment on economic growth of Nigeria: An econometric approach. J. Econ. Sustain. Dev. 2015, 6, 116–123. [Google Scholar]
- Sekwati, D.; Dagume, M.A. Effect of unemployment and inflation on economic growth in South Africa. Int. J. Econ. Financ. Issues 2023, 13, 35–45. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Stability and Hopf bifurcation analysis for the diffusive delay logistic population model with spatially heterogeneous environment. Appl. Math. Comput. 2021, 408, 126362. [Google Scholar] [CrossRef]
- Bianca, C.; Guerrini, L. On the Dalgaard-Strulik model with logistic population growth rate and delayed-carrying capacity. Acta Appl. Math. 2013, 128, 39–48. [Google Scholar] [CrossRef]
- Bianca, C.; Guerrini, L. Existence of limit cycles in the Solow Model with delayed-logistic population growth. Sci. World J. 2014, 2014, 207806. [Google Scholar] [CrossRef]
- ElFadily, S.; Khalid, N.; Kaddar, A. Stability Analysis of Bifurcated Limit Cycles in a Labor Force Evolution Model. In The International Congress of the Moroccan Society of Applied Mathematics; Springer: Cham, Switzerland, 2019; pp. 61–77. [Google Scholar]
- Xu, R.; Wang, Z.; Zhang, F. Global stability and Hopf bifurcations of an SEIR epidemiological model with logistic growth and time delay. Appl. Math. Comput. 2015, 269, 332–342. [Google Scholar] [CrossRef]
- Mamo, D.K.; Ayele, E.A.; Teklu, S.W. Modelling and Analysis of the Impact of Corruption on Economic Growth and Unemployment. In Operations Research Forum; Springer: Cham, Switzerland, 2024; Volume 5, p. 36. [Google Scholar]
- Hale, J.K.; Verduyn Lunel, S.M. Introduction to Functional Differential Equations; Springer: New York, NY, USA, 1993; Volume 99. [Google Scholar] [CrossRef]
- Kuang, Y. Delay Differential Equations; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Gopalsamy, K. Stability and Oscillations in Delay Differential Equations of Population Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 74. [Google Scholar]
- Breda, D.; Maset, S.; Vermiglio, R. Stability of Linear Delay Differential Equations: A Numerical Approach with MATLAB; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Shampine, L.F.; Thompson, S. Solving ddes in matlab. Appl. Numer. Math. 2001, 37, 441–458. [Google Scholar] [CrossRef]
- Shampine, L.F.; Thompson, S. Numerical Solution of Delay Differential Equations. In Delay Differential Equations; Springer: Boston, MA, USA, 2009; pp. 1–27. [Google Scholar]
- Jones, L.E.; Manuelli, R.E. A model of Optimal Equilibrium Growth; Graduate School of Business, Stanford University: Stanford, CA, USA, 1988. [Google Scholar]
- Mauro, P. Corruption and growth. Q. J. Econ. 1995, 110, 681–712. [Google Scholar] [CrossRef]
- Acemoglu, D.; Robinson, J. The Role of Institutions in Growth and Development; World Bank: Washington, DC, USA, 2008; Volume 10. [Google Scholar]
- Uddin, I.; Rahman, K.U. Impact of corruption, unemployment and inflation on economic growth evidence from developing countries. Qual. Quant. 2023, 57, 2759–2779. [Google Scholar] [CrossRef]
- Triatmanto, B.; Bawono, S. The interplay of corruption, human capital, and unemployment in Indonesia: Implications for economic development. J. Econ. Criminol. 2023, 2, 100031. [Google Scholar] [CrossRef]
- Moza, G.; Rocşoreanu, C.; Sterpu, M.; Oliveira, R. Stability and bifurcation analysis of a four-dimensional economic model. Carpathian J. Math. 2024, 40, 139–153. [Google Scholar] [CrossRef]
- Fernández-Díaz, A. Overview and perspectives of chaos theory and its applications in economics. Mathematics 2023, 12, 92. [Google Scholar] [CrossRef]







| Equilibrium Point | Stability | Hopf Bifurcation |
|---|---|---|
| Always unstable | No | |
| Always unstable | No | |
| Locally stable under certain conditions | Yes | |
| Locally stable under certain conditions | Yes | |
| Locally stable under certain conditions | Yes | |
| Locally stable under certain conditions | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ifeacho, O.; González-Parra, G. Mathematical Model for Economic Growth, Corruption and Unemployment: Analysis of the Effects of a Time Delay in the Economic Growth. AppliedMath 2025, 5, 57. https://doi.org/10.3390/appliedmath5020057
Ifeacho O, González-Parra G. Mathematical Model for Economic Growth, Corruption and Unemployment: Analysis of the Effects of a Time Delay in the Economic Growth. AppliedMath. 2025; 5(2):57. https://doi.org/10.3390/appliedmath5020057
Chicago/Turabian StyleIfeacho, Ogochukwu, and Gilberto González-Parra. 2025. "Mathematical Model for Economic Growth, Corruption and Unemployment: Analysis of the Effects of a Time Delay in the Economic Growth" AppliedMath 5, no. 2: 57. https://doi.org/10.3390/appliedmath5020057
APA StyleIfeacho, O., & González-Parra, G. (2025). Mathematical Model for Economic Growth, Corruption and Unemployment: Analysis of the Effects of a Time Delay in the Economic Growth. AppliedMath, 5(2), 57. https://doi.org/10.3390/appliedmath5020057







