Modelling Systems with a Finite-Capacity Queue: A Theoretical Investigation into the Design and Operation of Real Systems
Abstract
1. Introduction
2. Assessment of Physical Performance
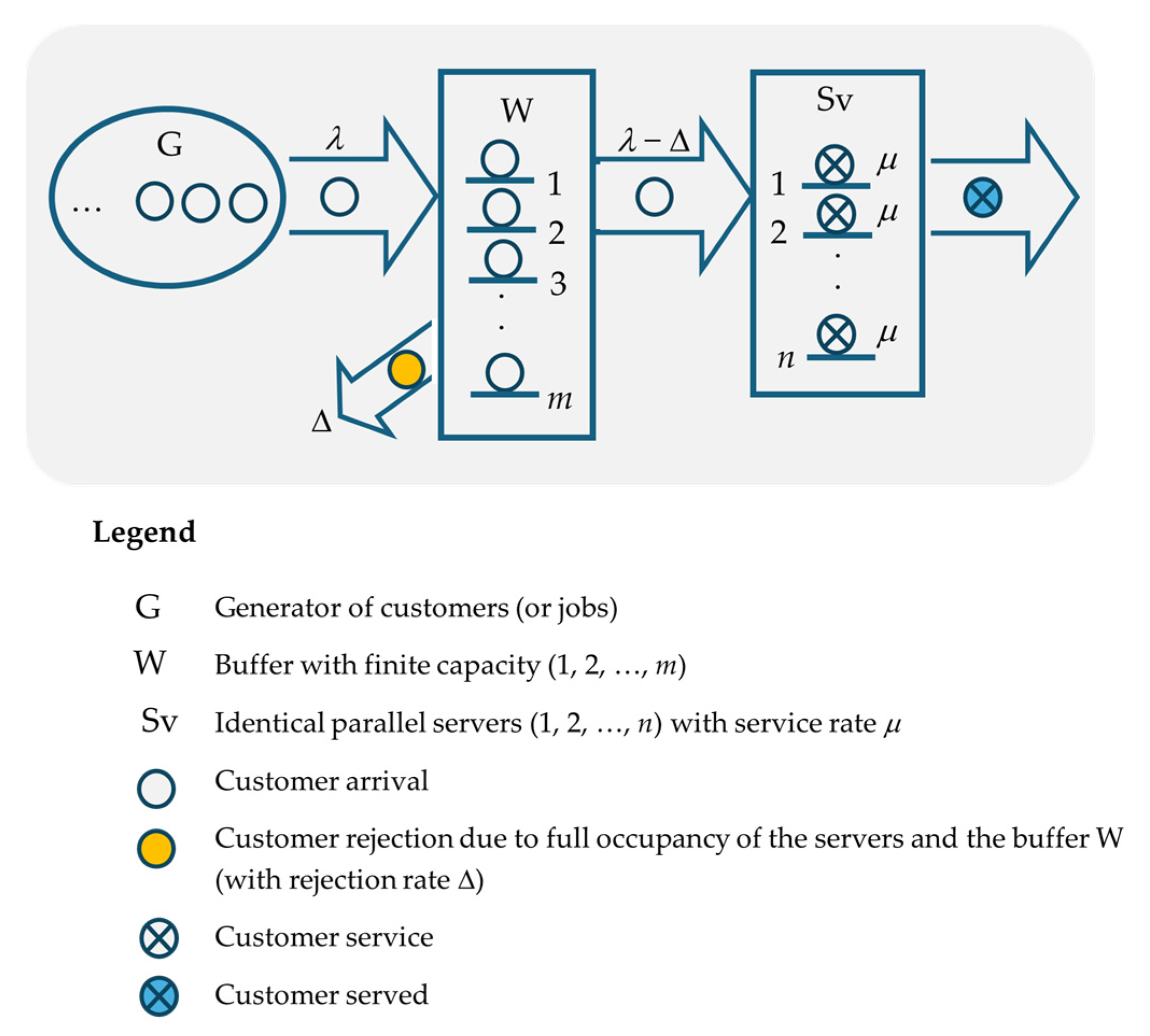
2.1. System Characteristics
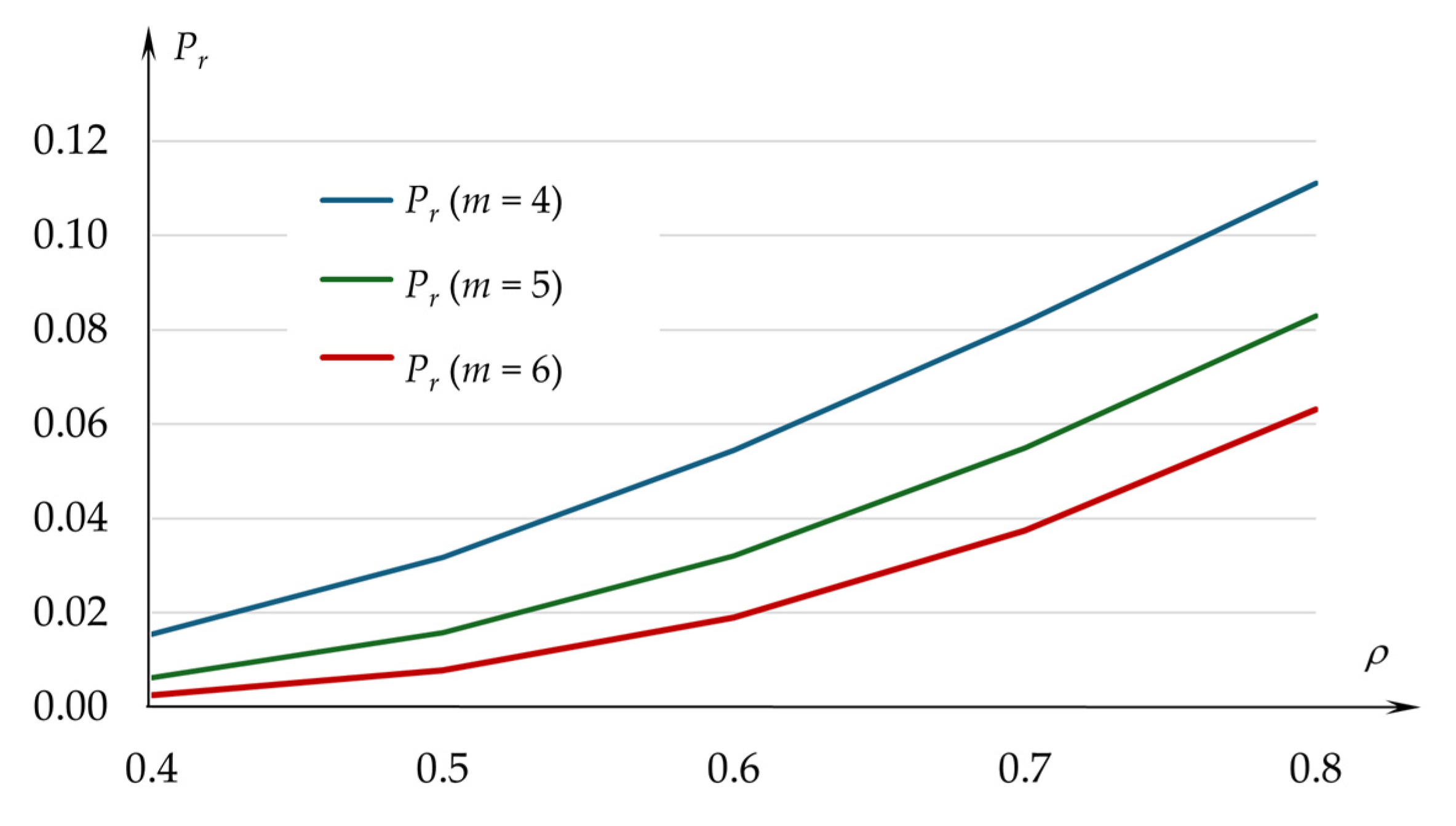
2.2. Probability of Customer Rejection
2.3. System Capacity with Waiting and Rejection
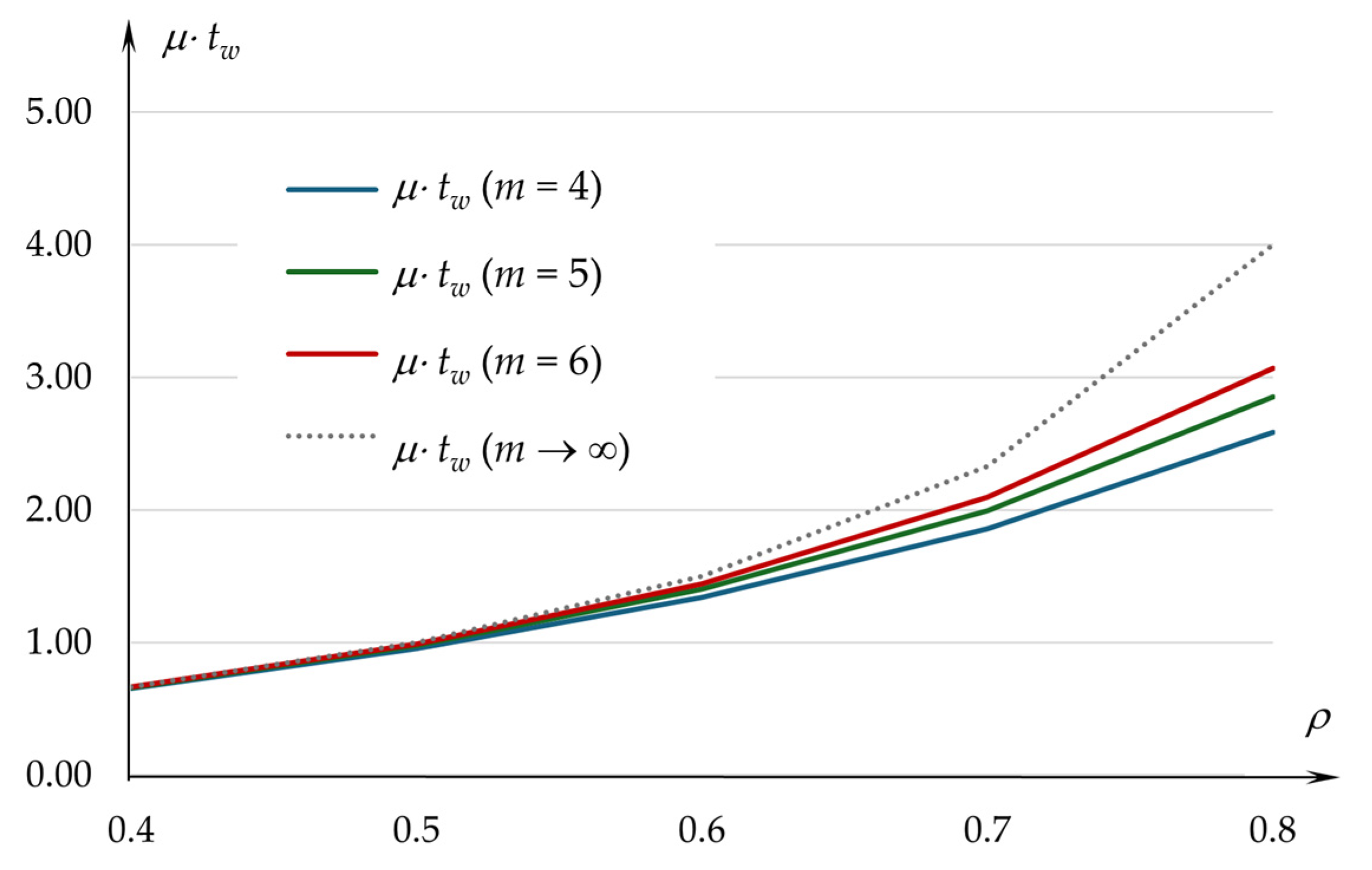
2.4. Average Waiting Time
- The probability of losing customers while the system is busy.
- The average waiting time compared to a specified threshold accepted for waiting time or total transit time.
3. Optimisation of the System Structure
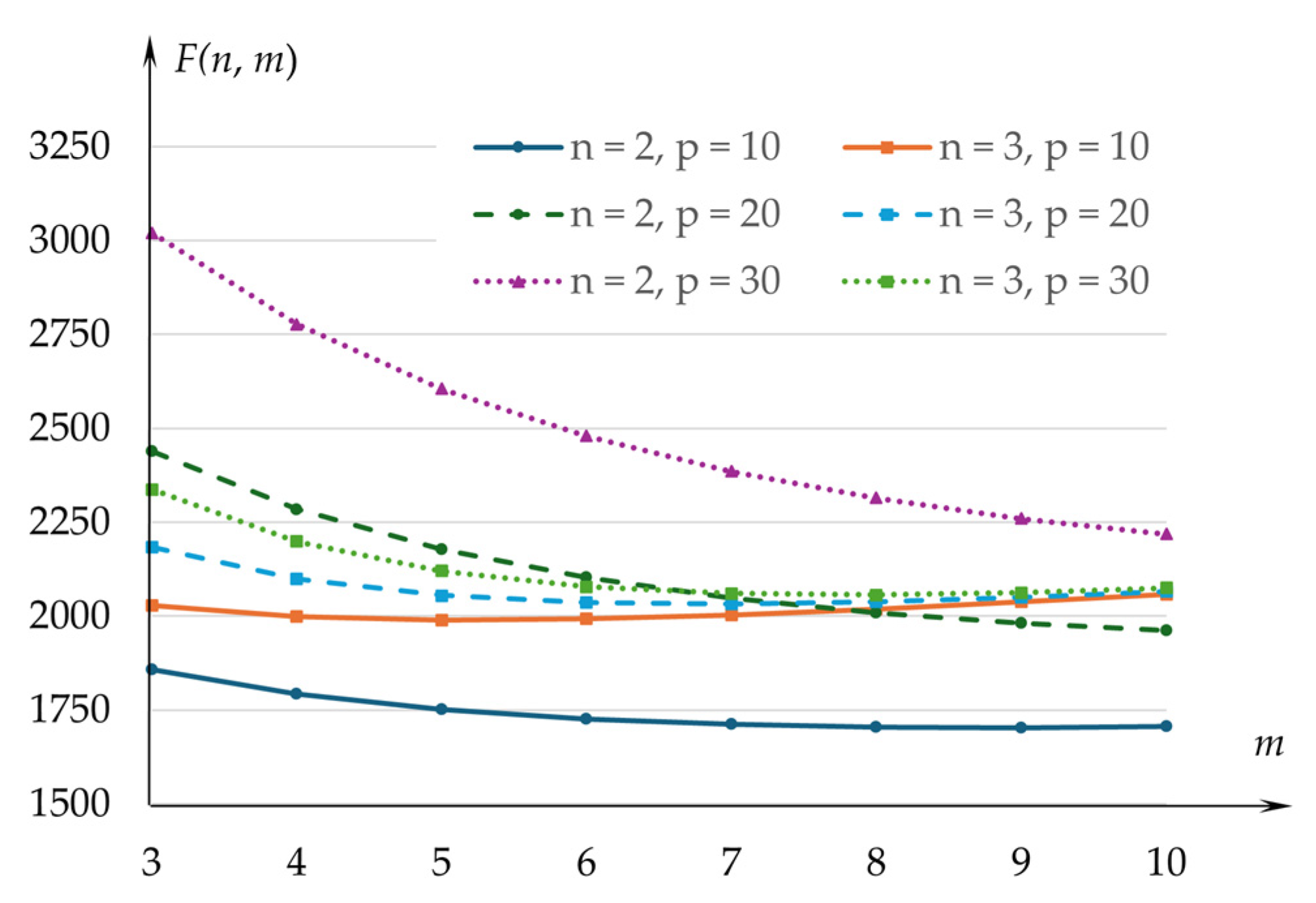
3.1. Cost Function Related to System Operation
- Pr—the probability of rejection given by Equation (4).
- v—the profit obtained for customer service.
- h—the cost associated with a place for waiting.
- c—the cost associated with a server
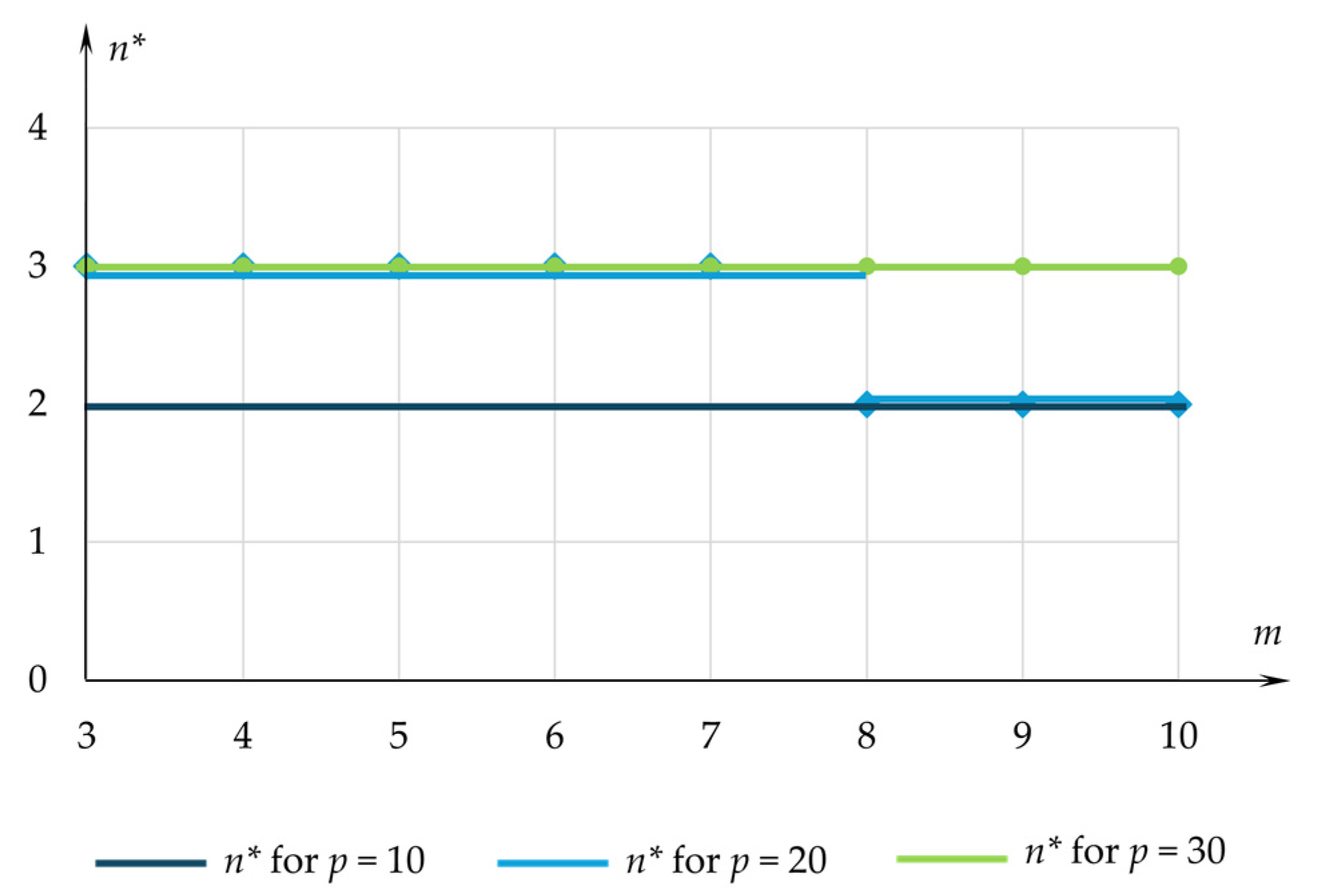
3.2. Number of Servers
- The arrival rate is 320 vehicles/day (λ = 320 vehicles/day).
- The service rate of a refuelling server is 160 vehicles/day (μ = 160 vehicles/day).
- There are six places for waiting for fuelling (m = 6).
- The fixed costs associated with a server comprise 600 monetary units/day (c = 600 m.u./day).
- The profit resulting from a vehicle fuelling comprises 10 monetary units/vehicle (v = 10 m.u./vehicle).
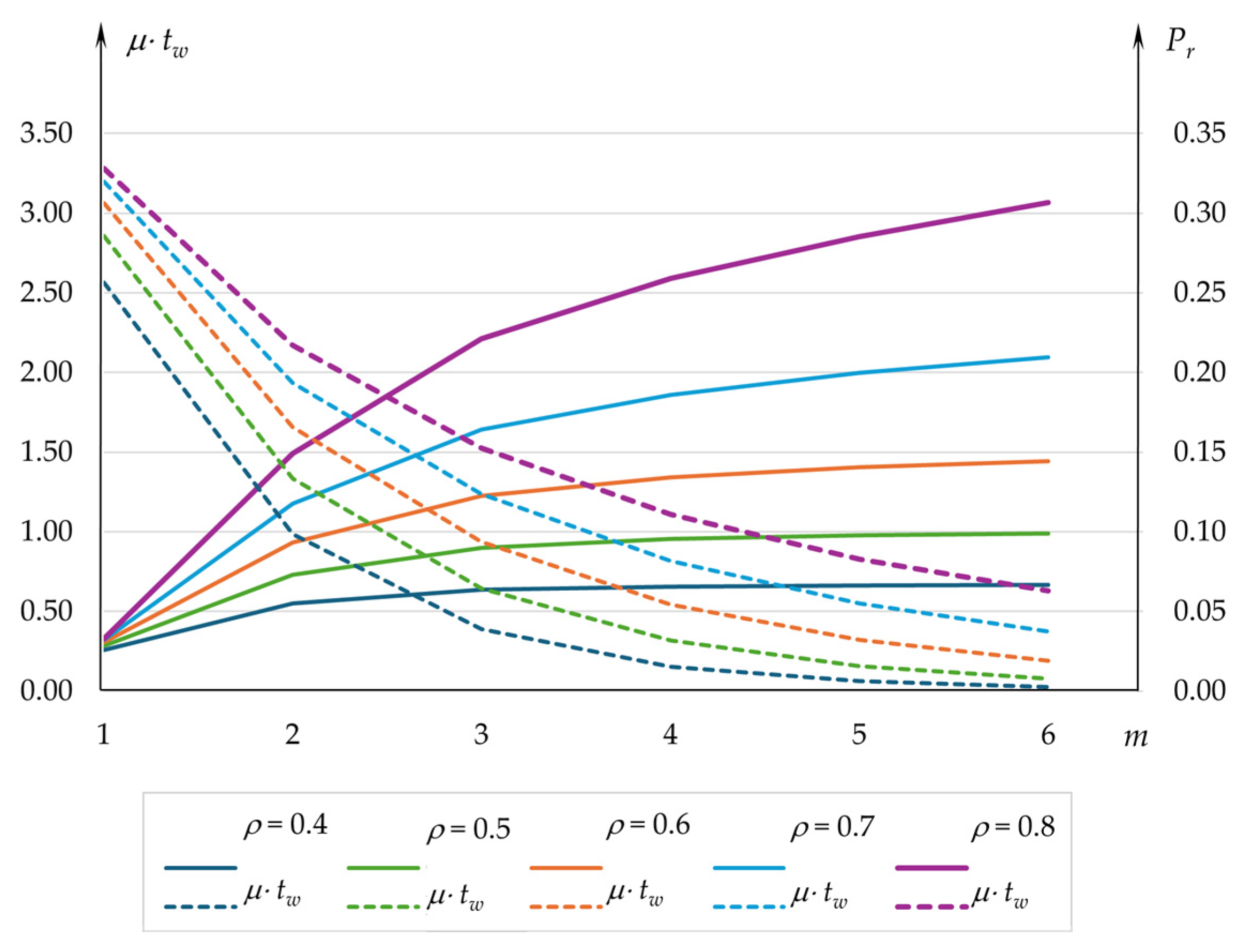
3.3. Number of Servers and Number of Waiting Places
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Asanjarani, A.; Nazarathy, Y.; Taylor, P. A survey of parameter and state estimation in queues. Queueing Syst. 2021, 97, 39–80. [Google Scholar] [CrossRef]
- Gross, D.; Shortie, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Hall, R.W. Queueing Methods for Services and Manufacturing; Prentice Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Barndorff-Nielsen, O.E.; Cox, D.R.; Kluppelberg, C. (Eds.) Complex Stochastic Systems, 1st ed.; CRC Press. Taylor & Francis Group: Boca Raton, FL, USA, 2000. [Google Scholar] [CrossRef]
- Kempa, W.M.; Kobielnik, M. Transient solution for the queue-size distribution in a finite-buffer model with general independent input stream and single working vacation policy. Appl. Math. Mod. 2018, 59, 614–628. [Google Scholar] [CrossRef]
- Sanga, S.S. Nidhi. Cost optimisation and ANFIS computing for M/M/(R+c)/N queue under admission control policy and server breakdown. Simul. Model. Pr. Theory 2025, 138, 103037. [Google Scholar] [CrossRef]
- Jain, M.; Sanga, S.S. State dependent queueing models under admission control F-policy: A survey. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 3873–3891. [Google Scholar] [CrossRef]
- Yang, D.Y.; Chiang, Y.C.; Tsou, C.S. Cost analysis of a finite capacity queue with server breakdowns and threshold-based recovery policy. J. Manuf. Syst. 2013, 32, 174–179. [Google Scholar] [CrossRef]
- Raicu, S.; Costescu, D.; Popa, M. Effects of the queue discipline on system performance. AppliedMath 2023, 3, 37–48. [Google Scholar] [CrossRef]
- Gupta, S.M. Interrelationship between controlling arrival and service in queueing systems. Comput. Oper. Res. 1995, 22, 1005–1014. [Google Scholar] [CrossRef]
- Tian, N.; Zhang, Z.G. Vacation Queueing Models. Theory and Applications; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Yang, D.Y.; Wang, K.H.; Wu, C.H. Optimization and sensitivity analysis of controlling arrivals in the queueing system with single working vacation. J. Comput. Appl. Math. 2010, 234, 545–556. [Google Scholar] [CrossRef]
- Huang, H.I.; Hsu, P.C.; Ke, J.C. Controlling arrival and service of a two-removable-server system using genetic algorithm. Expert Syst. Appl. 2011, 38, 10054–10059. [Google Scholar] [CrossRef]
- Yang, D.Y.; Yang, N.C. Performance and cost analysis of a finite capacity queue with two heterogeneous servers under F-policy. Int. J. Serv. Oper. Inform. 2018, 9, 101–115. [Google Scholar] [CrossRef]
- Jain, M.; Kumari, S.; Qureshi, R.; Shankaran, R. Markovian multi-server queue with reneging and provision of additional removable servers. In Performance Prediction and Analytics of Fuzzy, Reliability and Queuing Models. Asset Analytics; Deep, K., Jain, M., Salhi, S., Eds.; Springer: Singapore, 2019; pp. 203–217. [Google Scholar] [CrossRef]
- Abdul Rasheed, K.V.; Manoharan, M. Markovian queueing system with discouraged arrivals and self-regulatory servers. Adv. Oper. Res. 2016, 2016, 2456135. [Google Scholar] [CrossRef][Green Version]
- Jain, M.; Sanga, S.S. F-Policy for M/M/1/K retrial queueing model with state-dependent rates. In Performance Prediction and Analytics of Fuzzy, Reliability and Queuing Models. Asset Analytics; Deep, K., Jain, M., Salhi, S., Eds.; Springer: Singapore, 2019; pp. 127–138. [Google Scholar] [CrossRef]
- Kim, J.; Kim, B. A survey of retrial queueing systems. Ann. Oper. Res. 2016, 247, 3–36. [Google Scholar] [CrossRef]
- Artalejo, J.R.; Gómez-Corral, A. Retrial Queueing Systems. A Computational Approach; Springer: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- MacGregor Smith, J. System capacity and performance modelling of finite buffer queueing networks. Int. J. Prod. Res. 2014, 52, 3125–3163. [Google Scholar] [CrossRef]
- Pourvaziri, H.; Sarhadi, H.; Azad, N.; Afshari, H.; Taghavi, M. Planning of electric vehicle charging stations: An integrated deep learning and queueing theory approach. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103568. [Google Scholar] [CrossRef]
- Cox, D.R.; Smith, W. Queues, 1st ed.; Chapman & Hall/CRC: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Natvig, B. On the transient state probabilities for a queueing model where potential customers are discouraged by queue length. J. Appl. Probab. 1974, 11, 345–354. [Google Scholar] [CrossRef]



| n | Pr(n) | Pr(n) − Pr(n + 1) | Ratio (c/pλ) | Pr(n − 1) − Pr(n) |
|---|---|---|---|---|
| 1 | 0.5020 | - | - | - |
| 2 | 0.1177 | 0.1043 | 0.1875 | 0.3843 |
| 3 | 0.0134 | 0.0120 | 0.1875 | 0.1043 |
| 4 | 0.0014 | 0.0012 | 0.1875 | 0.0120 |
| 5 | 0.0001 | 0.0001 | 0.1875 | 0.0012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raicu, S.; Costescu, D.; Popa, M. Modelling Systems with a Finite-Capacity Queue: A Theoretical Investigation into the Design and Operation of Real Systems. AppliedMath 2025, 5, 17. https://doi.org/10.3390/appliedmath5010017
Raicu S, Costescu D, Popa M. Modelling Systems with a Finite-Capacity Queue: A Theoretical Investigation into the Design and Operation of Real Systems. AppliedMath. 2025; 5(1):17. https://doi.org/10.3390/appliedmath5010017
Chicago/Turabian StyleRaicu, Serban, Dorinela Costescu, and Mihaela Popa. 2025. "Modelling Systems with a Finite-Capacity Queue: A Theoretical Investigation into the Design and Operation of Real Systems" AppliedMath 5, no. 1: 17. https://doi.org/10.3390/appliedmath5010017
APA StyleRaicu, S., Costescu, D., & Popa, M. (2025). Modelling Systems with a Finite-Capacity Queue: A Theoretical Investigation into the Design and Operation of Real Systems. AppliedMath, 5(1), 17. https://doi.org/10.3390/appliedmath5010017









