Abstract
The basic reproduction, or reproductive number, is a useful index that indicates whether or not there will be an epidemic. However, it is also very important to determine whether an epidemic will eventually decrease and disappear or persist as an endemic. Different infectious diseases have different behaviors and mathematical models used to simulated them should capture the most important processes; however, the models also involve simplifications. Influenza epidemics are usually short-lived and can be modeled with ordinary differential equations without considering demographics. Delays such as the infection time can change the behavior of the solutions. The same is true if there is permanent or temporary immunity, or complete or partial immunity. Vaccination, isolation and the use of antivirals can also change the outcome. In this paper, we introduce several new models and use them to find the effects of all the above factors paying special attention to whether the model can represent an infectious process that eventually disappears. We determine the equilibrium solutions and establish the stability of the disease-free equilibrium using various methods. We also show that many models of influenza or other epidemics with a short duration do not have solutions with a disappearing epidemic. The main objective of the paper is to introduce different ways of modeling immunity in epidemic models. Several scenarios with different immunities are studied since a person may not be re-infected because he/she has total or partial immunity or because there were no close contacts. We show that some relatively small changes, such as in the vaccination rate, can significantly change the dynamics; for example, the existence and number of the disease-free equilibria. We also illustrate that while introducing delays makes the models more realistic, the dynamics have the same qualitative behavior.
1. Introduction
Influenza, or flu, is a contagious disease spread by contact with an infected individual. Seasonal influenza affects between 3% and 11% of the population in the United States every year [1]. The flu peaks from December to February of each year. Although some patients die from seasonal flu, it is not a particularly deadly disease with 0.2 deaths per 100,000 population [2]. Other contagious diseases that are short-lived are the common cold, Respiratory Syncytial Virus Disease and Streptococcus throat. There are many papers dealing with mathematical models for epidemics, both via direct contact and vector transmitted. Mathematical modeling of epidemics started in the early 20th century. One of the first efforts is [3] and the seminal paper of Kermack and McKendrick [4] is widely recognized as introducing the first compartmental epidemic model based on ordinary differential equations (ODEs). The use of ODEs is a good modeling assumption if the different populations are well-mixed and there is little or no spatial dependence. Kermack and McKendrick introduced the SIR (susceptible-infected-removed) model, which assumes that the population can be in one of three states: susceptible, infected or infective, and removed (recovered with permanent immunity or deceased). The SIR model and its many variations including the SIS (susceptible-infective-susceptible) and SIRS (susceptible-infective-recovered-susceptible) models have been very influential in understanding epidemics and their control. Among the modifications made to the original SIR model of Kermack and McKendrick, are the introduction of demographics (not important for seasonal flu), vaccinations, different age groups, use of anti-virals and isolation. One important modification is the addition of delays. Delays appear in epidemics due to the time it takes certain processes to occur, like the time it takes a susceptible to become infected after a contact with and infected individual, or the time it takes vaccines to become effective after being administered. The two main ways of introducing delays into a model based on ordinary differential equations are by using delay differential equations (DDEs) or by introducing and additional exposed or latent population. DDEs may have different dynamics than ODEs [5,6]. Among the possible differences are the introduction of oscillations, introduction of discontinuities in the time derivatives, non-uniqueness and different stability. While there is a wide range of literature about models of epidemics or disease transmission using delay differential equations, most books on DDEs have sparse coverage of contagious disease spread, and books on epidemics only have little material on DDEs. Two exceptions are the following books [7,8]. SIR models consider that after being infected, individuals recover and achieve permanent and total immunity from the disease. For seasonal influenza and other contagious diseases the immunity is temporal which leads to SIRS models in which the recovered individuals lose immunity completely after a certain time period. However, there are other possibilities: the individuals whom recovered lose total immunity but keep partial immunity forever; the individuals whom recovered lose total immunity and achieve partial immunity for a time period; some individuals whom recovered keep total and permanent immunity while others only keep partial permanent immunity, and so on. What happens depends on the particular infection and population. Vaccines may also confer total permanent immunity, or total immunity that wanes to partial immunity, or other scenarios.
One of the most important uses of mathematical models of contagious diseases is to predict whether there will be an epidemic or not. The basic reproduction number defined as the number of secondary infections produced by a newly infected individual at the start of the infective process is a useful index to determine whether the epidemic will die or not. It is usually calculated using the next generation matrix method [9,10]. It also gives the stability of the disease-free equilibrium (DFE) of the model. In case that the number of infectives grows initially, it is also very important to determine if the epidemic will eventually die or not. In this paper, we will develop mathematical models of short-lived contagious diseases liked seasonal influenza that include different assumptions about total, partial, permanent and temporal immunity. We will also add vaccinations with different immunity effects, and also add the use of anti-virals and isolation. The models will include delayed versions, using DDEs and also exposed populations. For these models we will study whether the epidemic persists or not. Ref. [11] compares some basic models for influenza that we will use as a starting point. The rest of the paper is organized as follows. In Section 2, we present several new models, that are extensions to the SIRS model, with different hypotheses about total and partial immunity and vaccination, determine their equilibria, and analyze the stability of their disease-free equilibria. In Section 3, numerical simulations and results are presented, including the effects of introducing delays. We also show that some relatively small changes in the models can significantly change the dynamics. Finally, in Section 4, the discussions and conclusions about the models and results are presented.
2. Materials and Methods
In this section, we introduce several new mathematical models of short-term epidemics with different types of immunities. We also add vaccination, the use of anti-virals and isolation or quarantine. To determine if an epidemic develops according to the model used, the equilibrium points need to be found. If there is an equilibrium point with no infectives and susceptibles equal to the total population, and if the number of infectives grows with time, then there will be an epidemic. An equilibrium with zero infectives is known as a disease-free equilibrium (DFE). There are different methods to determine if the number of infectives grows: the differential equation for the infectives has a positive right-hand side; the DFE is locally unstable; using the basic reproduction number gives ; the infective compartments subsystem of equations is locally unstable; the index calculated using the next generation matrix method is greater than 1 [10,12]. In case there is an epidemic, it is very important to establish if it will eventually die. This can be calculated by determining if there is a DFE for positive time that is locally asymptotically stable. This may happen for a finite time or only as time tends to infinity. This determination will be conducted in the following subsections for different models with no demographics. The first subsection is a review of the susceptible-infective-susceptible model (SIS), the susceptible-infective-recovered model (SIR) and the susceptible-infective-recovered-susceptible model (SIRS) with different immunities.
2.1. SIS, SIR and SIRS Models
A very simple epidemic model, for a total constant population N, consisting of only two population compartments, susceptibles S and infectives I is the SIS model. It assumes that a susceptible gets infected with probability by a contact with an infective, and then recovers with no immunity and returns to the susceptible compartment. The common cold is an example of a contagious disease that can be modeled by a SIS system of equations. The total population is usually considered constant which assumes that the disease is fast compared to the demographic effects. An almost equivalent assumption, since the death rate is very small compared to the time frame of the disease, is the number of births is equal to the number of deaths with no migration. The SIS model with no demographics is [13,14]
where is the recovery rate and is the total population. Since the population is constant, and we can eliminate one equation
The SIS model has two equilibrium states, and . The last one is physical only for . The basic reproduction number (also called basic reproductive number) is the number of secondary infectives generated by a single infective at the beginning of the infection process. For the SIS model it can be calculated as the product of the probability of a new infective, , times the number of susceptibles at the beginning of the infective process, N, times the average lifetime of an infection, . Therefore If the number of infectives increases away from the DFE, and the other equilibrium makes biological sense since all the states are non-negative. If the infection disappears and the DFE equilibrium is the only one that makes biological sense. implies that the DFE is locally asymptotically unstable so at least one the eigenvalues of the linearized system about the DFE has positive real part. To determine if the infection is growing it is only necessary to look at the infected compartment, . The next generation matrix method [9,10] is widely used to calculate the basic reproduction number in more complex models in epidemiology. Applying this method to the SIS model there is only one infective compartment, I, so the Jacobian J of this system is a 1 × 1 matrix. Decomposing this matrix as , with T the transmission and the transition matrices, produces and . The next generation matrix is . At the beginning of the infection , so the spectral radius of K, which is , can be approximated by . The local stability of the DFE can also be established by finding an index that states when the eigenvalue of the linearized system consisting of the disease compartment evaluated at the DFE has negative real part. A straightforward way of finding whether the number of infectives grows at the start of the epidemic is to the evaluate the differential equation for I at the initial state with :
which is positive for . Note that since at the start of the epidemic , . However, for large N, S can be taken equal to N. Another way of finding the stability of the DFE at the start of the infection can is by calculating the eigenvalues of the Jacobian matrix corresponding to the full system of equations, but the formulas are usually complicated or cannot be determined analytically. Using the characteristic polynomial and the Routh-Hurwitz criterion is another possibility [13,15].
Two delays may be added to the SIS model, the time in takes the disease to develop in a susceptible individual after being infected by a contact with an infective individual, and the time it takes for a newly infected individual to recover. This second delay is usually included implicitly since is the average recovery time. There are two ways to introduce the first delay. The first way is given by SIS Delay Model I:
The assumption is that a contact at produces a new infective at time t. The second way is given by SIS Delay Model II:
The assumption now is that an individual susceptible after contact with an infective turns into an infective but takes it a time to actually become infected with the disease and be able to infect. Both models make biological sense. Another approach to studying epidemic models is to consider them as chemical reactions, as shown, for example, in [16]. As an illustration, the reaction between an infective and a susceptible produces two infectives. For the reaction to happen both species should be at the same time, which is a caveat for Delay Model II. However, since both ways of introducing the infection delay are used in many papers, we include both to see if they produce the same dynamics qualitatively. The dynamics may be different since their characteristic equations are different. For other epidemic models that introduce the delay in the infection as was performed in Delay Model 1 see, for example, [17,18,19]. And for other applications using the delay as in Delay Model 2 see [20,21].
For the SIS model, the equilibrium solutions of both delay models are the same as those of the ODE model. To determine the stability of the DFE for model (3), let and . Then the linearized differential equation for i is . By taking we obtain the characteristic equation
This equation is transcendental and there is no exact solution, but only for . So we have the same as the for ODE model. A similar calculation for model (4) yields the same result. This method has been applied to other models by [20,22].
Another way of introducing the time it takes the infection to develop is to add another compartment for the exposed or latent population (E). After a contact with an infective, the susceptible individual goes into the exposed compartment and spends an average time equal to the infection time there. Exposed individuals cannot infect. The SIS model with an exposed population is
The DFE equilibrium of (5) is the same as that of (1). Its stability can be calculated using the next generation matrix method and gives So the stability is the same as that of (1). Exposed populations have been used in many epidemic models such as those in [23,24].
The SIR model of Kermack and McKendrick [4] considers that and infected recovers with total and permanent immunity. It adds the recovered (R) compartment to the SIS model:
Since the total population is constant, one equation can be eliminated using . The new system of equations is
The only steady solution of (6) is . At the start of the infection . The second equation of (6) states that at the initial time, , for . So for the DFE is unstable, and has its maximum value when . Furthermore, the solution as t tends to infinity is and [13]. So if there is an epidemic it does not disappear.
The delay due to the time of infection can be introduced in the two ways as conducted for the SIS model. The equilibrium solution of both delay models is the DFE with the same stability as for the no delay model. The same stability result for the DFE of the no delay ODE model is true for the SIR model with the exposed population.
A model for propagation of many different diseases in a population is the SIRS model with no demographics [13]. It consists of three populations: susceptibles (), infectives or infected () and recovered (). A susceptible turns into an infective with a given probability after a contact with an infective. An infective recovers with a rate . A recovered loses immunity at a rate and converts into a susceptible. The total population is assumed constant, , and the disease is assumed to be short enough so births and deaths need not be considered. The infection coefficient will be denoted by . All parameters are positive. The system of ordinary differential equations (ODEs) describing the model is [13,14]
Since the total population is constant, one equation can be eliminated using . The new system of equations is
The SIRS model has two equilibrium solutions: the DFE, , and the endemic equilibrium, . The basic reproduction number is .
There are several different methods of introducing delays in the infection into the model: The first one which we will call SIRS Model I [17,18,19] is given by
where the hypothesis is that an infective has contact with a susceptible and it takes a time for this susceptible to turn infective. It is not counted as a susceptible until that time. A second model is the SIRS Model II [25] described by:
where the assumption is that after a contact between a susceptible and an infective, a time passes before the susceptible turns into an infective and is then able to infect another susceptible.
Instead of considering a recovered population, where individuals spend an average time before losing immunity, infective individuals after stopping being infective have to wait a delay time before turning infectives. In [26], this is performed in addition to keeping the recovered compartment.
The two models with delays introduced above have the same equilibrium solutions but the actual time dependent solutions will be different. There is also the question of the influence of the initial conditions given in the history interval. For an epidemic they can always be given as the equilibrium solutions with no disease. That is, the natural assumption that the epidemic starts at can be used.
A model that takes into account the dependence in the past, caused by the delay in the transmission, by including an exposed population, E, is [27,28]
The additional parameter is . Models of this form are usually called SEIRS models. It has the same DFE and as the non-delay model.
2.2. Models with Different Immunities
The three models given in Section 2.1 have different types of immunity. The SIS model has no immunity, the SIR model has total and permanent immunity, and the SIRS model has total but temporal immunity. However, for different infections there may be different types of immunity such as partial and permanent or partial and temporal. Some papers considering immunity for influenza are [29,30,31]. Ref. [32] includes a reinfected class with different immunity. Ref. [33] models partial immunity of the recovered population and [34] includes that recovered lose immunity but not all infectives recover. Ref. [35] adds the effect of reinfection of influenza. Ref. [36] also takes into account waning immunity. Ref. [37] models the loss of immunity with time-dependent rates. We will consider several new models with different immunity based on the SIRS model. The first model assumes all infective individuals get partial but permanent immunity. Similar models are given by [34,38]. Susceptibles get infected and then move into susceptibles with partial immunity who can be reinfected with infection rate . The equations of the model are
Since the total population is constant, one equation can be eliminated using . The system has two equilibrium solutions: the DFE , and . At the start of the infection, so the equation for I is the same as that in system (6), and has the same value . The two delay models are constructed as before. The first model is
and the second is
They have the same equilibrium points as the no-delayed model. The model with the exposed population is constructed similarly and is given by
All these three models also have the same as (12).
The second partial immunity model assumes that all infectives get partial immunity but that it is only temporal. Susceptibles get infected, then go to susceptibles with partial immunity and then back to susceptibles with no immunity. The model is given by the following system of ODEs
Again since the total population is constant, one equation can be eliminated. The system has two equilibrium solutions: the DFE , and a second equilibrium with and . At the start of the infection, so the equation for I is the same as that in system (6) and . The two delay models are similarly constructed as before. They have the same equilibrium points as the non-delayed model. The model with the exposed population has this population added in the same form. All these three models also have the same as (12).
The third model assumes that all infectives get total immunity but that it is only temporal, and then get permanent partial immunity. Susceptibles get infected, then recover with total temporal immunity, then get partial permanent immunity as susceptibles with partial immunity. The model is given by
Again since the total population is constant, one equation can be eliminated. The system has two equilibrium solutions: the DFE , and a second equilibrium and . This second equilibrium solution only makes sense for . At the start of the infection, so the equation for I is the same as that in system (6) and . However, if , the epidemic will eventually disappear.
The fourth model assumes that all infectives get total immunity but that it is only temporal, and then get partial immunity which is also temporal. Susceptibles get infected, then recover with total temporal immunity, then get partial temporal immunity as susceptibles with partial immunity, that then convert to susceptibles. The model is given by
Again since the total population is constant, one equation can be eliminated. The system has two equilibrium solutions: the DFE and a second endemic equilibrium and . At the start of the infection, so the differential equation for I is the same as that in system (6) and .
2.3. Models with Loss of Immunity and Two Groups
Different individuals lose immunity at different rates. In this subsection for simplicity we will include two groups of individuals, but the models can be extended to more groups. Ref. [34] has a model with some recovered losing immunity. The first proposed model assumes that all infected get permanent immunity but the two groups lose it at different rates, and . One group has a stronger immune system due to among other things to previous exposure to a previous variation of influenza or vaccinations on previous seasons [29,30,31].
Here, is the fraction of the population in the first group. The two models with delay in the infection are given by
and
For both delay models, the differential equation at the beginning of the infection process for the infective compartment is the same as that of the SIS model (1), therefore the same procedure can be used to determine that . Also, for both models the equilibrium points are the same as those of the ODE model (19).
The model with an exposed population is
It has the same DFE as (19). The stability of the DFE at the beginning of the infection is still given by .
In the next model, a fraction f of the infectives gets total and permanent immunity, and the rest gets partial and permanent immunity. The ODEs of the model are
The next model assumes that a fraction f gets total and temporal immunity and the rest get partial and temporal immunity. The system of equations is
In the next model all infectives get total immunity for a finite time, then lose it different rates and , and get partial and permanent immunity with different rates of infection and .
2.4. Models with Vaccination and Immunity Loss
Vaccination is a very effective tool for achieving immunity to seasonal influenza. Usually the effect of the vaccine wanes with time. We consider that the immunity is permanent if it lasts until the next flu season with a new variant of the virus. The vaccinated population will be denoted by V. There are different ways of introducing the vaccination rate. The first way is that it is proportional to the number of susceptibles S [39,40,41]. Refs. [42,43,44] also consider the waning of the vaccine. Ref. [45] has a basic vaccination model based on the SIR model. A second way is to assume that only a percentage of susceptibles is willing to be vaccinated [46] which is a more realistic assumption [47]. This leads to a vaccination rate of the form . It can also be considered proportional to the total population or just constant [48,49]. Ref. [50] considers vaccination, partial immunity and reinfection. Refs. [40,51] also include quarantine. Our first model with vaccination assumes infectives recover and get total and temporal immunity for an average length of time . Vaccinated individuals get total immunity but it wanes with time at a rate . The model is
In this model the rate of vaccination is proportional to the number of susceptibles. Since the equation for the infective population is the same as that for (6), the value of is still . If the vaccines does not wane, , the system has only one equilibrium point, . If there are two equilibrium points, and and I given by the solution to . The first delay model is obtained by replacing and in the infection terms by and ). The second one by only replacing the term. Both have the same equilibrium points and as (26). The system with an exposed population has the same DFE equilibrium points since implies . The calculated by the next generation matrix method is still .
The second model with vaccination considers that the infective population gets total immunity for a fixed time and then gets partial permanent immunity. The vaccinated population gets total but temporal immunity, and then it wanes to partial permanent immunity. There is a new compartment, , representing susceptibles with partial immunity.
This model has a DFE . There is also an endemic equilibrium with . Since at the beginning of the infection, , using the differential equation for I, . The two delay models are obtained modifying (27) in a similar way as was performed for previous models. The equilibrium states and are the same as those of (27). The corresponding equation with an exposed population also has the same .
If the vaccination rate is modified to instead of , to make the model agree with not everybody wanting to be vaccinated, the modified model is
This model does not have a steady solution with for arbitrary values of the parameters. This an important difference in the dynamics with those of the other models.
The next model considers that all vaccinated get total immunity for a time, then a fraction keeps the total immunity, while the rest gets partial permanent immunity. All infectives get total temporal immunity after they recover.
If the DFE is . For the DFE is . Since , we have for both case . The two delay models and the exposed population models are derived from (29) as was performed for the previous models. All three models have the same DFE and as (29).
As a final and more complete model we will add the use of antivirals to reduce the infection time and isolation to reduce the number of active infectives. There is a new compartment, the quarantined or isolated population Q. Infectives recover with total and temporal immunity, vaccinated get total and temporal immunity and then partial permanent immunity. A fraction of the infected gets an antiviral and exit the compartment at a faster rate . A fraction of the infected gets quarantined at a rate and leaves the quarantine state at a rate . The average time that a quarantined individual spends in the infected and quarantined compartments is the same as the time a non-quarantined individual spends in the infective compartment. Therefore, . The model is
The DFE is . Since , for the infective compartment to grow we need . The delay versions and the model with exposed population have the same DFE and .
3. Results
In this section, we present numerical results for the models given in the previous section. The numerical simulations, including the DDE were performed using the package DifferentialEqns.jl [52,53]. The parameter values used for most simulations are given in Table 1. If a different value is used for a particular simulation, it will be noted in the caption of the corresponding figure. The values of and are based on those given [54] and CDC [1] corresponding to seasonal influenza. All the others are estimated. The value of has a large variation depending on the conditions: rural, urban, suburban, high density work places, etc. The values of and chosen for most simulations give . Ref. [55] also gives similar parameter values for influenza.

Table 1.
This table has the parameter values used in the simulations.
The initial conditions for all models are and all other populations equal to zero. The history for the delay models is , and all other delayed variables equal to zero in the interval . This corresponds to an epidemic starting at . All simulations, except where specified, have .
3.1. SIS, SIR and SIRS Models
The SIS, SIR and SIRS models are widely used for epidemics with infection by direct contact. In the SIS model, infectives do not get immunity, in the SIR model they get total and permanent immunity and in the SIRS model they get total but temporal immunity.
Figure 1 presents the plots for the SIS model, in the left for the susceptible population and in the right for the infective population. Since the solution tends to the endemic state. The infective plot for the model with the exposed population has a different limit since there are two infective classes, I and E, and only I is plotted. The solutions have the same form but the one for the ODE model reaches the equilibrium state the fastest. The solutions of the two delay system are all identical since the only difference is when a new infected stops being counted as a susceptible. The model with the exposed population has an average time in the exposed compartment equal to the delay but not the same delay for every individual. Real data is needed to determine which model is the best, since all the models, with no delay, with delay, and with an exposed population, have the same qualitative dynamics.
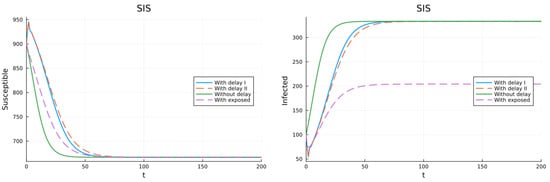
Figure 1.
SIS model. (left) Susceptible population. (right) Infective population.
Figure 2 presents the plots for the SIR model, in the left for the susceptible population and for the infective in the right. Note that for , there are multiple solutions . The simulated solutions depend on the initial values. The delay model I uses the history for both S and I, while all the other models only use .
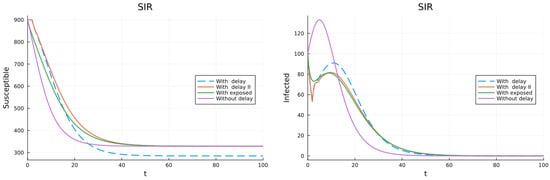
Figure 2.
SIR model. (left) Susceptible population. (right) Infective population.
Figure 3 presents the plots for the susceptible (left) and infective (right) populations for the SIR model. This model has total but temporal immunity. As expected, the simulated solutions tend to the endemic equilibrium. The ODE model gives the highest infection peak, but all the models have the same qualitative dynamics.
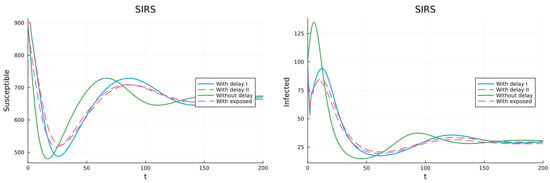
Figure 3.
SIR model. (left) Susceptible population. (right) Infective population.
3.2. Models with Different Immunities
In this subsection, we consider models with different immunities: total, partial, permanent and temporal in different combinations. The first model (12) considers that all infectives after recovering get partial and permanent immunity. Figure 4 has the simulated solutions for the infective population for two different values of the infection rate for the population with partial immunity, . On the left for and the solution tends to in spite of having , and on the right for and the solution tends to the endemic state. However, whether the epidemic ends or not depends on the values of which appears on the right-hand side of the differential equation for the infective population. The two delay models behave differently at the beginning since in the model with delay I, both S and I depend on the history, while for the model with delay II only I depends on the history.
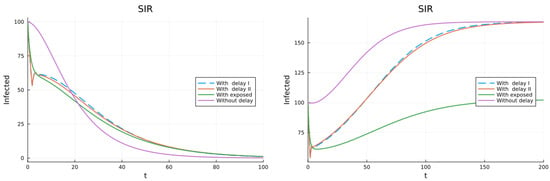
Figure 4.
Model with partial and permanent immunity (left) . (right) .
The next model (16) considers that all infectives recover with partial and temporal immunity. Figure 5 has the plots for the infective population, on the left for , and I tends to a small but non zero value, and on the right for , and I tends to a much larger value, showing the effect of .
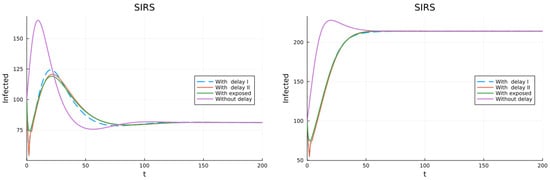
Figure 5.
Model with partial and temporal immunity (left) . (right) .
Model (17) is for an infection with total but temporary immunity and then partial and permanent immunity. Figure 6 has the simulated plots for the infective population for two values of . The figure on the left is for and I tends to the DFE; the figure on the right is for and I goes to an endemic equilibrium. For both simulations so initially the number of infectives grows. However, whether the epidemic ends or not depends on the values of . All models have the same equilibria.
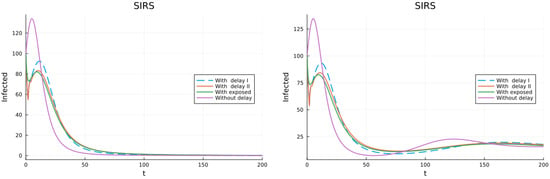
Figure 6.
Model with total temporal and then partial permanent immunity (left) . (right) .
The next model (18) supposes that after being infected an individual gets total immunity which is temporal, and then partial immunity that is also temporal, finally losing all immunity. Figure 7 shows the time solution of the infective population. On the left for and on the right for . In both cases the epidemic persists. The limit value for is slightly larger. Since all individuals eventually lose immunity completely, the epidemic does not end.
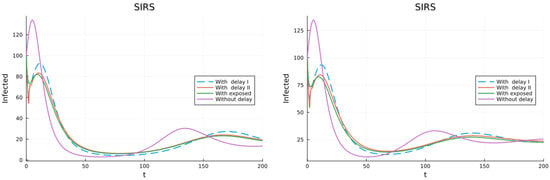
Figure 7.
Model with total temporal and then partial temporal immunity (left) . (right) .
3.3. Models with Loss of Immunity and Two Groups
Different individuals have different immune system reactions to an infection. For example, all individuals may get total immunity to the infection after recovering but may lose it at different rates. For seasonal influenza some of the reasons are that children have been exposed to fewer variants of the virus, that older individuals have weaker immune systems, or that some individuals may have other risk factors such as smoking. For simplicity we consider just two classes of individuals, but the models can be extended to an arbitrary number.
The first model with two distinct populations (19) considers that the two groups get total and temporal immunity after infection (the usual SIR assumption), but lose the immunity at different rates and , with fractions and , respectively. The simulations are in Figure 8. Both figures have , the left one with and the right one with . The limit value for the right figure is about twice that of the left showing the large influence that the infection rate has.
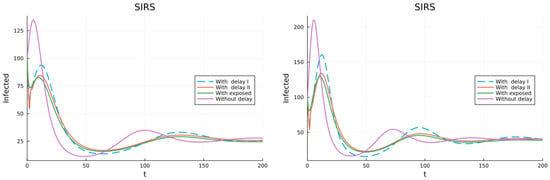
Figure 8.
Model with two populations with total temporal immunity leaving the R compartment at different rates. (left) . (right) .
The next model (23) assumes that one class gets total and permanent immunity, while the second gets partial and also permanent immunity. The fraction of individuals in both classes is taken to be . For the class with partial immunity . Since all individuals get permanent immunity it is expected that the epidemic will not persist. Figure 9 has two simulations for different values of . The left one for and the right one for . Even for the fairly large second value of , that corresponds to , the epidemic dies out.
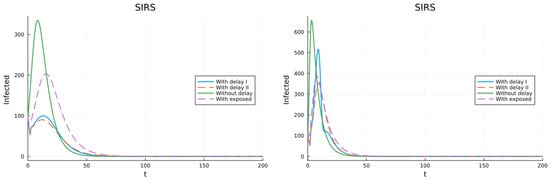
Figure 9.
Simulations for the model with two classes, one with total and permanent immunity, and the other with partial and permanent immunity. (left) . (right) .
Next we consider that half of the infective populations get total and temporal immunity, and half partial and also temporal immunity (24). Simulations were conducted for two values of , the infection rate of the population with partial immunity, (left plot of Figure 10) and , (right plot). In both cases the epidemic persists and the limit value of I has a relatively small change. The fact that all the individuals get immunity only for a finite time is the reason that the infection persists.
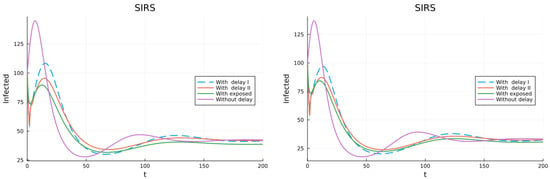
Figure 10.
Simulations for the model with two classes, one with total and immunity, and the other with partial immunity, both temporal. (left) . (right) .
Model (25) assumes that all infectives recover with total temporal immunity and then get partial and permanent immunity. A fraction has partial immunity with infection rate and loss of permanent immunity rate and the rest has infection rate and immunity loss rate (left plot of Figure 11). The solution tends to the endemic equilibrium. A second simulation was conducted changing the infection rates to and (right half of Figure 11). Now the solution tends to the DFE. In the second simulation and so when most recovered individuals have partial permanent immunity, the differential equation for I shows that I decreases.
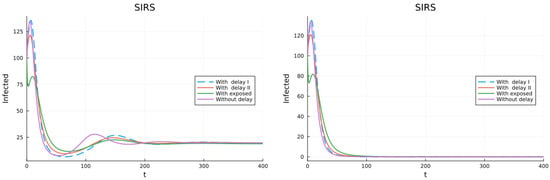
Figure 11.
Model with two population classes. Both get total immunity (compartment R) and then lose it to get partial immunity at different rates with different infection rates. (left) . (right) .
3.4. Models with Vaccination and Immunity Loss
Vaccines can help control seasonal influenza. Since the influenza virus mutates from season to season, it is hard to predict what is the efficiency of the vaccine. It is also difficult to determine if the vaccine gives total or partial immunity, or if the effect wanes. A vaccinated person may not get influenza due to the vaccine or just because the person was not in close contact with an infective. Similarly, a person becoming infected only once may be due to having acquired total and permanent immunity, or not having close contacts with infectives. In this subsection, we present simulations conducted for different scenarios all with vaccination.
The first scenario represents individuals that get vaccinated at a rate , and achieve total immunity. The immunity from becoming infected with the disease is total and disappears at a rate , (26). In the left part of Figure 12, the effect of the vaccine wanes at a rate . In the right part, the effect of the vaccines does not wane, . In both cases the solution tends to the DFE. In the first case there is also a second endemic equilibrium.
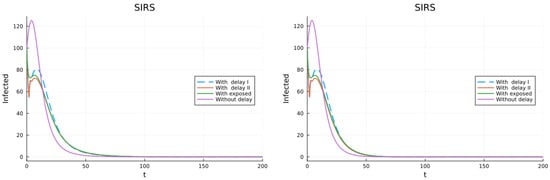
Figure 12.
Model with vaccination that gives total immunity. (left) Immunity does not wane. (right) Immunity wanes.
The model in the next scenario is similar to the model given by (26), except that when the vaccine wanes the individual still gets partial permanent immunity with . Figure 13 on the left shows the case with and the simulated solution almost gets to the DFE but then it rebounds. On the right, the plot corresponds to and the solution trends to the DFE. The figure shows the importance that the waning of the vaccine has.
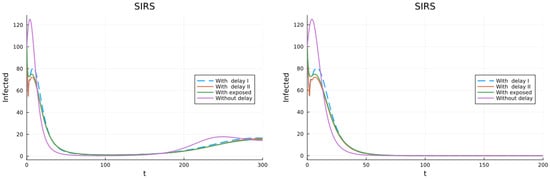
Figure 13.
Model with vaccination. Infected individuals get total immunity that wanes to partial and permanent immunity. Vaccinated individuals get total immunity that may wane or not. (left) Vaccination immunity wanes to partial permanent. (right) Vaccination immunity does not wane.
The next simulations were performed with model (28). The vaccination rate is . For this vaccination rate there is no DFE. The infected get to recovered that then get partial permanent immunity. Vaccinated get total immunity that, in one simulation wanes to partial permanent, and in the second one does not wane. We use , and the infection rate for the population with partial immunity . The left plot of Figure 14 is for the simulation with vaccination waning, and the one of the right for no waning. In both plots the infective solution approaches close to zero and then rebounds.
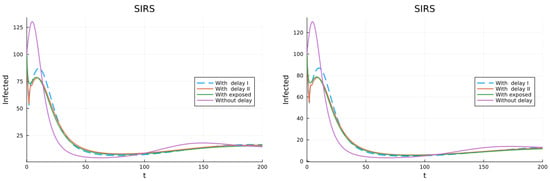
Figure 14.
Model with recovered getting partial permanent immunity and vaccinated getting total immunity that in one case wanes and in the other does not. (left) Vaccination immunity wanes. (right) Vaccination immunity does not wane.
The next simulations are performed with the model given by (29). The vaccination rate is with and a fraction of the vaccinated population gets total and permanent immunity while a fraction gets total immunity that wanes at a rate to partial and permanent immunity with infection rate . The immunity from an infection is total and temporal. The calculated solution tends to an endemic equilibrium. A second simulation was performed with no waning of the effect of the vaccine . The solution tends to the DFE. The plots are in Figure 15. This example shows the importance of the waning or not of the vaccine.
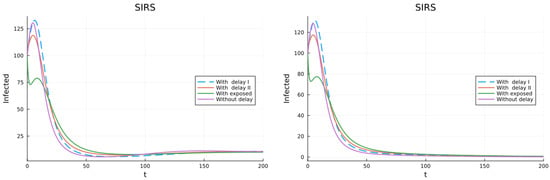
Figure 15.
Model with two classes of vaccinated individuals, one with total and permanent immunity and the other with total immunity that wanes to partial and permanent immunity. (left) Waning vaccination immunity. (right) Permanent vaccination immunity.
The final model considers vaccination, the use of antivirals and isolation. The vaccination rate is , a fraction of the vaccinated keeps the total immunity forever and the rest loses the total immunity and then gets permanent partial immunity with infection rate . The infected recover with total and temporal immunity. A fraction is given antivirals and is removed from the infective class at a rate . A fraction is removed from the infectives and isolated at a rate . Two simulations were performed. The first one with , that corresponds to , is shown in the plot in the left of Figure 16 and has a solution that tends to the DFE. The second one, with that gives , is shown in the right plot and the solution tends to an endemic equilibrium. The figure shows that while predicts whether an epidemic starts or not, it does not indicate whether it will eventually die out or not.
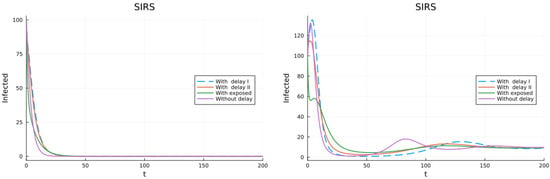
Figure 16.
Model with vaccination, antivirals and isolation (30). (left) . (right) .
4. Discussion
SIR-based models have been used for may infectious diseases transmitted by direct contact. In this paper, we used models with no demographics for short-lived infections such as seasonal influenza. The first reason is that the infection has a short duration and that it is not very deadly. Therefore, the number of births and deaths during the infection period is small. The second reason is that it allows us to concentrate on the effects of losing immunity. The basic reproduction number is a very important index that gives a criterion for determining whether there will be an epidemic or not. It is usually calculated as we did in this paper by assuming that at the start of the infection there is one infective and susceptibles with N the total population. For the majority of our examples it is and simplified to . If there is also an initial time of the infection number of vaccinated individuals , then . And, if for example without vaccination , by vaccinating more than 1/3 of the total population then and there is not an epidemic. A similar estimate can be performed if initially there is also a number of individuals with partial immunity and infection rate .
The models presented start with the simple SIS, SIR and SIRS, that have no immunity, total and permanent immunity, and total and temporal immunity. They were first extended to include other situations with combinations of total and partial immunity, both permanent and temporal. For diseases like seasonal influenza it is very difficult to determine if an infected and recovered individual received total or partial immunity after the infection. Or if that immunity disappears or not. The individual may not get infected again due to total immunity or partial immunity or just because the individual was not in close contact with any infective. The different models permit running scenarios with different hypotheses and comparing the results. Two population groups with different immune reactions were considered next and different scenarios were run. Finally, vaccination was introduced with the different models having different assumptions and the final model being more complete having also antivirals and isolation to reduce the infection. For the various models that had DFEs simulations were performed where the epidemic died and where it did not. The effect of introducing a delay in the time of infection was also studied. The delay was introduced in two different ways using DDEs and also adding an exposed compartment. Apart from the delayed solutions taking more time to reach the equilibrium states, the behavior is very similar to that of the corresponding ODE model. That is, they produce solutions with the same equilibrium states and the same basic reproduction number. However, adding the delay makes the model more realistic and it is expected that the delayed models will fit real data better.
The parameters related to the time between contact and infection and to the duration of the infection are well-known for seasonal influenza. The infection rates can be estimated from the number of infectives. They vary from city to city and from population group to population group. As mentioned above, the parameters related to partial immunity and vaccination effects are hard to estimate and not reported. Numerical simulations using different models and comparing with actual epidemic data can help determine the more realistic hypotheses.
Since the two delay versions of each model have different characteristic equations, their solution behaviors can be different from each other and different from the behavior of the solutions of the non-delayed model. However, for the parameter values used in the simulations that did not happen and the qualitative dynamics were all similar. Determining whether an individual has total or partial immunity or has not come into close contact is not an easy task. We proposed different models with different types of immunity. Comparisons with real data are needed to establish which one is more realistic.
Future work will consider different initial conditions, the introduction of randomness and spatial dependence. The use of other compartments such as asymptomatics is another route.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SIS | Susceptible, infective, susceptible |
| SIR | Susceptible, infective, recovered |
| SIRS | Susceptible, infective, recovered, susceptible |
| ODE | Ordinary differential equation |
| DDE | Delay differential equation |
| DFE | Disease-free equilibrium |
| Basic reproduction number |
References
- Centers for Disease Control. Influenza (Flu). 2024. Available online: https://www.cdc.gov/flu/about/keyfacts.htm#:~:text=Flu%20is%20a%20contagious%20respiratory,a%20flu%20vaccine%20each%20year (accessed on 24 April 2024).
- Centers for Disease Control. Influenza. 2024. Available online: https://www.cdc.gov/nchs/fastats/flu.htm (accessed on 24 April 2024).
- Ross, R.; Hudson, H.P. An application of the theory of probabilities to the study of a priori pathometry—Part III. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1917, 93, 225–240. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Ma, Z. Dynamical Modeling and Analysis of Epidemics; World Scientific: Singapore, 2009. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Singapore, 2021. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Edlund, S.; Kaufman, J.; Lessler, J.; Douglas, J.; Bromberg, M.; Kaufman, Z.; Bassal, R.; Chodick, G.; Marom, R.; Shalev, V.; et al. Comparing three basic models for seasonal influenza. Epidemics 2011, 3, 135–142. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Allen, L. An Introduction to Mathematical Biology; Pearson-Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Murray, J.D. Mathematical Biology I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Fages, F.; Soliman, S. On robustness computation and optimization in BIOCHAM-4. In Proceedings of the International Conference on Computational Methods in Systems Biolog, Brno, Czech Republic, 12–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 292–299. [Google Scholar]
- Cooke, K.L.; Yorke, J.A. Some equations modelling growth processes and gonorrhea epidemics. Math. Biosci. 1973, 16, 75–101. [Google Scholar] [CrossRef]
- Jackson, M.; Chen-Charpentier, B.M. Modeling plant virus propagation with delays. J. Comput. Appl. Math. 2017, 309, 611–621. [Google Scholar] [CrossRef]
- Khan, Q.J.A.; Krishnan, E.V. An Epidemic Model with a Time Delay in Transmission. Appl. Math. 2003, 48, 193–203. [Google Scholar] [CrossRef]
- Al Basir, F.; Takeuchi, Y.; Ray, S.A. Dynamics of a delayed plant disease model with Beddington-DeAngelis disease transmission. Math. Biosci. Eng. 2021, 18, 583–599. [Google Scholar] [CrossRef]
- Huang, G.; Ma, W.; Takeuchi, Y. Global analysis for delay virus dynamics model with Beddington–DeAngelis functional response. Appl. Math. Lett. 2011, 24, 1199–1203. [Google Scholar] [CrossRef]
- Wei, H.M.; Li, X.Z.; Martcheva, M. An epidemic model of a vector-borne disease with direct transmission and time delay. J. Math. Anal. Appl. 2008, 342, 895–908. [Google Scholar] [CrossRef]
- Chan, M.; Johansson, M.A. The incubation periods of dengue viruses. PLoS ONE 2012, 7, e50972. [Google Scholar] [CrossRef] [PubMed]
- Jeger, M.; Madden, L.; Van Den Bosch, F. Plant virus epidemiology: Applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 2018, 102, 837–854. [Google Scholar] [CrossRef]
- Liu, L. A delayed SIR model with general nonlinear incidence rate. Adv. Differ. Equ. 2015, 2015, 329. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Wang, N.; Fu, Y.; Zhang, H.; Shi, H. An evaluation of mathematical models for the outbreak of COVID-19. Precis. Clin. Med. 2020, 3, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Bjørnstad, O.N.; Shea, K.; Krzywinski, M.; Altman, N. The SEIRS model for infectious disease dynamics. Nat. Methods 2020, 17, 557–559. [Google Scholar] [CrossRef]
- Krammer, F. The human antibody response to influenza A virus infection and vaccination. Nat. Rev. Immunol. 2019, 19, 383–397. [Google Scholar] [CrossRef]
- Patel, M.M.; York, I.A.; Monto, A.S.; Thompson, M.G.; Fry, A.M. Immune-mediated attenuation of influenza illness after infection: Opportunities and challenges. Lancet Microbe 2021, 2, e715–e725. [Google Scholar] [CrossRef]
- Han, A.X.; de Jong, S.P.; Russell, C.A. Co-evolution of immunity and seasonal influenza viruses. Nat. Rev. Microbiol. 2023, 21, 805–817. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Maroto, G.; Atienza-Diez, I.; Ares, S.; Manrubia, S. Vaccination strategies in structured populations under partial immunity and reinfection. J. Phys. A Math. Theor. 2023, 56, 204003. [Google Scholar] [CrossRef]
- Katriel, G. Epidemics with partial immunity to reinfection. Math. Biosci. 2010, 228, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Mondal, B.; Ghosh, U. Dynamical behaviors of an epidemic model with partial immunity having nonlinear incidence and saturated treatment in deterministic and stochastic environments. Chaos Solitons Fractals 2023, 174, 113775. [Google Scholar] [CrossRef]
- Thieme, H.R.; Yang, J. An endemic model with variable re-infection rate and applications to influenza. Math. Biosci. 2002, 180, 207–235. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, R.M.; Childs, L.M.; Feng, Z.; Glasser, J.W.; Heffernan, J.M.; Li, J.; Röst, G. Modeling the waning and boosting of immunity from infection or vaccination. J. Theor. Biol. 2020, 497, 110265. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Adler, F.R. A time since recovery model with varying rates of loss of immunity. Bull. Math. Biol. 2012, 74, 2810–2819. [Google Scholar] [CrossRef]
- Viguerie, A.; Carletti, M.; Silvestri, G.; Veneziani, A. Mathematical Modeling of Periodic Outbreaks with Waning Immunity: A Possible Long-Term Description of COVID-19. Mathematics 2023, 11, 4918. [Google Scholar] [CrossRef]
- Alexander, M.E.; Bowman, C.; Moghadas, S.M.; Summers, R.; Gumel, A.B.; Sahai, B.M. A vaccination model for transmission dynamics of influenza. SIAM J. Appl. Dyn. Syst. 2004, 3, 503–524. [Google Scholar] [CrossRef]
- Sun, C.; Yang, W. Global results for an SIRS model with vaccination and isolation. Nonlinear Anal. Real World Appl. 2010, 11, 4223–4237. [Google Scholar] [CrossRef]
- Sahu, G.P.; Dhar, J. Analysis of an SVEIS epidemic model with partial temporary immunity and saturation incidence rate. Appl. Math. Model. 2012, 36, 908–923. [Google Scholar] [CrossRef]
- Moghadas, S.; Gumel, A. A mathematical study of a model for childhood diseases with non-permanent immunity. J. Comput. Appl. Math. 2003, 157, 347–363. [Google Scholar] [CrossRef]
- Saad-Roy, C.M.; Morris, S.E.; Metcalf, C.J.E.; Mina, M.J.; Baker, R.E.; Farrar, J.; Holmes, E.C.; Pybus, O.G.; Graham, A.L.; Levin, S.A.; et al. Epidemiological and evolutionary considerations of SARS-CoV-2 vaccine dosing regimes. Science 2021, 372, 363–370. [Google Scholar] [CrossRef]
- Goldberg, Y.; Mandel, M.; Bar-On, Y.M.; Bodenheimer, O.; Freedman, L.; Haas, E.J.; Milo, R.; Alroy-Preis, S.; Ash, N.; Huppert, A. Waning immunity after the BNT162b2 vaccine in Israel. N. Engl. J. Med. 2021, 385, e85. [Google Scholar] [CrossRef] [PubMed]
- Turkyilmazoglu, M. An extended epidemic model with vaccination: Weak-immune SIRVI. Phys. A Stat. Mech. Its Appl. 2022, 598, 127429. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.H.; He, D.; Eftimie, R. Mathematical models of transmission dynamics and vaccine strategies in Hong Kong during the 2017–2018 winter influenza season. J. Theor. Biol. 2019, 476, 74–94. [Google Scholar] [CrossRef] [PubMed]
- Reluga, T.C.; Medlock, J. Resistance mechanisms matter in SIR models. Math. Biosci. Eng. 2007, 4, 553–563. [Google Scholar] [PubMed]
- Scherer, A.; McLean, A. Mathematical models of vaccination. Br. Med. Bull. 2002, 62, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Safan, M.; Kretzschmar, M.; Hadeler, K.P. Vaccination based control of infections in SIRS models with reinfection: Special reference to pertussis. J. Math. Biol. 2013, 67, 1083–1110. [Google Scholar] [CrossRef]
- Krithika, B.; Tamilalagan, P. Unveiling the spread of epidemics involving partial immunity and reinfection: Insights from a time-delayed mathematical model. Eur. Phys. J. Spec. Top. 2023, 232, 2657–2673. [Google Scholar] [CrossRef]
- Arif, F.; Majeed, Z.; Rahman, J.U.; Iqbal, N.; Kafle, J. Mathematical modeling and numerical simulation for the outbreak of COVID-19 involving loss of immunity and quarantined class. Comput. Math. Methods Med. 2022, 2022, 3816492. [Google Scholar] [CrossRef] [PubMed]
- Rackauckas, C.; Nie, Q. DifferentialEquations.jl—A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia. J. Open Res. Softw. 2017, 5. Available online: https://app.dimensions.aion2019/05/05 (accessed on 24 April 2024). [CrossRef]
- Widmann, D.; Rackauckas, C. DelayDiffEq: Generating Delay Differential Equation Solvers via Recursive Embedding of Ordinary Differential Equation Solvers. arXiv 2022, arXiv:2208.12879. [Google Scholar]
- Colizza, V.; Barrat, A.; Barthelemy, M.; Valleron, A.J.; Vespignani, A. Modeling the worldwide spread of pandemic influenza: Baseline case and containment interventions. PLoS Med. 2007, 4, e13. [Google Scholar] [CrossRef]
- Kanyiri, C.W.; Mark, K.; Luboobi, L. Mathematical analysis of influenza A dynamics in the emergence of drug resistance. Comput. Math. Methods Med. 2018, 2018, 2434560. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).