New Bivariate Copulas via Lomax Distribution Generated Distortions

Abstract

We develop a framework for creating distortion functions that are used to construct new bivariate copulas. It is achieved by transforming non-negative random variables with Lomax-related distributions. In this paper, we apply the distortions to the base copulas of independence, Clayton, Frank, and Gumbel copulas. The properties of the tail dependence coefficient, tail order, and concordance ordering are explored for the new families of distorted copulas. We conducted an empirical study using the daily net returns of Amazon and Google stocks from January 2014 to December 2023. We compared the popular Clayton, Gumbel, Frank, and Gaussian copula models to their corresponding distorted copula models induced by the unit-Lomax and unit-inverse Pareto distortions. The new families of distortion copulas are equipped with additional parameters inherent in the distortion function, providing more flexibility, and are demonstrated to perform better than the base copulas. After analyzing the data, we have found that the joint extremes of Amazon and Google stocks are more likely for high daily net returns than for low daily net returns.

1. Introduction

Descriptions and measurements of correlation and dependence between risks and losses have been important in various fields, such as finance, risk management, and actuarial studies. Bivariate copulas of different dependence structures can model the tail dependence in extreme risks Ref. [1] but be independent of the marginal distributions of the risks. Ref. [2] numerically and graphically illustrated the types of relationships that various copula-based measures of association can detect. Ref. [3] addressed the mathematics of copula functions illustrated with a finance application to financial topics in derivative pricing and credit risk analysis. The seminal paper by [4] demonstrated their practical applications, such as the estimation of joint-life mortality and multi-decrement models. Extreme or tail losses tend to occur together; see [5]. Ref. [6] employed copulas to study the effect of tail dependence and tailedness by quantifying extreme risks. Refs. [7,8] applied copula modeling to investigate the increasing hydroclimatic extremes associated with a warming climate; see also [9] for flood and hydrological models. Overall, copula modeling has shown to be an effective tool in analyzing dependent structures between variables.

Sklar’s theorem [10] states that the joint cumulative distribution function (cdf) can be expressed as the product of the marginals and the copula, and conversely, the copula can be uniquely determined if we know the cdf and marginals. For instance, the Gaussian copula is derived from the bivariate Gaussian distribution and can also be used to generate new bivariate probability distributions via (A1) in the appendix; see [11] for summaries of the methods of constructing copulas. Necessary preliminaries on bivariate copulas corralled in Appendix A can be found in [11,12].

Most recently, Ref. [13] extended the traditional one-parameter Archimedean copulas by integrating the log-gamma-generated margins. Ref. [14] proposed a class of bivariate independence copula transformation of the form $C(u,v)=uvf\left(\right(1-u),(1-v\left)\right),$ where f is a twice differentiable. Let $\mathsf{\Pi }(u,v)=uv$ be the independence copula. Generalizing the FGM copula given by $\pi (u,v)+\alpha xy(1-u)(1-v)$, Refs. [15,16] constructed new copulas of the form $\mathsf{\Pi }(u,v)+Q(u,v;\alpha ),$ where Q is a perturbation function involving trigonometric, hyperbolic, logarithmic, or exponential functions. Ref. [7] used a truncation of the log-concave half-logistic distribution function F as a multiplicative Archimedean generator to construct the copulas of the form $F^{-1}\left(F\left(u\right)F\left(v\right)\right).$

In this paper, we are concerned with the construction of new bivariate copulas via distortion functions. A function T is called a distortion function if it is continuous and increasing on the unit interval $I=[0,1]$, with $T\left(0\right)=0$ and $T\left(1\right)=1.$ A new family of copulas born of the distortion is given by

$$\begin{array}{c}\hfill C_T(u,v)=T\left(C\left(T^{-1}\left(u\right),T^{-1}\left(v\right)\right)\right),u,v\in [0,1],\end{array}$$

(1)

T is termed as admissible distortion if (1) is a copula. If the initial copula is Archimedean with generator $\psi ,$ then $C_T$ is Archimedean with generator $\psi \circ T^{-1}$; see [17,18]. Theorem 3.3.3 in [11] (p. 96) shows that T is admissible if and only if T is increasing and convex; see also [19]. This key result dictates the convexity requirement and opens the door for explorations of admissible distortion functions. Ref. [20] showed that T is admissible if $T\circ exp:(-\infty ,0)\to [0,1]$ is log-convex and suggested several distortion functions. Ref. [21] proposed to apply the distortion to the copula function only, marginals only, or both. The induced copula in (1) is a result of distortions to both the copula and marginals.

Refs. [22,23] constructed new families of copulas via beta and Kumaraswamy cdf distortions.Ref. [24] employed the unit-Lomax distortion. Ref. [25] studied families of copulas generated by a unit-Weibull distortion. Ref. [26] investigated the properties of unit-Gompertz distorted copulas and applied them to analyze the anthropocentric data. The unit-Lomax, unit-Weibull, and unit-Gompertz distortions are derived from an exponential transformation of the Lomax, Weibull, and Gompertz random variables.

Motivated by the fact that the cdf of a continuous random variable with unit interval support meets the definition of a distortion function, we propose a transformation that converts a non-negative random variable to one with unit interval support, which, consequently, establishes a distortion function. The distortion can then be used to generate new families of copulas by distorting existing ones. Similar to the other constructions of new copulas in the literature, the aim is to obtain new families of copulas that may account for a wider range of tail dependence values. With the parameters in the distortion cdf, the distorted copulas have additional parameters in addition to those in the existing copulas, making them more flexible.

The paper is organized as follows. Section 2 begins with the proposed mechanism for generating new distortion functions and admissible parameter spaces of distortions to be studied further. Section 3 provides Archimedean generators for the new families of distorted copulas when the base copulas are independence, Clayton, Frank, and Gumbel. The family of distorted independence copulas is presented to serve as a validation of the results obtained in this paper. Section 4 and Section 5 investigate the properties of tail dependence, tail order, concordance order, and Kendall’s tau. Section 6 contains the numerical results of a simulation study and empirical application, followed by concluding remarks. Copula preliminaries and derivations of tail orders and concordance ordering are included in the Appendix A and Appendix B.

2. Proposed Method

Let Y be a non-negative continuous random variable with cdf $F.$ Consider the following transformation of the random variable Y:

$$\begin{array}{c}\hfill X={\displaystyle \frac{Y}{\theta +Y}},\theta >0.\end{array}$$

(2)

The random variable X has a support of the unit interval, and its cdf is given by

$$\begin{array}{cc}\hfill G\left(x\right)& =P(X\le x)=P\left(Y\le {\displaystyle \frac{\theta x}{1-x}}\right)=F\left({\displaystyle \frac{\theta x}{1-x}}\right).\hfill \end{array}$$

(3)

The cdf G and its quantile or inverse function may both serve as distortion functions to develop new copulas. If the variable Y assumes any value on the real number line, one may consider a transformation of its absolute value; that is, $\left|Y\right|/(1+|Y\left|\right)$, whose cdf is not as straightforward as (3).

We below demonstrate the method with F being the non-negative Lomax and inverse Lomax distributions, and derive the parameter space on which each of the distortions is convex. All the parameters in the generating distribution function F are assumed to be positive. The prime symbol, such as $G^{\prime }$ or $G^{″}$, denotes the derivative of a function.

Example 1.

Unit-Lomax (UL) distortion and its quantile (QUL). Let Y be a Lomax or Pareto Type II random variable with a cdf given by $F\left(y\right)=1-{\left[\beta /(\beta +y)\right]}^{\alpha },$ where $y>0.$ In this case, the transformation in (2) produces the distortion given by

$$\begin{array}{c}\hfill G\left(x\right)=1-{\left[\frac{\beta (1-x)}{\beta (1-x)+\theta x}\right]}^{\alpha },\end{array}$$

(4)

where $0<x<1.$ Note that, for example,

$$\begin{array}{c}\hfill {\left[\frac{2(1-x)}{2(1-x)+1x}\right]}^{\alpha }=\left[\frac{4(1-x)}{4(1-x)+2x}\right]={\left[\frac{8(1-x)}{4(1-x)+4x}\right]}^{\alpha }.\end{array}$$

(5)

Equation (5) demonstrates that multiple values of the parameters (β, θ) give rise to the same distortion in (4), and thus the parameters cannot be uniquely identified. Therefore, to solve this problem, with reparametrization, we consider the distortion $G_L$ (UL) and its inverse $Q_L$ (QUL) given by

$$\begin{array}{c}\hfill G_L\left(x\right)=1-{\left[\frac{(1-x)}{(1-x)+\theta x}\right]}^{\alpha };Q_L\left(x\right)={\displaystyle \frac{1}{1+\theta {[{(1-x)}^{-1/\alpha }-1]}^{-1}}}.\end{array}$$

Lemma 1.

The distortion $G_L\left(x\right)=1-{\left[(1-x){\left((1-x)+\theta x\right)}^{-1}\right]}^{\alpha }$ is convex on I if $0<\theta \le 1$ and $0<\alpha \le 1.$

Proof. 

Let $A\left(x\right)=(1-x)+\theta x,$ $B\left(x\right)=(1-x){\left[A\left(x\right)\right]}^{-1}$, and then $G_L\left(x\right)=1-{\left[B\left(x\right)\right]}^{\alpha }.$ For simplicity, the argument notation of $\left(x\right)$ is dropped. Note that ${\left(B\right)}^{-1}{\left(A\right)}^{-1}={(1-x)}^{-1}.$ The derivatives are given by

$$\begin{array}{ccc}\hfill B^{\prime }& =& -\theta A^{-2};G_L^{\prime }=\alpha \theta B^{\alpha -1}{A}^{-2}\hfill \\ \hfill G_L^{″}& =& -\alpha (\alpha -1){\theta }^2{B}^{\alpha -2}{A}^{-4}-2\alpha \theta B^{\alpha -1}{A}^{-3}(\theta -1)\hfill \\ & =& -\alpha \theta B^{\alpha -1}{A}^{-3}\left[{\displaystyle \frac{(\alpha -1)\theta }{1-x}}+2(\theta -1)\right].\hfill \end{array}$$

(6)

If $0<\theta \le 1$ and $0<\alpha \le 1$, then $G_L^{″}\left(x\right)\ge 0$ for all $x\in I.$ □

Lemma 2.

The distortion $Q_L\left(x\right)=1/\left[1+\theta {\left({(1-x)}^{-1/\alpha }-1\right)}^{-1}\right]$ is convex on I if $\theta \ge 1$ and $\alpha \ge 1.$

Proof. 

Since $Q_L$ is the inverse function of $G_L$, and $G_L$ is an increasing function, by (6), we obtain this lemma. □

Example 2.

Unit-inverse Pareto (UIP) distortion and its quantile (QUP). Consider the inverse Pareto random variable, defined to be the reciprocal of a Lomax random variable, with a cdf given by $F\left(y\right)={\left[y/(\beta +y)\right]}^{\alpha },$ where $y>0.$ In this case, (3) gives

$$\begin{array}{c}\hfill G\left(x\right)={\left[{\displaystyle \frac{\theta x}{\beta (1-x)+\theta x}}\right]}^{\alpha },\end{array}$$

where $0<x<1.$ For the same reason explained by (5), we propose the distortion $G_P$ (UIP) and its inverse $Q_P$ (QUP) given by

$$\begin{array}{c}\hfill G_P\left(x\right)={\left[{\displaystyle \frac{\theta x}{(1-x)+\theta x}}\right]}^{\alpha };Q_P\left(x\right)={\displaystyle \frac{1}{1+\theta (x^{-1/\alpha }-1)}}.\end{array}$$

Lemma 3.

The distortion $G_P\left(x\right)={\left[{\displaystyle \frac{\theta x}{(1-x)+\theta x}}\right]}^{\alpha }$ is convex on I if $0<\theta \le 1$ and $0<\alpha \le 1.$

Proof. 

Let $A\left(x\right)=(1-x)+\theta x$ and $B\left(x\right)=\theta x{\left[A\left(x\right)\right]}^{-1}$. Then ${\left[B\left(x\right)A\left(x\right)\right]}^{-1}=1/\left(\theta x\right)$ and $G_P\left(x\right)={\left[B\left(x\right)\right]}^{\alpha }.$ For simplicity, the argument notation of (x) is dropped. The relevant derivatives are given by

$$\begin{array}{ccc}\hfill B^{\prime }& =& \theta {\left(A\right)}^{-1}-\theta x{A}^{-2}(\theta -1)=\theta A^{-2};G_P^{\prime }=\alpha \theta B^{\alpha -1}{A}^{-2}\hfill \\ \hfill G_P^{″}& =& \alpha (\alpha -1){\theta }^2{B}^{\alpha -2}{A}^{-4}-2\alpha \theta B^{\alpha -1}{A}^{-3}(\theta -1)\hfill \\ & =& \alpha \theta B^{\alpha -1}{A}^{-3}{x}^{-1}\left[(\alpha -1)-2(\theta -1)x\right].\hfill \end{array}$$

(7)

If $0<\theta \le 1$ and $\alpha \ge 1$, then the second derivative $G_P^{″}\ge 0$ for all $x\in I.$ □

Lemma 4.

$Q_P\left(x\right)={[1+\theta (x^{-1/\alpha }-1)]}^{-1}$is convex onIif$\theta \ge 1$and$0<\alpha \le 1.$

Proof. 

This lemma follows since $Q_P$ is the inverse function of $G_P$ and $G_P$ is increasing and concave by (7) when $\theta \ge 1$ and $0<\alpha \le 1$. □

In summary, applying the proposed transformation in (2) to non-negative Lomax-related random variables, we are bestowed with four new admissible distortions tabulated in Table 1. Two functional forms are displayed as they would come in handy for calculations. Note that the admissible parameter spaces are only a sufficient condition for $C_T$ in (1) to be a copula. The dual power distortion is a special case of $G_L$ with $\theta =1.$ The power distortion is a special case of $G_P$ with $\theta =1.$ When $\theta =\alpha =1$, it is important to note that all the distortions in Table 1 become the identity function. This means that when these distortions are applied to a base copula, the resulting family of copulas offers a greater flexibility when fit to data because it includes the base copula as a special case.

Table 1. Proposed distortions and admissible parameter spaces.

Distortion	Function Form		Convex Parameter Space
U-Lomax (UL)	$G_L\left(x\right)$	$=1-{\left[{\displaystyle \frac{1-x}{1-x+\theta x}}\right]}^{\alpha }$	$0<\theta \le 1,$ $0<\alpha \le 1$
		$=1-{\displaystyle \frac{1}{{\{1+\theta [{(1-x)}^{-1}-1]\}}^{\alpha }}}$
Quantile U-Lomax (QL)	$Q_L\left(x\right)$	$={\displaystyle \frac{{(1-x)}^{-1/\alpha }-1}{\theta +{(1-x)}^{-1/\alpha }-1}}$	$\theta \ge 1,$ $\alpha \ge 1$
		$={\displaystyle \frac{1}{1+\theta {[{(1-x)}^{-1/\alpha }-1]}^{-1}}}$
U-Inverse Pareto (UIP)	$G_P\left(x\right)$	$={\left[{\displaystyle \frac{\theta x}{1-x+\theta x}}\right]}^{\alpha }$	$0<\theta \le 1$, $\alpha \ge 1.$
		$={\displaystyle \frac{1}{{[1+{\theta }^{-1}(x^{-1}-1)]}^{\alpha }}}$
Quantile U-Inverse Pareto (QUP)	$Q_P\left(x\right)$	$={\displaystyle \frac{x^{1/\alpha }}{x^{1/\alpha }+\theta (1-x^{1/\alpha })}}$	$\theta \ge 1, 0<\alpha \le 1$
		$={\displaystyle \frac{1}{1+\theta (x^{-1/\alpha }-1)}}$

Remark 1.

Let Y be a Lomax random variable. We also considered the cdf of $Y^{1/\tau }$, i.e., the Burr distribution, given by $F\left(y\right)=1-{(1+y^{\tau })}^{-\alpha },$ as the generating cdf. However, there does not exist a parameter space on which the resulting distortion is convex. Another generating cdf candidate is the exponentiated Lomax cdf of the form ${\left[1-F{\left(\gamma /(\gamma +y)\right)}^{\alpha }\right]}^{\gamma }$, which is more complex and will be investigated in the future.

Remark 2.

Instead of (2), the transformation of $X=1/(1+Y)$ also gives rise to a distortion cdf. The cdf of $X=1/[1+Y]$ is given by, for $0<x<1,$

$$\begin{array}{c}\hfill G\left(x\right)=P(X\le x)=1-F\left(Y\ge {\displaystyle \frac{1-X}{X}}\right).\end{array}$$

In this case, when Y has a Lomax distribution in Example 1, we derive the $G_P.$ When Y has a Lomax distribution in Example 2, we derive the $G_L.$

Remark 3.

There are a multitude of cdfs that may be used as the generating cdf F in (3). For instance, an exponential distribution with mean β. In this case, (3) gives a candidate distortion given by $1-exp\left(-x/\left[\beta \right(1-x\left)\right]\right).$ Another example, a generalized Pareto with a pdf given by

$$\begin{array}{c}\hfill f\left(y\right)=\frac{\mathsf{\Gamma }(\alpha +\tau )}{\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\tau \right)}\frac{{\theta }^{\tau }{y}^{\tau -1}}{{(y+\theta )}^{\alpha +\tau }}\end{array}$$

where $x>0,$ $\alpha >0,$ $\tau >0$, and $\theta >0.$

3. Families of New Distorted Copulas

The general form of copulas constructed by a distortion T is in (1). Archimedean copulas are widely used [27] and are recognized for their flexibility in modeling dependence within multivariate random variables. We formulate the Archimedean generators resulting from the distortions in Section 3.1 when the base copulas are independence, Clayton, Frank, and Gumbel; see Table A1 in Appendix A. The base copulas, except the independence copula, have a single parameter, and the families of the distorted copulas contain more parameters and are less restrictive. Let r denote the parameter in the base copula.

3.1. Archimedean Generators

Example 3

(Independence Copula). The Archimedean generators are

–

UL-independence generator: $log\left(\theta {\left[{(1-u)}^{-1/\alpha }-1\right]}^{-1}+1\right).$

–

QUL-independence generator: $-log\left(1-{\left[1+\theta \left({(1-u)}^{-1}-1\right)\right]}^{-\alpha }\right).$

–

UIP-independence generator: $log\left(1+\theta (u^{-1/\alpha }-1)\right).$

–

QUP-independence generator: $log{\left(1+{\theta }^{-1}(u^{-1}-1)\right)}^{\alpha }.$

Example 4

(Clayton Copula). In this case, we obtain the following:

–

UL-Clayton generator: $\left\{{\left[\theta {\left({(1-u)}^{-1/\alpha }-1\right)}^{-1}+1\right]}^{-r}-1\right\}/r.$

–

QUL-Clayton generator: $\left\{{\left[1-{\left(1+\theta ({(1-u)}^{-1}-1)\right)}^{-\alpha }\right]}^{-r}-1\right\}/r.$

–

UIP-Clayton generator: $\left\{{\left[1+\theta \left(u^{-1/\alpha }-1\right)\right]}^{-r}-1\right\}/r.$

–

QUP-Clayton generator: $\left\{{\left[1+{\theta }^{-1}(u^{-1}-1)\right]}^{\alpha r}-1\right\}/r.$

Example 5

(Frank Copula). When the base copula C is Frank, we obtain the following:

–

UL-Frank generator: $-log\left(1+\left[e^{-r{[\theta {({(1-u)}^{-1/\alpha }-1)}^{-1}+1]}^{-1}}-1\right]/(e^{-r}-1)\right).$

–

QUL-Frank generator: $-log\left(1+\left[e^{-r[1-{(1+\theta ({(1-u)}^{-1}-1))}^{-\alpha }]}-1\right]/(e^{-r}-1)\right).$

–

UIP-Frank generator: $-log\left(1+\left[e^{-r{[1+\theta (u^{-1/\alpha }-1)]}^{-1}}-1\right]/(e^{-r}-1)\right).$

–

QUP-Frank generator: $-log\left(1+\left[e^{-r{[1+{\theta }^{-1}(u^{-1}-1)]}^{-\alpha }}-1\right]/(e^{-r}-1)\right).$

Example 6

(Gumbel Copula). For Gumbel copula, we obtain the following:

–

UL-Gumbel generator: ${\left[-log\left(\theta {({(1-u)}^{-1/\alpha }-1)}^{-1}+1\right)\right]}^r.$

–

QUL-Gumbel generator: ${\left[-log\left(1-{(1+\theta ({(1-u)}^{-1}-1))}^{-\alpha }\right)\right]}^r.$

–

UIP-Gumbel generator: ${\left[log\left(1+\theta (u^{-1/\alpha }-1)\right)\right]}^r.$

–

QUP-Gumbel generator: ${\left[log{\left(1+{\theta }^{-1}(u^{-1}-1)\right)}^{\alpha }\right]}^r.$

3.2. Distortions of Independence Copula

We stage here the copula families constructed by distortions of the independent copula aiming to demonstrate the versatility of distortion and validate the results presented in this paper. The distortions proposed distort the parameter-free independent copula into diverse families of copulas adorned with two parameters and better flexibility.

Note that $G_L^{-1}=Q_L;$ see Table 1. For the UL-independence copula, $C(u,v)=uv$,

$$\begin{array}{ccc}\hfill C_{G_L}(u,v)& =& 1-{\left({\displaystyle \frac{1}{1+\theta \left\{{\left[1-C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)\right]}^{-1}-1\right\}}}\right)}^{\alpha }\hfill \\ \hfill & =& 1-{\left({\displaystyle \frac{\theta +{(1-u)}^{-1/\alpha }+{(1-v)}^{-1/\alpha }-2}{\theta +{(1-u)}^{-1/\alpha }{(1-v)}^{-1/\alpha }-1}}\right)}^{\alpha }.\hfill \end{array}$$

(8)

When $\alpha =\theta =1$, $C_{G_L}(u,v)=uv.$ Let $\overline{u}=(1-u)$ and $\overline{v}=(1-v).$ When $\theta =1$,

$$\begin{array}{ccc}\hfill C_{G_L}(u,v)& =& 1-({\overline{u}}^{1/\alpha }+{\overline{v}}^{1/\alpha }-{\overline{u}}^{1/\alpha }{\overline{v}}^{1/\alpha }{)}^{\alpha },\hfill \end{array}$$

(9)

which is the Joe or B5 copula. The Joe copula is given by $C(u,v)=1-\left({(1-u)}^r+{(1-v)}^r-{(1-u)}^r{(1-v)}^r\right),r\in [1,\infty ).$ It has ${\kappa }_L=2$ and ${\lambda }_U=2-2^{\alpha },0<\alpha \le 1,$ which endorses Proposition 1 in Section 4. The Joe copula in (9) is negatively ordered by $\alpha$. When $\alpha =1$, $C_{G_L}(u,v)=uv/\left[1-(1-\theta )\overline{u}\overline{v}\right],$ which is the Ali–Mikhail–Haq (AMH) copula [11] and is negatively ordered by the parameter $\theta .$ The AMH copula family has lower and upper tail dependence coefficients of zero, and is given by $C(u,v)=uv/[1-r(1-u\left)\right(1-v\left)\right],r\in [-1,1].$

For the QUL-independence copula, from Table 1,

$$\begin{array}{ccc}\hfill C_{Q_L}(u,v)& =& 1-{\displaystyle \frac{1}{\theta +{[1-C\left(Q_L^{-1}\left(u\right),Q_L^{-1}\left(u\right)\right)]}^{-1/\alpha }-1}},\mathrm{where}\hfill \\ \hfill C\left(Q_L^{-1}\left(u\right),Q_L^{-1}\left(u\right)\right)& =& \left(1-{\left[{\displaystyle \frac{1-u}{1-u+\theta u}}\right]}^{\alpha }\right)\left(1-{\left[{\displaystyle \frac{1-v}{1-v+\theta v}}\right]}^{\alpha }\right).\hfill \end{array}$$

(10)

When $\theta =1$, (10) produces the Joe copula in (9) with a different parametrization from the one in [12]. When $\alpha =1,$ (10) yields

$$\begin{array}{c}\hfill 1-{\displaystyle \frac{\overline{u}\overline{v}+\theta u\overline{v}+\theta \overline{u}v}{\theta \left(\overline{u}\overline{v}+\theta u\overline{v}+\theta \overline{u}v+\theta uv\right)}}.\end{array}$$

For the UIP-independence copula, from Table 1,

$$\begin{array}{ccc}\hfill C_{G_P}(u,v)& =& {\left({\displaystyle \frac{1}{1+{\theta }^{-1}\left\{{\left[C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)\right]}^{-1}-1\right\}}}\right)}^{\alpha }\hfill \\ \hfill & =& {\left[1+(u^{-1/\alpha }-1)+(v^{-1/a}-1)+\theta (u^{-1/\alpha }-1)(v^{-1/\alpha }-1)\right]}^{-\alpha }\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & =& uv{\left\{1-(1-\theta )\left[(1-u^{1/\alpha })(1-v^{1/a})\right]\right\}}^{-\alpha },\hfill \end{array}$$

(12)

which is the BB10 copula [12] with ${\kappa }_L={\kappa }_U=2.$ The BB10 copula is given by $C(u,v)=uv{[1-r_1(1-u^{1/r_2})(1-v^{1/r_2})]}^{-r_2},$ where $r_1\in [0,1)\mathrm{and}{r}_2>0$. As shown in Proposition 3, UIP-distorted copulas have the same upper and lower tail orders as the base copula.

For the QUP-independence copula, from Table 1,

$$\begin{array}{ccc}\hfill C_{Q_P}(u,v)& =& {\displaystyle \frac{1}{1+\theta \left[C{\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)}^{-1/\alpha }-1\right]}}\hfill \\ \hfill & =& {\left[1+{\displaystyle \frac{(1-u)(1-v)+\theta u(1-v)+\theta v(1-u)}{\theta uv}}\right]}^{-1}\hfill \\ \hfill & =& uv{\left[1-{\displaystyle \frac{\theta -1}{\theta }}(1-u)(1-v)\right]}^{-1},\hfill \end{array}$$

(13)

which is the AMH copula or a special case of the BB10 copula.

4. Tail Dependence Coefficients and Tail Orders

In this section, we investigate the tail dependence coefficients, tail orders, and concordances for the new families of copulas emerging from the four distortions in Table 1. The lengthy derivations of tail orders are stationed in Appendix B.

Let $t\left(u\right)=dT\left(u\right)/du$ and assume that the lower tail dependence (ltd) coefficient ${\lambda }_L$ of the base copula C and ${lim}_{\tau \to 0+}t\left(C(u,u)\right)/t\left(u\right)$ exist. By definition in (A3) and L’Hopital’s rule, the ltd coefficient for a T distortion-induced copula is given by

$$\begin{array}{ccc}\hfill {\lambda }_{T,L}& =& {\displaystyle \underset{u\to 0^{+}}{lim}}\frac{T\left(C(T^{-1}\left(u\right),T^{-1}\left(u\right))\right)}{u}\hfill \\ \hfill & =& {\displaystyle \underset{u\to 0^{+}}{lim}}\frac{T\left(C(u,u)\right)}{T\left(u\right)}={\displaystyle \underset{u\to 0^{+}}{lim}}\frac{t\left(C(u,u)\right)}{t\left(u\right)}\frac{dC(u,u)}{du}.\hfill \end{array}$$

(14)

Since ${lim}_{u\to 1^{-}}T\left(u\right)=1$, with the substitution of $v=T^{-1}\left(u\right),$ the upper tail dependence (utd) coefficient of $C_T$ is given by

$$\begin{array}{ccc}\hfill {\lambda }_{T,U}& =& 2-{\displaystyle \underset{u\to 1^{-}}{lim}}\frac{1-T\left(C(T^{-1}\left(u\right),T^{-1}\left(u\right))\right)}{1-u}\hfill \\ \hfill & =& 2-{\displaystyle \underset{v\to 1^{-}}{lim}}\frac{1-T\left(C(v,v)\right)}{1-T\left(v\right)}=2-{\displaystyle \underset{v\to 1^{-}}{lim}}\frac{t\left(C(v,v)\right)}{t\left(v\right)}\frac{dC(v,v)}{dv}.\hfill \end{array}$$

(15)

Below, we assume that the ltd coefficient ${\lambda }_L=0$ when ${\kappa }_L>1$ and the utd coefficient ${\lambda }_U=0$ when ${\kappa }_U>1$ for the base copula C. Furthermore, we assume that $C(u,u)\sim u^{{\kappa }_L}\mathrm{𝓁}\left(u\right)$ as $u\to 0^{+}$ and $\overline{C}(1-u,1-u)\sim u^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left(u\right)$ as $u\to 0^{+}$ for some slowly varying functions 𝓁 and ${\mathrm{𝓁}}_{\ast }$ at $0^{+}.$ Let the subscript denote a property owner, e.g., the subscript T in ${\lambda }_{T,U}$ is used to denote the ltd coefficient of a $T$-distorted copula.

Proposition 1

(Unit-Lomax Distortion). Let $C_{G_L}(u,v)$ be the $G_L$-distorted copula defined in (8), where $0<\theta \le 1$ and $0<\alpha \le 1.$ Then,

(i) 

${\kappa }_{G_L,L}={\kappa }_L$ and ${\lambda }_{G_L,L}={\lambda }_L.$

(ii) 

${\kappa }_{G_L,U}={\kappa }_U$ when $\alpha =1$ and ${\kappa }_{G_L,U}=1$ when $0<\alpha <1.$ And ${\lambda }_{G_L,U}=2-{(2-{\lambda }_U)}^{\alpha }.$

Proof. 

The tail orders are shown in (A9) and (A17) in Appendix B. The ltd coefficient, by (14) and L’Hopital’s rule, is given by

$$\begin{array}{cc}\hfill {\lambda }_{G_L,L}& ={\displaystyle \underset{u\to 0^{+}}{lim}}\left\{1-{\left({\displaystyle \frac{1-C(u,u)}{1-C(u,u)+\theta C(u,u)}}\right)}^{\alpha }\right\}/\left\{1-{\left[{\displaystyle \frac{1-u}{1-u+\theta u}}\right]}^{\alpha }\right\}\hfill \\ \hfill & ={\displaystyle \underset{u\to 0^{+}}{lim}}{\left\{{\displaystyle \frac{[1-C(u,u\left)\right]}{[1-C(u,u)+\theta C(u,u\left)\right]}}{\displaystyle \frac{\left[\right(1-u)+\theta u]}{(1-u)}}\right\}}^{\alpha -1}\hfill \\ \hfill & \times {\displaystyle \frac{C^{\prime }(u,u)}{{[1-C(u,u)+\theta C(u,u)]}^2}}{\displaystyle \frac{{[(1-u)+\theta u]}^2}{1}}={\lambda }_L\hfill \end{array}$$

since ${lim}_{u\to 0^{+}}C(u,u)/u={lim}_{u\to 0^{+}}dC(u,u)/du={\lambda }_L.$ The utd coefficient, by (15) and L’Hopital’s rule, we obtain that

$$\begin{array}{cc}\hfill {\lambda }_{G_L,U}& =2-{\displaystyle \underset{u\to 1-}{lim}}{\left\{{\displaystyle \frac{1-C(u,u)}{1-C(u,u)+\theta C(u,u)}}\right\}}^{\alpha }/{\left[{\displaystyle \frac{1-u}{1-u+\theta u}}\right]}^{\alpha }\hfill \\ \hfill & =2-{\displaystyle \underset{u\to 1-}{lim}}{\left\{{\displaystyle \frac{1-u+\theta u}{[1-C(u,u)+\theta C(u,u\left)\right]}}\right\}}^{\alpha }{\left[{\displaystyle \frac{1-C(u,u)}{1-u}}\right]}^{\alpha }=2-{(2-{\lambda }_U)}^{\alpha }\hfill \end{array}$$

since ${lim}_{u\to 1-}[1-C(u,u)]/(1-u)=2-{\lambda }_U.$ □

Proposition 2

(Quantile Unit-Lomax Distortion). Let $C_{Q_L}(u,v)$ be the $Q_L$-distorted copula defined in (10), where $\theta \ge 1$ and $\alpha \ge 1.$ Then,

(i) 

${\kappa }_{Q_L,L}={\kappa }_L$ and ${\lambda }_{Q_L,L}={\lambda }_L.$

(ii) 

${\kappa }_{Q_L,U}={\kappa }_U$ when $\alpha =1$ and ${\kappa }_{Q_L,U}=1$ when $\alpha >1.$ And ${\lambda }_{Q_L,U}=2-{(2-{\lambda }_U)}^{1/\alpha }.$

Proof. 

The tail orders are shown in (A10) and (A18) in Appendix B. By L’Hopital’s rule,

$$\begin{array}{cc}\hfill {\lambda }_{Q_L,L}& ={\displaystyle \underset{u\to 0^{+}}{lim}}{\displaystyle \frac{{\left(1-C(u,u)\right)}^{-1/\alpha }-1}{{\left(1-C(u,u)\right)}^{-1/\alpha }-1+\theta }}/{\displaystyle \frac{{(1-u)}^{-1/\alpha }-1}{{(1-u)}^{-1/\alpha }-1+\theta }}\hfill \\ \hfill & ={\displaystyle \underset{u\to 0^{+}}{lim}}{\displaystyle \frac{{[{(1-u)}^{-1/\alpha }-1+\theta ]}^2}{{[{\left(1-C(u,u)\right)}^{-1/\alpha }-1+\theta ]}^2}}{\displaystyle \frac{{\left(1-C(u,u)\right)}^{-1/\alpha -1}{C}^{\prime }(u,u)}{{(1-u)}^{-1/\alpha -1}}}={\lambda }_L\hfill \end{array}$$

since ${lim}_{u\to 0^{+}}C(u,u)/u={lim}_{u\to 0^{+}}dC(u,u)/du={\lambda }_L.$ By (15) and L’Hopital’s rule, the ltd coefficient is given by

$$\begin{array}{cc}\hfill {\lambda }_{Q_L,U}& =2-{\displaystyle \underset{u\to 1-}{lim}}{\displaystyle \frac{\theta }{{\left(1-C(u,u)\right)}^{-1/\alpha }-1+\theta }}/{\displaystyle \frac{\theta }{{(1-u)}^{-1/\alpha }-1+\theta }}\hfill \\ \hfill & =2-{\displaystyle \underset{u\to 1-}{lim}}{\left[{\displaystyle \frac{1-C(u,u)}{1-u}}\right]}^{1/\alpha +1}{\left[{\displaystyle \frac{dC(u,u)}{du}}\right]}^{-1}=2-{(2-{\lambda }_U)}^{1/\alpha }\hfill \end{array}$$

since ${lim}_{u\to 1-}[1-C(u,u)]/[1-u]=2-{\lambda }_U.$ □

Proposition 3

(Unit-Inverse Pareto Distortion). Let $C_{G_P}(u,v)$ be the $G_P$-distorted copula defined in (11), where $0<\theta \le 1$ and $\alpha \ge 1.$ Then,

(i) 

${\kappa }_{G_P,L}={\kappa }_L$ and ${\lambda }_{G_P,L}={\left({\lambda }_L\right)}^a.$

(ii) 

${\kappa }_{G_P,U}={\kappa }_U$ and ${\lambda }_{G_P,U}={\lambda }_U.$

Proof. 

The tail orders are shown in (A11) and (A19) in Appendix B. For the ltd, with the help of L’Hopital’s rule, we obtain that

$$\begin{array}{cc}\hfill & {\lambda }_{G_P,L}={\displaystyle \underset{u\to 0^{+}}{lim}}{\displaystyle \frac{{\{C(u,u)/[1-C(u,u)+\theta C(u,u)]\}}^{\alpha }}{{\{u/[1-u+\theta u]\}}^{\alpha }}}\hfill \\ \hfill & ={\displaystyle \underset{u\to 0^{+}}{lim}}{\left({\displaystyle \frac{C(u,u)}{u}}\right)}^{\alpha }{\left\{{\displaystyle \frac{1-C(u,u)+\theta C(u,u)}{1-u+\theta u}}\right\}}^{-\alpha }={\left({\lambda }_L\right)}^{\alpha }.\hfill \end{array}$$

The utd coefficient, by (15) and L’Hopital’s rule, is given by

$$\begin{array}{cc}\hfill {\lambda }_{G_P,U}& =2-{\displaystyle \underset{u\to 1-}{lim}}{\displaystyle \frac{1-{\{C(u,u)/[1-C(u,u)+\theta C(u,u)]\}}^{\alpha }}{1-{\{u/[1-u+\theta u]\}}^{\alpha }}}\hfill \\ \hfill & =2-{\displaystyle \underset{u\to 1-}{lim}}{\left({\displaystyle \frac{C(u,u)}{u}}\right)}^{(\alpha -1)}{\left\{{\displaystyle \frac{1-C(u,u)+\theta C(u,u)}{1-u+\theta u}}\right\}}^{-\alpha -1}{\displaystyle \frac{dC(u,u)}{du}}={\lambda }_U\hfill \end{array}$$

since ${lim}_{u\to 1-}C(u,u)=1$ and ${lim}_{u\to 1-}dC(u,u)/du=2-{\lambda }_U.$ □

Proposition 4

(Quantile Unit-Inverse Pareto Distortion). Let $C_{Q_P}(u,v)$ be the $Q_P$-distorted copula defined in (13), where $\theta \ge 1$ and $0<\alpha \le 1.$ Then,

(i) 

${\kappa }_{Q_P,L}={\kappa }_L$ and ${\lambda }_{Q_P,L}={\left({\lambda }_L\right)}^{1/\alpha }.$

(ii) 

${\kappa }_{Q_P,U}={\kappa }_U.$ If ${\kappa }_U=1,$ then ${\lambda }_{Q_P,U}={\lambda }_U.$

Proof. 

The tail orders are derived in (A13) and (A20) in Appendix B. For the ltd coefficient,

$$\begin{array}{cc}\hfill {\lambda }_{Q_P,L}& ={\displaystyle \underset{u\to 0^{+}}{lim}}{\displaystyle \frac{1/\left[1+\theta \left(C{(u,u)}^{-1/\alpha }-1\right)\right]}{1/[1+\theta (u^{-1/\alpha }-1)]}}={\displaystyle \underset{u\to 0^{+}}{lim}}{\displaystyle \frac{1+\theta (u^{-1/\alpha }-1)}{1+\theta \left(C{(u,u)}^{-1/\alpha }-1\right)]}}\hfill \\ \hfill & ={\displaystyle \underset{u\to 0^{+}}{lim}}{\left({\displaystyle \frac{C(u,u)}{u}}\right)}^{1+1/\alpha }{\displaystyle \frac{du}{dC(u,u)}}={\left({\lambda }_L\right)}^{1/\alpha }.\hfill \end{array}$$

The utd coefficient, by (15) and L’Hopital’s rule, is given by

$$\begin{array}{cc}\hfill {\lambda }_{Q_P,U}& =2-{\displaystyle \underset{u\to 1-}{lim}}{\displaystyle \frac{\theta [C{(u,u)}^{-1/\alpha }-1]}{1+\theta [C{(u,u)}^{-1/\alpha }-1]}}/{\displaystyle \frac{\theta (u^{-1/\alpha }-1)}{1+\theta (u^{-1/\alpha }-1)}}\hfill \\ \hfill & =2-{\displaystyle \underset{u\to 1-}{lim}}{\displaystyle \frac{1+\theta (u^{-1/\alpha }-1)}{1+\theta [C{(u,u)}^{-1/\alpha }-1]}}{\displaystyle \frac{C{(u,u)}^{-1/\alpha }-1}{(u^{-1/\alpha }-1)}}\hfill \\ \hfill & =2-{\displaystyle \underset{u\to 1-}{lim}}{\displaystyle \frac{1+\theta (u^{-1/\alpha }-1)}{1+\theta [C{(u,u)}^{-1/\alpha }-1]}}{\displaystyle \frac{{\left[C(u,u)\right]}^{-1/\alpha -1}}{u^{-1/\alpha -1}}}{\displaystyle \frac{dC(u,u)}{du}}={\lambda }_U\hfill \end{array}$$

since ${lim}_{u\to 1-}C(u,u)/u=1$ and ${lim}_{u\to 1-}dC(u,u)/du=2-{\lambda }_U.$ □

The results of the propositions are summarized in Table 2. The utd coefficients of UL- and QUL-distorted copulas differ from those of base copulas when $\alpha \ne 1$, while the ltd coefficients remain unchanged. The UL and QUL distortions render new copulas with upper tail dependence regardless of whether the base copula has it or not. Conversely, the UIP and QUP distortions form copulas with different ltd coefficients when $\alpha \ne 1$ from the base copula, while the utd coefficients remain the same. The Clayton copula has zero upper tail dependence. However, based on Table 2, by applying UL and QUL distortions to a Clayton copula, we create a new family of copulas that are more flexible in the sense that they can accommodate upper tail dependence values ranging from 0 to 1. This same conclusion can be applied to the Frank copula.

Table 2. Tail dependence coefficients of the distorted copulas.

	UL ($0<\mathit{\alpha }\le 1$)	QUL ($\mathit{\alpha }\ge 1$)	UIP ($\mathit{\alpha }\ge 1$)	QUP ($0<\mathit{\alpha }\le 1$)
${\lambda }_{T,L}$	${\lambda }_L$	${\lambda }_L$	${\left({\lambda }_L\right)}^{\alpha }$	${\left({\lambda }_L\right)}^{1/\alpha }$
${\lambda }_{T,U}$	$2-{(2-{\lambda }_U)}^{\alpha }$	$2-{(2-{\lambda }_U)}^{1/\alpha }$	${\lambda }_U$	${\lambda }_U$

We next construct the density contour plots for UL- and UIP-distorted copulas in Figure 1 and Figure 2. Contour plots and observations for QUL- and QUP-distorted copulas are displayed in Figure A1 and Figure A2 in Appendix B.1, respectively. The joint pdf of a copula is $\partial C(u,v)/\partial u\partial v.$ Note, if a contour plot is elongated along one direction, it signals a strong dependence in that direction. A circular contour shape indicates independence between variables. For example, the Clayton has lower tail dependence and no upper tail dependence, therefore, one expects to see a elongated or tightened contour line on the lower left-hand side. Let r be the parameter in the base copula. When $\theta =\alpha =1,$ both the UL and UIP distortions deliver us the base copulas shown in the first column of both figures.

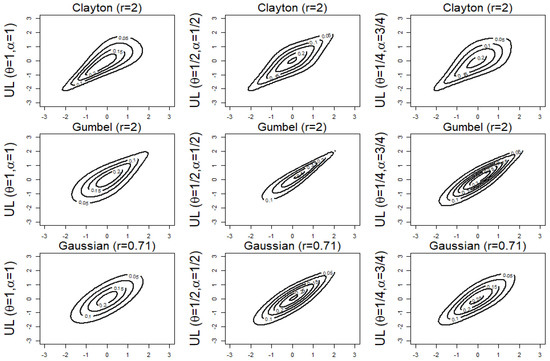
Figure 1. Density contour plots of the UL-Clayton, UL-Gumbel, and UL-Gaussian copulas with standard normal margins and parameters $(\theta ,\alpha )=(1,1),(1/2,1/2),$ and $(1/4,3/4).$ For Clayton, Gumbel, and Gaussian, the parameter r is selected so that the value of Kendall’s tau is $1/2$.

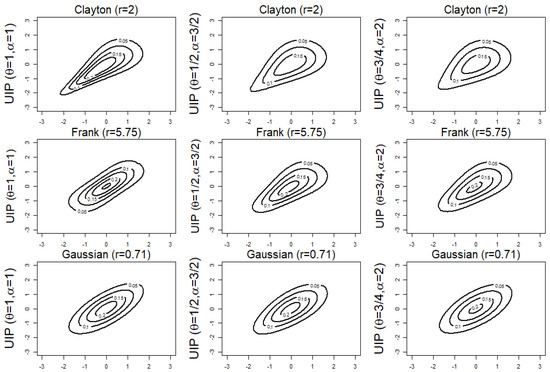
Figure 2. Density contour plots of the UIP-Clayton, UIP-Gumbel, and UIP-Gaussian copulas with standard normal margins and parameters $(\theta ,\alpha )=(1,1),(1/2,1/2),$ and $(1/4,3/4).$ For Clayton, Frank, and Gaussian, the parameter r is selected so that the value of Kendall’s tau is $1/2$.

While the Frank copula is tail-independent, the Clayton and Gumbel copulas are characterized by asymmetric tail dependence with only utd and ltd, respectively. As summarized in Table 2, UL distortions may yield new families of copulas with upper tail dependence. Copulas constructed using the UL distortion exhibit upper tail dependence and maintain the same patterns of lower tail behaviors as the base copula. Notably, UL-distorted Clayton copulas have both lower and upper tails.

As revealed in Table 2 and Figure 2, UIP-distorted copulas have similar characteristics to the base copulas in the first column. If the base copula has lower tail dependence, the family introduced an additional parameter to the ltd coefficient but retains the upper tail dependence of the base copula.

5. Concordance Order and Kendall’s Tau

In this section, we examine the concordance order and Kendall’s tau. We provide formulas for Kendall’s tau of the UL- and UIP-distorted copulas by using the Formula (16) and the Archimedean generators provided in Section 3. The formulas can be readily adapted to write programs to compute Kendall’s tau values at various parameter values.

5.1. Concordance Ordering

A family of copula functions $C_r(u,v)=C(u,v;r)$ with parameter r is positively ordered, denoted by $C_{r_1}\prec C_{r_2},$ if $C_{r_1}(u,v)\le C_{r_r}(u,v),$ and is negatively ordered, denoted by $C_{r_1}\succ C_{r_2},$ if $C_{r_1}(u,v)\ge C_{r_r}(u,v)$ for all $r_1\le r_2$ and $u,v\in I$. According to the definition of a concordance measure, if a family of copulas is ordered by a parameter, its Kendall’s tau is either nonincreasing or nondecreasing in the parameter; see [11].

One can compute the first derivative with respect to a parameter to determine if copula C is positively or negatively ordered by the parameter, which can be a daunting task. If a copula is of Archimedean class, in addition to Theorem A1 in Appendix C, we can utilize the following corollary to examine the concordance orderings in the parameters; see [11] or [28].

Theorem 1

([11]). Let $C_1$ and $C_2$ be Archimedean copulas with generators ${\psi }_1$ and ${\psi }_2$, respectively. Then $C_1\prec C_2$ holds if one of the following conditions is satisfied: (i) ${\psi }_1\circ {\psi }_2^{-1}$ is concave; (ii) ${\psi }_1/{\psi }_2$ is nondecreasing on I; and (iii) ${\psi }_1$ and ${\psi }_2$ are continuously differentiable on I and ${\psi }_1^{\prime }/{\psi }_2^{\prime }$ is nondecreasing on I.

If the base copula C is positively ordered, then, for $r_1\le r_2,$ $C(T^{-1}\left(u\right),T^{-1}\left(v\right);r_1)\le C(T^{-1}\left(u\right),T^{-1}\left(v\right);r_2)$ for all $u,v\in I.$ Since T is increasing, $T\left(C(T^{-1}\left(u\right),T^{-1}\left(v\right);r_1)\right)\le T\left(C(T^{-1}\left(u\right),T^{-1}\left(v\right);r2)\right).$ Similar arguments can be applied to a negatively ordered base copula. That is, a family of distortion copulas built by admissible distortions preserves the concordance order in the parameter of the base copula if the family of base copulas is ordered by the parameter; see also [24].

If the base copula is Archimedean with generator $\psi ,$ which is free of the parameters $\theta$ and $\alpha$, the new family of T-distorted copulas can be written as

$$T\left(C(T^{-1}\left(u\right),T^{-1}\left(v\right))\right)=T\circ {\psi }^{-1}\left(\psi \left(T^{-1}\left(u\right)\right)+\psi \left(T^{-1}\left(v\right)\right)\right),$$

with Archimedean with a generator given by $\psi \left(T^{-1}\left(u\right)\right),$ a continuous, strictly decreasing, convex function such that $\psi \left(T^{-1}\left(1\right)\right)=0.$ Assume below the base copula is Archimedean with generator $\psi .$ Let $T_1$ and $T_2$ be the T distortion evaluated at parameter values $r_1$ and $r_2$, where $r_1\le r_2,$ respectively.

Corollary 1.

Let $C_{T_1}$ and $C_{T_2}$ be Archimedean copulas with generators $\psi \circ T_1^{-1}$ and $\psi \circ T_2^{-1},$ respectively. If one of the following conditions holds: (i) $\psi \circ T_1^{-1}\circ T_2\circ {\psi }^{-1}$ is concave; (ii) $\psi \circ T_1^{-1}/\psi \circ T_2^{-1}$ is nondecreasing on $(0,1)$; or (iii) ψ is continuously differentiable on I and $({\psi }^{\prime }\circ T_1^{-1}/{\psi }^{\prime }\circ T_2^{-1})(T_2^{\prime }\circ T_2^{-1}/T_1^{\prime }\circ T_1^{-1})$ is nondecreasing on I holds, then $C_{T_1}\prec C_{T_2}$.

5.2. Kendall’s Tau

For the T distortion-induced copulas in (1), by substituting $T^{-1}\left(u\right)=x$ and $T^{-1}\left(v\right)=y$ in the definition of Kendall’s tau in (A5), then its Kendall’s tau can be expressed as

$$\begin{array}{c}\hfill \tau =1-4{\int }_0^1{\int }_0^1{\left[t\left(C(x,y)\right)\right]}^2{C}_{1|2}\left(x\right|y)C_{2|1}\left(y\right|x)dxdy,\end{array}$$

where $t\left(v\right)=dT\left(v\right)/dv,$ $C_{2|1}(u,v)=\partial C(u,v)/\partial u$ and $C_{1|2}(u,v)=\partial C(u,v)/\partial v$. Numerical integration methods will be required to compute Kendall’s tau. Define $\mathsf{\Psi }\left(u\right)=\psi \left(T^{-1}\left(u\right)\right).$ By (A6), Kendall’s tau for a distorted copula is given by

$$\begin{array}{ccc}\hfill \tau & =& 1+4{\int }_0^1\frac{\mathsf{\Psi }\left(u\right)}{{\mathsf{\Psi }}^{\prime }\left(u\right)}du=1+4{\int }_0^1\frac{\psi \left(v\right)}{{\psi }^{\prime }\left(v\right)}{t}^2\left(v\right)dv.\hfill \end{array}$$

(16)

We next present the explicit formulas of Kendall’s tau for UL and UIP distortions when the base copulas are independence, Clayton, Gumbel, and Frank copulas. The Archimedean generators for the base copulas are reported in Table A1 in Appendix A.

–

UL-independence copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha [{(1-u)}^{-1/\alpha }-1]log\left(\theta {[{(1-u)}^{-1/\alpha }-1]}^{-1}-1\right)}{\theta \left[{(1-u)}^{-1/\alpha -1}\right]{[\theta +{(1-u)}^{-1/\alpha }-1]}^{-1}}}du$.

–

UL-Clayton copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha \theta u(1-u^r)}{r{(1-u)}^2{[1+\theta (-1+{(1-u)}^{-1})]}^{\alpha +1}}}du$.

–

UL-Gumbel copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha \theta u(-logu)}{r{(1-u)}^2{[1+\theta (-1+{(1-u)}^{-1})]}^{\alpha +1}}}du$.

–

UL-Frank copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha \theta (1-e^{ru})}{r{(1-u)}^2{[1+\theta (-1+{(1-u)}^{-1})]}^{\alpha +1}}}log\left({\displaystyle \frac{e^{-ru}-1}{e^{-r}-1}}\right)du$.

–

UIP-independence copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha [1+\theta (u^{-1/a}-1)]log\left(1+\theta (u^{-1/a}-1)\right)}{\theta u^{-1/\alpha -1}}}du$.

–

UIP-Clayton copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha u(1-u^r)}{r\theta u^2{[1+{\theta }^{-1}(u^{-1}-1)]}^{\alpha +1}}}du.$

–

UIP-Gumbel copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha u(-logu)}{r\theta u^2{[1+{\theta }^{-1}(u^{-1}-1)]}^{\alpha +1}}}du.$

–

UIP-Frank copula: $1-4{\int }_0^1{\displaystyle \frac{\alpha (1-e^{ru})}{r\theta u^2{[1+{\theta }^{-1}(u^{-1}-1)]}^{\alpha +1}}}log\left({\displaystyle \frac{e^{-ru}-1}{e^{-r}-1}}\right)du.$

Example 7.

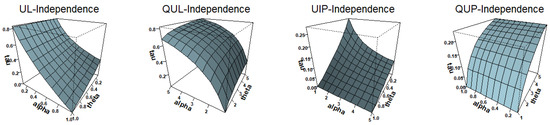
We here illustrate only the ordering in the parameter θ for UL and UIP distortions of the independence copula in Appendix C due to the page limit. While not all mathematically shown, Kendall’s tau surface plots in Figure 3 indicate that UL, QUL, UIP, and QUP distortions of the independence copula result in new families that are negatively ordered in the parameter θ and $\alpha .$ For the family of UIP-independence copulas in (12), the BB10 copula is negatively ordered by the parameter θ, see [12]. The family of QUP-independence copulas in (13) does not depend on the parameter α, and hence the flat lines along the α axis.

Figure 3. Surface plots of Kendall’s tau for UL-, QL-, QIP-, and QUP-independence copulas.

Not all families of distortion-generated copulas are ordered by concordance. For example, the UL-distorted Clayton family. When a family of copulas is ordered by a parameter, we expect Kendall’s tau values to increase or decrease with the parameter. Figure 4 exhibits Kendall’s tau surface plots when distortions are applied to the Clayton copula with parameter r. These plots indicate that the distortion copulas, just like the base Clayton copula, are positively ordered by the parameter r. The UL-Clayton copula with $r=15$ and the QUL-Clayton copula with $r=20$ are not ordered by the parameter $\alpha$. Regarding the UIP-Clayton copulas, the concordance order fails in the parameter $\alpha$ at $r=25$ and at $\theta =1/10$, as well as in the parameter $\theta$ when $\alpha =25$. Furthermore, depending on the $\alpha$ or r value, the QUL-Clayton copula can be positively or negatively ordered by the parameter $\theta$ when $r=2$ and $\alpha =3/4$.

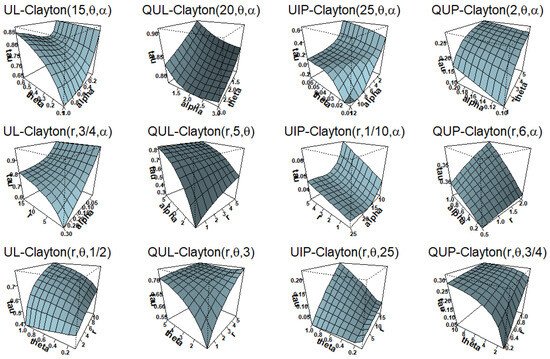
Figure 4. Surface plots of Kendall’s tau constructed at various combinations of parameter values for the UL-Clayton, QL-Clayton, UIP-Clayton, and QUP-Clayton copula.

6. Numerical Results

In this section, we run a simulation study to inspect how the newly minted families of UL distortion copulas perform when fit to data generated from the beloved Clayton, Gumbel, Gaussian, and Frank copulas, and vice versa. Additionally, the copula models are applied to a bivariate dataset consisting of the daily return rates of Amazon and Google stocks.

6.1. A Simulation Study

A general algorithm to generate draws from a bivariate copula C is the conditional distribution approach, as described by [19,24]. It consists of two steps: (i) generate two independent uniform random values $(u_1,v)$ and (ii) solve $C\left(u_2\right|u_1)-v=0$ for $u_2,$ where $C\left(u\right|v)=\partial C(u,v)/\partial v.$ The desired pair is $(u_1,u_2).$ Using this algorithm, we generated 2000 bivariate pseudo-observations from the Clayton, Gumbel, Gaussian, and Frank copulas. We also simulated the same number of pseudo-observations from the families of UL-distorted copulas, where the four copulas served as base copulas. We do not present the figures for QIP, QUL, and QUP distortions, as the conclusions are similar to those from UL distortion.

The values of parameters in the base copulas are selected so they have Kendall’s tau value of 0.5. The UL distortion has parameter values of $\alpha =1/2$ and $\theta =1/2$. We used the pseudo-likelihood estimation method [12] that maximizes (17) to fit the base copula and distorted copulas to the data. We then computed the empirical probabilities using the estimated copula models and constructed the probability–probability (PP) plots of the estimated probability distribution against the theoretical one. In the first row, the four base copulas are approximated by their UL-distorted counterparts, UL-Clayton, UL-Gumbel, UL-Gaussian, and UL-Frank copulas, and vice versa in the second row. The solid black line is the one that resulted from fitting the data to the copula model, from which observations were generated.

As another way of comparison, we also calculated the maximum distance in Table 3 between the theoretical and empirical probabilities at each data pair of $(u_1,u_2)$. The univariate Kolmogorov–Smirnov (KS) test came to mind, and for a sample size of 2000, the 95% critical value of 0.03 is used as an ad hoc threshold.

Table 3. Maximum distance between the theoretical and empirical copula distributions.

Distorted Copula	Approximating
	Clayton by	Gumbel by	Frank by	Gaussian by
UL-Clayton	$0.014$	$0.021$	$0.035$	$0.026$
UL-Gumbel	$0.028$	$0.012$	$0.019$	$0.008$
UL-Frank	$0.021$	$0.012$	$0.011$	$0.024$
UL-Gaussian	$0.031$	$0.021$	$0.031$	$0.016$
Base Copula	Approximating
	UL-Clayton by	UL-Gumbel by	UL-Frank by	UL-Gaussian by
Clayton	$0.035$	$0.047$	$0.042$	$0.042$
Gumbel	$0.050$	$0.013$	$0.034$	$0.033$
Frank	$0.046$	$0.024$	$0.030$	$0.032$
Gaussian	$0.021$	$0.019$	$0.017$	$0.022$

Based on Figure 5 and Table 3, the Clayton copula, which is represented in red in the second row of Figure 5, shows greater deviations from the 45-degree line when fit to the data generated from UL-distorted copulas. According to Lemma 1, the UL-distorted copula has an upd coefficient of $2-{(2-{\lambda }_U)}^{\alpha }$, which may be attuned to zero. Furthermore, it has zero ltd when the base copula has zero ltd. The Clayton copula does not have upper tail dependence, so one would expect it to perform poorly when fit to the data generated from the UL-distorted family. In contrast, e.g., the UL-Gumbel appears to do well when fit to the data generated from the Frank and Gaussian copulas. In general, the performance of a copula depends on its tail dependence characteristics, and the results show that the UL-distorted copulas are more flexible as they have extra parameters.

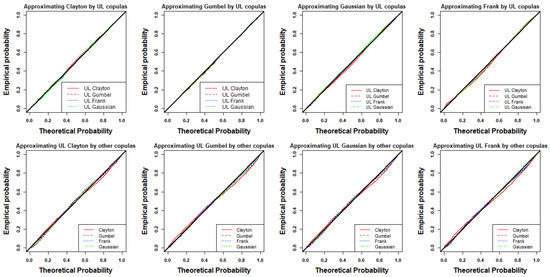
Figure 5. PP plots of UL and base copulas.

6.2. Empirical Application

We fit the proposed families of copula models to a bivariate dataset of daily return rates on Amazon and Google stocks. Historical data for the daily open, close, high, and low prices, and the adjusted closing price for stocks can be downloaded from Yahoo Finance. The adjusted closing price accounts for any splits and dividend distributions. We downloaded the data for Amazon and Google stocks for the period from January 2014 to December 2023, which amounts to a sample size of 2516 daily data points. The daily net return rates in percentages were then calculated based on the adjusted closing price. To calculate the return rate for today, the difference between today’s price and yesterday’s price is divided by yesterday’s price.

Table 4 displays the summary statistics for both variables. The sample Pearson correlation and Kendall’s tau are 0.71 (p-value < 0.001) and 0.49 (p-value < 0.001), respectively, both of which are significantly different from zero. Compared to Google, the center tendency measures for Amazon are smaller, but there is no significant difference in means. The Amazon daily rate return is significantly more variable based on the F test and is more skewed judging from the skewness measures and histograms in Figure 6.

Table 4. Descriptive statistics of the dataset.

	Mean	Sd	Min	1st Qu	Median	3rd Qu	Max	Skew
Amazon	$-0.01$	$1.60$	$-8.56$	$-0.86$	$-0.01$	$0.91$	$8.24$	−0.09
Google	$0.04$	$1.35$	$-5.76$	$-0.67$	$0.05$	$0.84$	$6.65$	−0.20

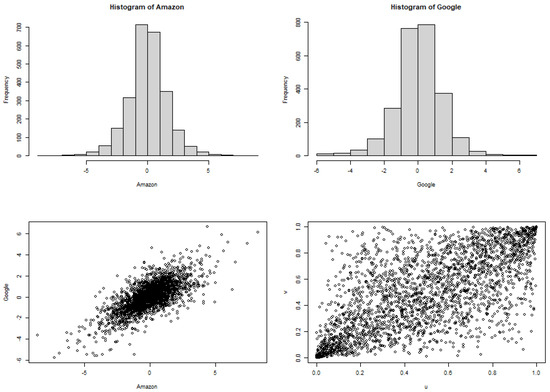
Figure 6. Histograms of daily return rates for Amazon and Google stocks, and scatter plots of Amazon against Google return rates and their corresponding pseudo-observations.

Let ${\{x_i,y_i\}}_{i=1}^n$ denote the bivariate observations. The pseudo-observations or scaled empirical distributions ${\{u_i,v_i\}}_{i=1}^n$ are defined to be $u_i={\sum }_{j=1}^{n}J(x_j\le x_i)/(n+1)$ and $v_i={\sum }_{j=1}^{n}J(y_j\le y_i)/(n+1),$ where $J(·)$ is the indicator function. Figure 6 contains the scatter plots of $y_i$ versus $x_i$ and $v_i$ versus $u_i.$ Based on the histograms, the return rates for both stocks are concentrated around their center, which is also reflected in the resulting scatter plot. However, the pseudo-observations computed using a scaled empirical distribution are uniformly distributed. Therefore, one would expect a more evenly dispersed scatter plot.

The maximum pseudo-likelihood estimation introduced by [18] is used to estimate the parameters. It maximizes the pseudo-log-likelihood function, i.e., the log-likelihood with the copula functions evaluated at pseudo-observations, given by

$$\begin{array}{c}\hfill L\left(\gamma \right)={\displaystyle \sum _{i=1}^n}log{c}_T(u_i,v_i;\gamma ),\end{array}$$

(17)

where $c_T$ is the copula pdf in (A1) and $\gamma$ is the parameter vector.

We did not fit a marginal distribution to each of the net returns. Our primary objective was to compare the new families of the distorted copula with the base copulas. Let r be the parameter in the base copula. Table 5 below reports the estimates with the estimated standard error in the parentheses, the maximum pseudo-likelihood (MPL), and the AIC values. All the parameter estimates fall within admissible spaces. Kendall’s tau estimates $\widehat{\tau }$ were computed by plugging parameter estimates into either the theoretical Kendall’s tau formula or (16).

Table 5. MPL, AIC, $\widehat{\tau }$, parameter estimates and their standard deviation in parentheses $\widehat{r}$, $\widehat{\theta }$, $\widehat{\alpha }$ for the base, UL-distorted, and UIP-distorted copula models.

Family	MPL	$\widehat{\mathit{\tau }}$	AIC	$\widehat{\mathit{r}}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\alpha }}$
Clayton	$756.0$	$0.488$	$-1510.1$	$1.907\left(0.055\right)$	–	–
Gumbel	$758.7$	$0.461$	$-1515.5$	$1.856\left(0.033\right)$	–	–
Frank	$754.3$	$0.491$	$-1506.7$	$5.582\left(0.165\right)$	–	–
Gaussian	$838.6$	$0.493$	$-1675.3$	$0.699\left(0.009\right)$	–	–
UL-Clayton	$877.3$	$0.450$	$-1748.6$	$4.855\left(0.192\right)$	$0.000$$\left(0.174\right)$	$0.562\left(0.029\right)$
UL-Gumbel	$906.4$	$0.461$	$-1806.9$	$1.256\left(0.043\right)$	$0.008\left(0.004\right)$	$0.873\left(0.056\right)$
UL-Frank	$900.0$	$0.476$	$-1794.0$	$4.223\left(0.319\right)$	$0.084\left(0.023\right)$	$0.640\left(0.019\right)$
UL-Gaussian	$901.9$	$0.484$	$-1797.9$	$0.527\left(0.034\right)$	$0.028\left(0.012\right)$	$0.686\left(0.026\right)$
UIP-Clayton	$748.3$	$0.353$	$-1490.6$	$1.413\left(0.097\right)$	$0.999\left(0.030\right)$	$1.296\left(0.108\right)$
UIP-Gumbel	$906.4$	$0.494$	$-1806.8$	$1.392\left(0.036\right)$	$0.010\left(0.006\right)$	$1.174\left(0.097\right)$
UIP-Frank	$748.5$	$0.481$	$-1494.9$	$9.281\left(0.443\right)$	$0.999\left(0.060\right)$	$3.484\left(0.043\right)$
UIP-Gaussian	$887.1$	$0.472$	$-1768.3$	$0.852\left(0.073\right)$	$0.022\left(0.062\right)$	$1.995\left(0.194\right)$

Based on the scatter plots, it appears that there is a weak dependence in both the lower and upper tails between the daily net returns of the two stocks. Table 5 shows that among the base copulas considered, the Gaussian copula performs the best in terms of MPL and AIC, followed by Gumbel. The estimated Kendall’s tau calculated from the Gaussian copula produces the closest match to the sample Kendall’s tau between Google and Amazon.

The Frank copula, which is supposedly suitable for data with weak tail dependence, performs the worst. Note that the Gumbel copula with a parameter value of 1 represents the independent copula where Kendall’s tau is equal to 0. It performs better than the Clayton copula, which suggests that there might be a stronger upd than ltd. Furthermore, a distortion copula that can accommodate a wider range of upper tail dependence, e.g., UL-distorted copulas, may do well in fitting this net return dataset.

Table 5 indicates that the UL-distorted copula model outperforms the corresponding base copula. The fitted UL-Clayton copula model has the largest AIC value, with the estimated lower and upper tail dependence coefficients of $0.44$ and $0.50.$ It is less satisfactory than other UL-distorted copula models, probably due to weak lower tail dependence in the data. Both the UL-distorted Frank and Gaussian copulas have an estimated upper tail dependence coefficient of 0.39 and perform better than the Gaussian copula in terms of MPL and AIC.

The UIP-Clayton and UIP-Frank copulas do not exhibit tail dependence behaviors and their performance is worse than their base copulas. The UL-Gumbel and UIP-Gumbel copulas are the best performers, with UL-Gumbel being slightly better than UIP-Gumbel in terms of MPL and AIC. The UIP-Gumbel model produces an estimated Kendall’s tau closer to the sample Kendall’s tau. Both models have upper tail dependence, but not lower tail tail dependence.

According to the copula models employed in this application, there is a moderate linear correlation between the daily net returns of Amazon and Google stocks. Additionally, there appears asymmetrical in the extreme co-movements; that is, joint extremes are more likely for high daily net return values than for low daily net return values.

7. Concluding Remarks

The framework advanced in the paper originates from the fact that a cumulative distribution function with unit interval support is a distortion function. It employs a transformation of a non-negative random variable into a variable with the support of the unit interval. The additional parameters in the distortion allow for more modeling flexibility. As demonstrated in Section 3.2, distortion of the independence copula creates a new family of copulas that includes the base copula and other existing copulas as its members and accommodates a wider range of tail dependence behaviors that the independence copula would never dream of having.

The tail behavior of a copula model is a crucial factor in determining whether it can adequately fit the data. The use of UL and QUL distortions can morph a family of base copulas without upper tail dependence into a new family of copulas with upper tail dependence. The upper tail dependence coefficient of the UL- and QUL-distorted copulas involves more parameters than the one of the base copula. The distortions can ultimately lead to a better accommodation of the upper tail dependence when compared to the base copula. The tail behaviors in the families of the UIP- and QUP-distorted copulas are similar to the ones in the base copula. However, they can accommodate better the lower tail dependence when compared to the base copulas.

We are not certain whether a more complicated generating cdf or distortion, e.g., one with more than two parameters, would result in a new family of copulas with both upper and lower tail dependence when applied to a base copula with no tail dependence behavior. The framework proposed in this article opens the door to a world of new distortions. Due to the page length limit, further exploration of the concordance ordering of the new family of distorted copulas will be pursued in more detail. The distortions of multivariate copulas of higher dimensions may also be of interest. Unlike the distortions of bivariate copulas, the distortions of multivariate copulas require more care and will be explored in the future.

Appendix B.1. Contour Plots

Figure A1 shows that the upper tail dependence tails of QUL-Clayton, QUL-Gumbel, and QUL-Gaussian appear more pronounced than the corresponding base copula for the selected $\alpha$ values, similar to those of UL-Clayton, UL-Gumbel, and UL-Gaussian, respectively. The UL- and QUL-distorted copulas have no lower tail dependence when the base copulas have no lower tail dependence. While the parameters are selected so that $\tau =0.5,$ the contour plots in Figure 1 and Figure A1 show various shapes and sparsities.

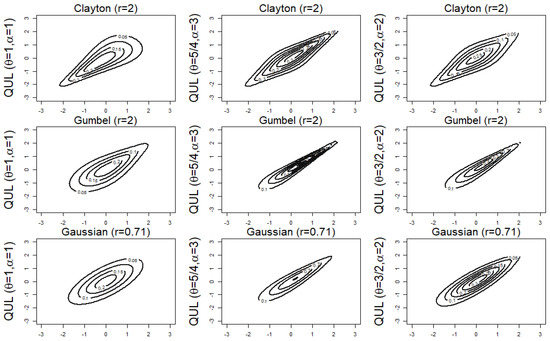
Figure A1. Density contour plots of the QUL-Clayton, QUL-Gumbel, and QUL-Gaussian copulas with standard normal margins and parameters $(\theta ,\alpha )=(1,1),(3/2,1/2),$ and $(2,3/4).$ For Clayton, Gumbel, and Gaussian, the parameter r is selected so that the value of Kendall’s tau is $1/2$.

Table 2 indicates that the upper tail dependence coefficient of the UIP- and QUP-distorted copulas is the same as that of the base copula. However, the lower tail dependence coefficients are ${\left({\lambda }_L\right)}^{\alpha }$ where $\alpha \ge 1$ and ${\left({\lambda }_L\right)}^{\alpha }$ where $0<\alpha \le 1,$ respectively. That is, the UIP distortion with $\alpha =3/2$ in Figure 2 and the QUP distortion with $\alpha =1/2$ in Figure A2 have similar if not the same shapes on the upper right side. Asymmetry is present in QUP-Frank and UIP-Frank when $\theta$ and $\alpha$ do not equal 1. The contour plots for UIP-Gaussian and QUP-Gaussian show little change.

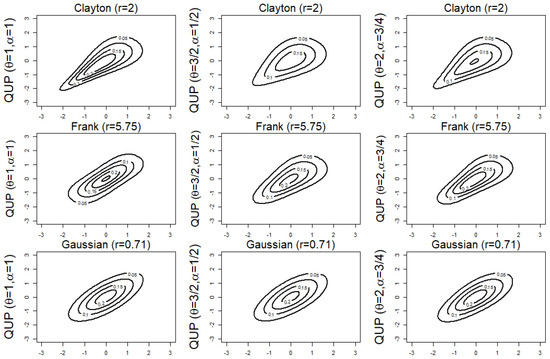
Figure A2. Density contour plots of the QUP-Clayton, QUP-Frank, and QUP-Gaussian copulas with standard normal margins and parameters $(\theta ,\alpha )=(1,1),(3/2,1/2),$ and $(2,3/4).$ For Clayton, Frank, and Gaussian, the parameter r is selected so that the value of Kendall’s tau is $1/2$.

Appendix B.2. Derivations of Tail Orders

The following Talyor’s series approximations are key workhorses for calculating the tail orders of proposed distortions. For two constants a and b, we have that

$$\begin{array}{c}{(1+u)}^a\sim 1+au,{\displaystyle \frac{1}{1+au}}\sim 1-au,{\displaystyle \frac{u}{1+au}}\sim u,{\displaystyle \frac{u}{b+au}}\sim {\displaystyle \frac{u}{b}}\mathrm{as}u\to 0.\end{array}$$

(A7)

Assume $C(u,u)\sim u^{{\kappa }_L}\mathrm{𝓁}\left(u\right)$ as $u\to 0^{+}$ and $\overline{C}(1-u,1-u)\sim u^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left(u\right)$ as $u\to 0^{+}$ for some slowly varying functions 𝓁 and ${\mathrm{𝓁}}_{\ast }$ at $0^{+}.$

Appendix B.3. Lower Tail Orders

Note that $G_L^{-1}=Q_L$ and $G_P^{-1}=Q_P.$ From (A7) and Table 1, we obtain that, as $u\to 0^{+},$

$$\begin{array}{c}{G}_L\left(u\right)=1-{\left(1-{\displaystyle \frac{\theta u}{1-(1-\theta )u}}\right)}^{\alpha }\sim 1-{\left(1-\theta u\right)}^{\alpha }\sim \alpha \theta u;\hfill \\ Q_L\left(u\right)={\displaystyle \frac{{(1-u)}^{-1/\alpha }-1}{\theta +{(1-u)}^{-1/\alpha }-1}}\sim {\displaystyle \frac{u/\alpha }{\theta +{(1-u)}^{-1/\alpha }-1}}\sim u/\left(\alpha \theta \right);\hfill \\ G_P\left(u\right)\sim {\theta }^{\alpha }{u}^{\alpha };Q_P\left(u\right)\sim u^{1/\alpha }/\theta .\hfill \end{array}$$

(A8)

For UL-distorted copulas, since $C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)\to 0$ as $u\to 0^{+},$ applying (A8) yields

$$\begin{array}{ccc}\hfill G_L\left(C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)\right)& =& 1-{\left[{\displaystyle \frac{1-C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)}{1-C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)+\theta C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)}}\right]}^{\alpha }\hfill \\ & \sim & \alpha \theta C\left(G_L^{-1}\left(u\right),G_L^{-1}\left(u\right)\right)\sim \alpha \theta {\left[Q_L\left(u\right)\right]}^{{\kappa }_L}\mathrm{𝓁}\left(Q_L\left(u\right)\right)\hfill \\ & \sim & u^{{\kappa }_L}{\left(\alpha \theta \right)}^{1-{\kappa }_L}\mathrm{𝓁}\left(Q_L\left(u\right)\right)\mathrm{as}u\to 0^{+}.\hfill \end{array}$$

(A9)

By (A8), $\mathrm{𝓁}\left(Q_L\left(u\right)\right)\sim \mathrm{𝓁}\left(u/\left(\alpha \theta \right)\right)$ and by definition, ${\left(\alpha \theta \right)}^{1-{\kappa }_L}\mathrm{𝓁}\left(Q_L\left(u\right)\right)$ is slowly varying.

For the QUL-distorted copulas, $Q_L$, by Table 1, (A7) and (A8), we have

$$\begin{array}{ccc}\hfill Q_L\left(C\left(Q_L^{-1}\left(u\right),Q_L^{-1}\left(u\right)\right)\right)& =& {\displaystyle \frac{{\left[1-C\left(Q_L^{-1}\left(u\right),Q_L^{-1}\left(u\right)\right)\right]}^{-1/\alpha }-1}{\theta +{\left[1-C\left(Q_L^{-1}\left(u\right),Q_L^{-1}\left(u\right)\right)\right]}^{-1/\alpha }-1}}\hfill \\ & \sim & {\left(\alpha \theta \right)}^{-1}C\left(Q_L^{-1}\left(u\right),Q_L^{-1}\left(u\right)\right)\sim {\left(\alpha \theta \right)}^{-1}{\left[G_L\left(u\right)\right]}^{{\kappa }_L}\mathrm{𝓁}\left(Q_L^{-1}\left(u\right)\right)\hfill \\ & \sim & u^{{\kappa }_L}{\left(\alpha \theta \right)}^{{\kappa }_L-1}\mathrm{𝓁}\left(G_L\left(u\right)\right)\mathrm{as}u\to 0^{+}.\hfill \end{array}$$

(A10)

By (A8), $\mathrm{𝓁}\left(G_L\left(u\right)\right)\sim \mathrm{𝓁}\left(\alpha \theta u\right)$ and by definition, ${\left(\alpha \theta \right)}^{{\kappa }_L-1}\mathrm{𝓁}\left(G_L\left(u\right)\right)$ is slowly varying.

For the UIP-distorted copulas, since $C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)\to 0$ as $u\to 0^{+}$ and by (A8),

$$\begin{array}{ccc}\hfill G_P\left(C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)\right)& =& {\left[{\displaystyle \frac{\theta C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)}{1-C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)+\theta C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)}}\right]}^{\alpha }\hfill \\ & \sim & {\theta }^{\alpha }{\left[C\left(G_P^{-1}\left(u\right),G_P^{-1}\left(u\right)\right)\right]}^{\alpha }\sim {\theta }^{\alpha }{\left\{{\left[Q_P\left(u\right)\right]}^{{\kappa }_L}\mathrm{𝓁}\left(Q_P\left(u\right)\right)\right\}}^{\alpha }\hfill \\ & \sim & u^{{\kappa }_L}{\theta }^{\alpha (1-{\kappa }_L)}{\left[\mathrm{𝓁}\left(Q_P\left(u\right)\right)\right]}^{\alpha }\mathrm{as}u\to 0^{+}.\hfill \end{array}$$

(A11)

Since $G_P\left(u\right)\sim {\theta }^{\alpha }{u}^{\alpha }$ and 𝓁 is slowly varying at $0^{+}$, for $s,\alpha >0,$

$$\begin{array}{c}{\displaystyle \underset{u\to 0+}{lim}}{\displaystyle \frac{\mathrm{𝓁}\left(su\right)}{\mathrm{𝓁}\left(u\right)}}={\displaystyle \underset{u\to 0+}{lim}}{\left[{\displaystyle \frac{\mathrm{𝓁}\left(su\right)}{\mathrm{𝓁}\left(u\right)}}\right]}^{\alpha }=1;\hfill \\ {\displaystyle \underset{u\to 0+}{lim}}{\displaystyle \frac{\mathrm{𝓁}\left(G_P\left(su\right)\right)}{\mathrm{𝓁}(G_P\left(u\right)}}={\displaystyle \underset{u\to 0+}{lim}}{\displaystyle \frac{\mathrm{𝓁}\left({\theta }^a{s}^{\alpha }{u}^{\alpha }\right)}{\mathrm{𝓁}\left({\theta }^a{u}^{\alpha }\right)}}={\displaystyle \underset{v\to 0+}{lim}}{\displaystyle \frac{\mathrm{𝓁}\left(s^{\alpha }v\right)}{\mathrm{𝓁}\left(v\right)}}=1.\hfill \end{array}$$

(A12)

Therefore, ${\left[\mathrm{𝓁}\left(Q_P\left(u\right)\right)\right]}^{\alpha }$ is slowly varying.

For the QUP-distorted copulas, $C\left(Q_P^{-1}\left(u\right),Q_P^{-1}\left(u\right)\right)\to 0$ and by (A8), we obtain

$$\begin{array}{ccc}\hfill Q_P\left(C\left(Q_P^{-1}\left(u\right),Q_P^{-1}\left(u\right)\right)\right)& =& {\displaystyle \frac{1}{1+\theta \{\left[C\left(Q_P^{-1}\left(u\right),Q_P^{-1}\left(u\right)\right){]}^{-1/\alpha }-1\right\}}}\hfill \\ & \sim & {\theta }^{-1}{\left[C\left(Q_P^{-1}\left(u\right),Q_P^{-1}\left(u\right)\right)\right]}^{1/\alpha }\sim {\theta }^{-1}{\left\{{\left[G_P\left(u\right)\right]}^{{\kappa }_L}\mathrm{𝓁}\left(G_P\left(u\right)\right)\right\}}^{1/\alpha }\hfill \\ & \sim & u^{{\kappa }_L}{\theta }^{{\kappa }_L-1}{\left[\mathrm{𝓁}\left(G_P\left(u\right)\right)\right]}^{1/\alpha }\mathrm{as}u\to 0^{+}.\hfill \end{array}$$

(A13)

By similar arguments in (A12), ${\left[\mathrm{𝓁}\left(G_P\left(u\right)\right)\right]}^{1/\alpha }$ can be shown to be slowly varying.

Appendix B.4. Upper Tail Orders

By the approximations in (A7), as $u\to 0^{+},$

$$\begin{array}{ccc}\hfill G_L(1-u)& =& 1-{\left[{\displaystyle \frac{u}{\theta +(1-\theta )u}}\right]}^{\alpha }\sim 1-{\left(u/\theta \right)}^{\alpha },\hfill \\ \hfill Q_L(1-u)& =& {\displaystyle \frac{u^{-1/\alpha }-1}{\theta +u^{-1/\alpha }-1}}=1-{\displaystyle \frac{\theta u^{1/\alpha }}{1+(\theta -1)u^{1/\alpha }}}\sim 1-\theta u^{1/\alpha },\hfill \\ \hfill G_P(1-u)& =& {\left[{\displaystyle \frac{\theta (1-u)}{u+\theta (1-u)}}\right]}^{\alpha }={\left[1-{\displaystyle \frac{u}{\theta +(1-\theta )u}}\right]}^{\alpha }\sim 1-\alpha u/\theta ,\hfill \\ \hfill Q_P(1-u)& =& {\displaystyle \frac{{(1-u)}^{1/\alpha }}{\theta +(1-\theta ){(1-u)}^{1/\alpha }}}\sim {\displaystyle \frac{1-u/\alpha }{\theta +(1-\theta )(1-u/\alpha )}}\hfill \\ & \sim & 1-{\displaystyle \frac{\theta u/\alpha }{1-u/\alpha +\theta u/a}}\sim 1-\theta u/\alpha .\hfill \end{array}$$

(A14)

By (A4), if $\widehat{C}(u,u)\sim u^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left(u\right)$ as $u\to 0^{+}$, $C(1-u,1-u)\sim 1-2u+u^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left(u\right)$, as $u\to 0^{+}.$ Therefore, by (A14),

$$\begin{array}{ccc}\hfill C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)& \sim & C\left(1-\theta u^{1/\alpha },1-\theta u^{1/\alpha }\right)\hfill \\ & \sim & 1-2\theta u^{1/\alpha }+{\left(\theta u^{1/\alpha }\right)}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left(\theta u^{1/\alpha }\right)=1-k_{G_L}\left(u\right),\hfill \\ \hfill C\left(Q_L^{-1}(1-u),Q_L^{-1}(1-u)\right)& \sim & C\left(1-{(u/\theta )}^{\alpha },1-{(u/\theta )}^{\alpha }\right)\hfill \\ & \sim & 1-2{(u/\theta )}^{\alpha }+{(u/\theta )}^{\alpha }{)}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left({(u/\theta )}^{\alpha }\right)=1-k_{Q_L}\left(u\right),\hfill \\ \hfill C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)& \sim & C\left(1-\theta u/\alpha ,1-\theta u/\alpha \right)\hfill \\ & \sim & 1-2\theta u/\alpha +{(\theta u/\alpha )}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }(\theta u/\alpha )=1-k_{G_P}\left(u\right),\hfill \\ \hfill C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right)& \sim & C\left(1-\alpha u/\theta ,1-\alpha u/\theta \right)\hfill \\ & \sim & 1-2\alpha u/\theta +{(\alpha u/\theta )}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }(\alpha u/\theta )=1-k_{Q_P}\left(u\right).\hfill \end{array}$$

(A15)

Note that the remainder terms $k_{G_L}\left(u\right),k_{Q_L}\left(u\right),k_{G_P}\left(u\right),$ and $k_{Q_P}\left(u\right)$ go to 0 as $u\to 0^{+}.$

For UL-distorted copulas, by (A14) and then (A7), $G_L\left(C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)\right)$ is given by

$$\begin{array}{c}1-{\left[{\displaystyle \frac{1-C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)}{1-C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)+\theta C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)}}\right]}^{\alpha }\hfill \\ \sim 1-{\left[{\displaystyle \frac{k_{G_L}\left(u\right)}{\theta +(1-\theta )k_{G_L}\left(u\right)}}\right]}^{\alpha }\sim 1-{\left[k_{G_L}\left(u\right)/\theta \right]}^{\alpha }.\hfill \end{array}$$

(A16)

Therefore, by (A4), for $0<\alpha \le 1,$ and ${\kappa }_U\ge 1,$ as $u\to 0^{+},$

$$\begin{array}{c}\widehat{G_L}\left(C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)\right)=2u-1+G_L\left(C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)\right)\hfill \\ \sim 2u-{\left[k_{G_L}\left(u\right)/\theta \right]}^{\alpha }=2u-{[2u^{1/\alpha }-{\theta }^{{\kappa }_U-1}{u}^{{\kappa }_U/\alpha }{\mathrm{𝓁}}_{\ast }\left(\theta u^{1/\alpha }\right)]}^{\alpha }\hfill \\ \sim u\left\{2-2^{\alpha }{[1-2^{-1}{\theta }^{{\kappa }_U-1}{u}^{({\kappa }_U-1)/\alpha }{\mathrm{𝓁}}_{\ast }\left(\theta u^{1/\alpha }\right)]}^{\alpha }\right\}\hfill \\ \sim u\left\{2-2^{\alpha }[1-\alpha 2^{-1}{\theta }^{{\kappa }_U-1}{u}^{({\kappa }_U-1)/\alpha }{\mathrm{𝓁}}_{\ast }\left(\theta u^{1/\alpha }\right)]\right\}\hfill \\ \sim {\theta }^{{\kappa }_U-1}{u}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left(\theta u\right)\mathrm{if}\alpha =1.\hfill \end{array}$$

(A17)

For QUL-distorted copulas, by (A15), $Q_L\left(C\left(Q_L^{-1}(1-u),Q_L^{-1}(1-u)\right)\right)$ is given by

$$\begin{array}{c}{\displaystyle \frac{{\left[1-C\left(Q_L^{-1}(1-u),Q_L^{-1}(1-u)\right)\right]}^{-1/\alpha }-1}{\theta +{\left[1-C\left(Q_L^{-1}(1-u),Q_L^{-1}(1-u)\right)\right]}^{-1/\alpha }-1}}={\displaystyle \frac{[k_{Q_L}{\left(u\right)]}^{-1/\alpha }-1}{\theta +{\left[k_{Q_L}\left(u\right)\right]}^{-1/\alpha }-1}}\hfill \\ =1-{\displaystyle \frac{\theta [k_{Q_L}{\left(u\right)]}^{1/\alpha }}{\theta {\left[k_{Q_L}\left(u\right)\right]}^{1/\alpha }+1-{\left[k_{Q_L}\left(u\right)\right]}^{1/\alpha }}}\sim 1-\theta [k_{Q_L}{\left(u\right)]}^{1/\alpha }.\hfill \end{array}$$

Therefore, for $\alpha \ge 1,$ and ${\kappa }_U\ge 1,$ as $u\to 0^{+},$

$$\begin{array}{c}\widehat{Q_L}\left(C\left(G_L^{-1}(1-u),G_L^{-1}(1-u)\right)\right)=2u-1+Q_L\left(C\left(Q_L^{-1}(1-u),Q_L^{-1}(1-u)\right)\right)\hfill \\ \sim 2u-\theta [k_{Q_L}{\left(u\right)]}^{1/\alpha }=2u-\theta {\left[2{(u/\theta )}^{\alpha }-{(u/\theta )}^{\alpha }{)}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }\left({(u/\theta )}^{\alpha }\right)\right]}^{1/\alpha }\hfill \\ =2u-2^{1/\alpha }u{\left[1-2^{-1}{(u/\theta )}^{\alpha ({\kappa }_U-1)}{\mathrm{𝓁}}_{\ast }\left({(u/\theta )}^{\alpha }\right)\right]}^{1/\alpha }\hfill \\ \sim u\left\{2-2^{1/\alpha }\left[1-2^{-1}{\alpha }^{-1}{(u/\theta )}^{\alpha ({\kappa }_U-1)}{\mathrm{𝓁}}_{\ast }\left({(u/\theta )}^{\alpha }\right)\right]\right\}\hfill \\ \sim {(u/\theta )}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }(u/\theta )\mathrm{if}\alpha =1.\hfill \end{array}$$

(A18)

For UIP-distorted copulas, by (A7) and (A15), $G_P\left(C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)\right)$ is given by

$$\begin{array}{c}{\left[{\displaystyle \frac{\theta C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)}{1-C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)+\theta C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)}}\right]}^{\alpha }\hfill \\ ={\left[{\displaystyle \frac{\theta [1-k_{G_P}\left(u\right)]}{k_{G_P}\left(u\right)]+\theta [1-k_{G_P}\left(u\right)]}}\right]}^{\alpha }={\left[1-{\displaystyle \frac{k_{G_P}\left(u\right)}{k_{G_P}\left(u\right)]+\theta [1-k_{G_P}\left(u\right)]}}\right]}^{\alpha }\hfill \\ \sim {\left[1-k_{G_P}\left(u\right)/\theta \right]}^{\alpha }\sim 1-\alpha {\theta }^{-1}{k}_{G_P}\left(u\right).\hfill \end{array}$$

Therefore, for $\alpha \ge 1,$ and ${\kappa }_U\ge 1,$ as $u\to 0^{+},$

$$\begin{array}{c}\widehat{G_P}\left(C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)\right)=2u-1+G_P\left(C\left(G_P^{-1}(1-u),G_P^{-1}(1-u)\right)\right)\hfill \\ \sim 2u-\alpha {\theta }^{-1}{k}_{G_P}\left(u\right)=2u-\alpha {\theta }^{-1}[2\theta u/\alpha -{(\theta u/\alpha )}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }(\theta u/\alpha )]\hfill \\ \sim \alpha {\theta }^{-1}{(\theta u/\alpha )}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }(\theta u/\alpha ).\hfill \end{array}$$

(A19)

For QIP-distorted copulas, by (A7) and (A15), $Q_P\left(C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right)\right)$ is given by

$$\begin{array}{c}{\displaystyle \frac{[C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right){]}^{1/\alpha }}{[C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right){]}^{1/\alpha }+\theta \{1-\left[C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right){]}^{1/\alpha }\right\}}}\hfill \\ ={\displaystyle \frac{{[1-k_{Q_P}\left(u\right)]}^{1/\alpha }}{[1-k_{Q_P}{\left(u\right)]}^{1/\alpha }+\theta \{1-\left[1-k_{Q_P}{\left(u\right)]}^{1/\alpha }\right\}}}\hfill \\ ={\displaystyle \frac{1-k_{Q_P}\left(u\right)/\alpha }{1-k_{Q_P}\left(u\right)/\alpha +\theta k_{Q_P}\left(u\right)/\alpha }}={\displaystyle \frac{\alpha -k_{Q_P}\left(u\right)}{\alpha -k_{Q_P}\left(u\right)+\theta k_{Q_P}\left(u\right)}}\hfill \\ =1-{\displaystyle \frac{\theta k_{Q_P}\left(u\right)}{\alpha -k_{Q_P}\left(u\right)+\theta k_{Q_P}\left(u\right)}}\sim 1-\theta k_{Q_P}\left(u\right)/\alpha .\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\widehat{Q_P}\left(C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right)\right)=2u-1+Q_P\left(C\left(Q_P^{-1}(1-u),Q_P^{-1}(1-u)\right)\right)\hfill \\ \sim 2u-\theta k_{Q_P}\left(u\right)/\alpha =2u-\theta {\alpha }^{-1}[2\alpha u/\theta -{(\alpha u/\theta )}^{{\kappa }_U}{\mathrm{𝓁}}_{\ast }(\alpha u/\theta )]\hfill \\ \sim u^{{\kappa }_U}{(\alpha /\theta )}^{{\kappa }_U-1}{\mathrm{𝓁}}_{\ast }(\alpha u/\theta ).\hfill \end{array}$$

(A20)

By applying similar arguments as in (A12), we can show that ${\mathrm{𝓁}}_{\ast }$ in (A17)–(A20) are slowly varying.