Dynamic Analysis of Neuron Models
Abstract
1. Introduction
2. Materials and Methods
2.1. The Generalized Model
2.2. The Simplified Models
3. Results
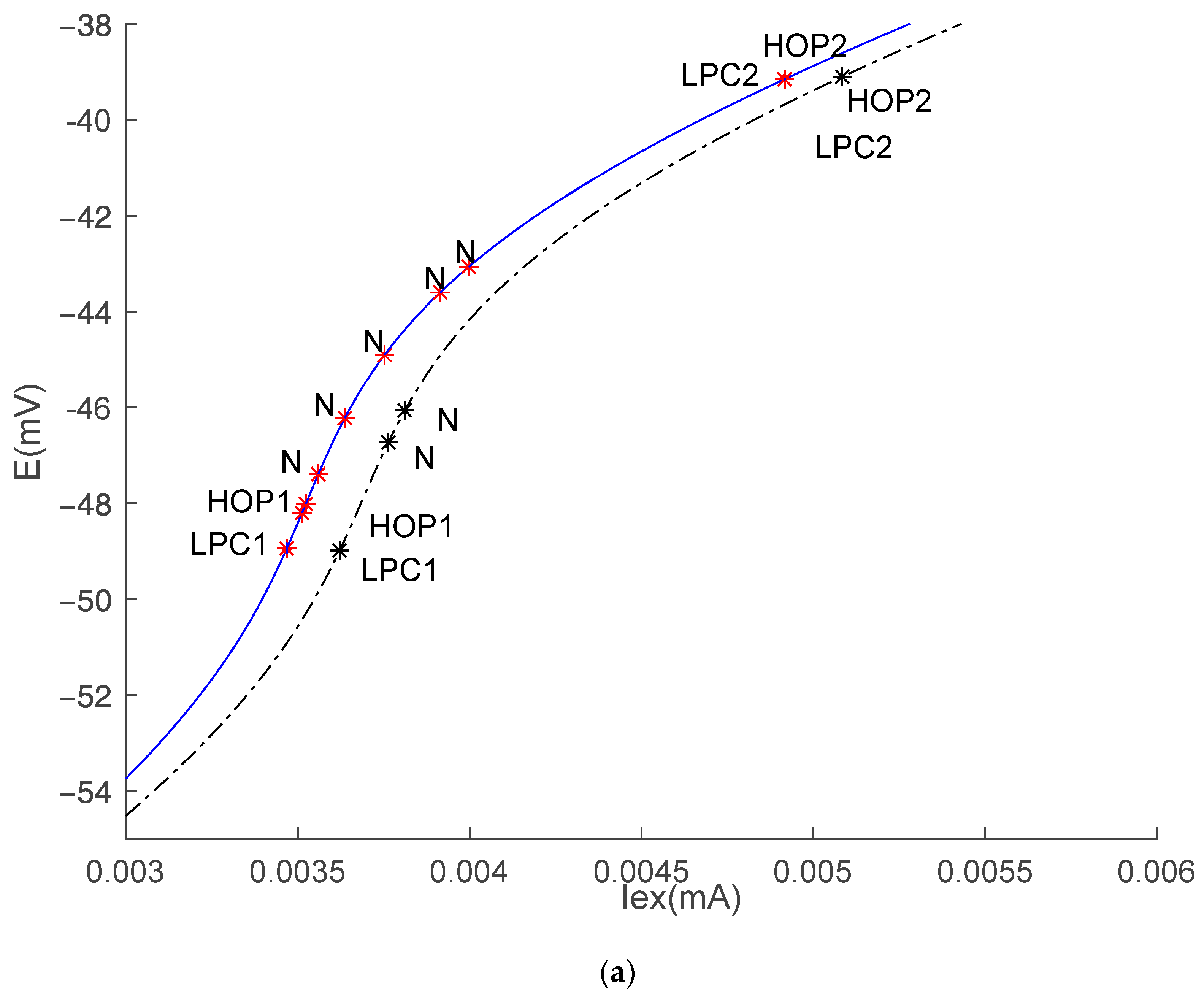
3.1. Equilibrium Point and Stability Analysis of HH Models
3.2. Equilibrium Point and Stability Analysis of the GHK Model
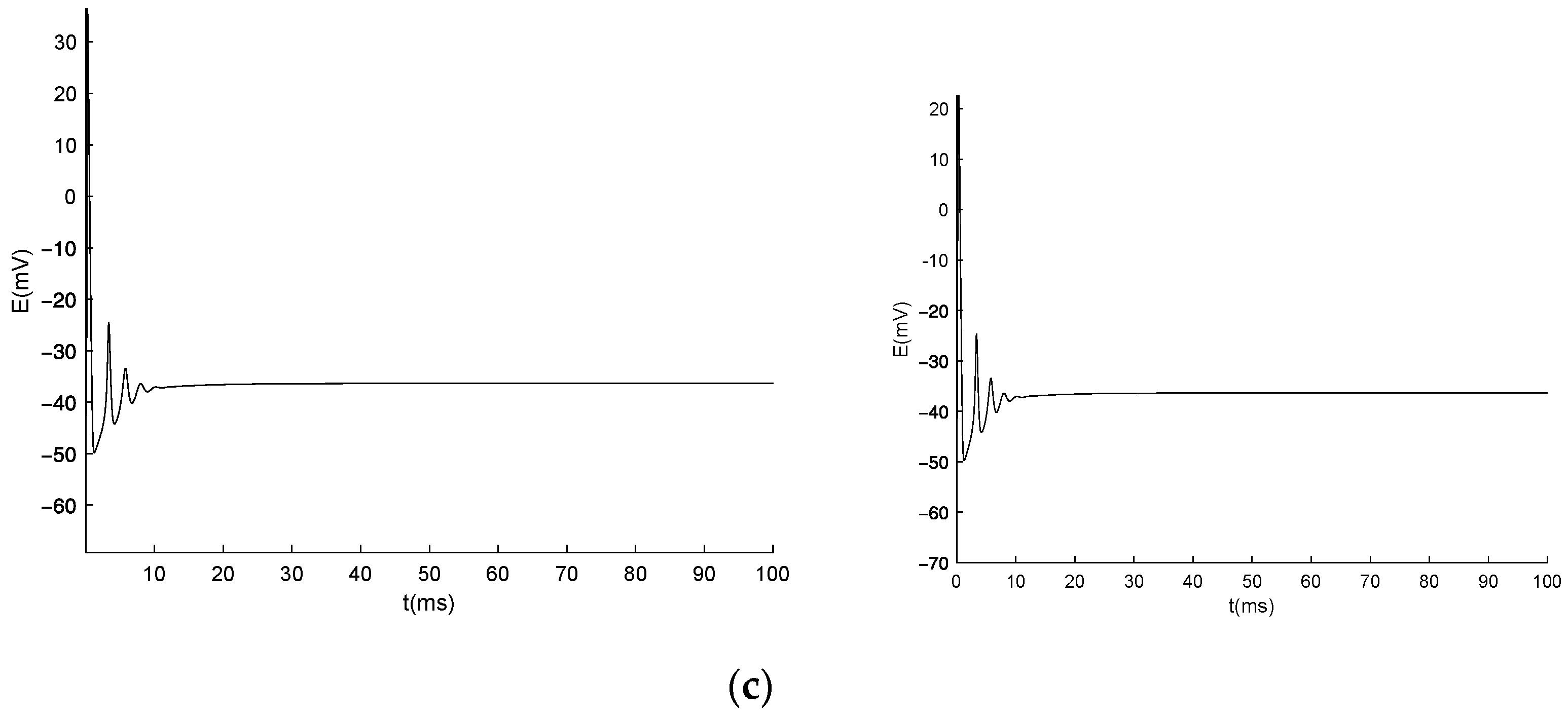
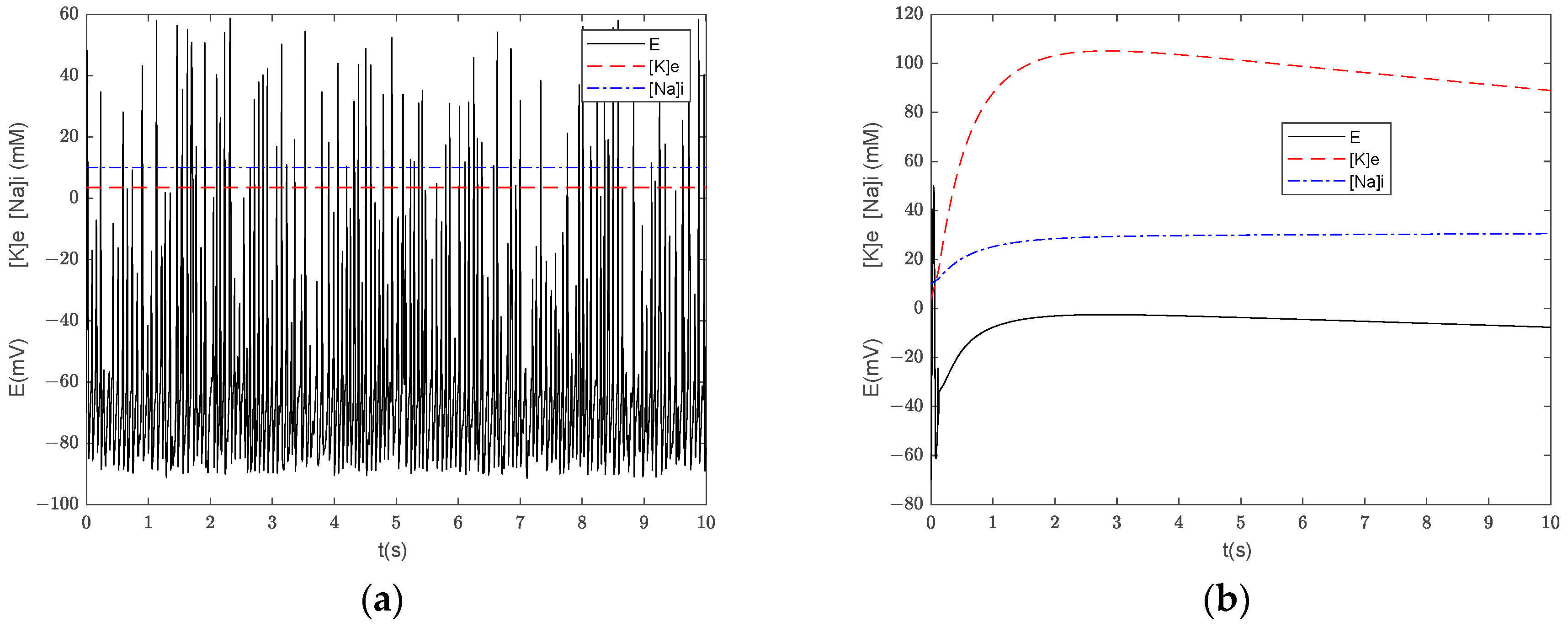
3.3. Numerical Simulation of the Generalized Model
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.; Xin, X.; Rinzel, J. Bistability at the onset of neuronal oscillations. Biol. Cybern. 2023, 117, 61–79. [Google Scholar] [CrossRef]
- Noble, D. How the Hodgkin cycle became the principle of biological relativity. J. Physiol. 2022, 600, 5171–5177. [Google Scholar] [CrossRef]
- FitzHugh, R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Morris, C.; Lecar, H. Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 1981, 35, 193–213. [Google Scholar] [CrossRef]
- Hindmarsh, J.L.; Rose, R.M. A model of the nerve impulse using two first-order differential equations. Nature 1982, 296, 162–164. [Google Scholar] [CrossRef]
- González-Zapata, A.M.; Tlelo-Cuautle, E.; Cruz-Vega, I.; León-Salas, W.D. Synchronization of chaotic artificial neurons and its application to secure image transmission under MQTT for IoT protocol. Nonlinear Dyn. 2021, 104, 4581–4600. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Neural excitability, spiking and bursting. Int. J. Bifurc. Chaos 2000, 6, 1171–1266. [Google Scholar] [CrossRef]
- Tóth, K.; Okun, M. Seventy years later: The legacy of the Hodgkin and Huxley model in computational neuroscience. J. Physiol. 2023, 601, 3009–3010. [Google Scholar] [CrossRef]
- Cooley, J.; Dodge, F.; Cohen, H. Digital computer solutions for excitable membrane models. J. Cell Comp. Physiol. 1965, 66, 99–109. [Google Scholar] [CrossRef]
- Rinzel, J. Repetitive activity in nerve. Fed. Proc. 1978, 37, 2793–2802. [Google Scholar]
- Aihara, K.; Matsumoto, G. Two stable steady states in the Hodgkin-Huxley axons. Biophys. J. 1983, 41, 87–89. [Google Scholar] [CrossRef]
- Rabinovich, M.I.; Varona, P.; Selverston, A.I.; Abarbanel, H.D.I. Dynamical principles in neuroscience. Rev. Mod. Phys. 2006, 78, 1213–1265. [Google Scholar] [CrossRef]
- Che, Y.; Wang, J.; Deng, B.; Wei, X.; Han, C. Bifurcations in the Hodgkin–Huxley model exposed to DC electric fields. Neurocomputing 2012, 81, 41–48. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Labouriau, J.S. Bifurcation of the Hodgkin and Huxley equations: A new twist. Bull. Math. Biol. 1993, 55, 937–952. [Google Scholar] [CrossRef]
- Fukai, H.; Nomura, T.; Doi, S.; Sato, S. Hopf bifurcations in multiple-parameter space of the Hodgkin-Huxley equations II. Singularity theoretic approach and highly degenerate bifurcations. Biol. Cybern. 2000, 82, 223–229. [Google Scholar] [CrossRef]
- Fukai, H.; Doi, S.; Nomura, T.; Sato, S. Hopf bifurcations in multiple-parameter space of the Hodgkin-Huxley equations I. Global organization of bistable periodic solutions. Biol. Cybern. 2000, 82, 215–222. [Google Scholar] [CrossRef]
- Yao, W.; Li, Y.; Ou, Z.; Sun, M.; Ma, Q.; Ding, G. Dynamic analysis of neural signal based on Hodgkin–Huxley model. Math. Methods Appl. Sci. 2022, 46, 4676–4687. [Google Scholar] [CrossRef]
- James Keener, J.S. Mathematical Physiology, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Yao, W.; Huang, H.; Miura, R.M. A Continuum Neuronal Model for the Instigation and Propagation of Cortical Spreading Depression. Bull. Math. Biol. 2011, 73, 2773–2790. [Google Scholar] [CrossRef][Green Version]
- Ma, Q.X.; Arneodo, A.; Ding, G.H.; Argoul, F. Dynamical study of Nav channel excitability under mechanical stress. Biol. Cybern. 2017, 111, 129–148. [Google Scholar] [CrossRef]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A. MATCONT: A Matlab Package for Numerical Bifurcation Analysis of ODEs. ACM Trans. Math. Softw. (TOMS) 2003, 29, 141–164. [Google Scholar] [CrossRef]
- Rinzel, J.; Huguet, G. Nonlinear Dynamics of Neuronal Excitability, Oscillations, and Coincidence Detection. Commun. Pure Appl. Math. 2013, 66, 1464–1494. [Google Scholar] [CrossRef] [PubMed]
- Kager, H.; Wadman, W.J.; Somjen, G.G. Simulated Seizures and Spreading Depression in a Neuron Model Incorporating Interstitial Space and Ion Concentrations. J. Neurophysiol. 2000, 84, 495–512. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.; Somjen, G.G. Na and K Concentrations, Extra- and Intracellular Voltages, and the Effect of TTX in Hypoxic Rat Hippocampal Slices. J. Neurophysiol. 2000, 83, 735–745. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Li, Y.; Yao, W. A Dynamic Model of Cytosolic Calcium Concentration Oscillations in Mast Cells. Mathematics 2021, 9, 2322. [Google Scholar] [CrossRef]
- Yao, W.; Huang, H.; Miura, R.M. Role of Astrocyte in Cortical Spreading Depression: A Quantitative Model of Neuron-Astrocyte Network. Commun. Comput. Phys. 2018, 23, 440–458. [Google Scholar] [CrossRef]
- Strous, L.; von Solms, S.; Zúquete, A. Security and privacy of the Internet of Things. Comput. Secur. 2021, 102, 102148. [Google Scholar] [CrossRef]
- Gonzalez-Zapata, A.M.; de la Fraga, L.G.; Ovilla-Martinez, B.; Tlelo-Cuautle, E.; Cruz-Vega, I. Enhanced FPGA implementation of Echo State Networks for chaotic time series prediction. Integration 2023, 92, 48–57. [Google Scholar] [CrossRef]





| Parameter/Unit | Value |
|---|---|
| Cm/F cm−2 | |
| gNa,T/S cm−2 | |
| gK,DR/S cm−2 | |
| gLeak/S cm−2 | |
| gNa,P/S cm−2 | |
| gK,A/S cm−2 | |
| [K]e/mM | 3.5 |
| [K]i/mM | 133.5 |
| [Na]e/mM | 10 |
| [Na]i/mM | 140 |
| αm,T | |
| βm,T | |
| αh,T | |
| βh,T | |
| αn,DR | |
| βn,DR | |
| αm,P | |
| βm,P | |
| αh,P | |
| βh,P | |
| αm,A | |
| βm.A | |
| αh,A | |
| βh,A | |
| Imax/mA cm−2 | 0.013 |
| S/cm2 | |
| Vi/cm3 |
| Model | Current Channel | Current Equation | Ion Concentration Change | Na-K Pump |
|---|---|---|---|---|
| HH1 | , , | Nernst equation | No | No |
| HH2 | All | Nernst equation | No | No |
| GHK | All | GHK formula | No | No |
| Generalized model without the Na-K pump | All | GHK formula | Yes | No |
| Generalized model | All | GHK formula | Yes | Yes |
| − | Model | Iex (mA) | E (mV) | First Lyapunov Coefficient |
|---|---|---|---|---|
| Hop1 | HH1 | 0.0036215335 | −48.99 | 0.293 |
| HH2 | 0.0036107258 | −48.98 | 0.275 | |
| Hop2 | HH1 | 0.0050838178 | −39.10 | −0.056 |
| HH2 | 0.0050715831 | −39.11 | −0.056 | |
| Neutral Saddle Equilibrium 1 | HH1 | 0.0037633645 | −46.73 | |
| 0.0038111984 | −46.06 | |||
| HH2 | 0.0036760695 | −47.93 | ||
| 0.00373672154 | −46.96 | |||
| 0.0038167752 | −45.85 | |||
| 0.004026353 | −43.88 | |||
| 0.0041198005 | −43.24 | |||
| LPC1 | HH1 | 0.0036189598 | 0.0036194737 | 0.0036174701 |
| HH2 | 0.0036087739 | |||
| LPC2 | HH1 | 0.0050838182 | ||
| HH2 | 0.0050715845 | |||
| PD | HH1 | 0.0036189602 | ||
| HH2 | 0.003608894 |
| Point Properties | Iex (mA) | E (mV) | First Lyapunov Coefficient |
|---|---|---|---|
| Hop1 | 0.00054 | −64.53 | −2.073 |
| Hop2 | 0.38712 | −34.44 | −0.013 |
| LP | 0.00054 | −64.34 | |
| LPC | 0.38712 | 1.14 | |
| N | 0.00049 | −63.25 | |
| 0.00052 | −63.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ding, G.; Yao, W. Dynamic Analysis of Neuron Models. AppliedMath 2023, 3, 758-770. https://doi.org/10.3390/appliedmath3040041
Wang Y, Ding G, Yao W. Dynamic Analysis of Neuron Models. AppliedMath. 2023; 3(4):758-770. https://doi.org/10.3390/appliedmath3040041
Chicago/Turabian StyleWang, Yiqiao, Guanghong Ding, and Wei Yao. 2023. "Dynamic Analysis of Neuron Models" AppliedMath 3, no. 4: 758-770. https://doi.org/10.3390/appliedmath3040041
APA StyleWang, Y., Ding, G., & Yao, W. (2023). Dynamic Analysis of Neuron Models. AppliedMath, 3(4), 758-770. https://doi.org/10.3390/appliedmath3040041







