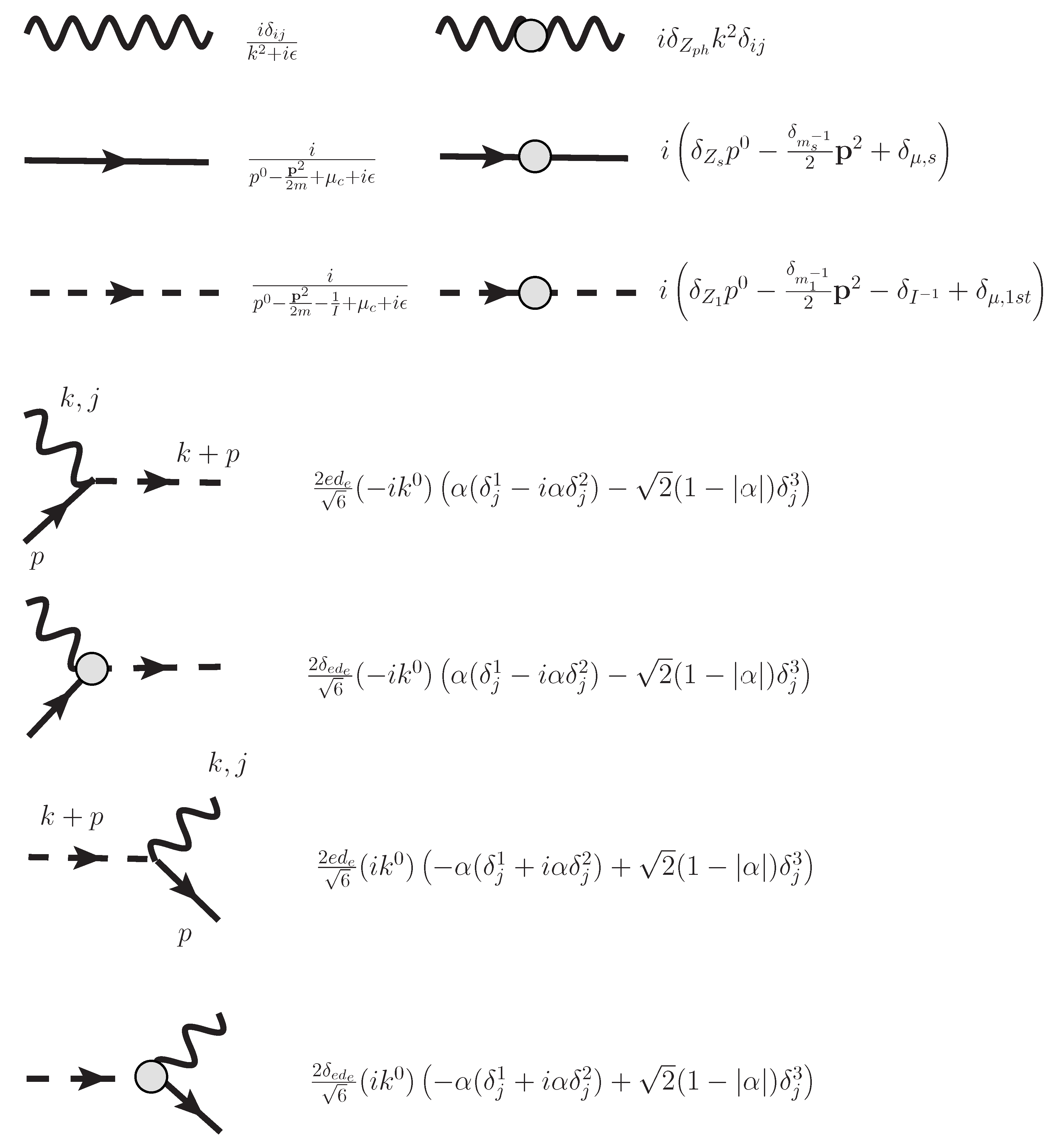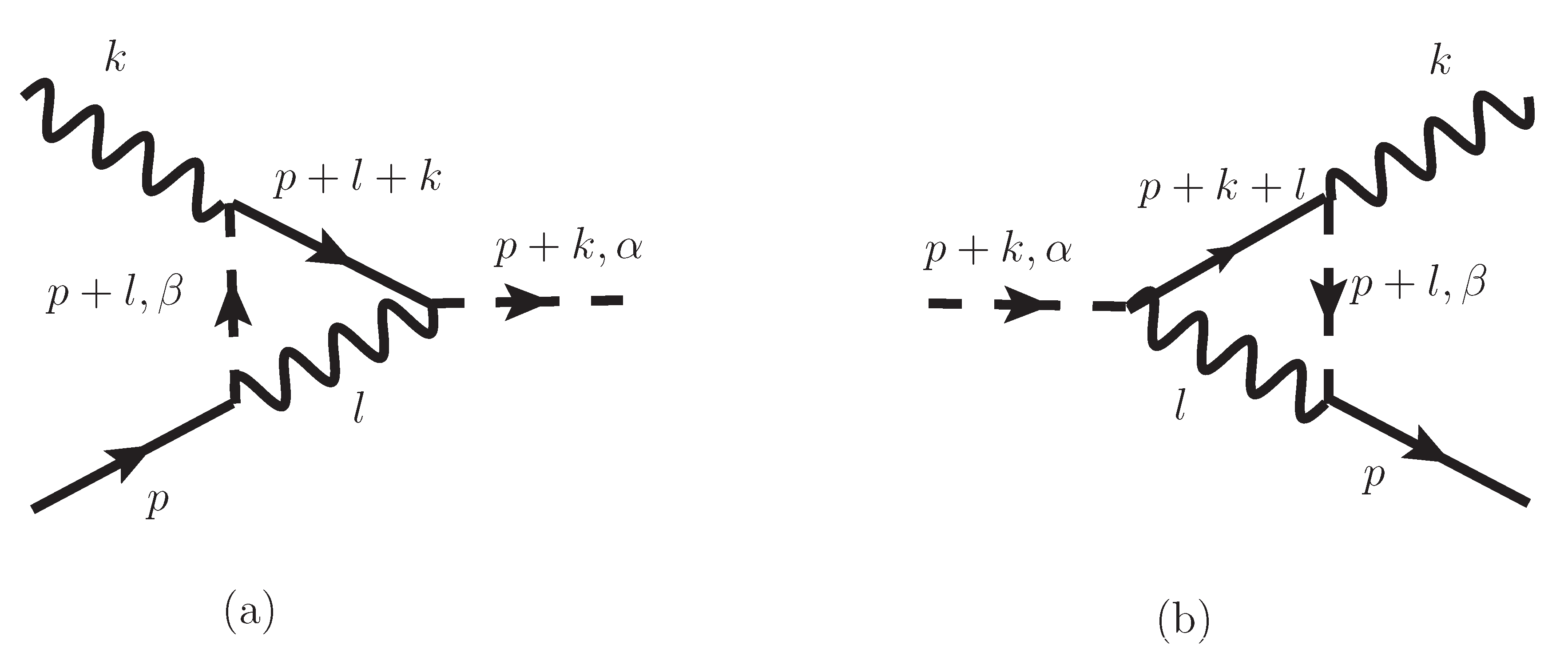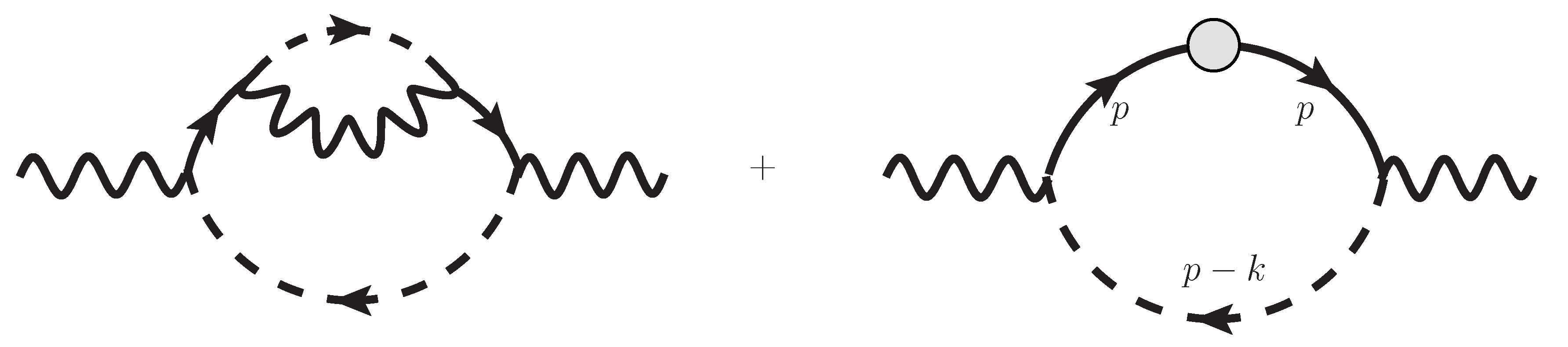Renormalization in Quantum Brain Dynamics

Abstract

We show renormalization in Quantum Brain Dynamics (QBD) in $3+1$ dimensions, namely Quantum Electrodynamics with water rotational dipole fields. First, we introduce the Lagrangian density for QBD involving terms of water rotational dipole fields, photon fields and their interactions. Next, we show Feynman diagrams with 1-loop self-energy and vertex function in dipole coupling expansion in QBD. The counter-terms are derived from the coupling expansion of the water dipole moment. Our approach will be applied to numerical simulations of Kadanoff–Baym equations for water dipoles and photons to describe the breakdown of the rotational symmetry of dipoles, namely memory formation processes. It will also be extended to the renormalization group method for QBD with running parameters in multi-scales.

1. Introduction

The human brain is one of the most complex and poorly understood biological structures studied by science. This is especially true regarding the molecular mechanisms of how the human brain works, especially its information processing and memory encoding functions. While much is known about the architecture of brain cells and their individual activities in terms of the action potential, ion channels and ionic currents [1], much less is known about such issues as where our memories are stored or which molecular mechanisms are involved in information processing and higher cognitive functions. Much has been speculated recently about the possibility of at least some cognitive functions requiring the operation at a level of quantum physics or even quantum field theory [2,3]. Experimental determination or even corroboration of such ideas is currently beginning to be achievable in view of the modern experimental methods and instrumentation available to researchers [4].

Electromagnetic (EM) field theories of consciousness propose that consciousness results when a brain produces an electromagnetic field with specific characteristics. Pockett [5] and McFadden [6] have proposed EM field theories; Some electromagnetic theories are also quantum mind theories of consciousness; examples include the Quantum Brain Dynamics (QBD) approaches of Jibu and Yasue [7] and Vitiello [8], who proposed a quantum field theory explanation of how memory is created. In general, quantum mind theories other than these QBD approaches do not treat consciousness as an electromagnetic phenomenon. The basis for McFadden and Pockett’s CEMI theory is the neuron’s firing, which generates an action potential that is then the trigger for a postsynaptic potential in the neighboring neuron. Moreover, this ionic current also perturbs the surrounding electromagnetic field. McFadden has proposed that the brain’s electromagnetic field represents an information-rich signal in the neurons. This hypothesis is supported by demonstrated effects of weak EM fields on the activity of the human brain, e.g., in well-documented reports on the so-called photobiomodulation [9,10]. McFadden has proposed that the digital information processed by neurons is integrated to create a conscious electromagnetic information (CEMI) field in the brain. Moreover, experiments performed by Christof Koch and his team demonstrated that external EM fields simulate the brain’s endogenous EM fields and influence neuronal firing patterns [11].

Following on from the seminal work of Stuart, Umezawa and Takahashi [12], the present authors have recently provided fundamental results for the realistic development of a quantum field theory of the dynamics of the brain that include hierarchical organization of the neurons, the microscopic intraneuronal structure, including the cytoskeleton and ordered water, as well as nonlinear dynamics [13,14,15]. The methodology adopted includes an open system, non-equilibrium and nonlinear approach to the field theoretic description that is seen as the most simplified adequate representation of Quantum Brain Dynamics. We have shown in this work how decoherence can be properly described within this framework and hence how to minimize it, which is a major issue in applying quantum concepts to the functioning of the brain. Although there are objections to the methodology adopting quantum coherence in brain dynamics represented by [16], we find quantum effects in magneto-reception, olfaction and photosynthesis in the context of quantum biology [17]. Moreover, a recent experimental result suggests that our brain adopts quantum entanglement by studying zero quantum coherence [18]. Considering recent experimental suggestions, it might be rash to exclude quantum effects in brain dynamics.

Quantum Brain Dynamics (QBD) represents one of the hypotheses expected to describe memory in the brain [19,20,21]. It originated with the monumental work by Ricciardi and Umezawa in 1967 [22]. They adopted vacua emerging in spontaneous symmetry breaking in quantum field theory (QFT) to describe memory. It was further developed by Stuart et al. at the end of the 1970s [12,23], where non-local memory storage and recall processes in the Takahashi model are described. Memory is vacua maintained by stability due to long-range correlation of massless Nambu–Goldstone (NG) bosons emerging in spontaneous symmetry breaking. The finite number of excitations of NG bosons represents memory recalling in the approach. In 1968, Fröhlich indicated that the physical coherence with long-range correlation might emerge in biological systems involving the boson condensation, where physical systems behave as a single entity, called the Fröhlich condensate [24,25]. In 1976, Davydov and Kislukha suggested a physical model for solitary waves propagating along protein $\alpha$-helical structures, called the Davydov soliton [26]. The Fröhlich condensate and the Davydov soliton appear as static and dynamical properties in the nonlinear Schrödinger equation involving an equivalent Hamiltonian [27]. In the 1980s, Del Giudice et al. studied quantum theory for biological systems [28,29,30,31]. Especially, the QFT for water-rotational fields and photon fields describe laser-like phenomena in water–photon systems [30]. In the 1990s, Jibu and Yasue provided concrete degrees of freedom in QBD, namely water electric dipole fields and photon fields. [32,33] In 1994, Jibu et al. suggested super-radiance phenomena induced by microtubules (spontaneous cooperative coherent photon emission) [34], which might induce holographic memory storage suggested by Pribram [14,35,36]. In 1997, Jibu suggested quantum tunneling of photons among coherent domains represented by Josephson phenomena to achieve information transfer in a brain [37]. In 1995, Vitiello proposed squeezed coherent states involving NG bosons in a dissipative model of QBD regarding a brain as an open system [8]. The heterogeneity of memories can be represented by diverse unitarily inequivalent squeezed coherent states emerging due to infinite degrees of freedom in QFT.

Experimentally, Zheng and Pollack discovered the Exclusion Zone (EZ) water around hydrophilic surfaces, which excludes solutes [38]. Del Giudice et al. suggested that the properties of EZ water resemble those in coherent water suggested in QFT [39]. Furthermore, it is experimentally suggested that the Near-Infrared spectra of liquid water indicate the existence of a coherent water state [40]. The fractality of water systems is then found to emerge as scale-free phenomena significant in the auto-organization of complex systems, such as ecosystems, neuron net and cellular metabolism. In a cortical system, neuronal avalanches indicate power-law behaviors and emerge as a scale-free phenomenon [41]. Moreover, magnetoencephalographic data suggest that fractal-like brain functional networks emerge [42]. Thus the analysis of fractal-like phenomena in a brain has been a prospective approach.

Fractals are isomorphic to squeezed coherent states, as suggested by Vitiello [43,44]. Self-similarity patterns in fractals represent scale-free phenomena in physical systems. Scale-free properties emerge as fixed points in the Renormalization Group (RG). The RG method was argued by Stüeckelberg and Petermann [45] and by Gell-Mann and Low [46] and applied to statistical physics by Wilson and Kogut [47]. In calculating quantum corrections in QFT, we encounter ultra-violet (UV) divergences. The divergences are renormalized by a finite number of counter-terms in each QFT model if the model is a renormalizable theory. In renormalization, we then encounter the arbitrariness of finite parts in counter-terms in renormalization prescription. To achieve the invariance of theory under renormalization prescription, physical parameters such as mass and coupling can evolve in changing physical scales as coarse graining procedures, which are described by RG equations [47,48,49]. In RG, the contributions in smaller scales are renormalized into parameters such as mass and coupling as coarse graining procedures, and we then encounter an effective theory in macroscopic scales (from microscopic scales) adopted to describe multi-scale brain functions in the beginning with the QBD Lagrangian and provide diversity in the effective theory for multi-scales in QBD. To derive RG equations for parameters, we need to analyze ultra-violet (UV) divergences appearing in self-energy and vertex corrections for cancellation of divergences by counter-terms in each QFT model. We might encounter fixed points where physical parameters become independent of renormalization scales for further coarse graining. The fixed points in RG represent scale-free fractal-like phenomena.

The aim of this paper is to cancel ultra-violet divergences in self-energy and vertex functions by counter-terms in the renormalization in QBD in $3+1$ dimensions. We begin with the Lagrangian density in QBD and expand terms involving counter-terms for renormalization. We next calculate self-energy and vertex functions and cancel ultra-violet divergences by counter-terms in renormalizations. We extend our analysis to the 2-Particle-Irreducible (2PI) effective action technique [50,51] in the derivation of Kadanoff–Baym (KB) equations [52,53,54]. Counter-terms will be adopted to achieve the cancellation of UV divergences in lattice simulations for the time-evolution of KB equations in QBD. Properties of divergences will be used in deriving RG equations in future studies, where fixed point solutions might describe the fractality of water–photon systems. Recently, we have shown a super-radiant solution in water–photon systems in $3+1$ dimensions, cooperative spontaneous photon emission [13]. Next, we have proposed the integration of QBD and holography using super-radiance and investigated the time-evolution of holograms [14]. Furthermore, we have provided control theory of coherent fields in the ${\varphi }^4$ model toward manipulating holograms or our subjective experiences [15]. The present work provides renormalization of UV divergences in quantum corrections in an interacting water–photon system, which will open up a new way to describe time-evolving holograms involving incoherent dipoles and photons, provide a control theory of holograms and introduce a RG method for QBD.

Our paper is organized as follows. In Section 2, we introduce the Lagrangian density for QBD with counter-terms. In Section 3, we calculate ultra-violet divergences in self-energy and vertex functions. In Section 4, we extend our approach to 2PI effective action technique. In Section 5, we discuss our results. In Section 6, we provide concluding remarks and perspectives. We adopt the natural unit with the light speed and the Planck constant divided by $2\pi$ set to unity. The metric tensor is set to be $g_{\mu \nu }=\mathrm{diag}(1,-1,-1,-1)$ with space-time subscript $\mu ,\nu =0,1,2,3$ and spatial subscript $i,j,n=1,2,3$.

2. Lagrangian Density

In this section, we introduce the Lagrangian density for Quantum Brain Dynamics in $3+1$ dimensions and show Feynman diagrams for propagators of renormalized fields and counter terms for mass and vertices.

First, we begin with the Lagrangian density for QBD in $3+1$ dimensions based on [13,30]. It is written by,

$$\begin{array}{ccc}\hfill \mathcal{L}& =& -\frac{1}{4}{F}^{\mu \nu }\left[A\left(x\right)\right]F_{\mu \nu }\left[A\left(x\right)\right]-\frac{{\left({\partial }^i{A}_i\right)}^2}{2\xi }+\int d\theta d\phi sin\theta {\mathsf{\Psi }}^{*}(x,\theta ,\phi )\left[i\frac{i\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}-\frac{{\mathbf{l}}^2}{2I}\right]\mathsf{\Psi }(x,\theta ,\phi )\hfill \\ & & +{\mu }_c\int d\theta d\phi sin\theta {\mathsf{\Psi }}^{*}(x,\theta ,\phi )\mathsf{\Psi }(x,\theta ,\phi )\hfill \\ & & +2e{d}_e\mathbf{E}·\int d\theta d\phi sin\theta {\mathsf{\Psi }}^{*}(x,\theta ,\phi )(sin\theta cos\phi ,sin\theta sin\phi ,cos\theta )\mathsf{\Psi }(x,\theta ,\phi ),\hfill \end{array}$$

(1)

with $F^{\mu \nu }={\partial }^{\mu }{A}^{\nu }-{\partial }^{\nu }{A}^{\mu }$ with electric scalar potential $A^0$ and magnetic vector potential $A^i$$(i=1,2,3)$, electric field $E_i=-{\partial }_i{A}_0+{\partial }_0{A}_i$, dipole fields ${\mathsf{\Psi }}^{(*)}(x,\theta ,\phi )$, the gauge fixing parameter $\xi =1$, mass of dipoles m, moment of inertia for dipoles I with $\frac{1}{I}=4\mathrm{meV}$, chemical potential ${\mu }_c$ and dipole moment for a water molecule $2e{d}_e$ with elementary charge e and $d_e=0.2\mathrm{\AA }$. We adopt the temporal axial gauge $A^0=0$. We assume the isotropic moment of inertia I for water dipoles. We adopt the two-energy-level approximation for angular momentum squared ${\mathbf{l}}^2=-\left(\frac{1}{{sin}^2\theta }\frac{{\partial }^2}{\partial {\phi }^2}+\frac{1}{sin\theta }\frac{\partial }{\partial \theta }\left(sin\theta \frac{\partial }{\partial \theta }\right)\right)$ for rotational degrees of freedom of water dipoles. We expand water electric dipole fields by the dipole field for the ground state ${\psi }_s\left(x\right)$ and the dipole fields for the 1st excited states ${\psi }_{\alpha }\left(x\right)$ with $\alpha =0,\pm 1$ as,

$$\begin{array}{ccc}\hfill \mathsf{\Psi }(x,\theta ,\phi )& =& {\psi }_s\left(x\right)Y_{00}(\theta ,\phi )+\sum _{\alpha =0,\pm 1}{\psi }_{\alpha }\left(x\right)Y_{1\alpha }(\theta ,\phi ),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\mathsf{\Psi }}^{*}(x,\theta ,\phi )& =& {\psi }_s^{*}\left(x\right)Y_{00}^{*}(\theta ,\phi )+\sum _{\alpha =0,\pm 1}{\psi }_{\alpha }^{*}\left(x\right)Y_{1\alpha }^{*}(\theta ,\phi ),\hfill \end{array}$$

(3)

using the spherical harmonics for the ground state $Y_{00}(\theta ,\phi )$ corresponding to the eigenvalue ${\mathbf{l}}^2=0$ and the 1st excited states $Y_{1\alpha }(\theta ,\phi )$ with $\alpha =0,\pm 1$ corresponding to eigenvalues ${\mathbf{l}}^2=2$ shown by,

$$\begin{array}{ccc}\hfill Y_{00}(\theta ,\phi )& =& \frac{1}{\sqrt{4\pi }},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill Y_{1\pm 1}(\theta ,\phi )& =& \mp i\sqrt{\frac{3}{8\pi }}sin\theta e^{\pm i\phi },Y_{10}(\theta ,\phi )=i\sqrt{\frac{3}{4\pi }}cos\theta .\hfill \end{array}$$

(5)

The 1st and 2nd terms in Equation (1) are rewritten as,

$$\begin{array}{c}\hfill -\frac{1}{4}{F}^{\mu \nu }\left[A\left(x\right)\right]F_{\mu \nu }\left[A\left(x\right)\right]-\frac{{\left({\partial }^i{A}_i\right)}^2}{2}=\frac{1}{2}\left({\partial }^{\mu }{A}_i\right)\left({\partial }_{\mu }{A}_i\right).\end{array}$$

(6)

The 3rd term in Equation (1) is then written as,

$$\begin{array}{ccc}\hfill \int d\theta d\phi sin\theta {\mathsf{\Psi }}^{*}(x,\theta ,\phi )\left[i\frac{i\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}-\frac{{\mathbf{l}}^2}{2I}\right]\mathsf{\Psi }(x,\theta ,\phi )& =& {\psi }_s^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}\right){\psi }_s\hfill \\ & & +\sum _{\alpha =0,\pm 1}{\psi }_{\alpha }^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}-\frac{1}{I}\right){\psi }_{\alpha }\hfill \end{array}$$

(7)

The 4th term in Equation (1) is written by,

$$\begin{array}{c}\hfill {\mu }_c\int d\theta d\phi sin\theta {\mathsf{\Psi }}^{*}(x,\theta ,\phi )\mathsf{\Psi }(x,\theta ,\phi )={\mu }_c\left({\psi }_s^{*}{\psi }_s+\sum _{\alpha }{\psi }_{\alpha }^{*}{\psi }_{\alpha }\right).\end{array}$$

(8)

The 5th term in Equation (1) with the electric fields $E_i=-F^{0i}$$(i=1,2,3)$ by,

$$\begin{array}{c}\hfill 2e{d}_e{\int }_0^{2\pi }d\phi {\int }_0^{\pi }d\theta sin\theta {\mathsf{\Psi }}^{*}{(sin\theta cos\phi ,sin\theta sin\phi ,cos\theta )}_i\mathsf{\Psi }{E}_i={\mathcal{M}}_i\left(x\right)E_i\left(x\right),\end{array}$$

(9)

with the dipole moment density ${\mathcal{M}}_i$$(i=1,2,3)$ defined as,

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1& =& \frac{2e{d}_{e}i}{\sqrt{6}}\left({\psi }_s^{*}{\psi }_{-1}-{\psi }_s^{*}{\psi }_1+{\psi }_1^{*}{\psi }_s-{\psi }_{-1}^{*}{\psi }_s\right),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\mathcal{M}}_2& =& \frac{2e{d}_e}{\sqrt{6}}\left({\psi }_s^{*}{\psi }_{-1}+{\psi }_s^{*}{\psi }_1+{\psi }_1^{*}{\psi }_s+{\psi }_{-1}^{*}{\psi }_s\right),\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\mathcal{M}}_3& =& \frac{2e{d}_{e}i}{\sqrt{3}}\left({\psi }_s^{*}{\psi }_0-{\psi }_0^{*}{\psi }_s\right).\hfill \end{array}$$

(12)

We can then rewrite as,

$$\begin{array}{ccc}\hfill {\mathcal{M}}_i\left(x\right)E_i\left(x\right)& =& \frac{2e{d}_e}{\sqrt{6}}[(i{E}_1+E_2)({\psi }_s^{*}{\psi }_{-1}+{\psi }_1^{*}{\psi }_s)+(-i{E}_1+E_2)({\psi }_s^{*}{\psi }_1+{\psi }_{-1}^{*}{\psi }_s)\hfill \\ & & +\sqrt{2}i{E}_3({\psi }_s^{*}{\psi }_0-{\psi }_0^{*}{\psi }_s)]\hfill \\ & =& \frac{2e{d}_e}{\sqrt{6}}\sum _{\alpha =0,\pm 1}[\left(-i\alpha \left(E_1+i\alpha E_2\right)+\sqrt{2}i(1-|\alpha \left|\right)E_3\right){\psi }_s^{*}{\psi }_{\alpha }\hfill \\ & & +\left(i\alpha \left(E_1-i\alpha E_2\right)-\sqrt{2}i(1-|\alpha \left|\right)E_3\right){\psi }_{\alpha }^{*}{\psi }_s].\hfill \end{array}$$

(13)

Next, we rewrite the Lagrangian density with several counter terms. Using the bare fields $A_{b,i}=Z_{ph}^{\frac{1}{2}}{A}_i$ with $i=1,2,3$ (with $E_{b,i}=Z_{ph}^{\frac{1}{2}}{E}_i$), ${\psi }_{b,s}^{(*)}=Z_s^{\frac{1}{2}}{\psi }_s^{(*)}$, and ${\psi }_{b,\alpha }^{(*)}=Z_1^{\frac{1}{2}}{\psi }_{\alpha }^{(*)}$ ($\alpha =0,\pm 1$) involving the renormalization coefficient $Z_{ph}$ with respect to wave functions for photons, coefficient $Z_s$ for dipoles in the ground state and coefficient $Z_1$ for dipoles in the 1st excited state, we write the Lagrangian density in QBD by the bare fields as,

$$\begin{array}{ccc}\hfill \mathcal{L}& =& -\frac{1}{4}{F}^{\mu \nu }\left[A_b\right]F_{\mu \nu }\left[A_b\right]-\frac{{\left({\partial }^i{A}_{b,i}\right)}^2}{2}\hfill \\ & & +{\psi }_{b,s}^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m_s}\right){\psi }_{b,s}+\sum _{\alpha =0,\pm 1}{\psi }_{b,\alpha }^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m_1}-\frac{1}{I_0}\right){\psi }_{b,\alpha }\hfill \\ & & +{\mu }_0\left({\psi }_{b,s}^{*}{\psi }_{b,s}+\sum _{\alpha }{\psi }_{b,\alpha }^{*}{\psi }_{b,\alpha }\right)\hfill \\ & & +\frac{2{\left(e{d}_e\right)}_0}{\sqrt{6}}\sum _{\alpha }[\left(-i\alpha \left(E_{b,1}+i\alpha E_{b,2}\right)+\sqrt{2}i\left(1-\left|\alpha \right|\right)E_{b,3}\right){\psi }_{b,s}^{*}{\psi }_{b,\alpha }\hfill \\ & & \left(i\alpha \left(E_{b,1}-i\alpha E_{b,2}\right)-\sqrt{2}i\left(1-\left|\alpha \right|\right)E_{b,3}\right){\psi }_{b,\alpha }^{*}{\psi }_{b,s}],\hfill \end{array}$$

(14)

where we adopt the bare mass $m_s$ and $m_1$, the bare moment of inertia $I_0$, the bare chemical potential ${\mu }_0$ and the bare dipole moment $2{\left(e{d}_e\right)}_0$. The above Lagrangian density is rewritten as,

$$\begin{array}{ccc}\hfill \mathcal{L}& =& -\frac{1}{4}{Z}_{ph}{F}^{\mu \nu }\left[A\right]F_{\mu \nu }\left[A\right]-Z_{ph}\frac{{\left({\partial }^i{A}_i\right)}^2}{2}\hfill \\ & & +Z_s{\psi }_s^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m_s}\right){\psi }_s+Z_1\sum _{\alpha =0,\pm 1}{\psi }_{\alpha }^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m_1}-\frac{1}{I_0}\right){\psi }_{\alpha }\hfill \\ & & +{\mu }_0\left(Z_s{\psi }_s^{*}{\psi }_s+Z_1\sum _{\alpha }{\psi }_{\alpha }^{*}{\psi }_{\alpha }\right)\hfill \\ & & +\frac{2{\left(e{d}_e\right)}_0}{\sqrt{6}}{Z}_{ph}^{\frac{1}{2}}{Z}_s^{\frac{1}{2}}{Z}_1^{\frac{1}{2}}\sum _{\alpha }[\left(-i\alpha \left(E_1+i\alpha E_2\right)+\sqrt{2}i\left(1-\left|\alpha \right|\right)E_3\right){\psi }_s^{*}{\psi }_{\alpha }\hfill \\ & & \left(i\alpha \left(E_1-i\alpha E_2\right)-\sqrt{2}i\left(1-\left|\alpha \right|\right)E_3\right){\psi }_{\alpha }^{*}{\psi }_s].\hfill \end{array}$$

(15)

Next, we introduce the parameters as follows,

$$\begin{array}{ccc}\hfill {\delta }_{Z_{ph}}=Z_{ph}-1,& {\delta }_{Z_s}=Z_s-1,& {\delta }_{Z_1}=Z_1-1,\hfill \\ \hfill {\delta }_{m_s^{-1}}=\frac{Z_s}{m_s}-\frac{1}{m},& {\delta }_{m_1^{-1}}=\frac{Z_1}{m_1}-\frac{1}{m},& {\delta }_{I^{-1}}=\frac{Z_1}{I_0}-\frac{1}{I},\hfill \\ \hfill {\delta }_{\mu ,s}=Z_s{\mu }_0-{\mu }_c,& {\delta }_{\mu ,1st}=Z_1{\mu }_0-{\mu }_c,& {\delta }_{e{d}_e}={\left(e{d}_e\right)}_0{Z}_{ph}^{\frac{1}{2}}{Z}_s^{\frac{1}{2}}{Z}_1^{\frac{1}{2}}-e{d}_e.\hfill \end{array}$$

(16)

Then the Lagrangian density is rewritten as,

$$\begin{array}{ccc}\hfill \mathcal{L}& =& \frac{1}{2}\left({\partial }^{\nu }{A}_i\right)\left({\partial }_{\nu }{A}_i\right)+{\psi }_s^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}+{\mu }_c\right){\psi }_s+\sum _{\alpha =0,\pm 1}{\psi }_{\alpha }^{*}\left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}-\frac{1}{I}+{\mu }_c\right){\psi }_{\alpha }\hfill \\ & & +\frac{2e{d}_e}{\sqrt{6}}\sum _{\alpha =0,\pm 1}[\left(-i\alpha \left(E_1+i\alpha E_2\right)+\sqrt{2}i(1-|\alpha \left|\right)E_3\right){\psi }_s^{*}{\psi }_{\alpha }\hfill \\ & & +\left(i\alpha \left(E_1-i\alpha E_2\right)-\sqrt{2}i(1-|\alpha \left|\right)E_3\right){\psi }_{\alpha }^{*}{\psi }_s]\hfill \\ & & +\frac{1}{2}{\delta }_{Z_{ph}}\left({\partial }^{\nu }{A}_i\right)\left({\partial }_{\nu }{A}_i\right)+{\psi }_s^{*}\left({\delta }_{Z_s}i\frac{\partial }{\partial x^0}+\frac{{\delta }_{m_s^{-1}}{\nabla }_i^2}{2}+{\delta }_{\mu ,s}\right){\psi }_s\hfill \\ & & +\sum _{\alpha }{\psi }_{\alpha }^{*}\left({\delta }_{Z_1}i\frac{\partial }{\partial x^0}+\frac{{\delta }_{m_1^{-1}}{\nabla }_i^2}{2}-{\delta }_{I^{-1}}+{\delta }_{\mu ,1st}\right){\psi }_{\alpha }\hfill \\ & & +\frac{2{\delta }_{e{d}_e}}{\sqrt{6}}\sum _{\alpha =0,\pm 1}[\left(-i\alpha \left(E_1+i\alpha E_2\right)+\sqrt{2}i(1-|\alpha \left|\right)E_3\right){\psi }_s^{*}{\psi }_{\alpha }\hfill \\ & & +\left(i\alpha \left(E_1-i\alpha E_2\right)-\sqrt{2}i(1-|\alpha \left|\right)E_3\right){\psi }_{\alpha }^{*}{\psi }_s].\hfill \end{array}$$

(17)

The 5th, 6th, 7th and 8th terms in the above Lagrangian represent counter-terms.

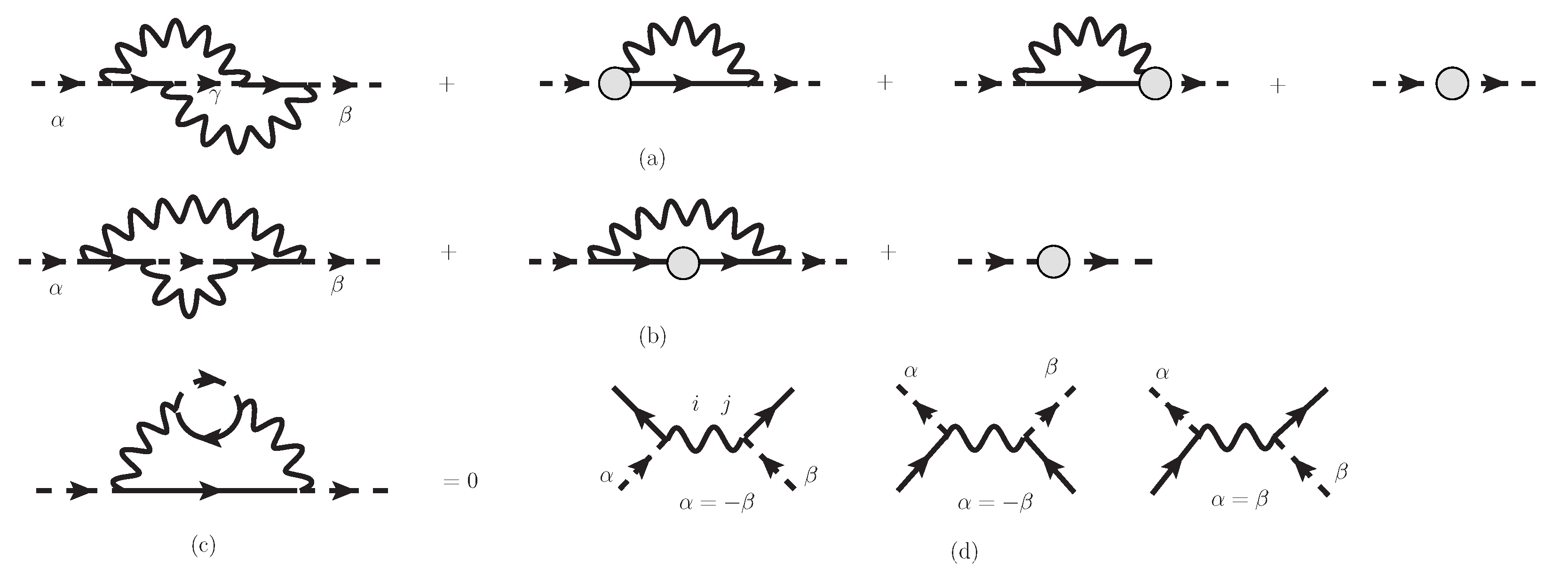
Finally, we show Feynman diagrams for propagators, vertices and counter-terms in Fourier transformation. Using the above Lagrangian density, we show the diagrams in Figure 1. The propagator for photons $D_{ij}\left(k\right)$, the propagator for dipoles in the ground state $G_{ss}\left(p\right)$ and the propagators for dipoles in the 1st excited states $G_{\alpha \alpha }\left(p\right)$ with $\alpha =0,\pm 1$ are written by,

$$\begin{array}{ccc}\hfill D_{ij}\left(k\right)& =& \frac{i{\delta }_{ij}}{k^2+iϵ},\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill G_{ss}\left(p\right)& =& \frac{i}{p^0-\frac{{\mathbf{p}}^{\mathbf{2}}}{2m}+{\mu }_c+iϵ},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill G_{\alpha \alpha }\left(p\right)& =& \frac{i}{p^0-\frac{{\mathbf{p}}^{\mathbf{2}}}{2m}-\frac{1}{I}+{\mu }_c+iϵ},\hfill \end{array}$$

(20)

respectively. The vertices represent,

$$\begin{array}{ccc}\hfill \frac{{\delta }^3{\int }_z\left(i{\mathcal{M}}_i\left(z\right)E_i\left(z\right)\right)}{\delta {\psi }_s\left(u_1\right)\delta {\psi }_{\alpha }^{*}\left(u_2\right)\delta A^j\left(u_3\right)}& =& \frac{2e{d}_e}{\sqrt{6}}{\int }_z\left[\alpha ({\delta }_j^1-i\alpha {\delta }_j^2)-\sqrt{2}(1-|\alpha \left|\right){\delta }_j^3\right]\hfill \\ & & \times \left({\partial }_z^0\delta (z-u_3)\right)\delta (z-u_1)\delta (z-u_2),\hfill \end{array}$$

(21)

with matrix element $\langle \alpha \left|·\right|k,s\rangle$ of ${\int }_z\left(i{\mathcal{M}}_i\left(z\right)E_i\left(z\right)\right)$ (shown in Equation (13)) describing processes of incoming photons with factor $e^{-ik·u_3}$, incoming dipoles in the ground state s with factor $e^{-ip·u_1}$ and outgoing dipoles in 1st excited states $\alpha$ with factor $e^{il·u_2}$ involving integration ${\int }_{u_1,u_2,u_3}$, and

$$\begin{array}{ccc}\hfill \frac{{\delta }^3{\int }_z\left(i{\mathcal{M}}_i\left(z\right)E_i\left(z\right)\right)}{\delta {\psi }_s^{*}\left(w_1\right)\delta {\psi }_{\alpha }\left(w_2\right)\delta A^j\left(w_3\right)}& =& \frac{2e{d}_e}{\sqrt{6}}{\int }_z\left[-\alpha ({\delta }_j^1+i\alpha {\delta }_j^2)+\sqrt{2}(1-|\alpha \left|\right){\delta }_j^3\right]\hfill \\ & & \times \left({\partial }_z^0\delta (z-w_3)\right)\delta (z-w_1)\delta (z-w_2),\hfill \end{array}$$

(22)

with $\langle k,s\left|·\right|\alpha \rangle$ representing processes of outgoing photons with factor $e^{ik·w_3}$, outgoing dipoles in the ground state with factor $e^{ip·w_1}$ and incoming dipoles in the 1st excited states with factor $e^{-il·w_2}$ involving integration ${\int }_{w_1,w_2,w_3}$. We show vertices in Figure 1. Here we find that the vertex with incoming dipoles in 1st excited states involves the factor with $\left(i{k}^0\right)\times ···$ and that the vertex with outgoing dipoles in 1st excited states involves the factor with $(-i{k}^0)\times ···$. Using Figure 1, we perform renormalization of self-energy and vertices in the next section.

3. Renormalization

In this section, we write Feynman diagrams for self-energy and vertices and cancel ultra-violet (UV) divergences by counter-terms. We have referred to [49] for calculations.

3.1. 1-Loop Self-Energy

In this section, we show a 1-loop self-energy for photons and dipoles, and we find that UV divergences are canceled by counter-terms.

First, we shall see the self-energy for photons ${\mathsf{\Pi }}_{ij}\left(k\right)$ in 1-loop order shown in Figure 2.

We find that 1-loop self-energy for photons contains the factor,

$$\begin{array}{ccc}\hfill {\int }_p{G}_{\alpha \alpha }(k+p)G_{ss}\left(p\right)& \sim & \int \frac{d{p}^0}{2\pi }\frac{i}{p^0-\frac{{\mathbf{p}}^{\mathbf{2}}}{2m}+{\mu }_c+iϵ}·\frac{i}{p^0-\frac{{\mathbf{p}}^{\mathbf{2}}}{2m}-\frac{1}{I}+{\mu }_c+iϵ}\hfill \\ & =& {\int }_0^{1}dx\int \frac{d{p}^0}{2\pi }\frac{-1}{{\left[p^0+x{k}^0-\frac{(1-x){\mathbf{p}}^2}{2m}-\frac{x{\left(\mathbf{p}+\mathbf{k}\right)}^2}{2m}-\frac{x}{I}+{\mu }_c+iϵ\right]}^2}\hfill \\ & =& 0,\hfill \end{array}$$

(23)

with ${\int }_p=\int \frac{d^{4}p}{{\left(2\pi \right)}^4}$, since the 1st derivative of residue $-1$ by $p^0$ is zero. Here we have used the Feynman’s formula,

$$\begin{array}{c}\hfill \frac{1}{AB}={\int }_0^{1}dx\frac{1}{{\left[xA+(1-x)B\right]}^2}.\end{array}$$

(24)

Similarly, we also find the relation,

$$\begin{array}{c}\hfill {\int }_p{G}_{ss}(k+p)G_{\alpha \alpha }\left(p\right)=0.\end{array}$$

(25)

As a result, the self-energy for photons in 1-loop order is zero. We then find ${\delta }_{Z_{ph}}=0$ or $Z_{ph}=1$ in 1-loop order.

Next, we shall see self-energy for dipoles in 1st excited states, as shown in Figure 3. Using the Feynman rules in Figure 1, the self-energy ${\mathsf{\Sigma }}_{\alpha \alpha }$ with $\alpha =0,\pm 1$ can be written by,

$$\begin{array}{ccc}\hfill {\mathsf{\Sigma }}_{\alpha \alpha }\left(p\right)& =& -\frac{4}{3}{\left(e{d}_e\right)}^2{\int }_k{\left(k^0\right)}^2\frac{i}{p^0-k^0-\frac{{\left(\mathbf{p}-\mathbf{k}\right)}^2}{2m}+{\mu }_c+iϵ}·\frac{i}{k^2+iϵ}.\hfill \end{array}$$

(26)

The detailed calculations are shown in Appendix A. The result is given by,

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{\alpha \alpha }\left(p\right)=-\frac{4i}{3}{\left(e{d}_e\right)}^2{\int }_0^{1}dx{\int }_{l_E}\frac{\left[\mathrm{numerator}1\right]}{{(l_E^2+x^2{m}^2)}^2},\end{array}$$

(27)

where the subscript E represents the Euclidean 4-dimensional momenta, and [numerator 1] represents,

$$\begin{array}{ccc}\hfill \left[\mathrm{numerator}1\right]& =& {\left(l_E^0\right)}^2\left[|{\mathbf{l}}_E|+(1-3x)\left(m+p^0+{\mu }_c\right)+\frac{{(1-x)}^2{\mathbf{p}}^2+m^2}{2|{\mathbf{l}}_E|}-\frac{{(1-x)}^2{\mathbf{p}}^2}{6|{\mathbf{l}}_E|}\right]\hfill \\ & & -x^2\left|{\mathbf{l}}_E\right|m\left(m+2\left(p^0+{\mu }_c\right)\right)-x^2(1-x)m^2\left(m+3\left(p^0+{\mu }_c\right)\right)\hfill \\ & & +\frac{4mx(1-x)}{l_E^2+x^2{m}^2}\left((1-3x){\left(l_E^0\right)}^{2}m+{\left(l_E^0\right)}^2\left|{\mathbf{l}}_E\right|\right)\left(p^0+{\mu }_c-\frac{{\mathbf{p}}^2}{2m}\right).\hfill \end{array}$$

(28)

We find ${\mathsf{\Sigma }}_{\alpha \alpha }\left(p\right)$ involves cubic, quadratic, linear and logarithmic divergences in Equation (27); for example, the term ${\left(l_E^0\right)}^2\left|{\mathbf{l}}_E\right|$ in [numerator 1] in Equation (28) induces cubic divergence. They are canceled by counter-terms in Figure 1 and Figure 3. We then find the relation,

$$\begin{array}{c}\hfill {\delta }_{Z_1}{p}^0-\frac{{\delta }_{m_1^{-1}}{\mathbf{p}}^2}{2}-{\delta }_{I^{-1}}+{\delta }_{\mu ,1st}=\frac{4}{3}{\left(e{d}_e\right)}^2{\int }_0^{1}dx{\int }_{l_E}\frac{\left[\mathrm{numerator}1\right]}{{(l_E^2+x^2{m}^2)}^2}.\end{array}$$

(29)

We find that ${\delta }_{Z_1}$ and ${\delta }_{m_1^{-1}}$ are independent of the chemical potential ${\mu }_c$.

Finally, we show counter-terms for ${\mathsf{\Sigma }}_{ss}$. Since we can write,

$$\begin{array}{ccc}\hfill {\mathsf{\Sigma }}_{ss}\left(p\right)& =& -\frac{4}{3}{\left(e{d}_e\right)}^2\sum _{\alpha =0,\pm 1}{\int }_k{\left(k^0\right)}^2\frac{i}{p^0-k^0-\frac{{\left(\mathbf{p}-\mathbf{k}\right)}^2}{2m}-\frac{1}{I}+{\mu }_c+iϵ}·\frac{i}{k^2+iϵ}\hfill \\ & =& -4{\left(e{d}_e\right)}^2{\int }_k{\left(k^0\right)}^2\frac{i}{p^0-k^0-\frac{{\left(\mathbf{p}-\mathbf{k}\right)}^2}{2m}-\frac{1}{I}+{\mu }_c+iϵ}·\frac{i}{k^2+iϵ},\hfill \end{array}$$

(30)

the counter-terms can be derived by changing coefficient $\frac{4}{3}$ to 4 and factor ${\mu }_c$ to ${\mu }_c-\frac{1}{I}$ for ${\mathsf{\Sigma }}_{\alpha \alpha }\left(p\right)$ in Equation (26). We can then derive,

$$\begin{array}{ccc}\hfill {\delta }_{Z_s}{p}^0-\frac{{\delta }_{m_s^{-1}}{\mathbf{p}}^2}{2}+{\delta }_{\mu ,s}& =& 4{\left(e{d}_e\right)}^2{\int }_0^{1}dx{\int }_{l_E}\frac{\left[\mathrm{numerator}2\right]}{{(l_E^2+x^2{m}^2)}^2},\hfill \end{array}$$

(31)

with,

$$\begin{array}{ccc}\hfill \left[\mathrm{numerator}2\right]& =& {\left(l_E^0\right)}^2\left[|{\mathbf{l}}_E|+(1-3x)\left(m+p^0+{\mu }_c-\frac{1}{I}\right)+\frac{{(1-x)}^2{\mathbf{p}}^2+m^2}{2|{\mathbf{l}}_E|}-\frac{{(1-x)}^2{\mathbf{p}}^2}{6|{\mathbf{l}}_E|}\right]\hfill \\ & & -x^2\left|{\mathbf{l}}_E\right|m\left(m+2\left(p^0+{\mu }_c-\frac{1}{I}\right)\right)-x^2(1-x)m^2\left(m+3\left(p^0+{\mu }_c-\frac{1}{I}\right)\right)\hfill \\ & & +\frac{4mx(1-x)}{l_E^2+x^2{m}^2}\left((1-3x){\left(l_E^0\right)}^{2}m+{\left(l_E^0\right)}^2\left|{\mathbf{l}}_E\right|\right)\left(p^0+{\mu }_c-\frac{1}{I}-\frac{{\mathbf{p}}^2}{2m}\right).\hfill \end{array}$$

(32)

3.2. 1-Loop 3-Point Vertex

In this section, we show a 1-loop 3-point vertex and find that UV divergences are canceled by a counter-term. We shall see a 1-loop 3-point vertex shown in Figure 4.

The UV divergences in this figure are canceled by counter-terms involving ${\delta }_{e{d}_e}$ for vertices in Figure 1. The diagram in Figure 4a represents the term given by,

$$\begin{array}{ccc}\hfill \mathrm{vertex}\left(\mathrm{a}\right)& =& {\int }_l\sum _{\beta }{\left(\frac{2e{d}_e}{\sqrt{6}}\right)}^3(-i{l}^0)\left[\beta \left({\delta }_j^1-i\beta {\delta }_j^2\right)-\sqrt{2}\left(1-\left|\beta \right|\right){\delta }_j^3\right]\hfill \\ & & \times (-i{l}^0)\left[\alpha \left({\delta }_n^1-i\alpha {\delta }_n^2\right)-\sqrt{2}\left(1-\left|\alpha \right|\right){\delta }_n^3\right]{\delta }^{jn}\hfill \\ & & \times \left(i{k}^0\right)\left[-\beta \left({\delta }_i^1+i\beta {\delta }_i^2\right)+\sqrt{2}\left(1-\left|\beta \right|\right){\delta }_i^3\right]\hfill \\ & & \times \frac{i}{l^2+iϵ}\times \frac{i}{p^0+l^0-\frac{{\left(\mathbf{p}+\mathbf{l}\right)}^2}{2m}-\frac{1}{I}+{\mu }_c+iϵ}\times \frac{i}{p^0+l^0+k^0-\frac{{\left(\mathbf{p}+\mathbf{l}+\mathbf{k}\right)}^2}{2m}+{\mu }_c+iϵ}.\hfill \end{array}$$

(33)

The detailed calculations are given in Appendix B. We encounter the counter-term ${\delta }_{e{d}_e}$ as,

$$\begin{array}{ccc}\hfill -\frac{2{\delta }_{e{d}_e}}{\sqrt{6}}& =& -4{\left(\frac{2e{d}_e}{\sqrt{6}}\right)}^3{\int }_0^{1}dx{\int }_0^{1}dy{\int }_{q_E}\frac{-1}{{(q_E^2+{(x+y)}^2{m}^2)}^3}\hfill \\ & & \times \left[{\left(q_E^0\right)}^2\right[{\left(q_E^0\right)}^2-(|{\mathbf{q}}_E{|}^2+6m^2(x+y)(x+y-1)+2m\left|\mathbf{q}\right|(1-3(x+y))+2m^2\hfill \\ & & +\frac{1}{I^2}\left(5{(y-x)}^2+\frac{3y^2-3y+1}{3}-\left({(1-x)}^2-y^2\right)-2y(1-x-y)mI\right)\left)\right]\hfill \\ & & +|{\mathbf{q}}_E^2|\left[{(x+y)}^2{m}^2+\frac{{(y-x)}^2}{I^2}\right]\hfill \\ & & -{\left(q_E^0\right)}^2\left({\left(q_E^0\right)}^2-{\left|{\mathbf{q}}_E\right|}^2\right)\frac{\frac{3}{I^2}(x^2-x-2xy)}{q_E^2+{(x+y)}^2{m}^2}].\hfill \end{array}$$

(34)

The vertex correction involves quadratic, linear and logarithmic divergences canceled by counter-terms with ${\delta }_{e{d}_e}$. We have derived the counter-term for 1-loop vertex correction. We can derive the same result from Figure 4b.

3.3. 2-Loop Self-Energy

In this section, we estimate divergences in self-energy in 2-loop order.

First, we shall investigate the self-energy 1 for photons in Figure 5. This diagram contains the following factor,

$$\begin{array}{c}\hfill {\int }_l{\left(l^0\right)}^2{\int }_p{G}_{ss}\left(p\right)G_{\alpha \alpha }(p-l)G_{ss}(p-l-k)G_{\beta \beta }(p-k)\\ \hfill \sim {\left(l^0\right)}^2{\int }_0^{1}dx{\int }_0^{1}dy{\int }_0^{1}dz{\int }_0^{1}dw\delta (x+y+z+w-1){\int }_{p^0}\frac{1}{{(p^0+f(x,y,z,w,\mathbf{p},k,l))}^4},\end{array}$$

(35)

where we have used the Feynman’s formula. The function f is independent of $p^0$. Since the 3rd derivative of residue one by $p^0$ is zero, the contribution of this diagram is zero.

Next, we shall estimate the self-energy 2 on the left of Figure 6. This diagram contains a divergent part of the propagator of dipoles in the ground state, which can be canceled by the right diagram with counter-term. Even if the finite part, such as $C{p}^0$ with finite constant C remains after the cancellation, by using Feynman’s formula,

$$\begin{array}{c}\hfill \frac{1}{A{B}^2}={\int }_0^{1}dx{\int }_0^{1}dy\delta (x+y-1)\frac{2y}{{(xA+yB)}^3},\end{array}$$

(36)

we encounter the form of

$$\begin{array}{c}\hfill {\int }_p\frac{i}{p^0-k^0-\frac{{\left(\mathbf{p}-\mathbf{k}\right)}^2}{2m}-\frac{1}{I}+{\mu }_c+iϵ}·\frac{i}{p^0-\frac{{\mathbf{p}}^2}{2m}+{\mu }_c+ϵ}·\frac{iC{p}^0}{p^0-\frac{{\mathbf{p}}^2}{2m}+{\mu }_c+ϵ}\sim {\int }_{p^0}\frac{C{p}^0}{{(p^0+g(x,y,\mathbf{p},k))}^3},\end{array}$$

(37)

where g is a function independent of $p^0$. Since the 2nd derivative of the residue $C{p}^0$ by $p^0$ is zero, the remaining part in the above equation is zero. The same estimation is possible for the case when the propagator of dipoles in the 1st excited states contains divergent self-energy in the inner loop. We find ${\delta }_{Z_{ph}}$ is zero or $Z_{ph}=1$ in 2-loop order.

Next, we shall estimate the self-energy for dipoles in the ground state in 2-loop order in the left diagram in Figure 7a. This diagram contains quadratic divergences from vertex correction times cubic divergences from the remaining part. The quadratic divergences from vertex corrections are canceled by the two middle diagrams in Figure 7a with counter-terms. The sum of the left diagram and these middle diagrams contains cubic divergence in their loops. The cubic divergence can be canceled by the right counter-term in a similar way to 1-loop self-energy. We estimate the self-energy in the left diagram in Figure 7b. This diagram involves cubic divergence in the inner loop. The cubic divergence is canceled by the middle diagram with a counter-term. The sum of the left and middle diagrams contains cubic divergence at most. The cubic divergence can be canceled by the right counter-term in a similar way to 1-loop self-energy. We can also estimate the self-energy in Figure 7c. This diagram contains zero contributions in inner loops so the contribution is zero.

Finally, we shall show the self-energy for dipoles in the 1st excited states in Figure 8. The estimation of divergences is similar to the cases of self-energy for dipoles in the ground state. We just need to show the labels of external lines for dipoles in the 1st excited states $\alpha$ and $\beta$ will be the same one. The labels $\alpha ,\beta =0,\pm 1$ represent the three 1st excited states in our model originating from spherical harmonics $Y_{1\alpha }$ for rotational degrees of freedom of dipoles. We can consider the three cases shown in Figure 8d, where there are two incoming dipoles in 1st excited states to vertices connected by photon propagator (left), two outgoing dipoles in 1st excited states to vertices connected by propagator (middle), and one incoming and one outgoing dipole in 1st excited states connected by propagator (right). In the right diagram, we encounter the factor,

$$\begin{array}{c}\hfill {\delta }^{ij}\left[\alpha ({\delta }_i^1-i\alpha {\delta }_i^2)-\sqrt{2}(1-|\alpha \left|\right){\delta }_i^3\right]\left[-\beta ({\delta }_j^1+i\beta {\delta }_j^2)+\sqrt{2}(1-|\beta \left|\right){\delta }_j^3\right]\\ \hfill =-\alpha \beta -{\alpha }^2{\beta }^2-2(1-|\alpha \left|\right)(1-|\beta \left|\right),\end{array}$$

(38)

where we have used the Feynman rules in Figure 1. In $\alpha =1$, this factor is nonzero only when $\beta =1$. (In $\alpha =0$, it is nonzero only when $\beta =0$). We find that this factor is nonzero only in the cases $\alpha =\beta$ in the right diagram in Figure 8d. We shall consider the middle diagram. It contains the factor

$$\begin{array}{c}\hfill {\delta }^{ij}\left[\alpha ({\delta }_i^1-i\alpha {\delta }_i^2)-\sqrt{2}(1-|\alpha \left|\right){\delta }_i^3\right]\left[\beta ({\delta }_j^1-i\beta {\delta }_j^2)-\sqrt{2}(1-|\beta \left|\right){\delta }_j^3\right]\\ \hfill =\alpha \beta -{\alpha }^2{\beta }^2+2(1-|\alpha \left|\right)(1-|\beta \left|\right).\end{array}$$

(39)

This factor is nonzero only in $\alpha =-\beta$. Similarly, we find that the left diagram is nonzero only in $\alpha =-\beta$. Using these rules, we find that nonzero contributions are only in $\alpha =-\gamma$ and $\gamma =-\beta$ in the left diagram in Figure 8a, so we find $\alpha =\beta$. In the left diagram in Figure 8b, we also find $\alpha =\beta$. In self-energy for dipoles in 1st excited states, the label of incoming dipoles $\alpha$ is equal to that of outgoing dipoles $\beta$ at least in 1-loop and 2-loop order.

4. Renormalization in 2-Particle-Irreducible Effective Action Technique

In this section, we write 2-Particle-Irreducible (2PI) effective action [50,51,55] with counter-terms in Quantum Brain Dynamics and describe how to cancel ultra-violet diagrams in self-energy by counter-terms in the Kadanoff–Baym equations.

Beginning with the Lagrangian density in QBD in Equation (17), we can derive 2PI effective action. The action ${\mathsf{\Gamma }}_{2\mathrm{PI}}$ is given by,

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{2\mathrm{PI}}& =& \frac{i}{2}ln{D}^{-1}+\frac{i}{2}\mathrm{Tr}{D}_0^{-1}D+iln{G}_{ss}^{-1}+i\mathrm{Tr}{G}_{0,ss}^{-1}{G}_{ss}\hfill \\ & & +\sum _{\alpha }\left[iln{G}_{\alpha \alpha }^{-1}+i\mathrm{Tr}{G}_{0,\alpha \alpha }^{-1}{G}_{\alpha \alpha }\right]+\frac{1}{2}{\mathsf{\Gamma }}_2[D,G_{ss},G_{\alpha \alpha }],\hfill \end{array}$$

(40)

where we have used the full propagator of photons $D_{ij}(x,y)=\langle \mathrm{T}{A}_i\left(x\right)A_j\left(y\right)\rangle$ (the brackets representing expectation values), that of dipoles in the ground state $G_{ss}(x,y)=\langle \mathrm{T}{\psi }_s\left(x\right){\psi }_s^{*}\left(y\right)\rangle$ and that of dipoles in 1st excited states $G_{\alpha \alpha }(x,y)=\langle \mathrm{T}{\psi }_{\alpha }\left(x\right){\psi }_{\alpha }^{*}\left(y\right)\rangle$ and shown the case of vanishing background fields $\langle A_i\rangle =0$, $\langle {\psi }_s^{(*)}\rangle =0$ and $\langle {\psi }_{\alpha }^{(*)}\rangle =0$. Here, $i{D}_{0,ij}$, $i{G}_{0,ss}^{-1}$ and $i{G}_{0,\alpha \alpha }^{-1}$ are written by,

$$\begin{array}{ccc}\hfill i{D}_{0,ij}^{-1}(x,y)& =& {\delta }_{ij}\left(-{\partial }_x^2-{\delta }_{Z_{ph}}{\partial }_x^2\right)\delta (x-y),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill i{G}_{0,ss}^{-1}(x,y)& =& \left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}+{\mu }_c+{\delta }_{Z_s}i\frac{\partial }{\partial x^0}+\frac{{\delta }_{m_s^{-1}}{\nabla }_i^2}{2}+{\delta }_{\mu ,s}\right)\delta (x-y),\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill i{G}_{0,\alpha \alpha }^{-1}(x,y)& =& \left(i\frac{\partial }{\partial x^0}+\frac{{\nabla }_i^2}{2m}-\frac{1}{I}+{\mu }_c+{\delta }_{Z_1}i\frac{\partial }{\partial x^0}+\frac{{\delta }_{m_1^{-1}}{\nabla }_i^2}{2}-{\delta }_{I^{-1}}+{\delta }_{\mu ,1st}\right)\delta (x-y).\hfill \end{array}$$

(43)

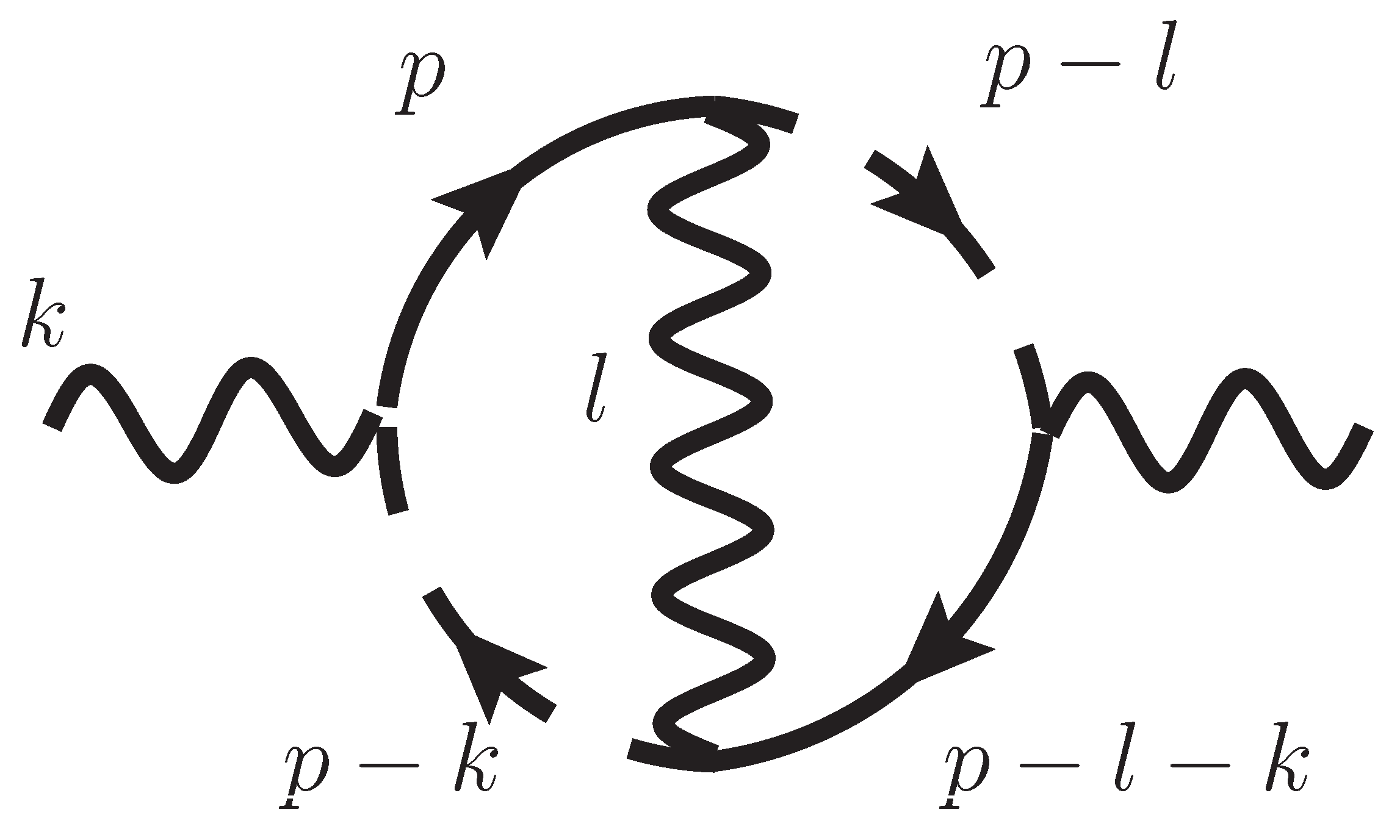
We find that counter-terms are in $i{D}_{0,ij}$, $i{G}_{0,ss}^{-1}$ and $i{G}_{0,\alpha \alpha }^{-1}$. In 2PI effective action, the term $\frac{{\mathsf{\Gamma }}_2}{2}$ represents all the 2-Particle-Irreducible loop diagrams in loop-expansion technique [53]. This term is expressed in Figure 9 for up to $O\left({\left(e{d}_e\right)}^4\right)$. We find diagrams involving counter-terms.

Differentiating 2PI action by propagators, we can derive the Kadanoff–Baym (KB) equations [52,53,54]. By the relation $\frac{\delta {\mathsf{\Gamma }}_{2\mathrm{PI}}}{\delta D}=0$, we can derive the KB equations for photons as,

$$\begin{array}{c}\hfill i\left(D_0^{-1}-\mathsf{\Pi }\right)=i{D}^{-1},\end{array}$$

(44)

with ${\mathsf{\Pi }}_{ij}(x,y)\equiv i\frac{\delta {\mathsf{\Gamma }}_2}{\delta D_{ji}(y,x)}$. ( $\mathsf{\Pi }$ is not renormalized due to ${\delta }_{Z_{ph}}=0$.) By the relation $\frac{\delta {\mathsf{\Gamma }}_{2\mathrm{PI}}}{\delta G_{ss}}=0$, we derive the KB equations for dipoles in the ground state as,

$$\begin{array}{ccc}\hfill i\left(G_{0,ss}^{-1}-{\mathsf{\Sigma }}_{ss}\right)& =& i{G}_{ss}^{-1},\hfill \end{array}$$

(45)

with ${\mathsf{\Sigma }}_{ss}\equiv \frac{i}{2}\frac{\delta {\mathsf{\Gamma }}_2}{\delta G_{ss}}$. In Fourier transformation in this equation, we can use the renormalized self-energy ${\mathsf{\Sigma }}_{ss,\mathrm{ren}}$ as,

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{ss,\mathrm{ren}}\left(p\right)={\mathsf{\Sigma }}_{ss}\left(p\right)+i\left(p^0{\delta }_{Z_s}-\frac{{\delta }_{m_s^{-1}}{\mathbf{p}}^2}{2}+{\delta }_{\mu ,s}\right),\end{array}$$

(46)

where we adopt counter-terms derived in perturbation theory in the previous section. In the relation $\frac{\delta {\mathsf{\Gamma }}_{2\mathrm{PI}}}{\delta G_{\alpha \alpha }}=0$, we derive the KB equations for dipoles in the 1st excited states as,

$$\begin{array}{ccc}\hfill i\left(G_{0,\alpha \alpha }^{-1}-{\mathsf{\Sigma }}_{\alpha \alpha }\right)& =& i{G}_{\alpha \alpha }^{-1},\hfill \end{array}$$

(47)

with ${\mathsf{\Sigma }}_{\alpha \alpha }\equiv \frac{i}{2}\frac{\delta {\mathsf{\Gamma }}_2}{\delta G_{\alpha \alpha }}$. Here we can use the renormalized self-energy ${\mathsf{\Sigma }}_{\alpha \alpha ,\mathrm{ren}}$ in Fourier transformation as,

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{\alpha \alpha ,\mathrm{ren}}\left(p\right)={\mathsf{\Sigma }}_{\alpha \alpha }\left(p\right)+i\left(p^0{\delta }_{Z_1}-\frac{{\delta }_{m_1^{-1}}{\mathbf{p}}^2}{2}-{\delta }_{I^{-1}}+{\delta }_{\mu ,1st}\right).\end{array}$$

(48)

The right-hand side in this equation is depicted in Feynman diagrams in Figure 10.

We adopt the same counter-terms as those in perturbation theory in the previous section.

5. Discussion

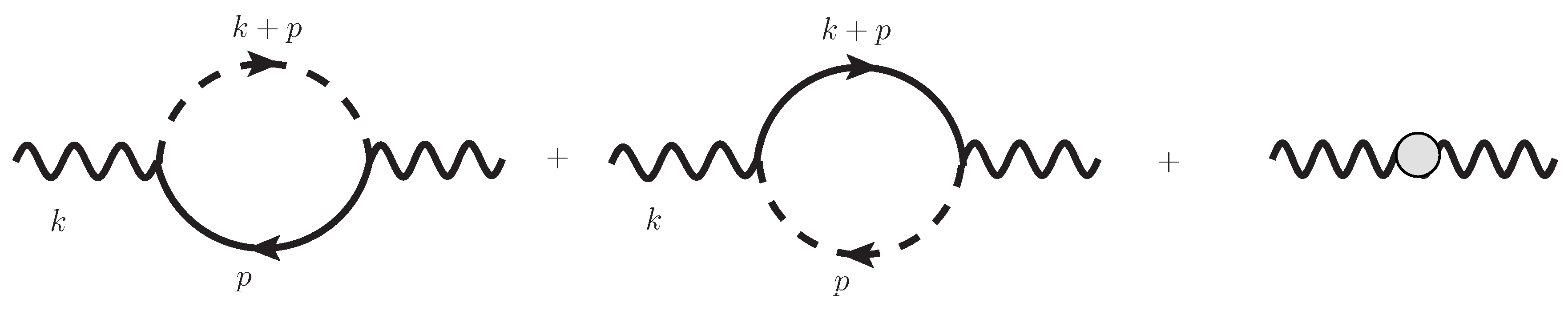
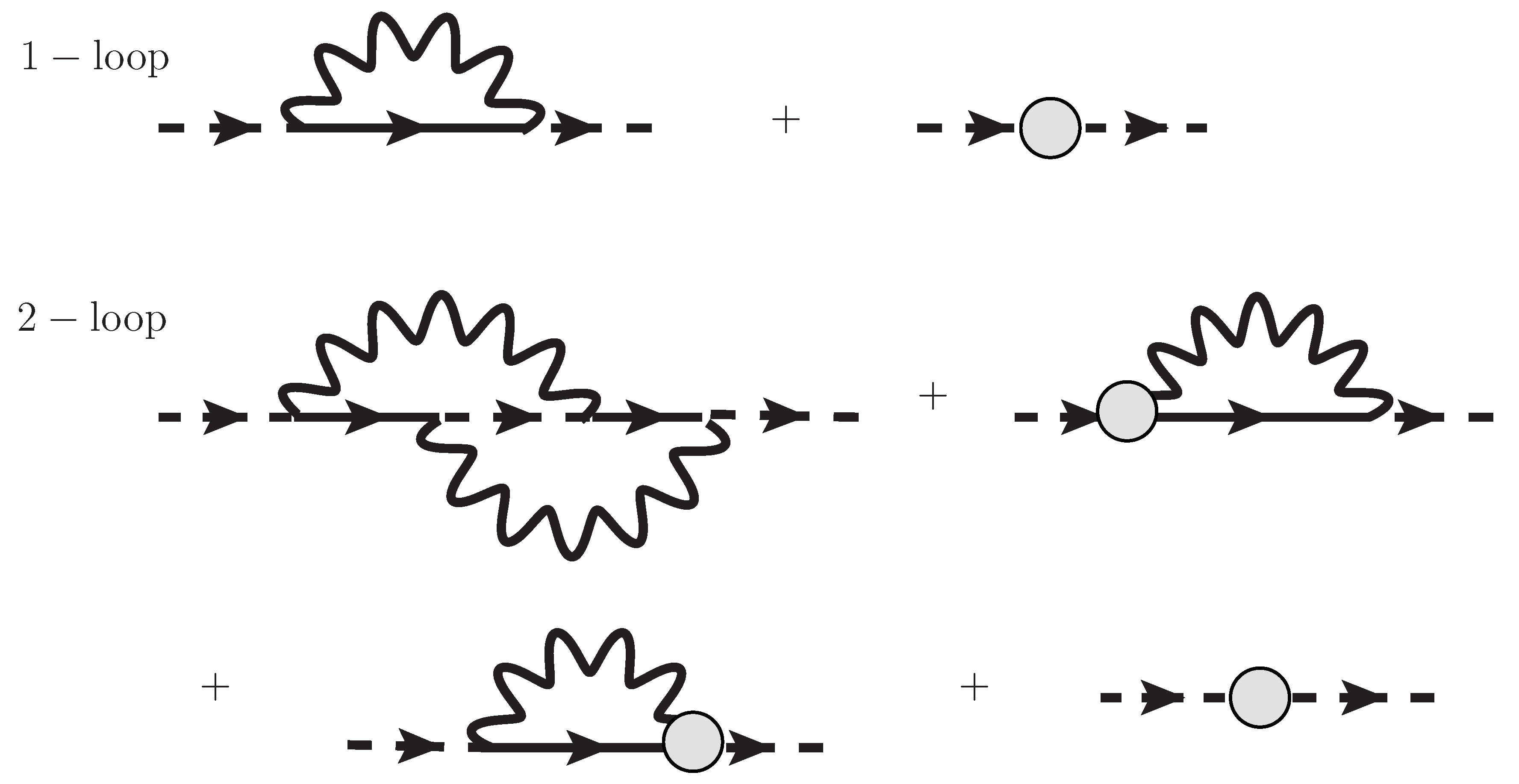
In this paper, we have introduced the Lagrangian density for Quantum Brain Dynamics (QBD) in $3+1$ dimensions and shown the Feynman rules for propagators, vertices and their counter-terms. We have investigated how to cancel ultra-violet (UV) divergences for 1-loop and 2-loop self-energy and 1-loop 3-point vertex corrections in the perturbation theory in the coupling expansion of $e{d}_e$. The photon self-energy has no UV divergent terms, at least in 2-loop order. The dipole self-energy involves, at most, cubic-divergent terms in 1-loop order canceled by counter-terms. The vertex corrections for 1-loop 3-point vertices involve, at most, quadratic divergent terms canceled by counter-terms. We can adopt these counter-terms derived in the perturbation theory to cancel UV divergences in the self-energy emerging in the Kadanoff–Baym (KB) equations derived in the 2-Particle-Irreducible effective action technique.

Using the counter-terms derived in this paper, we can cancel UV divergences in self-energy for dipoles in lattice simulations of the KB equations in QBD. We set the momenta $l^{\mu }\to \frac{2\pi n^{\mu }}{2a_s{N}_s}$ with $n^{\mu }=-N_s,-N_s+1,···N_s-1,N_s$ on the lattice with lattice spacing $a_s$. The finite UV cutoff $\mathsf{\Lambda }$ in the integral $\int d{l}^0$ is then $\pm \frac{\pi }{a_s}$. We can then calculate finite counter-terms in self-energy with a finite cutoff on the lattice. Using them in numerical simulations of time-evolution of KB equations, we might find convergent behaviors in increasing the cutoff on the lattice $\frac{\pi }{a_s}$ (decreasing lattice spacing $a_s$). Juchem et al. [56] have reported that the convergent behaviors appear in increasing cutoff by renormalizing the non-local sunset self-energy in the ${\varphi }^4$ model in $2+1$ dimensions. Without renormalization, the numerical results of KB equations are dependent on the cutoff in ${\varphi }^4$ theory. The convergent behaviors are also expected to appear in numerical simulations in KB equations in QBD using the counter-terms derived in this paper, although we require numerical costs involving parallel computations to check the convergence since we need to trace the time-evolution of KB equations in $3+1$ dimensions during equilibration on the lattice with several cutoffs and discuss numerical results in cases with and without renormalization.

We can consider the Ward–Takahashi identity in QBD. We shall consider the case when we do not adopt axial gauge fixing conditions, such as $A^0=0$, but adopt Lorentz invariant gauge fixing conditions. Using electric fields written by $E_i=-{\partial }_i{A}_0+{\partial }_0{A}_1$ and the 4th term in the Lagrangian density in Equation (17), the Feynman rules for vertices in Figure 1 are changed by,

$$\begin{array}{ccc}\hfill \frac{2e{d}_e}{\sqrt{6}}\left(i{k}^0\right)\left[-\alpha \left({\delta }_i^1+i\alpha {\delta }_i^2\right)+\sqrt{2}(1-|\alpha \left|\right){\delta }_i^3\right]& \to & \frac{2e{d}_e}{\sqrt{6}}[\left(i{k}^0\right)\left(-\alpha \left({\delta }_{\mu }^1+i\alpha {\delta }_{\mu }^2\right)+\sqrt{2}(1-|\alpha \left|\right){\delta }_{\mu }^3\right)\hfill \\ & & -i{\delta }_{\mu }^0\left(-\alpha \left(k^1+i\alpha k^2\right)+\sqrt{2}(1-|\alpha \left|\right)k^3\right)],\hfill \end{array}$$

(49)

and,

$$\begin{array}{ccc}\hfill \frac{2e{d}_e}{\sqrt{6}}(-i{k}^0)\left[\alpha \left({\delta }_i^1-i\alpha {\delta }_i^2\right)-\sqrt{2}(1-|\alpha \left|\right){\delta }_i^3\right]& \to & \frac{2e{d}_e}{\sqrt{6}}[(-i{k}^0)\left(\alpha \left({\delta }_{\mu }^1-i\alpha {\delta }_{\mu }^2\right)-\sqrt{2}(1-|\alpha \left|\right){\delta }_{\mu }^3\right)\hfill \\ & & +i{\delta }_{\mu }^0\left(\alpha \left(k^1-i\alpha k^2\right)-\sqrt{2}(1-|\alpha \left|\right)k^3\right)],\hfill \end{array}$$

(50)

with subscripts of spatial coordinate $i=1,2,3$ and subscripts of space-time coordinate $\mu =0,1,2,3$. We find that inner products with external momenta $k^{\mu }$ with the above vertices are zero. Using this property, Feynman diagrams involving inner products of vertices and momenta $k^{\mu }$ are zero even if the condition $k^2=0$ is not satisfied so we find the Ward–Takahashi identity in QBD. Using this identity, we find that the longitudinal component with $\frac{k^{\mu }{k}^{\nu }}{k^2}$ in propagators for photons does not contribute to physical quantities, such as the S-matrix.

We shall discuss the renormalizability in QBD in $3+1$ dimensions. We have investigated UV divergences in self-energy in the expansion of dipole moment $2e{d}_e$. Up to 2-loop order self-energy, we need not introduce new counter-terms in our Lagrangian density. However, we might need to introduce terms such as ${\psi }_s^{*}{\psi }_s{A}_i{A}_i$, ${\psi }_s^{*}{\psi }_s{\psi }_{\alpha }^{*}{\psi }_{\alpha }$ ($\alpha =0,\pm 1$), and so on, in higher loop order self-energy. Similar problems will occur in Quantum Electrodynamics for non-relativistic charged bosons labeled by field ${\phi }^{(*)}$ with interaction term $\partial A{\phi }^{*}\phi$, where we need to introduce additional ${\phi }^4$ interaction terms to renormalize 4-point vertices of ${\phi }^{(*)}$ appearing in $\langle {(\partial A{\phi }^{*}\phi )}^4\rangle$. In QBD, the terms such as ${\psi }_s^{*}{\psi }_s{A}_i{A}_i$ and ${\psi }^4$ might be introduced. If further additional terms need not emerge, we will arrive at renormalizable theory. Otherwise, the QBD Lagrangian in this paper is non-renormalizable and will represent a low-energy effective theory. We have introduced the hierarchy $k\left(\sim \frac{1}{I}\right)\ll m\ll \mathsf{\Lambda }$ with $\frac{1}{I}=4\mathrm{meV}$, mass $m=18\times 940\mathrm{MeV}$ for water molecules and cutoff $\mathsf{\Lambda }$. The dipole moment $2e{d}_e$ times $\frac{1}{I}=4\mathrm{meV}$ (or k) is the order ${10}^{-7}$ due to elementary charge $e=0.3$ and $d_e=0.2\times {10}^{-10}\mathrm{m}$ for water molecules. Then the perturbation is achieved for expansion with sufficiently small ${\left(2e{d}_e/I\right)}^n$$(n=2,3,4,···)$. However, if we expand by ${\left(2e{d}_e\mathsf{\Lambda }\right)}^n$ and our QBD Lagrangian is non-renormalizable, we find that the order of $\mathsf{\Lambda }$ is ${10}^4\mathrm{e}\mathrm{V}$ in $2e{d}_e\mathsf{\Lambda }\sim 1$ and that QBD is effective in typical frequency $p^0\ll \mathsf{\Lambda }\sim {10}^4\mathrm{e}\mathrm{V}$. Then we need to adopt the hierarchy $\frac{1}{I}\ll \mathsf{\Lambda }\ll 1/\left(2e{d}_e\right)\ll m$ with typical momenta $p^0\ll \mathsf{\Lambda }$. (Or we might adopt $\frac{1}{I}\ll 1/\left(2e{d}_e\right)\ll \mathsf{\Lambda }\ll m$ with expansions by $\frac{\mathsf{\Lambda }}{m}$.)

Our results will be applied to trace our decision-making or thinking processes in brain dynamics. Human decision-making is mathematically described in quantum-like theory in quantum cognition adopting quantum superposition and entanglement, which cannot be explained classically [57,58,59,60,61,62], although no physical degrees of freedom are provided in quantum cognition. QBD might provide concrete quantum degrees of freedom in quantum cognition. We adopt the theory of QBD and holography [14]. A single photon has a superposition state of two or more paths, as given by,

$$\begin{array}{c}\hfill |\Phi \rangle =\sum _i|\mathrm{path}i\rangle \to \sum _i|\mathrm{path}i\rangle |\mathrm{hologram}i\rangle \to \sum _i|\mathrm{path}i\rangle |\mathrm{hologram}i\rangle |\mathrm{decision}i\rangle .\end{array}$$

(51)

The photon superposition state propagating through two or more paths will provide a quantum state involving entanglement with holograms. Optical parallel information processing through holograms will provide quantum decision-making involving entanglement, as shown in the above equation. Increasing the number of photons, statistical properties of photons propagating through holograms in water–photon system will emerge. We then encounter quantum many-body problems in a water–photon system to describe our decision-making or thinking processes. Quantum many-body properties of water dipoles and photons can be described by the KB equation in quantum field theory. We can then adopt renormalization in an interacting water–photon system to trace our thinking processes in brain dynamics using KB equations.

In canceling UV divergences emerging in self-energy and vertex corrections by renormalization, we encounter arbitrariness in finite parts in counter-terms in renormalization prescription [48]. In achieving the invariance of the theory in renormalization prescriptions, parameters $(m,1/I,{\mu }_c,2e{d}_e)$ will become dependent on the renormalization scale $a_s$ (lattice spacing). The contributions from smaller scales than $a_s$ are renormalized into those parameters, so that the coarse graining procedures cause group, namely Renormalization Group (RG). The changes in parameters for scales $a_s$ are described by the RG equations in QBD. The RG equations describe running parameters of $(m,1/I,{\mu }_c,2e{d}_e)$ dependent on the renormalization scale $a_s$. In an increasing scale $a_s$ with renormalizing contributions from smaller scales, we might encounter the fixed point in RG equations independent of further coarse graining procedures. The fixed point represents scale-free physical phenomena in QBD. We then find the fractality in water–photon systems representing scale-invariant physics by solving fixed-point solutions in RG equations. Furthermore, when properties larger than the momentum cutoff $\mathsf{\Lambda }$ or those smaller scales than $a_s$ (with the momentum cutoff $\mathsf{\Lambda }\sim \frac{1}{a_s}$) are renormalized in QBD theory, we might encounter a new effective theory in macroscopic scales from microscopic water–photon dynamics. The effective theory might provide macroscopic conscious phenomena in brain functions. Renormalization in this work will be extended to describe the diversity in multi-scale brain dynamics involving running parameters, fractality in water–photon systems and so on.

Our paper, following on from a series of previous studies [13,14,15], provides a basis for the proper construction of the Hamiltonian structure of the Quantum Brain Dynamics with respect to a renormalization group application that shows the cancellation of divergent terms. Importantly, the resultant Hamiltonian exhibits fractal self-similar properties that could lead to a better understanding of the quantum degrees of freedom in the human brain in a hierarchical manner. We will explore these repercussions in the context of dipole–dipole interactions within neurons in future work.

6. Concluding Remarks and Perspectives

We have introduced the Lagrangian density in QBD in $3+1$ dimensions and shown the counter-terms in the Lagrangian. We have derived counter-terms for the cancellation of ultra-violet (UV) divergences in self-energy and vertex corrections in perturbation theory with the coupling expansion of the dipole moment. Counter-terms will be adopted to cancel UV divergences in numerical simulations of Kadanoff–Baym equations during equilibration. Our analysis will be extended to the renormalization group (RG) method in QBD to investigate running parameters of mass, dipole moment, moment of inertia and chemical potentials and show fractal-like properties for water–photon systems in fixed points in RG equations.