Approximate Nonlocal Symmetries for a Perturbed Schrödinger Equation with a Weak Infinite Power-Law Memory

Abstract

A nonlocally perturbed linear Schrödinger equation with a small parameter was derived under the assumption of low-level fractionality by using one of the known general nonlocal wave equations with an infinite power-law memory. The problem of finding approximate symmetries for the equation is studied here. It has been shown that the perturbed Schrödinger equation inherits all symmetries of the classical linear equation. It has also been proven that approximate symmetries corresponding to Galilean transformations and projective transformations of the unperturbed equation are nonlocal. In addition, a special class of nonlinear, nonlocally perturbed Schrödinger equations that admits an approximate nonlocal extension of the Galilei group is derived. An example of constructing an approximately invariant solution for the linear equation using approximate scaling symmetry is presented.

1. Introduction

The classical Schrödinger equation is one of the most fundamental models in non-relativistic quantum mechanics [1,2]. It is a linear partial differential equation describing the behavior of any quantum mechanical system via a wave function. At the same time, there are numerous nonlinear extensions of the Schrödinger equation that are relevant in many fields. Generally, such equations describe wave phenomena in nonlinear and dispersive media. For instance, nonlinear extensions have been used in hydrodynamics [3], nonlinear optics [4] and plasma physics [5]. Perturbed Schrödinger equations have been investigated in [6,7] and by many other researchers. Moreover, during the last two decades, several time- and space-fractional generalizations of linear and nonlinear Schrödinger equations have been proposed [8,9,10,11]. Such equations belong to the class of fractional partial differential equations [12,13], which allow the description of wave propagation in complex systems with power memory and spatial nonlocality.

Lie symmetry analysis [14,15,16,17] is a powerful mathematical technique frequently used for studying Schrödinger-type equations, especially nonlinear ones. In 1972, Niederer [18] proved that the free Schrödinger equation admits a 12-parameter Lie symmetry group containing time and space translations, dilations, the Galilei group, and a group of projective transformations. Two years later, he obtained the general potential–independent form of the maximal kinematical invariance groups for Schrödinger equations with arbitrary potentials, and found a classifying relation for invariance groups depending on potential [19]. In the same year, Boyer [20] performed a full group classification for these equations. It is important to note that recently this result has been revised by Nikitin [21]. At the same time, the symmetry approach to the separation of variables for stationary and nonstationary Schrödinger equations has been developed [22,23,24] (see also [25] and references therein). This approach is based both on classical Lie point symmetries and on higher (or Lie-Bäcklund) symmetries [16,26]. Higher symmetries of the Schrödinger equation with an arbitrary potential have been investigated, in particular, in [27,28,29]. We also mention here some recent papers on the investigation of the symmetry properties and construction of invariant solutions for time-dependent and time-independent Schrödinger equations [30,31,32,33].

Symmetry properties of nonlinear Schrödinger equations have been investigated by many researchers. Here we mention only some of them. Gagnon and Winternitz studied a generalized Schrödinger equation with a linear combination of the cubic and quintic terms in 3+1 dimensions. Lie symmetries of this equation have been obtained in [34], and different exact invariant solutions have been constructed in [35,36]. In [37], these authors analyzed the symmetry properties of a variable-coefficient nonlinear Schrödinger equation with three arbitrary complex functions in $1+1$ dimensions. Classical Lie point symmetries and invariant solutions, as well as higher symmetries, have been obtained by Fushchich et al. [29,38,39] for different classes of nonlinear Schrödinger-type equations (see also [40] and references therein). Results on symmetry group classification for nonlinear Schrödinger equations can be found in [41,42,43,44,45]. In [46], approximate symmetries for a perturbed nonlinear equation have been studied. For some more recent results on symmetry analysis we refer to recent papers [47,48,49].

During the last two decades, basic methods of the classical Lie group analysis have been extended to fractional differential equations (see [50,51,52] and references therein). In [53,54,55,56,57,58,59], these methods were successfully applied for investigating symmetry properties and finding exact solutions of time- and space-fractional Schrödinger equations. It is worth noting that fractional-order equations always have much fewer Lie point symmetries than integer-order ones. In particular, any time-fractional Schrödinger equation describing finite memory processes does not admit the group of time translations and the Galilei group. As a result, applying classical Lie group analysis methods to find exact solutions to fractional Schrödinger equations shows quite low efficiency.

Nevertheless, if the memory effect is weak in the modeled system, a corresponding small parameter can be introduced. For example, for time-fractional equations with a weak power-law memory, the order of fractional differentiation can be close to an integer. This is the so-called low-level fractionality case [60]. Such a fractional order can be written as the sum of an integer and a small parameter. As a result, the corresponding time-fractional equation can be approximated by a differential equation with a small nonlocal term. More details of such approximation technique can be found in [60,61,62,63].

At the end of the last century, Baikov, Gazizov and Ibragimov [64,65,66] developed the theory of approximate transformation groups (see also Part II in [17]). This theory gives the tools to investigate approximate symmetry properties of differential equations that have a small parameter. In [67,68,69], several methods of this theory were successfully extended to equations with nonlocal terms that arose during the approximation of time-fractional differential equations in the case of low-level fractionality. As a result, constructive algorithms for finding approximate symmetries and conservation laws for such equations have been developed. Note that the dimension of an approximate group of invariance for any perturbed equation with a small parameter is always larger than the dimension of an exact group of invariance for the corresponding unperturbed equation; therefore, much more approximate invariant solutions can be constructed.

In this paper, we dealt with the problem of finding approximate symmetries for a perturbed Schrödinger equation with a weak infinite power-law memory. Recently, Uchaikin [70,71] proved that the dynamics of an open system, which is considered as a subsystem of some closed Hamiltonian system, can be described by an integro-differential equation with a delayed time argument. This concept provides the physical background of the equation in question. We prove that the equation inherits all the symmetries of the classical Schrödinger equation. Moreover, we prove that approximate symmetries of the perturbed equation in question that corresponded to Galilean transformations and projective transformations of the unperturbed equation are nonlocal. To the best of this author’s knowledge, this is the first study on nonlocal symmetries for nonlocally perturbed equations obtained from fractional differential equations under the assumption of low-level fractionality. In addition, a class of nonlinear nonlocally perturbed Schrödinger equations that have approximate nonlocal Galilean-type symmetries is presented.

The paper is organized as follows. In Section 2, a formal approach to deriving a linear perturbed Schrödinger equation with infinite memory and low-level fractionality is proposed. Section 3 contains the results of an approximate symmetry analysis for this equation. A class of nonlinear Schrödinger equations with a small nonlocal term that have approximate nonlocal Galilean-type symmetries is discussed in Section 4. A semi-analytical example of finding an approximately invariant solution for the linear equation by using the obtained approximate scaling symmetry is given in Section 5. The last section contains a conclusion.

2. Perturbed Schrödinger Equation with a Weak Infinite Memory

It is well known that E. Schrödinger derived his famous equation from the optics-mechanics analogy [1,2]. Using this analogy for a particle, the representation for the phase velocity of a wave can be written (see, e.g., [1]) as

$$v={\displaystyle \frac{\hslash \omega }{\sqrt{2m}}}{\displaystyle \frac{1}{\sqrt{\hslash \omega -U}}},$$

(1)

where $\omega$ is the angular frequency; m is the mass of the particle; U is the potential energy of the particle in an external field; and ℏ is the reduced Planck constant (or the Dirac constant).

Next, the wave function for a monochromatic harmonic wave is of the form

$$\psi (t,x)=\widehat{\psi }\left(x\right)e^{-i\omega t},$$

(2)

which satisfies the classical wave equation

$${\psi }_{tt}=v^2\Delta \psi .$$

(3)

Substituting (1) and (2) in (3), and using the formal association

$$\omega \widehat{\psi }\to i{\psi }_t,$$

(4)

we obtain the classical Schrödinger equation

$$i\hslash {\psi }_t+{\displaystyle \frac{{\hslash }^2}{2m}}\Delta \psi -U\psi =0.$$

(5)

However, it is interesting to note that function (2) is a particular solution both for the classical (3), and the more general wave equations with an infinite power-law memory

$${\psi }_{tt}=a^2\Delta \psi +b_{\alpha }^2{}_{-\infty }^{}{I}_t^{\alpha }\Delta \psi ,\alpha \in (0,1),$$

(6)

where

$$\left({}_{-\infty }^{}{I}_t^{\alpha }f\right)(t,x)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_{-\infty }^t{\displaystyle \frac{f(\tau ,x)}{{(t-\tau )}^{1-\alpha }}}d\tau$$

is the Liouville fractional integral of order $\alpha$ [12]. Here $\alpha$ is a dimensionless number.

Note that (6) can be considered as a particular case of the wave equation with an infinite memory

$${\psi }_{tt}=a^2\Delta \psi +{\int }_0^{\infty }K\left(s\right)\Delta \psi (t-s,x)ds,$$

(7)

whenever

$$K\left(s\right)=b_{\alpha }^2{\displaystyle \frac{s^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}}.$$

Equation (7) is well known and has been investigated, for example, in [72,73,74]. In particular, this equation describes wave propagation in an open system considered as a part of a closed Hamiltonian system. More details of this approach can be found in [70,71].

Substituting (2) into (6), we get

$$-{\omega }^2\widehat{\psi }=a^2\Delta \widehat{\psi }+b_{\alpha }^2\Delta \widehat{\psi }{e}^{i\omega t}{}_{-\infty }^{}{I}_t^{\alpha }\left(e^{-i\omega t}\right).$$

For $\lambda >0$, we can use following expressions (see Table 9.2 in [12]):

$${}_{-\infty }^{}{I}_t^{\alpha }sin\left(\lambda t\right)={\omega }^{-\alpha }sin(\lambda t-\pi \alpha /2),$$

$${}_{-\infty }^{}{I}_t^{\alpha }cos\left(\lambda t\right)={\omega }^{-\alpha }cos(\lambda t-\pi \alpha /2).$$

Since

$$e^{-i\omega t}=cos\left(\right|\omega \left|t\right)-\mathrm{sign}\left(\omega \right)sin\left(\right|\omega \left|t\right),\omega \in \mathbb{R},$$

we have

$${}_{-\infty }^{}{I}_t^{\alpha }\left(e^{-i\omega t}\right)={\left|\omega \right|}^{-\alpha }{e}^{-i\omega t}{e}^{i\mathrm{sign}\left(\omega \right)\pi \alpha /2}.$$

(8)

As a result, we obtained the equation

$$-{\omega }^2\widehat{\psi }=a^2\Delta \widehat{\psi }+b_{\alpha }^2\Delta \widehat{\psi }{\left|\omega \right|}^{-\alpha }{e}^{i\mathrm{sign}\left(\omega \right)\pi \alpha /2}.$$

(9)

If $\alpha =0$, we have ${}_{-\infty }^{}{I}_t^{0}f=f$. Therefore, in this case (6) coincides with the classical wave Equation (3), and $a^2+b_0^2=v^2$. Assuming that

$$a^2=A^2{v}^2,b_{\alpha }^2=B_{\alpha }^2{v}^2,$$

(10)

where A and $B_{\alpha }$ do not depend on $\omega$, and $A^2+B_0^2=1$, we can rewrite (9) as

$$-{\displaystyle \frac{{\omega }^2}{v^2}}\widehat{\psi }=A^2\Delta \widehat{\psi }+B_{\alpha }^2\Delta \widehat{\psi }{\left|\omega \right|}^{-\alpha }{e}^{i\mathrm{sign}\left(\omega \right)\pi \alpha /2}.$$

In view of (1), we have

$$-(\hslash \omega -U)\widehat{\psi }={\displaystyle \frac{{\hslash }^2}{2m}}\left(A^2\Delta \widehat{\psi }+B_{\alpha }^2\Delta \widehat{\psi }{\left|\omega \right|}^{-\alpha }{e}^{i\mathrm{sign}\left(\omega \right)\pi \alpha /2}\right).$$

It follows from (8) that

$${\left|\omega \right|}^{-\alpha }{e}^{i\mathrm{sign}\left(\omega \right)\pi \alpha /2}\Delta \widehat{\psi }\to {}_{-\infty }^{}{I}_t^{\alpha }\Delta \psi .$$

Using this association and association (4), we obtained

$$i\hslash {\psi }_t+A^2{\displaystyle \frac{{\hslash }^2}{2m}}\Delta \psi +B_{\alpha }^2{\displaystyle \frac{{\hslash }^2}{2m}}{}_{-\infty }^{}{I}_t^{\alpha }\Delta \psi -U\psi =0.$$

(11)

This equation is a time-fractional generalization of the Shrödinger equation. If $\alpha =0$, it coincides with the classical Equation (5).

It is important to note that, generally, the second equality in (10) is physically quite restrictive. However, it is approximately valid for the case of a weak memory when $\alpha$ is small enough. Then we can write $\alpha =\epsilon$ ($0<\epsilon \ll 1$) and $B_{ϵ}^2\approx B_0^2$. In this case, the following expansion holds (see [12]) for the Liouville fractional integral:

$${}_{-\infty }^{}{I}_t^{\epsilon }f=f\left(t\right)+\epsilon \left(\gamma f+{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )f\left(\tau \right)d\tau \right)+o\left(\epsilon \right),$$

where $\gamma \approx 0.577215665$ is the Euler constant. Substituting this expansion in (11), we get

$$i\hslash {\psi }_t+(1+\epsilon B_0^2\gamma ){\displaystyle \frac{{\hslash }^2}{2m}}\Delta \psi +\epsilon B_0^2{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta \psi d\tau -U\psi =0.$$

(12)

This equation is the Shrödinger equation with a small nonlocal perturbations corresponding to infinite memory. In this equation $\epsilon$ is a dimensionless small numerical parameter.

Assuming that $0<\epsilon B_0^2\ll 1$, by the change of variables

$$t\to \hslash t,x\to {\displaystyle \frac{\hslash x}{\sqrt{2m}}},\epsilon \to {\displaystyle \frac{\epsilon }{B_0^2}},$$

we transform the Equation (12) to the simpler form

$$i{\psi }_t+(1+\epsilon \beta )\Delta \psi +\epsilon {\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta \psi d\tau -U\psi =0$$

(13)

with $\beta =\gamma +ln\hslash$ and a small parameter $\epsilon$. For simplicity, we call this equation the perturbed Schrödinger equation (PSE). If $\epsilon =0$ and $U=0$, this equation coincides with the free Schrödinger equation

$$i{\psi }_t+\Delta \psi =0.$$

(14)

3. Approximate Symmetries for PSE

3.1. Problem Statement

It is known that the free Schrödinger Equation (14) is invariant under the extended Galilei group, also known as the Schrödinger group [34,40]. Let $\psi (t,x)=u(t,x)+iv(t,x)$, $x\in {\mathbb{R}}^n$. Here u, v are real functions. Then (14) can be rewritten as the system of linear PDEs

$$u_t+\Delta v=0,-v_t+\Delta u=0.$$

(15)

A basis for the Lie algebra admitted by this system is provided (see, e.g., [34]) by a time translation T, n spatial translations $P_i$, n rotations $J_i$, n Galilean transformations $K_i$, one phase transformation M, two dilations I and D, and one projective transformation R:

$$\begin{array}{c}T={\displaystyle \frac{\partial }{\partial t}},P_i={\displaystyle \frac{\partial }{\partial x_i}},J_i=x_j{\displaystyle \frac{\partial }{\partial x_k}}-x_k{\displaystyle \frac{\partial }{\partial x_j}},\\ K_i=2t{\displaystyle \frac{\partial }{\partial x_i}}+x_i\left(u{\displaystyle \frac{\partial }{\partial v}}-v{\displaystyle \frac{\partial }{\partial u}}\right),M=u{\displaystyle \frac{\partial }{\partial v}}-v{\displaystyle \frac{\partial }{\partial u}},\\ I=u{\displaystyle \frac{\partial }{\partial u}}+v{\displaystyle \frac{\partial }{\partial v}},D=2t{\displaystyle \frac{\partial }{\partial t}}+x_i{\displaystyle \frac{\partial }{\partial x_i}},\\ R=t^2{\displaystyle \frac{\partial }{\partial t}}+t{x}_i{\displaystyle \frac{\partial }{\partial x_i}}-\left({\displaystyle \frac{n}{2}}tu+{\displaystyle \frac{1}{4}}{\left|x\right|}^{2}v\right){\displaystyle \frac{\partial }{\partial u}}-\left({\displaystyle \frac{n}{2}}tv-{\displaystyle \frac{1}{4}}{\left|x\right|}^{2}u\right){\displaystyle \frac{\partial }{\partial v}},\end{array}$$

(16)

where $i=1,\dots ,n$. Here summation over repeated indices is implied.

Since system (15) is linear, it also admits infinite transformations with the generator

$$X_{\infty }=f(t,x){\displaystyle \frac{\partial }{\partial u}}+g(t,x){\displaystyle \frac{\partial }{\partial v}},$$

where the functions $f(t,x)$ and $g(t,x)$ are solutions of the system

$$f_t+\Delta g=0,-g_t+\Delta f=0.$$

In this work, we investigated the question of how PSE (13), considered with $U=0$, inherits the symmetries (16) of the unperturbed Equation (14). Similarly to (15), we can rewrite (13) with $U=0$ as the system

$$\begin{array}{c}{u}_t+(1+\epsilon \beta )\Delta v+\epsilon \left(Sv\right)(t,x)=0,\hfill \\ -v_t+(1+\epsilon \beta )\Delta u+\epsilon \left(Su\right)(t,x)=0,\hfill \end{array}$$

(17)

where we denote for convenience

$${\displaystyle \left(Su\right)(t,x)={\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta u(\tau ,x)d\tau ,\left(Sv\right)(t,x)={\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta v(\tau ,x)d\tau .}$$

Since $\epsilon$ is assumed to be a small parameter in (17), we can try to find approximate symmetries for this system in the form

$$X=X^0+\epsilon X^1,$$

(18)

where $X^0$ is a symmetry of unperturbed system (15), i.e., any generator from (16). We will not assume that the operator $X^1$ is local because (17) is a nonlocally perturbed system and therefore it should admit nonlocal approximate symmetries.

The operator X defined by (18) is an approximate symmetry of (17) if and only if

$$\begin{array}{c}\tilde{X}\left[u_t+(1+\epsilon \beta )\Delta v+\epsilon Sv\right]\approx 0,\hfill \\ \tilde{X}\left[-v_t+(1+\epsilon \beta )\Delta u+\epsilon Su\right]\approx 0,\hfill \end{array}$$

whenever u and v satisfy (17). Here the approximate equality $F\approx 0$ means that $F=o\left(\epsilon \right)$, and $\tilde{X}$ denotes the prolongation of the operator X to all differential and integral variables in (17). We can rewrite the above system in a more convenient form:

$$\begin{array}{c}{\tilde{X}}^0(u_t+\Delta v)+\epsilon \left[{\tilde{X}}^1(u_t+\Delta v)+\beta {\tilde{X}}^0(\Delta v)+{\tilde{X}}^0\left(Sv\right)\right]\approx 0,\hfill \\ {\tilde{X}}^0(-v_t+\Delta u)+\epsilon \left[{\tilde{X}}^1(-v_t+\Delta u)+\beta {\tilde{X}}^0(\Delta u)+{\tilde{X}}^0\left(Su\right)\right]\approx 0.\hfill \end{array}$$

(19)

Note that the Equations of (19) cannot be split by $\epsilon$ because u and v satisfy (17), and therefore

$${\tilde{X}}^0(u_t+\Delta v)=O\left(\epsilon \right),{\tilde{X}}^0(-v_t+\Delta u)=O\left(\epsilon \right).$$

To obtain the determining equations for the operator $X^1$ from system (19) in an explicit form, the prolongations of a point transformation group defined by the infinitesimal generator $X^0$ to the nonlocal expressions $Su$ and $Sv$ have to be constructed. Further, we derive such prolongations for transformations defined by generators (16), and then find corresponding operators $X^1$.

3.2. Groups of Translations and Rotations

Let $X^0=T$. Then the corresponding infinitesimal transformations are

$$\overline{t}=t+a,\overline{x}=x,\overline{u}(\overline{t},\overline{x})=u(t,x),\overline{v}(\overline{t},\overline{x})=v(t,x),$$

where a is a group parameter. Applying this transformation to $Su$, we have

$$\begin{array}{c}{\displaystyle \left(Su\right)(t,x)={\displaystyle \frac{\partial }{\partial \overline{t}}}{\int }_{-\infty }^{\overline{t}-a}ln(\overline{t}-a-\tau ){\Delta }_{\overline{x}}u(\tau ,\overline{x})d\tau =|\overline{\tau }=\tau +a|}\\ {\displaystyle ={\displaystyle \frac{\partial }{\partial \overline{t}}}{\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\overline{\tau }){\Delta }_{\overline{x}}u(\overline{\tau }-a,\overline{x})d\overline{\tau }={\displaystyle \frac{\partial }{\partial \overline{t}}}{\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\overline{\tau }){\Delta }_{\overline{x}}\overline{u}(\overline{\tau },\overline{x})d\overline{\tau }\equiv \left(S\overline{u}\right)(\overline{t},\overline{x}).}\end{array}$$

(20)

Here we use the equality $u(\overline{\tau }-a,\overline{x})=\overline{u}(\overline{\tau },\overline{x})$ that follows from $\overline{u}(\overline{t},\overline{x})=u(\overline{t}-a,\overline{x})$ by a simple change of variable $\overline{t}\to \overline{\tau }$, and ${\Delta }_{\overline{x}}$ denotes the Laplace operator with respect to $\overline{x}=({\overline{x}}_1,\dots ,{\overline{x}}_n)$. Hence, the function $\left(Su\right)(t,x)$ is invariant under time translation, and therefore the corresponding prolongation of the generator T to $Su$ is equal to zero. The same is valid for $\left(Sv\right)(t,x)$. Since T has zero prolongations to $u_t$, $v_t$, $\Delta u$ and $\Delta v$, the equalities (19) are satisfied for $X^1=0$. Thus, the system (17) inherits the symmetry T, i.e., PSE admits any time translation. Note that this is due to the full memory in this system.

Similarly, one can easily prove that generators $P_i$ and $J_i$$(i=1,\dots ,n)$ also have zero prolongations to $\left(Su\right)(t,x)$ and $\left(Sv\right)(t,x)$. As a result, system (17) inherits these symmetries, i.e., PSE admits spatial translations and rotations.

Since the perturbed system admits time and space translations, it has different traveling wave solutions [75,76]. Note that time-fractional generalizations of Schrödinger’s equation with finite memory does not have such solutions.

3.3. Galilean Transformations

Now let us consider one of the most interesting cases of Galilean transformations: $X^0=K_i$. Corresponding infinitesimal transformations reads

$$\begin{array}{c}\overline{t}=t,{\overline{x}}_j=x_j(j\ne i),{\overline{x}}_i=x_i+2at+o\left(a\right),\\ \overline{u}=u-a{x}_{i}v+o\left(a\right),\overline{v}=v+a{x}_{i}u+o\left(a\right),\end{array}$$

(21)

where a is a group parameter.

At first, we find prolongations ${\zeta }_i^{Lu}$ and ${\zeta }_i^{Lv}$ of this group to integrals $\left(Lu\right)(t,x)$ and $\left(Lv\right)(t,x)$, where

$$\left(Lf\right)(t,x)={\int }_{-\infty }^{t}ln(t-\tau )f(\tau ,x)d\tau ,$$

such that

$$\left(L\overline{u}\right)(\overline{t},\overline{x})=\left(Lu\right)(t,x)+a{\zeta }_i^{Lu}+o\left(a\right),\left(L\overline{v}\right)(\overline{t},\overline{x})=\left(Lv\right)(t,x)+a{\zeta }_i^{Lv}+o\left(a\right).$$

For convenience, we introduce two vectors

$$z\left(s\right)=(x_1,\dots ,x_{i-1},x_i+as,x_{i+1},\dots ,x_n),\overline{z}\left(s\right)=({\overline{x}}_1,\dots ,{\overline{x}}_{i-1},{\overline{x}}_i-as,{\overline{x}}_{i+1},\dots ,{\overline{x}}_n).$$

By using the infinitesimal approach, we found from (21)

$$\overline{u}(\overline{t},\overline{x})=u(\overline{t},\overline{z}\left(2\overline{t}\right))-a{\overline{x}}_{i}v(\overline{t},\overline{x})+o\left(a\right),$$

and therefore

$$\overline{u}(\tau ,\overline{x})=u(\tau ,\overline{z}\left(2\tau \right))-a{\overline{x}}_{i}v(\tau ,\overline{x})+o\left(a\right)=u(\tau ,z(2t-2\tau ))-a{x}_{i}v(\tau ,x)+o\left(a\right).$$

Hence, the infinitesimal transformation of the integral $\left(L\overline{u}\right)(\overline{t},\overline{x})$ has the form

$$\begin{array}{c}{\displaystyle \left(L\overline{u}\right)(\overline{t},\overline{x})={\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\tau )\overline{u}(\tau ,\overline{x})d\tau }\\ {\displaystyle ={\int }_{-\infty }^{t}ln(t-\tau )[u(\tau ,z(2t-2\tau ))-a{x}_{i}v(\tau ,x)]d\tau +o\left(a\right)}\\ {\displaystyle ={\int }_{-\infty }^{t}ln(t-\tau )[u(\tau ,x)+2a(t-\tau )u_{x_i}(\tau ,x)-a{x}_{i}v(\tau ,x)]d\tau +o\left(a\right)}\\ =\left(Lu\right)(t,x)+2at\left(L{u}_{x_i}\right)](t,x)-2a\left[L\left(t{u}_{x_i}\right)\right](t,x)-a{x}_i\left(Lv\right)(t,x)+o\left(a\right).\end{array}$$

Thus, we obtain the prolongation formula

$${\zeta }_i^{Lu}=2t\left(L{u}_{x_i}\right)(t,x)-2\left[L\left(t{u}_{x_i}\right)\right](t,x)-x_i\left(Lv\right)(t,x).$$

(22)

Similarly, one can find the prolongation formula for the integral $\left(L\overline{v}\right)(\overline{t},\overline{x})$ as

$${\zeta }_i^{Lv}=2t\left(L{v}_{x_i}\right)(t,x)-2\left[L\left(t{v}_{x_i}\right)\right](t,x)+x_i\left(Lu\right)(t,x).$$

(23)

Now we can find prolongation of the Galilei group to the expressions $\left(Su\right)(t,x)$ and $\left(Sv\right)(t,x)$. Since

$$\left(Sf\right)(t,x)=\left({\displaystyle \frac{\partial }{\partial t}}L\Delta f\right)(t,x)=\left(\Delta {\displaystyle \frac{\partial }{\partial t}}Lf\right)(t,x),$$

we can write

$$\left(S\overline{u}\right)(\overline{t},\overline{x})=\left(Su\right)(t,x)+a{\zeta }_i^{Su}+o\left(a\right),\left(S\overline{v}\right)(\overline{t},\overline{x})=\left(Sv\right)(t,x)+a{\zeta }_i^{Sv}+o\left(a\right),$$

where ${\zeta }_i^{Su}$ and ${\zeta }_i^{Sv}$ are defined by the prolongation formulae

$${\zeta }_i^{Su}=\Delta D_t\left({\zeta }_i^{Lu}-2tL{u}_{x_i}\right)+2t\Delta D_t\left(L{u}_{x_i}\right)=\Delta D_t\left({\zeta }_i^{Lu}\right)-2\Delta \left(L{u}_{x_i}\right),$$

(24)

$${\zeta }_i^{Sv}=\Delta D_t\left({\zeta }_i^{Lv}-2tL{v}_{x_i}\right)+2t\Delta D_t\left(L{v}_{x_i}\right)=\Delta D_t\left({\zeta }_i^{Lv}\right)-2\Delta \left(L{v}_{x_i}\right).$$

(25)

Here $D_t$ is the total derivative to t. These formulae directly follow from the classical prolongation formulae to integer-order differential variables (see, e.g., [26]).

Substituting (22) into (24), we get

$$\begin{array}{c}{\zeta }_i^{Su}=\Delta D_t\left\{2tL{u}_{x_i}-2L\left(t{u}_{x_i}\right)-x_{i}Lv\right\}-2\Delta \left(L{u}_{x_i}\right)=\\ {\displaystyle =2{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^t(t-\tau )ln(t-\tau )\Delta u_{x_i}d\tau -2{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )v_{x_i}d\tau }\\ {\displaystyle -x_i{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta vd\tau -2{\int }_{-\infty }^{t}ln(t-\tau )\Delta u_{x_i}d\tau }\\ {\displaystyle =2{\int }_{-\infty }^t\Delta u_{x_i}d\tau -2{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )v_{x_i}d\tau -x_i{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta vd\tau .}\end{array}$$

Thus, we can write

$${\displaystyle {\zeta }_i^{Su}=2{\int }_{-\infty }^t\Delta u_{x_i}d\tau -2D_t\left(L{v}_{x_i}\right)-x_{i}Sv.}$$

(26)

Similarly, substituting (23) in (25), we find

$${\displaystyle {\zeta }_i^{Sv}=2{\int }_{-\infty }^t\Delta v_{x_i}d\tau -2D_t\left(L{u}_{x_i}\right)+x_{i}Su.}$$

(27)

Prolongations of the generator $K_i$ to $u_t$, $v_t$, $\Delta u$ and ${\Delta }_v$ are calculated by classical prolongation formulae. As a result, we found the prolonged generator in the form

$$\begin{array}{c}{\tilde{K}}_i=K_i-(x_i{v}_t+2u_{x_i}){\displaystyle \frac{\partial }{\partial u_t}}+(x_i{u}_t-2v_{x_i}){\displaystyle \frac{\partial }{\partial v_t}}-(x_i\Delta v+2v_{x_i}){\displaystyle \frac{\partial }{\partial \Delta u}}\\ +(x_i\Delta u+2u_{x_i}){\displaystyle \frac{\partial }{\partial \Delta v}}+{\zeta }_i^{Su}{\displaystyle \frac{\partial }{\partial Su}}+{\zeta }_i^{Sv}{\displaystyle \frac{\partial }{\partial Sv}},\end{array}$$

(28)

where ${\zeta }_i^{Su}$ and ${\zeta }_i^{Sv}$ are defined by (26) and (27). Substituting ${\tilde{X}}^0={\tilde{K}}_i$ into (19), in view of system (17), we obtain

$$\begin{array}{c}\epsilon \left[{\displaystyle (X^1(u_t+\Delta v)-2D_t\left(L{u}_{x_i}\right)+2{\int }_{-\infty }^t\Delta v_{x_i}d\tau +2\beta u_{x_i}}\right]\approx 0,\hfill \\ \epsilon \left[{\displaystyle X^1(-v_t+\Delta u)-2D_t\left(L{v}_{x_i}\right)+2{\int }_{-\infty }^t\Delta u_{x_i}d\tau -2\beta v_{x_i}}\right]\approx 0.\hfill \end{array}$$

(29)

Due to the multiplier $\epsilon$, this system should be approximately satisfied whenever u and v are the solutions of the unperturbed system (15).

We sought the operator $X^1$ in a quite general canonical form

$$X^1={\eta }^u{\displaystyle \frac{\partial }{\partial u}}+{\eta }^v{\displaystyle \frac{\partial }{\partial v}},$$

(30)

where functions ${\eta }^u$ and ${\eta }^v$ depend on t, x, u, v, as well as on any derivatives and integrals of u and v. Then we can rewrite system (29) as the system of determining equations for the functions ${\eta }^u$ and ${\eta }^v$:

$$\begin{array}{c}{\displaystyle D_t\left({\eta }^u\right)+\Delta {\eta }^v\approx 2D_t\left(L{u}_{x_i}\right)-2{\int }_{-\infty }^t\Delta v_{x_i}d\tau -2\beta u_{x_i},}\hfill \\ {\displaystyle -D_t\left({\eta }^v\right)+\Delta {\eta }^u\approx 2D_t\left(L{v}_{x_i}\right)-2{\int }_{-\infty }^t\Delta u_{x_i}d\tau +2\beta v_{x_i}.}\hfill \end{array}$$

(31)

In view of system (15), we have

$${\int }_{-\infty }^t\Delta u_{x_i}d\tau ={\int }_{-\infty }^t{v}_{\tau x_i}d\tau =v_{x_i}$$

and

$${\int }_{-\infty }^t\Delta v_{x_i}d\tau =-{\int }_{-\infty }^t{u}_{\tau x_i}d\tau =-u_{x_i}.$$

Here we use natural conditions

$$\underset{t\to -\infty }{lim}{u}_{x_i}=0,\underset{t\to -\infty }{lim}{v}_{x_i}=0.$$

Then system (31) takes the form

$$\begin{array}{c}{D}_t\left({\eta }^u\right)+\Delta {\eta }^v\approx 2D_t\left(L{u}_{x_i}\right)+2(1-\beta )u_{x_i},\hfill \\ D_t\left({\eta }^v\right)-\Delta {\eta }^u\approx -2D_t\left(L{v}_{x_i}\right)+2(1-\beta )v_{x_i}.\hfill \end{array}$$

(32)

Since the r.h.s. of equations in (32) contain the nonlocal operator L, the functions ${\eta }^u$ and ${\eta }^v$ should depend on nonlocal variables $L{u}_{x_i}$ and $L{v}_{x_i}$. To identify these functions, we gave several helpful relations. First of all, we proved that $D_t\left(Lf\right)=L{f}_t$. Indeed,

$$\begin{array}{c}{\displaystyle D_t\left(Lf\right)\equiv {\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )f(\tau ,x)d\tau =|s=t-\tau |={\displaystyle \frac{\partial }{\partial t}}{\int }_0^{\infty }lnsf(t-s,x)d\tau }\\ {\displaystyle ={\int }_0^{\infty }lns{f}_t(t-s,x)d\tau ={\int }_{-\infty }^{t}ln(t-\tau )f_{\tau }(\tau ,x)d\tau \equiv L{f}_t.}\end{array}$$

Next, by using this equality and system (15), we have

$$\Delta \left(L{u}_{x_i}\right)=L\Delta u_{x_i}=L\Delta u_{x_i}=L{v}_{t,x_i}=D_t\left(L{v}_{x_i}\right),$$

$$\Delta \left(L{v}_{x_i}\right)=L\Delta v_{x_i}=L\Delta v_{x_i}=-L{u}_{t,x_i}=-\left(D_{t}L{u}_{x_i}\right).$$

Therefore, if we set

$${\eta }^u=L{u}_{x_i}+{\tilde{\eta }}^u,{\eta }^v=-L{v}_{x_i}+{\tilde{\eta }}^v,$$

system (32) takes the form

$$\begin{array}{c}{D}_t\left({\tilde{\eta }}^u\right)+\Delta {\tilde{\eta }}^v\approx 2(1-\beta )u_{x_i},\hfill \\ D_t\left({\tilde{\eta }}^v\right)-\Delta {\tilde{\eta }}^u\approx 2(1-\beta )v_{x_i}.\hfill \end{array}$$

In view of system (15), it is easy to prove that a particular solution of this system is

$${\tilde{\eta }}^u=2(1-\beta )t{u}_{x_i},{\tilde{\eta }}^v=2(1-\beta )t{v}_{x_i}.$$

Thus, we found that $X^1$ is a nonlocal operator of the form

$$X^1=[2(1-\beta )t{u}_{x_i}+L{u}_{x_i}]{\displaystyle \frac{\partial }{\partial u}}+[2(1-\beta )t{v}_{x_i}-L{v}_{x_i}]{\displaystyle \frac{\partial }{\partial v}}.$$

We can also rewrite it as

$$X^1=2(\beta -1)t{\displaystyle \frac{\partial }{\partial x_i}}+L{u}_{x_i}{\displaystyle \frac{\partial }{\partial u}}-L{v}_{x_i}{\displaystyle \frac{\partial }{\partial v}}.$$

As a result, we concluded that the perturbed system (17) had n nonlocal approximate symmetries

$$K_i^{\epsilon }=2t[1+\epsilon (\beta -1)]{\displaystyle \frac{\partial }{\partial x_i}}+\left(-x_{i}v+\epsilon L{u}_{x_i}\right){\displaystyle \frac{\partial }{\partial u}}+\left(x_{i}u+\epsilon L{v}_{x_i}\right){\displaystyle \frac{\partial }{\partial v}},i=1,\dots ,n.$$

(33)

These symmetries are the nonlocal extensions of the generators $K_i$ of the Galilean transformations.

3.4. Group of Phase Transformation

Let us consider the case $X^0=M$ corresponding to the so-called phase transformation or to the rotation in the plane $(u,v)$. Then the infinitesimal transformations are

$$\overline{t}=t,{\overline{x}}_i=x_i(i=1,\dots ,n),\overline{u}=u-av+o\left(a\right),\overline{v}=v+au+o\left(a\right).$$

(34)

Applying this transformation to $S\overline{u}$, we have

$$\begin{array}{c}{\displaystyle \left(S\overline{u}\right)(\overline{t},\overline{x})={\displaystyle \frac{\partial }{\partial \overline{t}}}{\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\tau ){\Delta }_{\overline{x}}\overline{u}(\tau ,\overline{x})d\tau =}\\ {\displaystyle ={\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau ){\Delta }_x[u(\tau ,x)-av(\tau ,x)]d\tau +o\left(a\right)=\left(Su\right)(t,x)-a\left(Sv\right)(t,x)+o\left(a\right).}\end{array}$$

So, we get

$$\left(S\overline{u}\right)(\overline{t},\overline{x})=\left(Su\right)(t,x)+a{\zeta }_M^{Su}+o\left(a\right),{\zeta }_M^{Su}=-\left(Sv\right)(t,x).$$

Similarly, it is easy to obtain

$$\left(S\overline{v}\right)(\overline{t},\overline{x})=\left(Sv\right)(t,x)+a{\zeta }_M^{Sv}+o\left(a\right),{\zeta }_M^{Sv}=\left(Su\right)(t,x).$$

Thus, we have the following prolongation of the generator M:

$$\tilde{M}=M-v_t{\displaystyle \frac{\partial }{\partial u_t}}+u_t{\displaystyle \frac{\partial }{\partial v_t}}-\Delta v{\displaystyle \frac{\partial }{\partial \Delta u}}+\Delta u{\displaystyle \frac{\partial }{\partial \Delta v}}-Sv{\displaystyle \frac{\partial }{\partial Su}}+Su{\displaystyle \frac{\partial }{\partial Sv}}.$$

(35)

Substituting ${\tilde{X}}^0=\tilde{M}$ into (19), in view of system (17), we get

$$\begin{array}{c}-v_t+\Delta u+\epsilon [X^1(u_t+\Delta v)+\beta \Delta u+Su]\approx 0,\hfill \\ -u_t-\Delta u+\epsilon [X^1(-u_t-\Delta v)-\beta \Delta v-Sv]\approx 0.\hfill \end{array}$$

It is easy to see that if $X^1=0$, this system coincides with the initial perturbed system (17). It means that system (17) admits the phase transformation, i.e., this system has the Lie point symmetry M.

3.5. Groups of Dilations

Now we consider the dilation with the generator D. The corresponding infinitesimal transformations are

$$\overline{t}=t+2at+o\left(a\right),{\overline{x}}_i=x_i+a{x}_i+o\left(a\right),\overline{u}=u,\overline{v}=v.$$

Then for $Su$ we have

$$\begin{array}{c}{\displaystyle \left(S\overline{u}\right)(\overline{t},\overline{x})={\displaystyle \frac{\partial }{\partial \overline{t}}}{\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\overline{\tau }){\Delta }_{\overline{x}}\overline{u}(\overline{\tau },\overline{x})d\overline{\tau }=}\\ {\displaystyle ={\displaystyle \frac{1}{(1+2a){(1+a)}^2}}{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{(1+2a)t}ln(t+2at-\overline{\tau }){\Delta }_{x}u(\overline{\tau }-2a\overline{\tau },x)d\overline{\tau }+o\left(a\right)}\\ {\displaystyle =|\overline{\tau }=(1+2a)\tau |={\displaystyle \frac{1}{{(1+a)}^2}}{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln\left[(1+2a)(t-\tau )\right]{\Delta }_{x}u(\tau ,x)d\tau +o\left(a\right)}\\ {\displaystyle ={\displaystyle \frac{ln(1+2a)}{{(1+a)}^2}}\Delta u+{\displaystyle \frac{1}{{(1+a)}^2}}{\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau ){\Delta }_{x}u(\tau ,x)d\tau +o\left(a\right)}\\ =\left(Su\right)(t,x)+2a[\Delta u-(Su\left)\right(t,x\left)\right]+o\left(a\right).\end{array}$$

Similarly, for $Sv$ one can find

$$\left(S\overline{v}\right)(\overline{t},\overline{x})=\left(Sv\right)(t,x)+2a[\Delta v-\left(Sv\right)(t,x)]+o\left(a\right).$$

Hence, we can write the prolongation of the generator D as

$$\tilde{D}=D-2u_t{\displaystyle \frac{\partial }{\partial u_t}}-2v_t{\displaystyle \frac{\partial }{\partial v_t}}-2\Delta u{\displaystyle \frac{\partial }{\partial \Delta u}}-2\Delta v{\displaystyle \frac{\partial }{\partial \Delta v}}+2[\Delta u-Su]{\displaystyle \frac{\partial }{\partial Su}}+2[\Delta v+Sv]{\displaystyle \frac{\partial }{\partial Sv}}.$$

Setting ${\tilde{X}}^0=\tilde{D}$ in (19), in view of system (17), we obtain the system of determining equations for the coordinates of the operator $X^1$ from (30) as

$$\begin{array}{c}{D}_t{\eta }^u+\Delta {\eta }^v=-2\Delta v,D_t{\eta }^v-\Delta {\eta }^u=-2\Delta u.\hfill \end{array}$$

It is easy to prove that this system has the particular solution

$${\eta }^u=2t{u}_t,{\eta }^v=2t{v}_t.$$

Thus, the operator $X^1$ has the canonical form

$$X^1=2t{u}_t{\displaystyle \frac{\partial }{\partial u}}+2t{v}_t{\displaystyle \frac{\partial }{\partial v}},$$

or

$$X^1=-2t{\displaystyle \frac{\partial }{\partial t}}.$$

As a result, we concluded that system (17) has the approximate Lie point symmetry

$$D^{\epsilon }=2(1-\epsilon )t{\displaystyle \frac{\partial }{\partial t}}+x_i{\displaystyle \frac{\partial }{\partial x_i}}.$$

(36)

In the same way it can be proven that the perturbed system (17) also admits dilation with the generator I, which follows from the linearity of this system.

3.6. Group of Projective Transformations

At last, we find the approximate extension of the projective transformation R from (16). The infinitesimal transformation defined by R is

$$\begin{array}{c}\overline{t}=t+a{t}^2+o\left(a\right),{\overline{x}}_i=x_i+at{x}_i+o\left(a\right),\\ \overline{u}=u-{\displaystyle \frac{1}{4}}{a\left(\right|x|}^{2}v+2ntu)+o\left(a\right),\overline{v}=v+{\displaystyle \frac{1}{4}}{a\left(\right|x|}^{2}u-2ntv)+o\left(a\right).\end{array}$$

(37)

First, we consider the infinitesimal transformation of the integral $Lu$.

By using (37), we write

$$\overline{u}(\overline{t},\overline{x})=u(\overline{t}-a{\overline{t}}^2,\overline{x}-a\overline{t}\overline{x})-{\displaystyle \frac{1}{4}}a\left[\right|\overline{x}{|}^{2}v(\overline{t},\overline{x})+2n\overline{t}u(\overline{t},\overline{x})]+o\left(a\right),$$

or

$$\overline{u}(\overline{\tau },\overline{x})=u(\overline{\tau }-a{\overline{\tau }}^2,\overline{x}-a\overline{\tau }\overline{x})-{\displaystyle \frac{1}{4}}a\left[\right|\overline{x}{|}^{2}v(\overline{\tau },\overline{x})+2n\overline{\tau }u(\overline{\tau },\overline{x})]+o\left(a\right).$$

Then we have

$$\begin{array}{c}{\displaystyle \left(L\overline{u}\right)(\overline{t},\overline{x})={\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\tau )\overline{u}(\overline{\tau },\overline{x})d\overline{\tau }}\hfill \\ {\displaystyle ={\int }_{-\infty }^{\overline{t}}ln(\overline{t}-\overline{\tau })\left\{u(\overline{\tau }-a{\overline{\tau }}^2,\overline{x}-a\overline{\tau }\overline{x})-{\displaystyle \frac{1}{4}}a\left[\right|\overline{x}{|}^{2}v(\overline{\tau },\overline{x})+2n\overline{\tau }u(\overline{\tau },\overline{x})]\right\}d\overline{\tau }+o\left(a\right)}\hfill \\ {\displaystyle ={\int }_{-\infty }^{t+a{t}^2}ln(t+a{t}^2-\overline{\tau })}\hfill \\ \times \left\{u(\overline{\tau }-a{\overline{\tau }}^2,x+atx-a\overline{\tau }x)-{\displaystyle \frac{1}{4}}{a\left[\right|x|}^{2}v(\overline{\tau },x)+2n\overline{\tau }u(\overline{\tau },x)]\right\}d\overline{\tau }+o\left(a\right)\hfill \\ =|\overline{\tau }=\tau +a{\tau }^2,d\overline{\tau }=(1+2a)d\tau |\hfill \\ {\displaystyle ={\int }_{-\infty }^{t}ln(t+a{t}^2-\tau -a{\tau }^2)(1+2a\tau )}\hfill \\ \times \left\{u(\tau ,x+atx-a\tau x)-{\displaystyle \frac{1}{4}}{a\left[\right|x|}^{2}v(\tau ,x)+2n\tau u(\tau ,x)]\right\}d\tau +o\left(a\right)\hfill \\ {\displaystyle ={\int }_{-\infty }^t[ln(t-\tau )+a(t+\tau )](1+2a\tau )}\hfill \\ \times \left\{u(\tau ,x)+a(t-\tau )x_i{u}_{x_i}(\tau ,x)-{\displaystyle \frac{1}{4}}{a\left[\right|x|}^{2}v(\tau ,x)+2n\tau u(\tau ,x)]\right\}d\tau +o\left(a\right)\hfill \\ {\displaystyle ={\int }_{-\infty }^{t}ln(t-\tau )u(\tau ,x)d\tau +a{\int }_{-\infty }^t(t+\tau )u(\tau ,x)d\tau }\hfill \\ {\displaystyle +a{x}_i{\int }_{-\infty }^t(t-\tau )ln(t-\tau )u_{x_i}(\tau ,x)d\tau -a{\displaystyle \frac{{\left|x\right|}^2}{4}}{\int }_{-\infty }^{t}ln(t-\tau )v(\tau ,x)d\tau }\hfill \\ {\displaystyle -a{\displaystyle \frac{n}{2}}{\int }_{-\infty }^{t}ln(t-\tau )\tau u(\tau ,x)d\tau +2a{\int }_{-\infty }^{t}ln(t-\tau )u(\tau ,x)d\tau +o\left(a\right).}\hfill \end{array}$$

We can rewrite this result as

$$\left(L\overline{u}\right)(\overline{t},\overline{x})=\left(Lu\right)(t,x)+a{\zeta }_R^{Lu}+o\left(a\right)$$

with

$${\zeta }_R^{Lu}=-{\displaystyle \frac{{\left|x\right|}^2}{4}}Lv+\left(2-{\displaystyle \frac{n}{2}}\right)L\left(tu\right)+x_i\left[tL\left(u_{x_i}\right)-L\left(t{u}_{x_i}\right)\right]+{\int }_{-\infty }^t(t+\tau )u(\tau ,x)d\tau .$$

(38)

By using (38), we can now obtain the infinitesimal transformation of $Su$ as

$$\left(S\overline{u}\right)(\overline{t},\overline{x})=\left(Su\right)(t,x)+a{\zeta }_R^{Su}+o\left(a\right),$$

where ${\zeta }_R^{Su}$ is defined by

$$\begin{array}{c}{\zeta }_R^{Su}=\Delta D_t\left({\zeta }_R^{Lu}-t^2{D}_t\left(Lu\right)-t{x}_{i}L{u}_{x_i}\right)+t^2\Delta D_t^2\left(Lu\right)+t{x}_i\Delta D_t\left(L{u}_{x_i}\right)\\ =\Delta D_t\left({\zeta }_R^{Lu}\right)-2t{D}_t(L\Delta u)-\Delta \left(x_{i}L{u}_{x_i}\right)-t\Delta \left[x_i{D}_t\left(L{u}_{x_i}\right)\right]+t{x}_i\Delta D_t\left(L{u}_{x_i}\right).\end{array}$$

(39)

Substituting (38) in (39), we get

$$\begin{array}{c}{\zeta }_R^{Su}=-{\displaystyle \frac{1}{4}}{\Delta \left[\right|x|}^2{D}_t\left(Lv\right)]+\left(2-{\displaystyle \frac{n}{2}}\right)D_t\left[L(t\Delta u)\right]+\Delta \left[x_i{D}_t(tL\left(u_{x_i}\right)-L\left(t{u}_{x_i}\right))\right]\\ {\displaystyle +{\int }_{-\infty }^t\Delta u(\tau ,x)d\tau +2t\Delta u-2t{D}_t(L\Delta u)-\Delta \left(x_{i}L{u}_{x_i}\right)-t\Delta \left[x_i{D}_t\left(L{u}_{x_i}\right)\right]+t{x}_i\Delta D_t\left(L{u}_{x_i}\right).}\end{array}$$

By direct calculations it is easy to prove that for a smooth function $f=f(t,x)$ the following equalities are satisfied:

$$\Delta \left(\right|x^2\left|f\right)=2nf+4x_i{f}_{x_i}+{\left|x\right|}^2\Delta f,$$

and

$$\Delta \left(x_i{f}_{x_i}\right)=2\Delta f+x_i\Delta f_{x_i}.$$

We also have

$$D_t[tLf-L\left(tf\right)]=Lf+{\int }_{-\infty }^{t}f(\tau ,x)d\tau ,$$

or

$$D_t\left[L\left(tf\right)\right]=t{D}_t\left(Lf\right)-{\int }_{-\infty }^{t}f(\tau ,x)d\tau .$$

By using these formulae, after simple algebra we obtain the prolongation formula for $Su$ as

$$\begin{array}{c}{\zeta }_R^{Su}=-{\displaystyle \frac{n}{2}}{D}_t\left(Lv\right)-x_i{D}_t\left(L{v}_{x_i}\right)-{\displaystyle \frac{{\left|x\right|}^2}{4}}Sv-\left({\displaystyle \frac{n}{2}}+2\right)tSu+2t\Delta u\\ {\displaystyle +\left({\displaystyle \frac{n}{2}}+1\right){\int }_{-\infty }^t\Delta u(\tau ,x)d\tau +x_i{\int }_{-\infty }^t\Delta u_{x_i}(\tau ,x)d\tau .}\end{array}$$

(40)

Similarly, we get

$$\left(S\overline{v}\right)(\overline{t},\overline{x})=\left(Sv\right)(t,x)+a{\zeta }_R^{Sv}+o\left(a\right),$$

where ${\zeta }_R^{Sv}$ is defined by the prolongation formula

$$\begin{array}{c}{\zeta }_R^{Sv}={\displaystyle \frac{n}{2}}{D}_t\left(Lu\right)+x_i{D}_t\left(L{u}_{x_i}\right)+{\displaystyle \frac{{\left|x\right|}^2}{4}}Su-\left({\displaystyle \frac{n}{2}}+2\right)tSv+2t\Delta v\\ {\displaystyle +\left({\displaystyle \frac{n}{2}}+1\right){\int }_{-\infty }^t\Delta v(\tau ,x)d\tau +x_i{\int }_{-\infty }^t\Delta v_{x_i}(\tau ,x)d\tau .}\end{array}$$

(41)

Thus, we can write the prolongation of the generator R as

$$\tilde{R}=R+{\zeta }_R^{u_t}{\displaystyle \frac{\partial }{\partial u_t}}+{\zeta }_R^{v_t}{\displaystyle \frac{\partial }{\partial v_t}}+{\zeta }_R^{\Delta u}{\displaystyle \frac{\partial }{\partial \Delta u}}+{\zeta }_R^{\Delta v}{\displaystyle \frac{\partial }{\partial \Delta v}}+{\zeta }_R^{Su}{\displaystyle \frac{\partial }{\partial Su}}+{\zeta }_R^{Sv}{\displaystyle \frac{\partial }{\partial Sv}},$$

where ${\zeta }_R^{Su}$, ${\zeta }_R^{Su}$ are defined by (40) and

$$\begin{array}{c}{\zeta }_R^{u_t}=-{\displaystyle \frac{{\left|x\right|}^2}{4}}{v}_t-\left(2+{\displaystyle \frac{n}{2}}\right)t{u}_t-x_i{u}_{x_i}-{\displaystyle \frac{n}{2}}u,\hfill \\ {\zeta }_R^{v_t}={\displaystyle \frac{{\left|x\right|}^2}{4}}{u}_t-\left(2+{\displaystyle \frac{n}{2}}\right)t{v}_t-x_i{v}_{x_i}-{\displaystyle \frac{n}{2}}v,\hfill \\ {\zeta }_R^{\Delta u}=-{\displaystyle \frac{{\left|x\right|}^2}{4}}\Delta v-\left(2+{\displaystyle \frac{n}{2}}\right)t\Delta u-x_i{v}_{x_i}-{\displaystyle \frac{n}{2}}v,\hfill \\ {\zeta }_R^{\Delta v}={\displaystyle \frac{{\left|x\right|}^2}{4}}\Delta u-\left(2+{\displaystyle \frac{n}{2}}\right)t\Delta v+x_i{u}_{x_i}+{\displaystyle \frac{n}{2}}u.\hfill \end{array}$$

These representations were found by using the classical prolongation formulae.

Setting ${\tilde{X}}^0=\tilde{R}$ in (19), in view of system (17), we obtain the following system of determining equations for the coordinates of the operator $X^1$:

$$\begin{array}{c}{D}_t{\eta }^u+\Delta {\eta }^v=\left[(1-\beta ){\displaystyle \frac{n}{2}}+1\right]u+(1-\beta )x_i{u}_{x_i}-2t\Delta v-{\displaystyle \frac{n}{2}}{D}_t\left(Lu\right)-x_i{D}_t\left(L{u}_{x_i}\right),\hfill \\ D_t{\eta }^v-\Delta {\eta }^u=\left[(1-\beta ){\displaystyle \frac{n}{2}}+1\right]v+(1-\beta )x_i{v}_{x_i}+2t\Delta u-{\displaystyle \frac{n}{2}}{D}_t\left(Lv\right)-x_i{D}_t\left(L{v}_{x_i}\right).\hfill \end{array}$$

(42)

Here we take into account that due to system (17) and conditions

$$\underset{t\to -\infty }{lim}u=0,\underset{t\to -\infty }{lim}v=0,$$

the following approximate equalities hold:

$$\epsilon {\int }_{-\infty }^t\Delta u(\tau ,x)d\tau \approx \epsilon {\int }_{-\infty }^t{v}_t(\tau ,x)d\tau =\epsilon v,$$

$$\epsilon {\int }_{-\infty }^t\Delta v(\tau ,x)d\tau \approx -\epsilon {\int }_{-\infty }^t{u}_t(\tau ,x)d\tau =-\epsilon u.$$

Note that system (42) corresponds to the first order of the small parameter $\epsilon$.

Since the r.h.s. of equations in (42) contain nonlocal operators, the coordinates ${\eta }^u$ and ${\eta }^v$ of the operator $X^1$ also should be nonlocal. Here, we note that

$$\Delta \left({\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lf\right)\right)={\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t(L\Delta f)+x_i{D}_t\left(L{u}_i\right)+{\displaystyle \frac{n}{2}}{D}_t\left(Lf\right),$$

and

$$\epsilon D_t\left({\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lu\right)\right)=\epsilon {\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(L{u}_t\right)\approx -\epsilon {\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t(L\Delta v),$$

$$\epsilon D_t\left({\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lv\right)\right)=\epsilon {\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(L{v}_t\right)\approx \epsilon {\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t(L\Delta u).$$

Using these formulae, it is easy to prove that if we put

$${\eta }^u={\tilde{\eta }}^u+{\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lv\right),{\eta }^v={\tilde{\eta }}^v-{\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lu\right),$$

system (42) takes the form

$$\begin{array}{c}{D}_t{\tilde{\eta }}^u+\Delta {\tilde{\eta }}^v=\left[(1-\beta ){\displaystyle \frac{n}{2}}+1\right]u+(1-\beta )x_i{u}_{x_i}-2t\Delta v,\hfill \\ D_t{\tilde{\eta }}^v-\Delta {\tilde{\eta }}^u=\left[(1-\beta ){\displaystyle \frac{n}{2}}+1\right]v+(1-\beta )x_i{v}_{x_i}+2t\Delta u.\hfill \end{array}$$

(43)

A particular solution of this system is

$${\tilde{\eta }}^u=tu+t^2{u}_t-(1-\beta ){\displaystyle \frac{{\left|x\right|}^2}{4}}v,{\tilde{\eta }}^v=tv+t^2{v}_t+(1-\beta ){\displaystyle \frac{{\left|x\right|}^2}{4}}u.$$

Hence, we obtain the nonlocal operator

$$\begin{array}{c}{X}^1=\left[tu+t^2{u}_t-(1-\beta ){\displaystyle \frac{{\left|x\right|}^2}{4}}v+{\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lv\right)\right]{\displaystyle \frac{\partial }{\partial u}}\hfill \\ \hfill +\left[tv+t^2{v}_t+(1-\beta ){\displaystyle \frac{{\left|x\right|}^2}{4}}u-{\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lu\right)\right]{\displaystyle \frac{\partial }{\partial v}}.\end{array}$$

This operator can be also rewritten as

$$\begin{array}{c}{X}^1=-t^2{\displaystyle \frac{\partial }{\partial t}}+\left[tu-(1-\beta ){\displaystyle \frac{{\left|x\right|}^2}{4}}v+{\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lv\right)\right]{\displaystyle \frac{\partial }{\partial u}}\hfill \\ \hfill +\left[tv+(1-\beta ){\displaystyle \frac{{\left|x\right|}^2}{4}}u-{\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lu\right)\right]{\displaystyle \frac{\partial }{\partial v}}.\end{array}$$

Thus, we find that the perturbed system (17) has approximate nonlocal symmetry

$$\begin{array}{c}{R}^{\epsilon }=(1-\epsilon )t^2{\displaystyle \frac{\partial }{\partial t}}+t{x}_i{\displaystyle \frac{\partial }{\partial x_i}}\hfill \\ -\left[\left({\displaystyle \frac{n}{2}}-\epsilon \right)tu+(1+\epsilon (1-\beta )){\displaystyle \frac{{\left|x\right|}^2}{4}}v-\epsilon {\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lv\right)\right]{\displaystyle \frac{\partial }{\partial u}}\\ \hfill +\left[-\left({\displaystyle \frac{n}{2}}-\epsilon \right)tv+(1+\epsilon (1-\beta )){\displaystyle \frac{{\left|x\right|}^2}{4}}u-\epsilon {\displaystyle \frac{{\left|x\right|}^2}{4}}{D}_t\left(Lu\right)\right]{\displaystyle \frac{\partial }{\partial v}}.\end{array}$$

(44)

As a final remark, it should be noted that the perturbed system (17) also has the approximate symmetries $\epsilon T$, $\epsilon P_i$, $\epsilon J_i$, $\epsilon K_i$, $\epsilon M$, $\epsilon I$, $\epsilon D$, and $\epsilon R$. This result directly follows from (19) after the substitution $X^0=0$. All these symmetries are trivial but they should be taken into account for finding approximate invariant solutions. In addition, due to linearity, system (17) has infinite approximate symmetries

$$X_{\infty }=[f^0(t,x)+\epsilon f^1(t,x)]{\displaystyle \frac{\partial }{\partial u}}+[g^0(t,x)+\epsilon g^1(t,x)]{\displaystyle \frac{\partial }{\partial v}},$$

(45)

where $f^0$, $f^1$, $g^0$, and $g^1$ are a solution to the system

$$\begin{array}{cc}{f}_t^0+\Delta g^0=0,\hfill & f_t^1+\Delta g^1=-\beta \Delta g^0-S{g}^0,\hfill \\ g_t^0-\Delta f^0=0,\hfill & g_t^1-\Delta f^1=\beta \Delta f^0-S{f}^0.\hfill \end{array}$$

The results can be summarized as

Theorem 1.

The nonlocally perturbed system (17) inherits all symmetries of the unperturbed system (15). A corresponding basis of its approximate symmetry Lie algebra is provided by the exact local generators T, $P_i$, $J_i$, M, and I from (16), the local approximate generator $D^{\epsilon }$ from (36), nonlocal approximate generators $K_i^{\epsilon }$ and $R^{\epsilon }$ defined by (33) and (44), respectively, and corresponding local approximate generators $\epsilon T$, $\epsilon P_i$, $\epsilon J_i$, $\epsilon K_i$, $\epsilon M$, $\epsilon I$, $\epsilon D$, and $\epsilon R$. Also, this linear perturbed system has infinite approximate symmetries (45).

4. Nonlocally Perturbed Nonlinear Schrödinger Equation

Nonlinear Schrödinger equations play essential role in many areas of applied physics. An important class of such equations is invariant under the extended Galilei group. A basis of the Lie algebra corresponding to this group consists of the first 11 operators from (16): T, $P_i$, $J_i$, $K_i$ and M. In particular, this group is admitted by any nonlinear Schrödinger equation of the form

$$i{\psi }_t+\Delta \psi =F\left(\right|\psi \left|\right)\psi ,$$

where F is an arbitrary function (see, e.g., [34]).

Let us consider a corresponding nonlinear generalisation of PSE (13) of the form

$$i{\psi }_t+(1+\epsilon \beta )\Delta \psi +\epsilon {\displaystyle \frac{\partial }{\partial t}}{\int }_{-\infty }^{t}ln(t-\tau )\Delta \psi d\tau =F\left(\right|\psi \left|\right)\psi .$$

(46)

In this section, we solve the problem of finding the function $F\left(\right|\psi \left|\right)$ for which (46) admits approximate symmetries of the form (18) corresponding to the extended Galilei group.

We will assume that the function F depends on a small parameter $\epsilon$ and can be written as $F\left(\right|\psi \left|\right)=F^0\left(\right|\psi \left|\right)+\epsilon F^1\left(\right|\psi \left|\right)$. As previously, let $\psi (t,x)=u(t,x)+iv(t,x)$, $x\in R^n$. Also, we set $F^0=f^0(u^2+v^2)+i{g}^0(u^2+v^2)$ and $F^1=f^1(u^2+v^2)+i{g}^1(u^2+v^2)$. Here u, v, $f^0$, $f^1$, $g^0$ and $g^1$ are real functions. Then (46) can be rewritten as the system

$$\begin{array}{c}{u}_t+(1+\epsilon \beta )\Delta v+\epsilon \left(Sv\right)(t,x)=f^{0}v+g^{0}u+\epsilon (f^{1}v+g^{1}u),\hfill \\ -v_t+(1+\epsilon \beta )\Delta u+\epsilon \left(Su\right)(t,x)=f^{0}u-g^{0}v+\epsilon (f^{1}u-g^{1}v).\hfill \end{array}$$

(47)

The corresponding system of determining equations for the coordinates ${\eta }^u$ and ${\eta }^v$ of the operator $X^1$ from (30) can be written as

$$\begin{array}{c}\epsilon \left[D_t\left({\eta }^u\right)+\Delta {\eta }^v-{\eta }^u(g^0+2uv{\left(f^0\right)}^{\prime }+2u^2{\left(g^0\right)}^{\prime })-{\eta }^v(f^0+2v^2{\left(f^0\right)}^{\prime }+2uv{\left(g^0\right)}^{\prime })\right]\hfill \\ +{\tilde{X}}^0(u_t+\Delta v-f^{0}v-g^{0}u)+\epsilon {\tilde{X}}^0(\beta \Delta v+Sv-f^{1}v-g^{1}u)\approx 0,\hfill \\ \epsilon \left[-D_t\left({\eta }^v\right)+\Delta {\eta }^u-{\eta }^u(f^0+2u^2{\left(f^0\right)}^{\prime }-2uv{\left(g^0\right)}^{\prime })+{\eta }^v(g^0+2v^2{\left(g^0\right)}^{\prime }-2uv{\left(f^0\right)}^{\prime })\right]\hfill \\ +{\tilde{X}}^0(-v_t+\Delta u-f^{0}u+g^{0}v)+\epsilon {\tilde{X}}^0(\beta \Delta u+Su-f^{1}u+g^{1}v)\approx 0.\hfill \end{array}$$

(48)

Like the previous section, it is easy to prove that (47) admits Lie point transformation groups with the generators T, $P_i$ and $J_i$. In all of these cases we have ${\eta }^u=0$ and ${\eta }^v=0$. For the phase transformation M, we should set ${\tilde{X}}^0=\tilde{M}$, where $\tilde{M}$ is defined by (35). Then (48) takes the form

$$\begin{array}{c}\epsilon \left[D_t\left({\eta }^u\right)+\Delta {\eta }^v-{\eta }^u(g^0+2uv{\left(f^0\right)}^{\prime }+2u^2{\left(g^0\right)}^{\prime })-{\eta }^v(f^0+2v^2{\left(f^0\right)}^{\prime }+2uv{\left(g^0\right)}^{\prime })\right]\hfill \\ -v_t+\Delta u-f^{0}u+g^{0}v+\epsilon (\beta \Delta u+Su-f^{1}u+g^{1}v)\approx 0,\hfill \\ \epsilon \left[-D_t\left({\eta }^v\right)+\Delta {\eta }^u-{\eta }^u(f^0+2u^2{\left(f^0\right)}^{\prime }-2uv{\left(g^0\right)}^{\prime })+{\eta }^v(g^0+2v^2{\left(g^0\right)}^{\prime }-2uv{\left(f^0\right)}^{\prime })\right]\hfill \\ -u_t-\Delta v+f^{0}v+g^{0}u)-\epsilon (\beta \Delta u+Su-f^{1}v-g^{1}u)\approx 0.\hfill \end{array}$$

(49)

It can be seen that for ${\eta }^u=0$ and ${\eta }^v=0$ the system (49) coincides with the system (47). Therefore, the nonlinear nonlocal system (47) has symmetry M for any functions $f^0$, $g^0$, $f^1$ and $g^1$. As a result, the corresponding nonlocally perturbed nonlinear Schrödinger Equation (46) admits the phase transformation for any function F.

At last, we consider approximate extensions of Galilean transformations. Let ${\tilde{X}}^0={\tilde{K}}_i$ in (48), where ${\tilde{K}}_i$ is defined by (28). Then, in view of the system (47), we have

$$\begin{array}{c}{D}_t\left({\eta }^u\right)+\Delta {\eta }^v-{\eta }^u(g^0+2uv{\left(f^0\right)}^{\prime }+2u^2{\left(g^0\right)}^{\prime })-{\eta }^v(f^0+2v^2{\left(f^0\right)}^{\prime }+2uv{\left(g^0\right)}^{\prime })\hfill \\ {\displaystyle \approx 2D_t\left(L{u}_{x_i}\right)-2{\int }_{-\infty }^t\Delta v_{x_i}d\tau -2\beta u_{x_i},}\hfill \\ -D_t\left({\eta }^v\right)+\Delta {\eta }^u-{\eta }^u(f^0+2u^2{\left(f^0\right)}^{\prime }-2uv{\left(g^0\right)}^{\prime })+{\eta }^v(g^0+2v^2{\left(g^0\right)}^{\prime }-2uv{\left(f^0\right)}^{\prime })\hfill \\ {\displaystyle \approx 2D_t\left(L{v}_{x_i}\right)-2{\int }_{-\infty }^t\Delta u_{x_i}d\tau +2\beta v_{x_i}.}\hfill \end{array}$$

If $f^0=0$ and $g^0=0$, this system coincides with (31). As a result, we conclude that in this case the system (47) admits nonlocal approximate symmetries $K_i^{\epsilon }$$(i=1,\dots ,n)$ from (33).

Thus, the nonlocally perturbed nonlinear Schrödinger Equation (46) with $F\left(\right|\psi \left|\right)=\epsilon F^1\left(\right|\psi \left|\right)$ has the Lie point symmetries T, $P_i$, $J_i$, M, and the nonlocal approximate symmetries $K_i^{\epsilon }$.

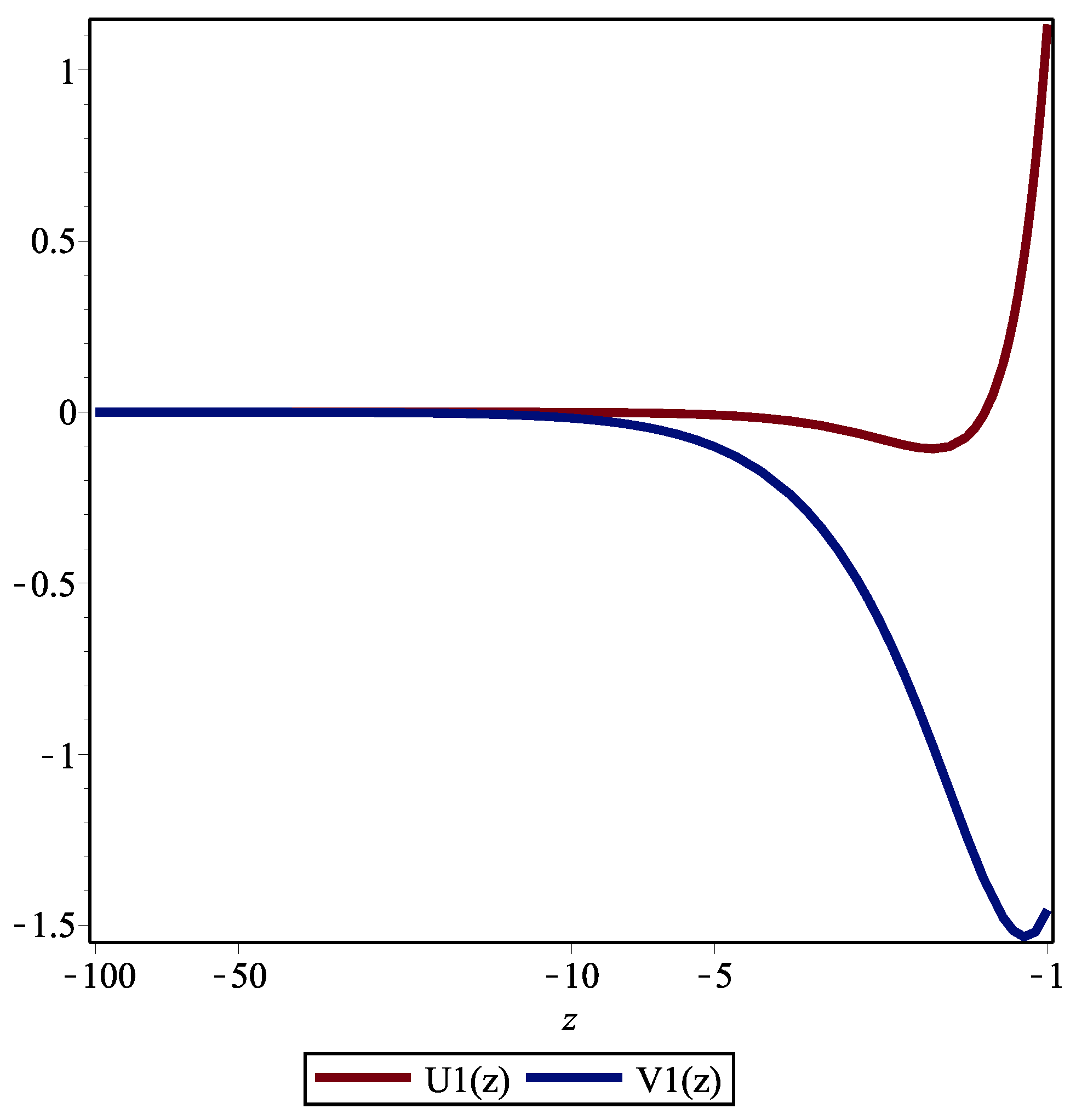
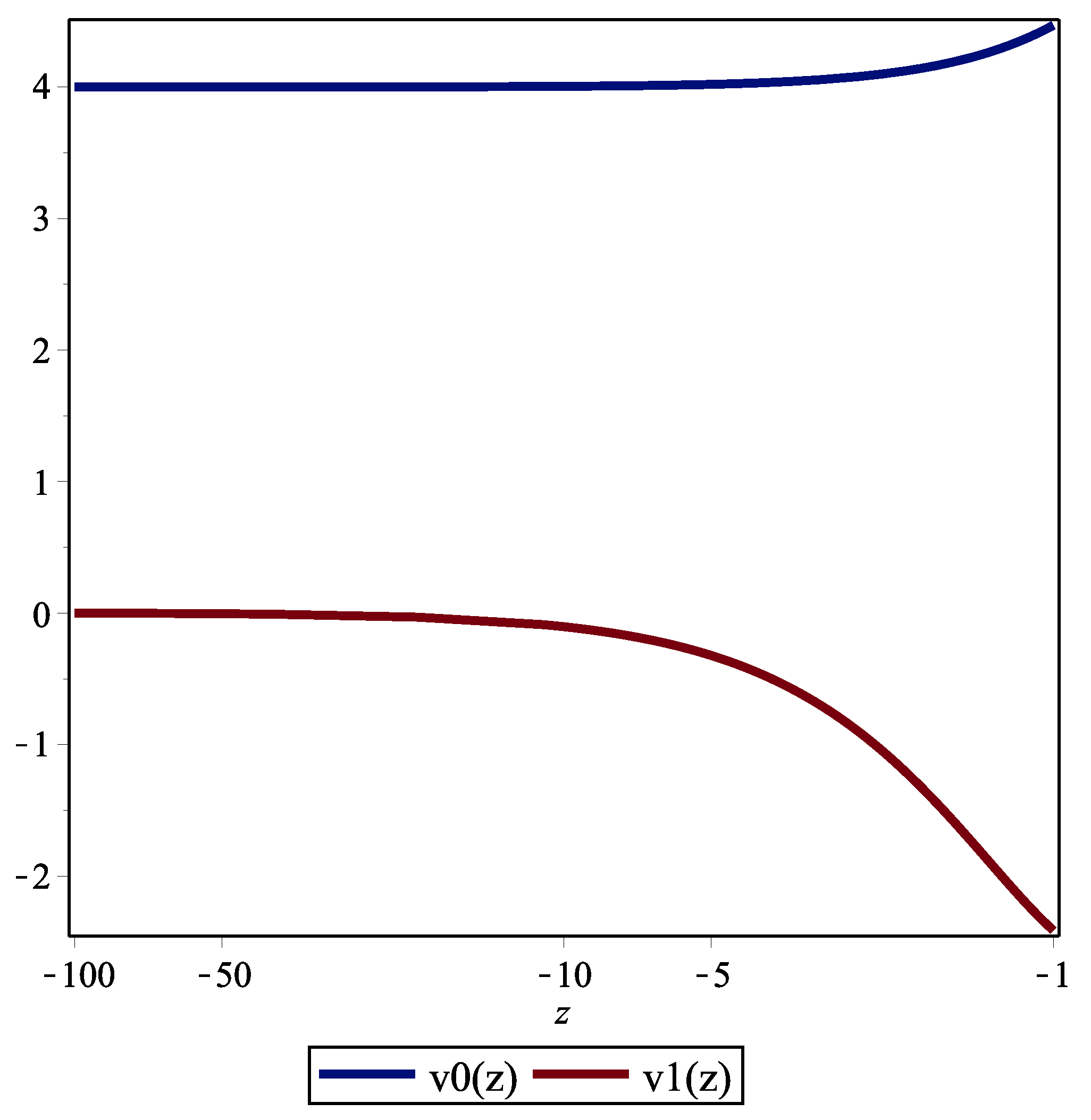
5. An Example of Approximate Solution

The symmetries in the previous section can be used to find approximate solutions to the system (17). To illustrate this possibility, we constructed an approximately invariant solution corresponding to the approximate scaling symmetry $D^{\epsilon }$ defined by (36). For simplicity, we considered the case of one spatial dimension ($x\in \mathbb{R}$).

First of all, it was necessary to find approximate invariants of the generator $D^{\epsilon }$. In the theory of approximate transformation groups [17] it has been proven that such invariants are written in the form

$$I(t,x,u,v,\epsilon )=I^0(t,x,u,v)+\epsilon I^1(t,x,u,v)+o\left(\epsilon \right),$$

and they are determined by the equation

$$D^{\epsilon }\left(I\right)=o\left(\epsilon \right).$$

In view of (36), this equation can be rewritten as the system

$$2t{\displaystyle \frac{\partial I^0}{\partial t}}+x{\displaystyle \frac{\partial I^0}{\partial x}}=0,2t{\displaystyle \frac{\partial I^1}{\partial t}}+x{\displaystyle \frac{\partial I^1}{\partial x}}=2t{\displaystyle \frac{\partial I^0}{\partial t}}.$$

Solving this system, we get three invariants:

$$u,v,{\displaystyle \frac{t}{x^2}}+2\epsilon lnx{\displaystyle \frac{t}{x^2}}.$$

As a result, we obtain the following form for the approximately invariant solutions of the system (17):

$$\begin{array}{c}u(t,x)=u_0\left(z\right)+2\epsilon lnxz{u}_0^{\prime }\left(z\right)+\epsilon u_1\left(z\right)+o\left(\epsilon \right),\hfill \\ v(t,x)=v_0\left(z\right)+2\epsilon lnxz{v}_0^{\prime }\left(z\right)+\epsilon v_1\left(z\right)+o\left(\epsilon \right),\hfill \end{array}$$

(50)

where $z=t{x}^{-2}$.

Substituting (50) into (17) and splitting the equations with respect to $\epsilon$, after simplification, we get

$$\begin{array}{c}{u}_0^{\prime }+6z{v}_0^{\prime }+2z^2{v}_0^{\prime \prime }=0,\hfill \\ -v_0^{\prime }+6z{u}_0^{\prime }+2z^2{u}_0^{\prime \prime }=0,\hfill \\ {\displaystyle u_1^{\prime }+6z{v}_1^{\prime }+2z^2{v}_1^{\prime \prime }=(10-6\beta )z{v}_0^{\prime }+(8-2\beta )z^2{v}_0^{\prime \prime }+{\displaystyle \frac{\partial }{\partial z}}{\int }_{-\infty }^{z}ln(z-s)u_0^{\prime }\left(s\right)ds,}\hfill \\ {\displaystyle -v_1^{\prime }+6z{u}_1^{\prime }+2z^2{u}_1^{\prime \prime }=(10-6\beta )z{u}_0^{\prime }+(8-2\beta )z^2{u}_0^{\prime \prime }-{\displaystyle \frac{\partial }{\partial z}}{\int }_{-\infty }^{z}ln(z-s)v_0^{\prime }\left(s\right)ds.}\hfill \end{array}$$

(51)

System (51) is a linear system of ordinary differential equations with respect to functions $u_0\left(z\right)$, $v_0\left(z\right)$, $u_1\left(z\right)$, $v_1\left(z\right)$. It can be also considered to be a first-order system with respect to functions

$$U_0\left(z\right)=u_0^{\prime }\left(z\right),V_0\left(z\right)=v_0^{\prime }\left(z\right),U_1\left(z\right)=u_1^{\prime }\left(z\right),V_1\left(z\right)=v_1^{\prime }\left(z\right).$$

(52)

Integration of the first and second equations in (51) yielded

$$U_0\left(z\right)={\displaystyle \frac{1}{z^3}}\left[C_{1}sin\left({\displaystyle \frac{1}{2z}}\right)+C_{2}cos\left({\displaystyle \frac{1}{2z}}\right)\right],$$

$$V_0\left(z\right)={\displaystyle \frac{1}{z^3}}\left[C_{2}sin\left({\displaystyle \frac{1}{2z}}\right)-C_{1}cos\left({\displaystyle \frac{1}{2z}}\right)\right].$$

Further, we restricted our consideration to the case $C_1=1$, $C_2=0$. The corresponding particular solution reads

$$U_0\left(z\right)={\displaystyle \frac{1}{z^3}}sin\left({\displaystyle \frac{1}{2z}}\right),V_0\left(z\right)=-{\displaystyle \frac{1}{z^3}}cos\left({\displaystyle \frac{1}{2z}}\right).$$

(53)

Integrating corresponding equations in (52), we obtained

$$u_0\left(z\right)={\displaystyle \frac{2}{z}}cos\left({\displaystyle \frac{1}{2z}}\right)-4sin\left({\displaystyle \frac{1}{2z}}\right),v_0\left(z\right)={\displaystyle \frac{2}{z}}sin\left({\displaystyle \frac{1}{2z}}\right)+4cos\left({\displaystyle \frac{1}{2z}}\right).$$

(54)

In view of (53), the third and fourth equations in (51) take the form

$$2z^2{V}_1^{\prime }+6z{V}_1+U_1=F\left(z\right),2z^2{U}_1^{\prime }+6z{U}_1-V_1=G\left(z\right),$$

(55)

where

$${\displaystyle F\left(z\right)={\displaystyle \frac{14}{z^2}}cos\left({\displaystyle \frac{1}{2z}}\right)+{\displaystyle \frac{4-\beta }{z^3}}sin\left({\displaystyle \frac{1}{2z}}\right)+{\displaystyle \frac{\partial }{\partial z}}{\int }_{-\infty }^z{\displaystyle \frac{ln(z-s)}{s^3}}sin\left({\displaystyle \frac{1}{2s}}\right)ds,}$$

(56)

$${\displaystyle G\left(z\right)=-{\displaystyle \frac{14}{z^2}}sin\left({\displaystyle \frac{1}{2z}}\right)-{\displaystyle \frac{4-\beta }{z^3}}cos\left({\displaystyle \frac{1}{2z}}\right)+{\displaystyle \frac{\partial }{\partial z}}{\int }_{-\infty }^z{\displaystyle \frac{ln(z-s)}{s^3}}cos\left({\displaystyle \frac{1}{2s}}\right)ds.}$$

(57)

Integrals in (56), (57) can be evaluated in closed form. In particular, for $z<0$ we have

$$\begin{array}{c}{\displaystyle {\int }_{-\infty }^z{\displaystyle \frac{ln(z-s)}{s^3}}sin\left({\displaystyle \frac{1}{2s}}\right)ds={\displaystyle \frac{2}{z}}\left[cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right)-sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right)\right]}\hfill \\ -4\left[cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right)+sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right)\right]+{\displaystyle \frac{2(ln2-\gamma )}{z}}cos\left({\displaystyle \frac{1}{2z}}\right)\\ \hfill -4(ln2-\gamma )sin\left({\displaystyle \frac{1}{2z}}\right)-8ln(-z)sin\left({\displaystyle \frac{1}{2z}}\right)+{\displaystyle \frac{4}{z}}ln(-z)cos\left({\displaystyle \frac{1}{2z}}\right)+4\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right),\end{array}$$

$$\begin{array}{c}{\displaystyle {\int }_{-\infty }^z{\displaystyle \frac{ln(z-s)}{s^3}}cos\left({\displaystyle \frac{1}{2s}}\right)ds=-{\displaystyle \frac{2}{z}}\left[cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right)+sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right)\right]}\hfill \\ -4\left[cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right)-sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right)\right]-{\displaystyle \frac{2(ln2-\gamma )}{z}}sin\left({\displaystyle \frac{1}{2z}}\right)\\ \hfill -4(ln2-\gamma )\left(1+cos\left({\displaystyle \frac{1}{2z}}\right)\right)-8ln(-z)cos\left({\displaystyle \frac{1}{2z}}\right)-{\displaystyle \frac{4}{z}}ln(-z)sin\left({\displaystyle \frac{1}{2z}}\right)-4\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right).\end{array}$$

Here

$$\mathrm{Si}\left(y\right)={\int }_0^y{\displaystyle \frac{sin\left(s\right)}{s}}ds,\mathrm{Ci}\left(y\right)=-{\int }_y^{\infty }{\displaystyle \frac{cos\left(s\right)}{s}}ds$$

are the sine and the cosine integrals, respectively. Substituting these representations for integrals in (56), (57), and performing the necessary calculations, we obtained

$$\begin{array}{c}F\left(z\right)={\displaystyle \frac{1}{z^3}}\left[18z+\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right)\right]cos\left({\displaystyle \frac{1}{2z}}\right)-{\displaystyle \frac{2}{z^2}}\hfill \\ \hfill +{\displaystyle \frac{1}{z^3}}\left[4-\beta +ln2-\gamma -4z^2+\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right)+2ln(-z)\right]sin\left({\displaystyle \frac{1}{2z}}\right),\end{array}$$

(58)

$$\begin{array}{c}G\left(z\right)=-{\displaystyle \frac{1}{z^3}}\left[18z+\mathrm{Si}\left(-{\displaystyle \frac{1}{2z}}\right)\right]sin\left({\displaystyle \frac{1}{2z}}\right)+{\displaystyle \frac{4}{z}}\hfill \\ \hfill +{\displaystyle \frac{1}{z^3}}\left[-4+\beta +ln2-\gamma -4z^2+\mathrm{Ci}\left(-{\displaystyle \frac{1}{2z}}\right)+2ln(-z)\right]cos\left({\displaystyle \frac{1}{2z}}\right).\end{array}$$

(59)

The general solution of system (55) with (58), (59) is

$$\begin{array}{c}{U}_1\left(z\right)={\displaystyle \frac{1}{z^3}}\left\{\left[C_{11}-2z-{\displaystyle \frac{2+ln\left(2\right)-\gamma +2ln(-z)}{2z}}\right]cos\left({\displaystyle \frac{1}{2z}}\right)+2z\right.\hfill \\ +\left[C_{21}+{\displaystyle \frac{4-\beta }{2}}-9ln(-z)\right]sin\left({\displaystyle \frac{1}{2z}}\right)+2\left[cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left({\displaystyle \frac{1}{2z}}\right)-sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left({\displaystyle \frac{1}{2z}}\right)\right]\\ \hfill \left.-{\displaystyle \frac{1}{2z}}\left[sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left({\displaystyle \frac{1}{2z}}\right)-cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left({\displaystyle \frac{1}{2z}}\right)\right]\right\},\end{array}$$

(60)

$$\begin{array}{c}{V}_1\left(z\right)={\displaystyle \frac{1}{z^3}}\left\{\left[C_{11}-2z-{\displaystyle \frac{2+ln\left(2\right)-\gamma +2ln(-z)}{2z}}\right]sin\left({\displaystyle \frac{1}{2z}}\right)+1\right.\hfill \\ +\left[-C_{21}+{\displaystyle \frac{4-\beta }{2}}+9ln(-z)\right]cos\left({\displaystyle \frac{1}{2z}}\right)+2\left[cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left({\displaystyle \frac{1}{2z}}\right)+sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left({\displaystyle \frac{1}{2z}}\right)\right]\\ \hfill \left.-{\displaystyle \frac{1}{2z}}\left[sin\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Ci}\left({\displaystyle \frac{1}{2z}}\right)-cos\left({\displaystyle \frac{1}{2z}}\right)\mathrm{Si}\left({\displaystyle \frac{1}{2z}}\right)\right]\right\},\end{array}$$

(61)

where $C_1$ and $C_2$ are arbitrary constants. For certainty, we set $C_{11}=C_{21}=0$. Both functions are plotted for $z<-1$ in Figure 1.

From (52) we have

$$u_1\left(z\right)=\int U_1\left(z\right)dz,v_1\left(z\right)=\int V_1\left(z\right)dz,$$

where $U_1\left(z\right)$ and $V_1\left(z\right)$ are defined by (60) and (61), respectively. Note that these integrals could not be evaluated explicitly, so we used numerical computations in Maple software.

The results of numerical computations for functions $u_1\left(z\right)$ and $v_1\left(z\right)$ are given in Figure 2 and Figure 3, respectively. The graphs of $u_0\left(z\right)$ and $v_0\left(z\right)$ from (54) are presented on the same figures. It can be seen that the functions $u_0\left(z\right)$ and $v_0\left(z\right)$ were positive for $z<-1$, whereas the functions $u_1\left(z\right)$ and $v_1\left(z\right)$ were negative. Therefore, in this example, the nonlocal terms in (17) were related to the opposite dynamics of the system.

To study the influence of a small parameter $\epsilon$ on the time dynamics of the system, approximate solutions of the form (50) were found at the point $x=1$ for three different values of $\epsilon$: 0.05, 0.1 and 0.2. The results of numerical computations are presented in Figure 4 and Figure 5. It can be seen that increasing the small parameter affected the dynamics significantly.

6. Conclusions

A nonlocally perturbed Schrödinger equation was derived in this paper by using a generalized nonlocal wave equation, which is used to investigate wave phenomena in an open system considered to be part of a closed Hamiltonian system under a weak coupling of these systems leading to weak infinite power-law memory effects. It has been proved that the linear nonlocally perturbed Schrödinger equation inherits all symmetries of the classical equation. In particular, this equation admits exact local groups of time and space translations, as well as the group of rotations. It means that the equation in question has exact classical, fundamental conservation laws, such as those for energy, momentum, and angular momentum. Moreover, the equation admits the exact group of phase transformations, and therefore the local conservation law for the probability density is fulfilled. The Galilei group and a group of projective transformations were inherited by the equation in a nonlocal sense. It meant that the corresponding conservation laws should also have been nonlocal ones. The group of dilations was inherited as an approximate local group of dilations; therefore, the equation possesses the property of approximate self-similarity.

Based on the exact and approximate symmetries, various approximate invariant solutions can be constructed for the nonlocally perturbed Schrödinger equation. Since this equation has exact time and space translation symmetries, it has different classes of traveling wave solutions. By using the approximate local scaling symmetry, a class of approximate self-similar solutions can be constructed for this equation. An example of a solution belonging to this class is presented in this paper. Next, the nonlocal Galilean-type and projective-type symmetries give the opportunity to find nonlocal approximate solutions for the equation. Classification of approximately invariant solutions can be performed based on an optimal system of subalgebras, which should be constructed for approximate symmetry algebra. These are topics for further research.