The Riemann–Liouville formulation will be defined slightly differently to (
1):
where
is the delayed-fractional order, which implies that, after the integral has been evaluated, the fractional order
is mapped to
. Notation-wise, the fractional order derivative operator (
19) will be written as
,
A similar scheme applies to the fractional integral operator (
2), which can be written as
. For the rest of the paper, only the derivative as defined by (
20) will be examined, for reasons of brevity, but the integral version of the integration of functions follows a similar argument. The proposition is that the fractional order can take a number of forms, such as:
In the conventional use of the fractional order, it is always taken as a constant
, with values that are real or complex,
or
. The second definition is a function that is independent of the integration variable
x. The third definition is a function of integration variable
x; however, when using this definition in (
21), it should be understood that this is not part of the integration. Only after the fractional derivative is obtained can
be used, as indicated by (
19) or (
20), i.e., this is a delayed order. The first case where
has always been dealt with in the literature. The second case
has recently been discussed in [
6]. The case of
will be examined here. On this basis, the definition for differentiation to functional order is straightforward: the fractional derivative of a function is obtained and the fractional order is replaced with an arbitrary continuous function
. Hence, the following notation is used:
This will represent the differentiation of a function
to functional order. This simple definition has some very powerful mathematical properties, which allow solutions to be obtained to a number of problems. In addition, differentiation to functional order allows for dualities to be found between distinct functions. In other words, two independent functions
and
can be made equivalent, in the sense that
Aside from functional orders
that satisfy the relation (
23), it should be noted that (
23) can also be used to obtain asymptotic solutions which can be thought of as ‘transitional’ functions or limits that are mixtures of the two functions
and
. Put another way, if the variable in the functional order is strictly time,
, then this has memory properties, encompassing past present and future states. If the functional order contains spatial dimensions, e.g.,
, then it has spatial correlation properties, a kind of spacial dimensional fading effect. In both cases, these are equivalent to or represented by the asymptotic solutions.
If the constant parameter
is added to the mathematical form of the functional order
, it can be used as the mechanism that picks out these asymptotic solutions. When
is set in the functional order, then
, and when
, then
, and the solutions provide the exact form of
. This requires solving the expression (
23) for
, which then makes it possible, through variations to
, to obtain
and
or any combination of them. Amongst other things, this establishes a duality between the two independent functions. In addition, the functional order
is an arbitrary continuous function with validity throughout the
x domain. If the entire domain is not required, then a more localised derivative order (approaching a constant or integer value) can be obtained by taking the series of
to any desired number of terms. In the following sections, differentiation to functional order will be demonstrated and, via the use of (
23), used to solve some interesting problems.
3.1. Applications of Functional Order Differentiation
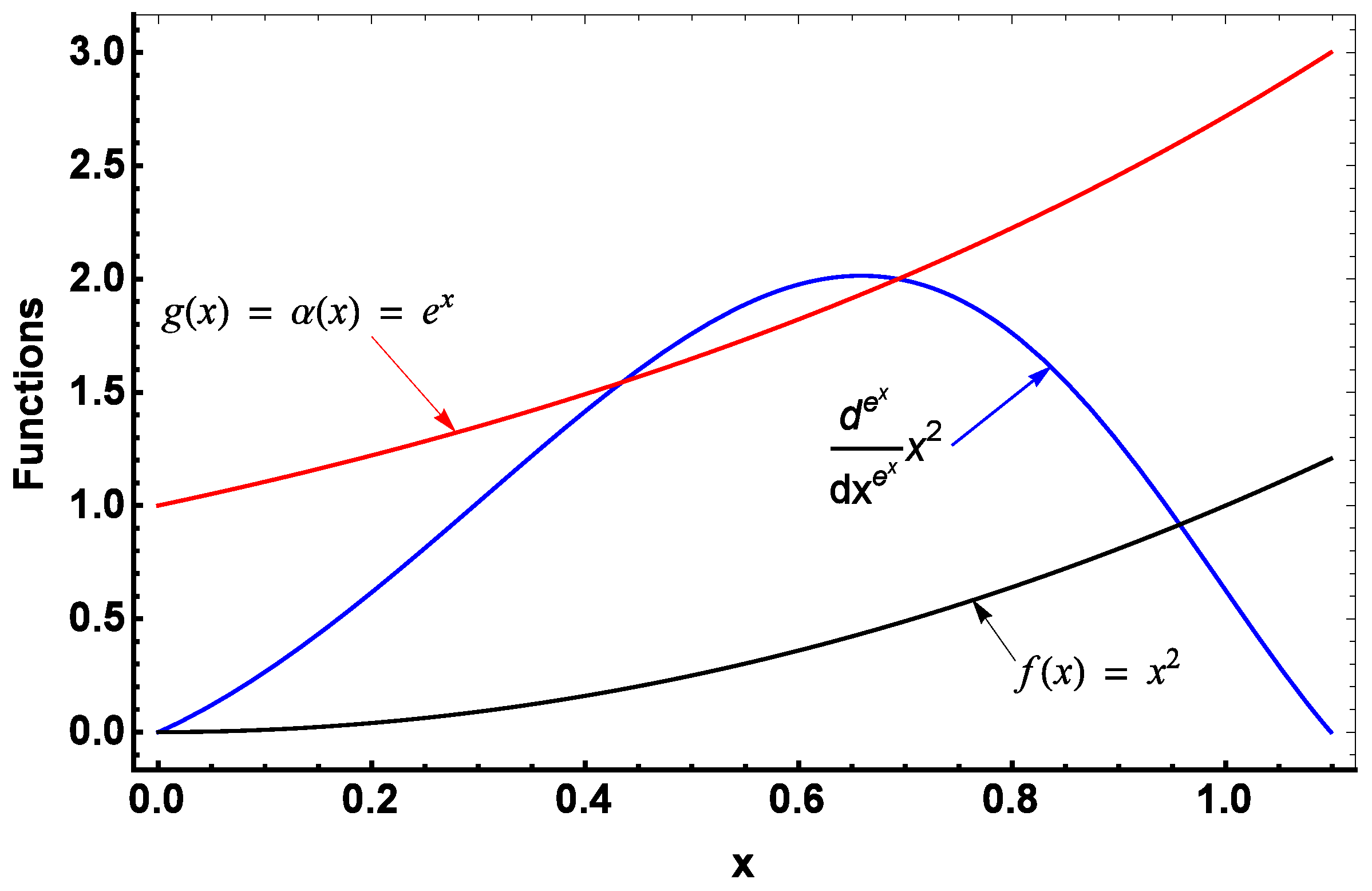
In this section, how functional differentiation can form dualities and asymptotic mixtures between various independent functions can be shown. Relating such functions is only possible via functional differentiation (integration). This is not possible with conventional fractional or integral differentiation. Consider the case of a monomial
, as discussed in
Section 2.1. Its derivative to functional order is given as follows:
for some functional orders,
. Equation (
24) can posses a number of interesting properties depending on the mathematical form of the functional order
. Suppose that the monomial is quadratic
with
, and let a second function be
. It is clear from
Figure 1 that
and
do not intersect for
. As they do not have any common solutions, they are independent functions. If the functional order is taken to be equal to the function
, for example, i.e.,
, then it is possible to relate the two independent functions so that they intersect. There are four solutions that are related by the derivative of
to functional order, as can be seen in
Figure 1. This is achieved via (
24) so that the derivative to functional order becomes:
Note that when
, (
25) reduces to the conventional integer derivative while the original function
corresponds to the case
in (
24). Hence, the function to the right of (
25) now encompasses solutions that belong to the two independent functions
and
.
Next, allow two alternative functions
and
to be considered. The solution that makes both of these functions equal and provides their asymptotic ‘transitions’ will be derived. Firstly, from (
23),
The left-hand side of (
26) has been calculated before; see (
17). Hence, (
26) becomes:
Equation (
27) holds if the functional order is given by:
with
. The constant
, but here this can be set to zero:
. Thus, the derivative of
to functional order
, as given by (
28) with
, provides the exact same result as function
. This is shown in
Figure 2, which also shows the function
, as well as asymptotic solutions corresponding to
,
and
. When
,
, so original function
is recovered. As the value of
increases from zero to
, the asymptotic solutions first resemble the function
, and then they approach and resemble
until the two are exact when
. Note that the asymptotic solutions approach the functions
and
from ‘above’, since the values for
are all less than
. However, they can also approach these functions asymptotically from ‘below’ if their values were
.
Another example of the use of differentiation to functional order is considered. From
Section 2, use can be made of the functional derivative of an exponential function:
Expanding the right-hand side of (
29) to the first order and setting the result to the original exponential function gives the following:
The functional order
that allows for expression (
30) to be exact is obtained as:
Substituting (
31) into (
30) and transposing gives the result:
Multiplying both sides by
a and setting
gives:
Taking the
n-th power of both sides and setting
gives,
Define the parameter
z as
and (
34) can be written as:
Equation (
36) is an equivalent way of writing the binomial expansion, i.e., it is an identity or there is a duality between the binomial expansion and the expression on the right of (
34). This duality may also allow for certain integrals to be performed more easily if, for example, integrals take the form:
or some variation of (
36). Here,
a and
b are functions or a combination of functions and constants, such that
. As an example, consider the relationship (
37) and its use to solve:
by setting
and
and where
and
is the exponential integral function. Thus, the complicated integral on the left is equivalent to a simple integral on the right, via the manipulation of (
37), which, in turn, can be determined in closed form. As another example, it can be shown that the integral on the left:
is equal to the closed form on the right, where
is the error-function,
and
and
. Similar expressions can be derived for other mathematical relations using the same approach as shown above. This highlights the power of using functional-order differentiation (integration) to form dualities between arbitrary and uniquely different functions. In what is to follow, functional order differentiation will be used to derive dualities and general relations in some physics and mathematics problems via the functional order.
3.2. Duality and Asymptotic Mixtures of Probability Densities
It is well-known that many physical, mathematical and engineering systems can be modelled via probability distributions. Using differentiation to functional order, a direct connection between different probability densities can be achieved when this is otherwise not possible. Consider the one-parameter Exponential-density with parameter
:
where the inverse of the parameter
is equal to the mean. In addition, consider the two-parameter Pareto-density, which has been extensively used in many research areas to model various processes. The ability to model some very important phenomena using the Pareto distribution has prompted its generalisation to a fractional form. Among other things, the fractional Pareto distribution has been successfully used to model the statistical properties of radar clutter returns in [
3], for example. The conventional Pareto density is given as follows:
The parameter
regulates the shape of the distribution and
is the support parameter. It is obvious that the two densities will have different distributions when compared to each other and cannot be equal, except for some cases where there is trivial overlap, typically at one or two intersections. No other solutions that make them both equal are possible. However, by using the differentiation to functional order approach, it will be shown that not only can they be made equal, but one can asymptotically approach the other. Let,
The left-hand side of (
42) for the Exponential-density involves the fractional differentiation of a negative exponential term, which was performed previously; see (
7). Then, replacing
with
provides the following form for (
42),
Observe that the conventional Exponential-density is recovered in (
43) when
. Furthermore, (
43) holds if, and only if, there is a functional order
that allows for this equivalence. In fact, this is true when
The substitution of (
44) into the left of (
43) collapses to the right side, i.e., the Pareto density. The functional-order (
44) can be rewritten as follows:
If
in (
45), this gives (
44) and, as a result, (
43) holds. Varying
above and below unity provides the asymptotic solutions to the Exponential density that, in the limit,
, tend towards and exactly match the Pareto density.
Figure 3 shows plots of the Pareto density for parameters
,
and the Exponential density parameter
for varying values of
, providing the exact curve that is produced by the Pareto density when
, and asymptotic solutions, as shown for
and
. Hence, via differentiation to functional order, a one-parameter density (Exponential model) produces the same mathematical properties as a two-parameter density (Pareto model). In this case, the Exponential density was not only generalised, but can also produce specific solutions corresponding to a different density, namely the Pareto, while also producing the asymptotic solutions that approach the latter in the limit
. Any
value that is greater than
, such as the one considered in
Figure 3, namely,
, will provide solutions that asymptotically approach the Pareto density from the right. As can be seen, solutions with
values approach the Pareto density from the left and, as
, solutions asymptotically approach the Exponential density, and equal it when
(not shown in
Figure 3 for reasons of brevity). The asymptotic solutions, as given by different values of
, except for
and
, are, in fact, mixed-probability densities consisting of a mixture of both the Exponential and Pareto densities, respectively.
3.3. Duality and Asymptotic Mixtures between the Gibbs–Shannon Entropy and the Hellinger Distance
As in the previous examples, consider another important application of differentiation to functional order that is of interest to physics, mathematics and engineering, including information geometry and information theory. Using the previously discussed differentiation method to functional-order, it will be shown that there is a duality between the Gibbs–Shannon entropy for a continuous probability density
and a metric distance between the same probability density and another density
with parameter space
and
, respectively, with
and
M providing the total number of parameters for each density. It has been shown that the fractional entropy for probability densities is given by [
6]:
where
is the domain of integration of the density and the modulus is used because the fractional-order
is not only real but can also be imaginary,
and
. It is worth pointing out that the analogue of (
46) for the discrete case of probability masses was derived by Ubriaco [
41]. The dissimilarity or divergence of the two probability densities can be determined using a metric distance, referred to as the Hellinger distance:
where (
47) is the square of the Hellinger distance. It should be obvious that both (
46) and (
47) will not provide the same result, as one is a measure of entropy and the other is a measure of the distance between the densities. Using differentiation to functional-order, it will be shown that there is a duality between the two formulations and both can give the same results. This duality will be established even though they each measure different properties between density/s: one being entropy and the other distance or divergence. In practice, this duality does not exist because the Gibbs–Shannon entropy is not a true distance metric as it is not symmetric and only measures entropy. On the other hand, the Hellinger formulation is symmetric and does obey the triangle inequality but measures distance and not entropy. Let the two densities be given as the Exponentials:
where their respective parameter spaces consist of only one parameter, namely,
and
. Equation (
46) is already in fractional form, so there is no need to obtain the fractional derivative. If
is substituted, this gives:
for the fractional entropy. A duality between the entropy and the Hellinger distance can be claimed for some functional-order
, such that:
In fact this is true and (
50) holds if
when
. It can be shown that when (
51) is substituted into the entropy on the left of (
50), it collapses to the Hellinger expression on the right, hence establishing a duality between them. This duality was achieved via the application of functional-order differentiation to conventional entropy.
Numerical solutions can be obtained for the parameter values
and
, for example. The conventional entropy then gives:
On the other hand, the square of the Hellinger distance between the densities
and
cannot be the same as the entropy for the density
, as expected. The square of the Hellinger distance becomes:
Using the fractional entropy and the functional-order
, as given by (
51), with
:
gives the value:
in agreement with the Hellinger distance (
53). Hence, a duality is established between them. Notice that if the square root of the right side is taken in (
53), then the same can be taken for (
55); they are equal either way. Asymptotic solutions between the Gibbs–Shannon and Hellinger formulations can also be obtained using (
51) for varying
, which will be referred to as asymptotic divergences. When
, the fractional entropy is equivalent to the Hellinger distance or divergence; that is, when
,
as established above. Setting
in (
51) provides the conventional entropy result, i.e.,
Figure 4 shows numerical values for the asymptotic divergences between the conventional entropy and the square of the Hellinger distance as a function of
. The numerical asymptotic divergence values that are bounded by the conventional entropy and Hellinger distance were plotted for
in steps of
. The first value on the left, corresponding to
, gives the exact solution as obtained from the Hellinger distance. As
varies and becomes equal to the last value on the right, i.e., when it is
, the solution is exactly the same as that given by the conventional entropy. For
values that lie between them, asymptotic divergence solutions are obtained, which are due to a ‘mixture’ of the two, depending on how close
is to one or the other. As a result, a minimum asymptotic divergence value exists between them when
. This indicates, among other things, where the conventional entropy and Hellinger distance have similar mathematical characteristics, while also minimising their respective probability densities. Finally, returning to the fact that (
49) and (
51) establish a duality between the conventional entropy and the Hellinger distance when
, it stands to reason that there can be other valid solutions, depending on the mathematical form of
. For example, if the functional order is a constant value instead of a function, i.e., if
, for example, then it is possible to obtain the same result for the fractional entropy as when the functional order
was a continuous function (
51). Substituting this into (
55) gives:
as before. This means that the entropy can also obtain the same result as the Hellinger formulation when the functional order is equal to a complex constant and not just a function. By differentiating the entropy to functional order, it was possible to find a duality between the conventional entropy and the Hellinger distance, as well as their asymptotic divergence solutions (mixture), not withstanding the fact that the two are completely different mathematical formulations.
3.4. Dualities between Higher-Dimensional Geometries and the Functional Order in Quantum Mechanics
Higher-dimensional spheres or hyperspheres have been of tremendous interest in the study of the effective properties of materials, since they exhibit interesting electromagnetic behaviour when they contain these hyperspheres as inclusions. The scattering effects of hyperspheres have been studied, and so has their use in metamaterial structures for example [
42]. Hyperspheres, and other hypergeometries such as hypercubes, are used in the study of error rate and data correction algorithms or in packing geometries. Functional-order differentiation will be used to examine the dualities between the functional order and the dimension of hyperspheres and hypercubes. These hypergeometries and, in particular, the geometry of hyperspheres, can represent quantum mechanical particles and their classical and relativistic properties. On this basis, consider the functional derivative
of the hypervolume of a hypersphere, which can be calculated from:
where
is the hypervolume of a hypersphere. The modulus is included because, in principle,
and
. From this, the functional variation in the hypervolume of a
d-dimensional sphere (hypersphere) is given by:
where
d is the dimension,
is the functional order and
R is the radius of the hypersphere.
The functional change in the hypervolume of a hypercube is obtained as follows:
where
L is the side length of the hypercube. The radius of a hypersphere
R is related to the length
L of a hypercube by the following:
where
. The functional order, which provides equal hypervolumes between hyperspheres and hypercubes is given by:
Hence, for the case represented in
Figure 5, the functional order can be determined from (
63) and is
. The hypervolume of the hypersphere starts from above 80 on the left in magenta and the hypervolume of the hypercube starts below 40 on the left in blue. The volume of a regular cube is constant as represented by the horizontal orange line. For the given parameters, the functional order
makes the hypervolumes/volume equal. The functional order
given by (
63) not only provides the duality or connection between the hyperspherical and hypercubic geometries, but also does the same for the relativistic energies of particles with such geometries. The relativistic energy of a hyperspherical particle is given by the following:
where
is the density of the mass,
c is the speed of light and
u is the speed of the hypersphere, respectively. Similarly, the energy of a hypercube particle is given by the following:
The rest energy
of a hypersphere or hypercube particle is given by (
64) and (
65) when
, respectively. For non-relativistic speeds
, the energies reduce to
(HyperSphere) and
(HyperCube), respectively:
and
where
is the rest energy (
64) and
is the rest energy (
65), i.e., when
. If a hypersphere and a hypercube particle have the same density and the same velocity, the ratio of their energies
is given by the following:
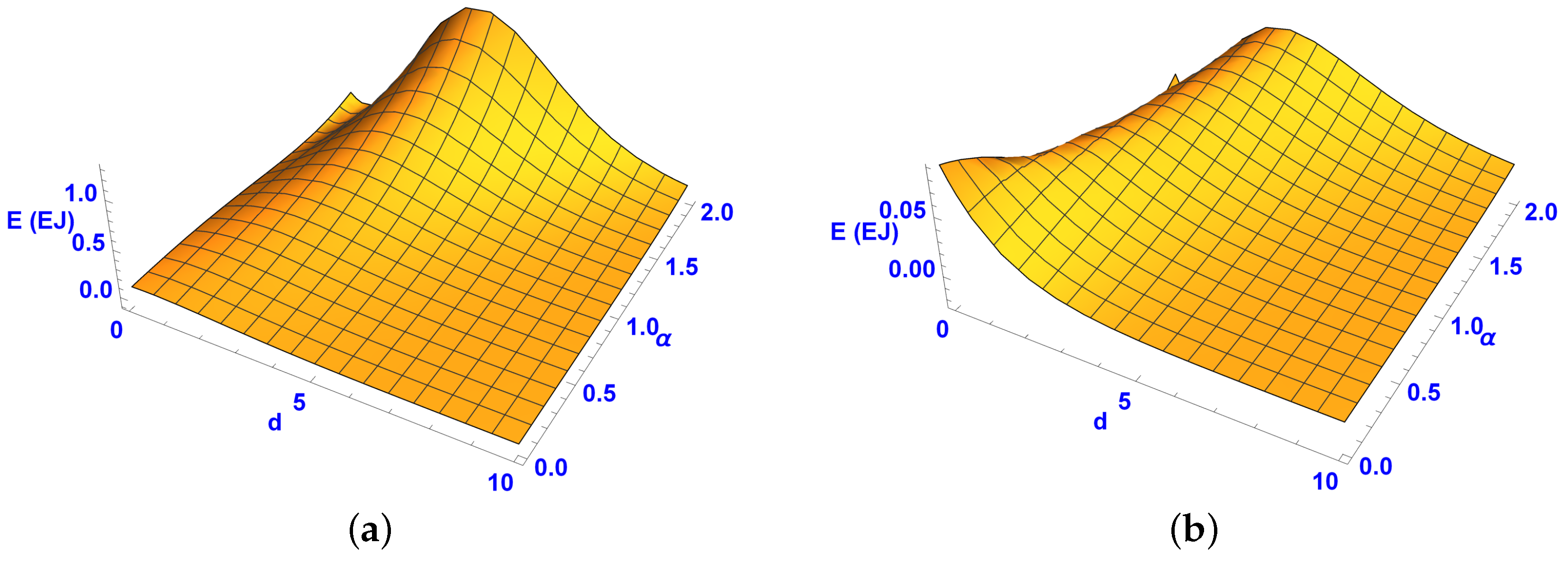
Figure 6 shows the relationship between the rest energy, functional order and fractal dimension of hypersherical and hypercube particles as a comparison. Referring to
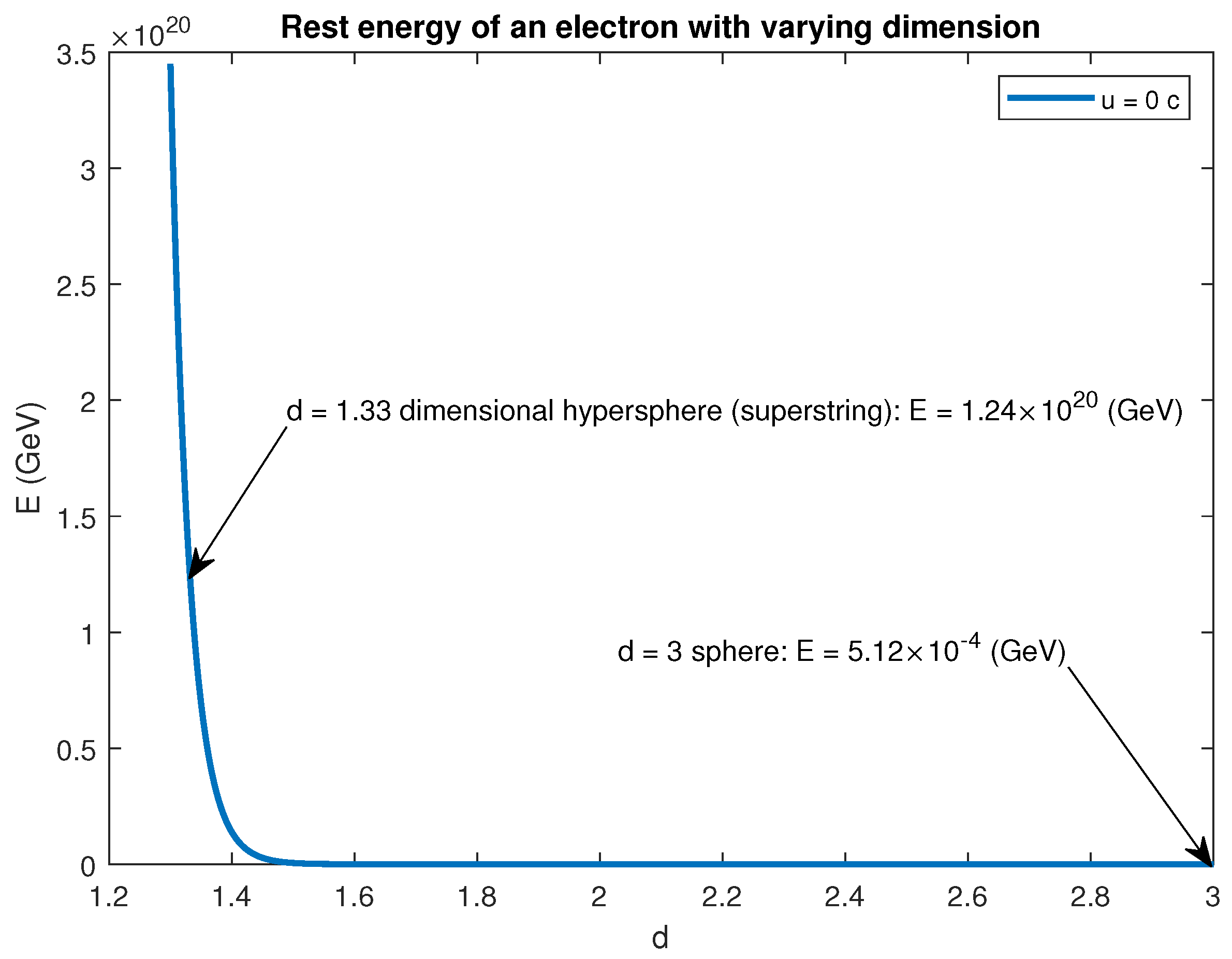
Figure 7 and
Figure 8, consider the case where an electron is assumed to be a hypersphere (functional order
). When the electron is assumed to have a spherical geometry,
, the corresponding energy agrees with the theory. When the same electron is assumed to have the energy of a typical open superstring of Planck length and energy, the dimension is fractal at
. Superstrings are considered to be approximately
dimensional from the macroscopic perspective but, in reality, they possess an internal geometry that arises from their vibration in Calabi–Yau manifolds. The figures show that the fractal dimension of the superstring (electron), namely,
, ‘drops’ out from extrapolating the dimension as the energies increase and match the expected values from the theory; see
Figure 7 for the particle at rest and
Figure 8 when it is moving at
. Revisiting the hypersphere volume (
60), a hyper-particle of radius
and even dimensions provides a hypervolume variation,
where
and
. Summing (
69) to infinity, i.e., summing all even dimensional hypervolumes to infinite dimensions, gives the closed form:
where
is the regularised generalised hypergeometric function. This means that the sum of all relativistic energies for even dimensional hyperparticles of radius one is given by the following:
If the velocity of the hyperparticles is
, then:
An interesting result is obtained for the sum of the rest energies of all the even-dimensional hyperparticles. If the hypervolume is considered, i.e.,
when
in (
71) or (
72), the total energy becomes:
This can easily be seen if one considers the sum in (
70)
In a similar way, for
and
, the energies become:
and
respectively, etc. These results are very interesting and raise a number of further questions that need to be answered, such as determining their physical interpretation.