Ayatutu as a Framework for Mathematics Education: Integrating Indigenous Philosophy with Cooperative Learning Approaches

Abstract

This article explores the integration of “Ayatutu”, a communal philosophy from Nigeria’s Tiv people, into mathematics education frameworks. Ayatutu—embodying collective responsibility and mutual assistance—aligns with contemporary cooperative learning approaches while offering unique cultural dimensions. Through analysis of the ethnomathematics literature, indigenous knowledge systems, and cooperative learning theories this article develops a theoretical framework for Ayatutu-based mathematics instruction built on the following five core elements: collective problem-solving, resource sharing, complementary expertise, process orientation, and intergenerational knowledge transfer. The framework demonstrates significant alignment with sociocultural learning theory, communities of practice, and critical pedagogy while also offering potential benefits including enhanced mathematical engagement, positive identity development, stronger learning communities, and cultural sustainability. Implementation challenges involving teacher preparation, structural constraints, cultural translation, and balancing individual with collective learning are examined. This research contributes to decolonizing mathematics education by positioning indigenous philosophical systems as valuable resources for creating culturally responsive and mathematically powerful learning environments that serve diverse student populations while honoring cultural wisdom.

1. Introduction

Mathematics education continues to evolve beyond conventional transmissive teaching approaches toward more collaborative, student-centered methodologies that emphasize conceptual understanding and mathematical thinking [1,2]. Despite these advancements, mathematics remains challenging for many students, particularly those from cultural backgrounds where traditional Western mathematical approaches may conflict with indigenous ways of knowing and learning [3,4,5]. In response, researchers and educators have increasingly advocated for culturally responsive mathematics pedagogy that incorporates diverse cultural perspectives and indigenous knowledge systems [6,7,8]. The need for such approaches is particularly evident when considering the disconnect many students experience between their cultural worldviews and conventional mathematics instruction, which often emphasizes individual achievement and competition rather than collaborative knowledge construction.

The Tiv people, residing predominantly in Nigeria’s Middle-Belt region, possess a rich cultural heritage characterized by communal living and collective responsibility. Central to their societal values is “Ayatutu”, which translates to “we, the Tiv, are the ones”, and embodies communal responsibility, collective problem-solving, and mutual assistance [9,10,11]. ‘Ayatutu’ underscores the importance of unity and shared purpose, serving as both a philosophical framework for understanding social relationships and a practical approach to addressing community challenges. This indigenous concept represents a worldview where knowledge and skills are shared resources and learning is a collective endeavor rather than an individual pursuit. Within Tiv communities, the application of Ayatutu principles facilitate social cohesion, resource distribution, conflict resolution, and knowledge transmission across generations, demonstrating its versatility as a cultural practice with implications extending beyond immediate social contexts. While Ayatutu has been examined within contexts of social organization, conflict resolution, and community development [12,13,14], its potential application in educational settings—particularly mathematics education—remains largely unexplored despite its natural alignment with contemporary educational theories emphasizing collaborative learning and social knowledge construction. This paper aims to bridge this gap by investigating how the Tiv philosophy of Ayatutu can be integrated theoretically into mathematics education frameworks to enhance collaborative problem-solving and cooperative learning. The research addresses the following questions:

• How do the principles of Ayatutu align with contemporary theories of cooperative learning in mathematics education?
• What might an Ayatutu-based mathematics learning environment look like in practice?
• What potential benefits might emerge from implementing Ayatutu principles in mathematics classroom settings?
• What challenges might educators face when integrating Ayatutu concepts into mathematics instruction?

These questions guide the theoretical exploration of Ayatutu as an indigenous philosophical framework with potential contributions to mathematics education practice and theory, particularly in contexts where cultural relevance and collaborative learning are valued educational goals. Examining these questions, this paper seeks to contribute to the ongoing discussions about decolonizing mathematics education and recognizing the value of indigenous knowledge systems in contemporary educational contexts. The investigation draws on the literature from mathematics education, cooperative learning theories, ethnomathematics, and cultural studies to develop a theoretical framework for Ayatutu-based mathematics instruction. This interdisciplinary approach acknowledges the complexity of integrating cultural philosophies into educational practice and the need to consider both cultural authenticity and educational effectiveness. The theoretical framework proposed in this paper synthesizes insights from these diverse fields to articulate how Ayatutu principles might manifest in mathematics classrooms, what structures would support their implementation, and how they might complement existing approaches to mathematics teaching and learning. The researcher hopes that this examination of indigenous philosophy through an educational lens will contribute to the growing body of research on culturally responsive mathematics pedagogy and indigenous knowledge systems in education, offering both theoretical insights and practical implications for creating mathematics learning environments that honor cultural wisdom while developing powerful mathematical understanding among diverse student populations.

Author’s Positionality

As a Tiv scholar born and raised in Tiv land (Benue State, Nigeria), my engagement with Ayatutu philosophy is deeply rooted in lived experience, cultural immersion, and personal identity. Ayatutu is not merely an academic subject for me—it forms the ethical and philosophical foundation of my upbringing, community life, and worldview. This insider perspective allows me to interpret and articulate Ayatutu not only through scholarly inquiry but also from the standpoint of someone who has internalized its principles from childhood through family, community interactions, and traditional practices.

My academic journey, however, has taken place within predominantly Western educational institutions, which inevitably shapes how I theorize and present indigenous knowledge systems like Ayatutu. I am conscious of the epistemological tensions that arise when indigenous philosophies are translated into academic discourse and I strive to navigate these tensions with cultural integrity and scholarly rigor.

This paper reflects a long-standing commitment to bridging indigenous Tiv philosophies and contemporary educational theory, especially in mathematics education. Over the past fifteen years, I have engaged in sustained collaboration with Tiv educators, community elders, and knowledge holders. Their insights and lived knowledge have critically informed the theoretical framework presented here. Rather than positioning myself as a detached observer, I approach this work as a cultural participant and academic facilitator, aiming to co-construct knowledge that honors the depth of Ayatutu while situating it meaningfully within global educational discourse.

By foregrounding my positionality, I acknowledge both the privileges and responsibilities that come with being a cultural insider interpreting indigenous knowledge within academic spaces. I invite readers to engage with this work as both a scholarly contribution and a culturally situated reflection that seeks to affirm the value and contemporary relevance of Tiv epistemologies.

2. Literature Review

2.1. Understanding Ayatutu: Principles and Practices

Ayatutu is a central philosophical concept in Tiv culture that represents the idea of communal living, shared responsibility, and collective problem-solving [9,11]. The term “Ayatutu” literally translates to “sitting together” or “working together”, embodying the Tiv belief that community challenges are best addressed through collaborative efforts [15]. This philosophy manifests in various aspects of traditional Tiv society, including economic activities (communal farming), social organization (age-grade systems), and governance structures (council of elders). Ref. [10], in his seminal ethnographic work on Tiv social structure, observed that Ayatutu serves as both a practical strategy for resource maximization and a moral framework that emphasizes mutual care and responsibility. The philosophy operates on the following key principles:

• Collective responsibility: Problems affecting individuals are considered community concerns requiring community responses [11].
• Resource sharing: Knowledge, skills, and material resources are shared for the collective benefit of the community [15].
• Complementary expertise: Different individuals contribute different skills and knowledge to solve problems collaboratively [10].
• Process orientation: The process of working together is valued as much as the outcome [16].
• Intergenerational knowledge transfer: Wisdom and knowledge flow between generations through collaborative activities [9].

Ref. [17] notes that Ayatutu extends beyond mere cooperation to encompass a holistic worldview where individual identity is intrinsically connected to community membership. This profound philosophical dimension positions Ayatutu not simply as a pragmatic approach to social organization but as a comprehensive ontological framework that shapes how Tiv people understand their place in the world and their relationships with others. The concept fundamentally challenges Western individualistic notions of selfhood by emphasizing the primacy of communal bonds and collective identity formation. This perspective resonates with Ubuntu, a philosophical concept originating specifically from Southern African cultures (particularly among the Nguni language groups, including Zulu, Xhosa, and Ndebele peoples), which emphasizes that “I am because we are” [18]. Ubuntu, with its roots in the Bantu languages of Southern Africa, has been articulated by scholars such as the authors of [19,20,21] as a philosophy emphasizing communality, human interdependence, and ethical responsibility toward others. While Ayatutu and Ubuntu emerged from different regions and cultural contexts within Africa, the resonance between these philosophies illustrates how certain indigenous African traditions share fundamental principles regarding the relational nature of human existence while still maintaining their distinct cultural characteristics and contextual expressions.

The comparison between Ayatutu and Ubuntu is not intended to homogenize African philosophical traditions but rather to illustrate how similar ethical and communal principles have emerged in different cultural contexts across the continent, each with their own unique expressions, applications, and historical developments. This recognition of both commonality and specificity helps position Ayatutu within broader philosophical discourse while respecting its distinct cultural origins and particular manifestations within Tiv society.

While Ayatutu has been documented primarily in anthropological and cultural studies, its educational dimensions remain largely unexplored in systematic research. The principles that guide communal living and collective problem-solving among the Tiv have not been extensively examined for their potential contributions to formal educational theory and practice, creating a significant gap in the literature. Ref. [22] briefly mentioned how traditional Tiv education incorporated Ayatutu principles through apprenticeship systems and communal learning activities, where knowledge was transmitted through participation in authentic community practices rather than through decontextualized instructions. However, this early account did not elaborate on specific pedagogical approaches or provide detailed analysis of the learning processes involved in these traditional educational contexts. This lack of educational research on Ayatutu represents a missed opportunity to understand how indigenous knowledge systems might inform contemporary educational practices, particularly in mathematics education where collaborative approaches are increasingly valued yet often implemented without cultural grounding.

2.2. Cooperative Learning in Mathematics Education

Cooperative learning represents a structured pedagogical approach where students work together in small groups toward shared academic goals while being held individually accountable for their learning [23,24]. This systematic instructional methodology differs significantly from casual group work by incorporating specific structures and processes designed to maximize both individual learning and group success through intentional collaboration. This approach has gained significant traction in mathematics education due to its demonstrated benefits for conceptual understanding, problem-solving abilities, and mathematical communication [25]. Educational researchers have documented how cooperative learning environments provide rich opportunities for students to articulate mathematical thinking, encounter diverse solution strategies, and develop deeper conceptual connections that often remain underdeveloped in traditional individualistic mathematics instruction [26,27,28].

Johnson and Johnson [23] identify the following five essential elements of effective cooperative learning:

• Positive interdependence: Requires that students perceive that they are linked with others such that one cannot succeed unless everyone succeeds, creating mutually beneficial relationships and shared commitment to learning outcomes.
• Individual accountability: Ensures that each group member is held accountable for their contribution and learning, preventing the “free-rider effect” that can undermine group effectiveness.
• Promotive interaction: Involves students encouraging and facilitating each other’s efforts through explanation, discussion, and mutual support in ways that advance collective understanding.
• Social skills: Requires students to develop and practice interpersonal and small-group skills essential for collaboration, including communication, trust-building, and conflict resolution.
• Group processing: Involves groups reflecting on and discussing how well they are achieving their goals and maintaining effective working relationships, fostering metacognitive awareness of both mathematical learning and collaborative processes.

These elements can be seen to align conceptually with several Ayatutu principles, suggesting potential compatibility between the Tiv philosophy and cooperative learning approaches, particularly in their shared emphasis on collective success, mutual support, and complementary contributions.

Research indicates that cooperative learning in mathematics produces significant benefits compared to individualistic or competitive approaches across diverse educational contexts and student populations. Ref. [29] found that cooperative learning improved mathematics achievement across multiple grade levels and mathematical topics, with effect sizes suggesting meaningful educational impact beyond statistical significance. Similarly, Ref. [30] documented improvements in mathematical problem-solving, reasoning, and communication skills among students engaged in cooperative learning activities, noting that these improvements extended to both procedural fluency and conceptual understanding. These findings are consistent with meta-analyses that have repeatedly demonstrated the effectiveness of well-structured cooperative learning in mathematics [24,31]. Beyond academic achievement, cooperative learning fosters positive interdependence, enhances student attitudes toward mathematics, reduces mathematics anxiety, and develops mathematical identity [32,33]. These affective and identity-related outcomes often persist beyond specific mathematical content learning, influencing students’ long-term relationship with mathematics and their willingness to pursue advanced mathematical study. These outcomes are particularly significant for students from underrepresented groups who may experience alienation in traditional mathematics classrooms [34,35] as cooperative approaches can create more inclusive learning communities that validate diverse perspectives and approaches to mathematical thinking.

2.3. Ethnomathematics and Culturally Responsive Mathematics Pedagogy

Ethnomathematics, a term coined by the authors of [36], refers to the study of mathematical practices and concepts within their cultural contexts. This field recognizes that mathematical thinking exists across all cultures, though it may manifest in forms different from conventional Western mathematics [5]. Ethnomathematics challenges the notion of mathematics as a culturally neutral discipline and advocates for acknowledging diverse mathematical traditions [4]. Research in ethnomathematics has documented sophisticated mathematical thinking embedded in cultural practices including weaving patterns, navigation systems, architectural designs, and games [3,37,38]. These studies demonstrate that mathematics emerges from human activities and cultural needs rather than existing solely as an abstract discipline.

Building on ethnomathematical perspectives, culturally responsive mathematics pedagogy seeks to incorporate students’ cultural backgrounds and experiences into teaching and learning [7,8]. This approach aims to make mathematics more accessible and relevant by connecting mathematical concepts to students’ lived experiences and cultural knowledge. Integrating cultural elements into mathematics education has been shown to enhance student engagement and understanding. For instance, African traditional games like Mancala have been utilized to teach mathematical concepts, demonstrating the effectiveness of culturally relevant pedagogy [39]. A study by the authors of Ref. [40] examined how incorporating Indigenous Papuan cultural contexts into math word problems helped students solve them more accurately, thereby reducing errors. Similarly, Ref. [41] explored the use of Akan traditional art to improve conceptual understanding in geometry among senior high school students, highlighting the effectiveness of culturally relevant pedagogy.

Culturally responsive mathematics pedagogy operates on the following principles:

• Cultural validation: Recognizing and valuing the mathematical knowledge embedded in students’ cultural backgrounds [42].
• Cultural bridge-building: Creating connections between students’ cultural knowledge and conventional mathematical concepts [34].
• Cultural competence: Developing students’ abilities to operate effectively within their home cultures and the broader mathematical community [8].
• Critical consciousness: Empowering students to recognize and challenge inequities in mathematics education [43].

Studies have shown that culturally responsive mathematics instruction positively impacts student engagement, mathematical identity development, and academic achievement across diverse educational contexts [44,45]. These benefits emerge when mathematics instruction acknowledges, incorporates, and builds upon the cultural knowledge, experiences, and perspectives that students bring to the classroom, creating learning environments where students see themselves and their communities reflected in mathematical activities. The research consistently demonstrates that when students perceive mathematical learning as connected to their cultural identities and everyday experiences they demonstrate greater persistence, deeper conceptual understanding, and more positive attitudes toward mathematics as a discipline [46,47,48]. This approach is particularly beneficial for students from non-dominant cultural backgrounds who may experience a disconnect between their cultural experiences and conventional mathematics instruction, which often implicitly privileges Western mathematical traditions and individualistic approaches to learning. For these students, culturally responsive mathematics instruction can help bridge the gap between home and school knowledge systems, reducing cognitive dissonance and providing more accessible entry points into mathematical concepts. The integration of indigenous philosophies like Ayatutu into mathematics education represents a promising avenue for culturally responsive pedagogy, particularly for students from cultural backgrounds where collective approaches to problem-solving are valued. By drawing on cultural resources such as Ayatutu, mathematics educators can create learning environments that not only honor students’ cultural identities but also leverage indigenous wisdom to enhance mathematical understanding through approaches that may align more closely with students’ ways of knowing and learning.

2.4. Indigenous Knowledge Systems in Education

Indigenous knowledge systems (IKSs) represent the accumulated wisdom, practices, and beliefs that indigenous communities have developed through generations of interaction with their environments [49]. These knowledge systems often embody holistic worldviews that integrate spiritual, ecological, social, and practical dimensions of life [50]. Within African contexts specifically, scholars such as [51,52,53] have demonstrated how indigenous knowledge systems provide epistemological foundations that challenge Eurocentric approaches to education. Refs. [51,54] argues that African indigenous knowledge systems are characterized by their relationality, communalism, and integration of spiritual and material dimensions of existence. Ref. [52] highlight how African IKSs emphasize learning through community participation, oral tradition, and apprenticeship—approaches that stand in contrast to the often individualistic and text-based learning privileged in Western educational systems.

Several distinctive characteristics define African indigenous knowledge systems in educational contexts. Ref. [55] identifies the holistic perspective, where knowledge is interconnected rather than compartmentalized into discrete subjects. Ref. [56] emphasizes contextual learning, where knowledge is deeply embedded in specific cultural, ecological, and social contexts. Ref. [57] discusses relational epistemology, where knowledge emerges from relationships between people and between people and their environment. These systems often prioritize the oral tradition and employ apprenticeship learning approaches [58].

In mathematics education specifically, researchers have explored how African indigenous knowledge systems inform mathematical thinking. Ref. [38] has extensively documented mathematical thinking in African cultural practices, particularly in relation to geometric patterns in crafts, architecture, and games. Ref. [59] has examined mathematical concepts embedded in indigenous South African games and their potential applications in formal mathematics education. These studies reveal sophisticated mathematical thinking that emerged from practical needs and esthetic considerations within African cultural contexts. The integration of Ayatutu into mathematics education builds upon this growing body of research on African indigenous knowledge systems, contributing to efforts to decolonize mathematics education by centering African philosophical approaches and cultural wisdom.

3. Theoretical Framework: Ayatutu-Based Mathematics Education

Building on the literature reviewed, this section proposes a theoretical framework for integrating Ayatutu principles into mathematics education. The framework, as shown in Figure 1, synthesizes elements from cooperative learning theories, ethnomathematics, and culturally responsive pedagogy while centering on the core principles of the Tiv Ayatutu philosophy.

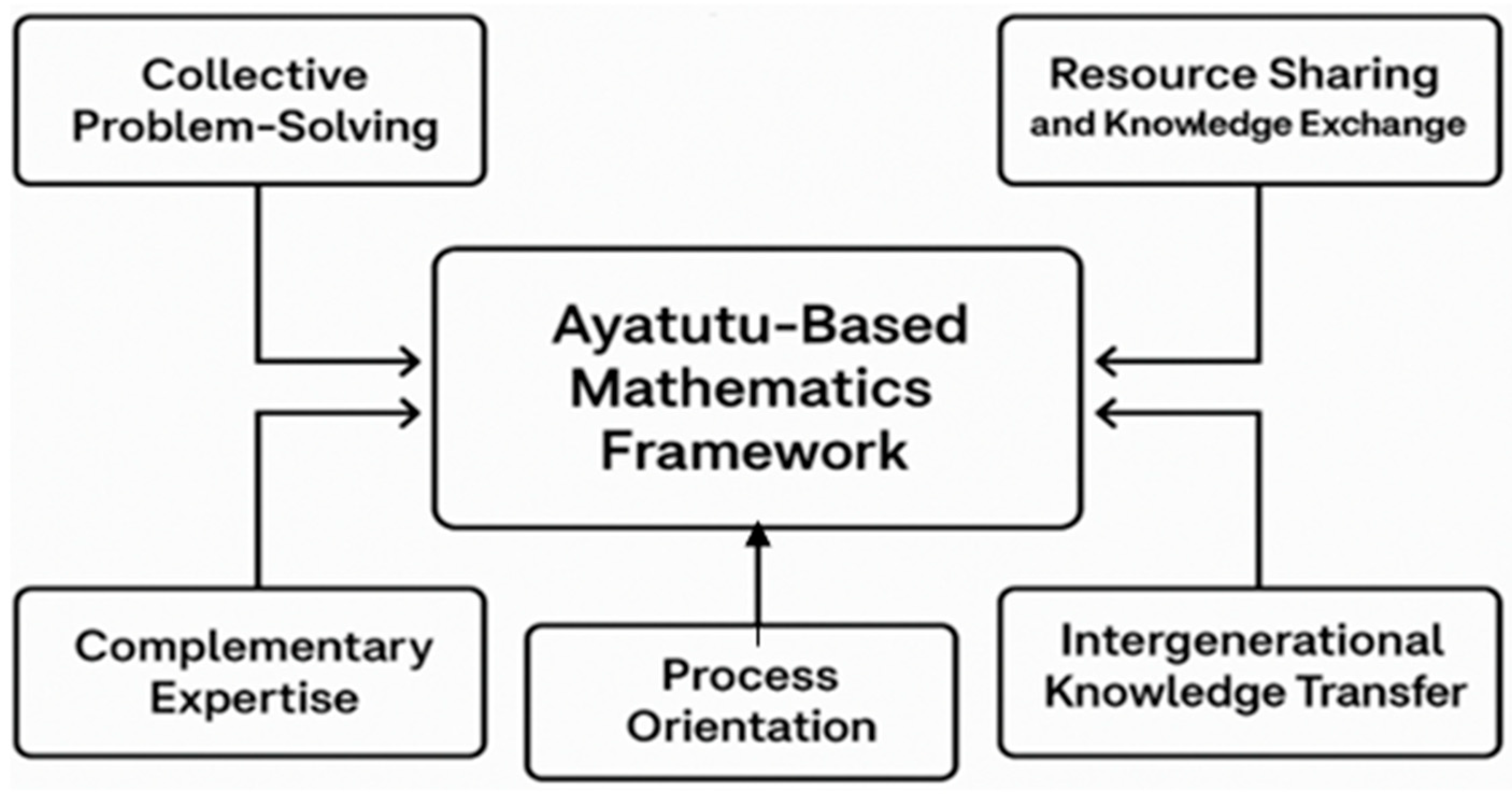
3.1. Core Elements of Ayatutu-Based Mathematics Framework

3.1.1. Collective Problem-Solving

At the heart of an Ayatutu-based mathematics framework is collective problem-solving, which is where mathematical challenges are approached as community endeavors rather than individual tasks. This aligns with both the Tiv philosophy of shared responsibility [11] and research on effective collaborative problem-solving in mathematics [60,61]. In practice, this element manifests through complex, open-ended problems designed to require diverse perspectives and complementary expertise [1]; group roles based on strengths that allow students to contribute their unique abilities while developing areas of growth [62]; and collective responsibility for understanding as group success is defined by ensuring all members understand the mathematical concepts, not merely by completing the task [63]. These approaches reflect the Ayatutu principle that community challenges require collective responses where each individual contributes according to their abilities.

3.1.2. Resource Sharing and Knowledge Exchange

The Ayatutu concept views knowledge and skills as communal resources to be shared rather than individual possessions [15]. In a mathematics context, this translates to structured knowledge exchange where students share mathematical insights, strategies, and understandings. Key practices would include structured explanation protocols that formalize processes for students to share mathematical thinking and reasoning [64]; reciprocal teaching where students take turns teaching mathematical concepts to peers [65]; and knowledge artifact creation involving collaborative development of mathematical representations, models, or explanations that capture group understanding [66]. These practices embody the Ayatutu principle of resource sharing while aligning with research on effective mathematical discourse and knowledge construction [67].

3.1.3. Complementary Expertise

Ayatutu recognizes that community members possess different skills and knowledge that, when combined, address complex challenges [10]. In mathematics education this principle acknowledges the diverse mathematical strengths students bring to group work. Implementation strategies include strength identification activities that help students recognize their mathematical strengths and areas for growth [33]; complex tasks requiring multiple skills that necessitate diverse approaches including visual representation, algebraic reasoning, pattern recognition, and conceptual explanation [1]; and expert groups using jigsaw-type structures where students develop expertise in specific mathematical approaches before sharing with home groups [68]. These approaches honor diverse mathematical thinking styles while ensuring all students develop comprehensive mathematical understanding.

3.1.4. Process Orientation

In Ayatutu philosophy the process of collaborative engagement is valued intrinsically, not merely as a means to an end. The Tiv recognize that how community members work together—the quality of their interactions, the inclusivity of their approach, and the respectful exchange of ideas—shapes not only immediate outcomes but also community cohesion and collective wisdom development. This process-centered value system contrasts with outcome-focused approaches that prioritize efficiency over relationship-building and learning. Ref. [16] notes that in traditional Tiv problem-solving contexts the journey toward resolution often holds equal importance to the resolution itself as it reinforces social bonds and establishes patterns of interaction that sustain community well-being beyond specific problem situations.

In mathematics education, this translates to an emphasis on mathematical processes—problem-solving, reasoning, and communication—rather than merely arriving at correct answers, as illustrated in Figure 1. This element manifests through metacognitive reflection with regular opportunities for students to reflect on both mathematical understanding and collaborative processes [69]; process portfolio assessment that captures students’ mathematical thinking processes, not just final products [70]; and mathematical discourse analysis that pays attention to how students communicate mathematically and build on each other’s thinking [71]. These practices align with both Ayatutu’s process orientation and research on effective mathematics learning that emphasizes mathematical practices alongside content (National Council of Teachers of Mathematics) [72].

3.1.5. Intergenerational Knowledge Transfer

Traditionally, Ayatutu involves knowledge transmission across generations, with elders sharing wisdom with younger community members [9]. In educational settings, this principle can be adapted through structured mentorship and cross-age learning opportunities. Implementation approaches include cross-grade mathematics partnerships with structured interactions between students of different ages around mathematical content [73]; community mathematics involvement that brings community members with mathematical expertise from various professional fields into classroom activities [74]; and mathematical oral history projects where students document mathematical practices and knowledge within their communities [75]. These approaches extend mathematical learning beyond classroom boundaries while honoring the Ayatutu principle of intergenerational knowledge sharing.

3.2. Theoretical Integration with Contemporary Educational Theories

The proposed Ayatutu-based mathematics framework integrates with several contemporary educational theories, positioning it within established educational discourse while offering unique contributions that extend and challenge aspects of these theories.

3.2.1. Alignment with and Extension of Sociocultural Learning Theory

The Ayatutu framework aligns with Vygotskian sociocultural theory, which posits that learning occurs through social interaction within cultural contexts [76]. Both approaches emphasize the zone of proximal development, where Ayatutu’s collective problem-solving creates natural conditions for students to work within their zones of proximal development with peer assistance [77]. This alignment extends to mediated learning as the knowledge exchange practices inherent in the Ayatutu approach provide multiple forms of mediation through peer explanation, collaborative representation, and group discourse that facilitate mathematical understanding [78].

However, Ayatutu extends conventional sociocultural theory in significant ways. While sociocultural learning theory recognizes the importance of social interaction in learning, Ayatutu introduces an ethical dimension often understated in Western interpretations of Vygotsky’s work—the responsibility knowledge-holders have toward others in their community. In Ayatutu, knowledge sharing is not merely a mechanism for cognitive development, but a moral obligation tied to community well-being. This perspective challenges the sometimes instrumental view of collaboration in educational settings where group work is valued primarily for its cognitive benefits rather than as an ethical practice of community building.

Additionally, the sociocultural emphasis on the internalization of social processes is reflected in the metacognitive reflection component of the Ayatutu framework, which supports students in internalizing the mathematical thinking made visible during group interactions [79]. Yet Ayatutu’s conception of internalization differs from conventional sociocultural approaches in its emphasis on the bidirectional nature of internalization—individuals not only internalize collective knowledge but also have a responsibility to contribute their internalized understandings back to the community, creating a continuous cycle of personal and collective knowledge development.

3.2.2. Connection to and Reconceptualization of Communities of Practice

The Ayatutu framework corresponds with Wenger’s [80] communities of practice theory, which describes learning as participation in social communities engaged in shared practices. This connection is evident in legitimate peripheral participation, in which the complementary expertise component allows students at different levels of mathematical understanding to participate meaningfully while developing greater competence through collaborative engagement with more knowledgeable peers [81].

Ayatutu, however, reconceptualizes certain aspects of communities of practice theory. While Wenger’s framework focuses primarily on the developmental trajectory from periphery to center (novice to expert), Ayatutu emphasizes the simultaneous validity of different types of expertise within a community. In Ayatutu the goal is not necessarily progression toward a single conception of expertise but rather the recognition and integration of diverse forms of expertise that complement one another. This perspective challenges linear models of expertise development and suggests a more multidimensional conception where different forms of knowledge are valued for their complementarity rather than positioned hierarchically.

Furthermore, the collective problem-solving approach requires students to negotiate shared understanding of mathematical concepts through discussion and collaborative work, reflecting Wenger’s emphasis on negotiation of meaning as central to communities of practice [82]. The process orientation element of the Ayatutu framework supports students in developing identities as capable mathematical thinkers within a community of mathematical practice, aligning with Wenger’s view that learning involves identity transformation through community participation [83]. However, Ayatutu expands this conception by emphasizing how individual identities remain fundamentally linked to collective identity, even as expertise develops—challenging Western notions of expertise as individual achievement and reinforcing the communal nature of knowledge ownership.

3.2.3. Relationship with and Transformation of Critical Pedagogy

The Ayatutu framework connects with critical pedagogy’s emphasis on education as an emancipatory practice that honors students’ cultural backgrounds [84]. This relationship appears in the validation of indigenous knowledge, with the framework explicitly valuing indigenous philosophical approaches to learning and problem-solving, challenging the often-implicit assumption that Western mathematical traditions represent the only legitimate approach to mathematical understanding [85].

Ayatutu transforms aspects of critical pedagogy by offering a non-Western philosophical foundation for educational liberation. While Freirean critical pedagogy emphasizes dialog, consciousness-raising, and praxis, it emerged from a particular Latin American context and reflects certain Western philosophical influences despite its critique of Western hegemony. Ayatutu provides an alternative philosophical grounding for critical mathematical practice—one that emerges from African philosophical traditions and centers communal rather than individual liberation. This perspective shifts the focus from individual conscientization toward collective empowerment, suggesting that mathematical liberation occurs through community solidarity rather than primarily through individual critical awareness.

The framework’s emphasis on collective responsibility and shared knowledge disrupts dominant Western individualistic educational models, aligning with critical pedagogy’s challenge to hegemonic educational practices [86]. The intergenerational knowledge transfer component connects classroom mathematics to community knowledge and practices, reflecting critical pedagogy’s insistence that education should be connected to students’ lived experiences and community contexts [75]. However, Ayatutu extends this by positioning community elders and knowledge holders not merely as contextual resources but as essential partners in the educational process, challenging conventional boundaries between formal and informal educational spaces and between academic and community knowledge.

3.3. Theoretical Contributions and Novelty of the Ayatutu Framework

The Ayatutu-based mathematics framework offers several unique theoretical contributions to the field of mathematics education that extend beyond existing approaches to cooperative learning and culturally responsive pedagogy.

3.3.1. Integration of Indigenous Philosophy and Mathematical Pedagogy

Unlike conventional cooperative learning approaches that are often grounded in Western psychological and educational theories, the Ayatutu framework introduces an indigenous philosophical system as its foundational structure. This represents a significant theoretical innovation by demonstrating how an entire indigenous philosophical system—not merely isolated cultural activities or examples—can serve as a coherent organizing framework for mathematics instruction. This approach moves beyond the common practice of incorporating cultural elements as supplementary features within existing Western educational structures, instead positioning indigenous philosophy as the generative foundation from which mathematical pedagogy emerges.

3.3.2. Reconceptualization of Mathematical Authority and Knowledge Construction

The framework challenges dominant conceptions of mathematical authority by positioning mathematical knowledge as collectively constructed and owned rather than individually possessed or institutionally controlled. This reconceptualization represents a theoretical departure from the traditional and progressive approaches to mathematics education which maintain that individual achievement is the ultimate goal, even when employing collaborative methods. By centering complementary expertise and collective problem-solving, the Ayatutu framework theorizes mathematical competence as inherently distributed across community members rather than concentrated in individuals, fundamentally shifting how mathematical ability is conceptualized.

3.3.3. Ethical Dimension of Mathematical Collaboration

The Ayatutu framework introduces an explicit ethical dimension to mathematical collaboration that is often absent in conventional approaches to cooperative learning. While traditional cooperative learning emphasizes structures that promote individual accountability alongside group interdependence [23], Ayatutu positions knowledge sharing as a moral responsibility tied to community well-being rather than merely an instructional strategy. This theoretical contribution suggests that mathematical learning has ethical implications beyond individual development, which is a perspective that challenges instrumental views of mathematics education and reconnects mathematical learning to broader questions of social responsibility and community care.

3.3.4. Temporally Extended View of Mathematical Learning Communities

Unlike many contemporary approaches to mathematical learning communities that focus primarily on immediate classroom contexts, the Ayatutu framework’s intergenerational knowledge transfer component theorizes mathematical learning communities as extending across time, connecting past, present, and future generations of mathematical thinkers. This temporally extended conception of mathematical community offers a novel theoretical perspective on mathematical learning, one which sees it as participation in knowledge traditions that transcend immediate educational contexts. This view positions students not just as learners for their own development but as links in an ongoing chain of mathematical knowledge transmission and transformation.

3.3.5. Process Prioritization over Product in Mathematical Achievement

The framework’s emphasis on process orientation offers a theoretical counterpoint to product-focused conceptions of mathematical achievement that dominate assessment and evaluation in mathematics education. By theorizing the process of mathematical collaboration as intrinsically valuable—not merely instrumentally valuable for producing better solutions—the Ayatutu framework challenges dominant outcome-oriented approaches to mathematical success. This theoretical contribution suggests alternative metrics for valuing mathematical work that prioritize the quality of mathematical thinking and interaction rather than solely the correctness of final answers.

Through these theoretical contributions the Ayatutu framework offers novel perspectives that extend current understandings of collaborative mathematics learning, culturally responsive pedagogy, and indigenous knowledge integration. The framework demonstrates how centering an indigenous philosophical system can generate fresh theoretical insights with practical implications for creating more inclusive, ethical, and mathematically powerful learning environments.

4. Potential Benefits of Ayatutu-Based Mathematics Education

The proposed Ayatutu-based mathematics framework offers several potential benefits for mathematics education, including enhanced engagement, mathematical identity development, community building, and cultural relevance.

4.1. Enhanced Mathematical Engagement and Understanding

Research suggests that collaborative approaches to mathematics learning improve student engagement and conceptual understanding [24,32]. The Ayatutu framework may further enhance these outcomes through distributed cognitive load, which is where complex mathematical problems become more accessible when approached collectively, potentially reducing mathematics anxiety and making challenging concepts more approachable for students who might otherwise struggle [87]. The framework also promotes multiple representations as group members bring diverse approaches to mathematical concepts, creating rich opportunities for students to encounter and work with varied ways of understanding mathematical ideas—a practice that research has consistently linked to deeper conceptual understanding [88].

Additionally, the structured knowledge exchange component of the Ayatutu framework promotes in-depth explanations that research shows benefit both the student providing the explanation and those listening, creating multiple pathways to understanding complex mathematical concepts [61]. The collective approach also provides scaffolding that helps students persist through productive struggle, allowing them to tackle challenging mathematical work with the support of peers rather than giving up when facing difficulties [89]. These mechanisms align with research on effective mathematics learning while implementing them through the cultural lens of Ayatutu, showing it may provide additional motivational benefits by connecting mathematical learning to cultural values and practices familiar to many students.

4.2. Mathematical Identity Development

Identity development represents a critical dimension of mathematics education, particularly for students from groups historically marginalized in mathematics [35,90]. The Ayatutu framework may support positive mathematical identity development through valued contributions as the complementary expertise component ensures all students have recognized mathematical strengths, allowing each student to experience being valued for their specific mathematical capabilities [91]. The emphasis on collective success, which defines achievement at the group level, may reduce the competitive aspects of mathematics that can undermine identity development, particularly for students who have previously struggled in traditional mathematics settings [32].

For students from communal cultural backgrounds, the approach provides cultural congruence that aligns with their existing cultural values, reducing potential identity conflicts that arise when school mathematics seems disconnected from or in opposition to cultural identities and values [92]. The knowledge exchange practices within the Ayatutu framework position students as mathematical authorities rather than passive recipients of knowledge, empowering them to see themselves as capable contributors to mathematical discourse and understanding [66]. These identity-supporting elements may be particularly beneficial for students from cultural backgrounds that value collectivism over individualism, allowing them to develop strong mathematical identities without compromising their cultural identities.

4.3. Community Building and Social Development

Mathematics classrooms implementing Ayatutu principles may foster stronger learning communities and develop important social competencies. Potential benefits include classroom cohesion, as the emphasis on collective responsibility can foster a stronger sense of classroom community and create an environment where students feel connected to one another and invested in each other’s success [93]. The framework naturally develops conflict resolution skills as navigating different mathematical perspectives requires developing constructive approaches to disagreement and learning to reconcile varying viewpoints productively—skills that extend well beyond the mathematics classroom [82].

Working closely with peers from diverse backgrounds helps students develop cultural perspective-taking abilities and intercultural competence as they learn to value and incorporate different approaches to mathematical thinking and problem-solving [7]. Regular engagement in collective mathematical work cultivates collaborative dispositions, developing collaboration as a habit of mind that students can apply across academic domains and in their lives beyond school [94]. These social outcomes extend beyond mathematical content knowledge to develop capacities essential for citizenship in diverse democratic societies, making the Ayatutu framework valuable not just for mathematical learning but for broader educational goals related to social development and civic preparation.

4.4. Cultural Relevance and Sustainability

For students from the Tiv community specifically, and for students from cultures with similar communal values more broadly, an Ayatutu-based approach offers particular benefits related to cultural relevance. Cultural validation occurs as centering an indigenous philosophy in academic learning demonstrates the value of indigenous knowledge systems, countering historical patterns of devaluing non-Western intellectual traditions in educational settings [95]. This approach helps reduce cultural dissonance by aligning classroom practices with cultural values, potentially minimizing the disconnect some students experience between home and school cultures that can interfere with learning and engagement [96].

The Ayatutu framework contributes to cultural sustainability by incorporating indigenous philosophical approaches that help sustain cultural knowledge and values within educational settings, ensuring that traditional wisdom continues to be transmitted even as students engage with conventional academic content [97]. This approach facilitates two-way knowledge exchange, enabling the integration of indigenous and conventional mathematical knowledge in ways that benefit all students, regardless of cultural background, by broadening mathematical perspectives and approaches [98]. These cultural benefits extend beyond immediate academic outcomes to address broader goals of cultural sustainability and educational equity, positioning the Ayatutu framework as a potential contributor to more inclusive and culturally responsive mathematics education.

5. Implementation Considerations and Challenges

While the Ayatutu-based mathematics framework offers promising benefits, its implementation would face several challenges that require careful consideration.

5.1. Teacher Preparation and Support

Implementing this approach would require teachers to develop specific competencies and receive ongoing support. Cultural knowledge development represents a critical area as teachers would need to understand Ayatutu philosophy and its educational applications, particularly if they are not from the Tiv community, requiring thoughtful immersion in both the philosophical concepts and their practical educational implications [7]. Teachers would also need to develop specialized facilitation skills for managing productive mathematical discourse and complex collaborative structures—skills that go beyond traditional mathematics instruction to include orchestrating meaningful group interactions, recognizing and building upon diverse student contributions, and fostering equitable participation patterns [99].

Additionally, assessment expertise would need significant development as evaluating both individual and collective mathematical understanding requires sophisticated assessment approaches that can capture the complex learning processes occurring within collaborative structures while still providing insight into individual student progress [100]. Professional development models would need to integrate cultural learning, mathematics pedagogy, and collaborative teaching strategies rather than addressing these as separate domains, creating cohesive learning experiences that help teachers see how these elements work together in practice and avoiding the fragmentation that often characterizes teacher professional development initiatives.

5.2. Structural Constraints

Conventional educational structures may present barriers to implementation. Time constraints pose a significant challenge as the reflective, process-oriented nature of the approach requires sustained engagement that may conflict with pacing requirements in many educational systems, potentially creating tension between the deep learning the approach aims to foster and the breadth of content coverage often expected in mathematics curricula [63]. The physical environment of many classrooms also presents challenges as effective collaboration requires classroom spaces designed for group interaction rather than the individual seat work arrangement common in many schools, necessitating rethinking of classroom layout, furniture, and resource organization to support the collective work central to the approach [101].

Furthermore, assessment systems focused on standardized testing and individual performance may undermine collective approaches unless carefully aligned, creating potential contradictions between the collaborative values of the Ayatutu approach and the individualistic measures often used to evaluate mathematical learning in conventional educational settings [102]. Addressing these structural challenges would require administrative support and potentially policy changes to create conditions conducive to Ayatutu-based mathematics education, including rethinking scheduling, classroom design, and assessment systems to better accommodate collaborative learning processes that may not fit neatly into existing educational structures.

5.3. Cultural Translation Challenges

Adapting an indigenous philosophy to contemporary educational contexts presents complex cultural translation challenges. Authentic representation stands as a primary concern as care must be taken to represent Ayatutu authentically rather than superficially appropriating cultural concepts, which requires deep engagement with Tiv community members and cultural knowledge holders throughout the development and implementation process [103]. Some aspects of Ayatutu may be deeply embedded in broader Tiv cultural contexts that cannot be fully replicated in classroom settings, requiring thoughtful consideration of how these cultural elements translate into educational contexts without losing their essential meaning or being reduced to simplified versions of complex cultural practices [85].

The approach must also balance honoring traditional Ayatutu practices with adapting them for contemporary educational needs, navigating the tension between preserving cultural authenticity and meeting the requirements of modern educational systems and mathematics learning objectives [104]. Addressing these challenges would require meaningful partnership with Tiv cultural knowledge holders and communities throughout development and implementation, creating ongoing dialog about how Ayatutu principles can be respectfully and authentically translated into educational practices while acknowledging the limitations of institutional educational settings and their ability to fully embody indigenous cultural systems.

5.4. Balancing Individual and Collective Learning

A significant implementation challenge involves balancing the collective emphasis of Ayatutu with the educational systems’ focus on individual student progress. Individual accountability mechanisms must be thoughtfully designed to ensure all students participate actively and develop mathematical understanding rather than relying excessively on peers, requiring structures that make individual thinking visible and valuable within collaborative contexts while maintaining the collective ethos of the approach [24]. Methods must be developed to evaluate individual mathematical understanding within collaborative contexts, creating assessment approaches that can distinguish between knowledge co-constructed in groups and that which has been internalized by individual students without undermining the collaborative values at the heart of the approach [100].

Furthermore, the approach must accommodate students’ differing needs while maintaining the collective orientation, addressing the challenge of differentiation within a framework that emphasizes shared responsibility and collective outcomes rather than individualized learning paths [105,106]. This balance requires the thoughtful design of both instructional activities and assessment approaches to honor Ayatutu principles while supporting individual student development, creating classroom structures that value collective achievement while still attending to the specific learning needs, strengths, and growth areas of each student within the community context.

6. Conclusions and Recommendations

This theoretical exploration suggests that the Tiv philosophy of Ayatutu offers valuable perspectives for enhancing mathematics education through collective problem-solving and cooperative learning. The proposed framework integrates indigenous wisdom with contemporary educational theories, potentially creating mathematics learning environments that are both culturally sustaining and mathematically powerful.

6.1. Research Recommendations

Future research could advance this theoretical framework through collaborative development initiatives that create meaningful partnerships between mathematics educators, Tiv community members, and educational researchers to develop specific Ayatutu-based mathematics modules, ensuring that the approach maintains cultural authenticity while addressing key mathematical learning objectives. These partnerships would ideally involve continuous dialog and co-creation, with indigenous knowledge holders playing central roles in determining how Ayatutu principles are translated into educational contexts.

Small-scale pilot implementation in diverse classroom settings would provide valuable insights into the practical challenges and opportunities that arise when implementing the framework, allowing for the iterative refinement of instructional approaches, materials, and assessment strategies before broader implementation efforts. Comparative studies examining Ayatutu-based mathematics instruction alongside conventional approaches across multiple outcome measures would help identify the specific strengths and limitations of the approach, considering not only academic outcomes but also measures of student engagement, mathematical identity development, and collaborative skills. Additionally, longitudinal studies examining how Ayatutu-based mathematics education affects students’ mathematical identities and dispositions over time would provide insights into the approach’s deeper and potentially more enduring impacts on how students relate to mathematical knowledge and see themselves as mathematical thinkers and problem-solvers. These research directions would provide the empirical grounding necessary to move the framework from theoretical proposition to evidence-based practice, while also maintaining respectful engagement with the indigenous philosophy at its core.

Framework Testing and Evaluation Approaches

To move from theoretical proposition to evidence-based practice the Ayatutu framework requires empirical testing using methodologies that align with the philosophy’s values while generating rigorous evidence of its effectiveness. The following approaches could be employed to assess each core element of the framework:

• Collective Problem-Solving Assessment

• Structured observation protocols using validated instruments such as the Reformed Teaching Observation Protocol (RTOP) adapted to include specific indicators of collective mathematical engagement.
• Discourse analysis examining patterns of student interaction during mathematical problem-solving, with particular attention to indicators of collective responsibility such as inclusive participation, mutual support, and collective sense-making.
• Comparative problem-solving tasks where student groups approach identical problems through either Ayatutu-based collective methods or conventional group work, with analysis of both solution quality and process quality.

• Resource Sharing Evaluation

• Knowledge mapping techniques that trace the flow of mathematical ideas within classroom communities, identifying patterns of knowledge exchange and resource distribution.
• Portfolio assessments that document individual students’ contributions to and benefits from collective knowledge building over time.
• Pre–post measures of mathematical concept understanding across student groups to assess whether knowledge sharing leads to a more equitable distribution of mathematical understanding.

• Complementary Expertise Measurement

• Social network analysis examining how different forms of mathematical expertise are recognized and utilized within classroom communities.
• Expertise identification surveys where students identify their own and peers’ mathematical strengths before and after implementation, assessing changes in recognition of diverse mathematical abilities.
• Task analysis evaluating how effectively student groups identify and leverage different forms of expertise to solve complex mathematical problems.

• Process Orientation Documentation

• Reflection protocols analyzing student metacognitive awareness of both mathematical and collaborative processes.
• Documentation of mathematical learning trajectories that capture the development of mathematical understanding through collaborative engagement rather than focusing solely on end points.
• Comparative analysis of student mathematical work that examines both process quality (mathematical reasoning, representation, and communication) and product quality (correctness, efficiency, and elegance).

• Intergenerational Knowledge Transfer Assessment

• Community-based participatory research methodologies involving community members in assessing the authenticity and effectiveness of knowledge transfer practices.
• Longitudinal studies examining how students integrate community mathematical knowledge with school mathematics over extended time periods.
• Mixed-methods approaches documenting both community members’ and students’ perspectives on the value and impact of intergenerational mathematical knowledge exchange.

These assessment approaches would need to be implemented through research designs that combine qualitative and quantitative methodologies to prioritize participant perspectives (particularly those of Tiv community members when working in Tiv contexts) and examine both immediate learning outcomes and longer-term impacts on mathematical identity, community relationships, and cultural sustainability. A critical aspect of empirical testing would be developing culturally appropriate metrics that align with Ayatutu values rather than imposing assessment frameworks that reflect contradictory educational philosophies.

6.2. Practice Recommendations

For educators interested in exploring Ayatutu principles in mathematics classrooms, starting with community building represents an essential first step, establishing classroom norms and structures that emphasize collective responsibility before implementing complex mathematical tasks. This foundational work creates the social environment necessary for genuine collaborative problem-solving, helping students develop the trust and interpersonal skills needed to engage meaningfully with challenging mathematical content as a community rather than as isolated individuals.

Developing task design expertise is equally important as educators need to create mathematical problems that genuinely require diverse perspectives and complementary expertise rather than tasks that could be completed individually but are simply assigned to groups. This requires careful attention to the mathematical demands of tasks, ensuring they have multiple entry points, benefit from various representation strategies, and are sufficiently complex to merit collective engagement. Building reflection routines should be a cornerstone of implementation, integrating regular opportunities for students to reflect on both mathematical understanding and collaborative processes, making the learning visible and helping students internalize both the mathematical concepts and the collaborative skills they are developing. Educators should also engage with local communities that value collective approaches to problem-solving whether or not they are specifically Tiv communities, creating connections between classroom mathematics and community practices that can enrich the learning experience and provide cultural context for collective problem-solving approaches. These practical steps can help educators begin implementing elements of the framework while formal research continues, allowing for classroom-based learning about how Ayatutu principles translate into effective mathematics instruction.

6.3. Policy Recommendations

Education policymakers could support an exploration of indigenous philosophies in mathematics education through curriculum flexibility policies that allow for innovative approaches that may not align with conventional pacing and assessment models. Such flexibility would create space for teachers to implement the more process-oriented, collaborative approaches central to Ayatutu-based mathematics education without feeling constrained by rigid pacing guides or narrowly defined learning progressions that might not accommodate the different learning trajectories that emerge in collaborative learning environments.

Dedicating professional development resources specifically for teacher learning related to indigenous knowledge systems and culturally responsive mathematics would build the capacity needed for effective implementation, helping teachers develop both the cultural understanding and the pedagogical skills necessary to bring Ayatutu principles into mathematics classrooms authentically and effectively. Community partnership support in the form of resources for schools to engage meaningfully with indigenous communities in curriculum development would ensure that cultural knowledge is respected and accurately represented, while also building relationships between schools and communities that can enrich educational experiences for all students. Research funding directed toward collaborative studies examining indigenous philosophical contributions to mathematics education would advance understanding of how diverse cultural perspectives can enhance mathematical learning, contributing to both theoretical knowledge and practical applications that make mathematics education more inclusive and effective. Such policy support would create conditions where innovative approaches like Ayatutu-based mathematics education could be meaningfully explored, evaluated, and refined, contributing to broader efforts to make education more culturally responsive and equitable.

6.4. Conclusions

The integration of Ayatutu philosophy into mathematics education represents one example of how indigenous knowledge systems can enrich educational practice. By bringing collective problem-solving principles from Tiv culture into dialog with contemporary mathematics education, this framework offers possibilities for creating learning environments that honor cultural wisdom while developing powerful mathematical understanding. The approach recognizes that indigenous philosophies contain sophisticated intellectual traditions that can contribute meaningfully to addressing current challenges in mathematics education, particularly regarding student engagement, mathematical identity development, and creating more inclusive learning environments.

As education systems worldwide strive to become more inclusive, culturally responsive, and effective, indigenous philosophies like Ayatutu provide valuable perspectives that can transform teaching and learning. These perspectives offer alternatives to individualistic approaches that have dominated Western educational models, suggesting ways to balance individual achievement with collective responsibility and to value diverse forms of mathematical thinking and problem-solving. The theoretical framework presented here offers a starting point for this transformative work, inviting educators, researchers, and communities to collaborate in reimagining mathematics education through the lens of collective wisdom. Such collaboration holds promise not only for enhancing mathematics education for students from indigenous backgrounds but for enriching mathematics learning for all students by introducing them to diverse ways of approaching mathematical challenges and building mathematical understanding collectively. Through respectful engagement with indigenous philosophies like Ayatutu, mathematics education can become both more culturally sustaining and more mathematically powerful, better serving diverse learners while honoring the intellectual contributions of cultures historically marginalized in educational contexts.