Exploring the Role of Metacognition in Measuring Students’ Critical Thinking and Knowledge in Mathematics: A Comparative Study of Regression and Neural Networks

Abstract

This article discusses the importance of open-ended problems in mathematics education. The traditional approach to teaching mathematics focuses on the repetitive practice of well-defined problems with a clear solution, leaving little room for students to develop critical thinking and problem-solving skills. Open-ended problems, on the other hand, open-ended problems require students to apply their knowledge creatively and flexibly, often with multiple solutions. We herein present a case study of a high school mathematics class that incorporated open-ended problems into its curriculum. The students were given challenging problems requiring them to think beyond what they had learned in class and develop their problem-solving methods. The study results showed that students exposed to open-ended problems significantly improved their problem-solving abilities and ability to communicate and collaborate with their peers. The article also highlights the benefits of open-ended problems in preparing students for real-world situations. By encouraging students to develop their problem-solving strategies, they are better equipped to face the unpredictable challenges of the future. Additionally, open-ended problems promote a growth mindset and a love for learning, as students are encouraged to take risks and explore new ideas. Overall, the article argues that incorporating open-ended problems into mathematics education is a necessary step towards developing students’ critical thinking skills and preparing them for success in the real world.

1. Introduction

Metacognition, which refers to the awareness and understanding of one’s thought processes, is an essential concept in learning and education [1]. Metacognition involves monitoring and regulating cognitive processes, including attention, memory, and problem-solving strategies. It goes beyond acquiring new knowledge or skills and encompasses the awareness of one’s learning strategies and the ability to reflect on and adapt them as needed [2].

In the study context, metacognition can be linked to the concept of self-awareness mentioned in relation to metagnosis. Metacognitive student capabilities include attentional control, spatial reasoning, working memory management, visual processing, and coordination with other body parts during the learning and practice of mathematics [1]. These metacognitive abilities play a crucial role in effective learning and problem-solving.

Furthermore, metacognition is intertwined with the self-exploration emphasized in the concept of metagnosis. It involves actively seeking new learning experiences, experimenting with different strategies, and reflecting on one’s own understanding and progress. Metacognition enables students to engage in higher-order thinking skills, such as analyzing, evaluating, and self-assessing their learning [3].

Teachers can play a vital role in promoting metacognition by providing opportunities for students to reflect on their learning processes, encouraging them to think about their thinking, and helping them develop effective metacognitive strategies. By fostering metacognitive awareness, teachers can empower students to take ownership of their learning, become more independent learners, and develop lifelong learning skills [4].

Integrating metacognition into mathematics education can support students in building a deep understanding of mathematical concepts and problem-solving strategies. It can also help them identify their strengths and weaknesses, set goals, and monitor their progress [2]. Educators can enhance students’ metacognitive abilities and facilitate their mathematical learning journey by explicitly teaching metacognitive strategies and fostering a metacognitive learning environment.

Other mathematical learning theories suggest that gnosis and metagnosis may induce learning and utilizing prior or new knowledge [5]. For example, researchers in mathematics use Piaget’s theory of learning to determine the best teaching methods available [5]. Piaget’s stages of a child’s cognition highly contribute to understanding how students learn about mathematical concepts [3].

His theory of learning indicates that even young children hold a particular understanding of numbers. Children can improve their numerical capabilities even at such an early stage if given the opportunity [6]. He has identified the mathematics learning probability at different stages of child development. It indicates the implication of metagnosis, which emphasizes exploration.

Piaget’s theory supports the definition of metagnosis, which indicates how children’s innate understanding helps them comprehend math’s complexity during education [7]. The ability to numerical understanding is natural, and children continue to explore it as they grow. According to Bobby Ojose [8], one of the significant challenges in teaching mathematics is how one connects mathematical concepts with routine activities.

For example, although children can recognize numbers, they don’t naturally apply them to mathematics. Thus, they may struggle to connect theory and practice [8]. In this situation, teachers need to provide adequate support. Therefore, Piaget’s approach links metagnosis to self-exploration, enhancing formal subjective understanding of numbers through mathematics [7].

According to Kushik Das, learning mathematics requires highly specialized knowledge [9]. Hence, in modern educational methods, students face several challenges. Different theories have presented improved teaching techniques that also include the use of gnosis and metagnosis theories. After Piaget’s theory, Vygotsky’s theories helped improve mathematical teaching by highlighting critical areas of consideration that can simplify math instruction [8].

The Vygotsky theory of learning in the context of mathematics can be improved by focusing on the proximal development zone [10]. According to research, the Vygotsky child zone of proximity can improve mathematics students’ poor and underperformance owing to idea-building issues. The proximity zone can be explored and mediated by teachers, field experts, and peer participation [11], and children can be helped to explore and understand mathematical concepts and promote collaborative learning by encouraging them to ask for help.

Furthermore, the educator must also determine each student’s proximity zone, which may prove challenging. Therefore, effectively managing each student based on their proximity zone while teaching can be challenging to apply for a mathematician [8]. Thus, the implication of Vygotsky’s theory can aid students in improving their performance during learning as it helps develop new knowledge (metagnosis).

The theory also emphasizes how the teacher should effectively deliver the instruction to the student [10]. The Vygotsky model’s proximity zone bridges the gap between students’ development and numerical problem-solving skills. Moreover, a child is more likely to learn mathematics if they receive enough support and guidance [9]. Thus, when working in a proximity zone, a teacher’s contribution is far more important than the students. Therefore, Vygotsky’s theory indicates how expert assistance is critical to identifying the proximity zone and eliminating challenges.

His theory also suggests that teachers should not assign mathematical problems as homework without considering students’ access to guidance since mathematical activities and problem-solving should be done mainly under the teacher’s supervision [8]. According to Vygotsky, mathematics can be enjoyable if students are assisted accordingly.

The constructive learning theory also supports gnosis. This theory supports that student should build their numeric concepts based on their prior knowledge and experiences [12]. This idea emphasizes experience and knowledge. The theory suggests that teachers should link what students have learned to what they will discover.

One of the significant issues that arise at this point is the level of variation in maths concept building among students, information which is critical for the teacher to have [12]. Some students are proficient in mathematics and can link themselves, while others with lousy math and problem-solving skills may struggle [13]. Thus, when adopting the gnosis theory, teachers must assess each student’s competency and devise solutions accordingly.

Maslow’s theory of knowledge also supports the implications of metagnosis in mathematical learning. It mainly revolves around fundamental needs, and according to him, needs are the source that increases one’s motivation [14]. A person will stay interested if their needs are met. Math is similar. Maslow’s theory suggests that teachers must meet their students’ needs, according to Fisher and Crawford [12].

Consequently, tackling students’ needs in class will improve motivation and decrease dissatisfaction and detachment. As a teacher, it is crucial to work equally with all students despite any lack of interest and coordination. In addition, along with some significant theoretical implications, there are advanced methods for improving mathematics teaching and learning [9]. Naturally, technology is boosting students’ and teachers’ learning experiences. Neural networking and intelligence systems simplify mathematics learning and boost students’ ability to tackle complex issues with improved digitalization [9].

2. Materials and Methods

2.1. Subject Problem Position

Learning mathematics is one of the most important subjects for students at any educational level, considering how frequently it is studied. Math is mostly a topic and a cognitive skill builder [14]. Mathematics is a subject in which students need to use prior knowledge and practice effectively. Yet, teaching arithmetic is complex. Math teaching theories abound [15].

Math students’ learning competency is affected by the subject’s complexity. Students believe that math is unmanageable and are therefore discouraged [13]. Another factor is the learner’s lack of effort because they lack a strong mathematical concept base and are, therefore, hesitant to seek assistance [15]. This lack of communication leads to difficulty in learning and teaching alike. Math learning also depends on other factors that strongly influence student learning competency.

Those factors also enforce the adoption of different teaching methods in mathematics. For example, a student’s ability to memorize, perpetual abilities, and other difficulties in learning mathematics [16]. For instance, cognitive, environmental, and affective factors also lead to challenges in teaching mathematics. As per various empirical studies, intellect and processing speed also complicate teaching. Students are eager to learn math in the early stages, but as problems get more challenging, they tend to lose interest [14].

Hence, this research aimed to identify the best learning theories to reduce errors in teaching mathematics. Thus, the research examines the implications of gnosis and metagnosis theories for teaching mathematics and determines which theory yields the best practical results.

This research also connects other theories with gnosis and metagnosis to indicate how learning impacts mathematics teaching. This study utilizes theories to improve learning and identify the most effective approaches to math teaching and learning issues. Mathematics is challenging for students and teachers due to the abovementioned challenges [13].

To overcome these issues and enhance math instruction, finding and presenting the best solution is essential [17]. Moreover, this research benefits learners and teachers alike. In addition, it equates two major learning theories, gnosis, and metagnosis, which generated the greatest results to simplify mathematics teaching in a real-world problem.

2.2. Probing Questions

The probing questions mainly focus on what key areas the research paper is emphasizing and what the intended aspects have been investigated in this paper. As identified from the importance of the research topic, this research aims to study teaching and learning development in the context of mathematics learning. Still, the main objective is to examine some significant theories within the teaching and mathematics learning settings. With the help of probing questions mentioned below, the dimensions of the research have been restricted to a particular domain to narrow down the research area and to mainly focus on some of the critical aspects [18].

It further facilitated deepening the understanding of the subject matter, effectively analyzing the intended research problem, and effectively answering the particular problem without deviating from the areas of interest. In addition, the main objective of separately mentioning the focused, probing question is to develop a deepened understanding of the topic. Mathematical learning and teaching can be done using different approaches, and some unlimited frameworks and theories support the improvement of both the teacher and learner [16]. Therefore, the research only identifies how well gnosis and metagnosis theories can facilitate mathematical learning.

Despite engaging and researching several theories of mathematical teaching and learning, the research mainly focuses on gnosis and metagnosis theories to develop a better framework to improve mathematical teaching aspects and improve learner abilities by reducing challenges in the light of related scholarly sources and models. Therefore, the probing question helped keep and align the research on its key aspects and remind the focused areas of the problem to eliminate errors and make the research authentic, apparent, specific, and in-depth information [18]. Thus, there are two main probing questions on which the whole research has been based, and in the Section 4, their answers have been discussed. The research aims to explore which theory is best for teaching mathematics. Therefore, the research question that has been examined and investigated in this research includes the following:

(a)

What is the implication of gnosis and metagnosis theories in teaching, and do they differentiate each other? How do gnosis and metagnosis theories contribute to teaching mathematics?

(b)

Which teaching theory is best and contributes highly to teaching mathematics? Is metagnosis better than gnosis for teaching mathematics?

2.3. Methodological Framework

The methodology is one of the most vital elements of any research, explaining how it was conducted, what methods were utilized, and why. The research is inclined to be conducted using a quantitative research method. Quantitative methods rely on numerical data [19]. The researcher determines how to collect, analyze, and interpret data through theoretical analysis. It provides information related to variables, relationships, causality, and measurement.

The researcher must also decide which data sources are ideal for answering the research questions when multiple types are needed. It assists in clarifying the way the study will be conducted, the methodologies used, the collection of data, and the interpretation of the results. Theoretical analysis also helps discuss and evaluate findings, placing the research in its historical, ethical, and philosophical context.

Understanding a research methodology’s theoretical background is essential to use it effectively. This research analyzed mathematical learning theories of gnosis and metagnosis using statistical regression and neural networking [20]. Statistical regression and neural networking are potent tools for predictive analysis used in data science and related fields of study. Statistical regression uses statistical modeling to analyze a set of predictor variables and one or more output variables.

Its primary purpose is to identify trends in existing data and predict future outcomes. The assumption is that data are related in a linear model where predictor variables can predict the output. Neural networks simulate human brain function, while a network links those layers of small neurons together [19].

Neural networks can learn from data, generating predictions and complex data patterns with relatively little input. Neural networks can be used for both regression and classification tasks, with regression being used to predict numerical output and classification being used to generate categorical output [21]. Neural networks can identify trends and correlations in data, while statistical regression can help understand the causation behind those correlations, making for an optimal combination.

Moreover, this combination allows for more complex tasks such as learning structured patterns, classifying data, and predicting numerical outcomes. Ultimately, this combination allows for improved accuracy and more reliable predictions, which can be used for decision-making in businesses, medical fields, and other areas.

Statistical regression and neural networks (NNs) in the Statistical Package for Social Sciences (SPSS) is an increasingly popular data analysis option. Regression and NNs are two established statistical techniques with many applications, from prediction to classification and clustering [21]. Regression can be used to forecast values of dependent variables, such as a stock’s closing price or a consumer’s likeliness to purchase a product when given independent variables.

Neural networks, on the other hand, recognize patterns and predict. Neurons, or nodes, form a NN, while complexity increases with nodes. NNs can identify non-linear relationships between variables that regression methods cannot detect [22].

SPSS regression and NNs improve data models. SPSS’s regression option simplifies yet powerfully analyzes almost any data set. It offers linear interpolation, polynomial, logistic, and multinomial regression models. Scatterplots, histograms, and other visual tools enable data visualization [20]. The neural network option within SPSS analyzes large and more complicated data sets where relationships between variables are difficult to predict.

SPSS can apply introductory artificial intelligence and machine learning methods to examine complex data. NNs can classify data, detect outliers, predict values, and cluster data into groups. SPSS uses regression and neural networks extensively. Both methods improve clarity and accuracy over traditional statistical methods [23]. SPSS provides powerful tools that allow both options to be utilized in identifying patterns, relationships, and trends within data. Metagnosis is intuitive, experiential knowledge, while gnosis is intellectual understanding.

Gnosis and metagnosis help students recognize and incorporate their foreknowledge. Metagnosis is a higher-level process that uses internal knowledge to treat something new in a context more significant than the part itself [22]. In mathematics, gnosis and metagnosis can be used to facilitate learning. Gnosis provides students with a solid foundation. It requires memorizing formulas, understanding concepts and terminology, and recognizing patterns.

Metagnosis involves applying knowledge in unfamiliar contexts beyond memorization and recognition. It often involves problem-solving, experimenting with different elements, analyzing results, and forming conclusions.

2.4. Method of Research Process

Most existing research has used school pupils’ data and quantitative research methods [21]. These points are directed at a specific audience, namely the graduate of numerical learning and arithmetic practical subjects. In terms of age, the pupil’s age ranges from 14 years to 17 years. All targeted partners of this research are teens, while both male and female students were targeted. All the juniors were associated with subordinate grades, while the sample size for the dossier collection and analysis was 58 scholars from mathematics history.

The central theme of this research was to find out how the theory of education can help mathematics students efficiently learn and attain a better understanding of numerical concepts [12]. Therefore, two main classifications have been introduced, called gnosis and metagnosis, while the research’s main objective is to label which individual is more productive for the educational outcomes of arithmetic students in the long term. For dossier collection, samples from undergraduates were collected. At this point, they were given some exercises to show the implication of the two theories in the knowledge process. This was carried out through focus groups placing each student group with the gnosis and metagnosis theory of learning, and their overall experience and knowledge process was traced.

In terms of sample size, the sample amount for this project was picked as limited because a limited sample size can more easily manage and integrate the outcomes, and the research theory can be examined and resolved effectively. In addition, this sample length of 58 students provided excellent support to understanding what learning methods mathematics teachers are amenable to applying in their teaching of mathematics students by eliminating all the learning and education barriers [23]. Moreover, taking the students as a target audience is rational because the central theme of this research paper is to understand the theoretical implication of mathematical learning and teaching among students; thus, students were the primary target participants in this research.

Moreover, the age categorization was limited to 14 to 17 because the research was limited to secondary-level students and narrowed down because secondary-level students face major mathematics issues [24]. Therefore, the primary motivation was to understand which theory is best for teaching mathematical concepts to secondary-level students. Quantitative research methods have been followed, wherein the student samples were analyzed using numerical values and statistical outcomes.

As mentioned above, for data collection, students’ working samples were collected from the focused groups, and their data were analyzed using SPSS. In the SPSS method, only two tests were considered for grasping the quantitative outcomes, which include statistical regression and neural networks. Using these two tests, the data were analyzed, and the outcomes were drawn. These tests are automatic and computer-generated and were used along with the numerical values and graphical representation to effectively understand the impact of the theoretical method [22].

Statistical regression is a data analysis method used in this research in which dependent and independent variables have been used [22]. It mainly focuses on drawing the relationship between the two variables. In this research, the relationships between gnosis and metagnosis have been with the students of mathematical learning were investigated to show which theory is more effective in teaching mathematical concepts. Several studies have evidenced and supported the effectiveness of statistical models and regression; therefore, this is an authentic and widely used methodology.

It has been identified that these analysis methods are not only practical and productive, but are also automotive, supportive, can handle the data, and enable great accuracy with a minimal proportion of errors [23]. On the other hand, another reason to use statistical regression is to identify the actual and unbiased relationships between the target variables to identify an accurate result with a higher level of effectiveness and realistic outcomes. On the other hand, the second method used herein, along with statistical regression, is neural networking, another method for data analysis that enables an understanding of processes and data patterns to identify the outcomes.

Using the SPSS neural network facilitated the presentation of the predictive capacity for the research outcomes, which enabled the answering of the target question [17]. It also elucidated a clear relationship between the associated variables targeted in this research. Using statistical regression and neural networks, the graphical representation of the input data was examined, and their interpretation was carried out through a discussion.

Using a neural network from SPSS provided an excellent opportunity to display and present accurate outcomes by reducing the probability of errors because it enabled us to identify the problems and present the best outcomes with a better predictive model. Both the statistical regression and neural network provided excellent support in analyzing the data and provided deep insight for better decision-making, which made the complex ideas and representation of data more straightforward and easier to understand and provided more authentic outcomes [18].

3. Data Collection

The study focused on students of numerical learning and practical arithmetic subjects. The targeted participants were students aged 14 to 17, male and female students from secondary grades. The sample size for data collection and analysis was 58 scholars from mathematics history. Written tests and group assignments were conducted in algebra (10th grade) and mathematics (11th grade) during the academic year 2022–2023. The tests and assignments had metacognitive content and aimed to assess critical thinking and metacognitive perception.

The collected data from the tests and assignments were analyzed using the Statistical Package for Social Sciences (SPSS). SPSS is a software tool used for statistical analysis and data management. The normality of the variables (test1, test2, and grades) was checked using the Kolmogorov–Smirnov test. The test results showed that all three variables followed a normal distribution. Descriptive statistics were calculated for the mean, median, mode, standard deviation, variance, minimum, and maximum values. Graphical representations, such as bar graphs, were used to visualize the data.

Regression analysis examined the relationship between the test1 and test2 variables. The model summary table provides information on the R-squared value, representing the percentage of total variability explained by the regression. This study aimed to determine if the values of test2 could be predicted from the values of test1. The results and findings were discussed in the context of the research objectives and theoretical implications. The study focused on understanding the effectiveness of different learning theories (gnosis and metagnosis) in teaching mathematical concepts to secondary-level students.

Testing for Normality of Variables

With the Kolmogorov–Smirnov test (

Table 1. The sample Kolmogorov–Smirnov test.

		Test1	Test2	Grades
N		58	58	58
Normal Parameters	Mean	6.8690	10.9466	15.1207
	Std. Deviation	5.66572	5.37565	3.00921
Most Extreme Differences	Absolute	0.176	0.164	0.109
	Positive	0.176	0.097	0.109
	Negative	−0.113	−0.164	−0.098
Kolmogorov-Smirnov Z		1.344	1.248	0.828
Asymp. Sig. (2-tailed)		0.054	0.089	0.499

), we checked the normality of our variables: test1, test2, and grades, which are the results of the tests submitted by the students.

We noticed that test1 had p = 0.054 > 0.05, and test2 had p = 0.089 > 0.05, and grades had p = 0.499 > 0.05.

Therefore, all three variables, test1, test2, and grades, followed the normal distribution, so the following conclusions are valid.

4. Results

The students participated in the metacognitive tests with the knowledge of typical teaching and practice in algorithmic-type exercises and theory that requires memorization and not particularly critical thinking. The tests were carried out at least two weeks at different intervals. The time order was as follows: test1 first, then test2, and finally, a combination of assignments and a written test called grades.

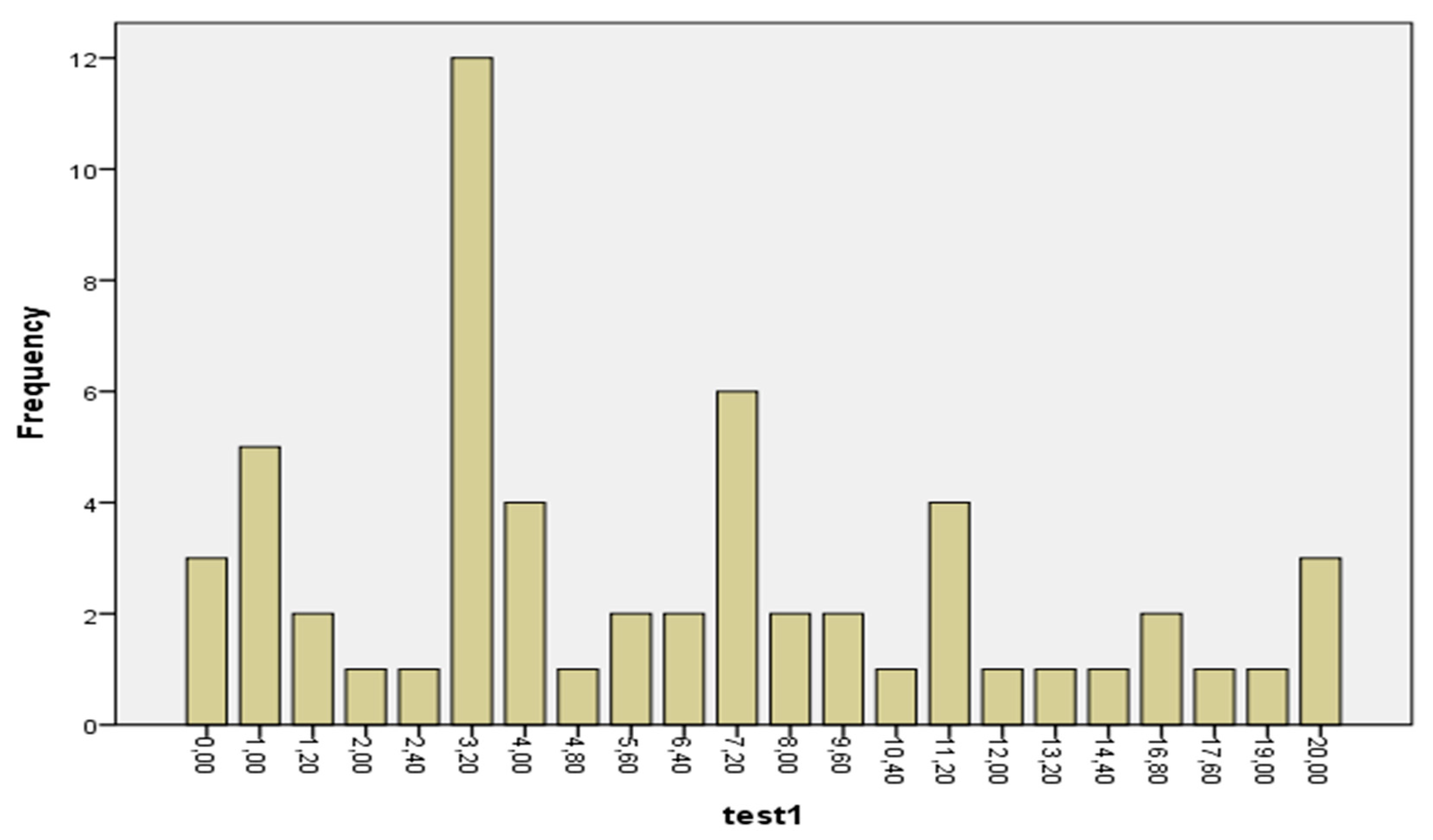
The results of test1 (

Table 2. Statistics.

		Test2	Test1	Grades
N	Valid	58	58	58
	Missing	0	0	0
Mean		10.9466	6.8690	15.1207
Median		12.0000	5.2000	15.0000
Mode		14.00	3.20	12.00
Std. Deviation		5.37565	5.66572	3.00921
Variance		28.898	32.100	9.055
Minimum		0.00	0.00	10.00
Maximum		20.00	20.00	20.00

, Figure 1) reflect the students’ inability to perform effectively in metacognitive- and holistic-type exercises and theory questions that challenge critical thinking.

The mean value of 6.890, the median of 5.2, and the overall value of 3.2 illustrate the intense weakness of the students in approaching and analyzing exercises with critical thinking and the combined content of concepts.

In the interval between test1 and test2, specialized teaching followed an emphasis on self-diagnostic questions between the students regarding the association of the concepts and their differences and similarities.

Exercises were solved using the dialectic method with questions and answers, leading the students’ thinking to dead ends, which they overcame by asking the right questions.

The result of this differentiated teaching is reflected in the improvement of the position measures of the variable test2 (Table 2, Figure 2).

The average value reached 10.9 from 6.8, the median 12 from 5.2, and the overall value 14 from 3.2.

In the time interval between the implementation of test2 and the recommended grading of the group assignments and the third test, the teaching continued based on metacognitive and holistic theories and exercises. The results were summarized in a graded record called grades (Table 2, Figure 3).

The results of the overall grading grades, as shown in Table 2, illustrate the development of the students in their ability to develop their critical thinking, understand the processes, and sense the concepts. The mean value was 15.12, the median was 15, and the prevailing value was 12.

4.1. Regression between Test1 and Test2 Variables

In the Variables Entered/Removed table (

Table 3. Variables entered/removed.

Model	Variables Entered	Variables Removed	Method
1	test1		Enter

),we we apply the linear regression between the variables test2 and test1.

In the ModelSummary table (

Table 4. Model summary.

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate	Change Statistics
					R Square Change	F Change	df1	df2	Sig. F Change
1	0.518	0.268	0.255	4.63891	0.268	20.543	1	56	0.000

), we are interested in the term AdjustedRsquare, which is 0.255 and expresses the percentage of the total variability present in the data and interpreted by the regression. We did not find an acceptable value.

We would have an acceptable value when the AdjustedRsquare term exceeds 0.7. The fact that the values of test2 cannot be interpreted from the values of test1 is expected. The grades of the two tests are the results of conventional teaching with a focus on mechanical processes, and memorization and teaching based on metacognitive- and holistic-type learning processes characterized by understanding and comparing new concepts with each other while at the same time allowing the student to shape the way they learn

4.2. Regression between Test2 and Grades Variables

In the Variables Entered/Removed table (

Table 5. Variables entered/removed.

Model	Variables Entered	Variables Removed	Method
1	grades		Enter

),we we apply the linear regression between the variables test2 and grades.

In the ModelSummary table (

Table 6. Model summary.

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate	Change Statistics					Durbin-Watson
					R Square Change	F Change	df1	df2	Sig. F Change
1	0.885	0.783	0.779	2.52899	0.783	201.539	1	56	0.000	1.923

), the term AdjustedRsquare is 0.779 and expresses the percentage of the total variability in the data as interpreted by the regression. We found an acceptable value.

We noticed a high correlation between the variables test2 and grades, which was expected since the same type of teaching was used among the two tests. The students continued to prepare for metacognitive exercises and theories of the right–wrong and multiple-choice types.

The ANOVA table (

Table 7. ANOVA.

Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	1289.001	1	1289.001	201.539	0.000
	Residual	358.164	56	6.396
	Total	1647.164	57

) shows whether the regression found by the software is statistically significant.

The value of F = 201,539 with sig. < 0.01 means that the regression found exists and is not a product of a sampling error. On the other hand, the F-test tests Hypothesis 1a:

Hypothesis 1a (H1a). 

$H_0:{\beta }_1={\beta }_2=\dots ={\beta }_k=0$ _με $H_1:\mathsf{\kappa }\mathsf{ά}\mathsf{\pi }\mathsf{o}\mathsf{\iota }\mathsf{o} {\beta }_i\ne 0$.

We then conducted a t-Test to determine which β is not 0.

In the coefficients table (

Table 8. Coefficients.

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	−12.949	1.716		−7.547	0.000
	grades	1.580	0.111	0.885 *	14.196	0.000

−y = b₀ + b₁x₁ + b₂x_2. Dependent = ConstantB + coefficient of independent B * independent Bi expresses the change in Y for a unit increase in X. In our case, y = −12.949 + 1.580 × x1 (Figure 4).

), we are interested in the B value, which gives us the regression equation:

4.3. Verify with Neural Networks

We used neural networks to examine the causality between the variables test1 and test2, followed by the causality between the variables test2 and grades.

The sum square error between the variables test2 and test1 (

Table 9. Model summary.

Training	The sum of Squares Error	11.840
	Relative Error	0.538
	Stopping Rule Used	one consecutive step(s) with no decrease in error
	Training Time	0:00:00.00
Testing	The sum of Squares Error	2.151
	Relative Error	0.545

) with the dependent variable test2 and the independent dependent variable test1 was SSE = 2.151 and the relative error = 0.545.

Contrary to Table 9, in which the dependent variable is the grades and the independent variable is test2, the sum square error was SSE = 1.081 and the relative error = 0.149 (

Table 10. Model summary.

Training	The sum of Squares Error	3.732
	Relative Error	0.191
	Stopping Rule Used	one consecutive step(s) with no decrease in error
	Training Time	0:00:00.00
Testing	The sum of Squares Error	1.081
	Relative Error	0.149

Dependent Variable: grades. Error computations are based on the testing sample.

).

We used the neural networks to verify the results given by the linear regression; since no significance was found between the variables test1 and test2, no regression is evident. In contrast, between test2 and grades, there was a regression.

Comparing our SSEs shows the exact correlation as 1.081 < 2.151, almost half.

5. Discussion

The quantitative analysis in this study using the variables of test1 and test2 scores indicated no correlation between them. This lack of correlation is expected, as the topics covered in test1 involve knowledge of definitions and algorithmic processes, that is, “knowledge.” On the other hand, the topics covered in test2 were more holistic and required “critical thinking,” that is, “metacognition.”

Initially, the students received standard instruction aimed at memorizing definitions and rules and learning algorithmic processes through repetition. The students were then tested on both test1 and test2, and the study demonstrated the inability of this specific type of instruction to help students cope with exercises that require holistic thinking and critical analysis.

In the second phase, a “metacognitive” type of instruction was implemented with the following structural elements:

Metacognition has become an essential instructional method as educational philosophy evolves from teaching simply “what” to reflecting on the “how.” Metacognition—sophisticated thinking—may be the precursor to modern education, dating back to Socrates himself.

A metacognitive procedure includes more than merely thinking about the concept of thinking. This technique requires students to “express their mental actions” and evaluate the resultant wisdom. As well as thoughtful emergent policies, learners must also be aware of themselves and their responsibilities. New policies must address a thinker’s abilities and flaws.

5.1. Why Is Teaching Metacognition Important?

When learners use metacognitive practices, their skills in simplifying their knowledge are enhanced. To achieve this, they must exceed the topic itself and obtain a level of attentiveness that reaches beyond it [24]. Metacognition abilities must be trained thoughtfully to nurture highly talented students. Mastering various metacognitive abilities takes recurrent practice, enabling students to develop their intelligence as they adjust to new motivations.

5.2. Metacognition Plans to Use in Classroom

It is essential to model metacognition and asks questions when coaching. Instructors can model metacognition by speaking aloud and asking students to mirror what they have discovered [25]. Specific guidance in questioning via tasks is critical to construct these capabilities in students. To broaden vital wondering, instructors ought to address both experts and beginners.

Classes of metacognitive techniques consist of making plans, tracking, and comparing. Within the thinking level, students interact in practices that address the query, “How will I accomplish the preferred studying results?” Students wonder by asking, “How am I doing with my plan execution and information?”; while tracking their wondering, students ask themselves, “Did it pass properly, and what can I do better next time?”.

5.3. Self-Questioning

Using self-thinking throughout the lesson is efficiently a matter of students posing inquiries to themselves and answering them [26]. Think–pair–share periods may be carried out informally. Developing a reflective magazine wherein students speak with themselves can also be helpful to the procedure. All through a lesson, students may want to ask themselves, “How am I achieving my goals nowadays?”, “How else may I achieve my goals?” and “Which sources can help me learn?”.

A student must reflect upon their studying after finishing an activity or lesson: “What did I research?”, “Is there something I nonetheless want to recognize?” or “Do I have any questions?” as well as “How would it be possible to reach a comparable challenge in a different way next time?”.

5.4. Pre-Assessments

In pre-tests, students are capable of taking a look at previous information on the subject matter. Instructors must ask students to study pre-tests to determine what subject matter questions they got right and how they might have reached it to enhance this exercise [25]. Metacognition occurs while pupils develop and execute a quiz or examination guidance approach. Before an evaluation, an instructor ought to have students examine study techniques. Students can also examine past pursuits to plan the most straightforward and efficient examination plan.

5.5. Identifying Confusions

In order to observe their thoughts on a subject, students can recognize misperception in a low-risk means. To notify the next day’s class, tutors can ask learners to note down what they create puzzling about a subject in their notebooks.

5.6. Active Learning Tasks

As part of active-learning activities, learners observe their studying [12]. Tasks contain, “Note down three activities that you have taught from today’s class and three questions you still have about this topic,” or “Note down yourself a letter clarifying that shows how you perform this task differently if you had to do it over.”

5.7. Post Assessments

If studying is the goal, post-assessments are of more excellent value than the assessments themselves [26]. When learners redirect on their presentation, training strategies, and potential methods, the exam turns into a coaching instrument and a model for future thoughts.

5.8. Exam Wrappers

These worksheets provide reflective questions that students may use to learn more about their performance on a quiz or test. Students should answer questions on their worksheets regarding how they prepared for the test and how they may improve their study methods [27].

5.9. Metacognitive Talks

The metacognitive conversation is the term for talking out loud while doing a job [26]. Students may use this to understand better how they think and concentrate. To put it into practice, one may guide a class through a job aloud to show them how it is done before letting them attempt it themselves. Pupils should verbalize their answers to the following questions aloud:

• What did I learn about this subject?
• Have I ever completed an assignment similar to this?
• What tactics were successful in the past?
• What must I complete first?
• How am I doing?
• What should I do after the task?
• Should I choose a different tactic?
• How can I get assistance?
• How did I perform on this assignment?

6. Limitations

The study utilized a small sample size of only 58 scholars from mathematics history. This small sample size may limit the generalizability of the findings to a larger population of school pupils. It focused on students aged 14 to 17 from secondary grades. This narrow age range may restrict the applicability of the findings to students of different age groups. The study collected data through written tests and group assignments, which may introduce subjectivity in assessing students’ metacognitive perception and critical thinking abilities. The subjective nature of the data collection method could affect the reliability and validity of the findings.

The study relied on quantitative methods such as statistical regression and neural networking. While these methods can provide valuable insights, they may overlook qualitative aspects of students’ learning experiences, such as their perceptions, attitudes, and motivations. It analyzed the data collected at different intervals but did not incorporate a longitudinal design to track the students’ progress over an extended period. Longitudinal studies can provide a better understanding of the long-term effects of teaching methods on students’ learning outcomes. The study utilized the Statistical Package for Social Sciences [SPSS] for data analysis. While SPSS is a widely used tool, relying solely on one software may limit the exploration of alternative analytical approaches or techniques.

7. Conclusions

This study investigated the effectiveness of different learning theories, namely metacognition, and metagnosis, in teaching mathematical concepts to secondary-level students. The research utilized quantitative methods and employed statistical regression and neural networking for data analysis. The study collected data from 58 scholars from mathematics history, consisting of students aged 14 to 17 from secondary grades.

The findings of the study indicated that both metacognition and metagnosis played significant roles in mathematical learning. Metacognition, which focuses on foundational knowledge and understanding, required memorization of formulas, recognition of patterns, and comprehension of concepts [2]. Metagnosis, on the other hand, involved the application of knowledge in unfamiliar contexts, problem-solving, analyzing results, and drawing conclusions [8].

The research utilized statistical regression and neural networks in the Statistical Package for Social Sciences (SPSS) for data analysis. Statistical regression allowed for identifying trends and relationships between variables, while neural networks simulated human brain function and facilitated predictions and complex data pattern recognition. The combination of these methods led to improved accuracy and reliable predictions, with potential applications in various fields, such as business and medicine.

The study’s methodology involved collecting data through written tests and group assignments, which were analyzed using SPSS. The normality of the variables was checked, and regression analysis was performed to examine the relationship between the variables. The results indicated that both test1 and test2 variables followed a normal distribution. The analysis showed that the students’ performances improved from test1 to test2, indicating the effectiveness of the differentiated teaching approach emphasizing self-diagnostic questions and critical thinking.

Overall, this study contributes to understanding the theoretical implications of mathematical learning theories and their impact on teaching mathematical concepts to secondary-level students. The findings highlight the importance of incorporating metacognition and metagnosis in the educational process to enhance students’ understanding and problem-solving abilities. The utilization of statistical regression and neural networks provides valuable insights and accurate predictions for decision-making in education and related fields.