Nonlinear Responses and Population-Level Coupling of Growth and MC-LR Production in Microcystis aeruginosa Under Multifactorial Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and Culture Conditions
2.2. Growth Curve Modeling
2.3. Modeling of Chlorophyll-A and Microcystin-LR Production
2.4. Statistical Analyses
3. Results
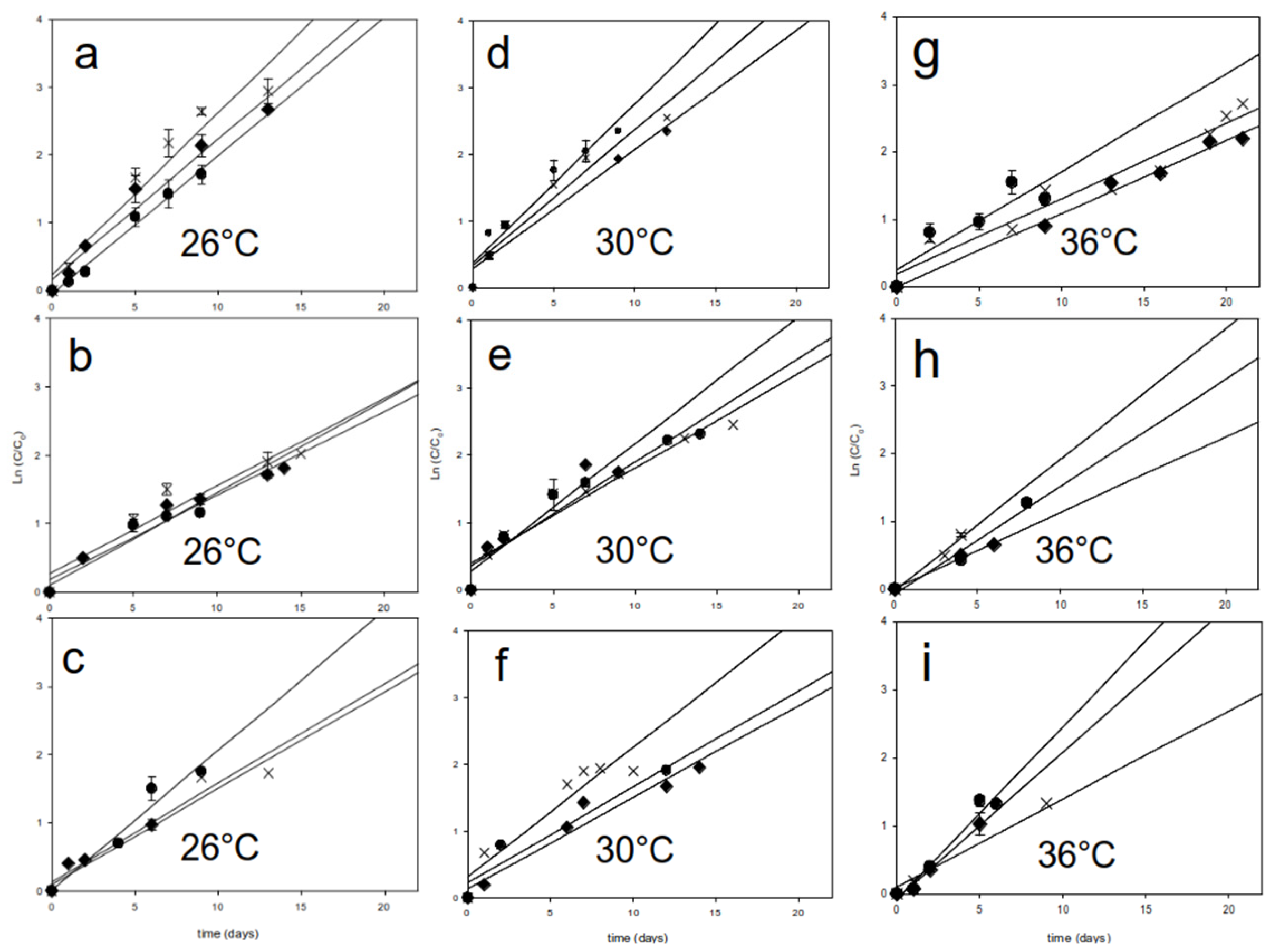
3.1. Growth Kinetics
3.2. Chlorophyll-A Production
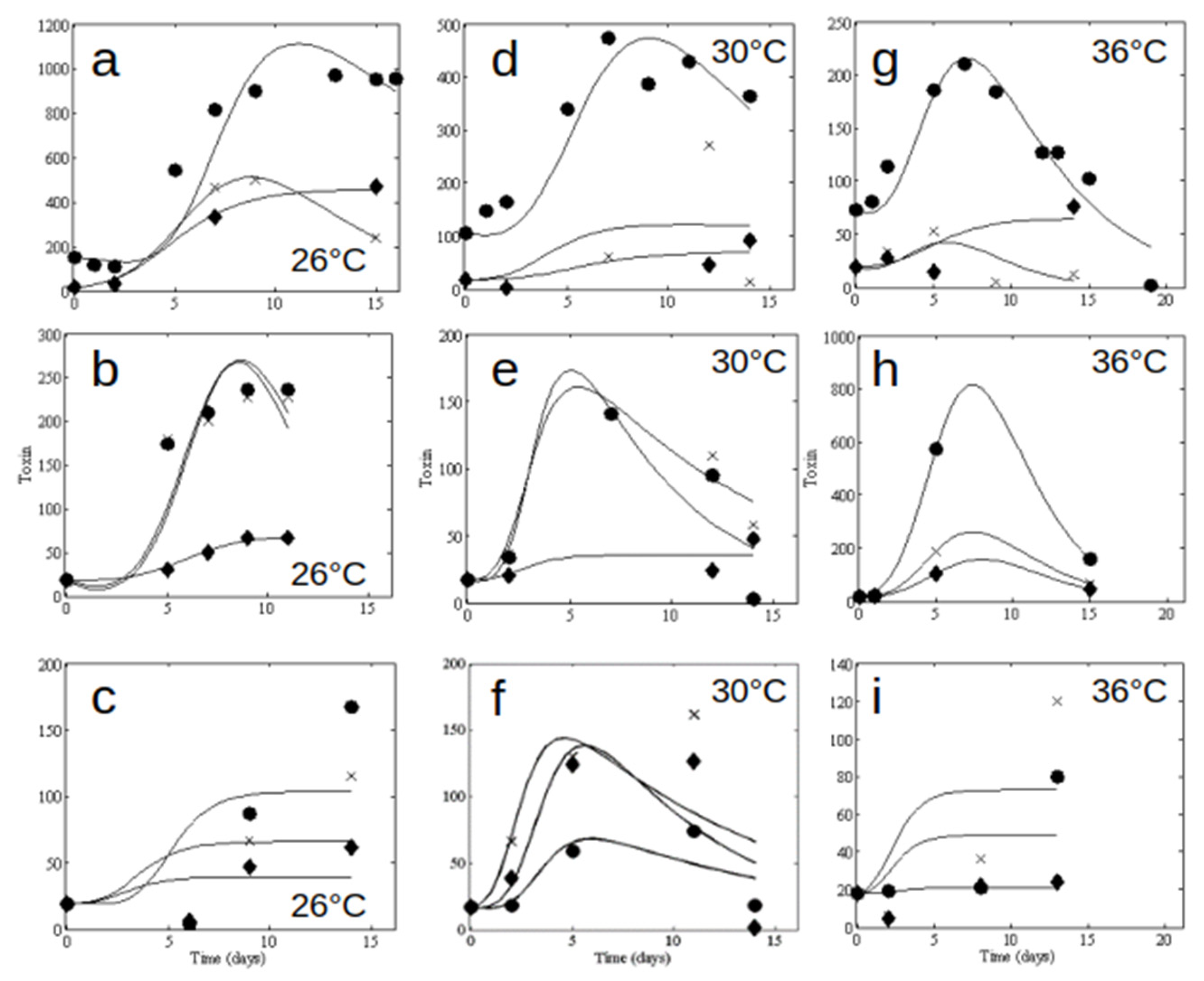
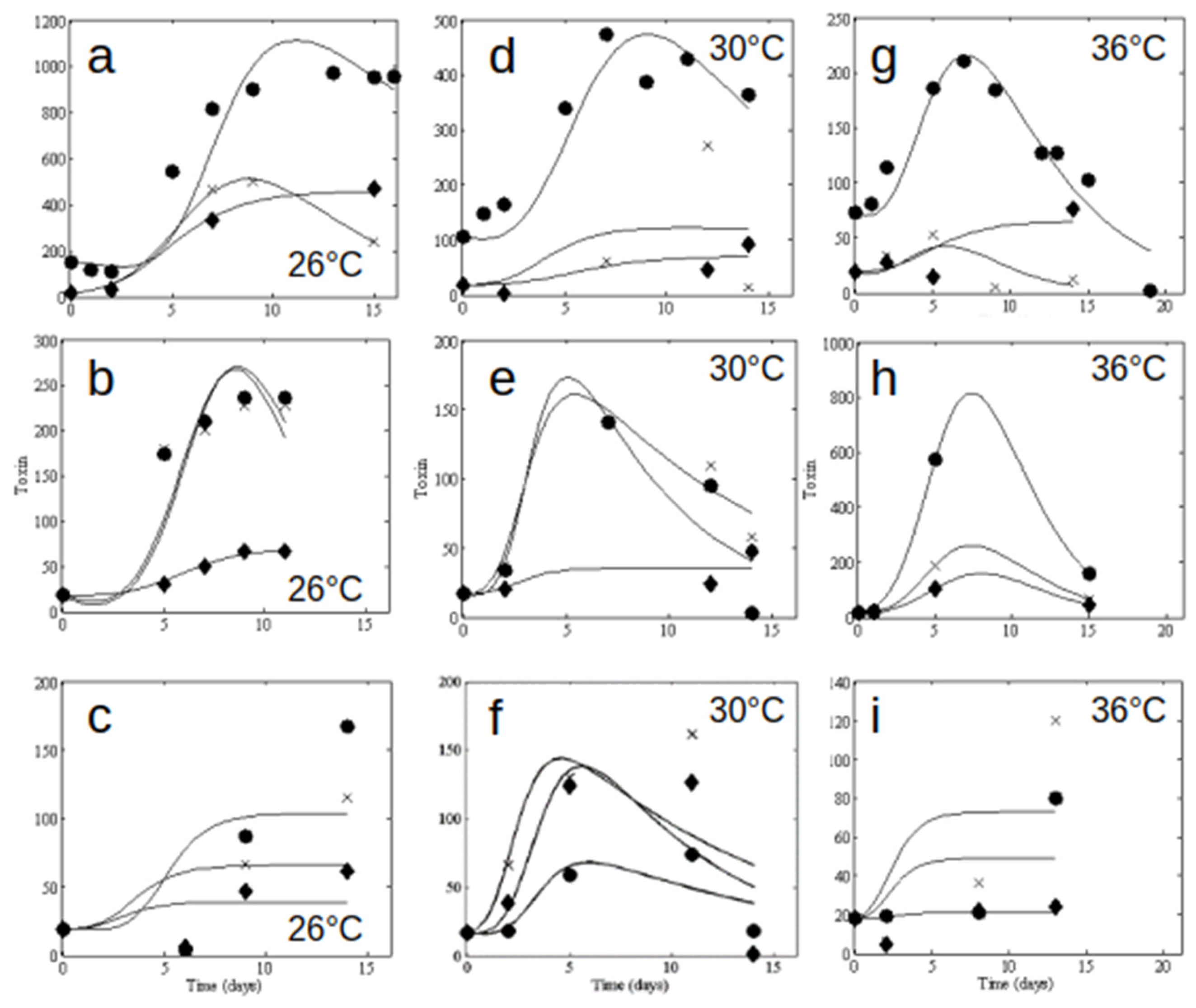
3.3. Microcystin-LR Production
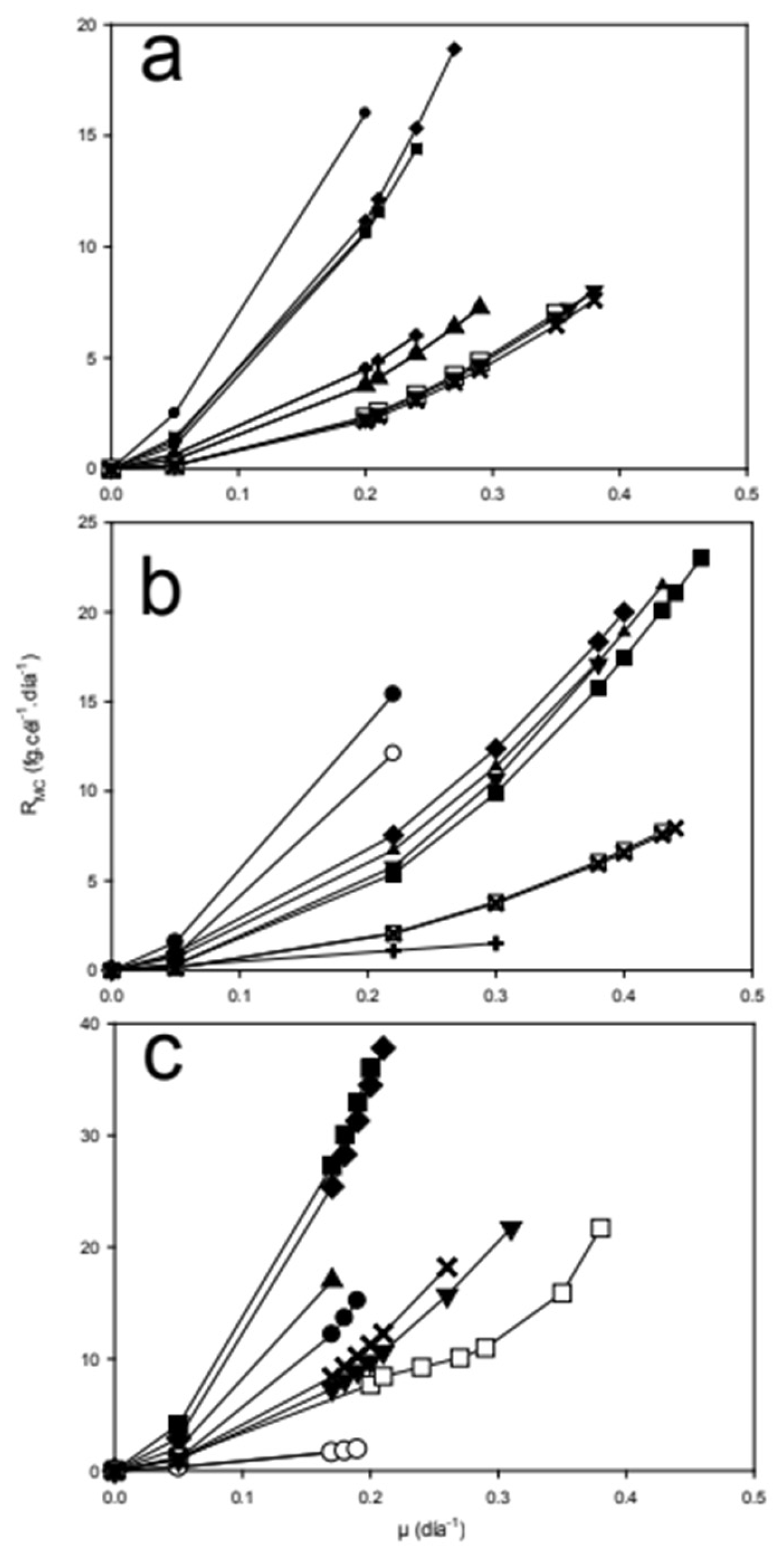
3.4. Long Model: Net Toxin Production and Growth Coupling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harke, M.J.; Steffen, M.M.; Gobler, C.J.; Otten, T.G.; Wilhelm, S.W.; Wood, S.A.; Paerl, H.W. A review of the global ecology, genomics, and biogeography of the toxic cyanobacterium, Microcystis spp. Harmful Algae 2016, 54, 4–20. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Yang, H.; Gao, X.; Li, M.; Zhang, M.; Dong, J.; Zhang, J.; Li, L.; Li, X.; Burford, M.A. Ecological damage of submerged macrophyte Myriophyllum spicatum by cell extracts from microcystin (MC)-and non-MC-producing cyanobacteria, Microcystis. J. Oceanol. Limnol. 2022, 40, 1732–1749. [Google Scholar] [CrossRef]
- Paerl, H.W.; Otten, T.G.; Kudela, R. Mitigating the expansion of harmful algal blooms across the freshwater-to-marine continuum. Environ. Sci. Technol. 2018, 52, 5519–5529. [Google Scholar] [CrossRef] [PubMed]
- Lürling, M.; Mucci, M. Mitigating eutrophication: In-lake measures are becoming inevitable in eutrophic waters in the Netherlands. Hydrobiologia 2020, 847, 4457–4477. [Google Scholar] [CrossRef]
- Becker, S.; Hu, W.; Wilhelm, S.W. The importance of interdependent environmental conditions in regulating cyanobacterial bloom dynamics. Front. Microbiol. 2021, 12, 661299. [Google Scholar]
- Li, Z.; An, L.; Yan, F.; Shen, W.; Du, W.; Dai, R. Evaluation of the Effects of Different Phosphorus Sources on Microcystis aeruginosa Growth and Microcystin Production via Transcriptomic Surveys. Water 2023, 15, 1938. [Google Scholar] [CrossRef]
- Van der Westhuizen, A.J.; Eloff, J.N. Effect of temperature and light on the toxicity and growth of the blue-green alga Microcystis aeruginosa (UV-006). Planta 1985, 163, 55–59. [Google Scholar] [CrossRef]
- Jähnichen, S.; Long, B.M.; Petzoldt, T. Microcystin production by Microcystis aeruginosa: Direct regulation by multiple environmental factors. Harmful Algae 2011, 12, 95–104. [Google Scholar] [CrossRef]
- Bortoli, S.; Oliveira-Silva, D.; Krüger, T.; Dörr, F.A.; Colepicolo, P.; Volmer, D.A.; Pinto, E. Growth and microcystin production of a Brazilian Microcystis aeruginosa strain (LTPNA 02) under different nutrient conditions. Rev. Bras. Farmacogn. 2014, 24, 389–398. [Google Scholar] [CrossRef]
- Long, B.M.; Jones, G.J.; Orr, P.T. Cellular microcystin content in N-limited Microcystis aeruginosa can be predicted from growth rate. Appl. Environ. Microbiol. 2001, 67, 278–283. [Google Scholar] [CrossRef]
- Lyck, S. Simultaneous changes in cell quotas of microcystin, chlorophyll a, protein and carbohydrate during different growth phases of a batch culture experiment with Microcystis aeruginosa. J. Plankton Res. 2004, 26, 727–736. [Google Scholar] [CrossRef]
- Wang, H.; Wang, B.; Zhang, C.; Liu, H.; Li, Y. Effects of temperature and nutrient loading on the growth and microcystin production of Microcystis aeruginosa. Sci. Total Environ. 2020, 708, 135150. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; Van’t Riet, K. Modeling of the bacterial growth curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef] [PubMed]
- Crettaz-Minaglia, M.C.; Rosso, L.; Aranda, J.O.; Goñi, S.; Sedan, D.; Andrinolo, D.; Giannuzzi, L. Mathematical modeling of Microcystis aeruginosa growth and [D-Leu1] microcystin-LR production in culture media at different temperatures. Harmful Algae 2017, 67, 13–25. [Google Scholar]
- Cottingham, K.L.; Weathers, K.C.; Ewing, H.A.; Greer, M.L.; Carey, C.C. Predicting the effects of climate change on freshwater cyanobacterial blooms requires consideration of the complete cyanobacterial life cycle. J. Plankton Res. 2020, 42, 421–430. [Google Scholar] [CrossRef]
- Ji, X.; Verspagen, J.M.H.; Van de Waal, D.B.; Rost, B.; Huisman, J. Phenotypic plasticity of carbon fixation stimulates cyanobacterial blooms at elevated CO2. Sci. Adv. 2020, 6, eaax2926. [Google Scholar] [CrossRef]
- Marrone, B.; Banerjee, S.; Talapatra, A.; Gonzalez-Esquer, R.; Pilania, G. Toward a predictive understanding of cyanobacterial harmful algal blooms through AI integration of physical, chemical, and biological data. ACS EST Water 2023, 3, 1611–1623. [Google Scholar] [CrossRef]
- Aragão, N.R.S.; dos Reis, K.C.; Souza, A.C.; Rocha, M.A.; Capelo Neto, J. Modeling total microcystin production by Microcystis aeruginosa using multiple regression. J. Water Supply Res. Technol. 2020, 69, 415–426. [Google Scholar] [CrossRef]
- Sakai, Y.; Katayama, H.; Oguma, K.; Ohgaki, S. Kinetics of Microcystis aeruginosa Growth and Intracellular Microcystins Release after UV Irradiation. Environ. Sci. Technol. 2009, 135, 78–85. [Google Scholar] [CrossRef]
- Howard, A. Modeling movement patternss of the cyanobacterium, Microcystis. Ecol. Appl. 2001, 11, 304–310. [Google Scholar] [CrossRef]
- Marker, A.F.H.; Crowther, C.A.; Gunn, R.J.M. Methanol and acetone as solvents for estimating chlorophyll a and phaeopigments by spectrophotometry. Arch. Hydrobiol. Beih. Ergebn. Limnol. 1980, 14, 52–69. [Google Scholar]
- Watanabe, M.F.; Oishi, S. Effects of environmental factors on toxicity of a cyanobacterium (Microcystis aeruginosa) under culture conditions. Appl. Environ. Microbiol. 1985, 49, 1342–1344. [Google Scholar] [CrossRef] [PubMed]
- Lürling, M.; Eshetu, F.; Faassen, E.J.; Kosten, S.; Huszar, V.L. Comparison of cyanobacterial and green algal growth rates at different temperatures. Freshw. Biol. 2013, 58, 552–559. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiao, P.; Yu, G.; Sano, T.; Pan, Q.; Li, R. Effects of irradiance on the growth and microcystin production of Microcystis viridis and Microcystis aeruginosa. Environ. Toxicol. 2012, 27, 342–349. [Google Scholar] [CrossRef]
- Robarts, R.D.; Zohary, T. Temperature effects on photosynthetic capacity, respiration, and growth rates of bloom-forming cyanobacteria. N. Z. J. Mar. Freshw. Res. 1987, 21, 391–399. [Google Scholar] [CrossRef]
- Queiroz, M.I.; Hornes, M.O.; da Silva-Manetti, A.G.; Jacob-Lopes, E. Single-cell oil production by cyanobacterium Aphanothece microscopica Nägeli cultivated heterotrophically in fish processing wastewater. Appl. Energy 2011, 88, 3438–3443. [Google Scholar] [CrossRef]
- Leloup, M.; Nicolau, R.; Pallier, V.; Yéprémian, C.; Feuillade-Cathalifaud, G. Organic matter produced by algae and cyanobacteria: Quantitative and qualitative characterization. J. Environ. Sci. 2013, 25, 1089–1097. [Google Scholar] [CrossRef]
- Yates, G.T.; Smotzer, T. On the lag phase and initial decline of microbial growth curves. J. Theor. Biol. 2007, 244, 511–517. [Google Scholar] [CrossRef]
- Giannuzzi, L.; Krock, B.; Minaglia, M.C.C.; Rosso, L.; Houghton, C.; Sedan, D.; Malanga, G.; Espinosa, M.; Andrinolo, D.; Hernando, M. Growth, toxin production, active oxygen species and catalase activity of Microcystis aeruginosa (Cyanophyceae) exposed to temperature stress. Comp. Biochem. Physiol. Part C Toxicol. Pharmacol. 2016, 189, 22–30. [Google Scholar] [CrossRef]
- Raps, S.; Wyman, K.; Siegelman, H.W.; Falkowski, P.G. Adaptation of the cyanobacterium Microcystis aeruginosa to irradiance. Plant Physiol. 1983, 72, 829–832. [Google Scholar] [CrossRef]
- Beversdorf, L.J.; Miller, T.R.; McMahon, K.D. The role of nitrogen fixation in cyanobacterial bloom toxicity in a eutrophic lake. PLoS ONE 2015, 10, e0148881. [Google Scholar] [CrossRef] [PubMed]
- Orr, P.T.; Jones, G.J. Relationship between microcystin production and cell division rates in nitrogen-limited Microcystis aeruginosa cultures. Limnol. Oceanogr. 1998, 43, 1604–1614. [Google Scholar] [CrossRef]
- Jähnichen, S.; Petzoldt, T.; Benndorf, J. Evidence for control of microcystin dynamics in Bautzen Reservoir (Germany) by cyanobacterial population growth rates and dissolved inorganic carbon. Arch. Für Hydrobiol. 2001, 150, 177–196. [Google Scholar] [CrossRef]
- Wicks, R.J.; Thiel, T. Environmental regulation of microcystin production. Toxicon 1990, 28, 883–890. [Google Scholar] [CrossRef]
- Runnegar, M.T.C.; Jackson, A.R.B.; Falconer, I.R. Toxicity of the cyanobacterium (blue-green alga) Microcystis aeruginosa in drinking water to growing pigs, as an animal model for human injury. Environ. Toxicol. Chem. 1983, 2, 377–385. [Google Scholar] [CrossRef]
- Babica, P.; Bláha, L.; Maršálek, B. Exploring the natural role of microcystins: A review of effects on aquatic organisms. Interdiscip. Toxicol. 2006, 2, 9–20. [Google Scholar] [CrossRef]
- Leão, P.N.; Vasconcelos, M.T.; Vasconcelos, V.M. Allelopathy in freshwater cyanobacteria. Crit. Rev. Microbiol. 2009, 35, 271–282. [Google Scholar] [CrossRef]

| RMSE | R2 | MPD (cells.mL−1) | LPD (d) | µ (d−1) | m | c | b | a | 26 °C | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.082 | 0.99 | 7.28 ± 0.02 a | 3.55 ± 0.07 a | 0.20 ± 0.05 a | 5.39 ± 0.06 | 0.54 ± 0.02 | 0.99 ± 0.01 | 6.29 ± 0.01 | N:P 10 | 30 µmol photon m−2.s−1 |
| 0.030 | 0.99 | 7.49 ± 0.03 a | 0.65 ± 0.26 b | 0.21 ± 0.05 a | 3.15 ± 0.07 | 0.40 ± 0.01 | 1.39 ± 0.02 | 6.10 ± 0.01 | N:P 100 | |
| 0.033 | 0.99 | 7.37 ± 0.05 a | 0.18 ± 0.40 b | 0.24 ± 0.07 a | 2.22 ± 0.09 | 0.49 ± 0.02 | 1.32 ± 0.03 | 6.06 ± 0.02 | N:P 150 | |
| 0.059 | 0.99 | 7.19 ± 0.03 b | 2.28 ± 0.36 a | 0.24 ± 0.07 a | 4.42 ± 0.05 | 0.47 ± 0.02 | 1.39 ± 0.02 | 5.80 ± 0.01 | N:P 10 | 50 µmol photon m−2.s−1 |
| 0.085 | 0.99 | 7.44 ± 0.03 b | 2.24 ± 0.38 b | 0.27 ± 0.06 a | 4.45 ± 0.06 | 0.45 ± 0.01 | 1.64 ± 0.02 | 5.80 ± 0.01 | N:P 100 | |
| 0.055 | 0.99 | 7.33 ± 0.05 b | 0.88 ± 0.43 b | 0.29 ± 0.08 a | 3.01 ± 0.09 | 0.47 ± 0.01 | 1.66 ± 0.03 | 5.67 ± 0.02 | N:C:\N:\PP 150 | |
| 0.040 | 0.99 | 7.35 ± 0.03 b | 2.54 ± 0.16 a | 0.35 ± 0.05 b | 3.71 ± 0.01 | 0.85 ± 0.01 | 1.11 ± 0.00 | 6.23 ± 0.00 | N:P 10 | 70 µmol photon m−2.s−1 |
| 0.075 | 0.99 | 7.22 ± 0.03 b | 0.72 ± 0.32 b | 0.38 ± 0.09 b | 1.94 ± 0.05 | 0.82 ± 0.03 | 1.27 ± 0.02 | 5.95 ± 0.02 | N:P 100 | |
| 0.021 | 0.99 | 7.05 ± 0.03 b | 0.56 ± 0.34 b | 0.36 ± 0.10 b | 1.66 ± 0.06 | 0.91 ± 0.07 | 1.09 ± 0.02 | 5.96 ± 0.01 | N:P 150 | |
| RMSE | R2 | MPD (cells.mL−1) | LPD (d) | µ (d−1) | m | c | b | a | 30 °C | |
| 0.033 | 0.99 | 7.39 ± 0.06 a.c | 0.94 ± 0.27 a | 0.22 ± 0.08 a | 3.10 ± 0.14 | 0.46 ± 0.02 | 1.31 ± 0.03 | 6.08 ± 0.03 | N:C:\N:\PP 10 | 30 µmol photon m−2.s−1 |
| 0.073 | 0.99 | 6.75 ± 0.07 a.d | 0.68 ± 0.46 a | 0.30 ± 0.12 a | 2.18 ± 0.10 | 0.66 ± 0.06 | 1.25 ± 0.04 | 5.50 ± 0.03 | N:P 100 | |
| 0.026 | 0.99 | 6.74 ± 0.09 a | 0.94 ± 0.62 a | 0.22 ± 0.11 a | 3.01 ± 0.18 | 0.48 ± 0.05 | 1.24 ± 0.05 | 5.49 ± 0.04 | N:P 150 | |
| 0.134 | 0.99 | 6.72 ± 0.06 b.c | 1.04 ± 0.25 a | 0.46 ± 0.14 b | 2.03 ± 0.06 | 1.01 ± 0.08 | 1.22 ± 0.03 | 5.49 ± 0.03 | N:P 10 | 50 µmol photon m−2.s−1 |
| 0.090 | 0.99 | 6.58 ± 0.06 b.d | 0.75 ± 0.38 a | 0.40 ± 0.12 b | 1.81 ± 0.08 | 0.95 ± 0.07 | 1.14 ± 0.03 | 5.44 ± 0.03 | N:P 100 | |
| 0.020 | 0.99 | 6.62 ± 0.08 b | 0.54 ± 0.38 a | 0.43 ± 0.15 b | 1.55 ± 0.07 | 1.00 ± 0.08 | 1.17 ± 0.04 | 5.45 ± 0.04 | N:P 150 | |
| 0.018 | 0.99 | 7.19 ± 0.06 a.c | 1.09 ± 0.44 a | 0.43 ± 0.08 b | 2.15 ± 0.11 | 0.94 ± 0.02 | 1.24 ± 0.03 | 5.95 ± 0.03 | N:P 10 | 70 µmol photon m−2.s−1 |
| 0.067 | 0.99 | 7.06 ± 0.02 a.d | 0.35 ± 0.23 a | 0.44 ± 0.08 b | 1.27 ± 0.03 | 1.08 ± 0.03 | 1.10 ± 0.01 | 5.96 ± 0.01 | N:P 100 | |
| 0.055 | 0.99 | 7.13 ± 0.06 a | 0.91 ± 0.61 a | 0.38 ± 0.06 b | 2.06 ± 0.16 | 0.87 ± 0.02 | 1.19 ± 0.04 | 5.94 ± 0.02 | N:P 150 | |
| RMSE | R2 | MPD (cells.mL−1) | LPD (d) | µ (d−1) | m | c | b | a | 36 °C | |
| 0.055 | 0.99 | 6.44 ± 0.07 a | 1.28 ± 0.60 a | 0.19 ± 0.04 a | 2.56 ± 0.19 | 0.50 ± 0.04 | 1.05 ± 0.04 | 5.39 ± 0.03 | N:C:\N:\PP 10 | 30 µmol photon m−2.s−1 |
| 0.070 | 0.99 | 6.41 ± 0.08 a | 0.90 ± 0.55 a | 0.18 ± 0.07 a | 2.02 ± 0.18 | 0.45 ± 0.02 | 1.09 ± 0.04 | 5.33 ± 0.04 | N:P 100 | |
| 0.576 | 0.99 | 6.46 ± 0.04 a | 1.25 ± 0.43 a | 0.19 ± 0.06 a | 2.62 ± 0.10 | 0.48 ± 0.02 | 1.07 ± 0.02 | 5.39 ± 0.02 | N:P 150 | |
| 0.058 | 0.99 | 6.46 ± 0.02 a | 1.21 ± 0.29 a | 0.20 ± 0.04 a | 3.32 ± 0.04 | 0.47 ± 0.01 | 1.14 ± 0.01 | 5.32 ± 0.01 | N:C:\N:\PP 10 | 50 µmol photon m−2.s−1 |
| 0.028 | 0.99 | 6.33 ± 0.06 a | 1.05 ± 0.51 a | 0.21 ± 0.08 a | 3.07 ± 0.13 | 0.49 ± 0.03 | 1.15 ± 0.03 | 5.32 ± 0.03 | N:C:\N:\PP 100 | |
| 0.030 | 0.99 | 6.50 ± 0.05 a | 0.78 ± 0.49 a | 0.17 ± 0.06 a | 3.37 ± 0.12 | 0.39 ± 0.02 | 1.21 ± 0.03 | 5.28 ± 0.03 | N:C:\N:\PP 150 | |
| 0.026 | 0.99 | 6.20 ± 0.03 b | 0.42 ± 0.31 b | 0.31 ± 0.08 b | 1.40 ± 0.05 | 1.01 ± 0.05 | 0.82 ± 0.01 | 5.38 ± 0.01 | N:C:\N:\PP 10 | 70 µmol photon m−2.s−1 |
| 0.026 | 0.99 | 6.13 ± 0.02 b | 0.29 ± 1.10 b | 0.26 ± 0.06 b | 1.37 ± 0.04 | 0.93 ± 0.03 | 0.75 ± 0.01 | 5.38 ± 0.01 | N:P 100 | |
| 0.071 | 0.99 | 6.27 ± 0.04 b | 0.51 ± 0.36 b | 0.31 ± 0.09 b | 1.55 ± 0.07 | 0.96 ± 0.06 | 0.89 ± 0.02 | 5.39 ± 0.02 | N:P 150 | |
| R2 | dtclo-a (d) | k0 (d−1) | 26 °C | |
|---|---|---|---|---|
| 0.99 | 3.46 ± 0.05 a | 0.20 ± 0.07 a | N:C:\N:\PP 10 | 30 µmol photon m−2.s−1 |
| 0.94 | 2.88 ± 0.05 a | 0.24 ± 0.08 a | N:P 100 | |
| 0.97 | 3.30 ± 0.06 a | 0.21 ± 0.09 a | N:P 150 | |
| 0.91 | 5.33 ± 0.06 b | 0.13 ± 0.09 a | N:P 10 | 50 µmol photon m−2.s−1 |
| 0.91 | 5.33 ± 0.04 b | 0.13 ± 0.06 a | N:P 100 | |
| 0.96 | 5.77 ± 0.06 b | 0.12 ± 0.09 a | N:P 150 | |
| 0.95 | 3.30 ± 0.03 b | 0.21 ± 0.04 a | N:P 10 | 70 µmol photon m−2.s−1 |
| 0.93 | 4.95 ± 0.05 b | 0.14 ± 0.08 a | N:P 100 | |
| 0.93 | 4.62 ± 0.05 b | 0.15 ± 0.07 a | N:P 150 | |
| R2 | dtclo-a (d) | k0 (d−1) | 30 °C | |
| 0.93 | 2.88 ± 0.06 a | 0.24 ± 0.09 a | N:C:\N:\PP 10 | 30 µmol photonm−2.s−1 |
| 0.94 | 3.46 ± 0.05 a | 0.20 ± 0.08 a | N:P 100 | |
| 0.95 | 3.85 ± 0.06 a | 0.18 ± 0.09 a | N:P 150 | |
| 0.93 | 4.62 ± 0.06 a | 0.15 ± 0.09 a | N:P 10 | 50 µmol photon m−2.s−1 |
| 0.93 | 4.95 ± 0.06 a | 0.14 ± 0.09 a | N:P 100 | |
| 0.91 | 3.64 ± 0.05 a | 0.19 ± 0.08 a | N:P 150 | |
| 0.93 | 4.95 ± 0.05 b | 0.14 ± 0.07 a | N:P 10 | 70 µmol photon m−2.s−1 |
| 0.95 | 3.64 ± 0.05 b | 0.19 ± 0.07 a | N:P 100 | |
| 0.95 | 4.95 ± 0.05 b | 0.14 ± 0.08 a | N:P 150 | |
| R2 | dtclo-a (d) | k0 (d−1) | 36 °C | |
| 0.93 | 4.95 ± 0.07 a | 0.14 ± 0.10 b | N:C:\N:\PP 10 | 30 µmol photon m−2.s−1 |
| 0.95 | 6.30 ± 0.06 a | 0.11 ± 0.09 b | N:P 100 | |
| 0.99 | 6.30 ± 0.05 a | 0.11 ± 0.08 b | N:P 150 | |
| 0.97 | 4.33 ± 0.06 a | 0.16 ± 0.09 b | N:C:\N:\PP 10 | 50 µmol photonm−2.s−1 |
| 0.98 | 3.64 ± 0.07 a | 0.19 ± 0.10 b | N:C:\N:\PP 100 | |
| 0.99 | 6.30 ± 0.05 a | 0.11 ± 0.08 b | N:P 150 | |
| 0.96 | 2.77 ± 0.06 a | 0.25 ± 0.09 b | N:P 10 | 70 µmol photon m−2.s−1 |
| 0.99 | 4.62 ± 0.05 a | 0.15 ± 0.08 b | N:C:\N:\PP 100 | |
| 0.98 | 3.30 ± 0.07 a | 0.21 ± 0.10 b | N:C:\N:\PP 150 | |
| R2 | dM (day−1) | p (fg.cell−1) | N:P | Irradiation (µmol.photon m−2.s−1 | Temperature |
|---|---|---|---|---|---|
| 0.97 | 6.36 × 10−2 ± 4.04 × 10−2 | 2.27 × 10−5 ± 6.17 × 10−6 | 10 | 30 | 26 °C |
| 0.98 | 1.77 × 10−1 ± 1.50 × 10−1 | 1.63 × 10−5 ± 9.24 × 10−6 | 100 | ||
| 0.99 | 1.00 × 10−6 ± 6.54 × 10−2 | 6.94 × 10−6 ± 3.53 × 10−6 | 150 | ||
| 0.91 | 1.31 × 10−1 ± 2.45 × 10−1 | 1.19 × 10−5 ± 9.83.10−6 | 10 | 50 | |
| 0.80 | 1.34 × 10−1 ± 3.89 × 10−1 | 5.83 × 10−6 ± 7.34 × 10−6 | 100 | ||
| 0.94 | 1.00 × 10−6 ± 1.33 × 10−1 | 7.43 × 10−7 ± 7.99 × 10−7 | 150 | ||
| 0.91 | 1.00 × 10−6 ± 3.68 × 10−1 | 8.09 × 10−7 ± 1.62 × 10−6 | 10 | 70 | |
| 0.87 | 1.00 × 10−6 ± 4.46 × 10−1 | 5.87 × 10−7 ± 1.07 × 10−6 | 100 | ||
| 0.77 | 1.00 × 10−6 ± 3.70 × 10−1 | 4.11 × 10−7 ± 1.43 × 10−6 | 150 | ||
| 0.96 | 7.86 × 10−2 ± 4.72 × 10−2 | 1.03 × 10−5 ± 2.97 × 10−6 | 10 | 30 | 30 °C |
| 0.18 | 4.17 × 10−4 ± 1.18 × 10−0 | 5.35 × 10−6 ± 6.32.10−5 | 100 | ||
| 0.94 | 1.01 × 10−6 ± 8.76 × 10−1 | 3.64 × 10−6 ± 1.74 × 10−5 | 150 | ||
| 0.77 | 1.85 × 10−1 ± 3.07 × 10−1 | 8.02 × 10−6 ± 1.39 × 10−5 | 10 | 50 | |
| 0.77 | 5.71.10−2 ± 3.46 × 10−1 | 6.35 × 10−6 ± 2.27 × 10−5 | 100 | ||
| 0.99 | 1.00 × 10−6 ± 1.75 × 10−1 | 7.21 × 10−7 ± 6.30 × 10−7 | 150 | ||
| 0.58 | 6.80 × 10−2 ± 2.15.10−1 | 7.00 × 10−7 ± 1.23 × 10−6 | 10 | 70 | |
| 0.40 | 7.49 × 10−2 ± 3.02 × 10−1 | 2.10 × 10−6 ± 4.30 × 10−6 | 100 | ||
| 0.59 | 1.34 × 10−1 ± 3.17 × 10−1 | 2.48 × 10−6 ± 4.73 × 10−6 | 150 | ||
| 0.81 | 2.30 × 10−1 ± 1.46 × 10−1 | 6.28 × 10−5 ± 3.79 × 10−5 | 10 | 30 | 36 °C |
| 0.88 | 4.91 × 10−1 ± 3.98 × 100 | 2.69 × 10−5 ± 2.13 × 10−4 | 100 | ||
| 0.99 | 1.00 × 10−6 ± 5.34 × 10−1 | 5.16 × 10−6 ± 1.70 × 10−5 | 150 | ||
| 0.99 | 4.56 × 10−1 ± 6.39 × 10−1 | 2.96 × 10−4 ± 2.73 × 10−4 | 10 | 50 | |
| 0.99 | 3.11 × 10−1 ± 1.94 × 10−1 | 7.15 × 10−5 ± 2.95 × 10−5 | 100 | ||
| 0.99 | 3.73 × 10−1 ± 2.15 × 10−1 | 6.05 × 10−5 ± 2.65 × 10−5 | 150 | ||
| 0.99 | 1.00 × 10−6 ± 1.61 × 10−1 | 4.71 × 10−6 ± 2.77 × 10−6 | 10 | 70 | |
| 0.99 | 1.00 × 10−6 ± 2.28 × 10−1 | 1.04 × 10−5 ± 6.56 × 10−6 | 100 | ||
| 0.40 | 1.00 × 10−6 ± 6.84 × 10−1 | 3.43 × 10−7 ± 1.35 × 10−6 | 150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crettaz-Minaglia, M.C.; Goñi, S.; Giannuzzi, L. Nonlinear Responses and Population-Level Coupling of Growth and MC-LR Production in Microcystis aeruginosa Under Multifactorial Conditions. Phycology 2025, 5, 26. https://doi.org/10.3390/phycology5020026
Crettaz-Minaglia MC, Goñi S, Giannuzzi L. Nonlinear Responses and Population-Level Coupling of Growth and MC-LR Production in Microcystis aeruginosa Under Multifactorial Conditions. Phycology. 2025; 5(2):26. https://doi.org/10.3390/phycology5020026
Chicago/Turabian StyleCrettaz-Minaglia, Melina Celeste, Sandro Goñi, and Leda Giannuzzi. 2025. "Nonlinear Responses and Population-Level Coupling of Growth and MC-LR Production in Microcystis aeruginosa Under Multifactorial Conditions" Phycology 5, no. 2: 26. https://doi.org/10.3390/phycology5020026
APA StyleCrettaz-Minaglia, M. C., Goñi, S., & Giannuzzi, L. (2025). Nonlinear Responses and Population-Level Coupling of Growth and MC-LR Production in Microcystis aeruginosa Under Multifactorial Conditions. Phycology, 5(2), 26. https://doi.org/10.3390/phycology5020026





