Emerging Near-Surface Solar MHD Dynamos
Abstract
1. Introduction
2. Magnetic Helicity and Distributed Chaos
2.1. Magnetic Helicity
2.2. Distributed Chaos in the Magnetic Field Driven by Magnetic Helicity
2.3. Spontaneous Breaking of Local Reflectional Symmetry
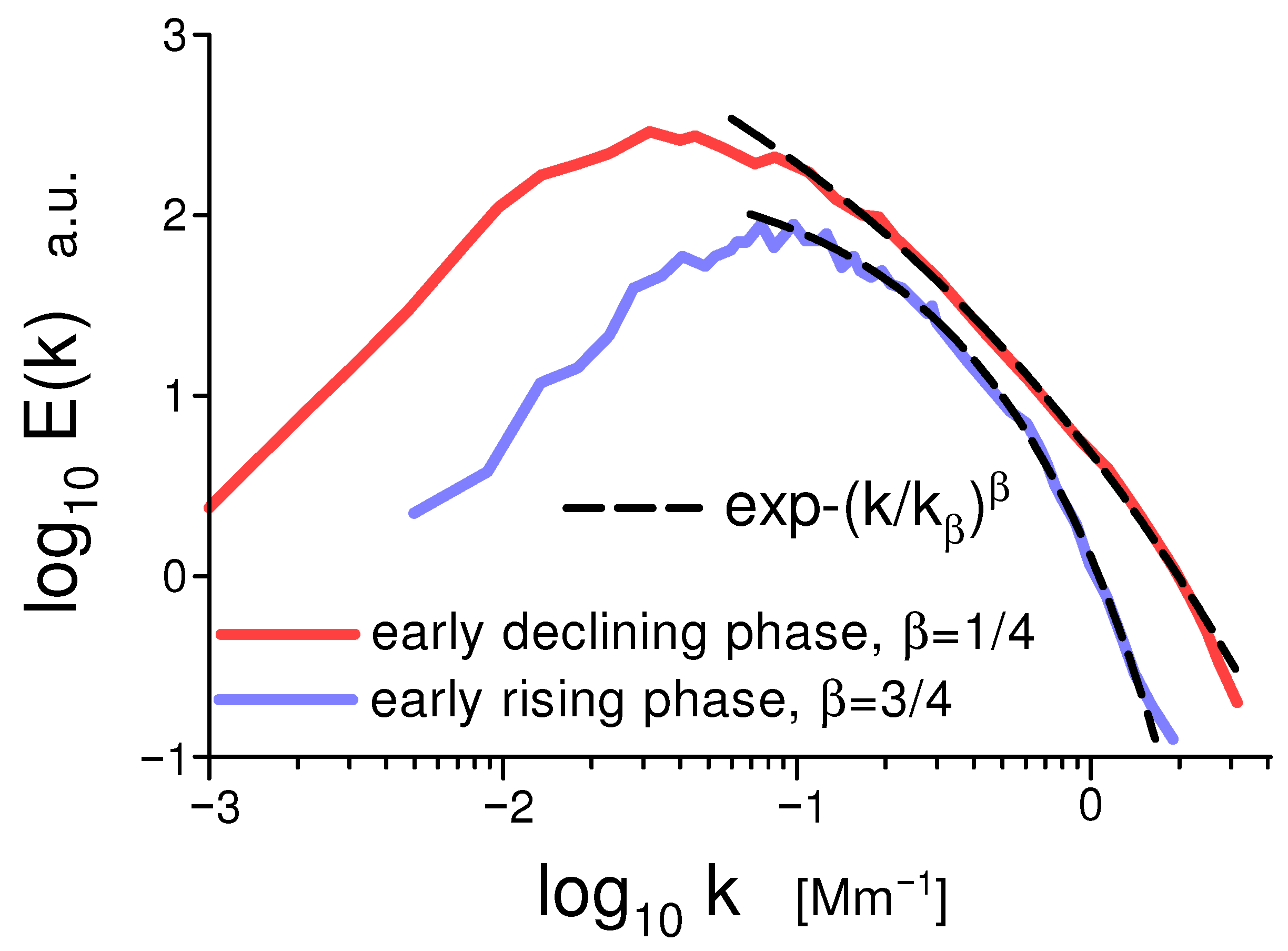
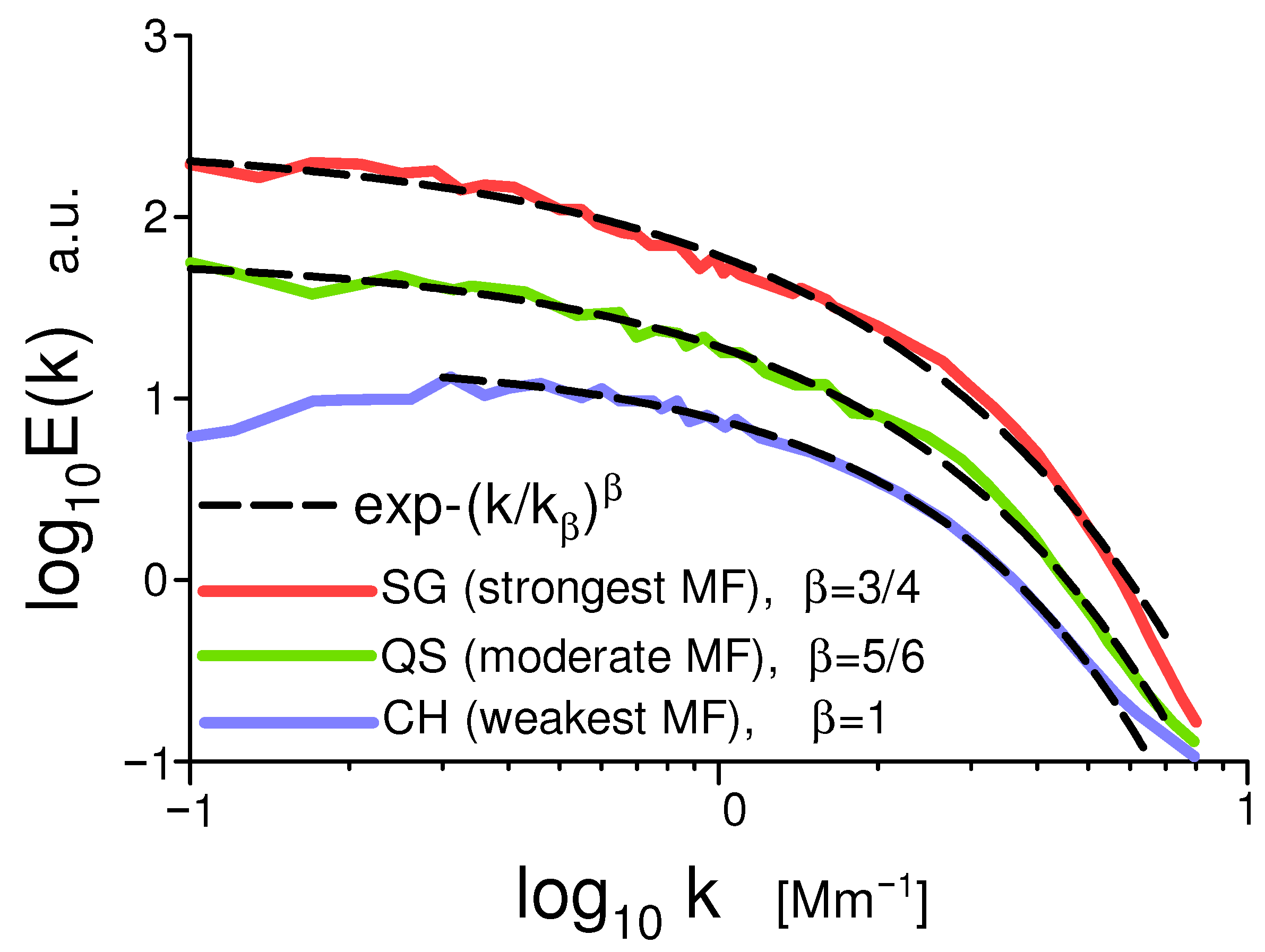
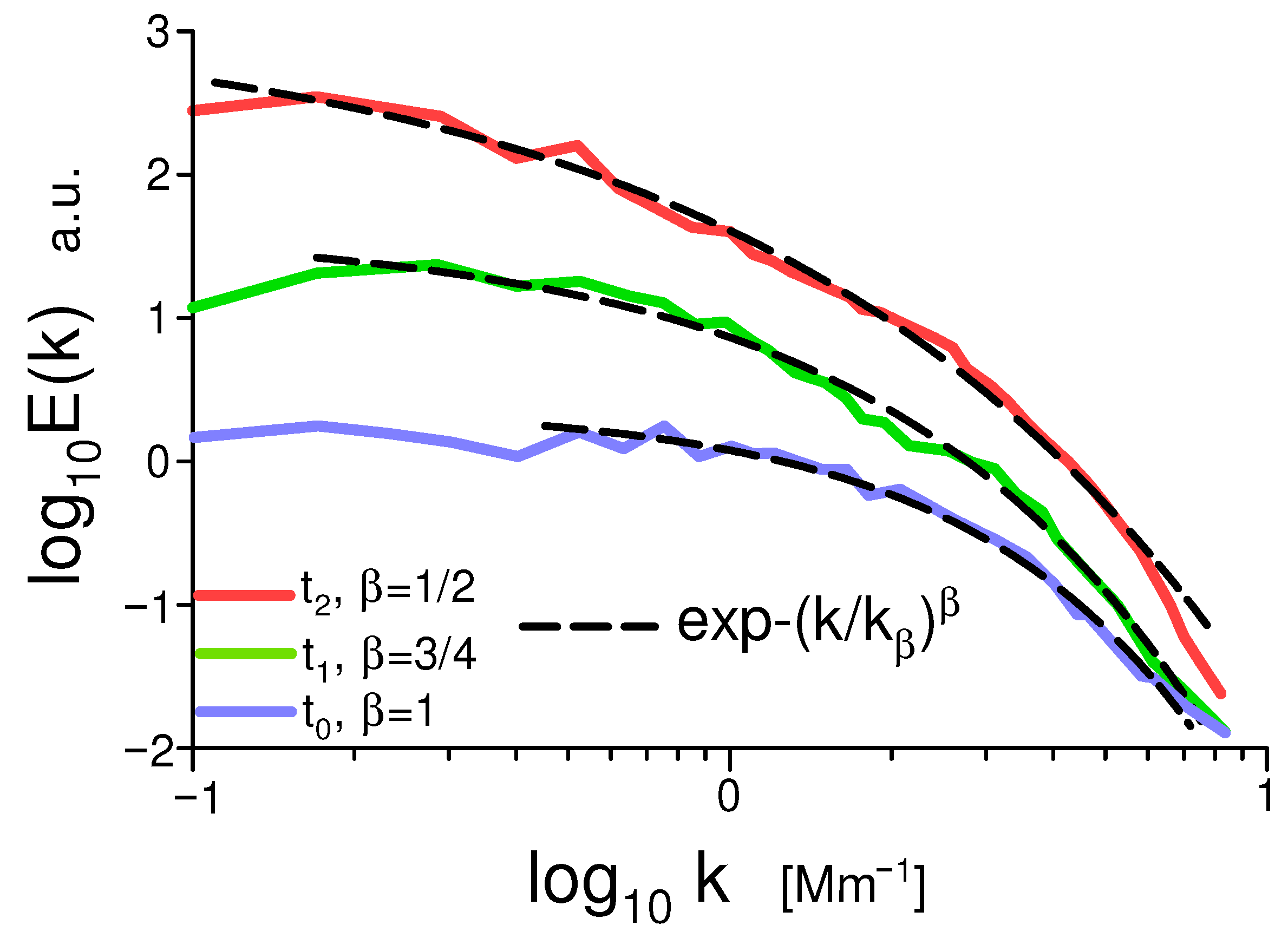
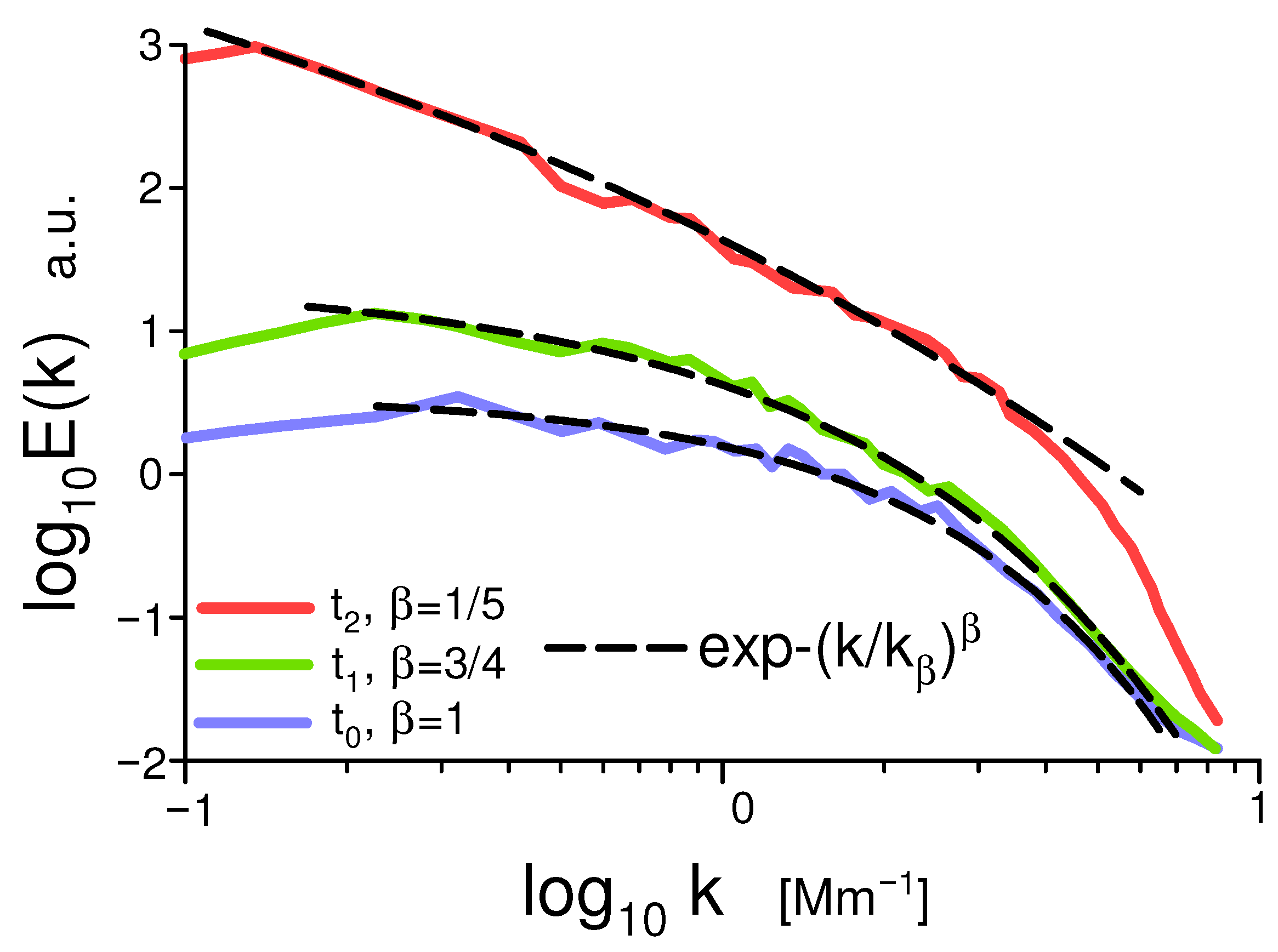
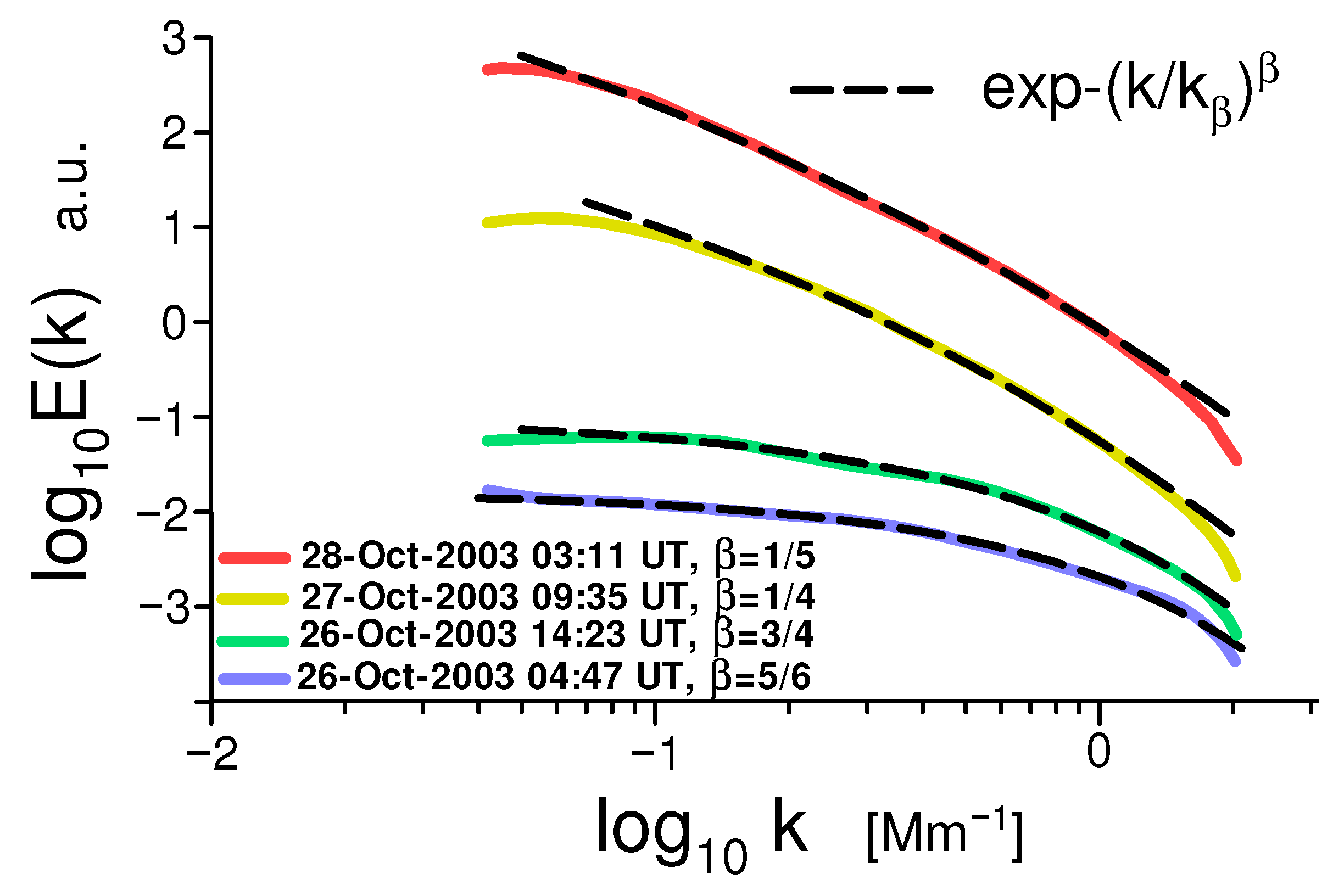
2.4. Examples
3. Magnetoinertial Range of Scales
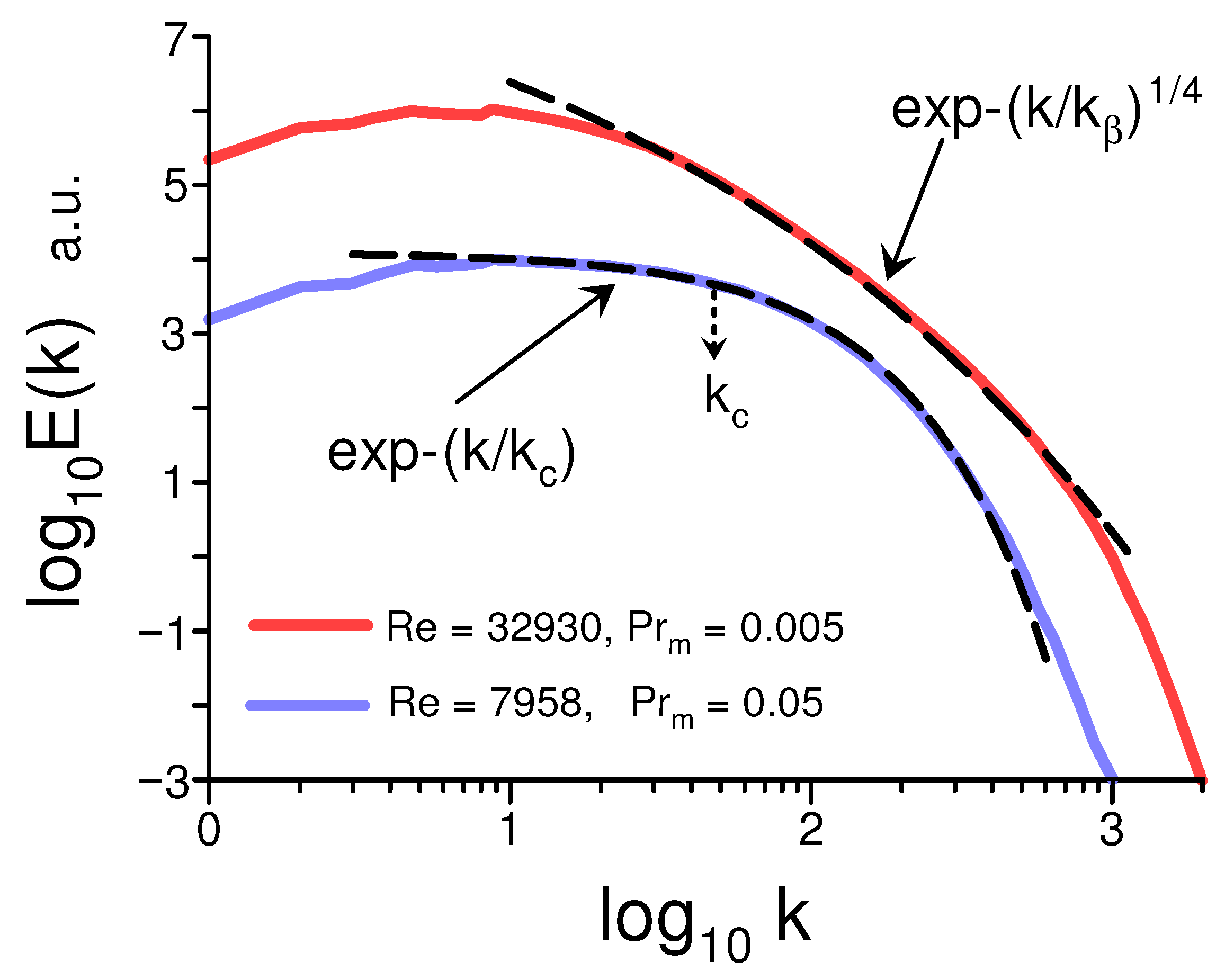
4. Dissipative Distributed Chaos
4.1. Dissipative MHD Invariants
4.2. Dissipative Distributed Chaos
5. Hall Magnetohydrodynamics
6. Solar Small-Scale MHD Dynamos
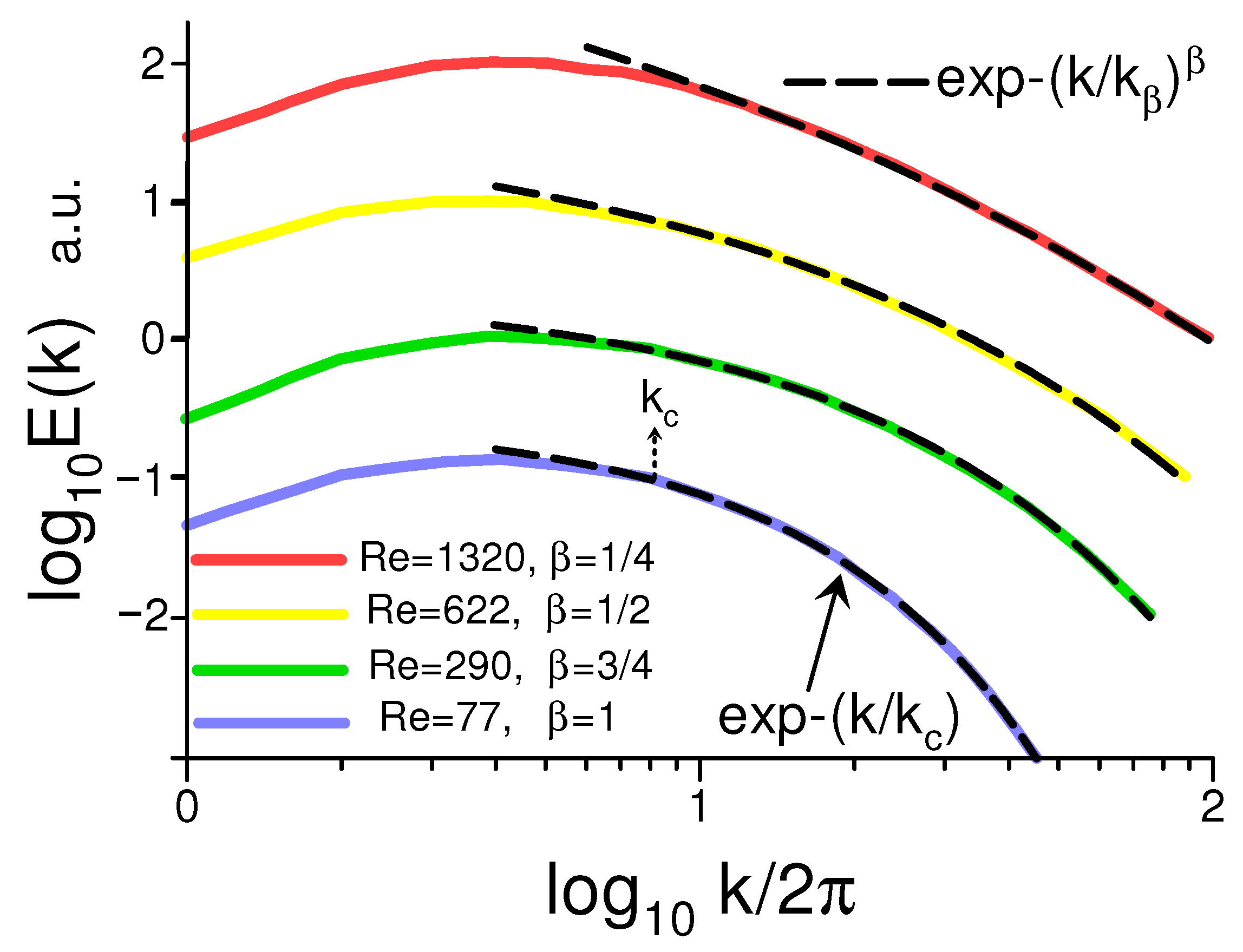
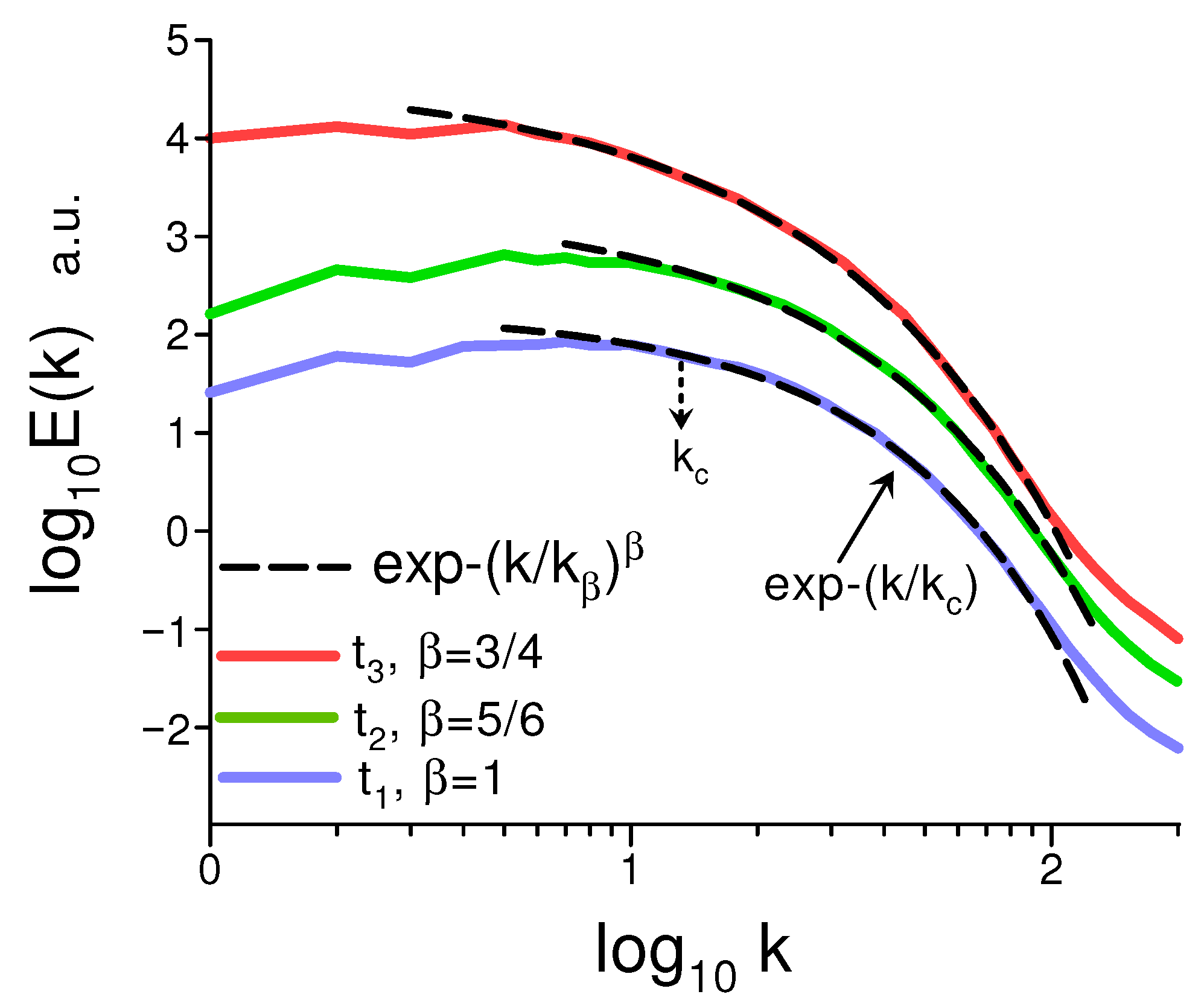
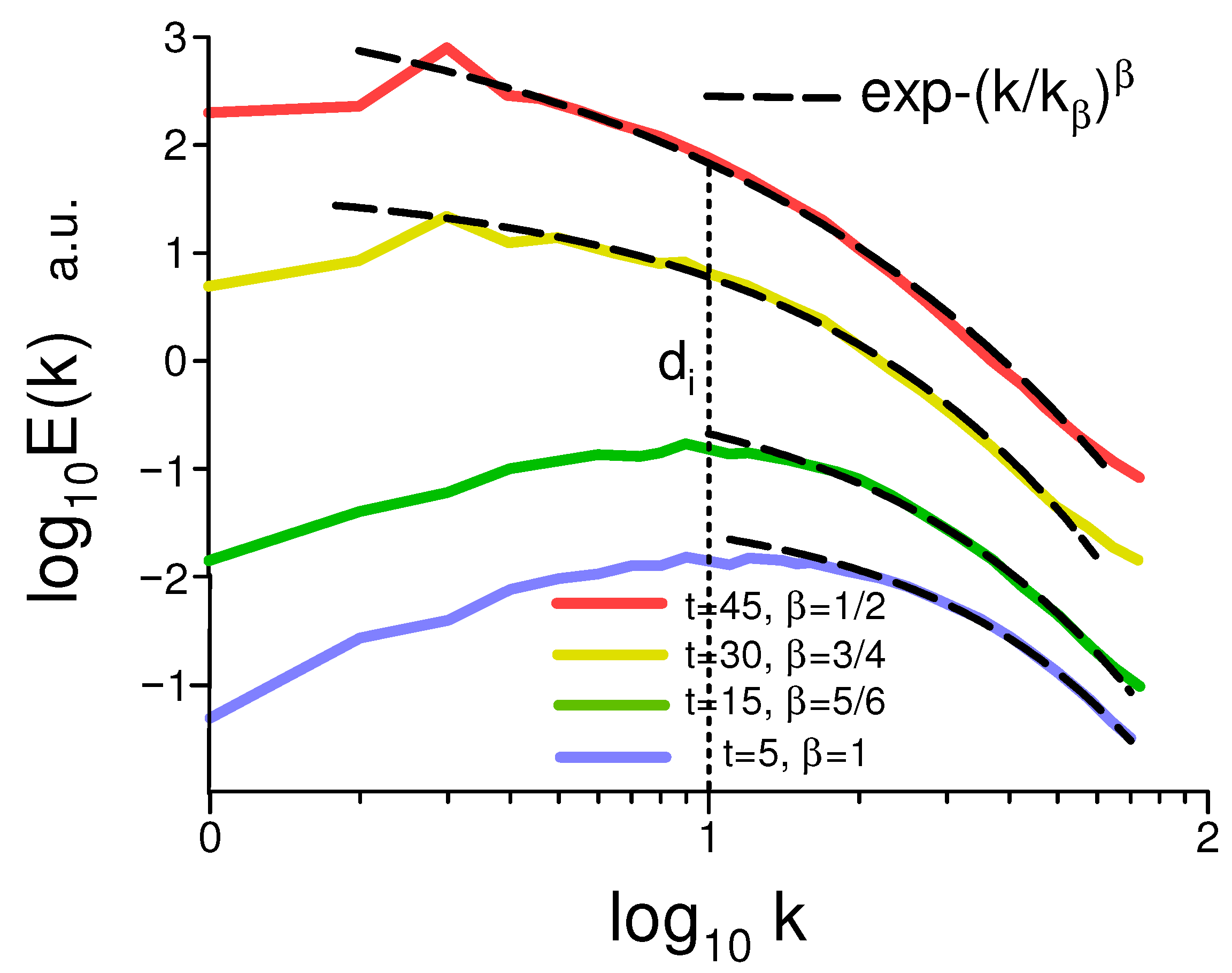
6.1. Numerical Simulations
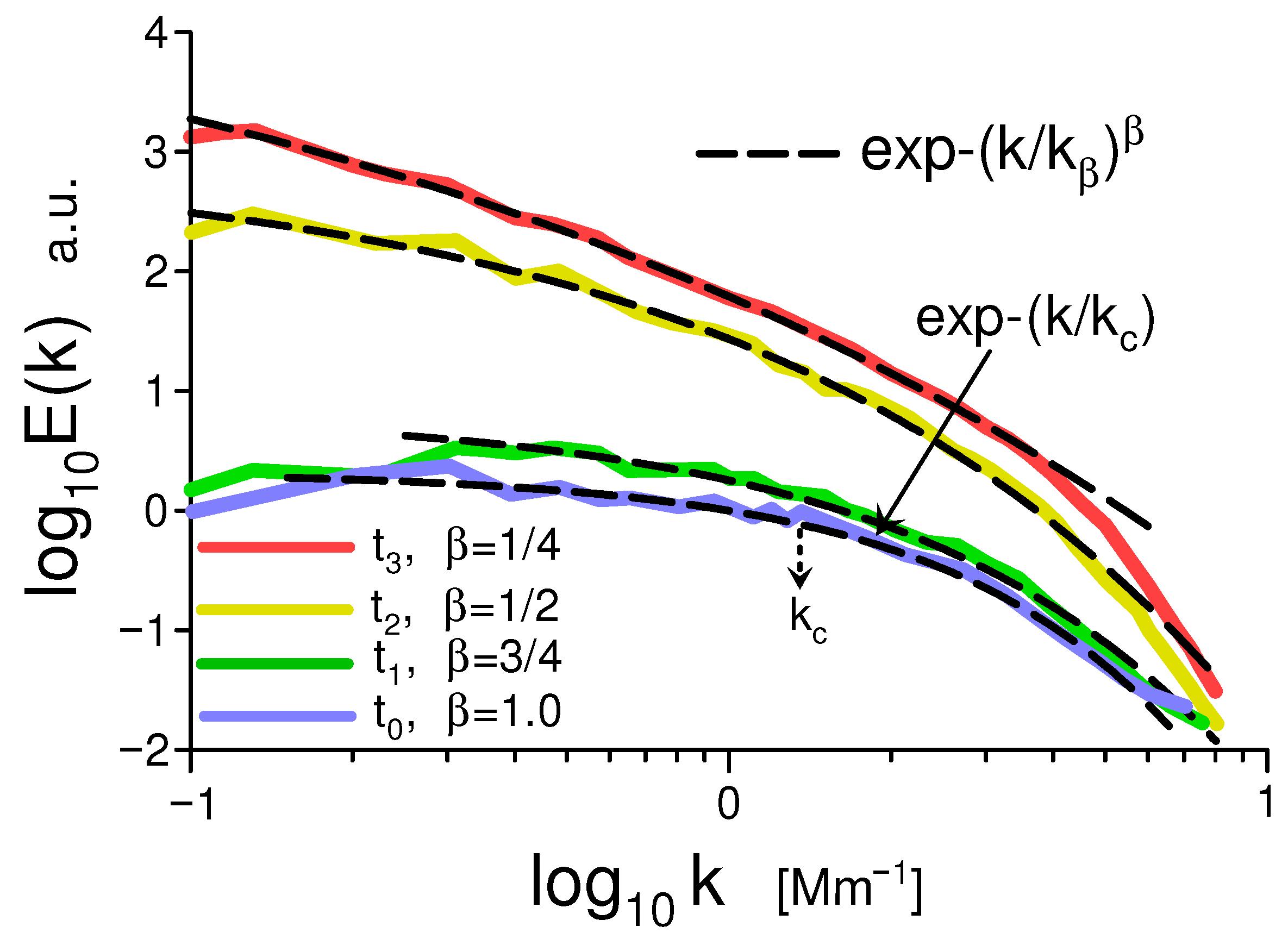
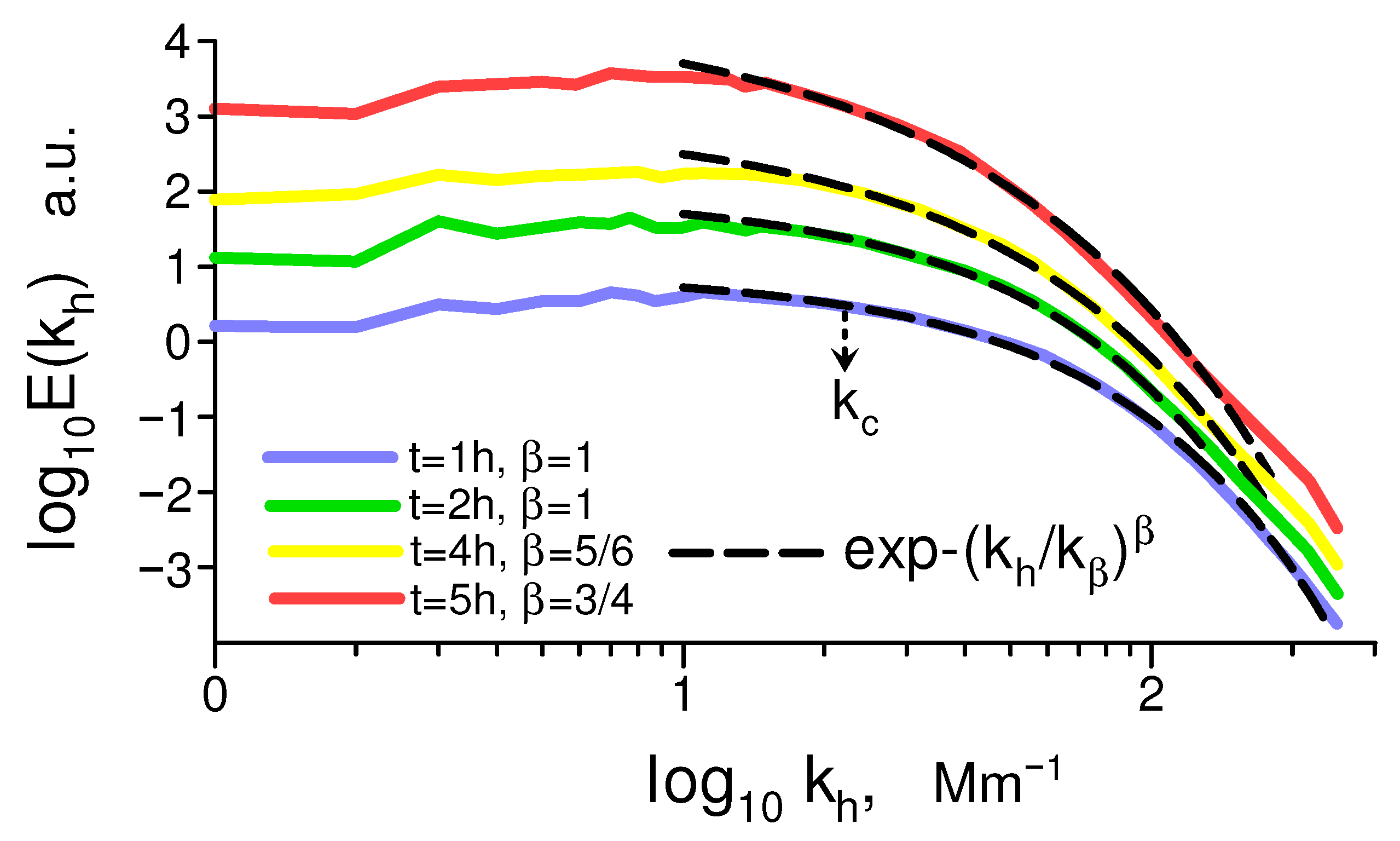
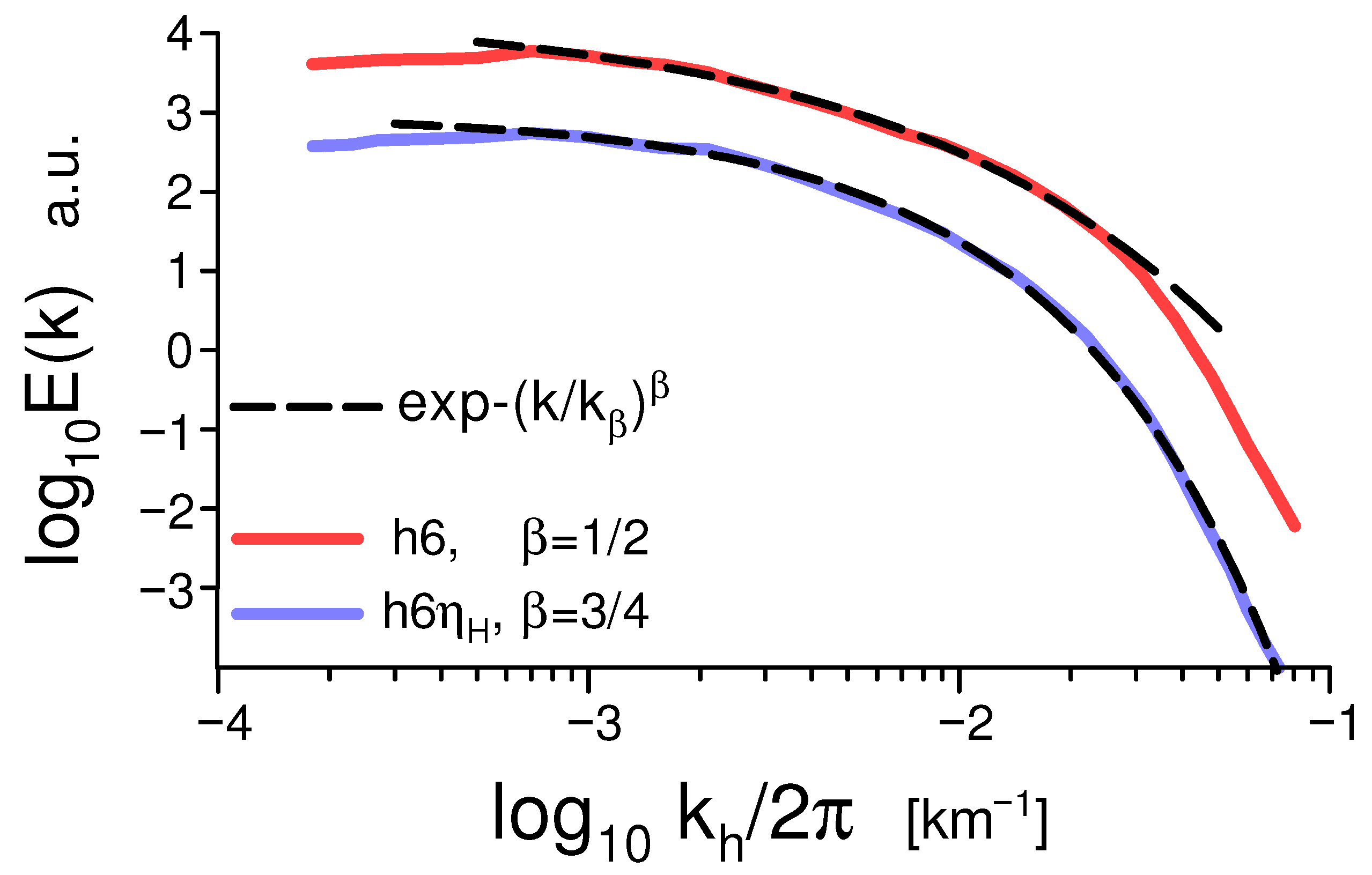
6.2. Solar Observations
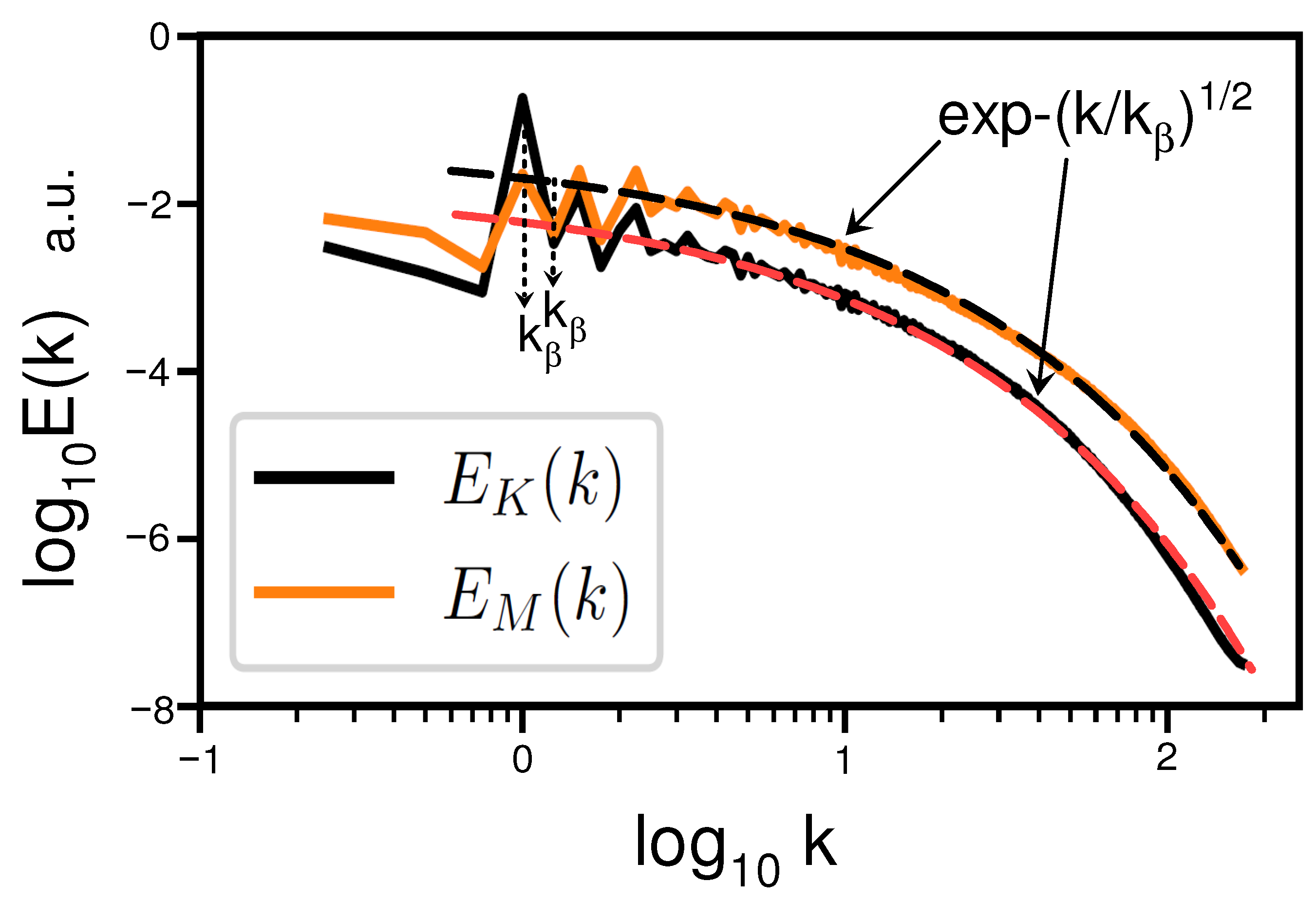
6.3. The Role of the Mean Magnetic Field
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Graham, J.P.; Cameron, R.H.; Schüssler, M. Turbulent small-scale dynamo action in solar surface simulations. Astrophys. J. 2010, 714, 1606. [Google Scholar] [CrossRef]
- Cameron, R.H.; Schüssler, M. Understanding solar cycle variability. Astrophys. J. 2017, 843, 111. [Google Scholar] [CrossRef]
- Rempel, M.; Bhatia, T.; Bellot, R.; Rubio, L.B.; Korpi-Lagg, M.J. Small-scale dynamos: From idealized models to solar and stellar applications. Space Sci. Rev. 2023, 219, 36. [Google Scholar] [CrossRef]
- Bershadskii, A. Subharmonic and chaotic resonances in solar activity. Europhys. Lett. 2010, 92, 50012. [Google Scholar] [CrossRef]
- Tanayveer, S.; Bhatia, T.S.; Cameron, R.H.; Solanki, S.K.; Hardi Peter, H.; Przybylski, D.; Witzk, V.; Shapiro, A. Small-scale dynamo in cool stars I. Changes in stratification and near-surface convection for main-sequence spectral types. Astron. Astrophys. 2022, 663, A166. [Google Scholar]
- Warnecke, J.; Korpi-Lagg, M.J.; Gent, F.A.; Rheinhardt, M. Numerical evidence for a small-scale dynamo approaching solar magnetic Prandtl numbers. Nat. Astron. 2023, 7, 662. [Google Scholar] [CrossRef]
- Vasil, G.M.; Lecoanet, D.; Augustson, K.; Burns, K.; Oishi, J.S.; Brown, B.P.; Brummell, N.; Julien, K. The solar dynamo begins near the surface. Nature 2024, 629, 769–772. [Google Scholar] [CrossRef] [PubMed]
- Gaire, B. Solar dynamo located near the surface. Nat. Astron. 2024, 8, 684. [Google Scholar] [CrossRef]
- Cameron, R.H.; Schüssler, M. Observationally guided models for the solar dynamo and the role of the surface field. Space Sci. Rev. 2023, 219, 60. [Google Scholar] [CrossRef]
- Shukurov, A.; Subramanian, K. The Fluctuation Dynamo. In Astrophysical Magnetic Fields: From Galaxies to the Early Universe; Cambridge University Press: Cambridge, UK, 2021; pp. 171–206. [Google Scholar]
- Maggs, J.E.; Morales, G.J. Generality of deterministic chaos, exponential spectra, and Lorentzian pulses in magnetically confined plasmas. Phys. Rev. Lett. 2011, 107, 185003. [Google Scholar] [CrossRef]
- Maggs, J.E.; Morales, G.J. Origin of Lorentzian pulses in deterministic chaos. Phys. Rev. E 2012, 86, 015401(R). [Google Scholar] [CrossRef]
- Maggs, J.E.; Morales, G.J. Exponential power spectra, deterministic chaos and Lorentzian pulses in plasma edge dynamics. Plasma Phys. Control. Fusion 2012, 54, 124041. [Google Scholar] [CrossRef]
- Khurshid, S.; Donzis, D.A.; Sreenivasan, K.R. Energy spectrum in the dissipation range. Phys. Rev. Fluids 2018, 3, 082601(R). [Google Scholar] [CrossRef]
- Wu, X.-Z.; Kadanoff, L.P.; Libchaber, A.; Sano, M. Frequency power spectrum of temperature fluctuations in free convection. Phys. Rev. Lett. 1990, 64, 2140–2143. [Google Scholar] [CrossRef]
- Schekochihin, A.A. MHD turbulence: A biased review. J. Plasma Phys. 2022, 88, 155880501. [Google Scholar] [CrossRef]
- Kutsenko, O.K.; Kutsenko, A.S.; Abramenko, V.I. Magnetic Power Spectra of Emerging Active Regions. Solar Phys. 2019, 294, 102. [Google Scholar] [CrossRef]
- Janßen, K.; Vögler, A.; Kneer, F. On the fractal dimension of small-scale magnetic structures in the Sun. Astron. Astrophys. 2003, 409, 1127–1134. [Google Scholar] [CrossRef]
- Zhou, S.; Feng, Y.; Wu, W.Y.; Li, Y.; Liu, J. Low-dimensional chaos and fractal properties of long-term sunspot activity. Res. Astron. Astrophys. 2014, 14, 104. [Google Scholar] [CrossRef]
- Abramenko, V.I. Fractal multi-scale nature of solar/stellar magnetic field. In Solar and Astrophysical Dynamos and Magnetic Activity Proceedings IAU Symposium; Kosovichev, A.G., de Gouviea Dal Pino, E.M., Yan, Y., Eds.; Cambridge University Press: Cambridge, UK, 2012; Volume 294. [Google Scholar]
- Rajkumar, B.; Haque, S. A fractal analysis of magnetograms within active regions. Sol. Phys. 2020, 295, 10. [Google Scholar] [CrossRef]
- Deng, L.H.; Li, B.; Xiang, Y.Y.; Dun, G.T. Comparison of chaotic and fractal properties of polar faculae with sunspot activity. Astr. J. 2016, 151, 2. [Google Scholar] [CrossRef]
- Moffatt, H.K.; Tsinober, A. Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 1994, 24, 281–312. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Goldstein, M.L. Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 1982, 87, 6011–6028. [Google Scholar] [CrossRef]
- Shebalin, J.V. Global invariants in ideal magnetohydrodynamic turbulence. Phys. Plasmas 2013, 20, 102305. [Google Scholar] [CrossRef]
- Bershadskii, A. Magneto-inertial range dominated by magnetic helicity in space plasmas. Fundam. Plasma Phys. 2024, 11, 100066. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics, Vol. II: Mechanics of Turbulence; Dover Publications: New York, NY, USA, 2013. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Kerr, R.M. Elementary Vortices and Coherent Structures. In Proceedings of the IUTAM Symposium, Kyoto, Japan, 26–28 October 2004; pp. 1–8. [Google Scholar]
- Holm, D.D.; Kerr, R.M. Helicity in the formation of turbulence. Phys. Fluids 2007, 19, 025101. [Google Scholar] [CrossRef]
- Moffatt, H.K. The degree of knottedness of tangled vortex lines. J. Fluid Mech. 1969, 35, 117–129. [Google Scholar] [CrossRef]
- Moffatt, H.K. Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. Part 1. Fundamentals. J. Fluid Mech. 1985, 159, 359–378. [Google Scholar] [CrossRef]
- Levich, E.; Tsinober, A. On the role of helical structures in three-dimensional turbulent flow. Phys. Lett. A 1983, 93, 293–297. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Cowley, S.C.; Dorland, W.; Hammett, G.W.; Howes, G.G.; Quataert, E.; Tatsuno, T. Astrophysical gyrokinetics: Kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. Ser. 2009, 182, 310–377. [Google Scholar] [CrossRef]
- Rincon, F. Helical turbulent nonlinear dynamo at large magnetic Reynolds numbers. Phys. Rev. Fluids 2021, 6, L121701. [Google Scholar] [CrossRef]
- Bershadskii, A.; Sreenivasan, K.R. Intermittency and the passive nature of the magnitude of the magnetic field. Phys. Rev. Lett. 2004, 93, 064501. [Google Scholar] [CrossRef]
- Johnston, D.C. Stretched exponential relaxation arising from a continuous sum of exponential decays. Phys. Rev. B 2006, 74, 184430. [Google Scholar] [CrossRef]
- Birkhoff, G. Fourier synthesis of homogeneous turbulence. Commun. Pure Appl. Math. 1954, 7, 19–44. [Google Scholar] [CrossRef]
- Saffman, P.G. The large-scale structure of homogeneous turbulence. J. Fluid. Mech. 1967, 27, 581–593. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The invariant theory of isotropic turbulence in magneto-hydrodynamics. Proc. R. Soc. Lond. Ser. A 1951, 204, 435–449. [Google Scholar]
- Politano, H.; Pouquet, A. von Kármán–Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 1998, 57, R21. [Google Scholar] [CrossRef]
- Wan, M.; Oughton, S.; Servidio, S.; Matthaeus, W.H. von Karmán self-preservation hypothesis for magnetohydrodynamic turbulence and its consequences for universality. J. Fluid Mech. 2012, 697, 296. [Google Scholar] [CrossRef]
- Sur, S.; Bhat, P.; Subramanian, K. Faraday rotation signatures of fluctuation dynamos in young galaxies. Mon. Not. R. Astron. Soc. Lett. 2018, 475, L72. [Google Scholar] [CrossRef]
- Banerjee, S.; Galtier, S. Chiral exact relations for helicities in Hall magnetohydrodynamic turbulence. Phys. Rev. E 2016, 93, 033120. [Google Scholar] [CrossRef]
- Polygiannakis, J.M. Moussas, X. A review of magneto-vorticity induction in Hall-MHD plasma. Plasma Phys. Control. Fusion 2001, 43, 195–221. [Google Scholar] [CrossRef]
- Galtier, S. von Kármán-Howarth equations for Hall magnetohydrodynamic flows. Phys. Rev. E 2008, 77, 015302(R). [Google Scholar]
- Mininni, P.D.; Alexakis, A.; Pouquet, A. Energy transfer in Hall-MHD turbulence: Cascades, backscatter, and dynamo action. J. Plasma Phys. 2007, 73, 377. [Google Scholar] [CrossRef]
- Kosovichev, A.G.; Mansour, N.N.; Wray, A.A. Mechanism of local dynamo action on the Sun. arXiv 2013, arXiv:1312.0982. [Google Scholar]
- Riva, F.; Steiner, O. Methodology for estimating the magnetic Prandtl number and application to solar surface small-scale dynamo simulations. Astron. Astrophys. 2022, 660, A115. [Google Scholar] [CrossRef]
- Prabhu, A. Towards Constraining the Solar Dynamo with Observational Studies of the Sun’s Magnetic Field. Ph.D. Thesis, University of Goettingen, Goettingen, Germany, 2021. Available online: https://ediss.uni-goettingen.de/handle/11858/14010 (accessed on 16 September 2025).
- Abramenko, V.I.; Kutsenko, O.K. Magnetic power spectrum in the undisturbed solar photosphere. Acta Astrophys. Taurica 2020, 1, 1. [Google Scholar] [CrossRef]
- Iroshnikov, R.S. Turbulence of a conducting fluid in a strong magnetic field. Astron. Zhurnal 1964, 40, 742, English translation in Sov. Astron. 1964, 7, 566. [Google Scholar]
- Bershadskii, A. Chaotic variability of the magnetic field at Earth’s surface driven by ionospheric and space plasmas. J. Atmos. Sol.-Terr. Phys. 2025, 269, 106456. [Google Scholar]
- Bershadskii, A. Foreground emission randomization due to dynamics of magnetized interstellar medium: WMAP and Planck frequency bands. Foundations 2025, 5, 21. [Google Scholar] [CrossRef]
- Kutsenko, A.S.; Abramenko, V.I.; Kutsenko, O.K. On the possibility of probing the flare productivity of an active region in the early stage of emergence. Mon. Not. R. Astron. Soc. 2021, 501, 6076–6082. [Google Scholar] [CrossRef]
- Hewett, R.J.; Gallagher, P.T.; McAteer, R.T.J.; Young, C.A.; Ireland, J.; Conlon, P.A.; Maguire, K. Multiscale analysis of active region evolution. Solar Phys. 2007, 248, 311–322. [Google Scholar]
- Moffatt, K.; Dormy, E. Self-Exciting Fluid Dynamos; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Tobias, S.M. The turbulent dynamo. J. Fluid Mech. 2021, 912, P1. [Google Scholar] [CrossRef]
- Shebalin, J.V. The Statistical Mechanics of Ideal Magnetohydrodynamic Turbulence and a Solution of the Dynamo Problem. Fluids 2024, 9, 46. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bershadskii, A. Emerging Near-Surface Solar MHD Dynamos. Foundations 2025, 5, 31. https://doi.org/10.3390/foundations5030031
Bershadskii A. Emerging Near-Surface Solar MHD Dynamos. Foundations. 2025; 5(3):31. https://doi.org/10.3390/foundations5030031
Chicago/Turabian StyleBershadskii, Alexander. 2025. "Emerging Near-Surface Solar MHD Dynamos" Foundations 5, no. 3: 31. https://doi.org/10.3390/foundations5030031
APA StyleBershadskii, A. (2025). Emerging Near-Surface Solar MHD Dynamos. Foundations, 5(3), 31. https://doi.org/10.3390/foundations5030031



