Cross-Analysis of Magnetic and Current Density Field Topologies in a Quiescent High Confinement Mode Tokamak Discharge

Abstract

In axisymmetric fusion devices like tokamaks, the winding of the magnetic field is characterized by its safety profile $q=q_{\mathbf{B}}$. Similarly, the winding of the current density field is characterized by $q_{\mathbf{J}}$. Currently, the relationship between $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ profiles and their effect on tokamak plasma confinement properties remains unexplored, as the $q_{\mathbf{J}}$ profile is neither computed nor considered. This study presents a reconstruction of the current density winding profile from experimental data in the quiescent H-mode. The topology analysis derived from $(q_{\mathbf{B}},q_{\mathbf{J}})$ was carried out using Hamada coordinates. It shows a large central plasma region unaffected by current filamentation-driven resonant magnetic perturbations, while the outer region harbors a spectrum of magnetic resonant modes, induced by current filaments located within the core plasma, which degrade peripheral confinement. These results suggest a QH-mode signature pattern needing further validation with additional data. Implementing $(q_{\mathbf{B}},q_{\mathbf{J}})$ real-time monitoring could provide insights into tokamak confinement regimes with significant implications.

1. Introduction

It has been shown that [1], in axisymmetric driven devices for fusion applications, such as the tokamak, both the magnetic and the current density fields have rotational transforms which allows a complete classification of modes according to their topology. At each given time, one can characterize the way that axisymmetric vector fields wind about the central axis through the well-known safety profile $q=q_{\mathbf{B}}$ for the magnetic field and its analogous $q_{\mathbf{J}}$ profile for the current density field or, equivalently, through their inverse functions that are traditionally named winding profiles. In the experiments, modern sophisticated codes can resolve the Grad–Shafranov equation in real time and reconstruct the equilibrium using the data derived from its diagnostics [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. This equilibrium reconstruction specifically allown $q_{\mathbf{B}}$ to be obtained in real time. Complementing this reconstruction with the computation of $q_{\mathbf{J}}$ can fully identify the nature of the perturbation modes and unveil the turbulence actuators. Indeed, as in neutral fluids, it is an empirical fact that vorticity filaments support (velocity) turbulence [21], and one may infer that current density filaments play a similar role in small-scale magnetic turbulence, which is the backbone of anomalous heat transport [22,23,24]. They have been extensively reported in experiments, e.g., in Refs. [25,26,27,28,29,30,31,32].

Currently, the study of the relationship between the $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ profiles in relation to the confinement properties of tokamak plasmas is a blank slate, as the $q_{\mathbf{J}}$ profile is neither computed nor taken into account. It is the objective of the present study to perform the first cross-analysis of the magnetic and current density field topologies. This will be carried out using the data of Pankin et al. [33] on the discharge 163518 from the DIII-D tokamak operating in the quiescent H-mode. Quiescent H-modes, also known as QH-modes, form an operational regime in tokamak plasmas that has garnered significant attention in the magnetic confinement fusion community. This has been achieved in tokamaks with advanced plasma control systems, which allow for precise control of the plasma shape, density, and temperature. QH mode was originally discovered on DIII-D [34,35] and was subsequently investigated on ASDEX-Upgrade [36,37,38], JT-60U [39,40] and JET [37]. QH modes form a subset of high (H) confinement-mode plasmas that exhibit a unique behavior as they operate at high confinement levels without the presence of large Edge-Localized Modes (ELMs).

2. Methods

2.1. Reconstruction Problem Formulation

To my knowledge, this work [1] contains the first evaluation of $q_{\mathbf{J}}$ in the convenient flux coordinates. Using the Grad–Shafranov equation, the expression of the $q_{\mathbf{J}}$ profile in the usual poloidal magnetic flux function variable is [1]

$$q_{\mathbf{J}}=q_{\mathbf{B}}\left(1+{\displaystyle \frac{{\mu }_0}{〈R^{-2}〉}}{\displaystyle \frac{p^{\prime }\left(\psi \right)}{F{F}^{\prime }\left(\psi \right)}}\right)$$

(1)

where p is the pressure and F is the diamagnetic function, $F\equiv R{B}_{\phi }$. Consequently, any classical equilibrium reconstruction code could freely add the evaluation line (1) to compute $q_{\mathbf{J}}$, as all the required information is known. Indeed, it should have converged to unfold the flux functions $p^{\prime }\left(\psi \right)$ and $F{F}^{\prime }\left(\psi \right)$, determined by minimizing the ${\chi }^2$ from the measured data and obtaining $q_{\mathbf{B}}$ from

$$q_{\mathbf{B}}={\displaystyle \frac{F}{4{\pi }^2}}〈R^{-2}〉v^{\prime }\left(\psi \right),$$

(2)

where v is the volume enclosed by the flux surface. Therefore it should have already computed the surface average function $〈R^{-2}〉$. Our objective here is to compute $q_{\mathbf{J}}$ using the expression (1). Figure 2 in Pankin et al.’s article [33] represents the flux surfaces computed with EFIT for the DIII-D discharge 163518 at 2350 ms. Also plotted are the total plasma pressure, the pressure gradient $p^{\prime }$, and the $F{F}^{\prime }$ and $q_{\mathbf{B}}$ profiles as functions of the normalized toroidal flux. Consequently, only the data for $〈R^{-2}〉$ as a function of the normalized toroidal flux is missing, and it needs to be estimated in order to use Equation (1).

2.2. Evaluation of the Flux Surface Averages

Here, we use the usual flux coordinates $\left(\psi ,{\theta }_g,{\phi }_g\right)$, where ${\theta }_g$ and ${\phi }_g$ are the poloidal and toroidal geometrical angles, respectively. Let us recall the definition of the flux surface average as

$$〈X〉\doteq {\left({\oint }_{\psi }{\displaystyle \frac{d{\theta }_g^{\prime }}{\mathbf{B}.\nabla {\theta }_g^{\prime }}}\right)}^{-1}{\oint }_{\psi }{\displaystyle \frac{Xd{\theta }_g^{\prime }}{\mathbf{B}.\nabla {\theta }_g^{\prime }}}={\displaystyle \frac{\partial }{\partial v}}{\int }_{V}Xd{v}^{\prime }.$$

(3)

Using the expression of the poloidal magnetic field, Equation (3) yields

$${〈R^{\alpha }〉}_{\psi ={\psi }_0}={\displaystyle \frac{{\oint }_{\psi ={\psi }_0}{R}^{\alpha +1}\frac{dl}{∥\nabla \psi ∥}}{{\oint }_{\psi ={\psi }_0}R\frac{dl}{∥\nabla \psi ∥}}}.$$

(4)

The closed line integrals are evaluated here using [41], for any point function f,

$${\oint }_{\psi ={\psi }_0}f\left(P\right){\displaystyle \frac{dl}{∥\nabla \psi ∥}}={\displaystyle \frac{d}{d{\psi }_0}}\left({\int }_{S\left({\psi }_0\right)}f\left(P\right)ds\right),$$

(5)

where $S\left(\psi \right)$ denotes the area of the surface of the poloidal cross-section enclosed by the flux surface $\psi$. We therefore have

$$〈R^{\alpha }〉\left({\psi }_0\right)={\displaystyle \frac{\frac{d}{d{\psi }_0}\left({\int }_{S\left({\psi }_0\right)}{R}^{\alpha +1}ds\right)}{\frac{d}{d{\psi }_0}\left({\int }_{S\left({\psi }_0\right)}Rds\right)}}.$$

(6)

In the above expression, it is possible to use the normalized poloidal magnetic flux, ${\psi }_N$, instead of the poloidal magnetic flux, $\psi$. This connects with the dimensionless (normalized) effective-radius $\rho$ based on the toroidal magnetic flux enclosed by the flux surface $\psi$ defined as

$$\pi {\rho }^2={\displaystyle \frac{\int B_{\phi }ds}{B_0{S}_b}}$$

(7)

where $S_b$ denotes the surface of the poloidal cross-section of the plasma within the last closed flux surface. The connection is made using the expression of ${\psi }_N$ as

$${\psi }_N\left(\rho \right)={\displaystyle \frac{{\int }_0^{\rho }\frac{s}{q_{\mathbf{B}}\left(s\right)}ds}{{\int }_0^1\frac{s}{q_{\mathbf{B}}\left(s\right)}ds}}.$$

(8)

2.3. Principles of the Analysis

It has been proposed in Ref. [1] to inspect the resonant or non-resonant character of any perturbation with respect to both the magnetic and current density field lines. In toroidal geometry, the appropriate framework to do this is to use the Hamada coordinates $(v,{\theta }_H,{\zeta }_H)$, which are a canonical set of variables for both the magnetic and current density field lines. In the Hamada coordinates [42], if $\delta {\mathbf{B}}_{m,n}\propto e^{i(m{\theta }_H-n{\zeta }_H)}$ then $\delta {\mathbf{J}}_{m,n}={\mu }_0^{-1}\nabla \times \delta {\mathbf{B}}_{m,n}\propto e^{i(m{\theta }_H-n{\zeta }_H)}$. This allows a mode-by-mode topological classification [1]. Moreover, the $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ profiles of the axisymetric equilibria are intrinsic quantities that do not depend on the coordinate system, as long as the same magnetic surfaces are parameterized, so that $q_{\mathbf{B}}\left(\psi \right)=q_{\mathbf{B}}\left(v\right)$ and $q_{\mathbf{J}}\left(\psi \right)=q_{\mathbf{J}}\left(v\right)$. Let us now consider some current density perturbation $(m,n)$. This can be resonant for the current density field lines if, at some $\psi$, or equivalently corresponding v or $\rho$, one has $q_{\mathbf{J}}\left(\rho \right)=m/n$, i.e., $q_{\mathbf{J}}^{-1}\left(\rho \right)=n/m$. It can also be resonant for the magnetic field lines if there exists some ${\rho }_{\mathbf{B}}$, such that $q_{\mathbf{B}}^{-1}\left({\rho }_{\mathbf{B}}\right)=n/m$. Let us use an example. Suppose that $q_{\mathbf{J}}^{-1}$ is smaller than 0.2 everywhere, whereas $q_{\mathbf{B}}$ is above 1 so that $q_{\mathbf{B}}^{-1}$ has positive values smaller than 1. Then, the mode $(m,n)=(3,1)$ is magnetically resonant but is not associated with a resonant current density perturbation as $1/3>0.2$. The same is true for all the modes $(m,n)$ such that $n/m>0.2$.

In the following sections of the paper, modes are considered in the Hamada setting. A $(m,n)$ mode in the Hamada coordinates does not correspond to a single $(m,n)$ mode in flux coordinates. It projects onto a spectrum of $(m+k,n)$ modes in flux coordinates, where $k\in \mathbb{Z}$ and where the dominant contribution comes from the $(m,n)$ mode. In the cylindrical limit, this would be the only contribution. Consequently, in the toroidal geometry, a $(m,n)$ Hamada $\mathbf{J}$-resonance generally amounts in the real space to a superposition of filaments.

3. Results

3.1. Computation of Flux Surface Averages

The plasma domain was extracted and digitized from Figure 2 of Ref. [33]. The last closed flux surface is the inner bold curve of Figure 1. In order to compute the flux surface averages of $R^{-2}$ using Equation (6), one needs to know the flux contours. To achieve this, the Grad–Shafranov equation was solved using this last closed flux surface as the boundary of the computational domain. Figure 1 depicts the obtained approximation of the flux contours and the red dot reports the location of the magnetic axis obtained from Figure 2 of Ref. [33]. One can then proceed to the evaluation of the flux surface averages of $R^{-2}$. The resulting estimates are depicted in Figure 2. To account for some inevitable imprecision, a confidence band is drawn around the estimated curve, spanning values between 0.93 and 1.07 times the estimated $〈R^{-2}〉$.

Figure 1. Reconstruction of the magnetic flux contours. The red dot stands for the magnetic axis.

Figure 1. Reconstruction of the magnetic flux contours. The red dot stands for the magnetic axis.

Figure 2. Evaluation of the flux surface average $〈R^{-2}〉$ as a function of $\rho$. At $\rho =0$, the flux surface average of $R^{-2}$ should be $R_{ax}^{-2}$ with $R_{ax}$ the radius of the magnetic axis. The reconstructed curve shows some discrepancy compared to this value in the limit $\rho \to 0$. To account for some inevitable imprecision, a confidence band is shown around the estimated curve, spanning values between 0.93 and 1.07 times the estimated $〈R^{-2}〉$.

Figure 2. Evaluation of the flux surface average $〈R^{-2}〉$ as a function of $\rho$. At $\rho =0$, the flux surface average of $R^{-2}$ should be $R_{ax}^{-2}$ with $R_{ax}$ the radius of the magnetic axis. The reconstructed curve shows some discrepancy compared to this value in the limit $\rho \to 0$. To account for some inevitable imprecision, a confidence band is shown around the estimated curve, spanning values between 0.93 and 1.07 times the estimated $〈R^{-2}〉$.

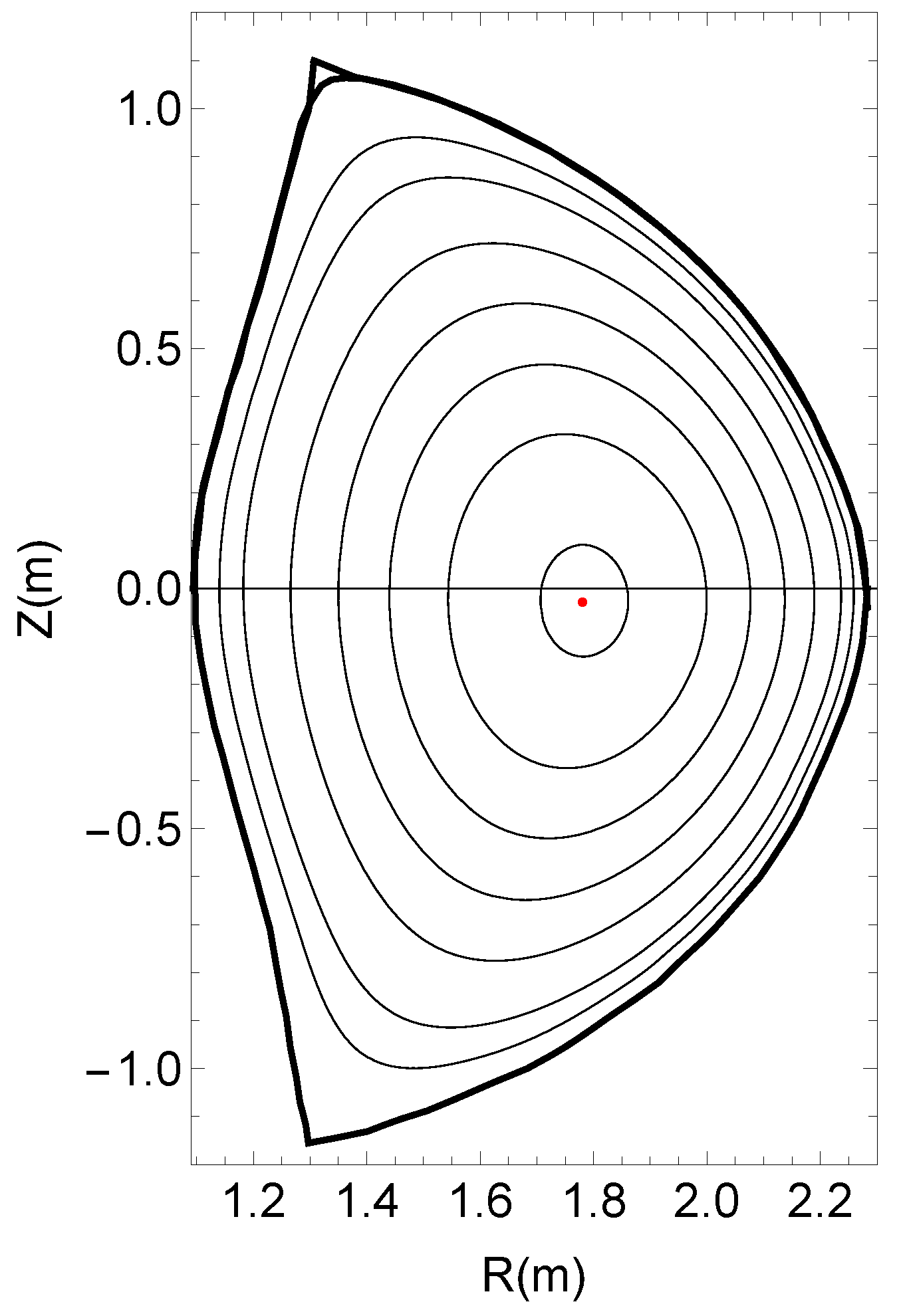
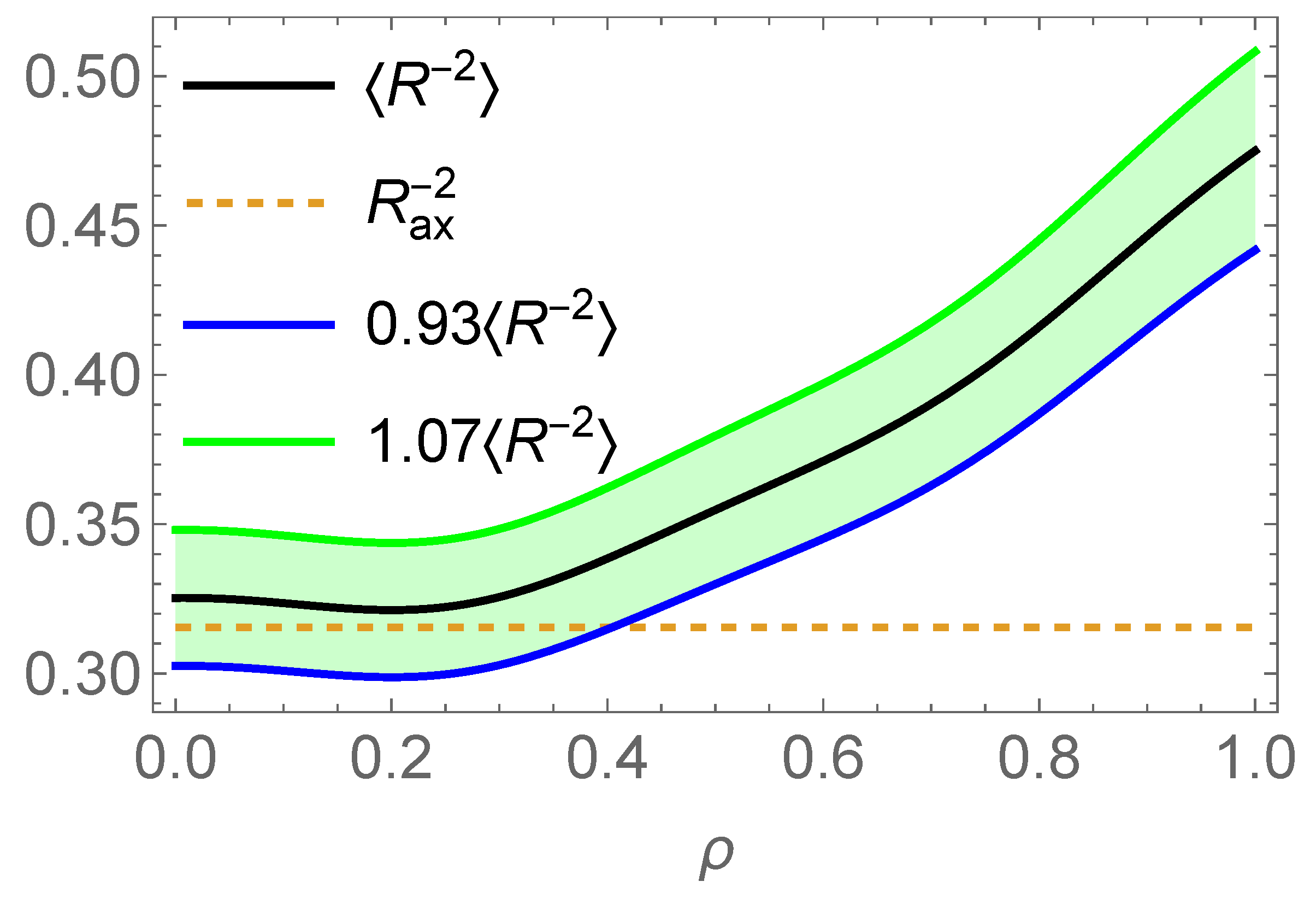
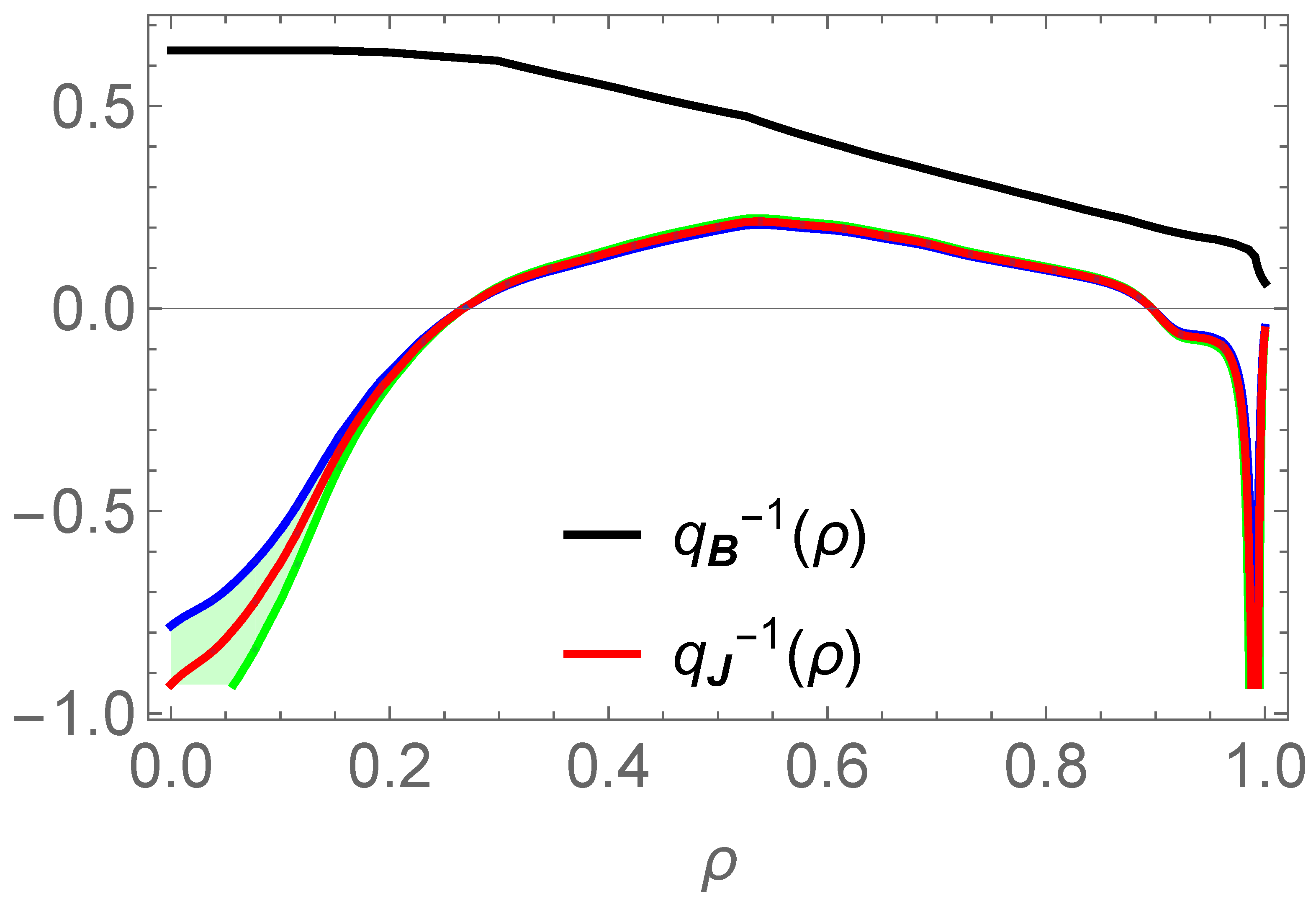
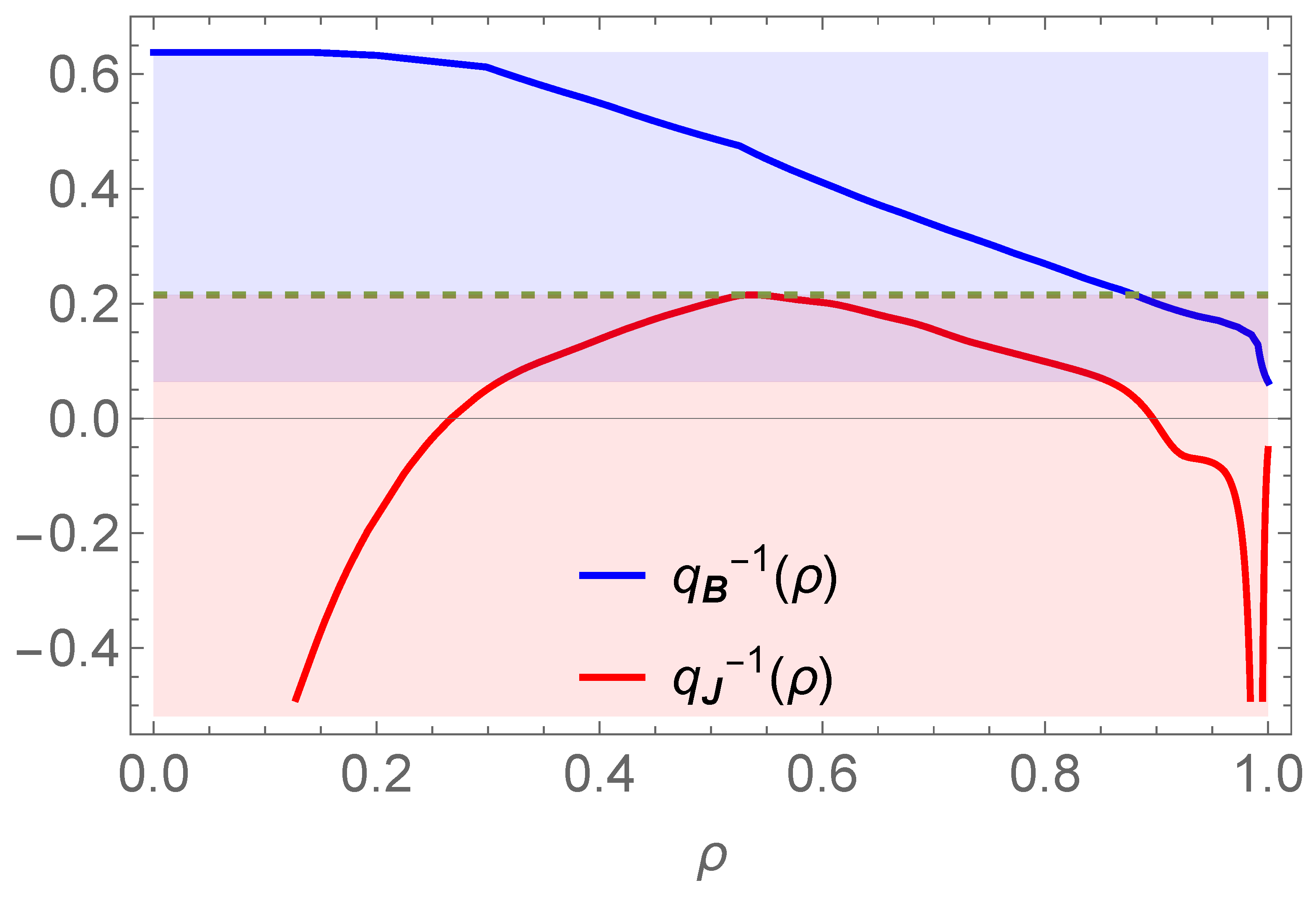
3.2. Equilibrium Reconstruction of the $q_{\mathbf{J}}$-Profile

We then have all the requested information to compute the winding profile, $q_{\mathbf{J}}^{-1}$, of the current density field lines. The reconstructed $q_{\mathbf{J}}^{-1}$ profile is shown on Figure 3.

Figure 3 represents the confidence band introduced by some uncertainty in the evaluation of the flux surface averages of $R^{-2}$. To be thoroughly rigorous, we must also test the robustness of the computation of $q_{\mathbf{J}}$ against errors in curve digitization. Let us then estimate the uncertainty in the evaluation of $q_{\mathbf{J}}$ introduced by the digitization of the data. Considering $q_{\mathbf{J}}$ as a function of $q_{\mathbf{B}}$, $〈R^{-2}〉$, $p^{\prime }$ and $F{F}^{\prime }$, the Laplace–Gauss uncertainty propagation formula yields, for the uncertainty on $q_{\mathbf{J}}$,

$$\begin{array}{ccc}\hfill \Delta q_{\mathbf{J}}& =& \left[{\left({\displaystyle \frac{\partial q_{\mathbf{J}}}{\partial q_{\mathbf{B}}}}\Delta q_{\mathbf{B}}\right)}^2+{\left({\displaystyle \frac{\partial q_{\mathbf{J}}}{\partial 〈R^{-2}〉}}\Delta 〈R^{-2}〉\right)}^2\right.\hfill \\ & & +{\left.{\left({\displaystyle \frac{\partial q_{\mathbf{J}}}{\partial p^{\prime }}}\Delta p^{\prime }\right)}^2+{\left({\displaystyle \frac{\partial q_{\mathbf{J}}}{\partial F{F}^{\prime }}}\Delta F{F}^{\prime }\right)}^2\right]}^{1/2}.\hfill \end{array}$$

(9)

After some calculations using Equation (1), Equation (9) gives

$$\begin{array}{ccc}& & {\left({\displaystyle \frac{\Delta q_{\mathbf{J}}}{q_{\mathbf{J}}}}\right)}^2-{\left({\displaystyle \frac{\Delta q_{\mathbf{B}}}{q_{\mathbf{B}}}}\right)}^2\hfill \\ & =& {\left(1-{\displaystyle \frac{q_{\mathbf{B}}}{q_{\mathbf{J}}}}\right)}^2\left[{\left({\displaystyle \frac{\Delta 〈R^{-2}〉}{〈R^{-2}〉}}\right)}^2+{\left({\displaystyle \frac{\Delta p^{\prime }}{p^{\prime }}}\right)}^2+{\left({\displaystyle \frac{\Delta F{F}^{\prime }}{F{F}^{\prime }}}\right)}^2\right].\hfill \end{array}$$

Assuming that all the uncertainties are similar with $\Delta q_{\mathbf{B}}/q_{\mathbf{B}}=\Delta 〈R^{-2}〉/〈R^{-2}〉=\Delta p^{\prime }/p^{\prime }=\Delta F{F}^{\prime }/F{F}^{\prime }=\delta$ yields

$${\displaystyle \frac{\Delta q_{\mathbf{J}}}{q_{\mathbf{J}}}}=\delta {\left[1+3{\left(1-{\displaystyle \frac{q_{\mathbf{B}}}{q_{\mathbf{J}}}}\right)}^2\right]}^{1/2}.$$

(10)

For $\delta =0.04$, one computes the uncertainty band shown in Figure 4.

The obtained confidence band for the evaluation of the current density winding profile is very similar to that plotted in Figure 3. This shows that the result obtained for $q_{\mathbf{J}}^{-1}$ is highly robust to small perturbations in the data, except in a very central zone of the tokamak plasma (roughly within $\rho <0.15$) where its knowledge is less precise and the confidence interval is larger. The negative value of $q_{\mathbf{J}}$ in this region renders this point irrelevant in terms of the topological properties of magnetic and current density modes: in this region, irrespective of the point located within the confidence interval, filamentation modes (i.e., current density resonances) are not associated with magnetic islands but with non-resonant magnetic perturbations.

3.3. Important Remark

It turns out that the shape of the current density winding profile, $q_J^{-1}\left(\rho \right)$, could have been inferred simply by the inspection of the functions $dp/d\psi \left(\rho \right)$ and $FdF/d\psi \left(\rho \right)$ plotted in Figure 2 of Ref. [33]. Indeed, this shows that $dp/d\psi <0$ for $0\le \rho \le 1$, while $FdF/d\psi$ is positive in the core, changes sign, and becomes negative in an inner region before returning to positive in the edge domain. The locations where $FdF/d\psi$ vanishes correspond to the two zeros of $q_J^{-1}$ shown in the $q_J^{-1}\left(\rho \right)$ plots. The height of the positive bump can be inferred by any rough geometrical estimate for the surface average $〈R^{-2}〉$. Indeed, Figure 3 shows that the maximal value of the current density winding profile is very robust to variations in $〈R^{-2}〉$.

4. Analysis and Discussion

4.1. Classification of Modes

Let us now analyse Figure 5 and first consider the current density winding profile.

Any mode $(m,n)$ where there exists some $\rho$ for which $q_{\mathbf{J}}\left(\rho \right)=m/n$ is resonant for the current density field, and therefore, when isolated, takes the form of a current filamentation mode. Yet, in tokamaks, the magnetic and current density field are, at any time, related by Ampère’s law, as the displacement current is substantially lower than the plasma current. This filamentation mode is then, by Ampère’s law, associated with some magnetic perturbation. This magnetic perturbation can be either resonant for magnetic field lines if $m/n=q_{\mathbf{B}}\left(\rho \right)$, or non-resonant otherwise. In the red stripe, the spectrum of tiny filamentation modes is associated by Ampère’s law with a spectrum of non-resonant magnetic modes that has a negligible impact on electron heat transport. On the contrary, in the violet stripe, the spectrum of tiny filamentation modes is associated by Ampère’s law to a spectrum of resonant magnetic modes that may impact the electron heat transport. Finally, in the blue stripe, there is no resonant mode for the current density field. Therefore, the potentially resonant magnetic modes can only arise there from smooth, non-resonant, modes of deformation of the equilibrium current density field lines.

Figure 6 shows the spatial distribution of magnetic modes, categorized according to the scheme outlined in Figure 5.

The broad central region on the poloidal cross-section, depicted in blue in this figure, as in Figure 5, is devoid of magnetic modes originating from the current filament spectrum. This region extends up to $\rho \approx 0.88$. This value is obtained from Figure 5 as the $\rho$-value at which the function $q_{\mathbf{J}}^{-1}$ enters the violet stripe. In the outer region, depicted in violet, the resonant magnetic modes are conversely originating from a spectrum of current filamentation modes. This is due to the superposition of numerous current filaments that permeate the plasma in the region spanning from $\rho \approx 0.32$ to $\rho \approx 0.85$ where the image of $q_{\mathbf{J}}^{-1}$ is in the violet stripe in Figure 5.

Consequently, the comparison of the $q=q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ profiles (or, equivalently, of their inverses), in an example of QH-mode occurrence, uncovers a key feature. It reveals the existence of two distinct plasma zones: a central region unaffected by magnetic turbulence caused by current filaments, and a thin peripheral zone where there exists a spectrum of magnetic modes associated to current filaments. Let us now briefly review some experimental facts about QH-modes before interpreting this result.

4.2. Overview of QH-Mode Phenomenology

In the standard H-modes, ELMs result in substantial transient spikes of particle and heat fluxes to the divertor components, which could potentially cause unacceptable damage in future fusion devices. In QH-modes, the plasma remains stable and quiet, without the deleterious ELM events. In terms of confinement, QH modes are similar to H modes. Their performance indicators are at the same level. Furthermore, although the quiescent H-modes do not experience ELMs, the edge particle transport in QH-mode is still rapid enough to provide some beneficial particle exhaust, which is a crucial requirement for future fusion reactors in order to remove impurities and helium ash. The QH-mode differs then from the standard ELM-free H-mode, where the density and radiated power exhibit a monotonic increase. An edge electromagnetic mode, the edge harmonic oscillation (EHO), provides enhanced edge particle transport that, when time-averaged, surpasses the transport produced by ELMs. This enhanced, time-averaged particle transport provided by the EHO allows for the constant density operation observed in the QH mode [43]. Notably, the EHO is self-generated by the plasma, and therefore the QH mode does not require the additional coils needed for ELM suppression via resonant magnetic perturbations [44].

4.3. Discussion

Generically, any perturbation to the tokamak equilibrium current density decomposes into a spectrum of modes, including a resonant spectrum that is a superposition of small current density filaments. In a Poincaré plot, the overlap of the current density field resonances (filaments modes) may result in some chaotic braiding of the current density field lines, with only possibly large filaments emerging from an overall chaotic sea. Yet, the corresponding magnetic perturbations may or may not be resonant depending on $q_{\mathbf{B}}$. In the context of the QH-mode considered here, the Figure 5 tells us that only in the violet stripe does the spectrum of tiny current density resonances produce a spectrum of resonant magnetic perturbations triggering magnetic braiding [45]. This happens here in the edge plasma region of the tokamak represented on Figure 6. Conversely, the large central zone of the plasma, colored in blue, is preserved from this current-driven small-scale magnetic turbulence. Figure 6 is therefore consistent with the phenomenological properties of QH-modes: the fact that, in the whole plasma center, the spectrum of magnetic modes associated with small current density filaments is non-resonant and, therefore, does not affect the integrity of the magnetic field lines is consistent with an improved heat confinement. This makes this operating mode similar to an H-mode. Conversely, in the edge plasma, the spectrum of small current density filaments spoils the integrity of the magnetic field lines. This is consistent with a low heat and electron confinement in the edge region. This is also consistent with edge particle exhaust enabling the constant density operation in QH-mode.

In addition to these general outcomes, the present reconstruction concerns the discharge 163518 from the DIII-D tokamak at time $t=2350\mathrm{ms}$, where a clear EHO, a coherent edge magnetic activity characteristic of many QH-mode plasmas, with dominant $n=1$ mode is observed. This magnetic activity can be inferred to be related to magnetic resonant modes at $q_{\mathbf{B}}=5$ or $q_{\mathbf{B}}=6$, having dominant mode numbers $(m,n)=(5,1)$ or $(6,1)$ being associated with some plasma current filamentation present at $q_{\mathbf{J}}=5$ or $q_{\mathbf{J}}=6$ that takes place close to $\rho =0.55$, according to Figure 5.

5. Conclusions

As advocated in Ref. [1], if the axisymmetric fusion device could be driven so as to disconnect $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$, in the sense that the intersection of the images of the functions $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ is empty, then all the resonant magnetic modes would only originate from smooth modes of deformation of the current but not from current density resonances. All the small magnetic perturbations produced by the tiny current filaments necessarily coming in from the distortion to axisymmetry about the resonant $q_{\mathbf{J}}$ surfaces would then not affect the integrity of the magnetic surfaces, being nonresonant. Thus, by forcing the operating regime of a tokamak to allow the $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ profiles to be separated, the magnetic surfaces could be preserved from magnetic perturbations due to current filamentation modes. This could be a favorable route for preserving heat confinement.

This work presents the first cross-analysis of magnetic and current density field topologies. This uses experimental data obtained in the promising QH-mode regime. If the pattern of the magnetic and current density winding profiles displayed in Figure 5 characterizes the QH-modes, which needs further investigation, then the central region of the tokamak plasma, in which $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ are disconnected, supports the above scenario as heat confinement is preserved there. On the contrary, the hump in the current density winding profile taking place in the violet stripe signals that the outer plasma region is the home of a spectrum of current filament-produced resonant magnetic modes degrading the peripheral confinement. This stochastization may explain the absence of edge-localized modes and allows some beneficial particle exhaust.

Overall, the present results point to a possible signature pattern of the QH-modes to be further reinforced and substantiated by additional data. Implementing the $(q_{\mathbf{B}},q_{\mathbf{J}})$ real-time monitoring could help uncover insights into the diverse tokamak confinement regimes with possibly important implications for magnetic confinement fusion. In particular, similar analyses could focus on uncovering the signatures associated with the emergence of ELMs. In the case of ELMs, one hypothesis is that the $q_{\mathbf{B}}$ and $q_{\mathbf{J}}$ profiles are locally equal to some $m_0/n_0$ in the edge region in coincidence with a local vanishing of the pressure gradient and the $(m_0,n_0)$ current filament flowing within the $(m_0,n_0)$ magnetic island.