Methods for Controlling Electrostatic Discharge and Electromagnetic Interference in Materials
Abstract
1. Introduction
2. Electrostatic Discharge and EM/RF Interference in Materials
3. Effective Medium Theory
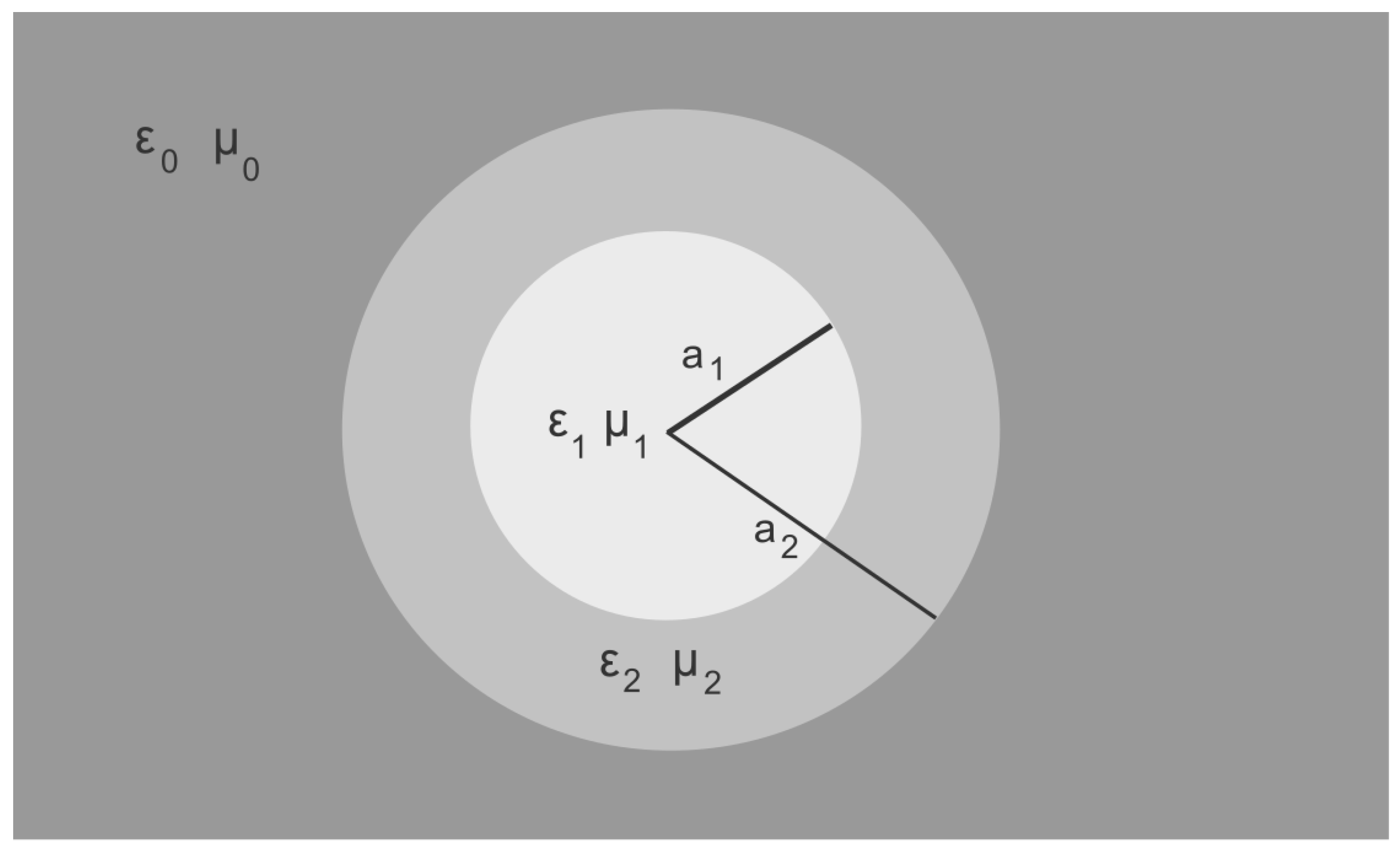
3.1. Effective Medium Theory of Inhomogeneous Hyperspheres
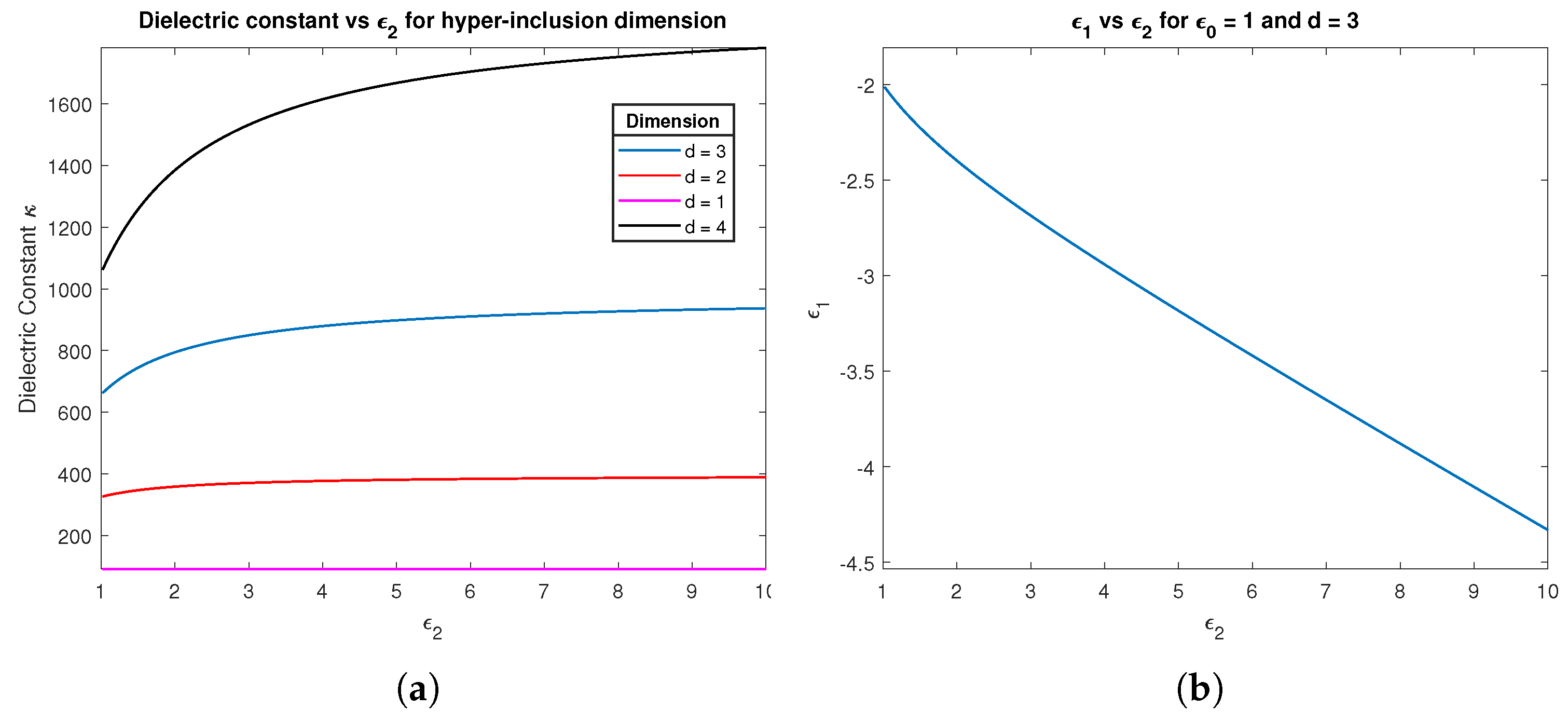
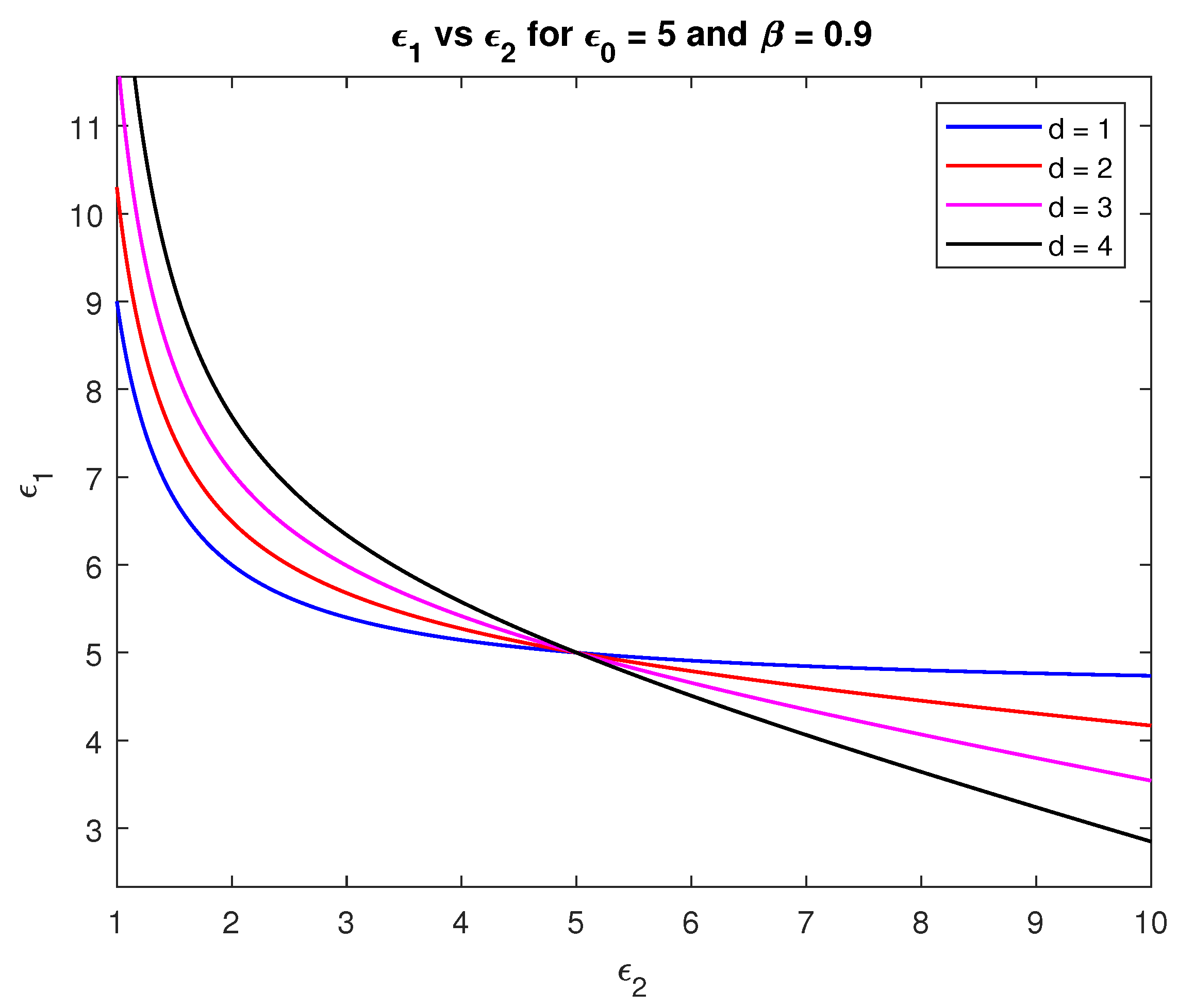
3.2. The Limit : Maximising the Dielectric Function
3.3. The Limit : The Perfect Conducting Limit
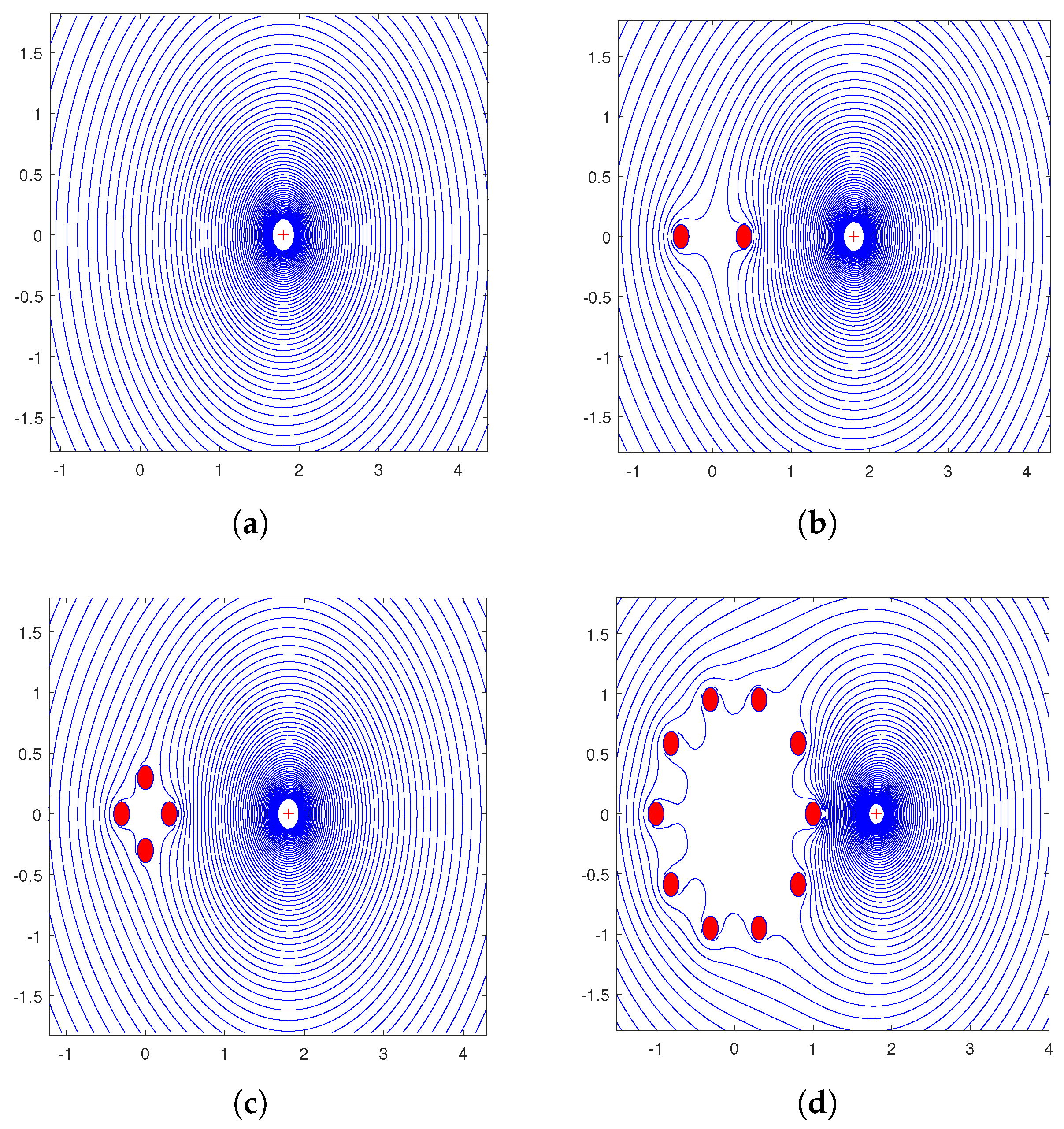
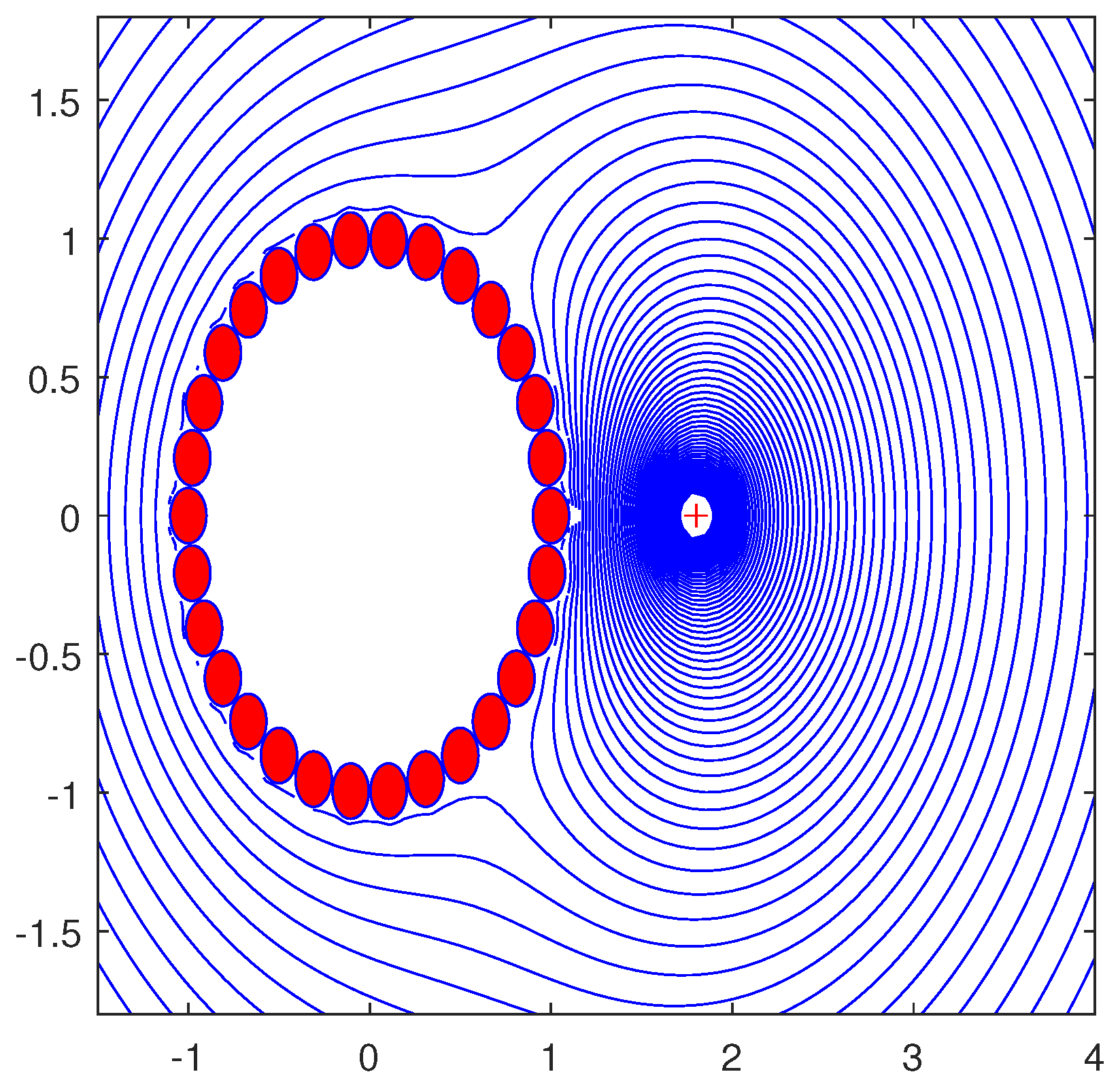
3.4. The Limit : EMI/RFI Cancellation
4. Transformation Medium Theory
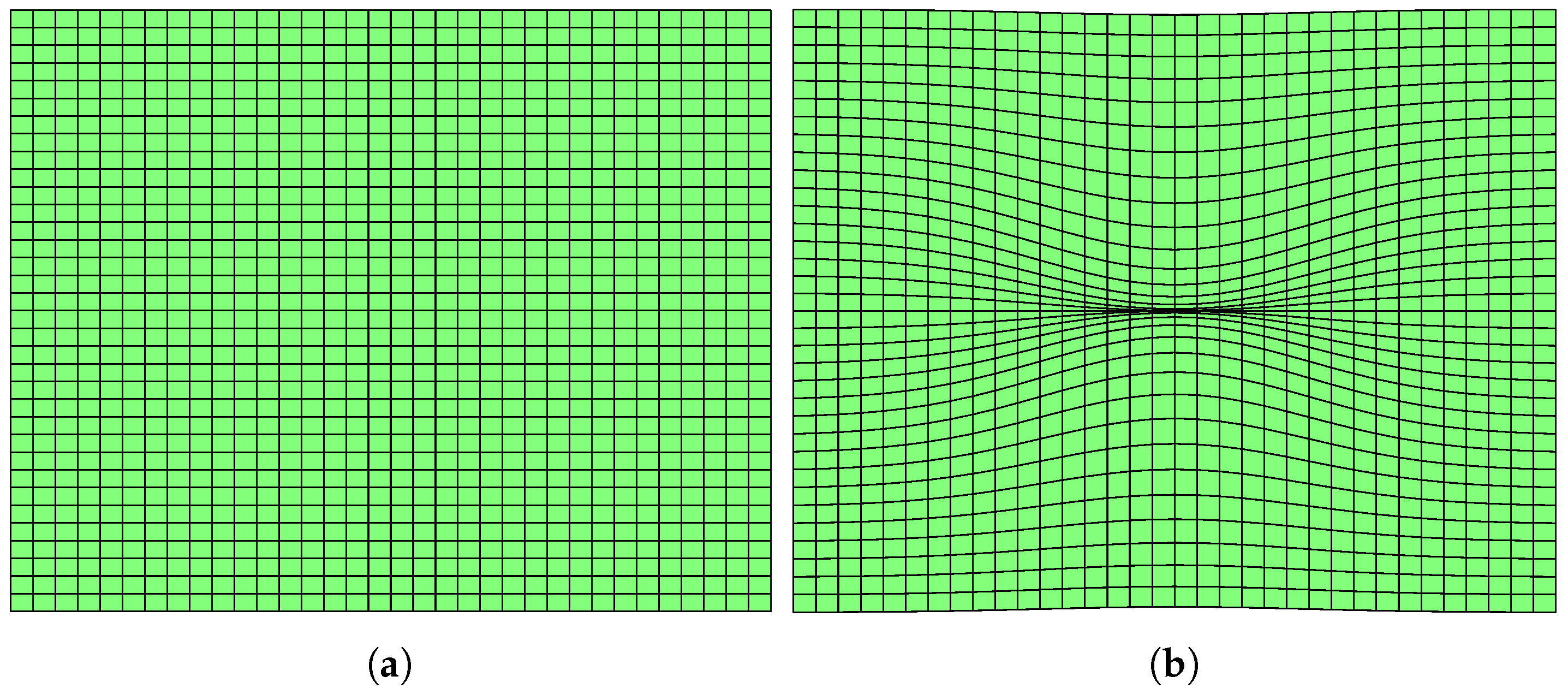
4.1. Determining the Equations and Geodesics of Electromagnetic Fields in a Material
4.2. Transformation of the Constitutive Parameters in Maxwell’s Equations
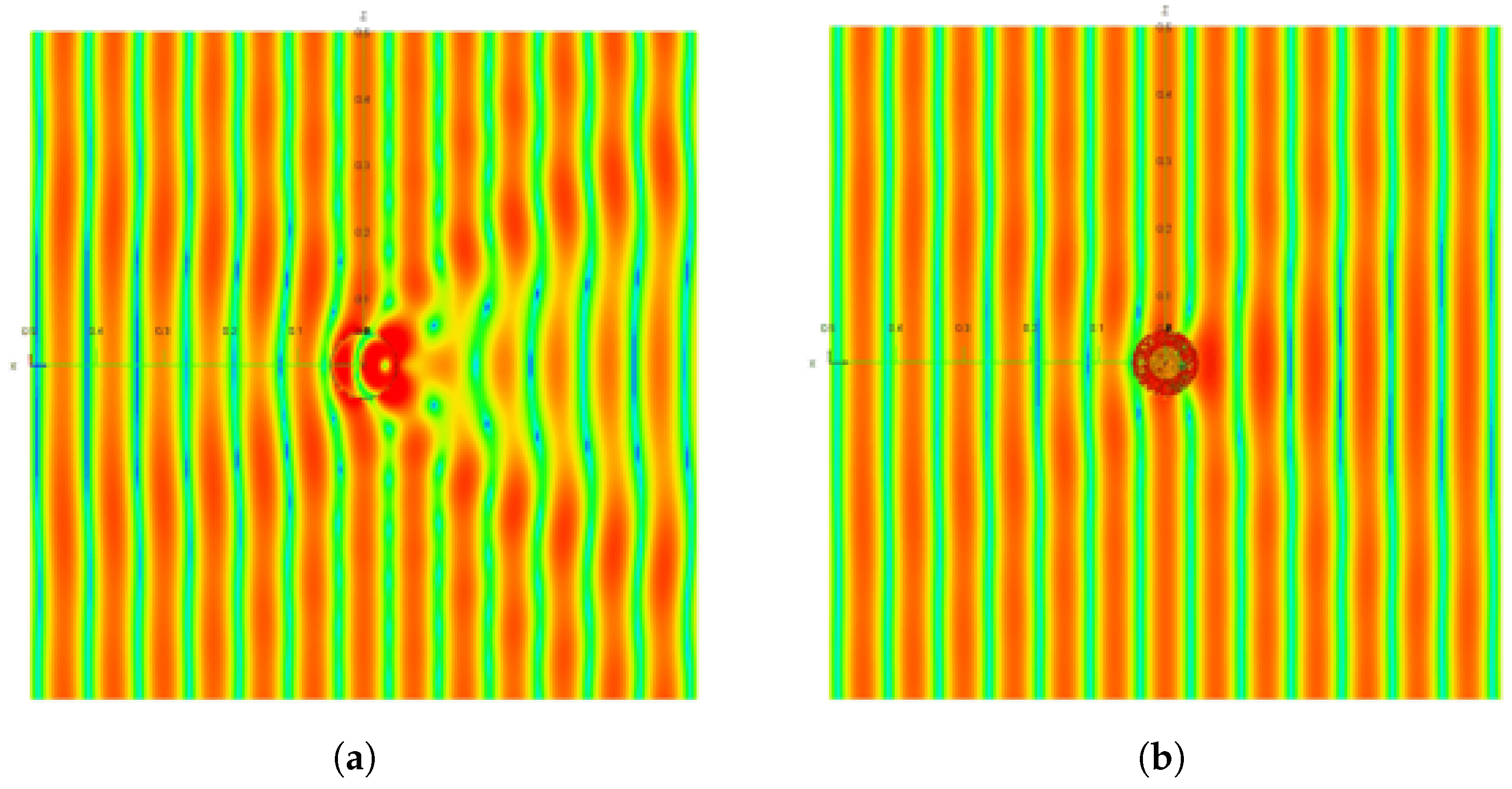
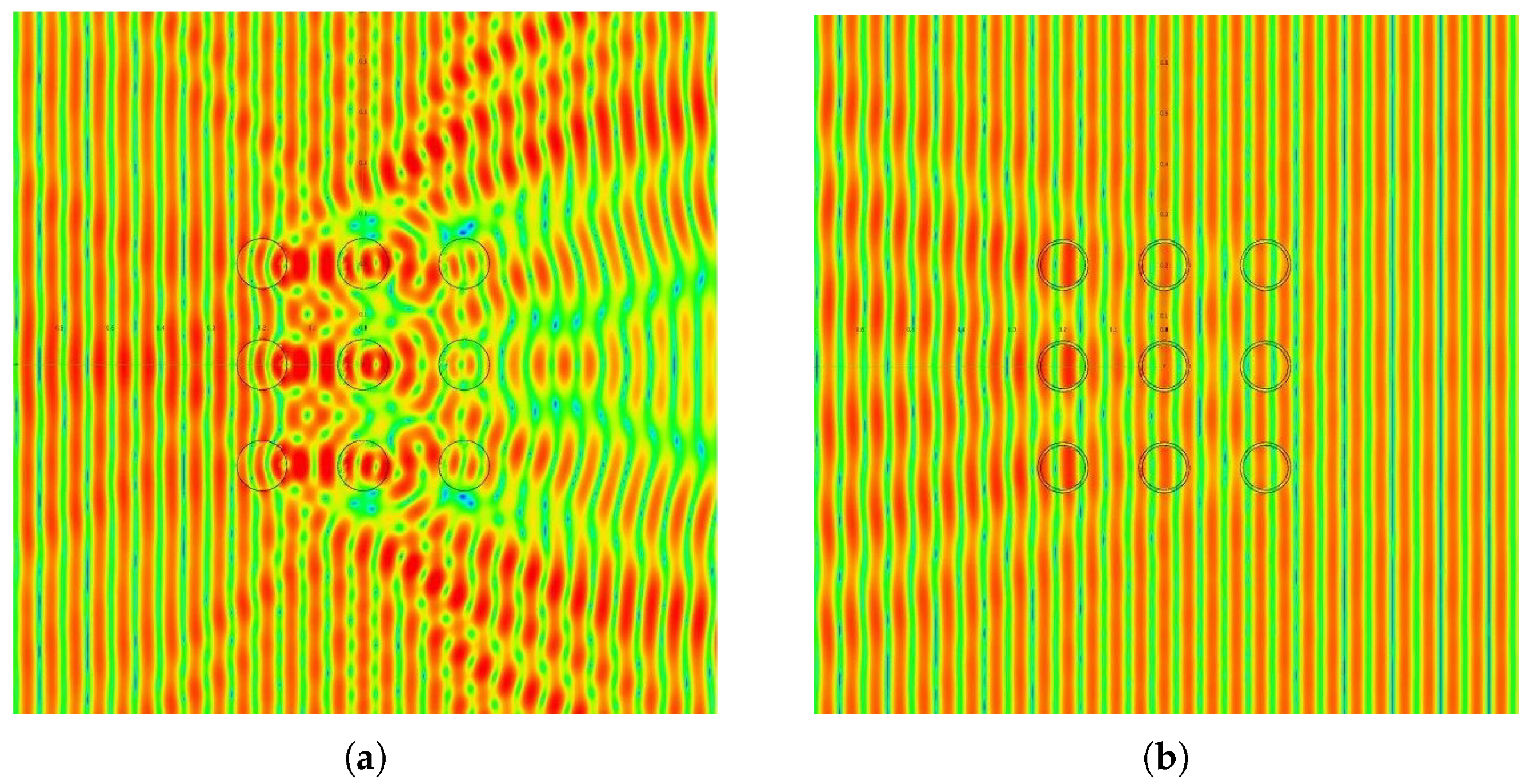
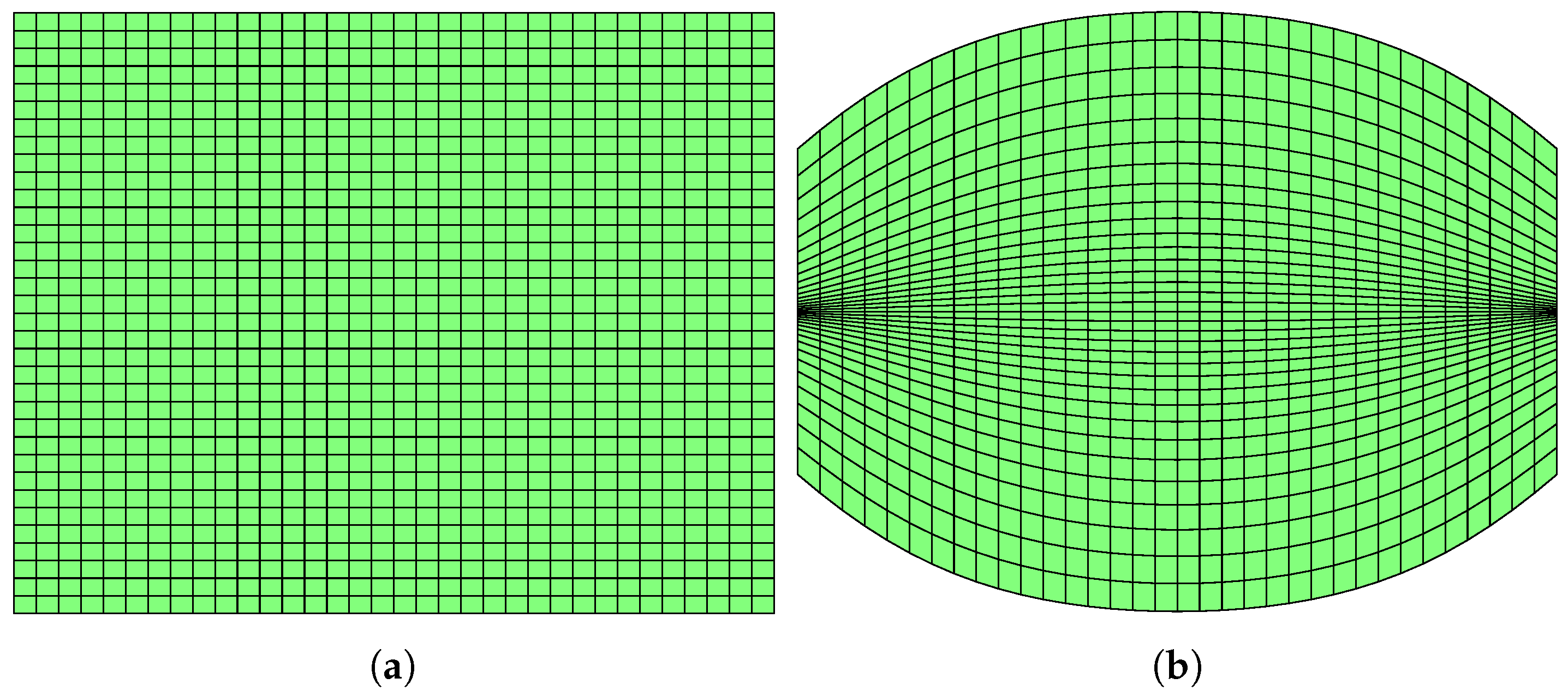
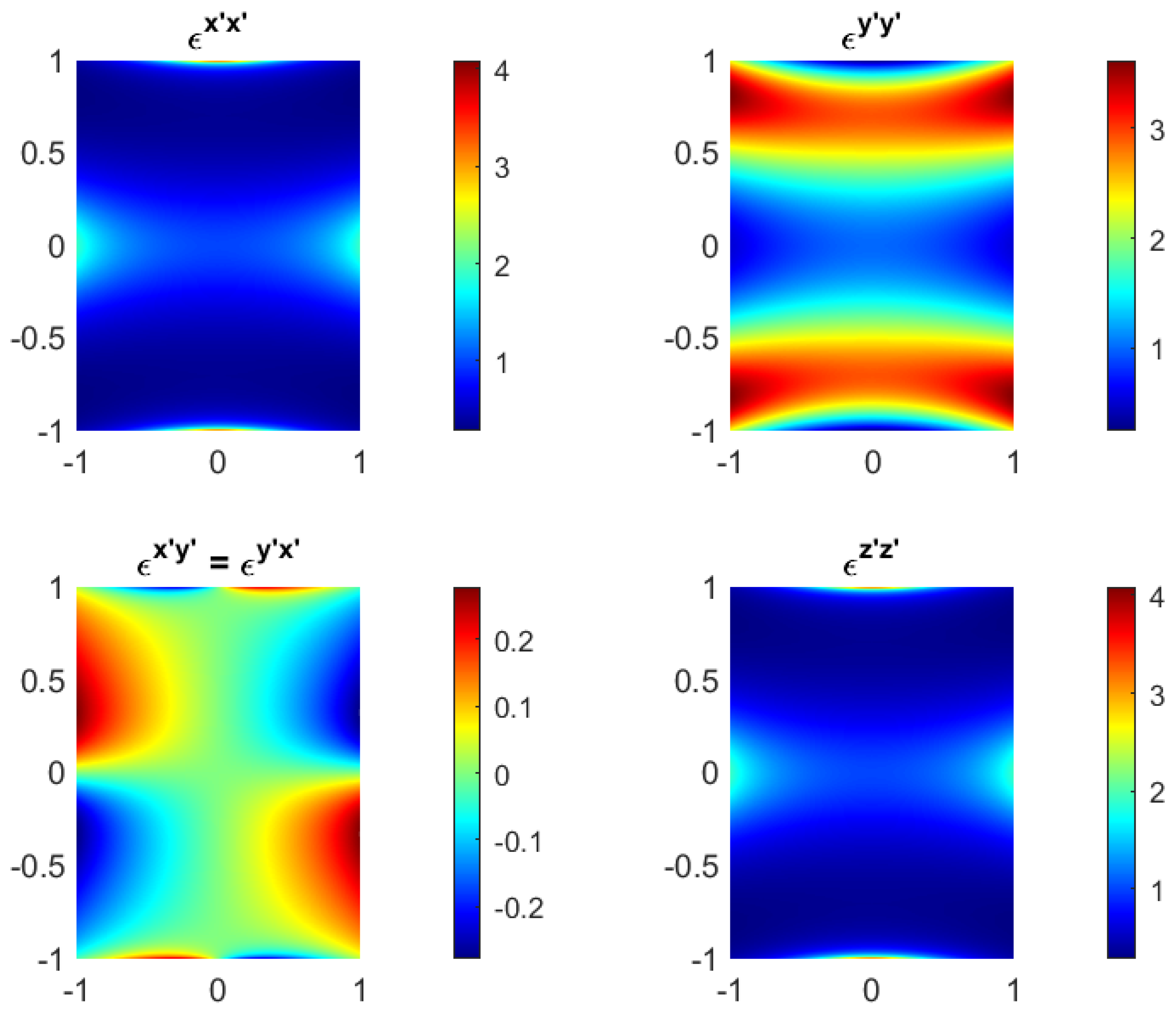
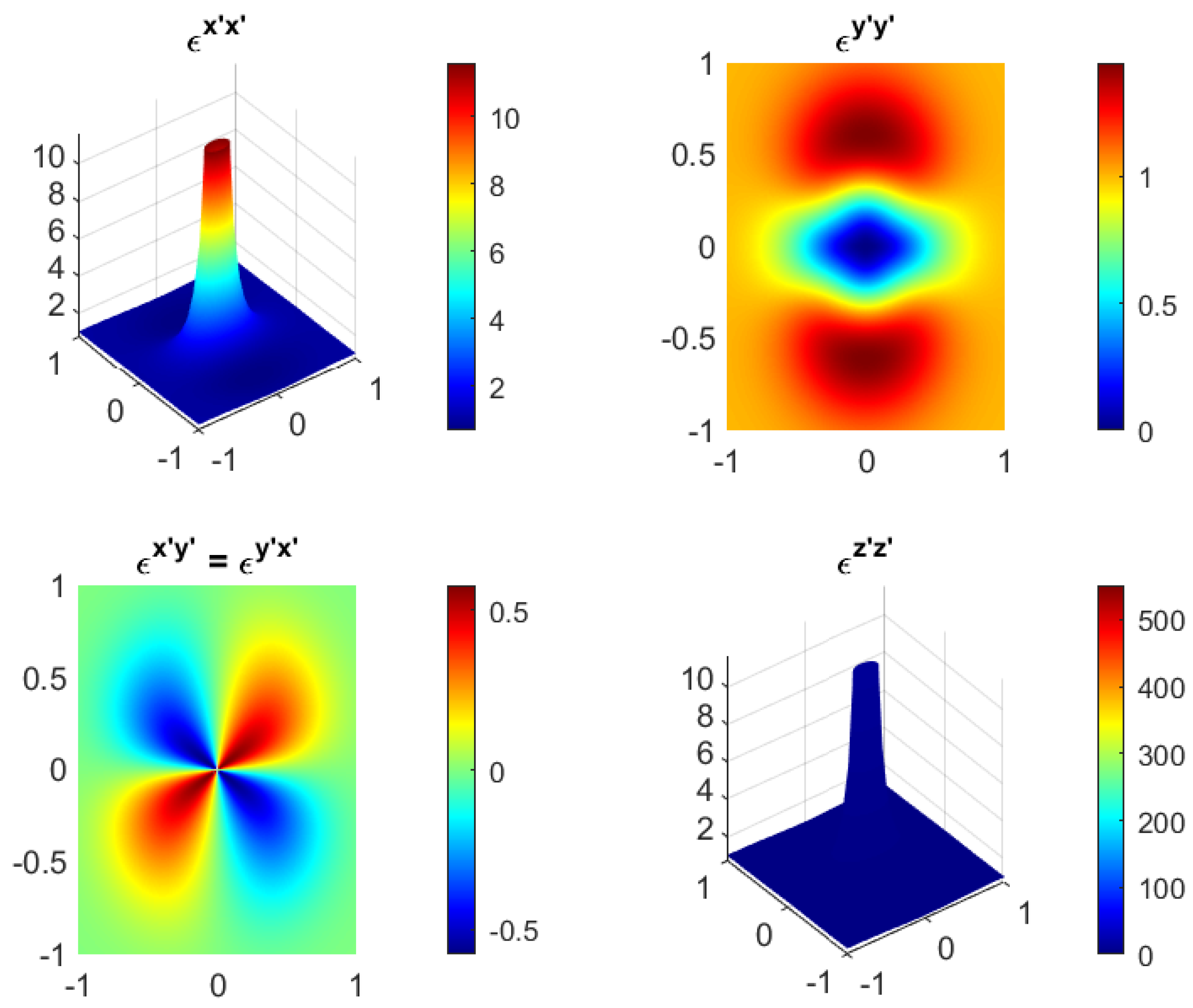
4.3. Controlling EM Fields in Different Regions of a Material
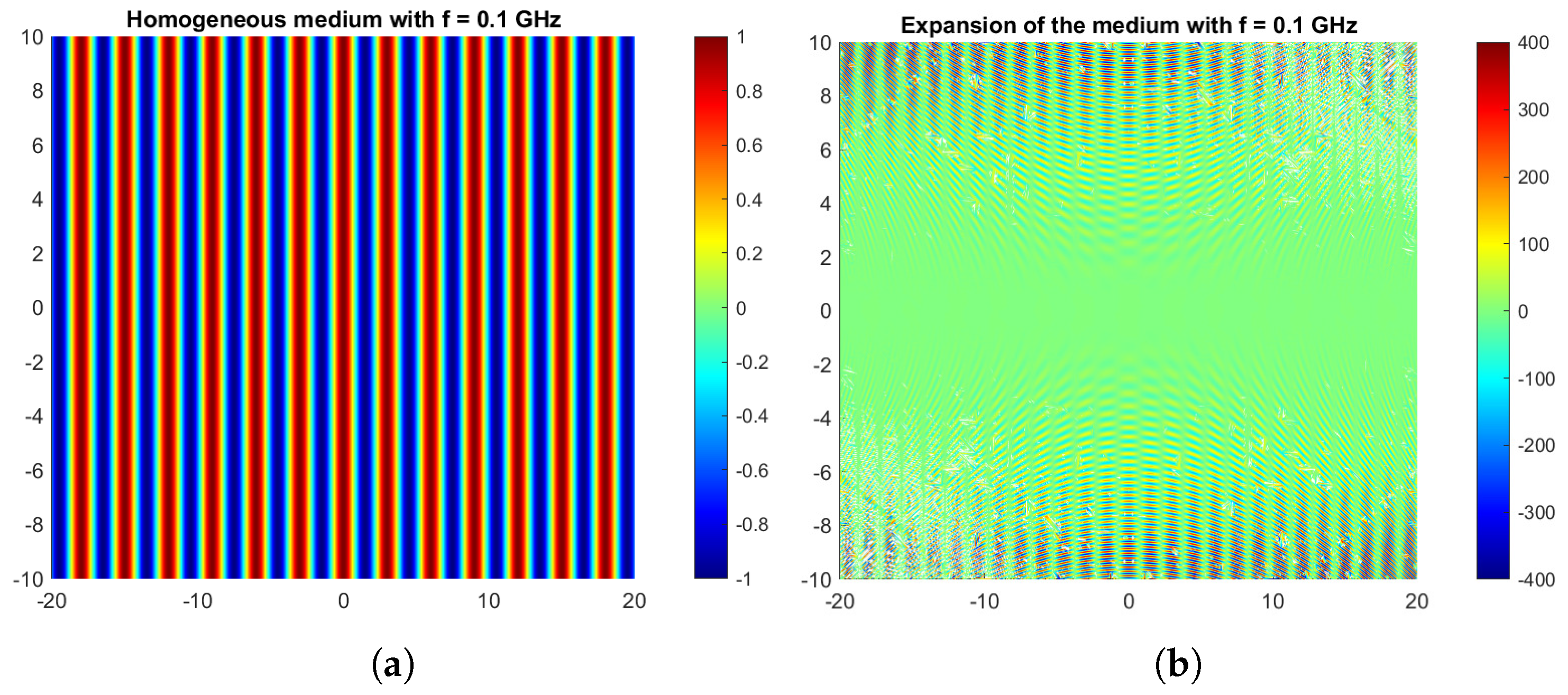
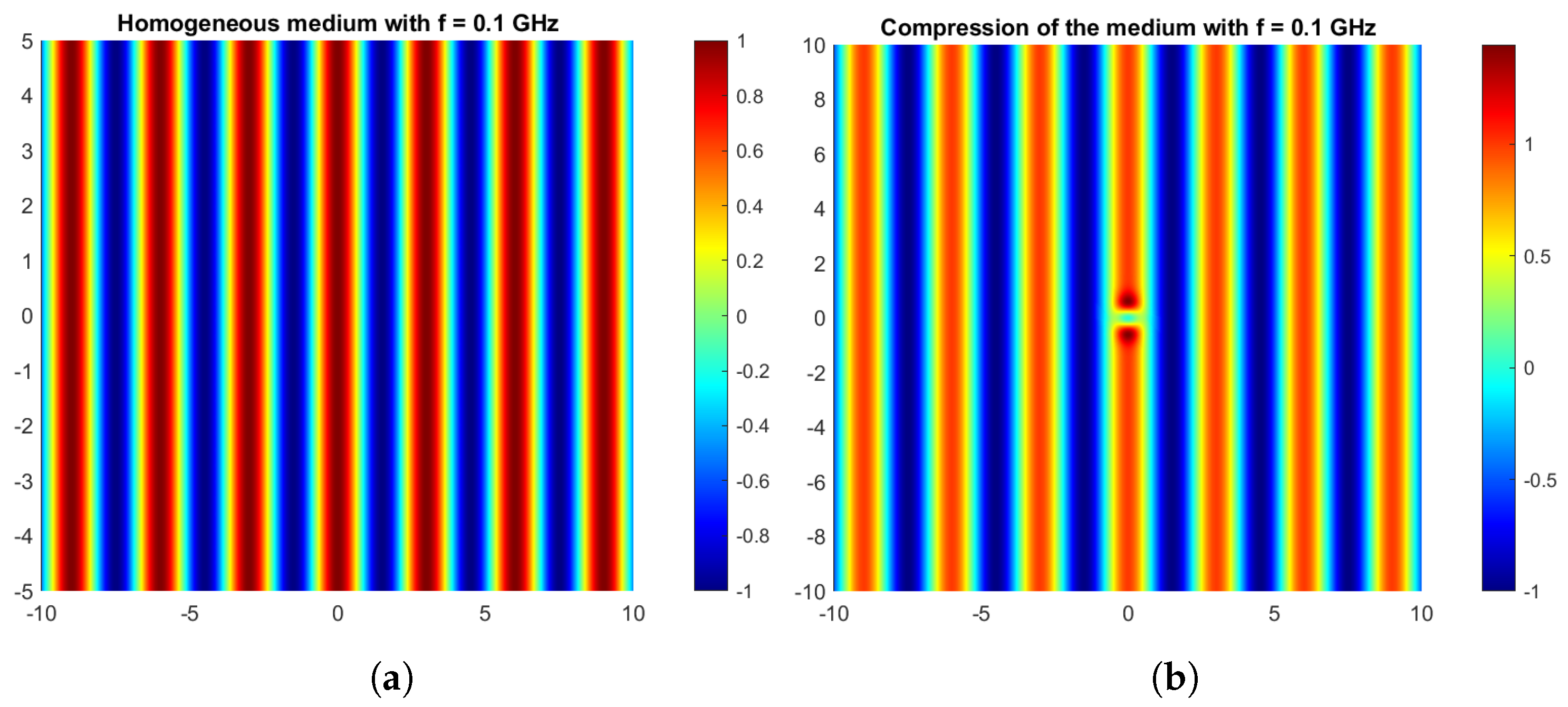
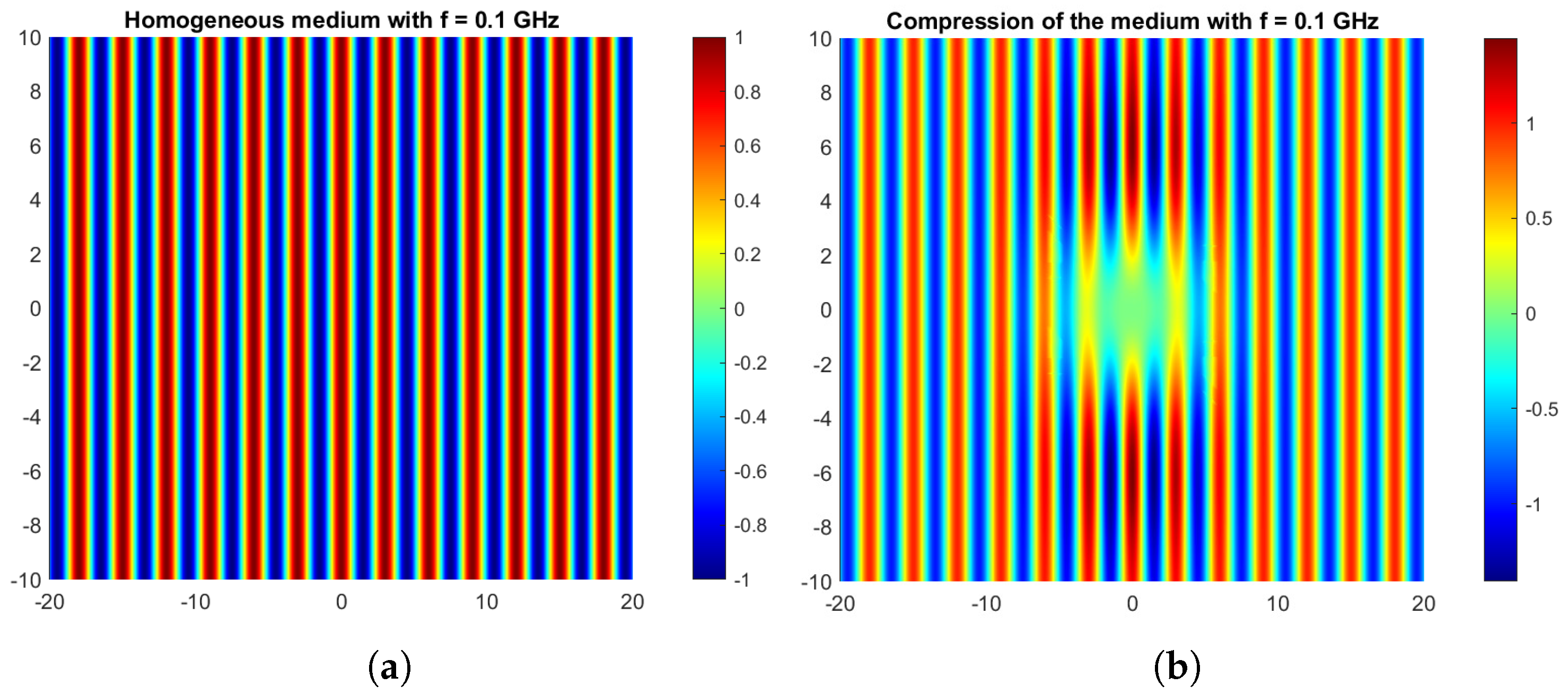
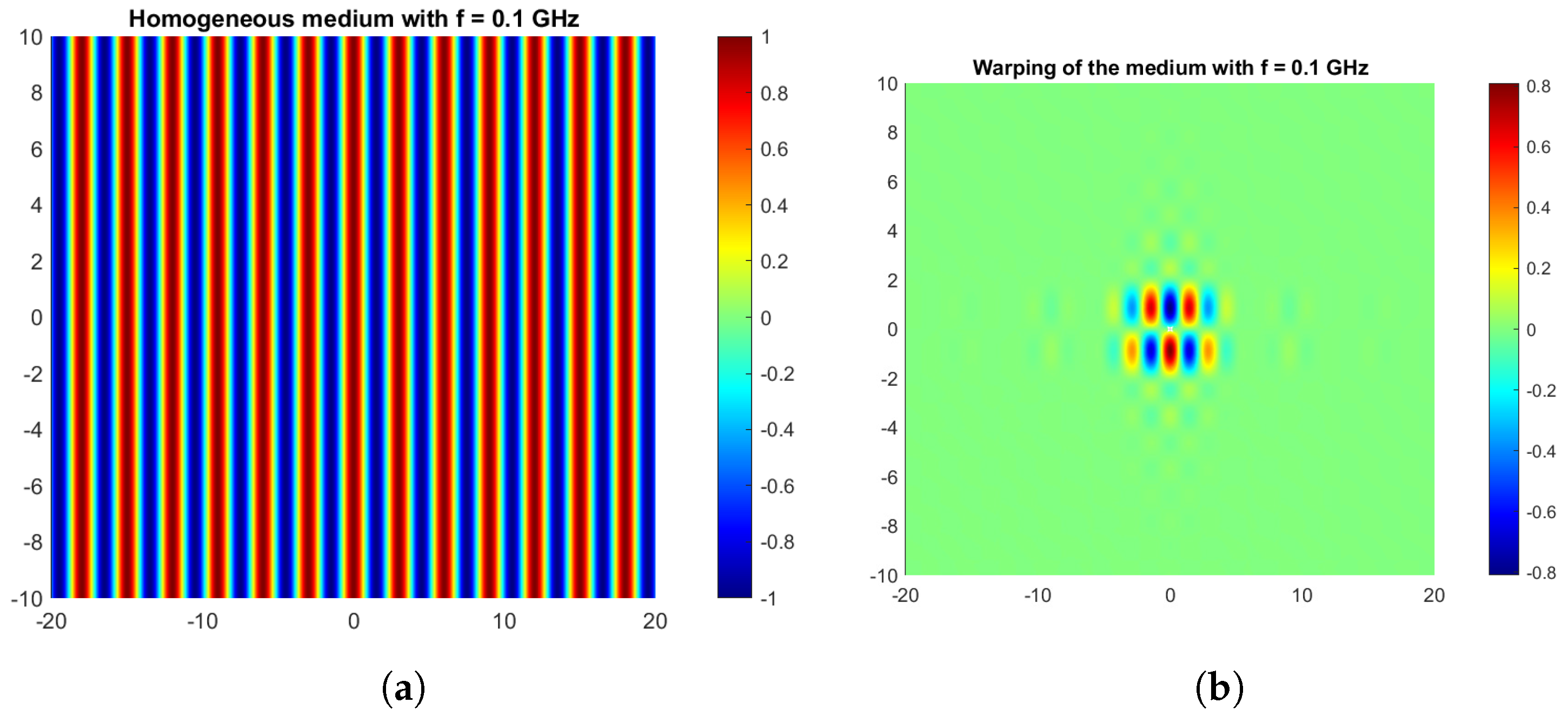
4.4. Propagation of the Fields along Their Geodesics in Inhomogeneous Materials
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Engelhart, D.P.; Plis, E.A.; Ferguson, D.; Johnston, W.R.; Cooper, R.; Hoffmann, R.C. Space plasma interactions with spacecraft materials. In Plasma Science and Technology-Basic Fundamentals and Modern Applications; IntechOpen: London, UK, 2019; pp. 225–245. [Google Scholar] [CrossRef]
- Ferguson, D.C.; Vayner, B.V.; Galofaro, J.T.; Hillard, G.; Vaughn, J.; Schneider, T. NASA GRC and MSFC Space Plasma Arc Testing Procedures. IEEE Trans. Plasma Sci. 2006, 34, 1948–1958. [Google Scholar] [CrossRef]
- Koons, H.C.; Mazur, J.E.; Selesnick, R.S.; Blake, J.B.; Fennell, J.F.; Roeder, J.L.; Anderson, P.C. The Impact of the Space Environment on Space Systems. In Space and Environment Technology Center Technology Operations. 1999. Available online: https://apps.dtic.mil/sti/pdfs/ADA376872.pdf (accessed on 10 June 2024).
- Monnereau, N.; Caignet, F.; Tremouilles, D.; Nolhier, N.; Bafleur, M. A System Level Electrostatic-Discharge-Protection Modeling Methodology for Time-Domain Analysis. IEEE Trans. Electromagn. Compat. 2013, 55, 45–57. [Google Scholar] [CrossRef]
- Fennell, J.R.; Koons, H.C.; Roeder, J.L.; Blake, J.B. Spacecraft Charging: Observations and Relationship to Satellite Anomalies. In Proceedings of the 7th International SCTC, Noordwijk, The Netherlands, 23–27 April 2001. [Google Scholar]
- Fredrickson, A.R.; Holeman, E.G.; Mullen, E.G. Characteristics of Spontaneous Electrical Discharges of Various Insulators in Space Radiation. IEEE Trans. Nucl. Sci. 1992, 39, 1773–1782. [Google Scholar] [CrossRef]
- Garrett, H.B. The Charging of Spacecraft Surfaces. Rev. Geophys. Space Phys. 1981, 19, 577–616. [Google Scholar] [CrossRef]
- Garrett, H.B.; Whittlesey, A.C. Spacecraft Charging-An Update, AIAA 96-0143. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996. [Google Scholar]
- Katz, I. Current Collection by High-Voltage Spacecraft, in The Behaviour of Systems in the Space Environment. In Proceeding NATO Advanced Study Institute 245; DeWitt, R.N., Duston, D., Hyder, A.K., Eds.; Kluwer Academic Publishers: Norwell, MA, USA, 1993; pp. 713–730. [Google Scholar]
- Liemohn, H. Single Event Upset of Spacecraft Electronics. In Proceedings of the Spacecraft Anomalies Conference, NOAA, San Francisco, CA, USA, 24–26 January 1984. [Google Scholar]
- Samir, U.; Wrenn, G.L. The Dependence of Charge and Potential Distribution Around a Spacecraft on Ionic Composition. Planet Space Sci. 1969, 17, 693. [Google Scholar] [CrossRef]
- Greason, W.D. Analysis of the Charge Discharge Processes for the Basic ESD Models. IEEE IAS 1993, 29, 887–895. [Google Scholar] [CrossRef]
- Honda, M. Impulsive Fields Generated by Low-Voltage ESD. In Proceedings of the Conference Record of the 1991 IEEE Industry Applications Society Annual Meeting, Dearborn, MI, USA, 28 September–4 October 1991; Volume I, pp. 577–580. [Google Scholar]
- Wilson, F.P.; Ma, M.T. Field radiated by electrostatic discharges. IEEE Tran. EMC 1991, 33, 10–18. [Google Scholar] [CrossRef]
- Huang, J. Measurement of transient electromagnetic field radiated by electrostatic discharge. In Proceedings of the 1999 IEEE AUTOTESTCON’99 (Proceedings), San Antonio, TX, USA, 30 August–2 September 1999; pp. 265–268. [Google Scholar]
- Pommerenke, D. ESD: Transient fields arc simulation and rise time limit. J. Electrost. 1995, 36, 31–54. [Google Scholar] [CrossRef]
- Mukund, P.R.; Omid, B. Electromagnetic Interference and Compatibility, and Electrostatic Discharge. In Spacecraft Power Systems; CRC Press: Boca Raton, FL, USA, 2023; pp. 231–243. [Google Scholar]
- Song, B.-P.; Zhou, R.D.; Yang, X.; Zhang, S.; Yang, N.; Fang, J.Y.; Song, F.L.; Zhang, G.J. Surface electrostatic discharge of charged typical space materials induced by strong electromagnetic interference. J. Phys. D Appl. Phys. 2021, 54, 275002. [Google Scholar] [CrossRef]
- Lu, W.; Guan, H. Multi-functional electromagnetic interference (EMI) shielding materials. In Electromagnetic Wave Absorption and Shielding Materials; CRC Press: Boca Raton, FL, USA, 2024; pp. 267–315. [Google Scholar]
- Chung, D.D.L. Materials for electromagnetic interference shielding. Mater. Chem. Phys. 2020, 255, 123587. [Google Scholar] [CrossRef]
- Hong, J.; Xu, P. Electromagnetic Interference Shielding Anisotropy of Unidirectional CFRP Composites. Materials 2021, 14, 1907. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Y. Modeling Study of Power-On and Power-Off System-Level Electrostatic Discharge Protection. IEEE Trans. Electromagn. Compat. 2021, 63, 979–987. [Google Scholar] [CrossRef]
- Liu, J.; Yu, M.-Y.; Yu, Z.-Z.; Nicolosi, V. Design and advanced manufacturing of electromagnetic interference shielding materials. Mater. Today 2023, 66, 245–272. [Google Scholar] [CrossRef]
- Smallwood, J.M. Electrostatic discharge charge transfer measurements in electrostatic hazard evaluation. J. Electrost. 2023, 125, 103817. [Google Scholar] [CrossRef]
- Nguyen, Q.-D.; Choi, C.-G. Recent advances in multifunctional electromagnetic interference shielding materials. Heliyon 2024, 10, e31118. [Google Scholar] [CrossRef] [PubMed]
- Wolf, K.F.J.; Daout, B. Alternative test set-up for testing the immunity of spacecraft equipment against discharge of electrostatic energy (ESD). IEEE Electromagn. Compat. Mag. 2020, 9, 69–76. [Google Scholar] [CrossRef]
- Bagotia, N. Electromagnetic (EM radiation) interference shielding material epicenter to carbon filler-based composite. Adv. Radiat. Shield. Mater. 2024, 9, 155–194. [Google Scholar]
- Gittleman, J.I.; Abeles, B. Comparison of the Effective Medium and the Maxwell-Garnett Predictions for the Di electric Constants of Granular Metals. Phys. Rev. B 1977, 15, 3273–3275. [Google Scholar] [CrossRef]
- Davis, V.A.; Schwartz, L. Electromagnetic Propagation in Close-packed Disordered Suspensions. Phys. Rev. B 1985, 31, 5155–5165. [Google Scholar] [CrossRef]
- Geigenmuller, U.; Mazur, P. The Effective Dielectric Constant of a Dispersion of Spheres. Phys. A 1986, 136, 316–369. [Google Scholar] [CrossRef]
- Claro, F.; Rojas, R. Correlation and Multipolar Effects in the Dielectric Response of Particulate Matter: An Iterative Mean-field Theory. Phys. Rev. B 1991, 43, 6369–6375. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Macedo, P.B.; Resca, L. Analytic Approach to the Interfacial Polarization of Heterogeneous Systems. Phys. Rev. B 1993, 47, 13818–13829. [Google Scholar] [CrossRef]
- Mackay, T.G.; Lakhtakia, A.; Weiglhofer, W.S. Third-order Implementation and Convergence of the Strong-property-fluctuation Theory in Electromagnetic Homogenization. Phys. Rev. E 2001, 64, 066616. [Google Scholar] [CrossRef]
- Cheng, H.; Torquato, S. Electric-field fluctuations in random dielectric composites. Phys. Rev. B Solid State 1997, 56, 8060–8068. [Google Scholar] [CrossRef]
- Alexopoulos, A. Second-order interactions in a medium containing perfect-conducting hyperspherical inclusions. J. Phys. A Math. Gen. 2004, 37, 11911–11933. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in Metal Glasses and in Metallic Films. Philos. Trans. R. Soc. Lond. Ser. A 1904, 203, 385–420. [Google Scholar]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef]
- Greenleaf, A.; Kurylev, Y.; Lassas, M.; Uhlmann, G. Electromagnetic worm holes and virtual magnetic monopoles from metamaterials. Phys. Rev. Lett. 2007, 99, 183901. [Google Scholar] [CrossRef]
- Chen, H.Y.; Miao, R.X.; Li, M. Transformation optics that mimics the system outside a schwarzschild black hole. Opt. Express 2010, 18, 15183–15188. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smithand, D.R.; Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U.; Philbin, T.G. Transformation optics and the geometry of light. Prog. Opt. 2009, 53, 69–152. [Google Scholar]
- Smith, D.R.; Schurig, S. Electromagnetic wave propagation in media with indefinite permittivity and permeability tensors. Phys. Rev. Lett. 2003, 90, 077405. [Google Scholar] [CrossRef] [PubMed]
- Available online: www.comsol.com (accessed on 20 July 2024).
- Available online: https://altair.com/feko (accessed on 20 July 2024).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexopoulos, A.; Neudegg, D. Methods for Controlling Electrostatic Discharge and Electromagnetic Interference in Materials. Foundations 2024, 4, 376-410. https://doi.org/10.3390/foundations4030025
Alexopoulos A, Neudegg D. Methods for Controlling Electrostatic Discharge and Electromagnetic Interference in Materials. Foundations. 2024; 4(3):376-410. https://doi.org/10.3390/foundations4030025
Chicago/Turabian StyleAlexopoulos, Aris, and David Neudegg. 2024. "Methods for Controlling Electrostatic Discharge and Electromagnetic Interference in Materials" Foundations 4, no. 3: 376-410. https://doi.org/10.3390/foundations4030025
APA StyleAlexopoulos, A., & Neudegg, D. (2024). Methods for Controlling Electrostatic Discharge and Electromagnetic Interference in Materials. Foundations, 4(3), 376-410. https://doi.org/10.3390/foundations4030025




