An Image-Processing Tool for Size and Shape Analysis of Manufactured Irregular Polyethylene Microparticles
Abstract
1. Introduction
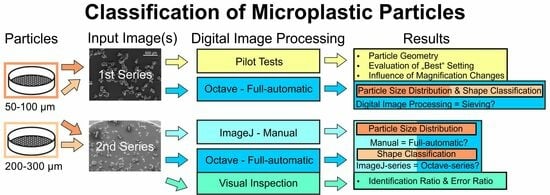
2. Materials and Methods
2.1. Materials and Sample Preparation
2.2. Scanning Electron Microscopy
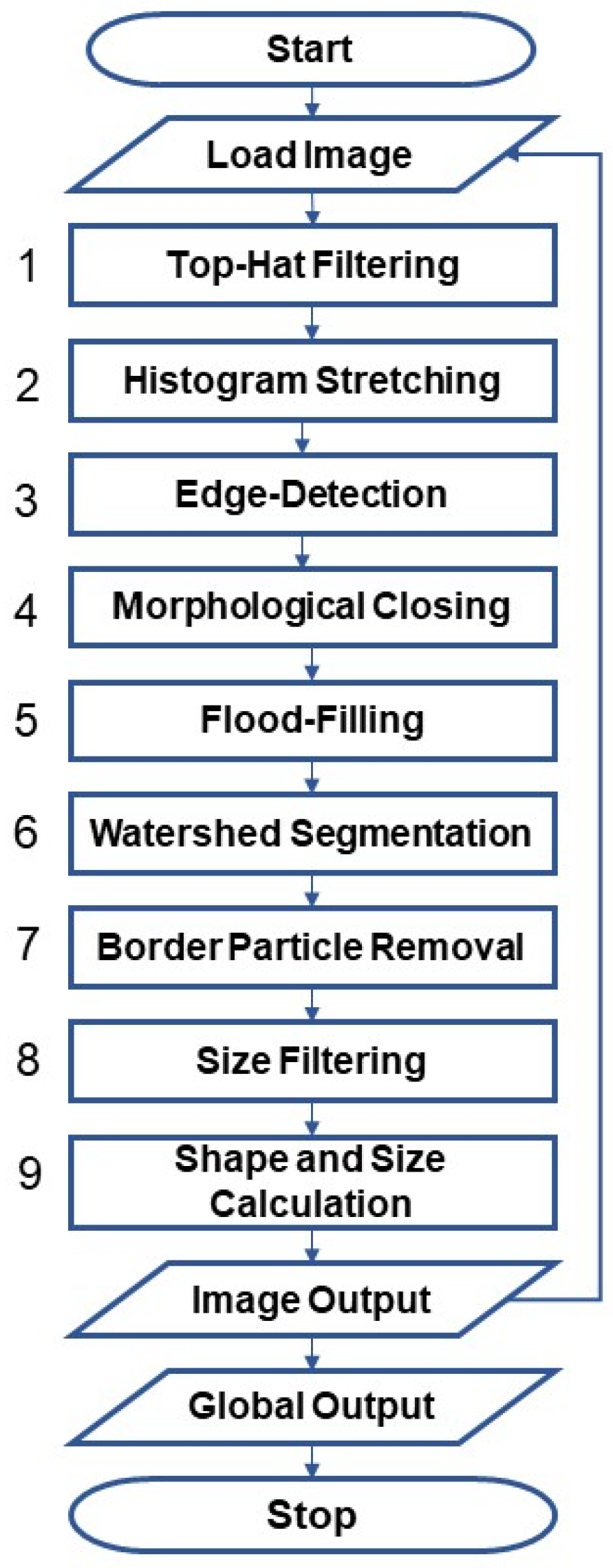
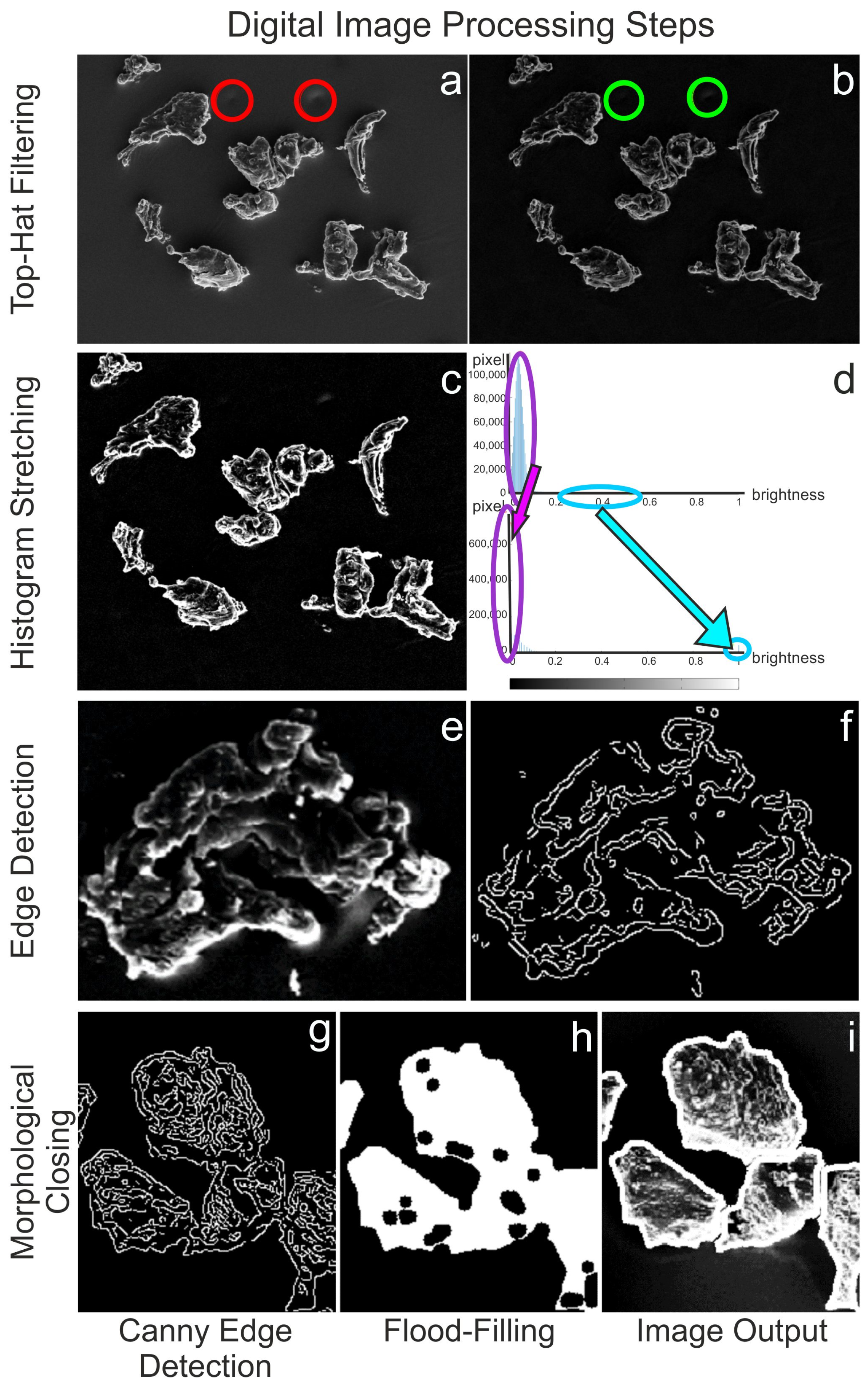
2.3. Software and Digital Image Processing (DIP)
2.4. Implemented Formula
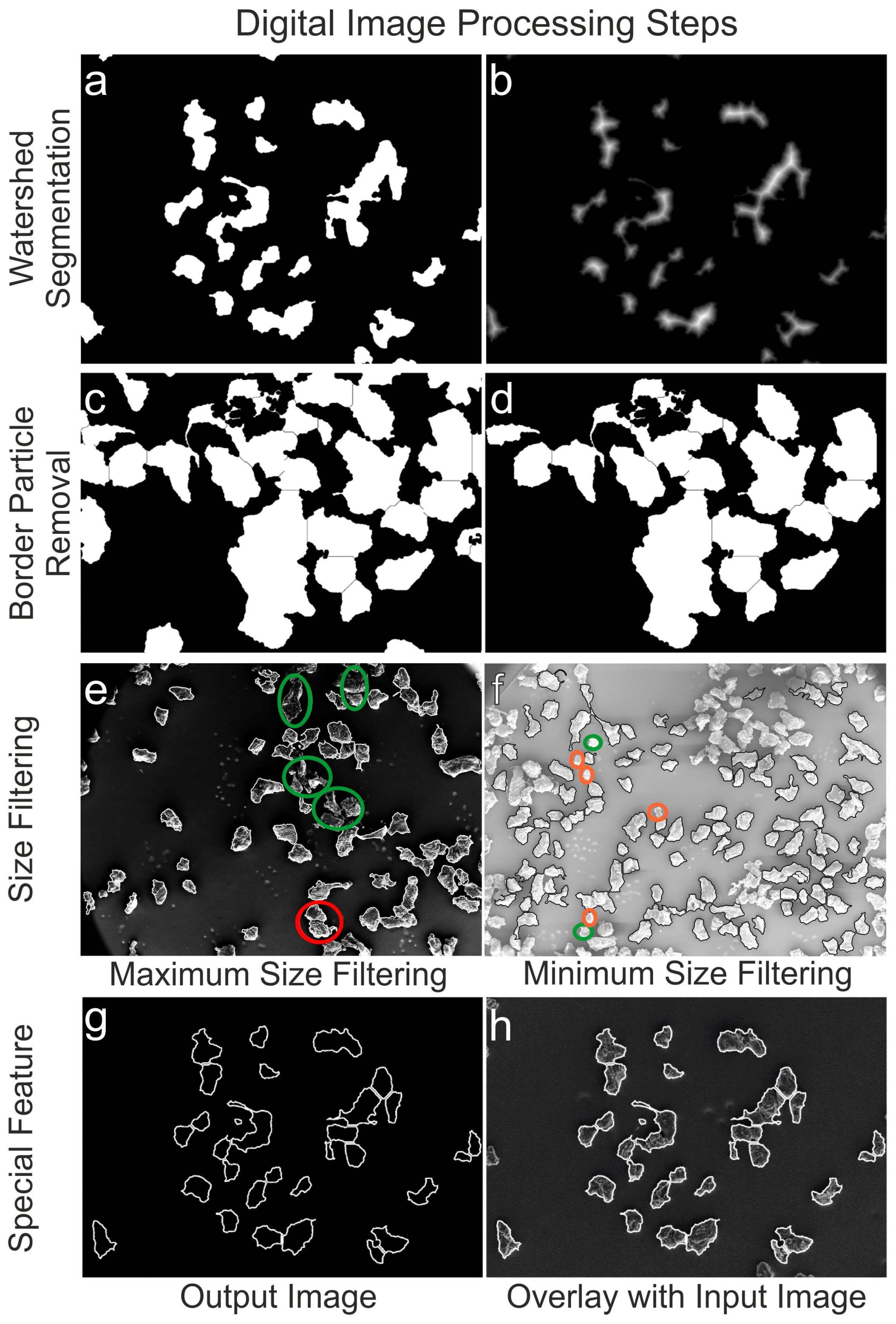
2.4.1. Watershed Segmentation
2.4.2. Particles and Sieve Pores
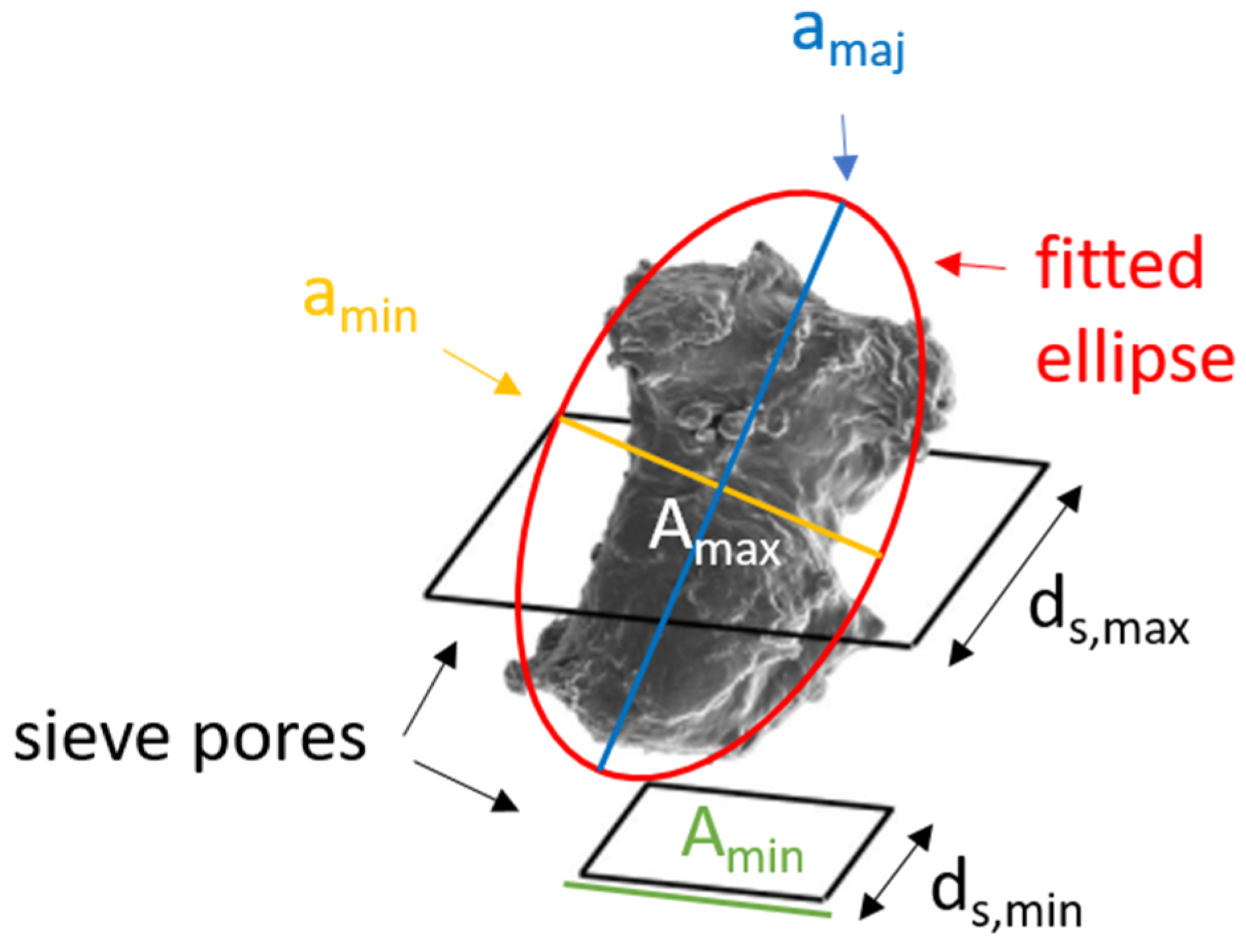
2.4.3. Particle Size Determination
2.4.4. Particle Shape Analysis
3. Results and Discussion
3.1. Pilot Testing
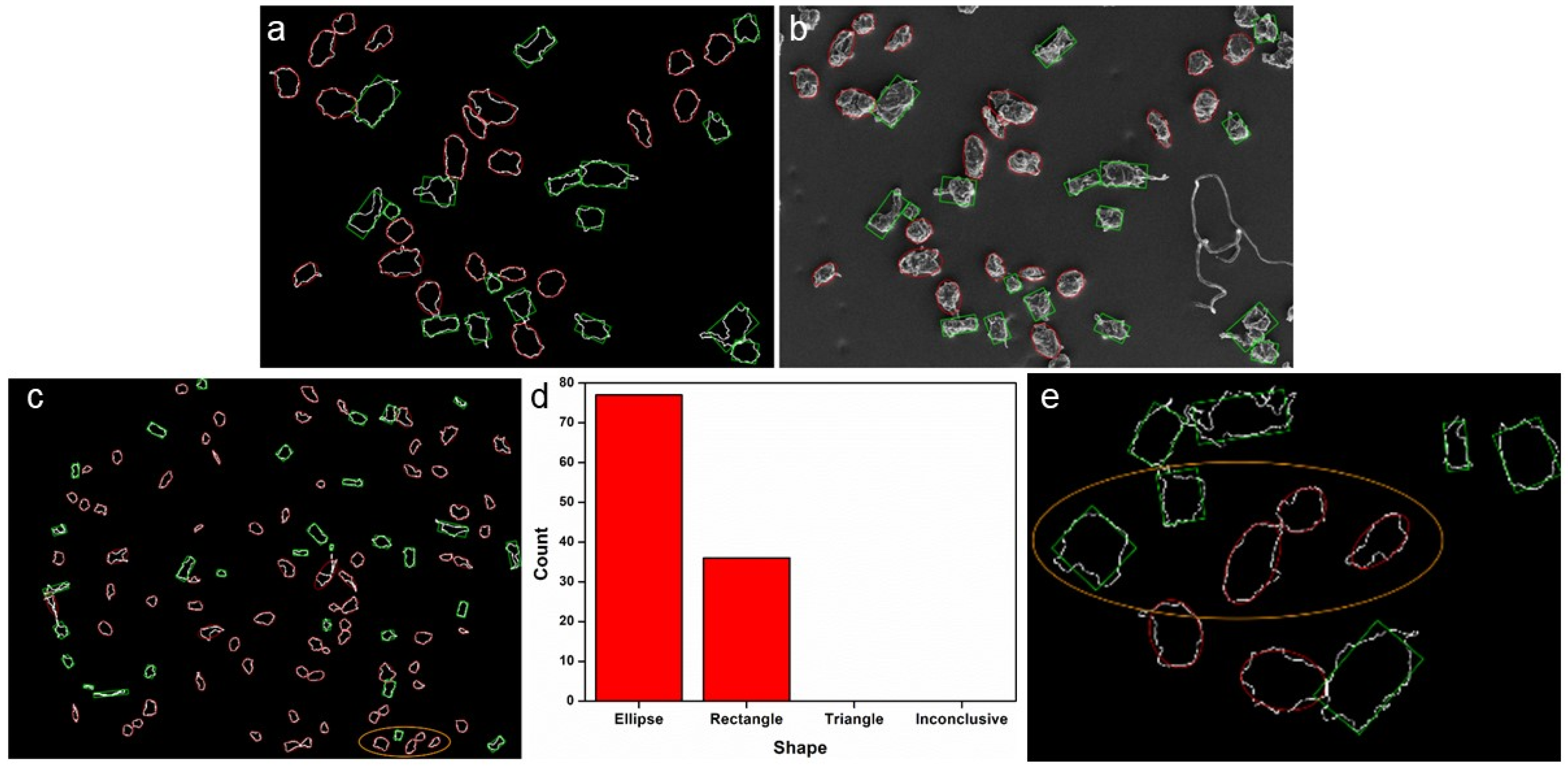
3.1.1. Particle Geometry
3.1.2. Evaluation of “Best” Setting
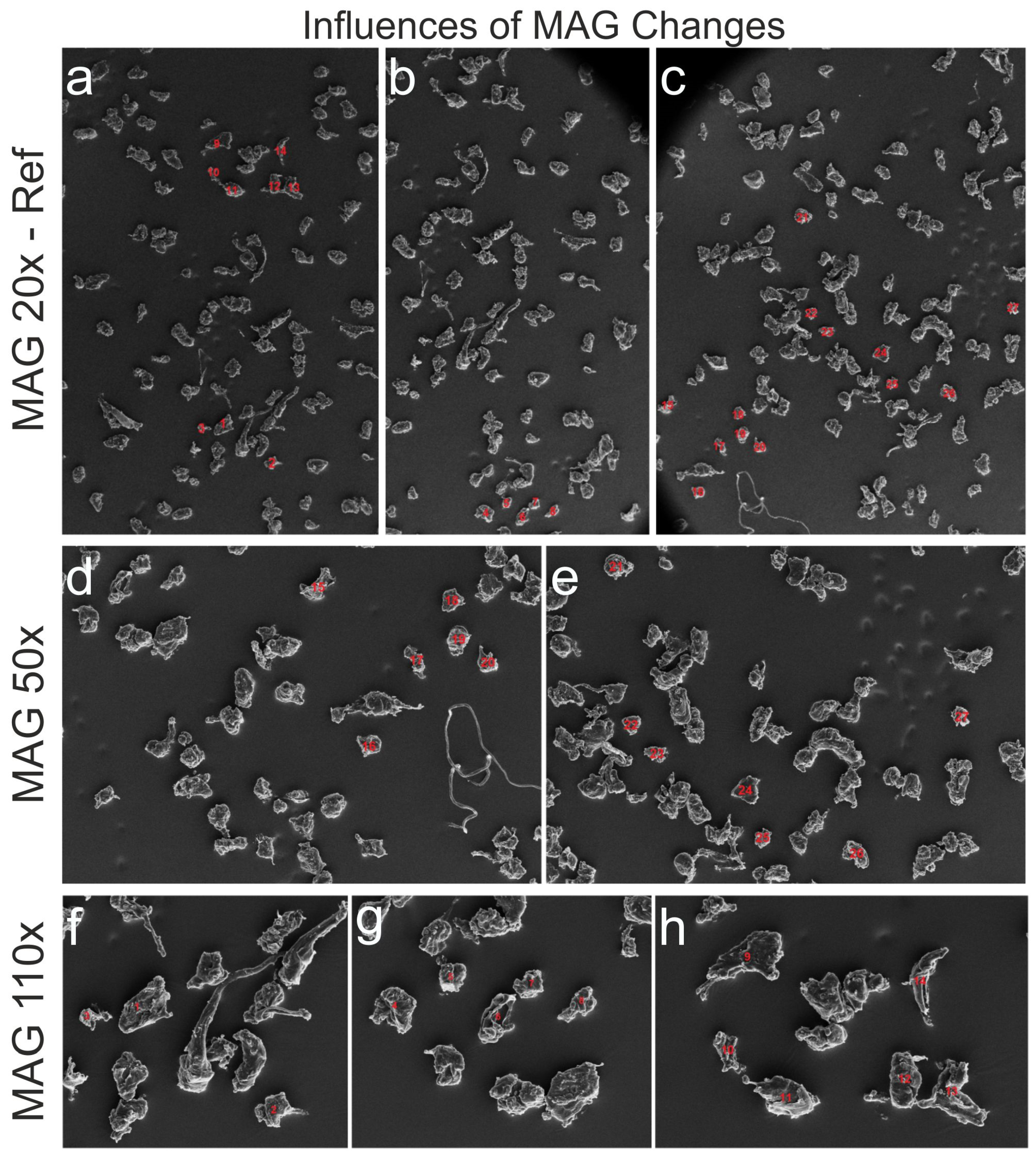
3.1.3. Influences of Magnification Changes
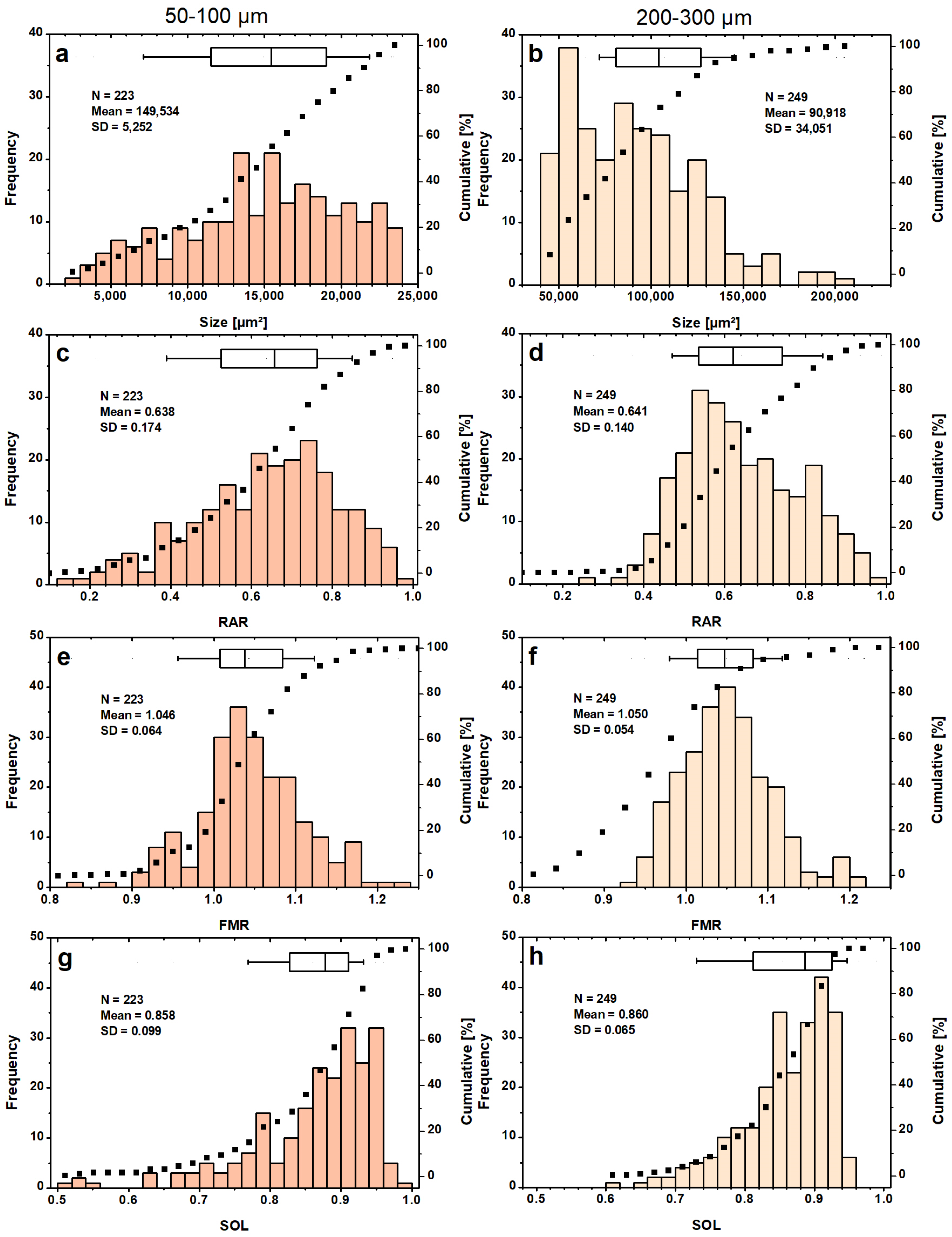
3.2. PSDs and Shape Classification for the 1st Series of Known Sieve Fractions
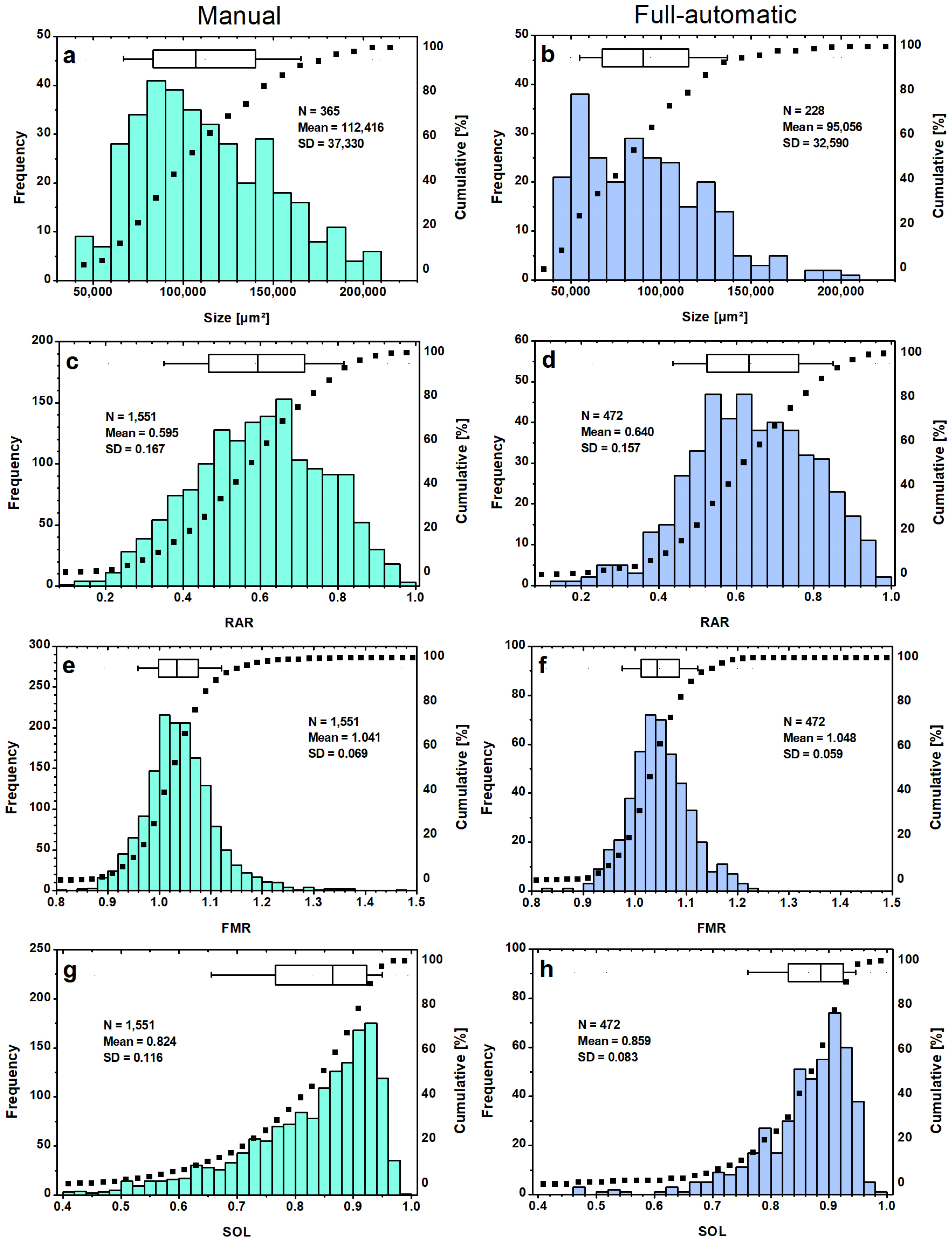
3.3. Evaluation of the Same Sieve Fraction Full-Automatic and Manual
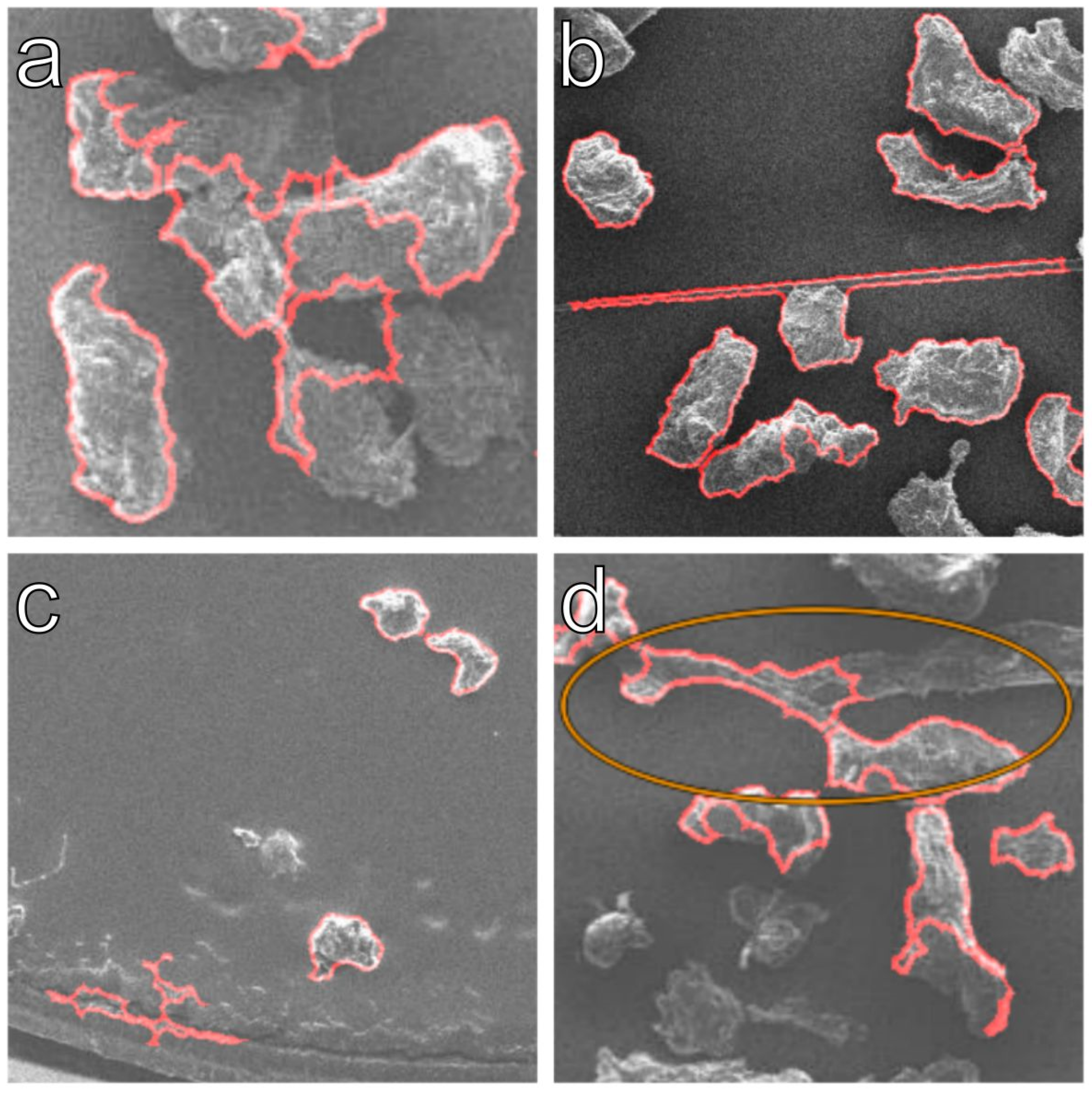
3.4. Visual Inspection of Fully Automatic Analyzed Image Series
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gigault, J.; ter Halle, A.; Baudrimont, M.; Pascal, P.-Y.; Gauffre, F.; Phi, T.-L.; El Hadri, H.; Grassl, B.; Reynaud, S. Current opinion: What is a nanoplastics? Environ. Pollut. 2018, 235, 1030–1034. [Google Scholar] [CrossRef] [PubMed]
- Blair, R.M.; Waldron, S.; Phoenix, V.; Gauchotte-Lindsay, C. Micro- and Nanoplastic Pollution of Freshwater and Wastewater Treatment Systems. Springer Sci. Rev. 2017, 5, 19–30. [Google Scholar] [CrossRef]
- Sharma, S.; Chatterjee, S. Microplastic pollution, a threat to marine ecosystem and human health: A short review. Environ. Sci. Pollut. Res. 2017, 24, 21530–21547. [Google Scholar] [CrossRef] [PubMed]
- Haegerbaeumer, A.; Mueller, M.T.; Fueser, H.; Traunspurger, W. Impacts of micro- and nano-sized plastic particles on benthic invertebrates: A literature review and gap analysis. Front. Environ. Sci. 2019, 7, 17. [Google Scholar] [CrossRef]
- Gebhardt, C.; Forster, S. Size-selective feeding of Arenicola marina promotes long-term burial of microplastic particles in marine sediments. Environ. Pollut. 2018, 242, 1777–1786. [Google Scholar] [CrossRef] [PubMed]
- Wegner, A.; Besseling, E.; Foekema, E.M.; Kamermans, K.; Koelmans, A.A. Effects of nanopolystyrene on the feeding behavior of the blue mussel (Mytilus edulis L.). Environ. Toxicol. Chem. 2012, 31, 2490–2497. [Google Scholar] [CrossRef] [PubMed]
- Vroom, R.J.E.; Koelmans, A.A.; Besseling, E.; Halsband, C. Aging of microplastics promotes their ingestion by marine. Environ. Pollut. 2017, 231, 987–996. [Google Scholar] [CrossRef]
- Foster, K.A.; Yazdanian, M.; Audus, K.L. Microparticulate uptake mechanisms of in-vitro cell culture models of the respiratory epithelium. J. Pharm. Pharmacol. 2001, 53, 57–66. [Google Scholar] [CrossRef]
- Kwon, W.; Kim, D.; Kim, H.-Y.; Jeong, S.W.; Lee, S.-G.; Kim, H.-C.; Lee, Y.-J.; Kwon, M.K.; Hwang, J.-S.; Han, J.E.; et al. Microglial phagocytosis of polystyrene microplastics results in immune alteration and apoptosis in vitro and in vivo. Sci. Total Environ. 2022, 807, 150817. [Google Scholar] [CrossRef]
- Ragusa, A.; Svelato, A.; Santacroce, C.; Catalano, P.; Notarstefano, V.; Carnevali, O.; Papa, F.; Rongioletti, M.C.A.; Baiocco, F.; Draghi, S.; et al. Plasticenta: First evidence of microplastics in human placenta. Environ. Int. 2021, 146, 106274. [Google Scholar] [CrossRef]
- Frère, L.; Paul-Pont, I.; Moreau, J.; Soudant, P.; Lambert, C.; Huvet, A.; Rinnert, E. A semi-automated Raman micro-spectroscopy method for morphological and chemical characterizations of microplastic litter. Mar. Pollut. Bull. 2016, 113, 461–468. [Google Scholar] [CrossRef]
- Anger, P.M.; von der Esch, E.; Baumann, T.; Elsner, M.; Niessner, R.; Ivleva, N.P. Raman microspectroscopy as a tool for microplastic particle analysis. TrAC Trends Anal. Chem. 2018, 109, 214–226. [Google Scholar] [CrossRef]
- Löder, M.G.J.; Kuczera, M.; Mintenig, S.; Lorenz, C.; Gerdts, G. Focal plane array detector-based micro-Fourier-transform infrared imaging for the analysis of microplastics in environmental samples. Environ. Chem. 2015, 12, 563–581. [Google Scholar] [CrossRef]
- Löder, M.G.J.; Gerdts, G. Methodology Used for the Detection and Identification of Microplastics—A Critical Appraisal. In Marine Anthropogenic Litter; Bergmann, M., Gutow, L., Klages, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 201–227. [Google Scholar] [CrossRef]
- Primpke, S.; Wirth, M.; Lorenz, C.; Gerdts, G. Reference database design for the automated analysis of microplastic samples based on Fourier transform infrared (FTIR) spectroscopy. Anal. Bioanal. Chem. 2018, 410, 5131–5141. [Google Scholar] [CrossRef] [PubMed]
- Mintenig, S.M.; Bäuerlein, P.S.; Koelmans, A.A.; Dekker, S.C.; Van Wezel, A.P. Closing the gap between small and smaller: Towards a framework to analyse nano- and microplastics in aqueous environmental samples. Environ. Sci. Nano 2018, 5, 1640–1649. [Google Scholar] [CrossRef]
- Peez, N.; Janiska, M.C.; Imhof, W. The first application of quantitative 1H NMR spectroscopy as a simple and fast method of identification and quantification of microplastic particles (PE, PET, and PS). Anal. Bioanal. Chem. 2019, 411, 823–833. [Google Scholar] [CrossRef] [PubMed]
- Peez, N.; Becker, J.; Ehlers, S.M.; Fritz, M.; Fischer, C.B.; Koop, J.H.E.; Winkelmann, C.; Imhof, W. Quantitative analysis of PET microplastics in environmental model samples using quantitative 1H-NMR spectroscopy: Validation of an optimized and consistent sample clean-up method. Anal. Bioanal. Chem. 2019, 411, 7409–7418, Erratum in Anal. Bioanal. Chem. 2019, 411, 7603. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez Chialanza, M.; Sierra, I.; Pérez Parada, A.; Fornaro, F. Identification and quantitation of semi-crystalline microplastics using image analysis and differential scanning calorimetry. Environ. Sci. Pollut. Res. 2018, 25, 16767–16775. [Google Scholar] [CrossRef] [PubMed]
- Elert, A.M.; Becker, R.; Duemichen, E.; Eisentraut, P.; Falkenhagen, J.; Sturm, H.; Braun, U. Comparison of different methods for MP detection: What can we learn from them, and why asking the right question before measurements matters? Environ. Pollut. 2017, 231, 1256–1264. [Google Scholar] [CrossRef]
- Stock, F.; Kochleus, C.; Bänsch-Baltruschat, B.; Brennholt, N.; Reifferscheid, G. Sampling techniques and preparation methods for microplastic analyses in the aquatic environment—A review. TrAC Trends Anal. Chem. 2019, 113, 84–92. [Google Scholar] [CrossRef]
- Hidalgo-Ruz, V.; Gutow, L.; Thompson, R.C.; Thiel, M. Microplastics in the marine environment: A review of the methods used for identification and quantification. Environ. Sci. Technol. 2012, 46, 3060–3075. [Google Scholar] [CrossRef] [PubMed]
- Koelmans, A.A.; Nor, N.H.M.; Hermsen, E.; Kooi, M.; Mintenig, S.M.; De France, J. Microplastics in freshwaters and drinking water: Critical review and assessment of data quality. Water Res. 2019, 155, 410–422. [Google Scholar] [CrossRef] [PubMed]
- Uurasjärvi, E.; Hartikainen, S.; Setälä, O.; Lehtiniemi, M.; Koistinen, A. Microplastic concentrations, size distribution, and polymer types in the surface waters of a northern European lake. Water Environ. Res. 2020, 92, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Conkle, J.L.; Báez Del Valle, C.D.; Turner, J.W. Are We Underestimating Microplastic Contamination in Aquatic Environments? Environ. Manag. 2018, 61, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Hanvey, J.S.; Lewis, P.J.; Lavers, J.L.; Crosbie, N.D.; Pozo, K.; Clarke, B.O. A review of analytical techniques for quantifying microplastics in sediments. Anal. Methods 2017, 9, 1369–1383. [Google Scholar] [CrossRef]
- Wills, B.A.; Finch, J.A. Particle Size Analysis. In Wills’ Mineral Processing Technology—An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery, 8th ed.; Wills, B.A., Finch, J.A., Eds.; Butterworth-Heinemann: Boston, MA, USA, 2016; pp. 91–107. [Google Scholar] [CrossRef]
- Buhr, E.; Senftleben, N.; Klein, T.; Bergmann, D.; Gnieser, D.; Frase, C.G.; Bosse, H. Characterization of nanoparticles by scanning electron microscopy in transmission mode. Meas. Sci. Technol. 2009, 20, 084025. [Google Scholar] [CrossRef]
- Peregrina-Barreto, H.; Terol-Villalobos, I.R.; Rangel-Magdaleno, J.J.; Herrera-Navarro, A.M.; Morales-Hernández, L.A.; Manríquez-Guerrero, F. Automatic grain size determination in microstructures using image processing. Measurement 2013, 46, 249–258. [Google Scholar] [CrossRef]
- Wang, Z.-M.; Wagner, J.; Ghosal, S.; Bedi, G.; Wall, S. SEM/EDS and optical microscopy analyses of microplastics in ocean trawl and fish guts. Sci. Total Environ. 2017, 603–604, 616–626. [Google Scholar] [CrossRef]
- Shanthi, C.; Kingsley Porpatham, R.; Pappa, N. Image analysis for particle size distribution. Int. J. Eng. Technol. 2014, 6, 1340–1345. [Google Scholar]
- Altuhafi, F.; O’Sullivan, C.; Cavarretta, I. Analysis of an Image-Based Method to Quantify the Size and Shape of Sand Particles. J. Geotech. Geoenvironmental Eng. 2013, 139, 1290–1307. [Google Scholar] [CrossRef]
- Chen, S.; Li, Y.; Mawhorte, C.; Legoski, S. Quantification of microplastics by count, size and morphology in beverage containers using Nile Red and ImageJ. J. Water Health 2020, 19, 79–88. [Google Scholar] [CrossRef]
- Girão, A.V. SEM/EDS and Optical Microscopy Analysis of Microplastics. In Handbook of Microplastics in the Environment; Rocha-Santos, T., Costa, M., Mouneyrac, C., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 1–22. [Google Scholar] [CrossRef]
- Cabernard, L.; Roscher, L.; Lorenz, C.; Gerdts, G.; Primpke, S. Comparison of Raman and Fourier Transform Infrared Spectroscopy for the Quantification of Microplastics in the Aquatic Environment. Environ. Sci. Technol. 2018, 52, 13279–13288. [Google Scholar] [CrossRef] [PubMed]
- Igathinathane, C.; Pordesimo, L.O.; Columbus, E.P.; Batchelor, W.D.; Methuku, S.R. Shape identification and particles size distribution from basic shape parameters using ImageJ. Comput. Electron. Agric. 2008, 3, 168–182. [Google Scholar] [CrossRef]
- Moaveni, M.; Wang, S.; Hart, J.M.; Tutumluer, E.; Ahuja, N. Evaluation of Aggregate Size and Shape by Means of Segmentation Techniques and Aggregate Image Processing Algorithms. Transp. Res. Rec. 2013, 2335, 50–59. [Google Scholar] [CrossRef]
- Olson, E.W. Particle Shape Factors and Their Use in Image Analysis—Part 1: Theory. J. GXP Compliance 2011, 15, 85–96. [Google Scholar]
- Damadipour, M.; Nazarpour, M.; Alami, M.T. Evaluation of Particle Size Distribution Using an Efficient Approach Based on Image Processing Techniques. Iran J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 429–441. [Google Scholar] [CrossRef]
- Kooi, M.; Koelmans, A. Simplifying Microplastic via Continuous Probability Distributions for Size, Shape, and Density. Environ. Sci. Technol. Lett. 2019, 6, 551–557. [Google Scholar] [CrossRef]
- Moura, D.S.; Pestana, C.J.; Moffat, C.F.; Hui, J.; Irvine, J.T.S.; Lawton, L. Characterisation of microplastics is key for reliable data interpretation. Chemosphere 2023, 331, 138691. [Google Scholar] [CrossRef]
- Brandt, J.; Fischer, F.; Kanaki, E.; Enders, K.; Labrenz, M.; Fischer, D. Assessment of Subsampling Strategies in Microspectroscopy of Environmental Microplastic Samples. Front. Environ. Sci. 2021, 8, 579676. [Google Scholar] [CrossRef]
- Valsesia, A.; Parot, J.; Ponti, J.; Mehn, D.; Marino, R.; Melillo, D.; Muramoto, S.; Verkouteren, M.; Hackley, V.A.; Colpo, P. Detection, counting and characterization of nanoplastics in marine bioindicators: A proof of principle study. Micropl. Nanopl. 2021, 1, 5. [Google Scholar] [CrossRef]
- Le, T.-T.; Miclet, D.; Heritier, P.; Piron, E.; Chateauneuf, A.; Berducat, M. Morphology characterization of irregular particles using image analysis. Application to solid inorganic fertilizers. Comput. Electron. Agric. 2018, 147, 146–157. [Google Scholar] [CrossRef]
- Hajihashemi, M.R.; Jiang, H. Gaussian random ellipsoid geometry-based morphometric recovery of irregular particles using light scattering spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 2013, 11, 886–895. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sun, H.Q.; Luo, Y.J. Adaptive watershed segmentation of binary particle image. J. Microsc. 2009, 233, 326–330. [Google Scholar] [CrossRef] [PubMed]
- Kwon, D.; Yeom, E. Shape evaluation of highly overlapped powder grains using U-Net-based deep learning segmentation network. J. Vis. 2021, 24, 931–942. [Google Scholar] [CrossRef]
- Ivleva, N.P. Chemical Analysis of Microplastics and Nanoplastics: Challenges, Advanced Methods, and Perspectives. Chem. Rev. 2021, 121, 11886–11936. [Google Scholar] [CrossRef] [PubMed]
- Zarfl, C. Promising techniques and open challenges for microplastic identification and quantification in environmental matrices. Anal. Bioanal. Chem. 2019, 411, 3743–3756. [Google Scholar] [CrossRef] [PubMed]
- Schwaferts, C.; Schwaferts, P.; von der Esch, E.; Elsner, M.; Ivleva, N.P. Which particles to select, and if yes, how many? Subsampling methods for Raman microspectroscopic analysis of very small microplastic. Anal. Bioanal. Chem. 2021, 413, 3625–3641. [Google Scholar] [CrossRef]
- Anger, P.M.; Prechtl, L.; Elsner, M.; Niessner, R.; Ivleva, N.P. Implementation of an open source algorithm for particle recognition and morphological characterisation for microplastic analysis by means of Raman microspectroscopy. Anal. Methods 2019, 11, 3483–3489. [Google Scholar] [CrossRef]
- Dąbrowska, A.; Mielańczuk, M.; Syczewski, M. The Raman spectroscopy and SEM/EDS investigation of the primary sources of microplastics from cosmetics available in Poland. Chemosphere 2022, 308, 136407. [Google Scholar] [CrossRef]
- Kefer, S.; Friedenauer, T.; Langowski, H.C. Characterisation of different manufactured plastic microparticles and their comparison to environmental microplastics. Powder Technol. 2022, 412, 117960. [Google Scholar] [CrossRef]
- Von Der Esch, E.; Kohles, A.J.; Anger, P.M.; Hoppe, R.; Niessner, R.; Elsner, M.; Ivleva, N.P. TUM-ParticleTyper: A detection and quantification tool for automated analysis of (microplastic) particles and fibers. PLoS ONE 2020, 15, e0234766. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, S.M.; Manz, W.; Koop, J.H.E. Microplastics of different characteristics are incorporated into the larval cases of the freshwater caddisfly Lepidostoma basale. Aquat. Biol. 2019, 28, 67–77. [Google Scholar] [CrossRef]
- Solomon, C.; Breckon, T. Fundamentals of Digital Image Processing: A Practical Approach with Examples in Matlab; Wiley-Blackwell: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- McAndrew, A. A Computational Introduction to Digital Image Processing, 2nd ed.; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jaglom, I.M.; Boltjanski, W.G. Convex Figures; Holt Rinehart and Winston: New York, NY, USA, 1961. [Google Scholar]
- Preparata, F.P.; Shamos, M.I. Computational Geometry: An Introduction; Springer: New York, NY, USA, 1985. [Google Scholar]
- Huang, Z.; Hu, B.; Wang, H. Analytical methods for microplastics in the environment: A review. Environ. Chem. Lett. 2023, 21, 383–401. [Google Scholar] [CrossRef] [PubMed]


| (i) LDPE Fractions < 300 µm, Mesh Size [µm] | (ii) LDPE Fractions < 800 µm, Mesh Size [µm] |
|---|---|
| >500 | |
| 400–500 | |
| >300 | 300–400 |
| 200–300 | 200–300 |
| 150–200 | 150–200 |
| 125–150 | 125–150 |
| 100–125 | 100–125 |
| 50–100 | 50–100 |
| 25–50 |
| Settings | Total Particles | Identified Particles | Total Errors | Identification Ratio [%] | Error Ratio [%] |
|---|---|---|---|---|---|
| A | 95 | 472 | 81 | 51.4 | 17.2 |
| B | 513 | 97 | 55.8 | 18.9 | |
| C | 409 | 76 | 44.5 | 18.6 | |
| D | 498 | 120 | 54.2 | 24.1 |
| Sample | MAG 20× (Baseline) | MAG 50× | MAG 110× |
|---|---|---|---|
| Mean A% [%] | −18.8 ± 1.9 | −15.0 ± 3.1 | −22.3 ± 1.8 |
| Std. dev. σ [%] | 9.8 | 11.3 | 6.7 |
| SEM-Image | (d) | (e) | (f) | (g) | (h) |
|---|---|---|---|---|---|
| Mean A% [%] | −24.2 ± 2.2 | −4.0 ± 2.0 | −24.6 ± 1.5 | −22.8 ± 4.2 | −19.9 ± 3.8 |
| Std. dev. σ [%] | 5.3 | 4.9 | 3.6 | 7.3 | 8.6 |
| Sieve Fractions [µm] | Total Particles | Identified Particles | Total Errors | Identification Ratio [%] | Error Ratio [%] |
|---|---|---|---|---|---|
| 125–150 | 396 | 166 | 43 | 41.9 | 25.9 |
| 150–200 A | 151 | 87 | 32 | 57.6 | 36.8 |
| 150–200 B | 219 | 133 | 39 | 60.7 | 29.3 |
| 200–300 | 270 | 137 | 44 | 50.7 | 32.1 |
| Sum | 1036 | 523 | 158 | 50.5 | 30.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fritz, M.; Deutsch, L.F.; Wijaya, K.P.; Götz, T.; Fischer, C.B. An Image-Processing Tool for Size and Shape Analysis of Manufactured Irregular Polyethylene Microparticles. Microplastics 2024, 3, 124-146. https://doi.org/10.3390/microplastics3010008
Fritz M, Deutsch LF, Wijaya KP, Götz T, Fischer CB. An Image-Processing Tool for Size and Shape Analysis of Manufactured Irregular Polyethylene Microparticles. Microplastics. 2024; 3(1):124-146. https://doi.org/10.3390/microplastics3010008
Chicago/Turabian StyleFritz, Melanie, Lukas F. Deutsch, Karunia Putra Wijaya, Thomas Götz, and Christian B. Fischer. 2024. "An Image-Processing Tool for Size and Shape Analysis of Manufactured Irregular Polyethylene Microparticles" Microplastics 3, no. 1: 124-146. https://doi.org/10.3390/microplastics3010008
APA StyleFritz, M., Deutsch, L. F., Wijaya, K. P., Götz, T., & Fischer, C. B. (2024). An Image-Processing Tool for Size and Shape Analysis of Manufactured Irregular Polyethylene Microparticles. Microplastics, 3(1), 124-146. https://doi.org/10.3390/microplastics3010008