1. Introduction
Many attempts have been made to derive gravitation from the electric force in order to simplify the theoretical foundations or predict new, previously unknown physical phenomena [
1,
2,
3]. However, none of these approaches have yet been accepted by the majority of the scientific community or have led to new technological applications [
4]. Gravitation and the electromagnetic force are therefore still considered different fundamental forces, particularly because gravitation is often not interpreted as a real force but instead is considered as a geometric effect of spacetime (e.g., [
5,
6,
7]).
This article presents a simple and intuitive hypothesis that requires only a few plausible assumptions and is based on the relational, non-relativistic electrodynamics used by engineers. Relational, in this context, means that force and acceleration of a point charge do not depend on the speed of an uninvolved observer, as in the theory of relativity, but are determined only by Galilean-invariant relational quantities between the source of the force and its recipient (The quantities (
4) and (
5) are purely relational, thus the force (
2) is also relational). It is inspired by an article by A. K. T. Assis published approximately three decades ago in the context of Weber electrodynamics [
8].
Because Weber electrodynamics was considered obsolete and did not appear to be compatible with Maxwell’s equations, insufficient attention was paid to Assis’ work. However, it is now known that the Weber force is the solution of Maxwell’s equations for sufficiently slow and uniformly moving point charges in the Galilean limit. This article revisits Assis’ concept and shows that both magnetism and gravitation might be interpreted in the same way as residual forces of the electric force.
The starting point comprises the four Maxwell equations, which have been considered valid since Maxwell’s time and are foundational to not only modern physics but also the physics used in electrical engineering. In electrical engineering, Maxwell’s equations have recently been found to be solvable for non-relativistic but otherwise arbitrarily moving point charges [
9]. The final result is a formula that is similar to the Coulomb force but clearly shows that the electric force always propagates at the speed of light
c between the two charges, regardless of the relative speed between them.
This solution to Maxwell’s equations for point charges is highly practical and enables many technical problems to be modeled quickly and inexpensively, because the use of relativity is avoided, and no differential equations must be solved [
10]. Potential applications include the propagation of electromagnetic waves as well as electromagnetic induction. In addition, phenomena of classical wave optics and even key experiments of quantum mechanics can be simulated, as previously demonstrated [
11]. That article and the present study demonstrate that the solution to Maxwell’s equations for point charges provides a new, largely unexplored and innovative approach to interpret a broad spectrum of physical phenomena.
The solution to Maxwell’s equations for point charges contains terms representing the time delay for the propagation of the electromagnetic force. However, point charges are often so close to one another that the trajectories of the point charges in this short period of time are nearly linear. In this case, the general formula [
9] for the electromagnetic force
can be simplified, thus yielding the approximation
Here,
is the Coulomb force, and
is a direction-dependent Lorentz factor, which, like the usual Lorentz factor
, depends on the ratio
. However,
is additionally dependent on the angle
between
and
, because
.
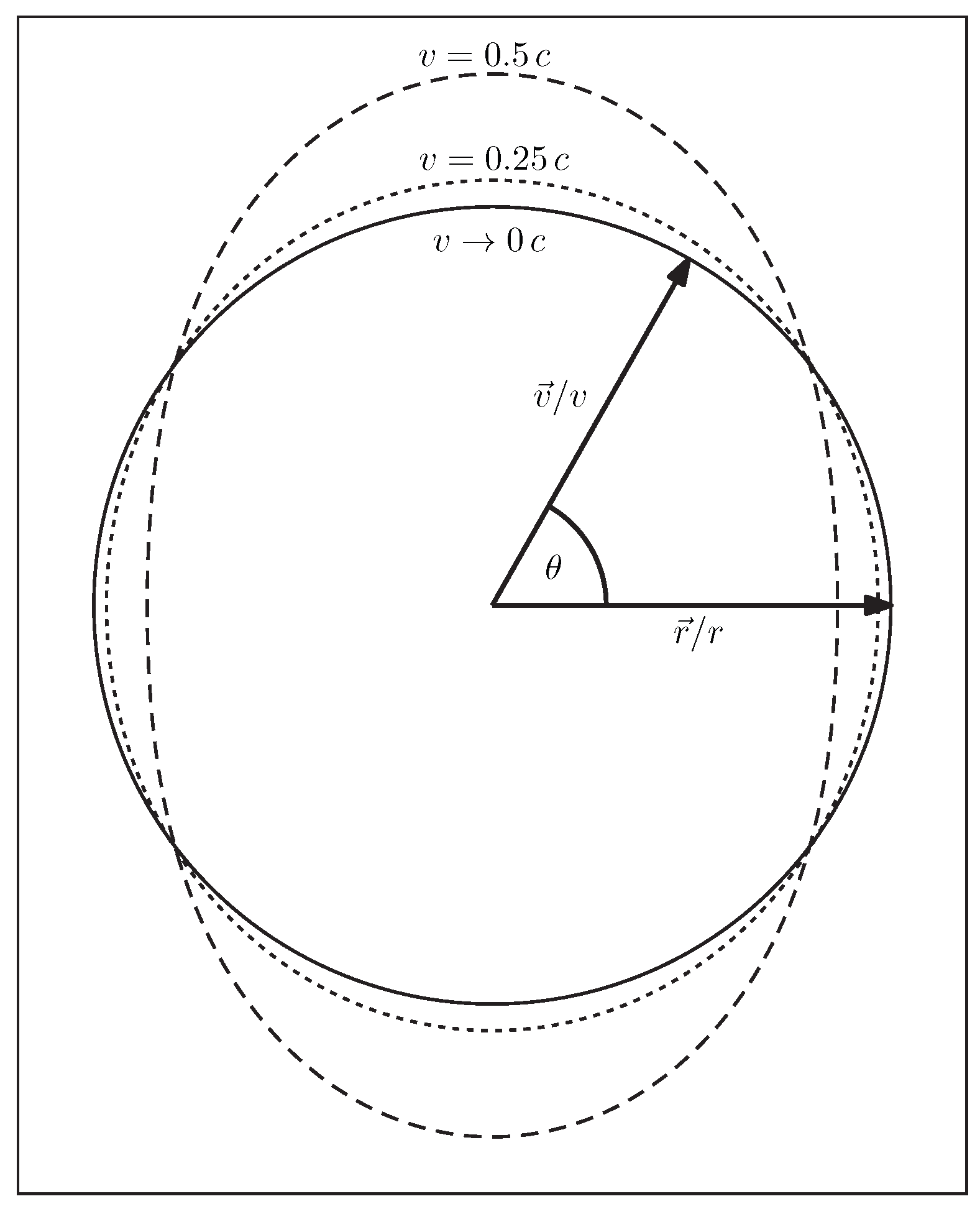
Figure 1 illustrates the deformation of the field as a function of the angle between velocity and distance vector at different speeds
v.
is the distance vector between the force-receiving charge
and the force-producing charge
. Therefore,
applies, with
being the trajectory of the charge
, i.e., the location of the charge at the current (non-retarded) time
t. Correspondingly,
is the trajectory of the charge
.
r is the Euclidean norm of the vector
, i.e.,
. A similar relation exists between
and
v. Because the force Formula (
1) strictly applies only to uniformly moving point charges, the relative velocity
is a constant that does not depend on the time
t.
Importantly, the pre-factor
is a scalar quantity and therefore has no influence on the direction of the force but influences only its strength. As can be verified by substitution,
if the two point charges move exactly on the connecting line (
). However, in the case in which
and
are perpendicular to each other, (
),
applies. This effect of the deformation of the electric force at high velocity is usually attributed to a Lorentz contraction [
12]. Because
is a scalar quantity, the force (
1) is, as a matter of principle, a central force, i.e., a force directed toward or away from the location of the point charge
.
Of note, Formula (
1) is the force formula from Weber electrodynamics in an alternative representation. For small
, Equation (
1) becomes the classical formula of Gauss from 1835 ([
13], p. 617). Formula (
1) fulfills the conservation of momentum, the conservation of energy and the conservation of angular momentum [
14].
Formula (
1) appears to suggest that the force propagates infinitely quickly. Some scientists believe that the Coulomb field requires no time to spread infinitely far. Although this question has not yet been conclusively answered, the structure of the exact solution to Maxwell’s equations for point charges strongly suggests that this is untrue. Instead, the radially symmetric Coulomb field of the force appears to propagate at finite speed and move relative to the source
as long as
is not accelerated.
A natural and straightforward explanation of this phenomenon would be to assume that point charges emit force carriers, which then behave similarly to projectiles fired from a moving ship. However, such a corpuscular theory violates the basic principle that the force cannot propagate faster than the speed of light in every arbitrarily chosen frame of reference. Therefore, Einstein, who initially favored this explanation, ultimately rejected the corpuscular theory [
15]. However, he and Lorentz did not consider an explanation suggested by Arago approximately 80 years prior ([
16], pp. 548–568): if we postulate that a point charge
can only perceive force carriers which have sublight speed in its frame of reference, this inevitably leads to the conclusion that the force between two point charges can never propagate faster than the speed of light (This corresponds to a temporal cross-section: a force carrier can only interact with a particle of matter if it remains in the vicinity of the particle of matter for a sufficiently long time). As becomes apparent, a intuitive, relational explanation exists in addition to the Lorentz transformation which is inherently compatible with Maxwell’s equations and Einstein’s seemingly contradictory postulates.
Since this conceptual model does not require relativity nor spacetime with its inherent difficulties, it is particularly valuable in electrical engineering because it allows engineers to work with the much simpler Galilean relativity. Moreover, the conceptual model corresponds directly to the mathematical structure of the exact solution to Maxwell’s equations for point charges. Furthermore, it is not only applicable to uniformly moving objects (like the special theory of relativity) and explains why the Coulomb force must be multiplied by the scalar pre-factor (
3) when relative velocities are present.
The decisive aspect for this field deformation (
Figure 1) is that a point charge moving directly toward another point charge perceives less of the Coulomb field the faster it moves. Similarly, a point charge moving away in a straight line perceives field components that appear to come from the opposite direction of the source. This also weakens the Coulomb force and one gets ultimately the elliptically shaped field (
1).
This article shows that this elliptical field deformation of the Coulomb force (Lorentz contraction) leads to magnetism, and further shows that this field deformation might also explain the existence of the gravitational force. This suggests that magnetism and gravitation might be closely related.
2. The Plasma Droplet Model
The starting point for consideration is the model of a very small, almost point-shaped object with total charge , which follows the trajectory . This postulated object is referred to as a plasma droplet in the context of this article. Numerous individual charges inside the plasma droplet can be imagined to move chaotically, as in a gas. Note that the plasma droplet is a mathematical abstraction chosen for analytical tractability, not a physically realistic model. It ensures that only velocity distributions—not spatial distributions—need be treated as random variables.
Let
be the probability distribution of the velocities
of the charges inside the plasma droplet. This function is a measure of the probability that a particle in the plasma droplet has velocity
. According to the laws of probability theory, the force of the plasma droplet on an external point charge at location
with velocity
can be calculated with the integral
(
,
,
). Of note,
represents the expected value of the probability distribution of the force, because the force is likewise a random variable, because of the randomness of
. Recall that
is the distance vector
, with
, in this case, representing the movement of the center of gravity of the plasma droplet.
is the approximately constant relative velocity
.
If Formula (
1) is substituted into integral (
6), an expression that can be evaluated only numerically is usually obtained. However, if we assume that the speed
u is much smaller than the speed of light
c, we can express
as a second order Taylor series with respect to
. In this case,
applies. With this approximation, integral (
6) can be solved independently of the specific form of the probability distribution
. We therefore obtain
with
being the expected value of the function
.
This article demonstrates how Newton’s law of universal gravitation can be derived with Formula (
8). However, it first demonstrates that Equation (
8) is also suitable for deriving the magnetic force.
3. Magnetism
Consider a point charge
that moves very slowly at a constant speed
. Although this is a deterministic movement, it can nonetheless be expressed with the probability distribution
, where
represents the Dirac delta function. Therefore,
and
. Insertion into Equation (
8) yields
If we assume that the velocity
v of the test charge
is not too high,
applies. By substituting into Equation (
10), we obtain the equation
for very low speeds
w and low speeds
v. If we now imagine a second, oppositely charged, stationary point charge at the same location as the moving point charge, the first term disappears, and we obtain the equation
by using the formula of the Coulomb force (
2). By means of the volume element
, the point charges can also be represented by charge densities
and
. Thus, we obtain the current densities
and
, and we can use the formula
to transform Equation (
13) into
We now see that Equation (
14) corresponds to Ampere’s original force law, from which, as repeatedly demonstrated in the specialist literature, the Lorentz force and the basic laws of magnetostatics can be derived [
17,
18,
19]. This shows that magnetic field lines are a conceptual model of magnetostatics and are used only for convenience (Note that the Lorentz force can be derived not only by using Ampere’s original force law (
14) by integrating over a closed current loop, but that there are also alternative formulas, e.g., the Biot-Savart law. However, none of these alternatives allows the electromagnetic force of a point charge to be expressed as a central force. In electrodynamics, however, the alternatives are no longer equivalent. The introduction of Maxwell’s addition transforms Maxwell’s equations into a wave equation. The solution of this wave equation is the Feynman–Jefimenko formula. Since the electric field strength in the rest frame of a test charge is proportional to the force on this test charge, the force formula can be transformed into another frame of reference by means of a Galilean transformation, provided that the point charges are not too fast. An analysis reveals that the transformed force formula contains already the magnetism. This not only makes the explicit definition of the Lorentz force and the magnetic field superfluous, but also transforms the electromagnetic force into a central force. Furthermore, it becomes obvious that Weber electrodynamics represents the limit of Maxwell’s electrodynamics for small relative velocities and small accelerations. Furthermore, it becomes apparent that the framework consisting of magnetic field, Biot-Savart law, and Lorentz force represents a relic of the quasistatic approximation that was originally developed to describe only the magnetic forces generated by closed current loops [
9]).
5. Assessment of Plausibility
The discussion in the previous section leads to far-reaching implications, although it is unfortunately not yet possible to determine whether these considerations are heading in the right direction. For a more reliable assessment, the calculations would need to be repeated using the full solution of Maxwell’s equations, which also applies to accelerated point charges and can describe wave phenomena. Due to the complexity involved, these calculations will have to be carried out in future works. At this stage, only a few plausibility considerations can be made.
The basic statement of the previous discussion is that electric charge in Brownian motion has a different gravitational mass and thus a different weight from the same amount of charge at rest. Wouldn’t that mean that an object that changes its temperature also changes its weight? The answer to this question is no, because heating only alters the velocity variance of the atoms contained in the object in their entirety. The change in weight due to the higher velocity variance of the electron shells is compensated for by the opposite change in weight of the atomic nuclei. Heating or cooling should therefore not lead to a measurable change in the weight of electrically neutral matter.
What might occur for an electrically charged copper sphere with a radius of, for example,
? This has a capacitance of
in relation to a very distant reference. With a static charge to a voltage of
, this metal sphere has a charge imbalance of
, which corresponds to approximately
missing electrons. The velocity variance of the copper ions can be roughly estimated by using the formula
. Here,
is the Boltzmann constant,
T is the absolute temperature, and
is the mass of a copper atom. At
(20 °C), a velocity variance of
38,546
results. Inserting this velocity variance into Equation (
28) yields
Therefore, the positively charged copper sphere should be slightly heavier at 20 °C than at the absolute zero point. However, the expected mass discrepancy is very small. If this phenomenon were noticed during an experiment, one would probably be tempted to explain it with electrostatic forces, because the sphere is electrically charged, and therefore electric forces with nearby objects such as the floor (electrostatic influence) are to be expected.
In the next thought experiment, we analyze two horizontally aligned, parallel copper rods 1 meter long, which are very close together and fixed to each other. A strong direct current of flows through each of the copper rods. We also assume that the current flows in one direction in one copper rod and in the other direction in the other copper rod. Both copper rods generate a magnetic field. However, because both rods are very close to each other, the magnetic fields can be assumed to approximately cancel each other out.
The current
I in the copper rods corresponds to movement of electrons whose average speed
v can be estimated with equation
Here
is the electron density, i.e., the number of electrons per volume, and
A is the cross-sectional area of a copper rod. The amount of charge
q moving in the two rods can also be calculated with the charge carrier density
. The formula is
where
L is the length of the copper rod. If Equations (
32) and (
33) are used in Equation (
28), we obtain the estimate
perpendicular to the two rods, owing to
. The electron density
for copper is
, as can be calculated with Avogadro’s constant. If we assume that the copper rods have a diameter of
, then we obtain
. We can therefore estimate that the mass change is again only very small despite the fairly strong current, because after insertion of all parameters into Formula (
34), we obtain a mass change of only approximately
. Since the currents do not flow in exactly the same place, magnetic fields are also present in practice. The small force could therefore also be explained as an interaction with the Earth’s magnetic field.
These and similar considerations indicate that Formula (
28) does not contradict everyday physics. The main difficulty in experimentally investigating the interpretation presented in this article is that both the electric force and magnetism are disproportionately stronger than gravity and can be tested only under conditions in which the other two forces are perfectly shielded.
6. Summary and Conclusions
The article demonstrated that the solution to Maxwell’s equations for sufficiently slow and uniformly moving point charges can be used to derive magnetism and, formally, Newton’s law of universal gravitation. The derivation is based on the fact that Coulomb’s law applies exactly only when the two point charges are at rest relative to each other. For uniformly moving point charges, the electric force remains a central force, but the field exhibits an elliptical deformation that depends on the relative velocity.
As demonstrated herein, this dependence on relative velocity inevitably leads to the magnetic force. The demonstration that the magnetic force can be derived from a central force is not new but was well known to many physicists of the 19th century, such as Gauss, Weber and Maxwell ([
21], p. 161). However, because of the definition of the Lorentz force formula, which is exactly valid for only magnetic forces generated by direct currents, this fact was largely forgotten at the beginning of the 20th century. For a long time, Newton’s law of universal gravitation was not recognized to also be derivable according to the same logic. A corresponding approach was first demonstrated by Assis at the end of the 20th century. However, because Assis used Weber electrodynamics as the starting point, which was considered outdated, the approach did not receive sufficient attention.
On the basis of the new insight that the Weber force represents a specific solution to Maxwell’s equations for sufficiently uniformly moving point charges in the Galilean limit, this approach is gaining new relevance, given that Maxwell’s electrodynamics has been well proven in practice for more than a century and is justifiably considered the standard theory of electrical engineering. The approach presented in this article does not completely correspond to that followed by Assis 30 years ago. However, both approaches are similar in that they use the relational field deformation of the Coulomb force as the starting point.
The considerations presented herein suggest that gravity and magnetism might be two aspects of the electric force. In summary, magnetic forces can be concluded to arise whenever two plasmas have a velocity standard deviation relative to each other, usually referred to as electric current. Gravity, in contrast, could be the result of two plasmas having different velocity variances. This aspect might explain why kinetic energy is released when mass is decreased. Furthermore, the derivation provides an hypothesis for why antimatter and photons exist alongside normal matter. However, the current considerations regarding gravity remain inconclusive, as they are based solely on the simplified Formula (
1) and apply only to stationary plasma droplets. To obtain experimentally verifiable results, the analysis must be extended to moving plasma droplets and carried out using the exact solution of Maxwell’s equations.