Analysis and Design of a Brushless WRSM with Harmonic Excitation Based on Electromagnetic Induction Power Transfer Optimization

Abstract

This paper proposes a method to analyze the effect of the rotor’s harmonic winding design and the output of a brushless wound rotor synchronous machine (WRSM) for optimal excitation power transfer. In particular, the machine analyzed by the finite-element method was a 48-slot eight-pole 2D model. The subharmonic magnetomotive force was additionally created in the air gap flux, which induces voltage in the harmonic winding of the rotor. This voltage is rectified and fed to the field winding through a full bridge rectifier. Eventually, a direct current (DC) flows to the field winding, removing the need for external excitation through brushes and sliprings. The effect of the number of harmonic winding turns is analyzed and the field winding turns were varied with respect to the available rotor slot space. Optimization of the harmonic excitation part of the machine will maximize the rotor excitation for regulation purposes and optimize the torque production at the same time. Two-dimensional finite-element analysis has been performed in ANSYS Maxwell 19 to obtain the basic results for the design of the machine.

1. Introduction

Ever since the advent of high-energy permanent magnet (PM) materials, research on PM machines has attracted significant consideration and attention, which has continued to the present day. Some of the recent advancements have been in exploiting the power density limits of interior permanent magnet synchronous machines (IPMSMs) [1,2]. Specifically, the wide-speed range operation of PM Vernier machines has been specifically investigated for use in electric vehicles and other variable-speed applications [3,4]. However, the applicable machine structure along with the drive system becomes costly, mainly due to the use of PM in applications where the product cost is a main consideration [5,6,7]. The high-energy rare-earth materials to be used in manufacturing PMs have their own issues to be solved, ranging from trade disputes to end-use recycling [8,9]. In a parallel world, a new issue has emerged: whether the rare-earth PM motors will be removed from electric vehicles (EVs), and what type of motors can be used in place of them [7,10]. In recent years, wound rotor synchronous machines (WRSMs) have been investigated as an alternative, owing to the cheaper structure manufacturing and wide-speed range capabilities given the degree of freedom for flux weakening, which is comparable to the PM machines [11,12,13,14,15,16,17,18]. Additionally, a PM-less rotor exhibits no PM loss; the machine features improved safety through direct field control during inverter fault conditions, and there is no problem of demagnetization [19,20,21].

However, WRSM has an inherent problem regarding the assembly of brushes and sliprings. Because of the problem associated with WRSM, comparative investigation always favors the use of a PMSM instead of WRSM in many applications. To address the problems, many brushless excitation techniques have been proposed for WRSMs [22,23,24,25,26,27].

The design of a large synchronous machine incorporates an extended-shaft brushless exciter to control the high power excitation currents [28,29,30,31]. However, on a small scale, this exciter can be integrated into the main machine for compact brushless and/or self-excitation purposes, reducing the cost and volume of the system [32,33].

One solution is generating harmonic flux in the air gap along with the fundamental flux to induce voltage in an additionally provided winding on the rotor, which is connected to the field winding of the rotor through a rectifier for brushless excitation [34,35,36,37]. However, when the higher harmonic flux is injected into the stator windings through modified inverters or pulse width modulation (PWM) techniques, the core losses due to additional high-frequency harmonics need to be considered. Alternatively, special stator winding designs have also been proposed in the literature for generating a subharmonic component of the air gap flux with either single or dual-inverter schemes [38,39,40,41,42,43,44].

Stator winding topology optimization with fractional-slot concentrated windings and alternative coil pitch designs can be used to suppress certain space harmonics by canceling their magnetomotive force (MMF) contributions, thereby reducing associated torque ripples and losses. Alternatively, hybrid design approaches using harmonic windings with carefully chosen pole numbers and placement can further reduce coupling of unwanted harmonics into the rotor.

In ref. [44], two inverters supply current to two three-phase winding sets, each located in half of the stator, to create a subharmonic MMF for brushless operation. The arrangement of stator armature winding with different magnitudes of currents in each set of armature winding creates a subharmonic MMF in the air gap, which is used to induce voltage on the rotor harmonic winding. The voltage is then rectified, and a DC power is fed to the field winding for brushless field excitation. However, the insertion of harmonic winding occupies a definite volume of the rotor slot area, which reduces the rotor flux generation capability from the field winding for torque production.

In this paper, the problem of the effect of harmonic winding turns inserted into the rotor by compensating field winding turns for a given slot area is addressed in subharmonic brushless schemes. A brushless WRSM based on subharmonic excitation topology [44] is analyzed for rotor harmonic and field winding turns to improve output performance by maximizing harmonic power transfer and obtaining high torque.

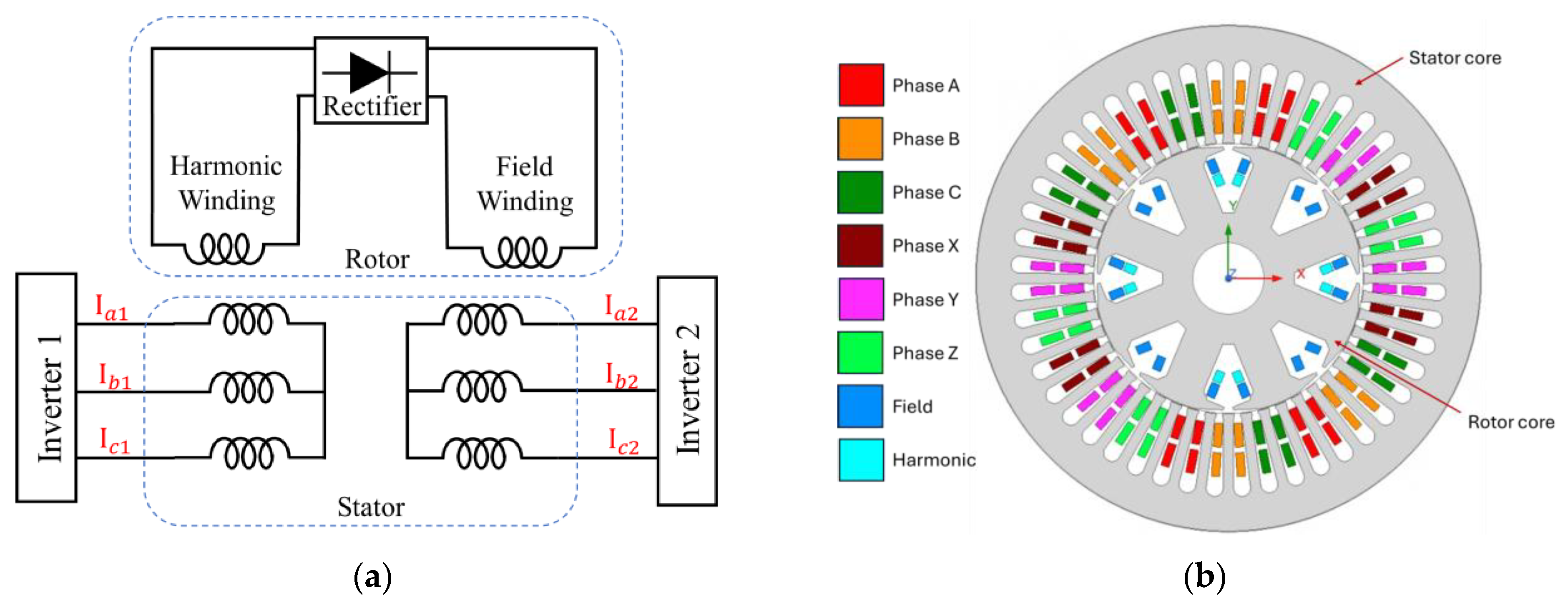
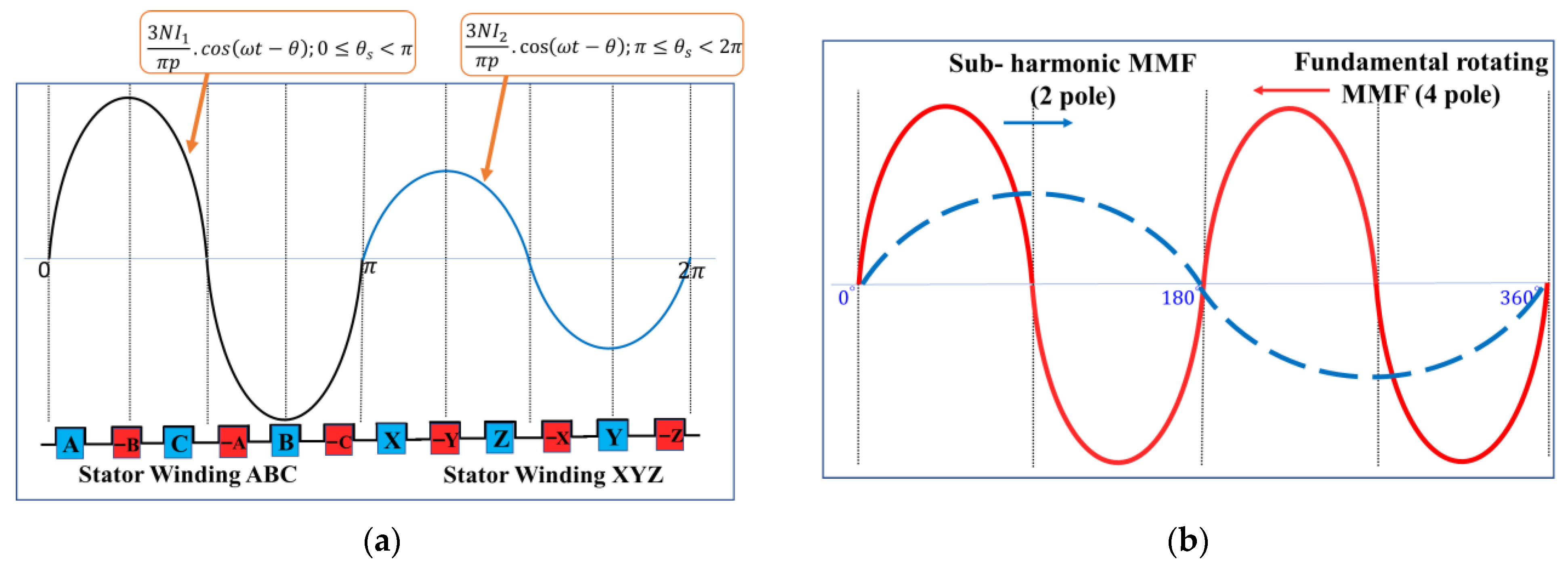
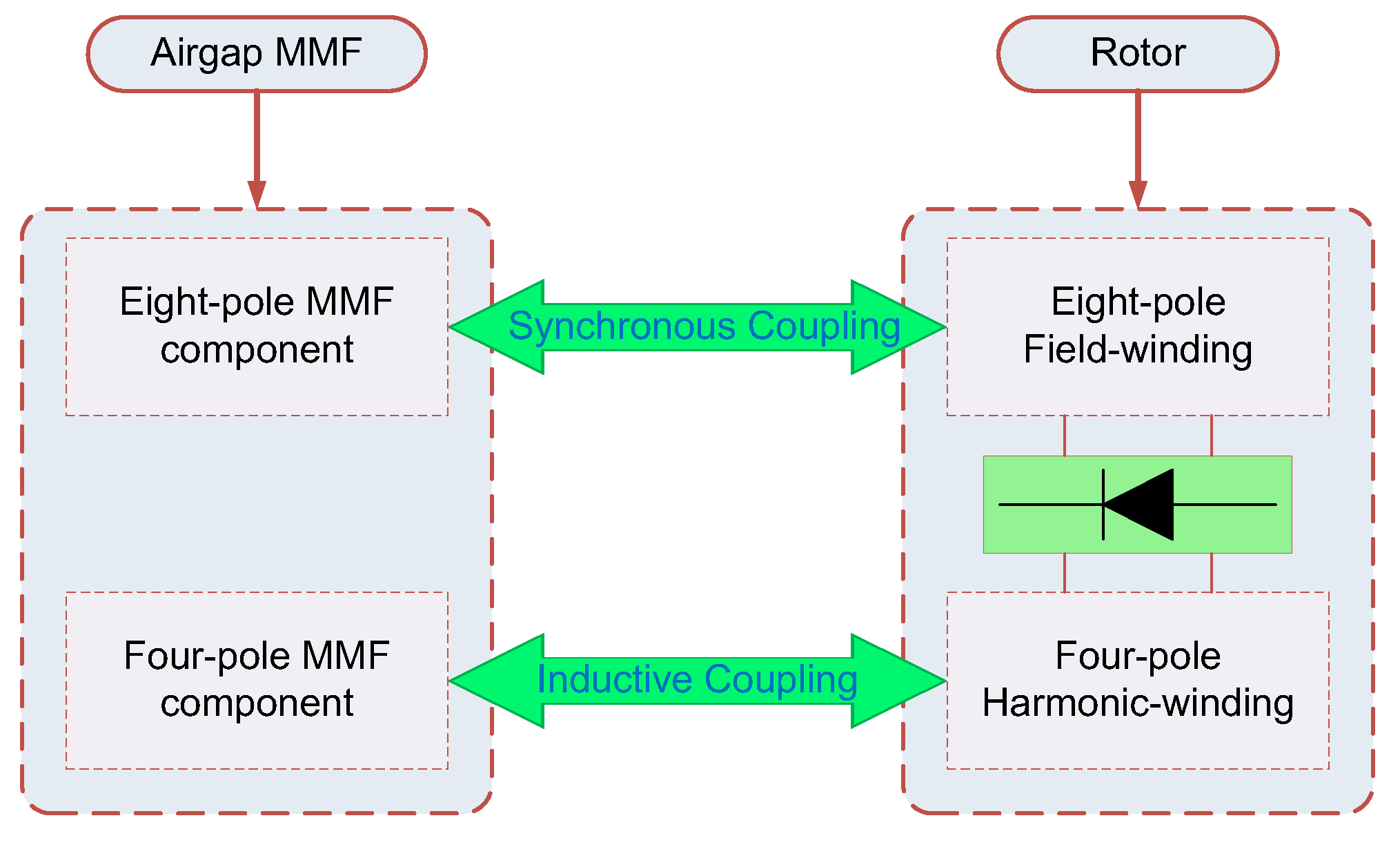
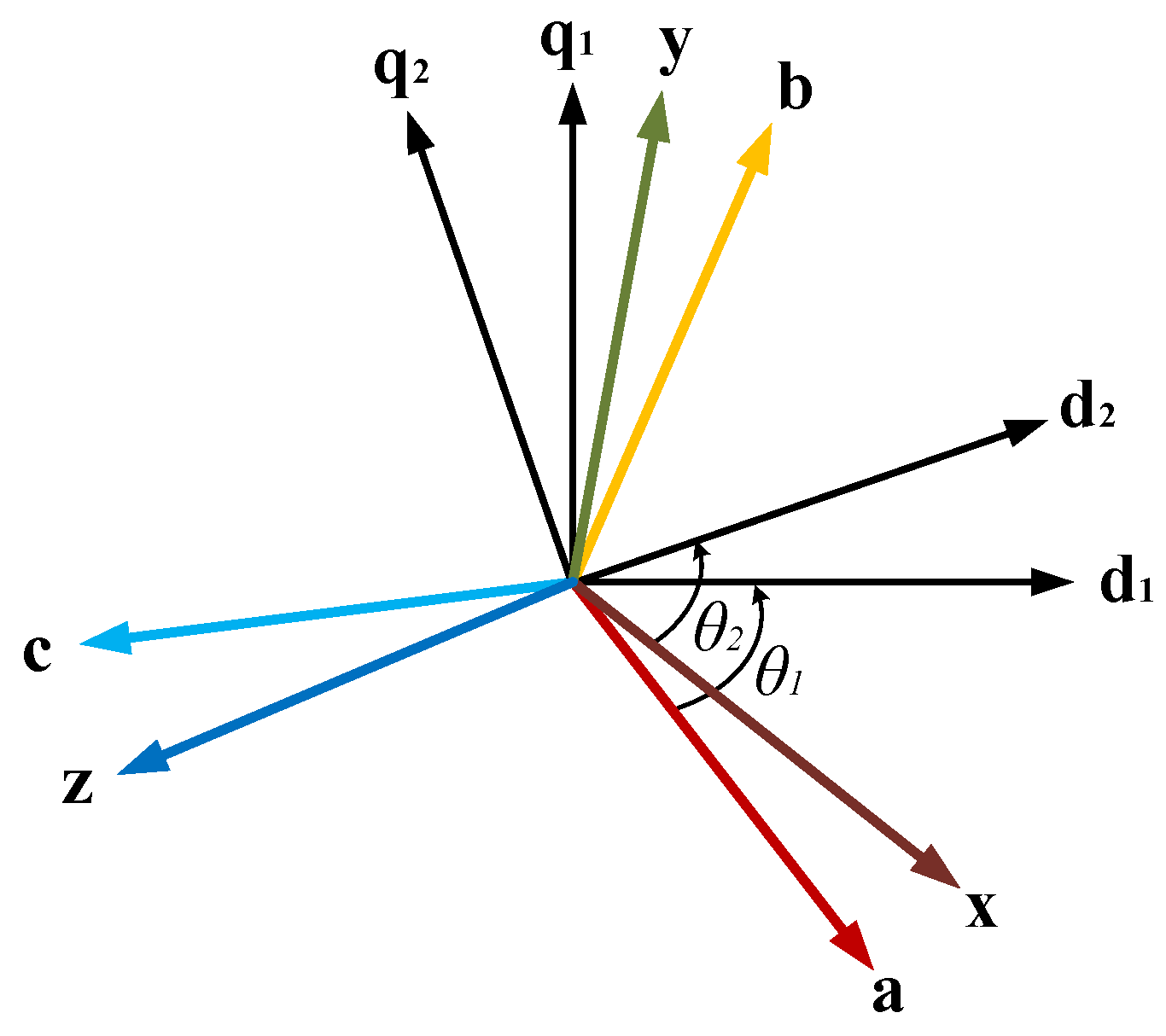
2. Topology and Working Principles

A WRSM drive scheme and 2D model based on subharmonic field excitation are shown in Figure 1, and the machine parameters are given in Table 1. Two inverters supply currents to two sets of three-phase stator armature windings, each with a separate neutral connection. The resulting air gap magnetic field in two portions of the machine is illustrated in Figure 2a. However, when it is decomposed as a Fourier series, two main magnetic field components can be observed as illustrated in Figure 2b. The two magnetic fields exist in the same air gap. Hence, the interaction of both fields generated from the stator side will interact with the rotor of the machine. It must be noted that in the proposed machine, the harmonic winding and the field winding share the limited rotor slot space which simultaneously interact with the two superimposed air gap magnetic fields. Higher harmonic current levels may result in superposition effects, influencing both slot harmonics and thermal performance. However, potential design approaches that can balance winding space utilization with harmonic suppression can be adopted. Some of them are discussed as follows:

• Layered winding arrangement: By placing the harmonic winding and the field winding in separate radial layers within the slot, mutual interference can be reduced. This configuration also helps manage insulation stress and thermal dissipation.
• Magnetic barriers or slot wedges: Introducing magnetic barriers (such as low-permeability slot liners or flux diverters) can reduce the coupling of higher-order harmonics while preserving available copper space for the windings.
• Optimized slot geometry: Adjusting slot opening and tooth width allows for a trade-off between winding accommodation and harmonic suppression without significantly increasing rotor size.

Figure 1. (a) Topology. (b) Stator winding configuration [44].

Figure 1. (a) Topology. (b) Stator winding configuration [44].

Figure 2. Waveform illustration of the MMF (a) based on winding configuration of ABC and XYZ and (b) decomposition into fundamental and subharmonic components.

Figure 2. Waveform illustration of the MMF (a) based on winding configuration of ABC and XYZ and (b) decomposition into fundamental and subharmonic components.

Table 1. Design parameters of the machine.

Parameter	Value	Unit
Stator outer diameter	120	mm
Stator inner diameter	72	mm
Air gap length	1	mm
Stack length	120	mm
Number of slots	48	-
Number of poles	8	-
Base speed	900	-
Core material	M-19	-

Table 1. Design parameters of the machine.

Parameter	Value	Unit
Stator outer diameter	120	mm
Stator inner diameter	72	mm
Air gap length	1	mm
Stack length	120	mm
Number of slots	48	-
Number of poles	8	-
Base speed	900	-
Core material	M-19	-

These approaches are feasible and worth exploring to further improve harmonic suppression and space utilization. A general flow of fundamental and subharmonic magnetic fields and their interaction with the machine components is shown in Figure 3. It is important that for maximum harmonic power transfer, the two-pole field should be maximally coupled with the harmonic winding of the rotor.

Currents from both inverters are given as

$$\begin{array}{l}{I}_A=I_1\mathit{sin}{\omega }_{e}t\\ I_B=I_1\mathit{sin}({\omega }_{e}t-{\displaystyle \frac{2\pi }{3}})\\ I_C=I_1\mathit{sin}({\omega }_{e}t+{\displaystyle \frac{2\pi }{3}})\end{array}$$

(1)

$$\begin{array}{l}{I}_X=m{I}_2\mathit{sin}{\omega }_{e}t\\ I_Y=m{I}_2\mathit{sin}({\omega }_{e}t-{\displaystyle \frac{2\pi }{3}})\\ I_Z=m{I}_2\mathit{sin}({\omega }_{e}t+{\displaystyle \frac{2\pi }{3}})\end{array}$$

(2)

where I₁ and I₂ are used to denote the amplitude of the fundamental currents of ABC-winding and XYZ-winding, respectively, m is the coefficient of difference between the currents I₁ and I₂, and ω_e is the electrical angular frequency. The back-EMF of the machine can be calculated from a general form such as

$$E_{ph}=4.44\cdot k_w\cdot f\cdot N\cdot \varphi$$

(3)

where $k_w$ is winding factor, N is the number of turns per phase, and $\varphi$ is flux per pole. When a current is injected into the armature phase windings, a rotating electromagnetic torque is produced due to the interaction between the magnetic field produced by the current and the rotor magnetic field, which is calculated as

$$T={\displaystyle \frac{3E_{ph}\cdot I_{ph}\cdot \mathit{cos}\phi }{{\omega }_r}}$$

(4)

where $I_{ph}$ is the phase current, and $\phi$ is the power factor angle. The dual three-phase quantities are converted into the dq reference frame, as shown in Figure 4, using Park’s transformation matrix P_dq for simplicity, identifying the control and state vectors. Accordingly, the DQ reference frame’s currents and voltages will be

$$\left[\begin{array}{c}{I}_{d1}\\ I_{q1}\\ I_{d2}\\ I_{q2}\end{array}\right]={\mathbf{P}}_{\mathit{d}\mathit{q}}.\left[\begin{array}{c}\begin{array}{c}{I}_a\\ I_b\\ I_c\end{array}\\ I_x\\ I_y\\ I_z\end{array}\right]; \left[\begin{array}{c}{V}_{d1}\\ V_{q1}\\ V_{d2}\\ V_{q2}\end{array}\right]={\mathbf{P}}_{\mathit{d}\mathit{q}}.\left[\begin{array}{c}\begin{array}{c}{V}_a\\ V_b\\ V_c\end{array}\\ V_x\\ V_y\\ V_z\end{array}\right]$$

(5)

where ${\mathbf{P}}_{\mathit{d}\mathit{q}}$ is given as

$${\mathbf{P}}_{\mathit{d}\mathit{q}}={\displaystyle \frac{2}{3}}\left[\begin{array}{cccccc}\mathit{cos}\left({\theta }_1\right)& \mathit{cos}\left({\theta }_1-{\displaystyle \frac{2\pi }{3}}\right)& \mathit{cos}\left({\theta }_1+{\displaystyle \frac{2\pi }{3}}\right)& \mathit{cos}\left({\theta }_2\right)& \mathit{cos}\left({\theta }_2-{\displaystyle \frac{2\pi }{3}}\right)& \mathit{cos}\left({\theta }_2+{\displaystyle \frac{2\pi }{3}}\right)\\ -\mathit{sin}{\theta }_1& -\mathit{sin}\left({\theta }_1-{\displaystyle \frac{2\pi }{3}}\right)& -\mathit{sin}\left({\theta }_1-{\displaystyle \frac{2\pi }{3}}\right)& -\mathit{sin}{\theta }_2& -\mathit{sin}\left({\theta }_2-{\displaystyle \frac{2\pi }{3}}\right)& -\mathit{sin}\left({\theta }_2-{\displaystyle \frac{2\pi }{3}}\right)\end{array}\right]$$

(6)

The two sets are wound alternately on the stator teeth so that from 0 to π/2 radians spatial angle, the MMF is generated with winding set ABC, and from π/2 to π radians the MMF is generated with winding set XYZ. The configuration repeats through angle π to 2π radians for an eight-pole synchronous machine, as shown in Figure 1 and Figure 2. From the basic topology, it is shown that an additional air gap MMF of subharmonic frequency will exist with the given winding configuration when the machine is supplied with two different amplitude currents from the two inverters. The additional MMF component is then utilized to induce a voltage on a harmonic winding on the rotor. The harmonic winding works as a source for field winding excitation. Eventually, the external DC voltage source, along with the sliprings and brushes can be removed. The equation for the rotating MMF in both the ABC and XYZ parts of the machine is calculated from the MMF equation of conventional WRSM. Neglecting the effect of harmonics, the MMF equation for the rotating flux is derived by

$$F_{total}=\left\{\begin{array}{c}{\displaystyle \frac{3N{I}_1}{\pi p}}\cdot \mathit{cos}(\omega t-\theta );0\le {\theta }_s<\pi \\ {\displaystyle \frac{3N{I}_2}{\pi p}}\cdot \mathit{cos}(\omega t-\theta );\pi \le {\theta }_s<2\pi \end{array}\right.$$

(7)

where N is the number of turns, I₁ is the peak current in winding set ABC, I₂ is the peak current in winding set XYZ, p is pole pairs, ω is mechanical speed, t is time, and θs is the spatial angle.

The MMF from 0 to π radian is generated by ABC currents, and from π to 2π radian, the MMF is generated by XYZ currents as illustrated in Figure 2a. Neglecting the higher harmonics, the composite MMF can be decomposed into fundamental and subharmonic components as illustrated in Figure 2b. The fundamental component of the MMF is employed to produce torque by synchronizing with the field winding flux, while the subharmonic component induces voltage in a harmonic winding on the rotor, which has half the number of poles of the field winding. The voltage induced in the rotor’s harmonic winding can be calculated as

$$V_h=K{.\omega \lambda }_{sub}$$

(8)

where K is the subharmonic coupling factor and ${\lambda }_{sub}$ is the flux linkage of the harmonic winding with the subharmonic air gap magnetic field. This voltage is rectified to energize the field winding from the rotating rectifier mounted on the same rotor connected with both the rotor windings. The rectifier connection with both the field winding and the harmonic winding is shown in Figure 5.

With the diode forward voltage $V_D$ being constant for the semiconductor material used, the voltage across the field winding can be approximated as

$$V_f\approx {\sqrt{2}V}_{h\left(RMS\right)}-{2V}_D$$

(9)

where $V_{h\left(RMS\right)}$ is the rms value of voltage across the harmonic winding. As the closed-circuit rotor allows current to flow in the field winding, a uniform magnetic flux is generated to achieve brushless operation and develop torque. Hence, it can be extracted from (9) that the field voltage is directly proportional to the induced harmonic voltage, which is directly proportional to the ratio m controlled by the difference between the currents from the two inverters.

$$V_f\propto V_{h\left(RMS\right)}$$

(10)

Therefore,

$$V_f\propto m$$

(11)

It is also important to note that feeding the proposed machine with a dual-inverter may exacerbate current harmonics if no countermeasures are taken. Several current control strategies have been reported in the literature to suppress undesired harmonic components while maintaining the subharmonic excitation required for brushless operation. Selective Harmonic Elimination (SHE) and optimized PWM patterns can be employed to eliminate specific low-order harmonics at the inverter side while retaining the target subharmonic component. Model Predictive Control (MPC) methods, including finite-control-set MPC, can minimize harmonic currents and torque ripple by directly optimizing inverter switching states [45]. Resonant and adaptive resonant current controllers are also effective in suppressing defined harmonic orders in the air gap while allowing the desired subharmonic to persist. Other options include predictive harmonic current control with disturbance observers for fast compensation, and the use of virtual impedance or adaptive virtual harmonic resistors to attenuate problematic harmonic frequencies. In practice, such active control methods can be complemented with modest passive measures such as phase reactors or small L-filters to further reduce iron loss and torque ripple. A comprehensive comparison of these algorithms and their implementation for dual-inverter WRSM drives is left for future work, as it requires detailed controller design and experimental validation beyond the steady-state analysis presented here.

In addition to conventional PWM and resonant control strategies, recent work has demonstrated more advanced methods for harmonic disturbance suppression. For example, predictive current control with selective harmonic mitigation has been shown to effectively reduce harmonic distortion in multiphase drives [46], while adaptive current regulation schemes have been applied to suppress torque ripple and iron losses across varying operating conditions [45]. These approaches offer promising prospects for extending the present dual-inverter WRSM toward enhanced harmonic robustness.

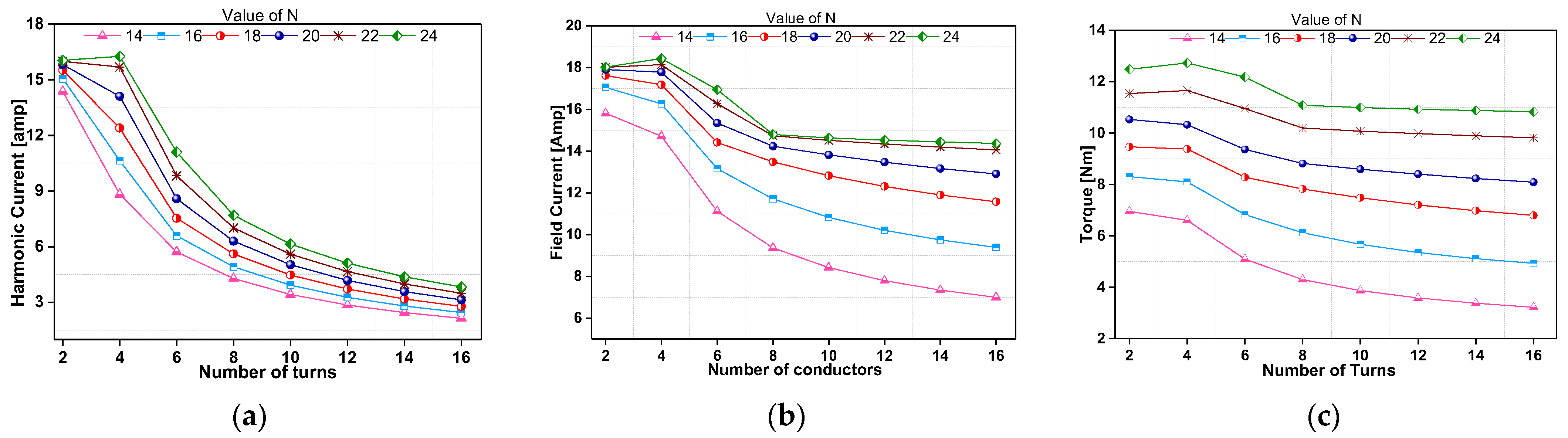
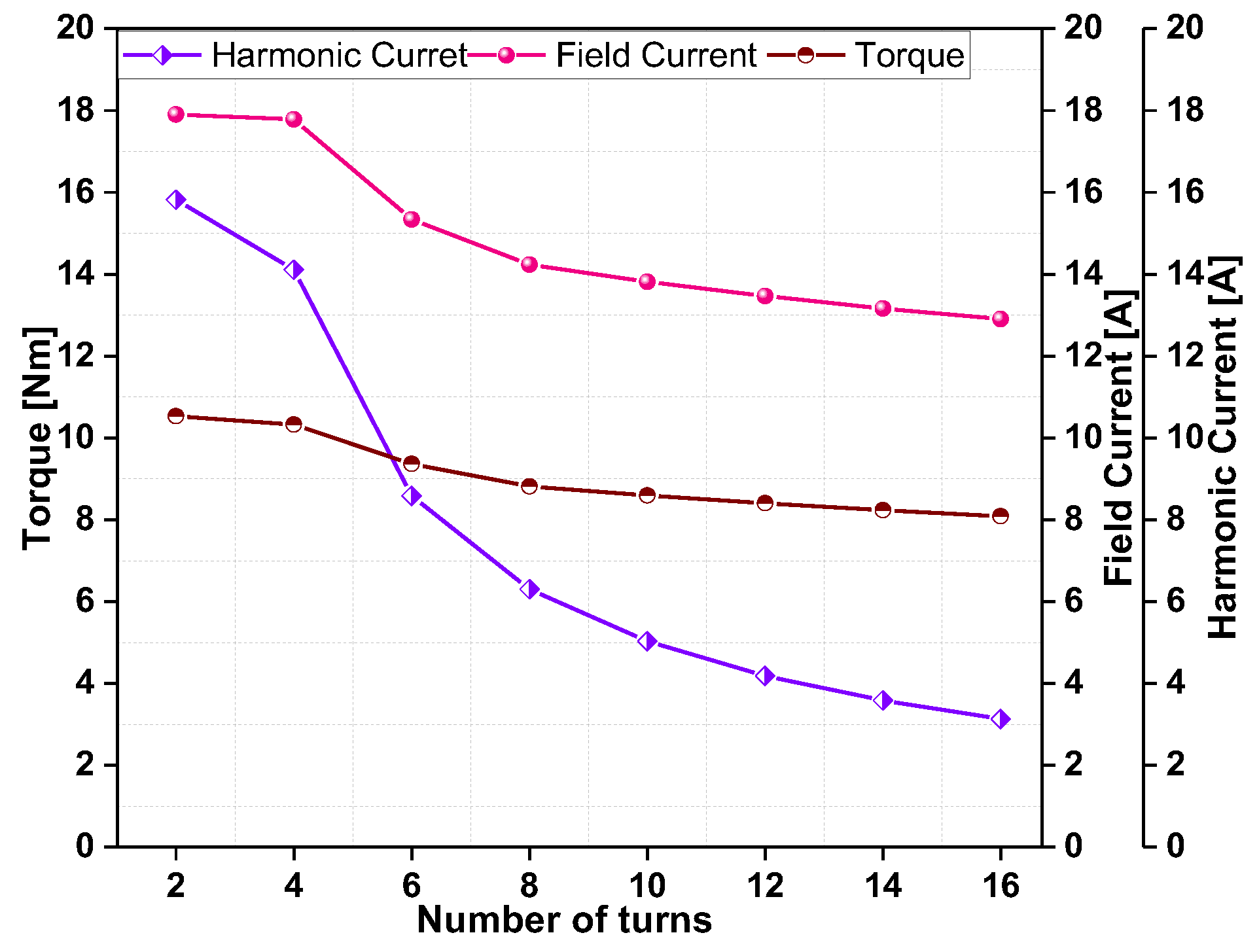
3. Effect of Harmonic Winding Turns with Fixed Field Winding Turns

Since field winding turns are not changed in this case, harmonic winding turns are varied, with a lower number of turns having a higher value of current. Therefore, copper loss due to high current in the harmonic winding increases exponentially, whereas the decrease in copper loss is only linear due to a lower number of harmonic winding turns. The copper loss in the harmonic winding is

$$\begin{gathered} P_{CH}={I_H}^{2}R \\ {P}_{CH}={I_H}^2\left({\displaystyle \frac{\rho N_c{L}_t}{A_w}}\right) \end{gathered}$$

(12)

where I_H is the RMS value of harmonic winding current, R is the total resistance of the harmonic winding, ρ is the resistivity of copper material, and L_t is the average length of the conductor, including end turn length. Since the average length of the conductor and the resistivity of copper can be constant, Equation (12) can be rewritten as

$$P_{CH}={I_H}^2\left({\displaystyle \frac{N_c}{A_w}}\right)\times \mathrm{Constant}$$

(13)

Thus, to keep the power loss limited to a constant value, the cross-sectional area of the conductor will have to be increased as the number of harmonic winding conductors decreases. Therefore,

$$A_w\propto {I_H}^2\times N_c$$

(14)

However, Equation (14) can be considered to keep the copper loss constant, which may affect the fill factor of the rotor given by

$$Fill-Factor={\displaystyle \frac{A_w\times N_c}{A_{slot}}}$$

(15)

where A_w is the cross-sectional area of the conductor, N_c is the number of conductors per slot, and Aslot is the area of the slot. Therefore, for a given fill factor,

$$\begin{gathered} A_w\times N_c=Fill-Factor\times A_{slot}=\mathrm{Constant} \\ \Rightarrow A_w\times N_c=\mathrm{Constant} \end{gathered}$$

(16)

3.1. Turn Variations in Harmonic Winding with a Different Number of Armature Windings

An eight-pole 48-slot machine model was used for finite-element analysis (FEA), and the results are shown in Figure 6. As the harmonic winding turns are increased from 2 turns per pole to 16 turns per pole, the harmonic winding current, field winding current, and the torque, as shown in Figure 6a–c, respectively, vary with a non-linear pattern. Since the harmonic current varies with respect to the number of harmonic winding turns, the field current, which is rectified and fed to the field winding also varies accordingly. Similarly, the torque of the machine also varies since the field current varies.

The simulation results show that the harmonic current increases with a lower number of turns of harmonic winding until four turns per pole. Similar results are obtained at different numbers of armature winding turns. However, less than four harmonic turns affect the current decrease. It is obtained from the simulation results that for the referred machine parameters, if only the harmonic winding turns are decreased to four turns, the maximum harmonic and field currents are obtained, and eventually, the torque output can be increased. At the same time, however, the copper losses of both the rotor windings, the harmonic and field winding, will increase due to increased current, and the current density will also increase, which can create rotor heating and insulation problems in the rotor windings.

3.2. Turn Variations in Harmonic Winding with the Same Number of Armature Winding Turns

The results indicate that the harmonic current decreases as the turns for harmonic winding is reduced to a certain number of turns. Neglecting the difference in harmonic power extraction from the air gap flux due to a change in the number of turns, the decrease in the number of turns increases the current to be equal to the power extraction. Keeping in mind the voltage limits of harmonic winding and the current density limit, the number of turns of harmonic winding is kept at four turns per harmonic pole. The limit is decided by the upper limit of current in the harmonic winding, which increases the field current, and eventually, a maximum torque average is achieved. It is established that for given design parameters, increasing the number of turns results in higher field current and average torque. Figure 7 shows the variation in harmonic and field winding currents and the output torque at different numbers of harmonic winding turns.

It can be observed that the currents and the torque output are highest at the lowest number of harmonic winding turns. However, it should also be noted that there will be a limit on the lowest number of harmonic winding turns used for a given design parameter of the machine owing to increased copper losses, which generate heat and higher current density, which requires a higher diameter of the winding conductors.

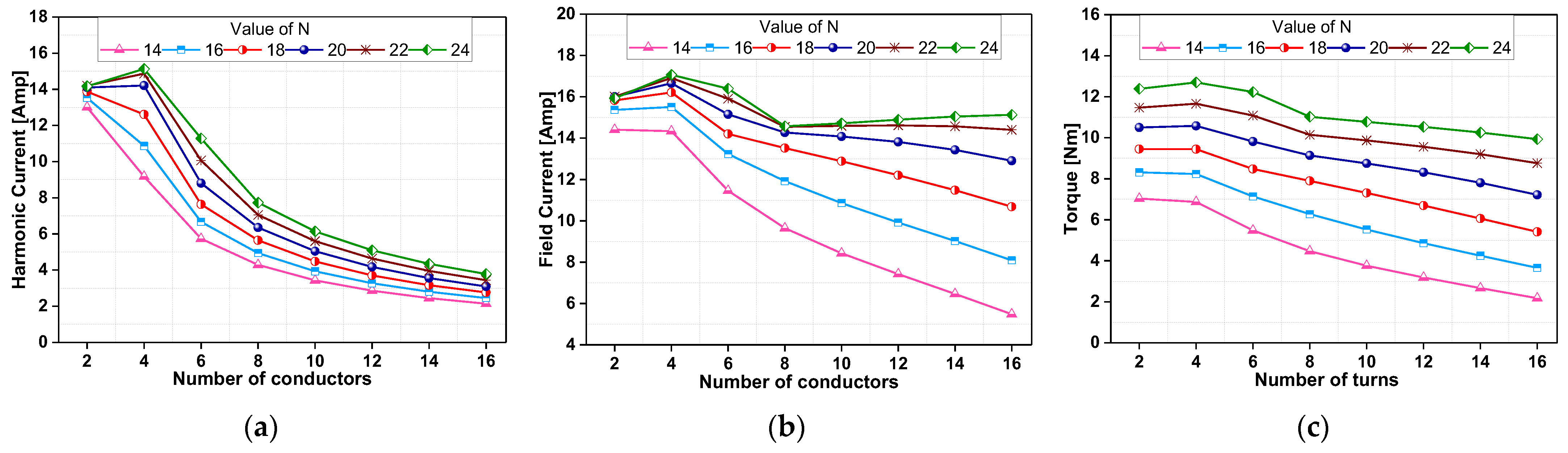
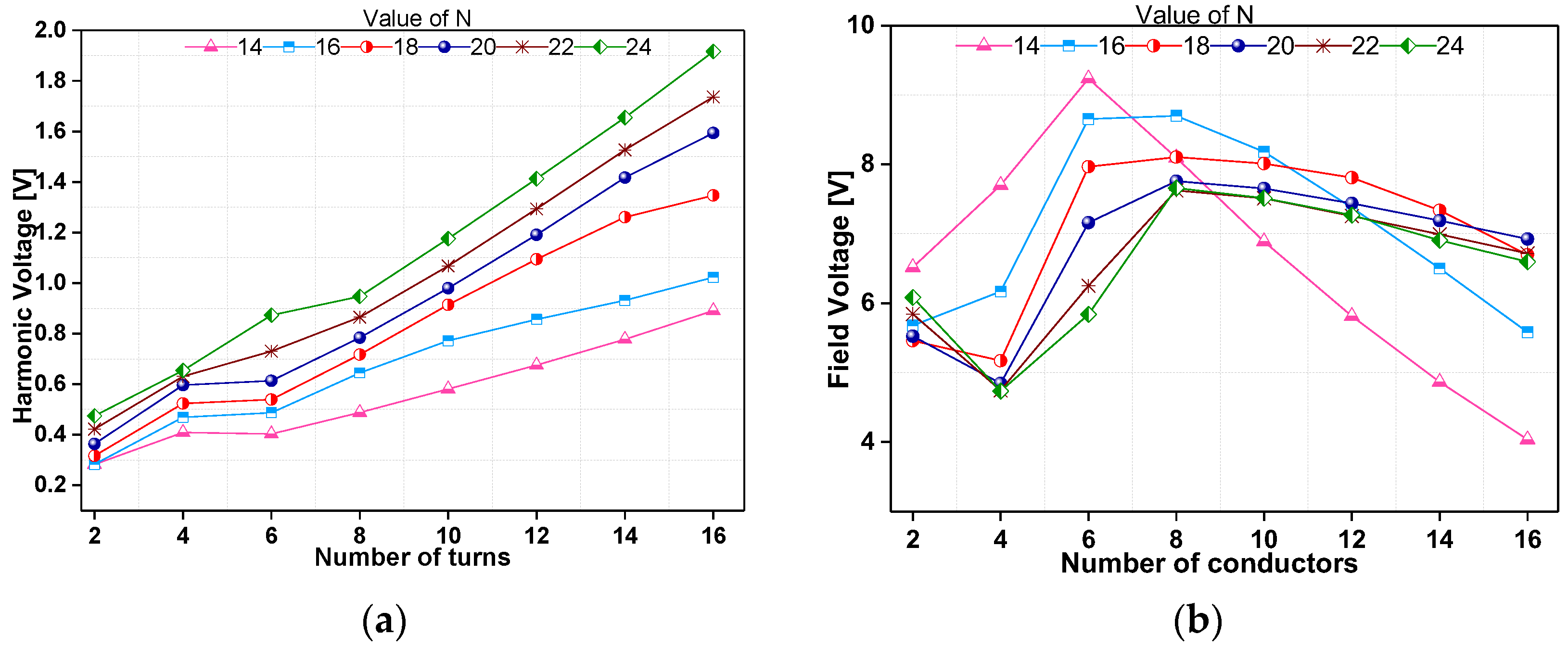
4. Effect of Harmonic Winding Turns Considering Variation in Field Winding Turns

Consider that the same diameter of the harmonic winding space created by using a lower number of harmonic winding turns can be used to increase the field winding turns by the same number. In this case, a constant fill factor is considered instead of copper loss.

4.1. Turn Variations in Harmonic Winding with a Different Number of Armature Windings

It can be observed from the results, as shown in Figure 8, that the harmonic current variation curves show approximately the same pattern as in the case where field turns are kept the same, as shown in Figure 6. It can be deduced that the harmonic current is not affected by the turn variation in the field winding. However, the same power is being fed to the field winding. Since the current of the harmonic winding decreases as the number of turns is increased, the voltage should also change accordingly.

Since the harmonic component of the air gap flux resulting from the stator winding currents did not change, it should induce the same power in the harmonic winding of the rotor. As shown in Figure 9, the voltage increases in the harmonic winding as the current decreases while changing the number of turns. However, this pattern is not observed in the voltage waveforms of the field winding. This discrepancy arises from the self-induced voltage generated by the tooth-harmonic fields, which adds an extra component. As a result, the total voltage across the field winding does not exhibit the regular pattern seen in the harmonic winding voltage.

4.2. Turn Variations in Harmonic Winding with the Same Number of Armature Winding Turns

Figure 10 shows the obtained current variation curves and the output torque curve with varying harmonic winding turns. In this case, the basic machine model is considered, with 20 armature winding turns, and the field winding turns are adjusted according to the available space in the rotor, considering the fill factor.

It can be observed that torque varies approximately linearly with respect to harmonic winding turns, with a higher torque at a lower number of harmonic winding turns. However, the current in the harmonic winding increases exponentially until the harmonic winding number of turns is four. Similarly, the field winding current changes irregularly from 2 to 4 turns but tends to change linearly after 6 to 16 turns. As discussed in the previous sections, smaller turns should be kept to increase torque output, given the limits of rotor copper loss and fill factor.

The stator and rotor cores were modeled using M-19 grade non-oriented silicon steel, selected for its favorable compromise between low core losses and high magnetic saturation capability, which is appropriate for medium-speed synchronous machines. The stator employs semi-closed rectangular slots designed to reduce leakage while maintaining structural strength, whereas the rotor slots are rectangular with rounded corners to facilitate placement of both the harmonic and field windings. The effective slot fill factor used in the finite-element model was approximately 0.5.

To provide further insight into electromagnetic behavior, Figure 11 illustrates the finite-element distribution of magnetic vector potential and flux density in the machine cross-section. The plot confirms the expected flux paths in both the stator and rotor, as well as the effective coupling of the subharmonic stator MMF with the rotor harmonic winding.

5. Conclusions

This paper describes the analysis of the effect of changing the rotor’s harmonic winding turns to obtain high output torque. The factors limiting the performance based on harmonic winding turns were analyzed, which depict the relationship of the harmonic winding turns with the currents in both harmonic and field windings and the output torque of a WRSM. The effect of the number of harmonic winding turns is analyzed by changing the harmonic winding turns at different armature winding turns, keeping the field winding turns constant in one section and varying the field winding turns with respect to the available rotor slot space. It is found that the currents in the rotor harmonic winding and field winding are not linearly dependent on the number of turns of the harmonic winding. Eventually, the torque is dependent on the field current but not on the turn variation directly. However, the results show a comprehensive pattern that can be used to design the machine parameters while fixing the number of harmonic winding turns within the constraints of the rated parameters.

While this paper has focused on steady-state characteristics at rated speeds to establish the feasibility of the proposed brushless harmonic excitation scheme, several aspects remain open for future work. Dynamic performance under starting low-speed, torque ripple analysis across transient operating ranges, and high-speed field-weakening operations will be investigated in subsequent studies. Moreover, to mitigate additional harmonic components that may arise in the dual-inverter system, current control strategies such as SHE, MPC, and resonant or predictive harmonic controllers, combined with virtual impedance methods or modest passive filtering, will be explored. These measures are expected to further enhance efficiency and suppress torque ripple while maintaining the required subharmonic excitation for brushless operation.

Overall, the proposed design establishes a practical foundation for brushless WRSM excitation, with clear pathways identified for extending the approach to dynamic and wide-speed operation in future work.

These results not only confirm the effectiveness of the proposed motor design but also provide a comprehensive understanding of its magnetic behavior, supporting future optimization and practical implementation.