Effect of the Non-Magnetic Ion Doping on the Magnetic Behavior of MgCr2O4
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
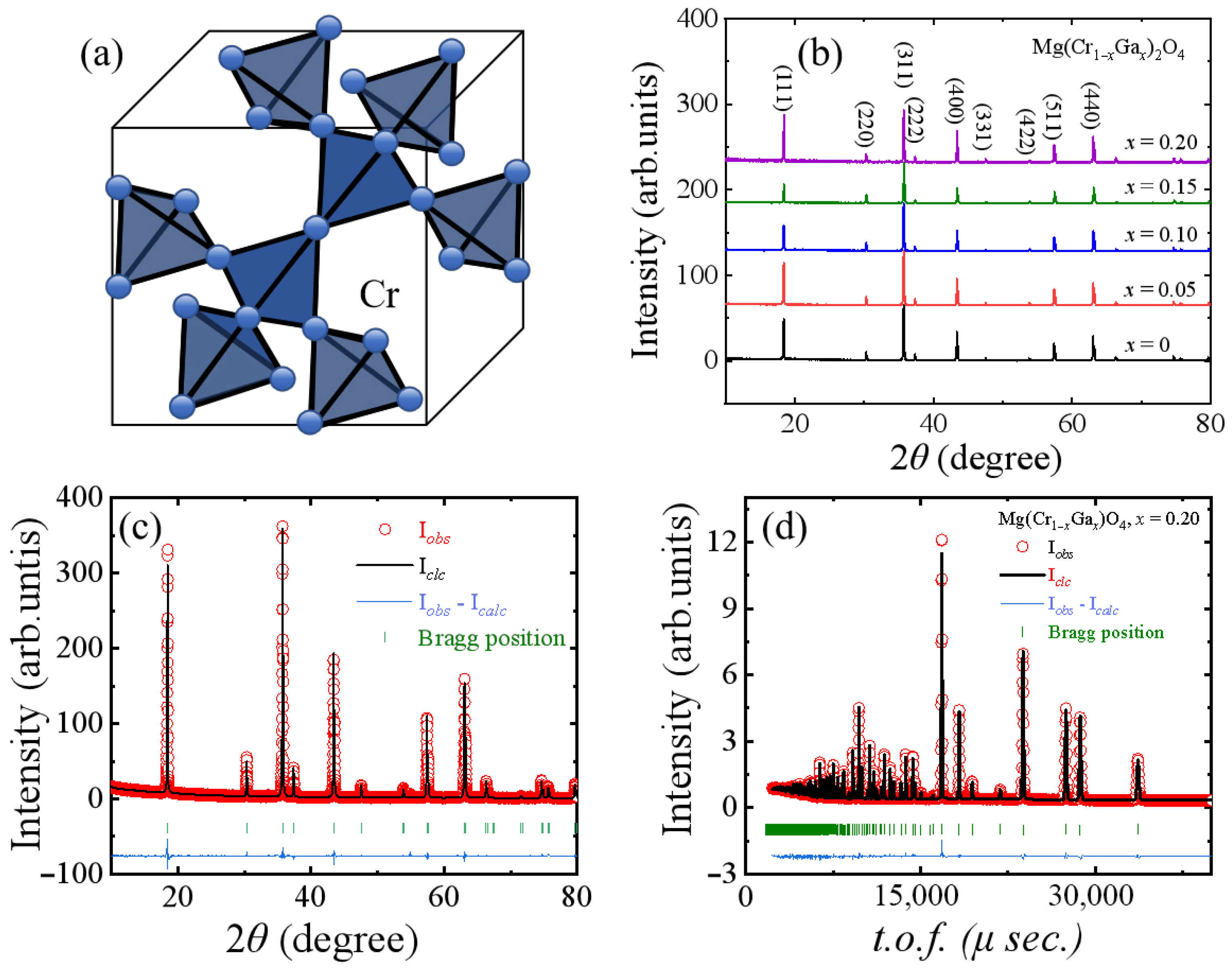
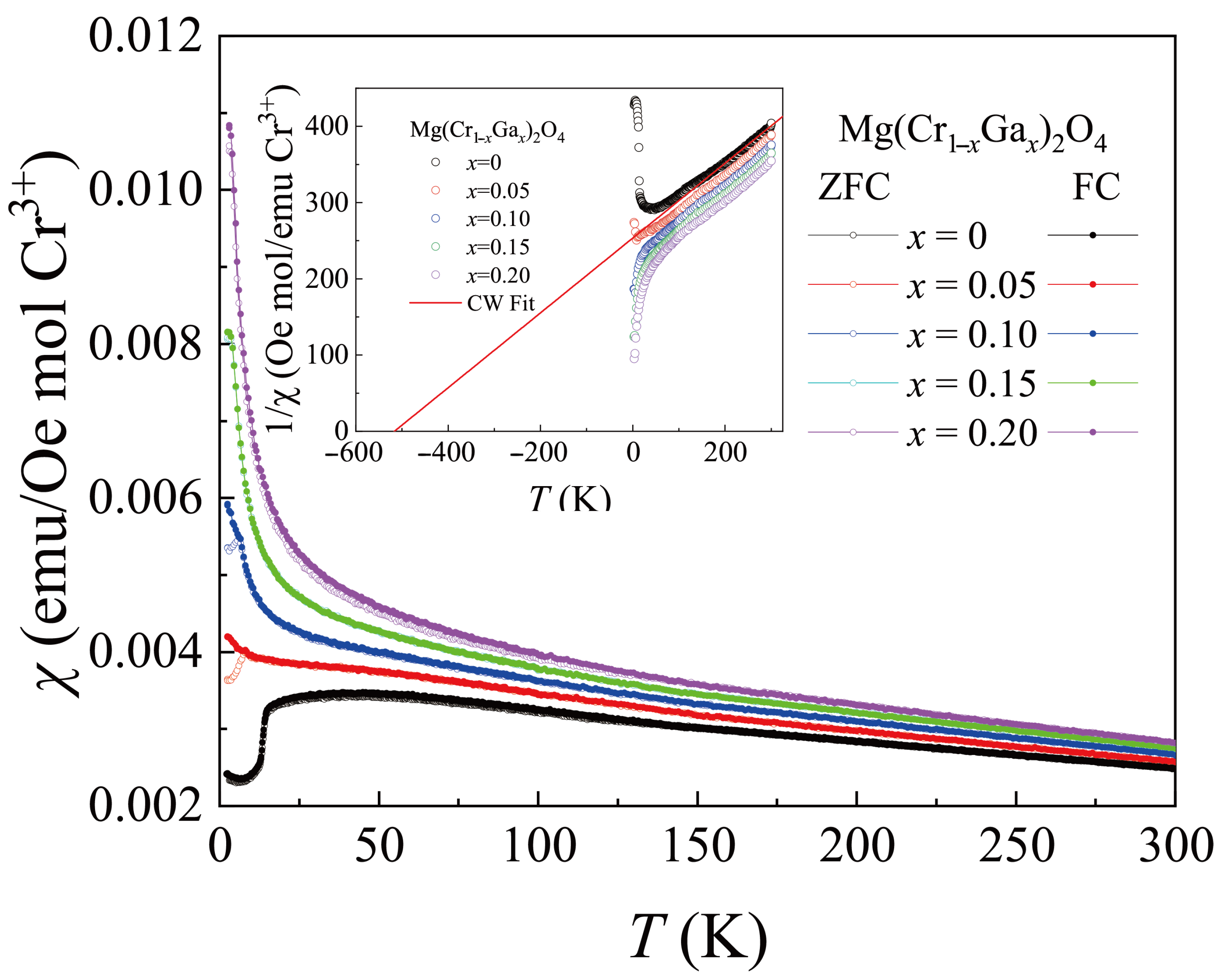
3.1. MgCr2O4 Doped with Ga
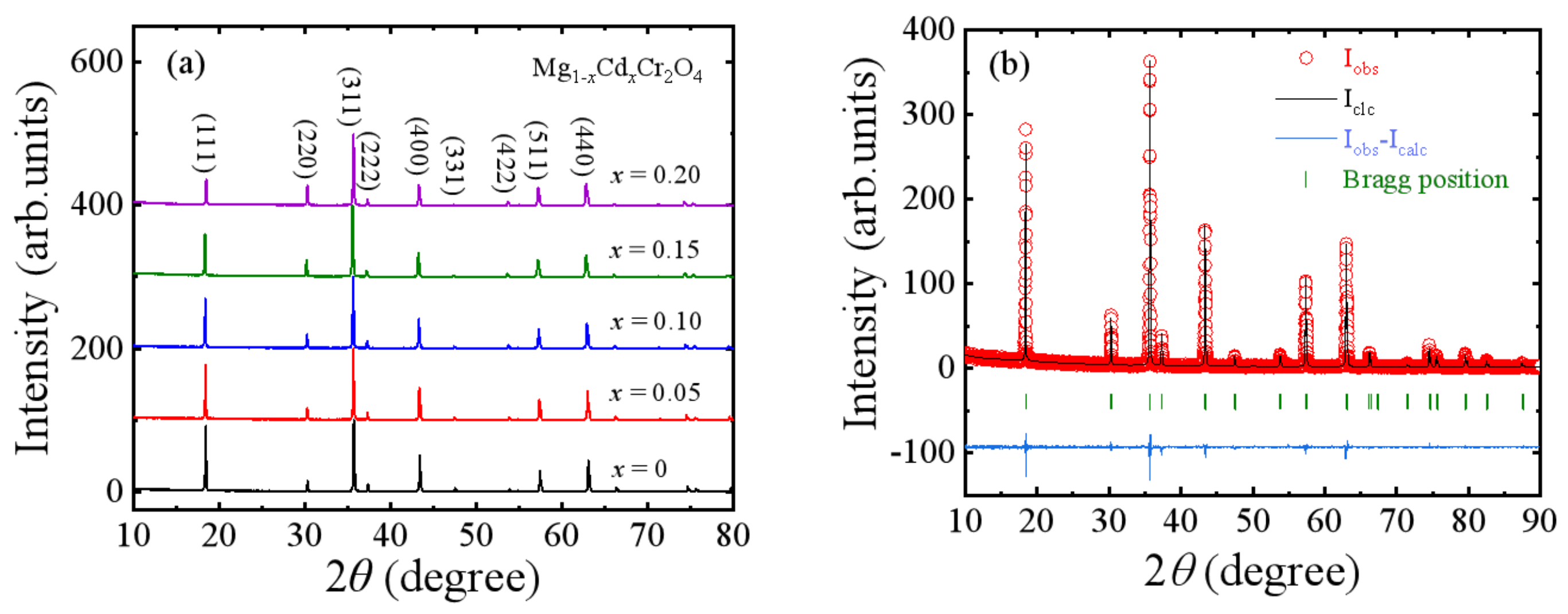
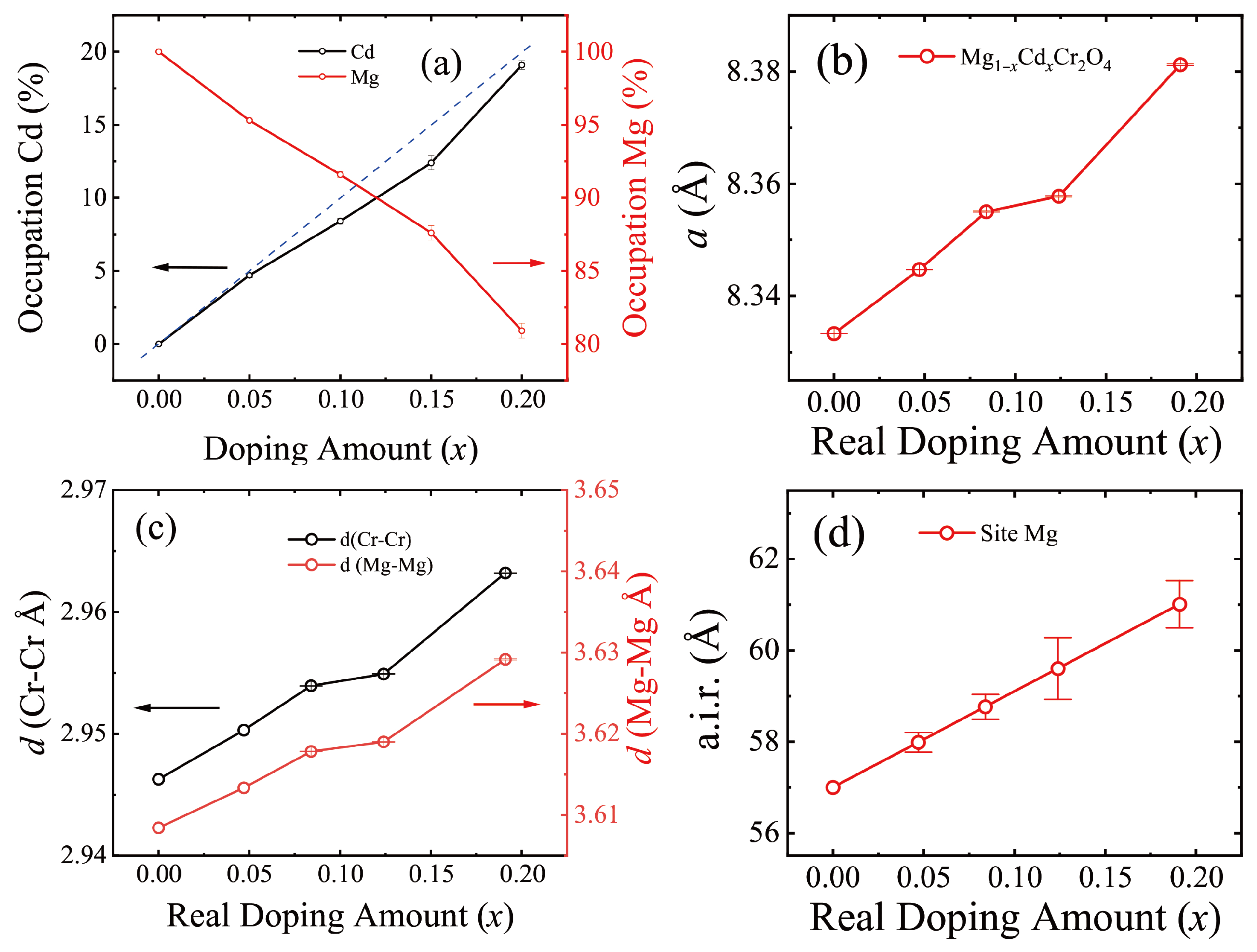
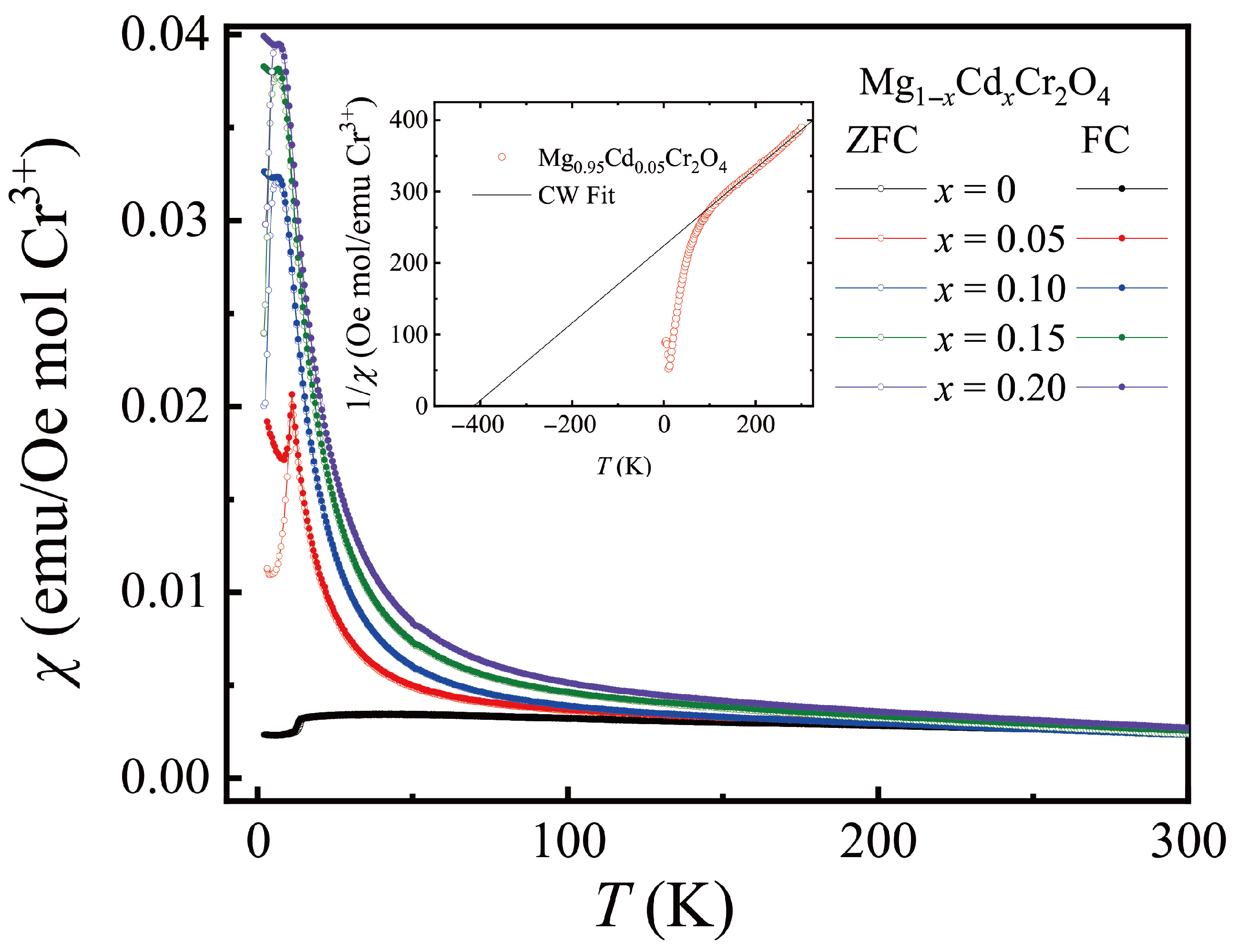
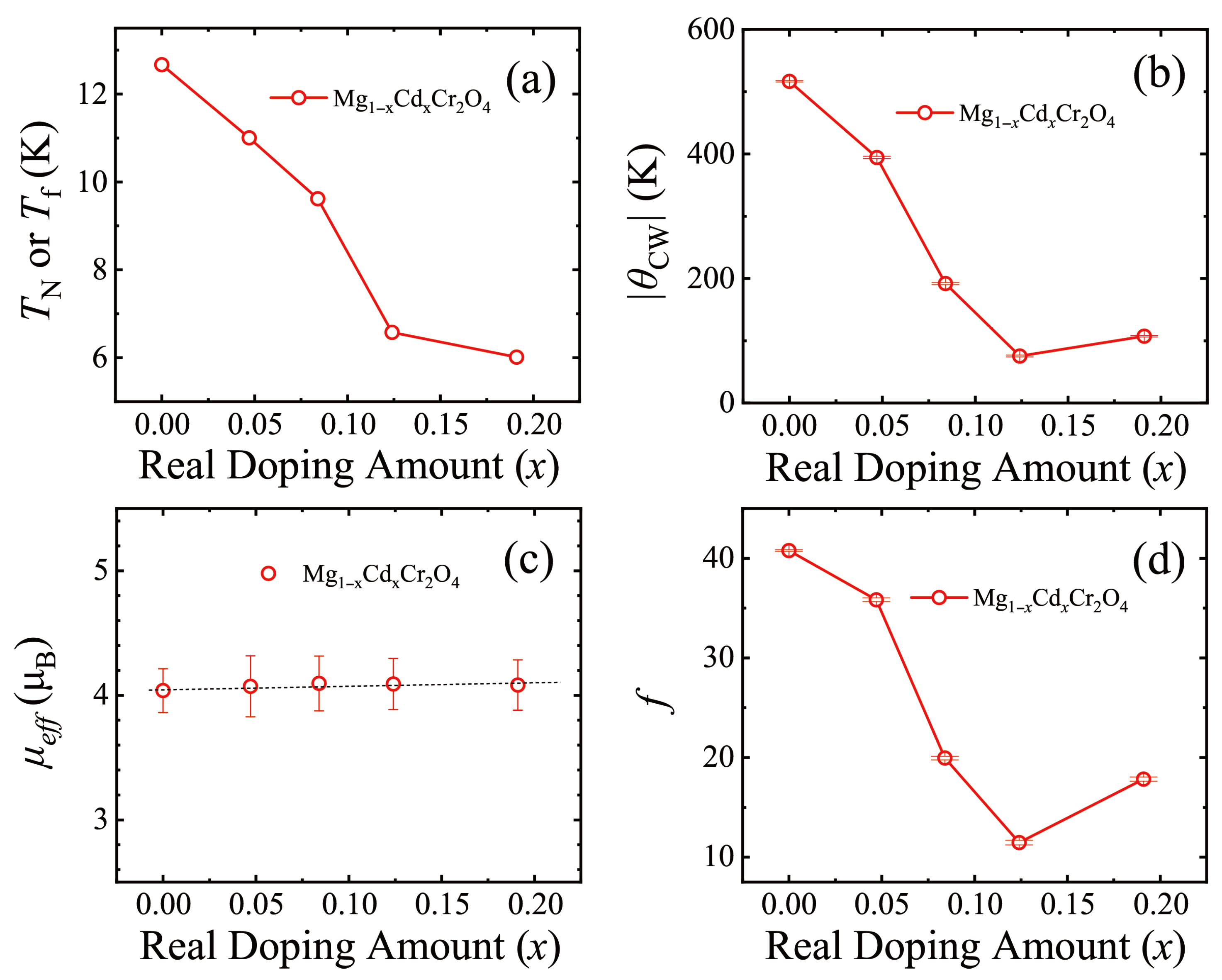
3.2. MgCr2O4 Doped with Cd
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Atom | Wyckoff Position | x | y | z |
|---|---|---|---|---|
| O | 32e | 0.26004 | 0.26004 | 0.26004 |
| Cr | 16d | 0.50000 | 0.50000 | 0.50000 |
| Ga(1) | 16d | 0.50000 | 0.50000 | 0.50000 |
| Mg | 8a | 0.12500 | 0.12500 | 0.12500 |
| Ga(2) | 8a | 0.12500 | 0.12500 | 0.12500 |
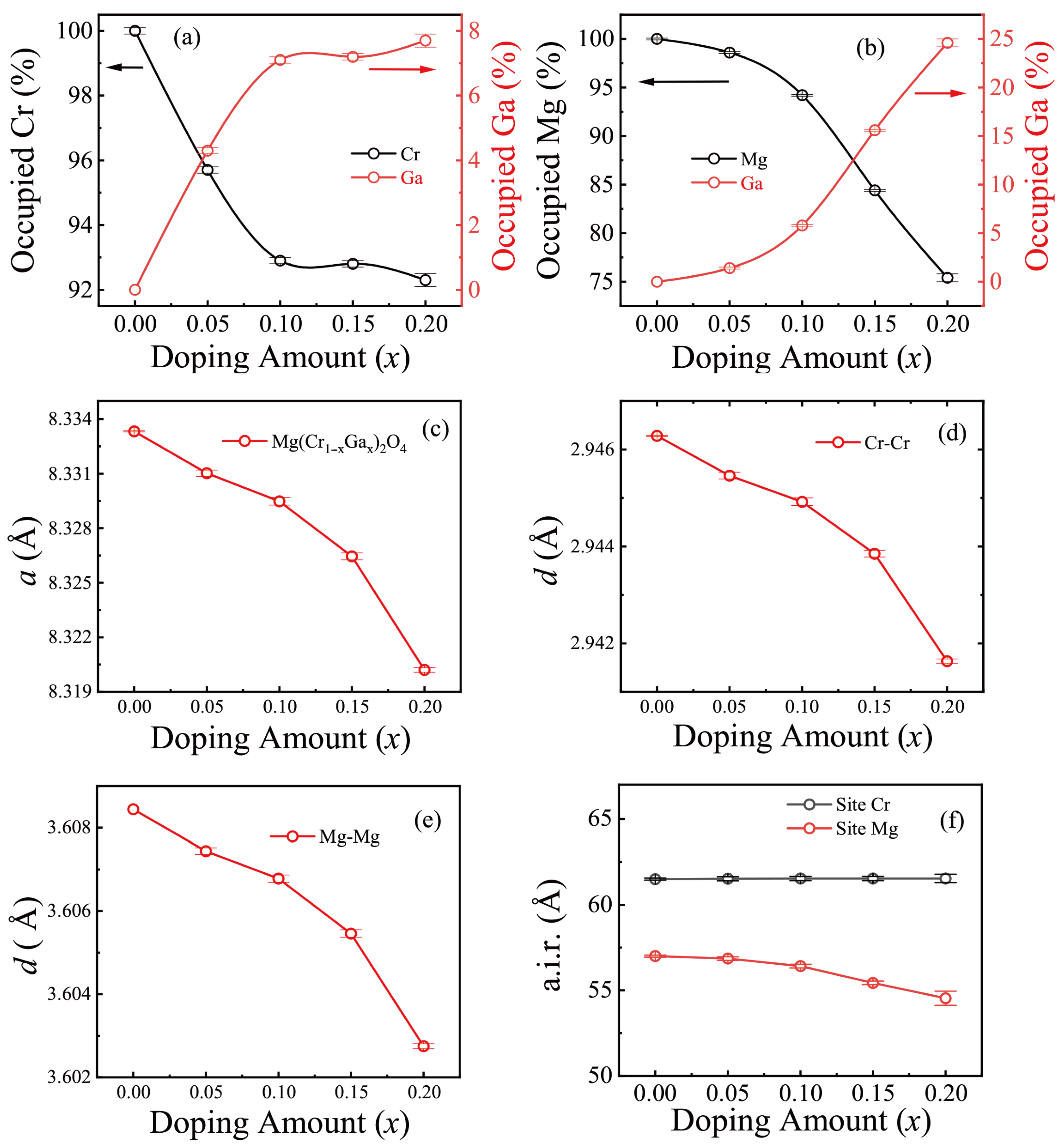
| x | a (Å) | B-Site Occupancy (%) | A-Site Occupancy (%) | ||||
|---|---|---|---|---|---|---|---|
| Cr | Ga | Mg | Ga | ||||
| 0 | 8.33333 (3) | 3.60844 (0) | 2.94628 (0) | 100.0 (1) | 0 | 100.0 (1) | 0 |
| 0.05 | 8.33293 (17) | 3.60744 (8) | 2.94546 (7) | 95.7 (1) | 4.3 (1) | 98.6 (1) | 1.4 (1) |
| 0.10 | 8.33111 (21) | 3.60678 (9) | 2.94492 (8) | 92.9 (1) | 7.1 (1) | 94.2 (1) | 5.8 (1) |
| 0.15 | 8.32714 (19) | 3.60546 (9) | 2.94385 (7) | 92.8 (1) | 7.2 (1) | 84.4 (1) | 15.6 (1) |
| 0.20 | 8.32183 (13) | 3.60275 (6) | 2.94163 (5) | 92.3 (2) | 7.7 (2) | 75.4 (2) | 24.6 (2) |
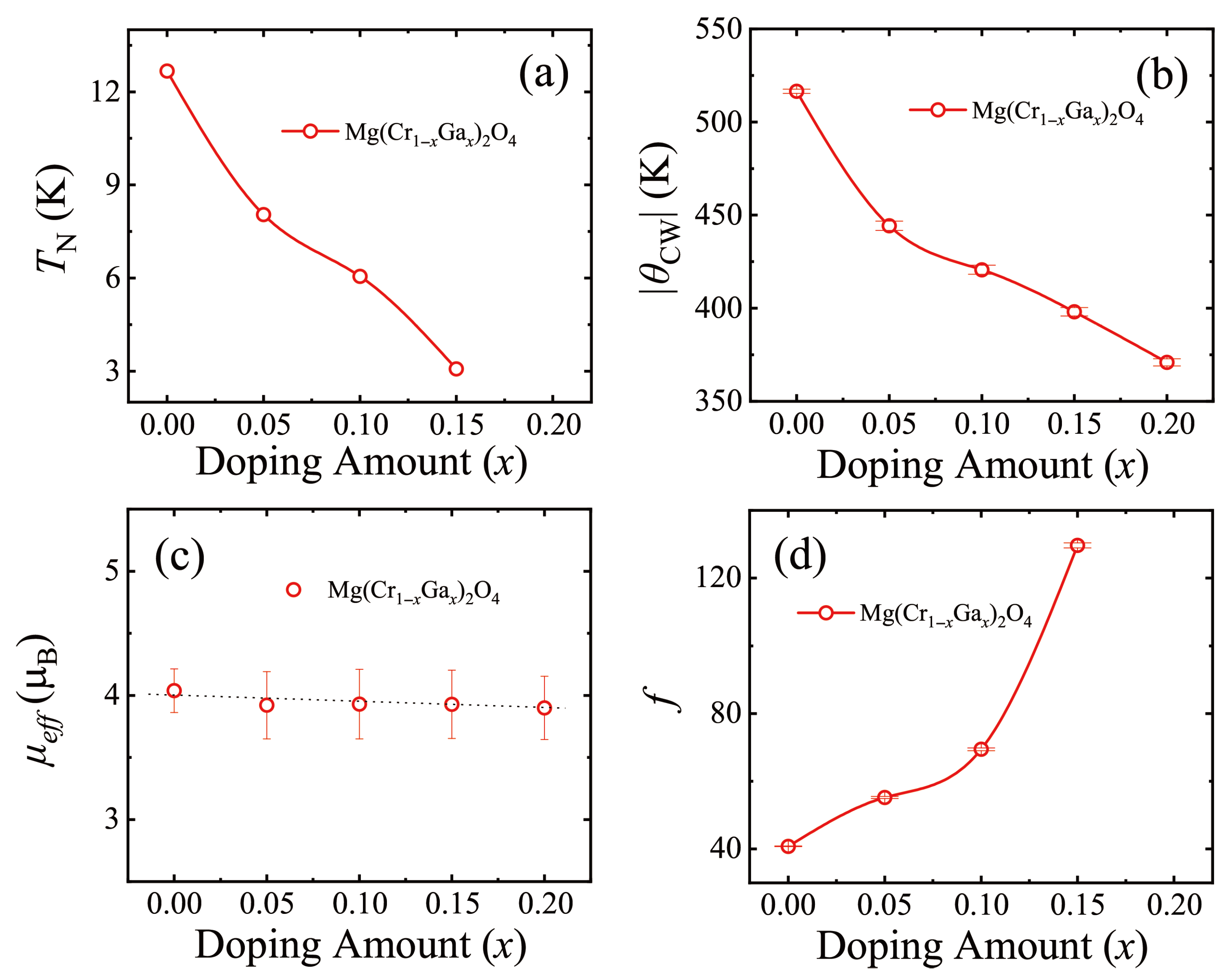
| Mg(Cr1−xGax)2O4 | (K) | (K) | () | f |
|---|---|---|---|---|
| 0 | 12.6 | −516.498 (11) | 4.04 (18) | 40.77 (9) |
| 0.05 | 8.0 | −444.311 (25) | 3.92 (27) | 55.23 (31) |
| 0.10 | 6.1 | −420.684 (25) | 3.93 (28) | 69.46 (41) |
| 0.15 | 3.1 | −398.092 (23) | 3.93 (27) | 129.67 (75) |
| 0.20 | <2.0 | −370.944 (19) | 3.90 (25) | >123.49 (64) |
| x | a (Å) | A-Site Occupancy (%) | |||
|---|---|---|---|---|---|
| Mg | Cd | ||||
| 0 | 8.33333 (3) | 2.94628 (0) | 3.60844 (0) | 100.0 (1) | 0 |
| 0.05 | 8.34472 (4) | 2.9503 (0) | 3.61337 (0) | 95.3 (2) | 4.7 (2) |
| 0.10 | 8.35502 (9) | 2.95395 (4) | 3.61783 (4) | 91.6 (2) | 8.4 (2) |
| 0.15 | 8.35776 (13) | 2.95491 (5) | 3.61902 (6) | 87.6 (5) | 12.4 (5) |
| 0.20 | 8.38121 (14) | 2.96321 (6) | 3.62917 (7) | 80.9 (5) | 19.1 (3) |
| Mg1− xCdxCr2O4 | (K) | (K) | () | f |
|---|---|---|---|---|
| 0 | 12.667 | −516.5 (11) | 4.04 (18) | 40.77 (9) |
| 0.05 | 11.004 | −394.3 (19) | 4.07 (24) | 35.84 (17) |
| 0.10 | 9.616 | −191.8 (17) | 4.10 (22) | 19.95 (17) |
| 0.15 | 6.579 | −75.4 (15) | 4.09 (21) | 11.46 (23) |
| 0.20 | 6.015 | −107.2 (13) | 3.08 (20) | 17.83 (21) |
References
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Moessner, R.; Ramirez, A.P. Geometrical frustration. Phys. Today 2006, 59, 24–29. [Google Scholar] [CrossRef]
- Rao, X.; Hussain, G.; Huang, Q.; Chu, W.J.; Li, N.; Zhao, X.; Dun, Z.; Choi, E.S.; Asaba, T.; Chen, L.; et al. Survival of itinerant excitations and quantum spin state transitions in YbMgGaO4 with chemical disorder. Nat. Commun. 2021, 12, 4949. [Google Scholar] [CrossRef]
- Helton, J.S.; Matan, K.; Shores, M.P.; Nytko, E.A.; Bartlett, B.M.; Qiu, Y.; Nocera, D.G.; Lee, Y.S. Dynamic scaling in the susceptibility of the spin-1/2 kagome lattice antiferromagnet Herbertsmithite. Phys. Rev. Lett. 2010, 104, 147201. [Google Scholar] [CrossRef]
- Khuntia, P.; Velazquez, M.; Barthélemy, Q.; Bert, F.; Kermarrec, E.; Legros, A.; Bernu, B.; Messio, L.; Zorko, A.; Mendels, P. Gapless ground state in the archetypal quantum kagome antiferromagnet ZnCu3(OH)6Cl2. Nat. Phys. 2020, 16, 469–474. [Google Scholar] [CrossRef]
- Han, T.H.; Helton, J.S.; Chu, S.; Nocera, D.G.; Rodriguez-Rivera, J.A.; Broholm, C.; Lee, Y.S. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 2012, 492, 406–410. [Google Scholar] [CrossRef]
- Schweika, W.; Valldor, M.; Lemmens, P. Approaching the ground state of the kagomé antiferromagnet. Phys. Rev. Lett. 2007, 98, 067201. [Google Scholar] [CrossRef]
- Stewart, J.R.; Ehlers, G.; Mutka, H.; Fouquet, P.; Payen, C.; Lortz, R. Spin dynamics, short-range order, and spin freezing in Y0.5Ca0.5BaCo4O7. Phys. Rev. B—Condensed Matter Mater. Phys. 2011, 83, 024405. [Google Scholar] [CrossRef]
- Okamoto, Y.; Nohara, M.; Aruga-Katori, H.; Takagi, H. Spin-liquid state in the S = 1/2 hyperkagome antiferromagnet Na4Ir3O8. Phys. Rev. Lett. 2007, 99, 137207. [Google Scholar] [CrossRef] [PubMed]
- Gardner, J.S.; Gingras, M.J.P.; Greedan, J.E. Magnetic pyrochlore oxides. Rev. Mod. Phys. 2010, 82, 53–107. [Google Scholar] [CrossRef]
- Siddharthan, R.; Shastry, B.S.; Ramirez, A.P.; Hayashi, A.; Cava, R.J.; Rosenkranz, S. Ising pyrochlore magnets: Low-temperature properties, “ice rules,” and beyond. Phys. Rev. Lett. 1999, 83, 1854. [Google Scholar] [CrossRef]
- Gingras, M.J.P.; McClarty, P.A. Quantum spin ice: A search for gapless quantum spin liquids in pyrochlore magnets. Rep. Prog. Phys. 2014, 77, 056501. [Google Scholar] [CrossRef]
- Bramwell, S.T.; Gingras, M.J.P. Spin ice state in frustrated magnetic pyrochlore materials. Science 2001, 294, 1495–1501. [Google Scholar] [CrossRef] [PubMed]
- Matsuhira, K.; Hinatsu, Y.; Tenya, K.; Amitsuka, H.; Sakakibara, T. Low-temperature magnetic properties of pyrochlore stannates. J. Phys. Soc. Jpn. 2002, 71, 1576–1582. [Google Scholar] [CrossRef]
- Shapiro, M.C.; Riggs, S.C.; Stone, M.B.; de la Cruz, C.R.; Chi, S.; Podlesnyak, A.A.; Fisher, I.R. Structure and magnetic properties of the pyrochlore iridate Y2Ir2O7. Phys. Rev. B 2012, 85, 214434. [Google Scholar] [CrossRef]
- Xu, J.; Anand, V.K.; Bera, A.K.; Frontzek, M.; Abernathy, D.L.; Casati, N.; Siemensmeyer, K.; Lake, B. Magnetic structure and crystal-field states of the pyrochlore antiferromagnet Nd2Zr2O7. Phys. Rev. B 2015, 92, 224430. [Google Scholar] [CrossRef]
- Das, D.; Ghosh, S. Density functional theory based comparative study of electronic structures and magnetic properties of spinel ACr2O4 (A = Mn, Fe, Co, Ni) compounds. J. Phys. D Appl. Phys. 2015, 48, 425001. [Google Scholar] [CrossRef]
- Ali, A.; Singh, Y. A magnetocaloric study on the series of 3d-metal chromites ACr2O4 (A = Mn, Fe, Co, Ni, Cu and Zn). J. Magn. Magn. Mater. 2020, 499, 166253. [Google Scholar] [CrossRef]
- Kassem, M.A.; El-Fadl, A.A.; Nashaat, A.M.; Nakamura, H. Structure, optical and varying magnetic properties of insulating MCr2O4 (M = Co, Zn, Mg and Cd) nanospinels. J. Alloys Compd. 2019, 790, 853–862. [Google Scholar] [CrossRef]
- Moureen, C.K.; Stephanie, L.M.; Lucy, E.D.; Ram, S.; Matthew, R.S.; Daniel, P.S.; Katharine, P.; Joan, S. Structural ground states of (A,A′)Cr2O4 (A = Mg, Zn; A′ = Co, Cu) spinel solid solutions: Spin-Jahn-Teller and Jahn-Teller effects. Phys. Rev. B 2014, 89, 174410. [Google Scholar]
- Ohgushi, K.; Okimoto, Y.; Ogasawara, T.; Miyasaka, S.; Tokura, Y. Magnetic, optical, and magnetooptical properties of spinel-type ACr2X4 (A = Mn, Fe, Co, Cu, Zn, Cd; X = O, S, Se). J. Phys. Soc. Jpn. 2008, 77, 034713. [Google Scholar] [CrossRef]
- Lau, G.C.; Ueland, B.G.; Freitas, R.S.; Dahlberg, M.L.; Schiffer, P.; Cava, R.J. Magnetic characterization of the sawtooth-lattice olivines ZnL2S4 (L = Er, Tm, Yb). Phys. Rev. B 2006, 73, 012413. [Google Scholar] [CrossRef]
- Zhandun, V.S. The magnetic, electronic, optical, and structural properties of the AB2O4 (A = Mn, Fe, Co; B = Al, Ga, In) spinels: Ab initio study. J. Magn. Magn. Mater. 2021, 533, 168015. [Google Scholar] [CrossRef]
- Ortega-San-Martin, L.; Williams, A.J.; Gordon, C.D.; Klemme, S.; Attfield, J.P. Low temperature neutron diffraction study of MgCr2O4 spinel. J. Phys. Condens. Matter 2008, 20, 104238. [Google Scholar] [CrossRef]
- Dutton, S.E.; Huang, Q.; Tchernyshyov, O.; Broholm, C.L.; Cava, R.J. Sensitivity of the magnetic properties of the ZnCr2O4 and MgCr2O4 spinels to nonstoichiometry. Phys. Rev. B 2011, 83, 064407. [Google Scholar] [CrossRef]
- Bai, X.; Paddison, J.A.M.; Kapit, E.; Koohpayeh, S.M.; Wen, J.-J.; Dutton, S.E.; Savici, A.T.; Kolesnikov, A.I.; Granroth, G.E.; Broholm, C.L.; et al. Magnetic excitations of the classical spin liquid MgCr2O4. Phys. Rev. Lett. 2019, 122, 097201. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.D.; Zhao, Z.Y.; Sun, X.F.; Suarez, M.N.; Rivas-Murias, B.; Tsurkan, V.; Deisenhofer, J.; Zapf, V.S.; Rivadulla, F. Low-temperature spin excitations in frustrated ZnCr2O4 probed by high-field thermal conductivity. Phys. Rev. B 2013, 87, 174436. [Google Scholar] [CrossRef]
- Matsuda, M.; Ueda, H.; Kikkawa, A.; Tanaka, Y.; Katsumata, K.; Narumi, Y.; Inami, T.; Ueda, Y.; Lee, S.-H. Spin–lattice instability to a fractional magnetization state in the spinel HgCr2O4. Nat. Phys. 2007, 3, 397–400. [Google Scholar] [CrossRef]
- Ueda, H.; Mitamura, H.; Goto, T.; Ueda, Y. Field-induced metamagnetic transitions in S = 3/2 Heisenberg antiferromagnets MCr2O4. Prog. Theor. Phys. Suppl. 2005, 159, 256–259. [Google Scholar] [CrossRef]
- Rudolf, T.; Kant, C.; Mayr, F.; Hemberger, J.; Tsurkan, V.; Loidl, A. Spin-phonon coupling in antiferromagnetic chromium spinels. New J. Phys. 2007, 9, 76. [Google Scholar] [CrossRef]
- Shaked, H.; Hastings, J.M.; Corliss, L.M. Magnetic structure of magnesium chromite. Phys. Rev. B 1970, 1, 3116. [Google Scholar] [CrossRef]
- Suzuki, H.; Tsunoda, Y. Spinel-type frustrated system MgCr2O4 studied by neutron scattering and magnetization measurements. J. Phys. Chem. Solids 2007, 68, 2060–2063. [Google Scholar] [CrossRef]
- Gao, S.; Guratinder, K.; Stuhr, U.; White, J.S.; Mansson, M.; Roessli, B.; Fennell, T.; Tsurkan, V.; Loidl, A.; Hatnean, M.C.; et al. Manifolds of magnetic ordered states; and excitations in the almost Heisenberg pyrochlore antiferromagnet MgCr2O4. Phys. Rev. B 2018, 97, 134430. [Google Scholar] [CrossRef]
- Tomiyasu, K.; Suzuki, H.; Toki, M.; Itoh, S.; Matsuura, M.; Aso, N.; Yamada, K. Molecular spin resonance in the geometrically frustrated magnet MgCr2O4 by inelastic neutron scattering. Phys. Rev. Lett. 2008, 101, 177401. [Google Scholar] [CrossRef]
- Yong, W.; Botis, S.; Shieh, S.R.; Shi, W.; Withers, A.C. Pressure-induced phase transition study of magnesiochromite (MgCr2O4) by Raman spectroscopy and X-ray diffraction. Phys. Earth Planet. Inter. 2012, 196, 75–82. [Google Scholar] [CrossRef]
- Lee, S.-H.; Ratcliff, W., II; Huang, Q.; Kim, T.H.; Cheong, S.-W. Néel to spin-glass-like phase transition versus dilution in geometrically frustrated ZnCr2−2xGa2xO4. Phys. Rev. B 2008, 77, 014405. [Google Scholar] [CrossRef]
- Yu, J.; Wang, L.; Ying, Y.; Zheng, J.; Li, W.; Qiao, L.; Cai, W.; Li, J.; Zhang, L.; Che, S. Magnetic Exchange Interactions in Geometrically Frustrated Antiferromagnet of ZnCr2−xGaxO4. J. Supercond. Nov. Magn. 2019, 32, 1095–1098. [Google Scholar] [CrossRef]
- Martinho, H.; Moreno, N.O.; Sanjurjo, J.A.; Rettori, C.; Âa-Adeva, A.J.G.; Huber, D.L.; Oseroff, S.B.; Ratcliff, W., II; Cheong, S.-W.; Pagliuso, P.G.; et al. Magnetic properties of the frustrated antiferromagnetic spinel ZnCr2O4 and the spin-glass Zn1−xCdxCr2O4 (x = 0.05, 0.10). Phys. Rev. B 2001, 64, 024408. [Google Scholar] [CrossRef]
- Ohta, H.; Okubo, S.; Kikuchi, H.; Ono, S. Millimetre-wave ESR (electron-spin resonance) measurements of frustrated system ZnCr2xGa2−2xO4. Can. J. Phys. 2001, 79, 1387–1391. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Found. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Kant, C.; Deisenhofer, J.; Tsurkan, V.; Loidl, A. Magnetic susceptibility of the frustrated spinels ZnCr2O4, MgCr2O4 and CdCr2O4. J. Phys. Conf. Ser. 2010, 200, 032032. [Google Scholar] [CrossRef]
- Nassar, L.S.; Lane, H.; Haberl, B.; Graves-Brook, M.; Winn, B.; Koohpayeh, S.M.; Mourigal, M. Pressure control of magnetic order and excitations in the pyrochlore antiferromagnet MgCr2O4. Phys. Rev. B 2024, 109, 064415. [Google Scholar] [CrossRef]
- Niu, X.; Liu, C.; Zong, B. Investigation on the microstructure and magnetic properties of Mg(Ga2−XFex)O4 Spinel Ferrites. J. Mater. Sci. Mater. Electron. 2023, 34, 118. [Google Scholar] [CrossRef]
- Das, A.; Ranaut, D.; Pal, P.; Pal, R.; Mandal, P.; Pal, A.N.; Moulick, S.; Das, M.; Topwal, D.; Mukherjee, K.; et al. Tuning of magnetic frustration and emergence of a magnetostructural transition in Mn1−XCdxCr2O4. Phys. Rev. B 2023, 108, 064426. [Google Scholar] [CrossRef]
- Koohpayeh, S.M.; Wen, J.-J.; Mourigal, M.; Dutton, S.E.; Cava, R.J.; Broholm, C.L.; McQueen, T.M. Optical floating zone crystal growth and magnetic properties of MgCr2O4. J. Cryst. Growth 2013, 384, 39–43. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; He, Z.; Cheng, D.; Ge, H.; Zhang, W.; Wang, X.; Zhou, P.; Luo, W.; Fu, Z.; Liu, X.; et al. Effect of the Non-Magnetic Ion Doping on the Magnetic Behavior of MgCr2O4. Magnetism 2025, 5, 19. https://doi.org/10.3390/magnetism5030019
Zhou F, He Z, Cheng D, Ge H, Zhang W, Wang X, Zhou P, Luo W, Fu Z, Liu X, et al. Effect of the Non-Magnetic Ion Doping on the Magnetic Behavior of MgCr2O4. Magnetism. 2025; 5(3):19. https://doi.org/10.3390/magnetism5030019
Chicago/Turabian StyleZhou, Fuxi, Zheng He, Donger Cheng, Han Ge, Wenjing Zhang, Xiao Wang, Pengfei Zhou, Wanju Luo, Zhengdong Fu, Xinzhi Liu, and et al. 2025. "Effect of the Non-Magnetic Ion Doping on the Magnetic Behavior of MgCr2O4" Magnetism 5, no. 3: 19. https://doi.org/10.3390/magnetism5030019
APA StyleZhou, F., He, Z., Cheng, D., Ge, H., Zhang, W., Wang, X., Zhou, P., Luo, W., Fu, Z., Liu, X., Wu, L., He, L., Zhao, Y., & Feng, E. (2025). Effect of the Non-Magnetic Ion Doping on the Magnetic Behavior of MgCr2O4. Magnetism, 5(3), 19. https://doi.org/10.3390/magnetism5030019







