1. Introduction
With the emergence of the field of molecular magnetism [
1,
2], the rapid expansion in the synthesis of exchange-coupled clusters, along with their physical and spectroscopic characterization—such as their temperature-dependent magnetic susceptibilities, electron paramagnetic resonance (EPR), and inelastic neutron-scattering spectra—has made theoretical modeling based on effectively treating the open-shell metal ions as spin centers increasingly important [
3,
4]. The most common description is the Heisenberg model of pairwise scalar coupling, Equation (1),
where
is a local spin vector, which also arises in other contexts, such as the coupling between nuclear spins in NMR [
5]. While the direction-dependent properties observed in EPR require the inclusion of anisotropic terms, these effects can often be treated via perturbation theory [
3].
The levels of such an isotropic Hamiltonian are characterized by a total-spin value
S and comprise
states with magnetic quantum numbers
(eigenvalues of the
z-component
). Molecular symmetry manifests in terms of the permutations of spin sites [
6,
7], allowing each level to be additionally assigned to an irreducible representation (irrep)
of the respective point group (PG). Point-group symmetry follows from choosing the isotropic couplings in a way that reflects the desired molecular symmetry; anisotropic interactions explicitly encode the geometric structure [
8,
9].
Given the rapidly increasing dimensions of the Hilbert space with the number of centers, it becomes essential, when aiming for exact diagonalization (ED), to exploit all available symmetries to factor the Hamiltonian into smaller blocks, each characterized by labels
S and
[
10]. Beyond facilitating computations, a classification of levels can be useful for deriving selection rules [
11,
12] or for separating the geometric and dynamic features of spectra [
11,
12,
13].
Combining PG and
symmetry by working from a basis of uncoupled configurations
(also known as a Zeeman product basis [
5]) defined by local
z-projections with the sum
M, as in Equation (2),
is straightforward [
6,
14]. In addition, for
, spin-flip symmetry can be used to separate sectors with an even or odd
S [
14]. Such approaches have been applied widely, e.g., in the full ED of symmetric polyhedra [
15] or in calculations of the thermodynamic properties of lattice fragments with up to
sites using the finite-temperature Lanczos method (FTLM) [
16]. However, factorization of the Hamiltonian in terms of
and
S, which involves constructing eigenfunctions of
(rather than only
), is considered more demanding and has been pursued in just a few cases. The most prominent strategy used for this task [
6,
10,
17,
18,
19] is based on genealogical coupling (GC) [
3,
20], where individual spins are coupled into subunits of increasing size until a multiplet with the total spin
S is obtained. The calculation of the Hamiltonian elements from such a basis makes use of irreducible tensor–operator techniques and proceeds by successive decoupling through Wigner-9
j symbols [
3]. However, a complication arises from PG adaption [
6]: for most systems, there is no compatible coupling scheme, i.e., PG operations may produce states belonging to different schemes, related to the original basis by their respective site permutations, and transforming them back can become prohibitively demanding as it requires the computation of a large number of square roots and Wigner-6
j symbols [
10,
17]. Resorting to the use of a subgroup that enables the construction of a compatible coupling scheme [
6,
10] to avoid such transformations presents two drawbacks: it neither produces the smallest possible Hamiltonian matrix blocks, nor does it provide a comprehensive labeling of eigenstates.
GC is not the only method used for constructing spin eigenfunctions [
20], but Sahoo et al. [
21] briefly reviewed why various other techniques are also difficult to apply in conjunction with arbitrary point groups. To overcome this limitation, these authors suggested transformations between uncoupled and valence bond (VB) states. In a VB state, each site
is replaced by
auxiliary spin-1/2 objects,
of which are singlet-paired according to Rumer–Pauling rules, supplemented by the restriction that no pairs are formed within the same center. As PG symmetrization and setting up the Hamiltonian would require complicated transformations between different diagrams, VB states are transformed into the uncoupled basis set (using Clebsch–Gordan coefficients), where the PG projectors and the Hamiltonian have simple representations. Thus, coupled and uncoupled bases are utilized for spin and PG adaptation, respectively. This approach is extendable to fermionic systems [
22] and can be applied to all types of point groups, but it has not been widely adopted. Since full ED was only demonstrated for a rather small system with a cubic arrangement of 14
sites (the dimension of the largest symmetry subspace was 219) [
21], it remains uncertain how well the procedure would scale to more challenging cases.
Our present strategy of applying spin and PG projectors to uncoupled states is suitable for arbitrary point groups, and it is simpler than the GC or VB methods. Note that Bernu et al. [
23] combined Löwdin’s spin-projection operator [
24]—
in Equation (6) below—with a spatial-symmetry projector in a Lanczos process to compute a small number of lowest states for clusters of up to 36 spin-1/2 centers. We recently used a similar approach to obtain analytical solutions for particularly small clusters [
25]. In contrast, the present aim is the full numerical diagonalization of systems that would be challenging to solve without using all available symmetries. Details on forming spin eigenfunctions based on a group-theoretical formulation of
(a procedure that we investigated recently [
26]) and on the construction of the Hamiltonian in each
subspace are provided in the following Theory and Computational Details section. In the Results and Discussion section, we assess the numerical accuracy of this approach and present several cases that represent some of the largest fully solved spin models to date, including systems that cannot be practically handled using the conventional GC method.
2. Theory and Computational Details
In the following, we explain the combined spin and PG adaptation of uncoupled configurations to set up a generalized eigenvalue problem (GEP) defined by the Hamiltonian and the overlap matrix in a symmetry subspace characterized by the quantum numbers
S and
. We start with a discussion of PG adaptation. The projection onto a specific component
of a possibly multidimensional irrep
is given in Equation (3):
where
h is the order of the group, the sum runs over all elements
g,
is a symmetry operation that permutes the
z-projections
, and
is a diagonal element of the representation matrix
(the asterisk * denotes complex conjugation). Note that, when employing characters
instead of specific matrix elements
, the components are not separated; see Equation (4).
We work with Equation (3) instead of Equation (4) in order to reduce the size of the Hamiltonian matrix in each respective sector by the number of components
n (the dimension of
), i.e.,
. The subspace dimension can be represented as the weighted sum of Equation (5), where
is the matrix representation of
in the basis set with the selected
M. To compute the traces of individual operations,
, we examine each
and check whether it is mapped onto itself under the action of
.
The irreps of the cyclic group
, which is relevant for spin rings, are one-dimensional and characterized by a crystal momentum
associated with the eigenvalues
of the site permutation
corresponding to a rotation of
. Except when
(Mulliken label A) or
(label B, for even
N),
k and
comprise degenerate pairs spanning two-dimensional irreps (
,
, etc.) of the dihedral group
. Therefore, when working with the
group, ED can be restricted to the sectors
for even
N or
for odd
N. A few guidelines for the simple construction of the required matrices for more complicated groups like icosahedral
or octahedral
were provided in our previous work [
26]: permutation and representation matrices [
27] are explicitly set up only for the group generators, and the permutations are pairwise-compounded until a closed set of elements is obtained; whenever a new element is found, the corresponding pair of representation matrices is similarly multiplied to obtain the new representation matrix.
In many cases—including in cyclic groups—a complete and orthogonal basis in a
sector can be constructed by ensuring that each uncoupled state appears in at most one linear combination. The configurations
selected by this rule form a complete orthogonal space
upon the application of
and are stored in the columns of the matrix
(each column of
has exactly one entry of 1). While it was previously assumed that each
would always contribute to at most one linear combination [
25], we have observed that this does not generally hold for multidimensional irreps of the icosahedral group, where a
may appear in multiple states for a given
, provided its coefficients have different magnitudes in different states. A small threshold on the number of these distinct absolute amplitudes (e.g., two or three) suffices to generate the complete
space. The resulting
is generally overcomplete with respect to
. However, rather than directly pruning linear dependencies, a single rank-revealing selection (as discussed below) is performed later to choose configurations for simultaneous spin and PG projection.
For large , we typically stop the generation of once approximately 20% more states have been collected than the number of levels. If the subsequent spin adaptation step fails to fully span the space with this truncated set, then additional configurations can be considered. However, we found that to produce a suitable truncated set, the should be processed in a random order, not sequentially. (For example, for , a listing according to a binary representation, where and represent 1 and 0, would not be adequate; the ordering should be randomized for generating a truncated PG-adapted basis.)
Turning now to the construction of spin eigenfunctions, we note that the direct application of Löwdin’s projector, Equation (6),
can induce significant numerical rounding errors due to the repeated matrix–vector multiplications needed to isolate the subspace with the desired
S [
23,
26]. To circumvent these issues, we employ a group-theoretical integral formulation of
[
28],
where
is a diagonal element of the Wigner rotation matrix for spin
S. Evaluating the wave function
, i.e., Equation (8), obtained by applying
to a state
with
, is greatly simplified by the integral formulation.
The integrals over Euler angles
and
(corresponding to rotations about the
z-axis) are trivial. The remaining integration over
involves the element
of the small Wigner matrix and is reduced to a standard integral for spin-1/2 systems [
29], which leads to a closed-form expression for
, Equation (9), in terms of a special kind of so-called Sanibel coefficient [
30] involving only a sign factor and a binomial coefficient,
where
k is the number of sites where
and
is the number of
sites in the reference configuration, i.e.,
,
. For
, the wave function becomes a linear combination of standard integrals [
26] (one may alternatively evaluate the integrals numerically on a grid). As we recently demonstrated [
26], this analytical group-theoretical approach to evaluating the action of
provides numerical advantages over Löwdin’s projector. Accordingly, we exclusively employ this method in the present work.
The number of multiplets with spin
S transforming according to
is calculated from Equation (5), assuming
. The
level is symmetric under all spin-permutations; thus,
, where
is the totally symmetric irrep.
A subset (see the next section on the selection procedure) of
columns from
comprises the matrix
R. These configurations span a complete, linearly independent
basis once the projectors have been applied. With
and
denoting their respective matrices (here and in the following, to avoid clutter, we will typically just refer to Γ for simplicity and let
denote
, while keeping in mind that the projection is always performed onto a specific component
μ), and considering the Hermiticity and idempotency of projection operators, the Hamiltonian and overlap matrices in a
sector are formulated as in Equations (11) and (12).
The Hamiltonian
H (in the uncoupled basis where
) is generated in a sparse format and is multiplied by the PG adapted states
, which are also in a sparse format. The spin adaptation works as described above, cf. Equation (9) for
, but as spin eigenfunctions are dense vectors, fully storing
may require excessive memory. Therefore, a single row (or a limited number of rows) of
is multiplied with the entire
to construct
(as well as
) sequentially. A symmetrization of
and
should be performed to eliminate numerical rounding errors, which would slow down the subsequent solution of the GEP and could lead to small imaginary components in the eigenvalues. The nonorthogonality of the symmetry-adapted basis is a feature shared with the GC and VB methods mentioned in the Introduction [
17,
21]. Rather than performing an explicit orthogonalization, we solve the GEP using the
eig function in
MATLAB R2024a.
We now discuss the selection of
states
from
for the combined application of
and
. As explained, the columns of
span the (possibly truncated) space
under
. Note that for pure spin projection in spin-1/2 systems, the so-called Löwdin theorem specifies how configurations ought to be selected so that under the action of
they span a complete, linearly independent basis in the
sector [
20]. We have recently generalized Löwdin’s theorem to systems with arbitrary local spin quantum numbers [
26] but observed that it does not constitute the most numerically stable procedure in terms of the conditioning of the overlap matrix (i.e., eigenvalues can approach zero within numerical precision). Instead, we proposed an iterative pivoted Cholesky decomposition [
31,
32] (PCD). This strategy efficiently selects a linearly independent subset for constructing a well-conditioned GEP. A practical alternative is a rank-revealing QR factorization with column-pivoting, which is directly available in MATLAB without additional coding, unlike PCD.
To our knowledge, there is no analogue to Löwdin’s theorem for selecting configurations for the combined action of
and
, and we thus build on the iterative strategy described previously to construct a
basis [
26]. However, this procedure is now applied in a slightly modified fashion (our explanation focuses specifically on PCD, but the iterative approach for state selection could be performed similarly for QR factorization with column-pivoting): rather than initially selecting a minimal number
of candidate states from
, we choose roughly 10–20% more to reduce the likelihood of multiple iterations (if
is a complete set of PG-adapted states generated from an ordered list of uncoupled configurations, its columns should be selected randomly). From these selected states, provisional overlap and Hamiltonian matrices
and
are formed, and the rank
r of
is computed at a reasonable tolerance well above numerical accuracy. At each step, the PCD routine identifies the pivot—the index of the largest diagonal element of the current residual matrix (initially set to
)—and then forms a normalized scaling vector to update that matrix. This procedure is repeated until
r pivots have been recorded, as detailed in
Figure 1. States failing the selection are removed, and if the rank of
in the subset of the selected pivot indices remains below
, then an additional batch of states is appended. If the process stagnates, the tolerance for rank determination may be reduced. Each iteration only updates
and
for any newly added states, thereby avoiding a recomputation of matrix elements.
In our implementation, the construction of spin eigenstates by analytically evaluating the group-theoretical integral of Equation (7) tends to lead to a computational bottleneck for . We therefore accelerate the construction of and by processing uncoupled states in parallel. With respect to assembling and solving the GEP, different sectors are independent—aside from the minor overhead of constructing the same uncoupled basis and Hamiltonian H for a given S but different Γ—thus permitting the straightforward distribution of these computations across the nodes of a computer cluster.
3. Results and Discussion
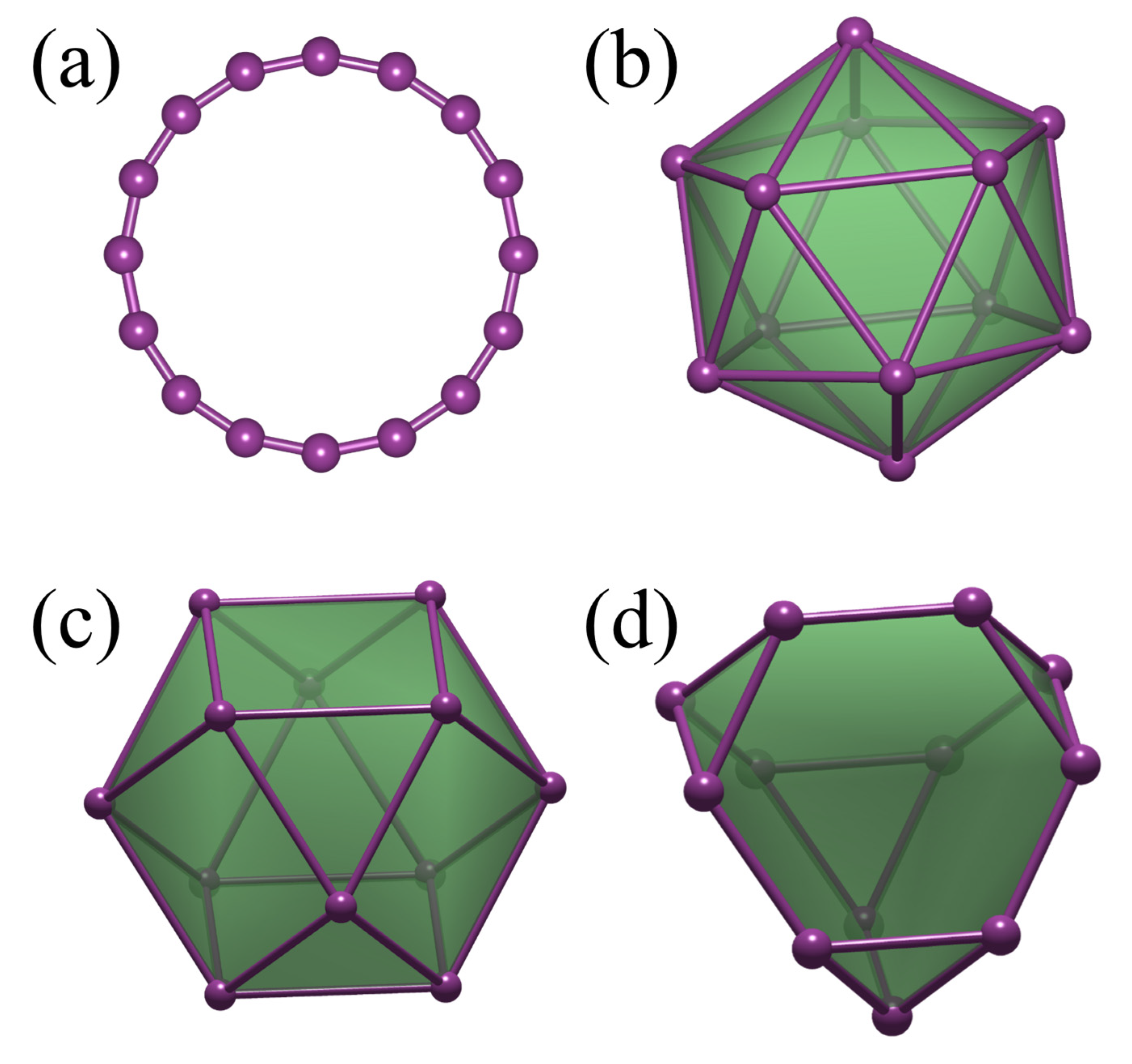
We consider spin rings and polyhedra—specifically, the icosahedron, cuboctahedron and truncated tetrahedron (see
Figure 2)—to illustrate the exact diagonalization procedure that uses a complete symmetry factorization of the Heisenberg spin Hamiltonian. Throughout, we assume nearest-neighbor couplings with
, which represent antiferromagnetic interactions. We note that our projection operator approach applies to any spin Hamiltonian exhibiting both total spin and point-group symmetries and is therefore not limited to the antiferromagnetic Heisenberg model.
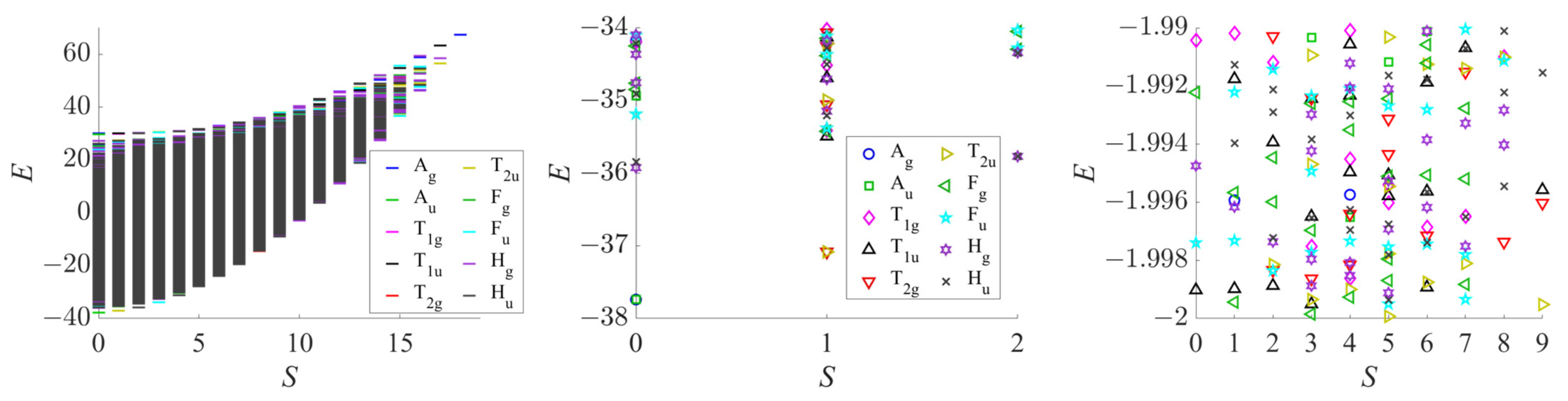
Spin ring. As the first example, we compare the results of two methods when factoring the spin Hamiltonian for an
,
ring: (1) using the straightforward PG adaptation of uncoupled states, labeling sectors by
(quantum numbers
S can be assigned to the levels using one of two methods: (i) calculating the spectra in all
subspaces, and if a level appears in a specific
M subspace but not in
, it corresponds to
, or (ii) diagonalizing only in the space with the smallest absolute value of
M (
or
) and assigning
S from the expectation value
, which requires access to the eigenfunctions); and (2) combining PG adaptation with total spin projection, labeling sectors by
. The first method involves a standard eigenvalue problem, while the second requires solving a generalized eigenvalue problem (GEP). The numerical accuracy of the
approach is guaranteed to be at approximately machine precision because all Hamiltonian elements are computed using exact algebraic expressions in MATLAB’s standard double-precision arithmetic. This ensures that the eigenvalues serve as a reliable benchmark for comparison with the
-based results. In the
approach, the spin projection is performed exactly, using Sanibel coefficients, as detailed above. This procedure avoids the numerical problems that could arise when using Löwdin’s projector or if the group-theoretical projection integral were discretized over a grid. However,
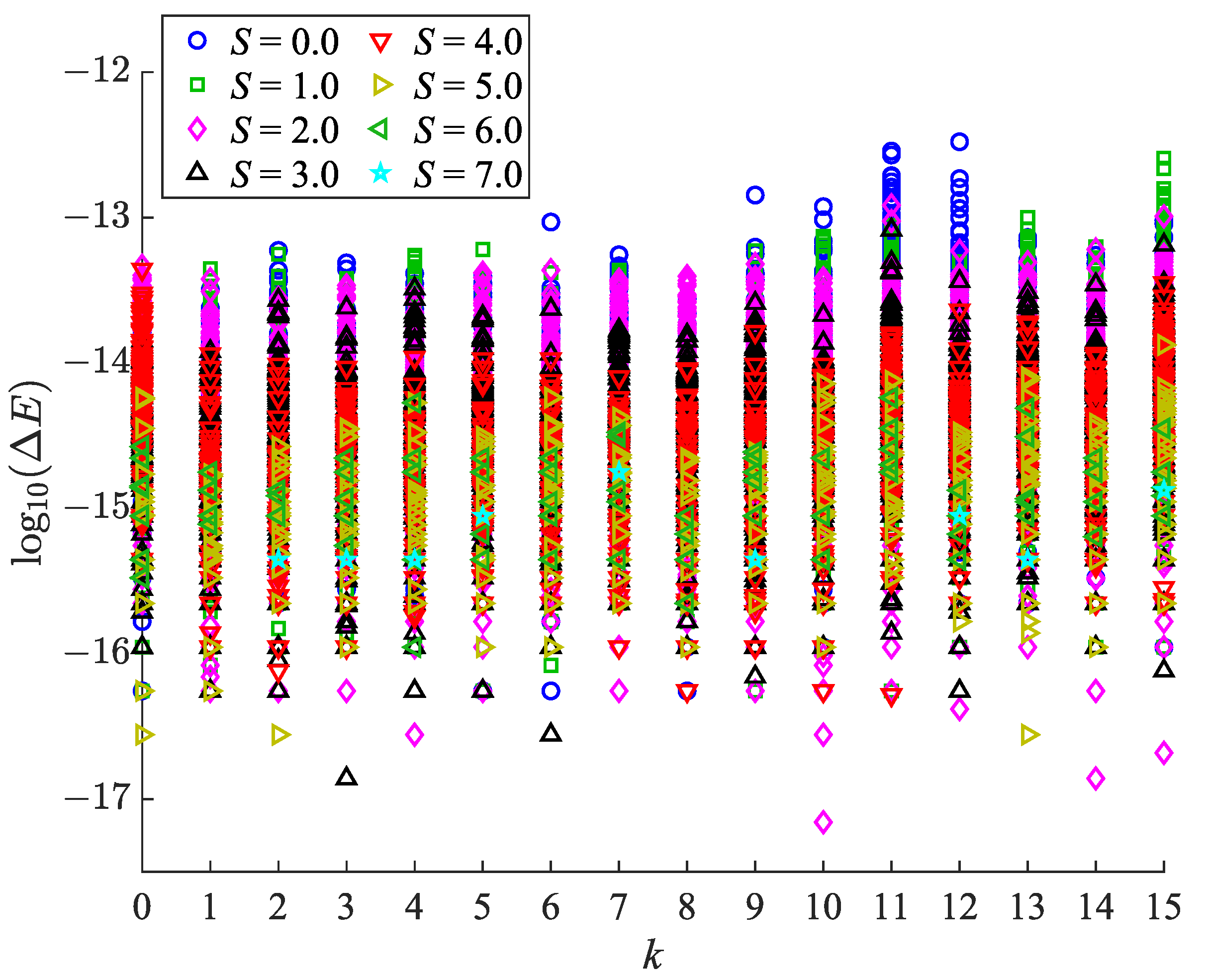
adaptation inherently involves solving a GEP, which may introduce errors due to the conditioning of the overlap matrix and the limitations of the numerical solver. As noted in the Theory and Computational Details section, we verify that the rank of the overlap matrix corresponds to the full dimension of the symmetry subspace within a reasonable tolerance.
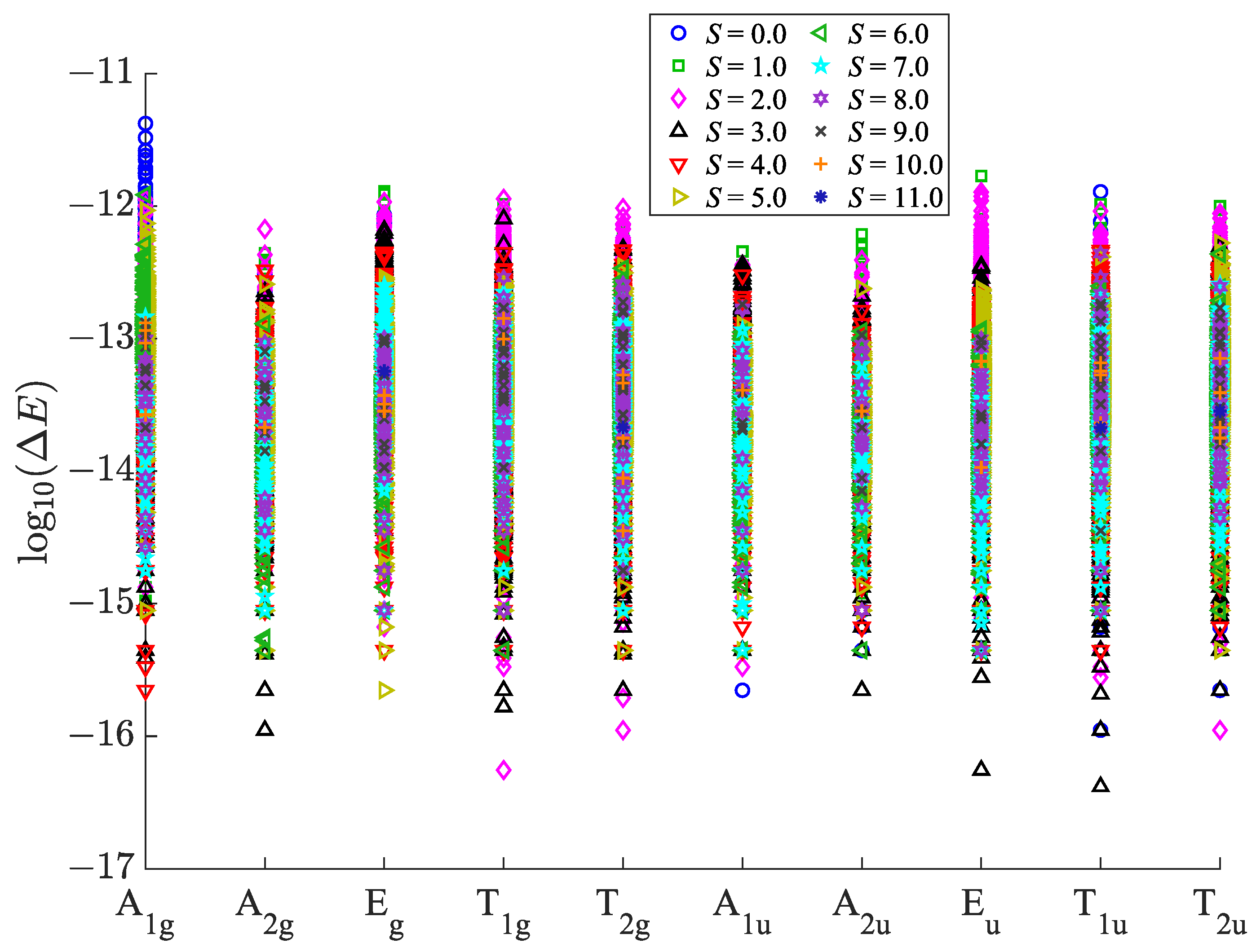
Figure 3 demonstrates that the energy errors for all levels are negligibly small for practical purposes, confirming the reliability of our
adaptation.
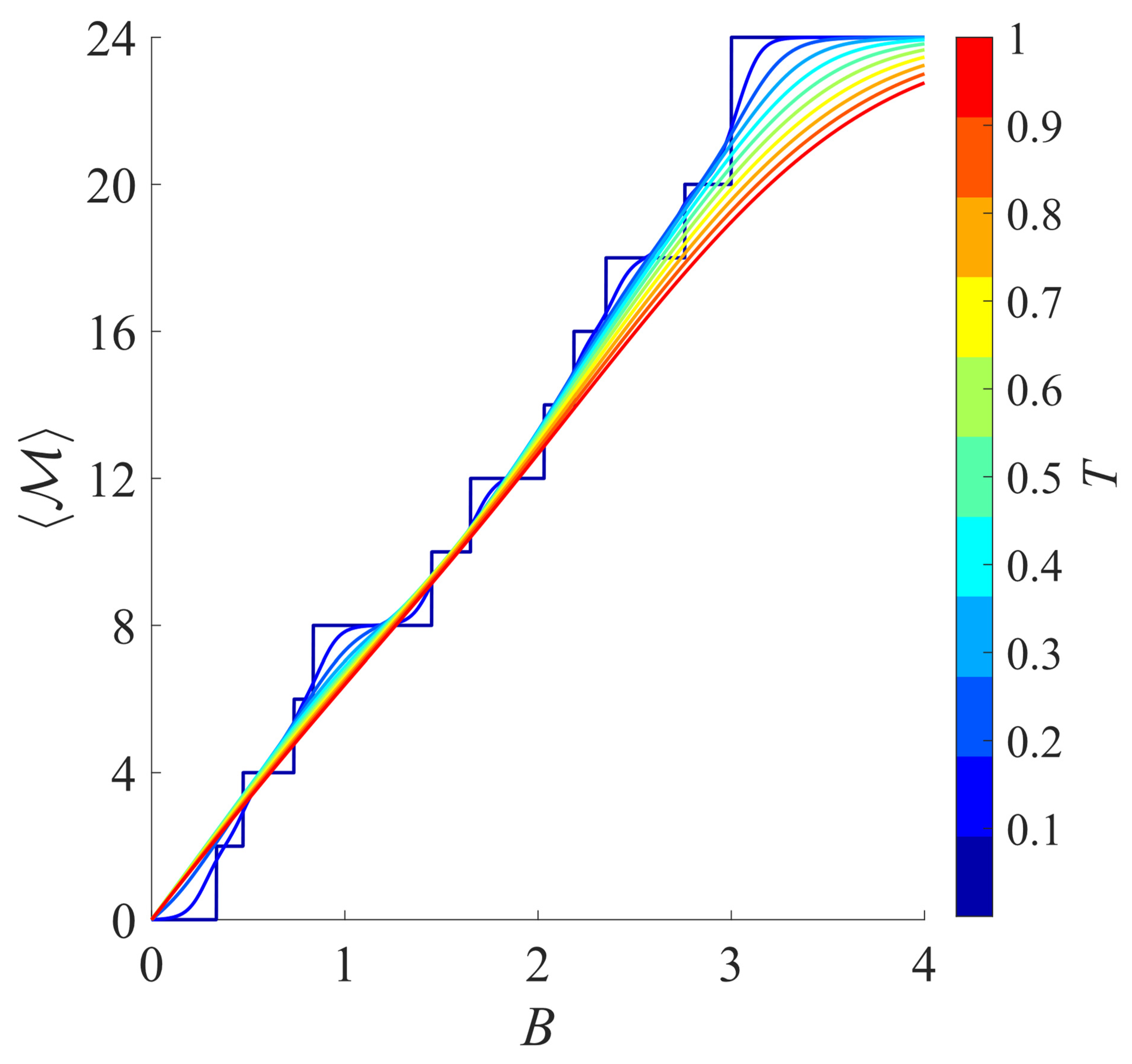
To illustrate the utility of the spectrum, we follow Ref. [
17] by focusing on two thermodynamic properties: magnetization and magnetic heat capacity, which are functions of the temperature and magnetic field. Both quantities can be readily computed using the complete set of eigenvalues. The thermal average
of the magnetization is given by Equation (13):
where
is the magnetic quantum number for state
i,
is the molecular partition function,
, and
represents the total energy, which includes the field-free energy
obtained from ED and a Zeeman contribution that depends on the external magnetic field
B, where
g and
denote the isotropic
g-factor and the Bohr magneton, respectively.
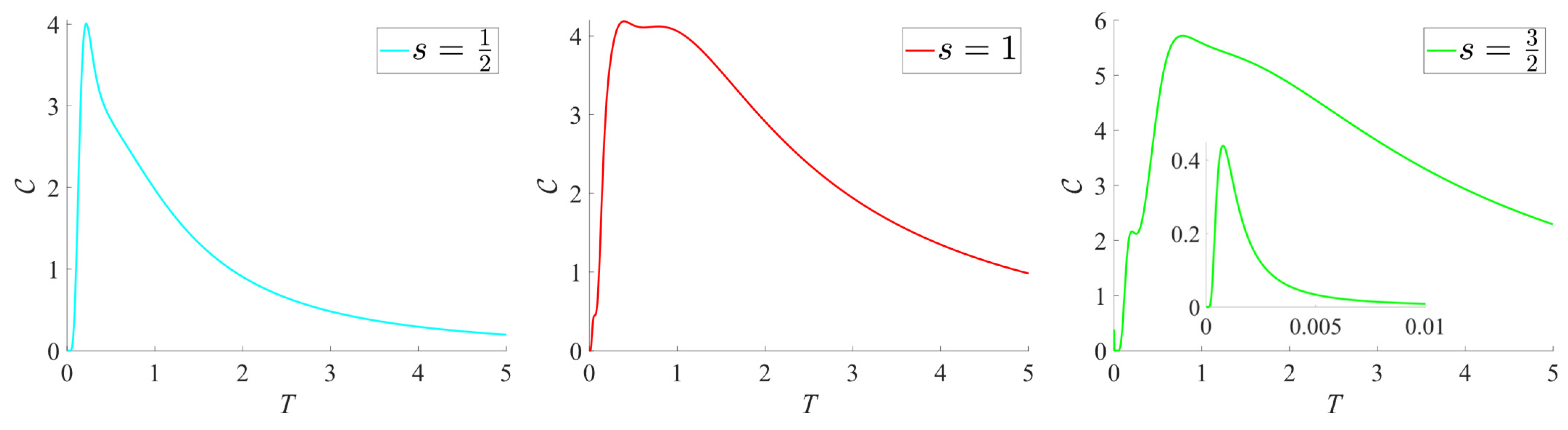
The heat capacity
, defined in Equation (14),
is expressed in terms of the internal energy
and can be calculated from the thermal-energy fluctuation, as shown in Equation (15):
where
.
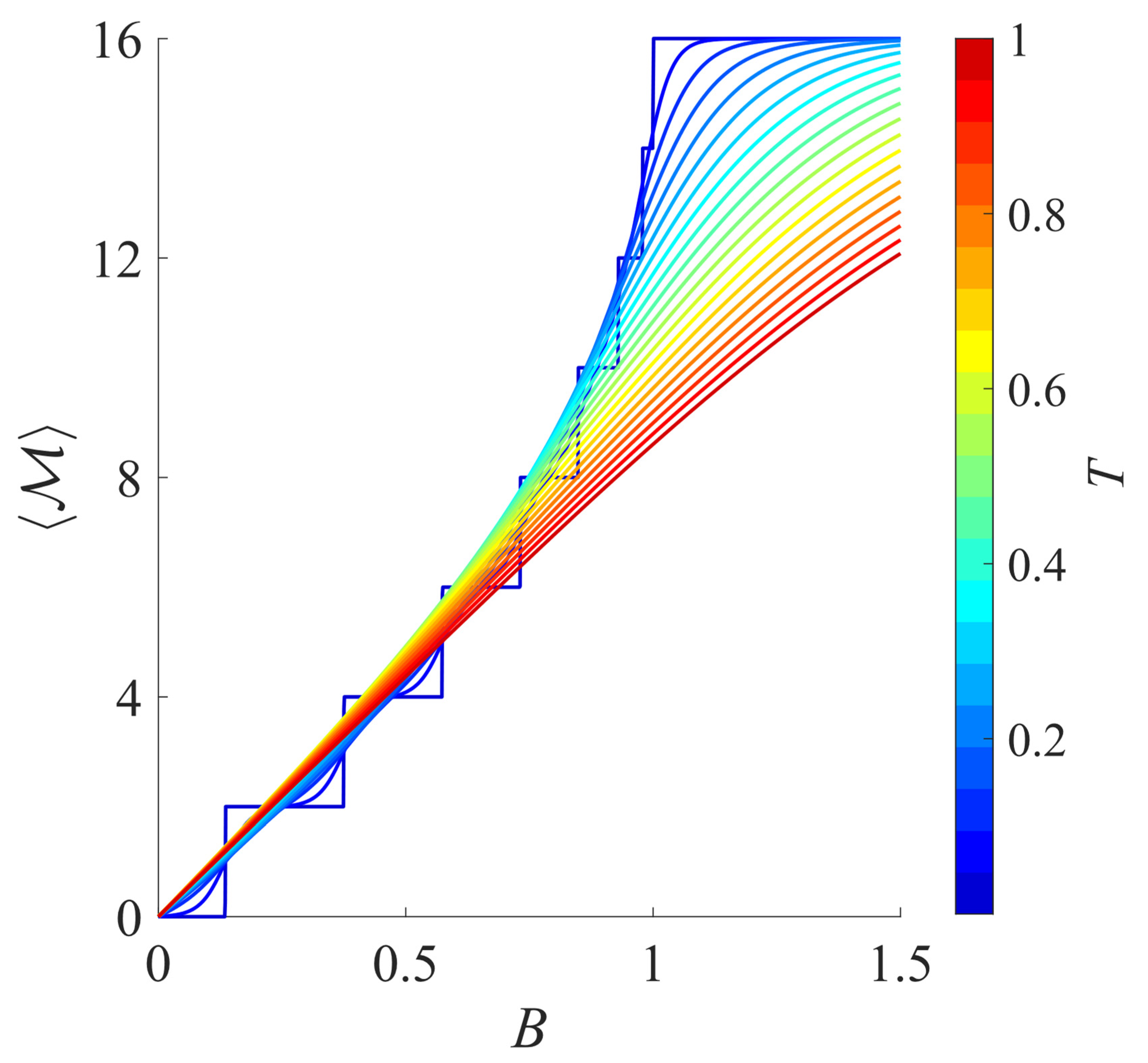
and
are plotted in
Figure 4 and
Figure 5, respectively, for the
,
ring; we set
and
.
The magnetization of an
,
ring (a Kramers system, with half-integer spin) is non-zero at
T = 0 in the zero-field limit; see
Figure 6. In real systems at low temperatures, however, anisotropic effects—such as local zero-field splitting (ZFS) and anisotropic
g-tensors—can also influence the magnetization.
Icosahedron. By employing the
point group and
(and spin-flip) symmetries, low-energy spectra for various values of
s have been obtained [
33], and the
icosahedron has been fully diagonalized by Konstantinidis [
15]. However, full diagonalization for
with such an approach would be challenging due to the significantly larger state-space dimension (cf.
Table A1 in
Appendix A). Although the Hamiltonian and overlap matrices in the
basis are stored in a memory-efficient sparse format, exploiting this advantage for complete diagonalization would require specialized libraries. The built-in eig function in MATLAB, which computes a full spectrum for (generalized) eigenvalue problems, does not accept sparse inputs; sparse matrices must thus be converted into their full counterparts. On the other hand, the iterative solver eigs is designed to compute only a subset of the eigenvalues (and eigenvectors) of sparse matrices.
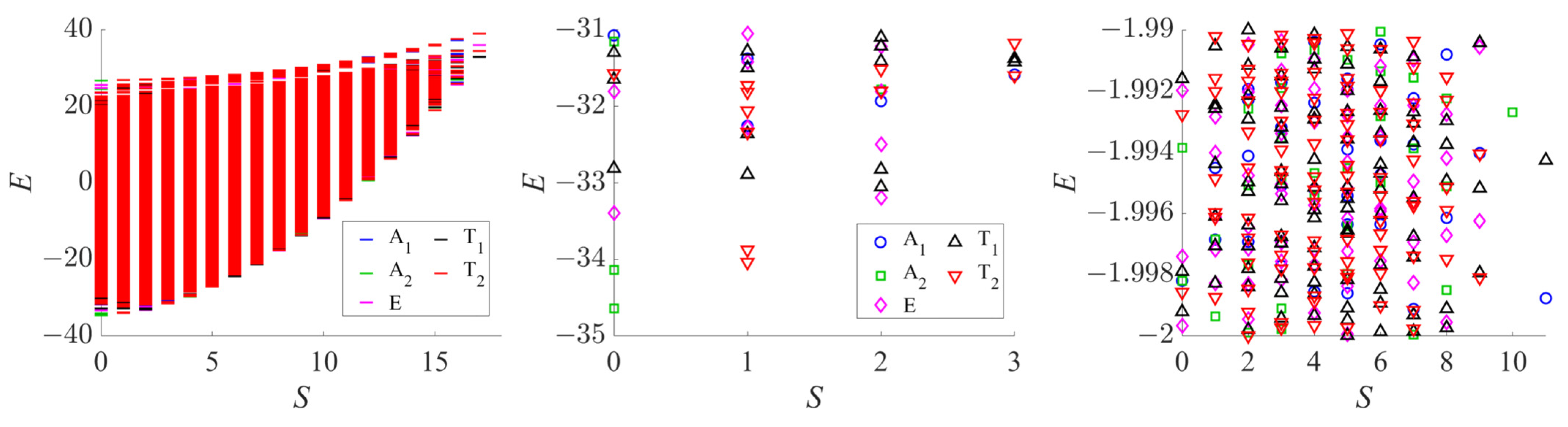
Using the GC method, it took three days on 128 processors to construct the Hamiltonian in the largest subspace in the
icosahedron (dimension 3315,
,
), primarily due to the computationally demanding transformations between coupling schemes [
10]. Using our current projection method on a desktop computer with six CPU cores, setting up the GEP in the same space (as explained in the Theory and Computational Details section, we separate the five components of
, reducing the matrix dimensions in the
,
space to
; see
Table A2 in
Appendix A) took only a few seconds, and determining the full spectrum took two minutes (this estimate is provided primarily for illustrative purposes, as it is likely possible to improve the implementation of our method to reduce the runtime). In our current implementation, the main bottleneck encountered is the construction of spin eigenstates, which requires evaluating the analytical form of the group-theoretical integral of Equation (7). The spin adaptation for
is more demanding for
systems of similar Hilbert-space dimensions because the integral—as explained in Ref. [
26]—decomposes into a sum of analytically evaluable standard integrals, and the number of terms in the sum grows steeply as
s increases. In contrast, for
systems, only a single standard integral needs to be evaluated.
Even with 256 processors, a full adaptation with respect to the total spin and
symmetry for the
icosahedron could not be completed using the GC approach [
10]. Instead, this system was diagonalized by adopting the
subgroup of
, which permits the construction of a compatible coupling scheme; however, the Hamiltonian blocks are significantly larger compared to full
symmetry. With our approach, we are now able to adapt to
within the complete
point group without any difficulty: the determination of the full spectrum of the
icosahedron took us approximately 16 h on a cluster node with 64 GB RAM and eight CPU cores. The dimensions of the respective subspaces are collected in
Table A3 and spectra are illustrated in
Figure 7. If only spin symmetry were used (as is done, e.g., in the MAGPACK program [
34]) instead of combined spin and PG symmetry, then the matrices are considerably larger and the relevant dimensionrs can be derived from the table in the
Appendix A. For example, for
S = 4, if one takes into account the degrees of degeneracy of the PG irreps, this results in a prohibitive matrix dimension of 258,192, according to Equation (16).
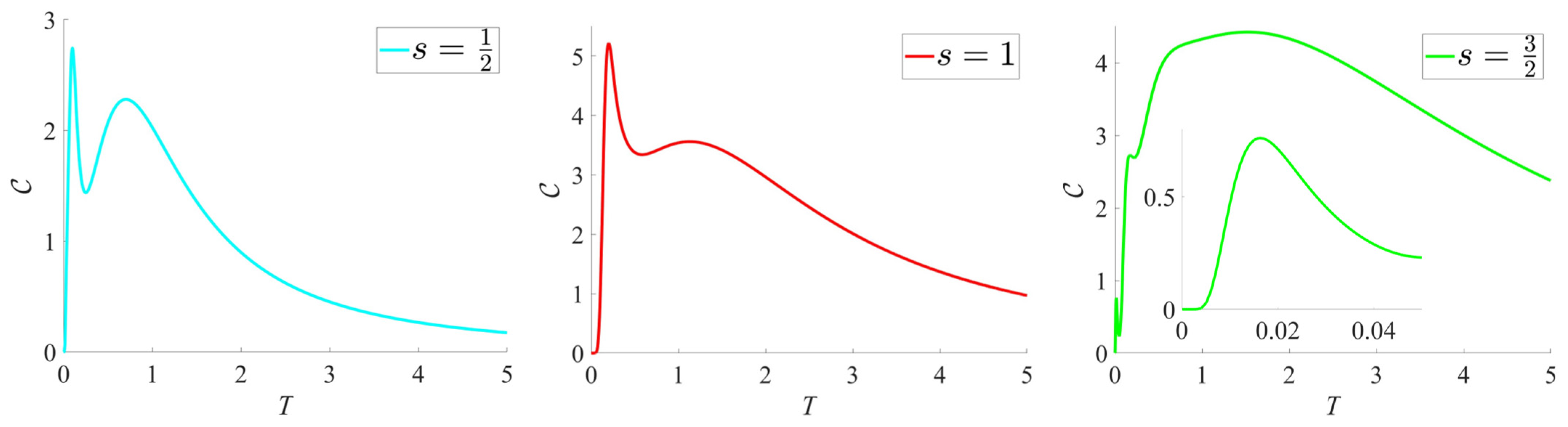
The magnetic heat capacities in the zero field for icosahedrons with
,
, and
are shown in
Figure 8. Note that for
and
heat capacity values have also been plotted in Ref. [
15] (albeit with a logarithmic temperature axis). There are two peaks in the low-temperature part of the curve for the
system. The first peak at
is due to a near-degeneracy of the ground state, as the lowest levels in sectors
and
have energies of
and
, respectively. We verified the curve for
s = 1/2 with exact diagonalization and without using symmetries, and the curves for
s = 1 and
s = 3/2 were confirmed through FTLM calculations employing only
symmetry [
35].
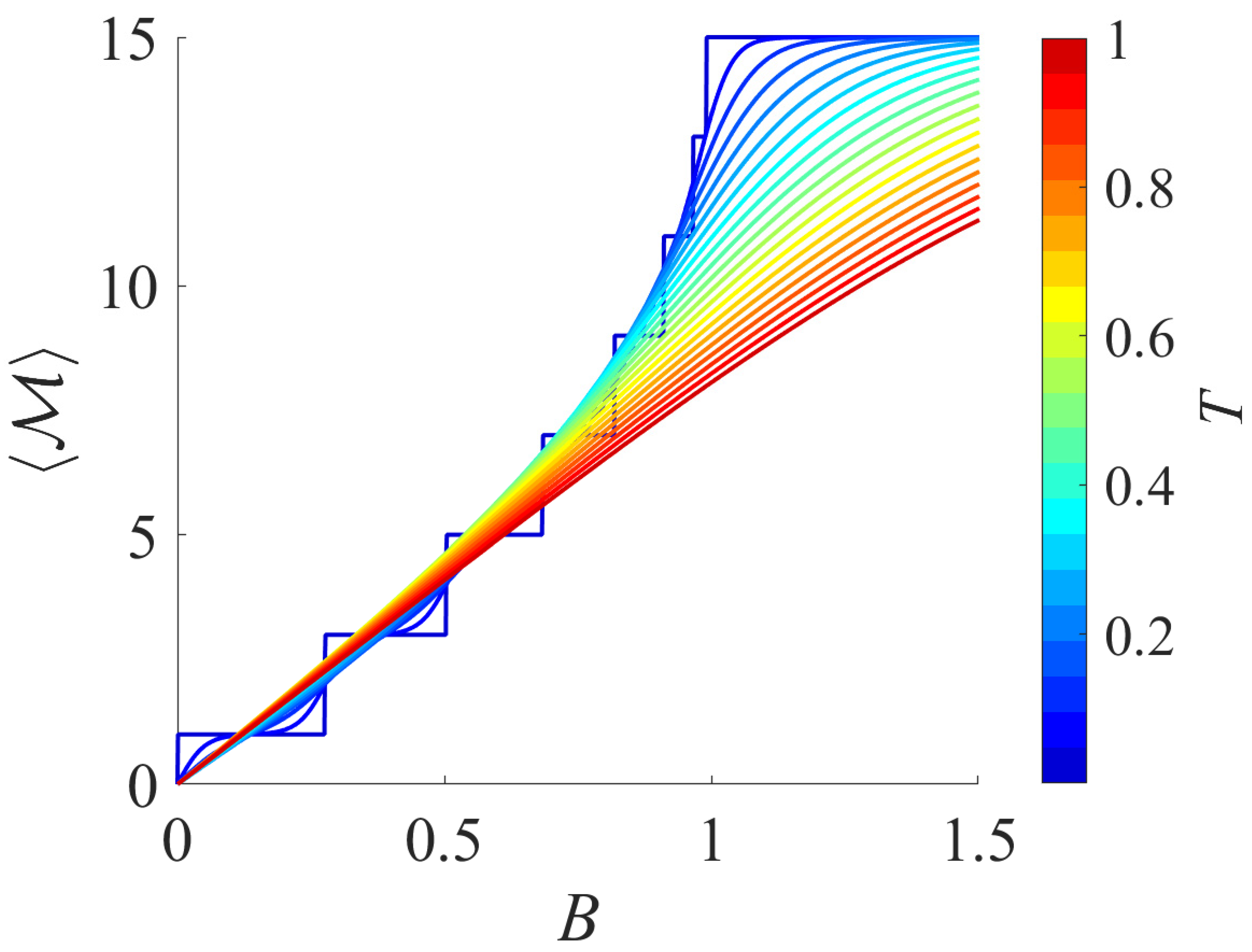
Cuboctahedron. A comparison between diagonalization in the
and
spaces for the
cuboctahedron, as shown in
Figure 9, again demonstrates the good agreement of our approach. The magnetization is plotted as a function of
B and
T in
Figure 10.
The
system was solved by Schnalle and Schnack in the compatible
subgroup, while only the low-energy part of the spectrum was fully resolved with respect to
[
10,
19]. Here, we have for the first time obtained a full symmetry classification of the entire spectrum (the subspace dimensions are given in
Table A4 in
Appendix A); see
Figure 11.
We plot the magnetic heat capacities of the cuboctahedron in
Figure 12. A comparison with Ref. [
10] reveals that our calculated curves coincide with theirs if the temperature axis is scaled by a factor of two. This difference could arise from a distinct choice of conventions in defining the exchange constant
J in the Heisenberg Hamiltonian. However, our convention for energies matches those in Ref. [
10], as is apparent from
Figure 5 and
Figure 6 in that work, implying an inconsistency in the treatment of
J-conventions [
35].
Truncated Tetrahedron. Finally, we consider the truncated tetrahedron, which, to the best of our knowledge, has never been fully diagonalized for
. This may be attributed to the fact that the relevant
point group (which is isomorphic to the octahedral group
), with only five irreps comprising a total of 10 components, is smaller than
or
, which have 10 irreps each and 20 and 30 components, respectively. Consequently, the matrices involved are significantly larger but still manageable if the full symmetry is exploited (see
Table A5 in
Appendix A). The spectrum of the
truncated tetrahedron is presented in
Figure 13, and the heat capacities of the
,
, and
systems are shown in
Figure 14.