Stability of Noncentrosymmetric Square Skyrmion Crystals with Easy-Axis and Easy-Plane Magnetic Anisotropy
Abstract
1. Introduction
2. Model and Method
3. Results
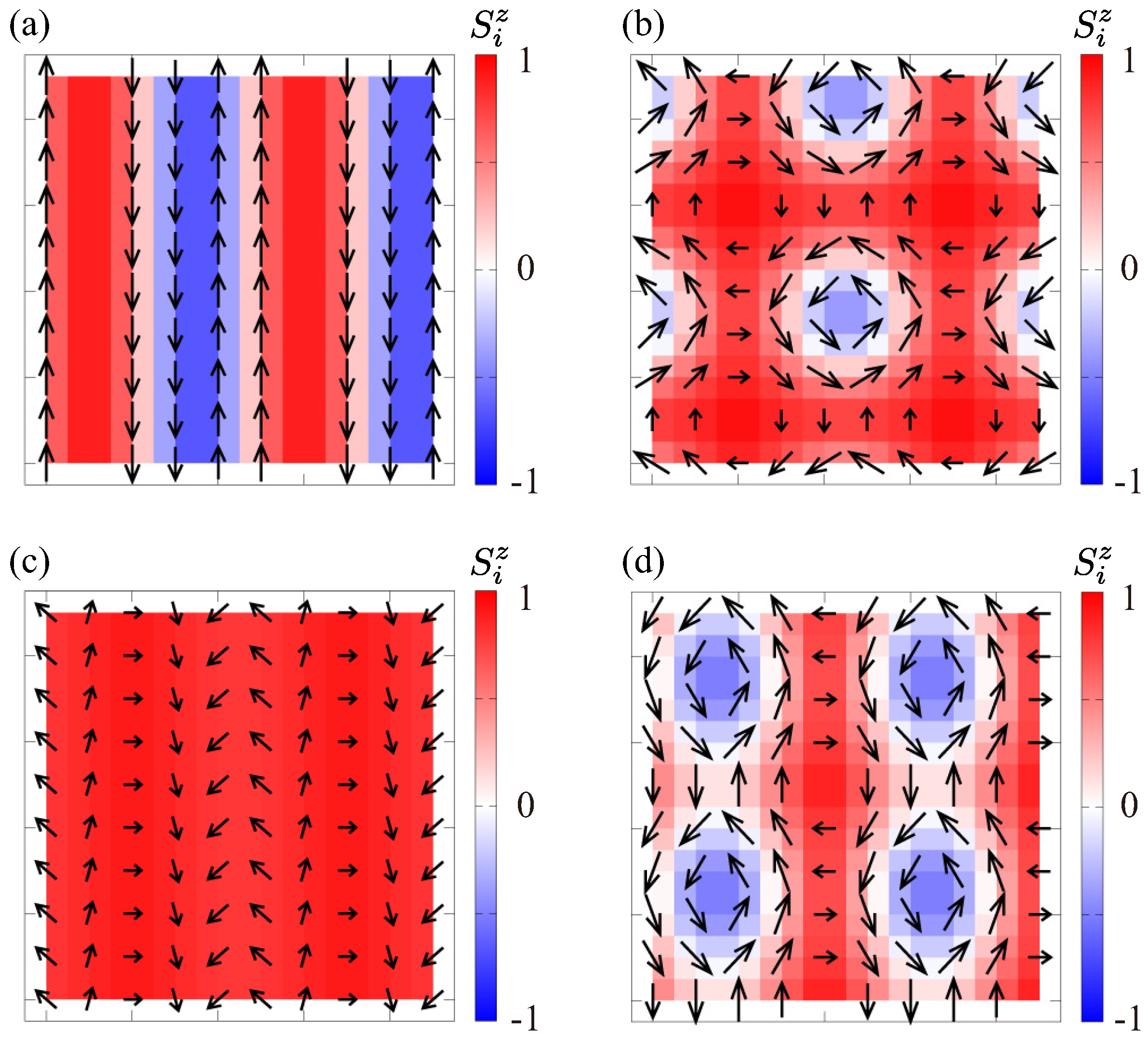
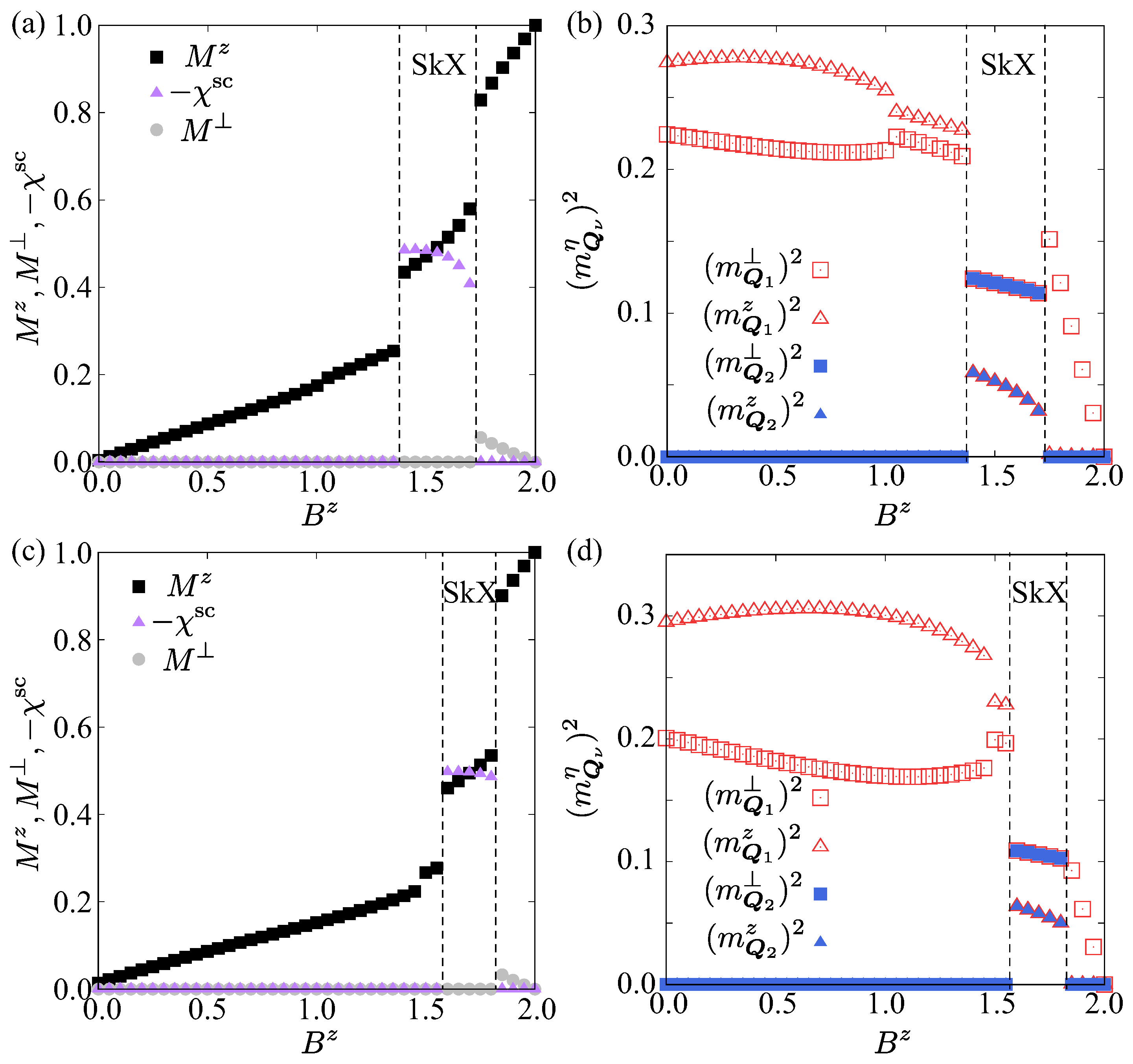
3.1. In an Out-Of-Plane Magnetic Field
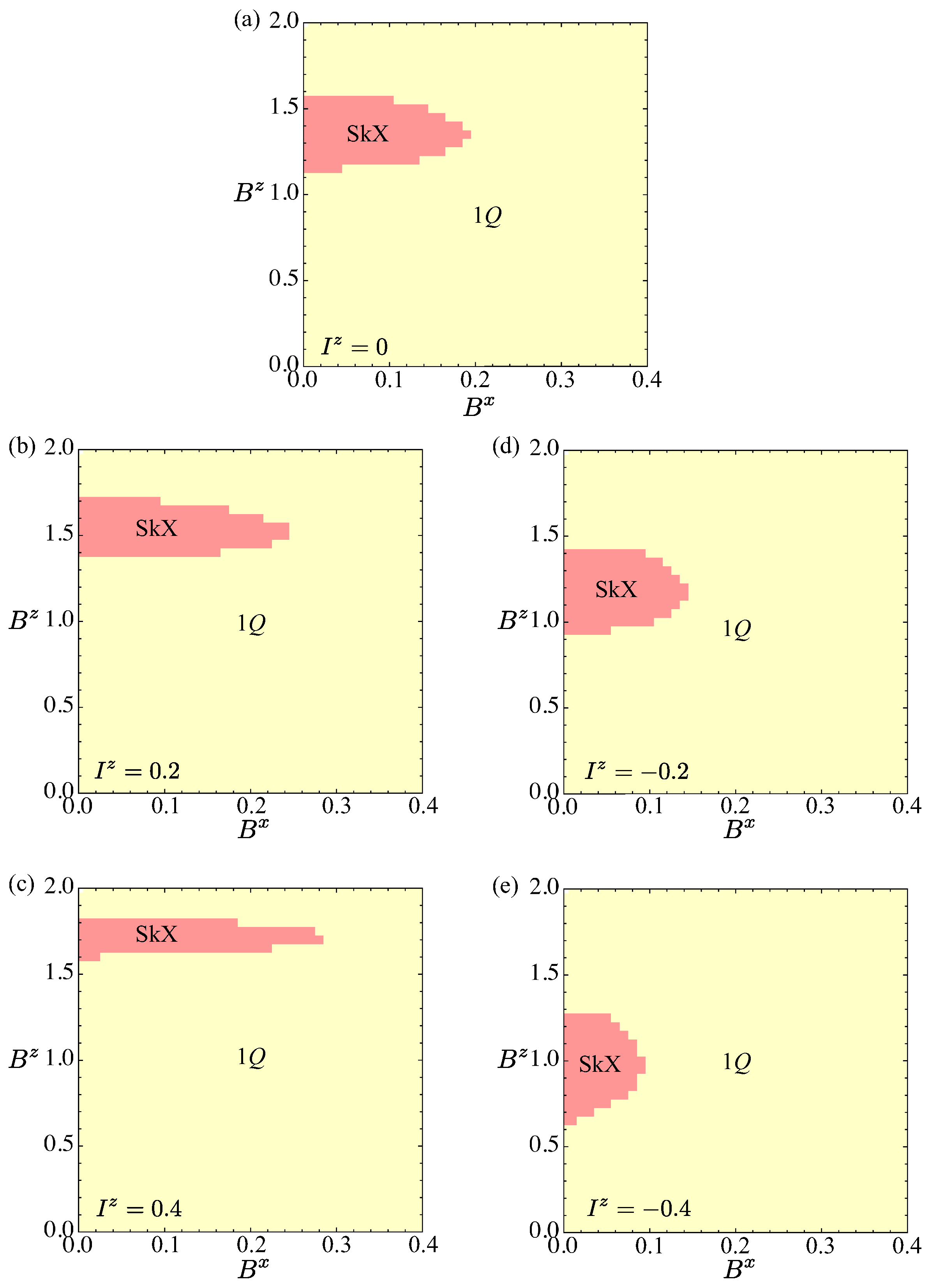
3.2. In a Tilted Magnetic Field
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aizu, K. Polarization, Pyroelectricity, and Ferroelectricity of Ionic Crystals. Rev. Mod. Phys. 1962, 34, 550–576. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Frigeri, P.A.; Agterberg, D.F.; Sigrist, M. Spin susceptibility in superconductors without inversion symmetry. N. J. Phys. 2004, 6, 115. [Google Scholar] [CrossRef]
- Palazzese, S.; Landaeta, J.; Subero, D.; Bauer, E.; Bonalde, I. Strong antisymmetric spin–orbit coupling and superconducting properties: The case of noncentrosymmetric LaPtSi. J. Phys. Condens. Matter. 2018, 30, 255603. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403(R). [Google Scholar] [CrossRef]
- Rashba, E.I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Ishizaka, K.; Bahramy, M.; Murakawa, H.; Sakano, M.; Shimojima, T.; Sonobe, T.; Koizumi, K.; Shin, S.; Miyahara, H.; Kimura, A.; et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 2011, 10, 521–526. [Google Scholar] [CrossRef]
- Bahramy, M.S.; Arita, R.; Nagaosa, N. Origin of giant bulk Rashba splitting: Application to BiTeI. Phys. Rev. B 2011, 84, 041202(R). [Google Scholar] [CrossRef]
- Sunko, V.; Rosner, H.; Kushwaha, P.; Khim, S.; Mazzola, F.; Bawden, L.; Clark, O.; Riley, J.; Kasinathan, D.; Haverkort, M.; et al. Maximal Rashba-like spin splitting via kinetic-energy-coupled inversion-symmetry breaking. Nature 2017, 549, 492–496. [Google Scholar] [CrossRef]
- Takashima, R.; Fujimoto, S. Supercurrent-induced skyrmion dynamics and tunable Weyl points in chiral magnet with superconductivity. Phys. Rev. B 2016, 94, 235117. [Google Scholar] [CrossRef]
- Wang, B.Z.; Lu, Y.H.; Sun, W.; Chen, S.; Deng, Y.; Liu, X.J. Dirac-, Rashba-, and Weyl-type spin-orbit couplings: Toward experimental realization in ultracold atoms. Phys. Rev. A 2018, 97, 011605(R). [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699. [Google Scholar] [CrossRef] [PubMed]
- Ugeda, M.M.; Bradley, A.J.; Shi, S.F.; Felipe, H.; Zhang, Y.; Qiu, D.Y.; Ruan, W.; Mo, S.K.; Hussain, Z.; Shen, Z.X.; et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 2014, 13, 1091. [Google Scholar] [CrossRef] [PubMed]
- Kormányos, A.; Zólyomi, V.; Drummond, N.D.; Burkard, G. Spin-Orbit Coupling, Quantum Dots, and Qubits in Monolayer Transition Metal Dichalcogenides. Phys. Rev. X 2014, 4, 011034. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Dissipationless quantum spin current at room temperature. Science 2003, 301, 1348–1351. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Spin-Hall Insulator. Phys. Rev. Lett. 2004, 93, 156804. [Google Scholar] [CrossRef]
- Sinova, J.; Culcer, D.; Niu, Q.; Sinitsyn, N.A.; Jungwirth, T.; MacDonald, A.H. Universal Intrinsic Spin Hall Effect. Phys. Rev. Lett. 2004, 92, 126603. [Google Scholar] [CrossRef]
- Fujimoto, S. Emergent Nodal Excitations due to Coexistence of Superconductivity and Antiferromagnetism: Cases with and without Inversion Symmetry. J. Phys. Soc. Jpn. 2006, 75, 083704. [Google Scholar] [CrossRef]
- Fujimoto, S. Fermi liquid theory for heavy fermion superconductors without inversion symmetry: Magnetism and transport coefficients. J. Phys. Soc. Jpn. 2007, 76, 034712. [Google Scholar] [CrossRef]
- Edelstein, V.M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. [Google Scholar] [CrossRef]
- Yip, S.K. Two-dimensional superconductivity with strong spin-orbit interaction. Phys. Rev. B 2002, 65, 144508. [Google Scholar] [CrossRef]
- Fujimoto, S. Magnetoelectric effects in heavy-fermion superconductors without inversion symmetry. Phys. Rev. B 2005, 72, 024515. [Google Scholar] [CrossRef]
- Yoda, T.; Yokoyama, T.; Murakami, S. Orbital Edelstein Effect as a Condensed-Matter Analog of Solenoids. Nano Lett. 2018, 18, 916–920. [Google Scholar] [CrossRef] [PubMed]
- Massarelli, G.; Wu, B.; Paramekanti, A. Orbital Edelstein effect from density-wave order. Phys. Rev. B 2019, 100, 075136. [Google Scholar] [CrossRef]
- Roy, A.; Cerasoli, F.T.; Jayaraj, A.; Tenzin, K.; Nardelli, M.B.; Sławińska, J. Long-range current-induced spin accumulation in chiral crystals. npj Comput. Mater. 2022, 8, 243. [Google Scholar] [CrossRef]
- Tenzin, K.; Roy, A.; Cerasoli, F.T.; Jayaraj, A.; Nardelli, M.B.; Sławińska, J. Collinear Rashba-Edelstein effect in nonmagnetic chiral materials. Phys. Rev. B 2023, 108, 245203. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Seki, S.; Okamura, Y.; Kondou, K.; Shibata, K.; Kubota, M.; Takagi, R.; Kagawa, F.; Kawasaki, M.; Tatara, G.; Otani, Y.; et al. Magnetochiral nonreciprocity of volume spin wave propagation in chiral-lattice ferromagnets. Phys. Rev. B 2016, 93, 235131. [Google Scholar] [CrossRef]
- Giordano, A.; Verba, R.; Zivieri, R.; Laudani, A.; Puliafito, V.; Gubbiotti, G.; Tomasello, R.; Siracusano, G.; Azzerboni, B.; Carpentieri, M.; et al. Spin-Hall nano-oscillator with oblique magnetization and Dzyaloshinskii-Moriya interaction as generator of skyrmions and nonreciprocal spin-waves. Sci. Rep. 2016, 6, 36020. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740. [Google Scholar] [CrossRef] [PubMed]
- Yokouchi, T.; Hoshino, S.; Kanazawa, N.; Kikkawa, A.; Morikawa, D.; Shibata, K.; Arima, T.H.; Taguchi, Y.; Kagawa, F.; Nagaosa, N.; et al. Current-induced dynamics of skyrmion strings. Sci. Adv. 2018, 4, eaat1115. [Google Scholar] [CrossRef] [PubMed]
- Hoshino, S.; Nagaosa, N. Theory of the magnetic skyrmion glass. Phys. Rev. B 2018, 97, 024413. [Google Scholar] [CrossRef]
- Bar’yakhtar, V.G.; Danilevich, A.G.; Krivoruchko, V.N. Magnetochiral nonreciprocity of spin wave damping in long-period structures. Phys. Rev. B 2019, 99, 104407. [Google Scholar] [CrossRef]
- dos Santos, F.J.; dos Santos Dias, M.; Lounis, S. Nonreciprocity of spin waves in noncollinear magnets due to the Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2020, 102, 104401. [Google Scholar] [CrossRef]
- Seki, S.; Garst, M.; Waizner, J.; Takagi, R.; Khanh, N.; Okamura, Y.; Kondou, K.; Kagawa, F.; Otani, Y.; Tokura, Y. Propagation dynamics of spin excitations along skyrmion strings. Nat. Commun. 2020, 11, 256. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M. Nonlinear nonreciprocal transport in antiferromagnets free from spin-orbit coupling. Phys. Rev. B 2022, 106, 014420. [Google Scholar] [CrossRef]
- Katsura, H.; Nagaosa, N.; Balatsky, A.V. Spin Current and Magnetoelectric Effect in Noncollinear Magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef]
- Mostovoy, M. Ferroelectricity in Spiral Magnets. Phys. Rev. Lett. 2006, 96, 067601. [Google Scholar] [CrossRef]
- Cheong, S.W.; Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater. 2007, 6, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Bulaevskii, L.N.; Batista, C.D.; Mostovoy, M.V.; Khomskii, D.I. Electronic orbital currents and polarization in Mott insulators. Phys. Rev. B 2008, 78, 024402. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef] [PubMed]
- White, J.S.; Levatić, I.; Omrani, A.; Egetenmeyer, N.; Prša, K.; Živković, I.; Gavilano, J.L.; Kohlbrecher, J.; Bartkowiak, M.; Berger, H.; et al. Electric field control of the skyrmion lattice in Cu2OSeO3. J. Phys. Condens. Matter. 2012, 24, 432201. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Mochizuki, M.; Seki, S. Dynamical magnetoelectric phenomena of multiferroic skyrmions. J. Phys. Condens. Matter 2015, 27, 503001. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I. Magnetoelectric effect and orbital magnetization in skyrmion crystals: Detection and characterization of skyrmions. Phys. Rev. B 2019, 99, 060406. [Google Scholar] [CrossRef]
- Kurumaji, T. Spiral spin structures and skyrmionsin multiferroics. Phys. Sci. Rev. 2020, 5, 20190016. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef]
- Balasubramanian, B.; Manchanda, P.; Pahari, R.; Chen, Z.; Zhang, W.; Valloppilly, S.R.; Li, X.; Sarella, A.; Yue, L.; Ullah, A.; et al. Chiral Magnetism and High-Temperature Skyrmions in B20-Ordered Co-Si. Phys. Rev. Lett. 2020, 124, 057201. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef] [PubMed]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Shiomi, Y.; Kanazawa, N.; Shibata, K.; Onose, Y.; Tokura, Y. Topological Nernst effect in a three-dimensional skyrmion-lattice phase. Phys. Rev. B 2013, 88, 064409. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Zadorozhnyi, A.; Dahnovsky, Y. Topological Hall effect in three-dimensional centrosymmetric magnetic skyrmion crystals. Phys. Rev. B 2023, 107, 054436. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Zhang, J.; Yuan, Y.; Wen, Y.; Li, Y.; Zheng, D.; Zhang, Q.; Hou, Z.; Yin, G.; et al. Room-Temperature Magnetic Skyrmions and Large Topological Hall Effect in Chromium Telluride Engineered by Self-Intercalation. Adv. Mater. 2023, 35, 2205967. [Google Scholar] [CrossRef]
- Jonietz, F.; Mu¨hlbauer, S.; Pfleiderer, C.; Neubauer, A.; Mu¨nzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Bo¨ni, P.; Duine, R.A.; et al. Spin Transfer Torques in MnSi at Ultralow Current Densities. Science 2010, 330, 1648. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Kanazawa, N.; Zhang, W.; Nagai, T.; Hara, T.; Kimoto, K.; Matsui, Y.; Onose, Y.; Tokura, Y. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 2012, 3, 988. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Wang, X.; Benjamin Jungfleisch, M.; Pearson, J.E.; Cheng, X.; Heinonen, O.; Wang, K.L.; et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162–169. [Google Scholar] [CrossRef]
- Yu, X.; Morikawa, D.; Nakajima, K.; Shibata, K.; Kanazawa, N.; Arima, T.h.; Nagaosa, N.; Tokura, Y. Motion tracking of 80-nm-size skyrmions upon directional current injections. Sci. Adv. 2020, 6, eaaz9744. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.T.; Sisodia, N.; Di Manici, I.; Urrestarazu-Larrañaga, J.; Bairagi, K.; Pelloux-Prayer, J.; Guedas, R.; Buda-Prejbeanu, L.D.; Auffret, S.; Locatelli, A.; et al. Fast current-induced skyrmion motion in synthetic antiferromagnets. Science 2024, 384, 307–312. [Google Scholar] [CrossRef]
- Song, D.; Wang, W.; Zhang, S.; Liu, Y.; Wang, N.; Zheng, F.; Tian, M.; Dunin-Borkowski, R.E.; Zang, J.; Du, H. Steady motion of 80-nm-size skyrmions in a 100-nm-wide track. Nat. Commun. 2024, 15, 5614. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, S.; Ahn, H.B.; Moon, K.W.; Ju, T.S.; Im, M.Y.; Han, H.S.; Lee, J.; Park, S.y.; Lee, C.; et al. Direct Observation of Room-Temperature Magnetic Skyrmion Motion Driven by Ultra-Low Current Density in Van Der Waals Ferromagnets. Adv. Mater. 2024, 36, 2312013. [Google Scholar] [CrossRef]
- Birch, M.T.; Belopolski, I.; Fujishiro, Y.; Kawamura, M.; Kikkawa, A.; Taguchi, Y.; Hirschberger, M.; Nagaosa, N.; Tokura, Y. Dynamic transition and Galilean relativity of current-driven skyrmions. Nature 2024, 633, 554–559. [Google Scholar] [CrossRef]
- Jiang, W.; Upadhyaya, P.; Zhang, W.; Yu, G.; Jungfleisch, M.B.; Fradin, F.Y.; Pearson, J.E.; Tserkovnyak, Y.; Wang, K.L.; Heinonen, O.; et al. Blowing magnetic skyrmion bubbles. Science 2015, 349, 283–286. [Google Scholar] [CrossRef]
- Büttner, F.; Lemesh, I.; Schneider, M.; Pfau, B.; Günther, C.M.; Hessing, P.; Geilhufe, J.; Caretta, L.; Engel, D.; Krüger, B.; et al. Field-free deterministic ultrafast creation of magnetic skyrmions by spin–orbit torques. Nat. Nanotechnol. 2017, 12, 1040–1044. [Google Scholar] [CrossRef] [PubMed]
- Hrabec, A.; Sampaio, J.; Belmeguenai, M.; Gross, I.; Weil, R.; Chérif, S.M.; Stashkevich, A.; Jacques, V.; Thiaville, A.; Rohart, S. Current-induced skyrmion generation and dynamics in symmetric bilayers. Nat. Commun. 2017, 8, 15765. [Google Scholar] [CrossRef] [PubMed]
- Ahrens, V.; Kiesselbach, C.; Gnoli, L.; Giuliano, D.; Mendisch, S.; Kiechle, M.; Riente, F.; Becherer, M. Skyrmions Under Control—FIB Irradiation as a Versatile Tool for Skyrmion Circuits. Adv. Mater. 2023, 35, 2207321. [Google Scholar] [CrossRef] [PubMed]
- de Jong, M.C.H.; Smit, B.H.M.; Meijer, M.J.; Lucassen, J.; Swagten, H.J.M.; Koopmans, B.; Lavrijsen, R. Controlling magnetic skyrmion nucleation with Ga+ ion irradiation. Phys. Rev. B 2023, 107, 094429. [Google Scholar] [CrossRef]
- Li, S.; Wang, X.; Rasing, T. Magnetic skyrmions: Basic properties and potential applications. Interdiscip. Mater. 2023, 2, 260–289. [Google Scholar] [CrossRef]
- Wang, X.; Li, M.; Li, B.; Li, Y.; Li, Y.; Zheng, F.; Liu, L. Efficient generation and deterministic annihilation of a single skyrmion via pure localized heating. J. Appl. Phys. 2024, 135, 143902. [Google Scholar] [CrossRef]
- Butenko, A.B.; Leonov, A.A.; Rößler, U.K.; Bogdanov, A.N. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Lin, S.Z.; Saxena, A.; Batista, C.D. Skyrmion fractionalization and merons in chiral magnets with easy-plane anisotropy. Phys. Rev. B 2015, 91, 224407. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. N. J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Leonov, A.O.; Kézsmárki, I. Asymmetric isolated skyrmions in polar magnets with easy-plane anisotropy. Phys. Rev. B 2017, 96, 014423. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Néel- and Bloch-Type Magnetic Vortices in Rashba Metals. Phys. Rev. Lett. 2018, 121, 137202. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S. Rectangular and square skyrmion crystals on a centrosymmetric square lattice with easy-axis anisotropy. Phys. Rev. B 2022, 105, 174437. [Google Scholar] [CrossRef]
- Tokunaga, Y.; Yu, X.; White, J.; Rønnow, H.M.; Morikawa, D.; Taguchi, Y.; Tokura, Y. A new class of chiral materials hosting magnetic skyrmions beyond room temperature. Nat. Commun. 2015, 6, 7638. [Google Scholar] [CrossRef]
- Karube, K.; White, J.; Reynolds, N.; Gavilano, J.; Oike, H.; Kikkawa, A.; Kagawa, F.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; et al. Robust metastable skyrmions and their triangular–square lattice structural transition in a high-temperature chiral magnet. Nat. Mater. 2016, 15, 1237. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Morikawa, D.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Yu, X.; Tokunaga, Y.; Arima, T.h.; Rønnow, H.M.; et al. Disordered skyrmion phase stabilized by magnetic frustration in a chiral magnet. Sci. Adv. 2018, 4, eaar7043. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Ukleev, V.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; Taguchi, Y. Metastable skyrmion lattices governed by magnetic disorder and anisotropy in β-Mn-type chiral magnets. Phys. Rev. B 2020, 102, 064408. [Google Scholar] [CrossRef]
- Henderson, M.E.; Bleuel, M.; Beare, J.; Cory, D.G.; Heacock, B.; Huber, M.G.; Luke, G.M.; Pula, M.; Sarenac, D.; Sharma, S.; et al. Skyrmion alignment and pinning effects in the disordered multiphase skyrmion material Co8Zn8Mn4. Phys. Rev. B 2022, 106, 094435. [Google Scholar] [CrossRef]
- Chacon, A.; Heinen, L.; Halder, M.; Bauer, A.; Simeth, W.; Mühlbauer, S.; Berger, H.; Garst, M.; Rosch, A.; Pfleiderer, C. Observation of two independent skyrmion phases in a chiral magnetic material. Nat. Phys. 2018, 14, 936–941. [Google Scholar] [CrossRef]
- Takagi, R.; Yamasaki, Y.; Yokouchi, T.; Ukleev, V.; Yokoyama, Y.; Nakao, H.; Arima, T.; Tokura, Y.; Seki, S. Particle-size dependent structural transformation of skyrmion lattice. Nat. Commun. 2020, 11, 5685. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef] [PubMed]
- Khanh, N.D.; Nakajima, T.; Hayami, S.; Gao, S.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Takagi, R.; Motome, Y.; Tokura, Y.; et al. Zoology of Multiple-Q Spin Textures in a Centrosymmetric Tetragonal Magnet with Itinerant Electrons. Adv. Sci. 2022, 9, 2105452. [Google Scholar] [CrossRef]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef] [PubMed]
- Yoshimochi, H.; Takagi, R.; Ju, J.; Khanh, N.; Saito, H.; Sagayama, H.; Nakao, H.; Itoh, S.; Tokura, Y.; Arima, T.; et al. Multistep topological transitions among meron and skyrmion crystals in a centrosymmetric magnet. Nat. Phys. 2024, 20, 1001. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Topological spin crystals by itinerant frustration. J. Phys.: Condens. Matter 2021, 33, 443001. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Ullah, A.; Balamurugan, B.; Zhang, W.; Valloppilly, S.; Li, X.Z.; Pahari, R.; Yue, L.P.; Sokolov, A.; Sellmyer, D.J.; Skomski, R. Crystal structure and Dzyaloshinski–Moriya micromagnetics. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Ullah, A.; Balasubramanian, B.; Tiwari, B.; Giri, B.; Sellmyer, D.J.; Skomski, R.; Xu, X. Topological spin textures and topological Hall effect in centrosymmetric magnetic nanoparticles. Phys. Rev. B 2023, 108, 184432. [Google Scholar] [CrossRef]
- Berg, B.; Luscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Locking of skyrmion cores on a centrosymmetric discrete lattice: Onsite versus offsite. Phys. Rev. Res. 2021, 3, 043158. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Hayami, S. Multiple-Q magnetism by anisotropic bilinear-biquadratic interactions in momentum space. J. Magn. Magn. Mater. 2020, 513, 167181. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Nakamura, S.; Sakakibara, T.; Hedo, M.; Nakama, T.; et al. Giant Hall resistivity and magnetoresistance in cubic chiral antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2018, 87, 023701. [Google Scholar] [CrossRef]
- Kaneko, K.; Frontzek, M.D.; Matsuda, M.; Nakao, A.; Munakata, K.; Ohhara, T.; Kakihana, M.; Haga, Y.; Hedo, M.; Nakama, T.; et al. Unique Helical Magnetic Order and Field-Induced Phase in Trillium Lattice Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 013702. [Google Scholar] [CrossRef]
- Tabata, C.; Matsumura, T.; Nakao, H.; Michimura, S.; Kakihana, M.; Inami, T.; Kaneko, K.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic Field Induced Triple-q Magnetic Order in Trillium Lattice Antiferromagnet EuPtSi Studied by Resonant X-ray Scattering. J. Phys. Soc. Jpn. 2019, 88, 093704. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Takeuchi, T.; Harima, H.; Hedo, M.; Nakama, T.; et al. Unique Magnetic Phases in the Skyrmion Lattice and Fermi Surface Properties in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 094705. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ganesan, V. A-phase, field-induced tricritical point, and universal magnetocaloric scaling in EuPtSi. Phys. Rev. B 2019, 100, 125113. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic field versus temperature phase diagram for H‖[001] in the trillium lattice antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 053703. [Google Scholar] [CrossRef]
- Matsumura, T.; Tabata, C.; Kaneko, K.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Single helicity of the triple-q triangular skyrmion lattice state in the cubic chiral helimagnet EuPtSi. Phys. Rev. B 2024, 109, 174437. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Angle Dependence of the Magnetic Phase Diagram in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2020, 89, 093703. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Sakakibara, T.; Nakamura, S.; Kittaka, S.; Kakihana, M.; Hedo, M.; Nakama, T.; Onuki, Y. Magnetic Phase Transitions of the 4f Skyrmion Compound EuPtSi Studied by Magnetization Measurements. J. Phys. Soc. Jpn. 2021, 90, 064701. [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Hayami, S. Skyrmion crystal and spiral phases in centrosymmetric bilayer magnets with staggered Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 105, 014408. [Google Scholar] [CrossRef]
- Hayami, S. Multifarious skyrmion phases on a trilayer triangular lattice. Phys. Rev. B 2022, 105, 184426. [Google Scholar] [CrossRef]
- Lin, S.Z. Skyrmion lattice in centrosymmetric magnets with local Dzyaloshinsky-Moriya interaction. Mater. Today Quantum 2024, 2, 100006. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Stability of Noncentrosymmetric Square Skyrmion Crystals with Easy-Axis and Easy-Plane Magnetic Anisotropy. Magnetism 2024, 4, 368-382. https://doi.org/10.3390/magnetism4040024
Hayami S. Stability of Noncentrosymmetric Square Skyrmion Crystals with Easy-Axis and Easy-Plane Magnetic Anisotropy. Magnetism. 2024; 4(4):368-382. https://doi.org/10.3390/magnetism4040024
Chicago/Turabian StyleHayami, Satoru. 2024. "Stability of Noncentrosymmetric Square Skyrmion Crystals with Easy-Axis and Easy-Plane Magnetic Anisotropy" Magnetism 4, no. 4: 368-382. https://doi.org/10.3390/magnetism4040024
APA StyleHayami, S. (2024). Stability of Noncentrosymmetric Square Skyrmion Crystals with Easy-Axis and Easy-Plane Magnetic Anisotropy. Magnetism, 4(4), 368-382. https://doi.org/10.3390/magnetism4040024





