Far-Field Spatial Response of Off-Diagonal GMI Wire Magnetometers. Application to Magnetic Field Sources Sensing
Abstract
1. Introduction
2. Magnetometer
2.1. GMI Sensor
2.2. Magnetometer Characteristics
3. Setup
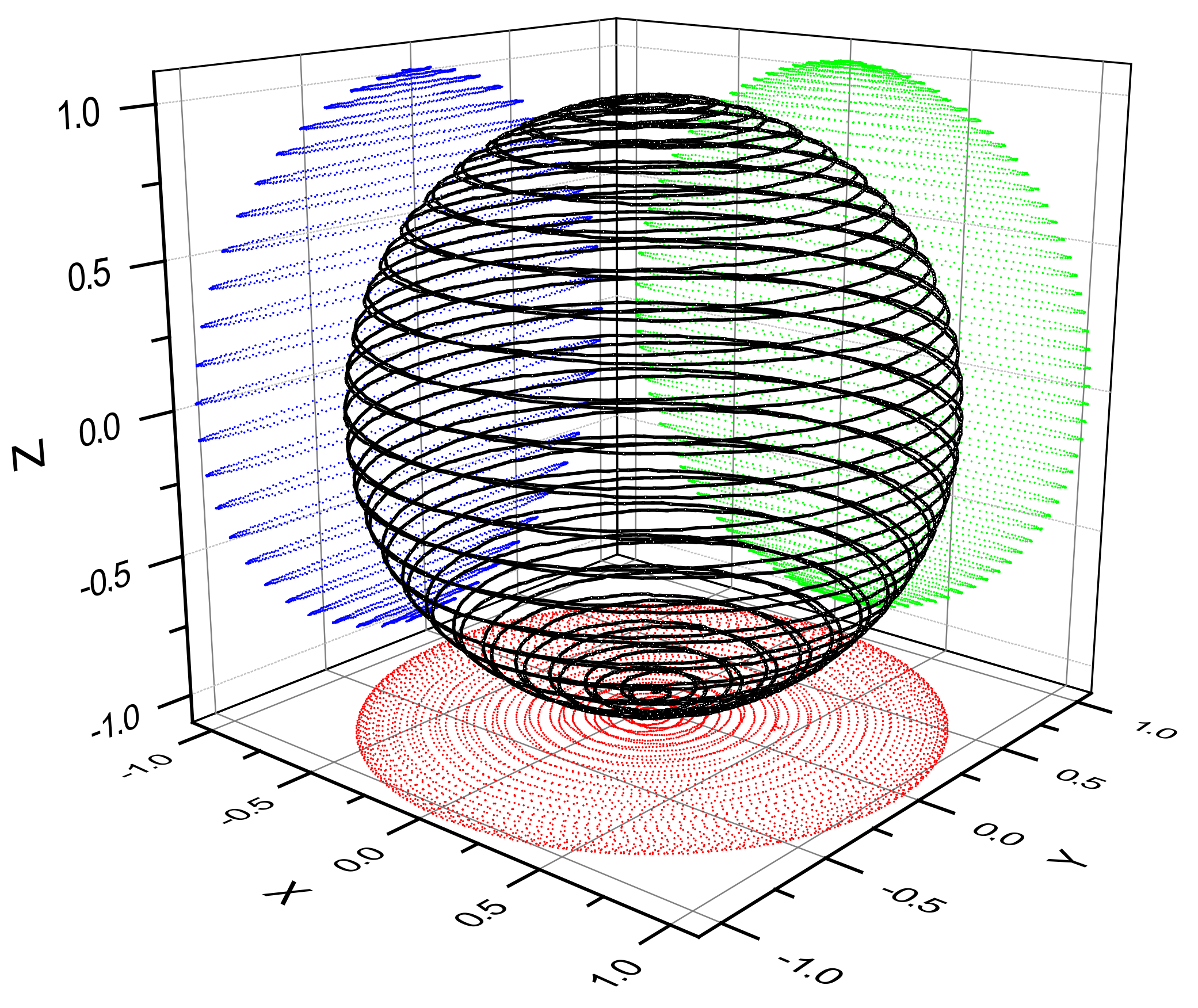
3.1. Three-Dimensional Helmholtz Coil System
3.2. The Rotating Magnetic Field
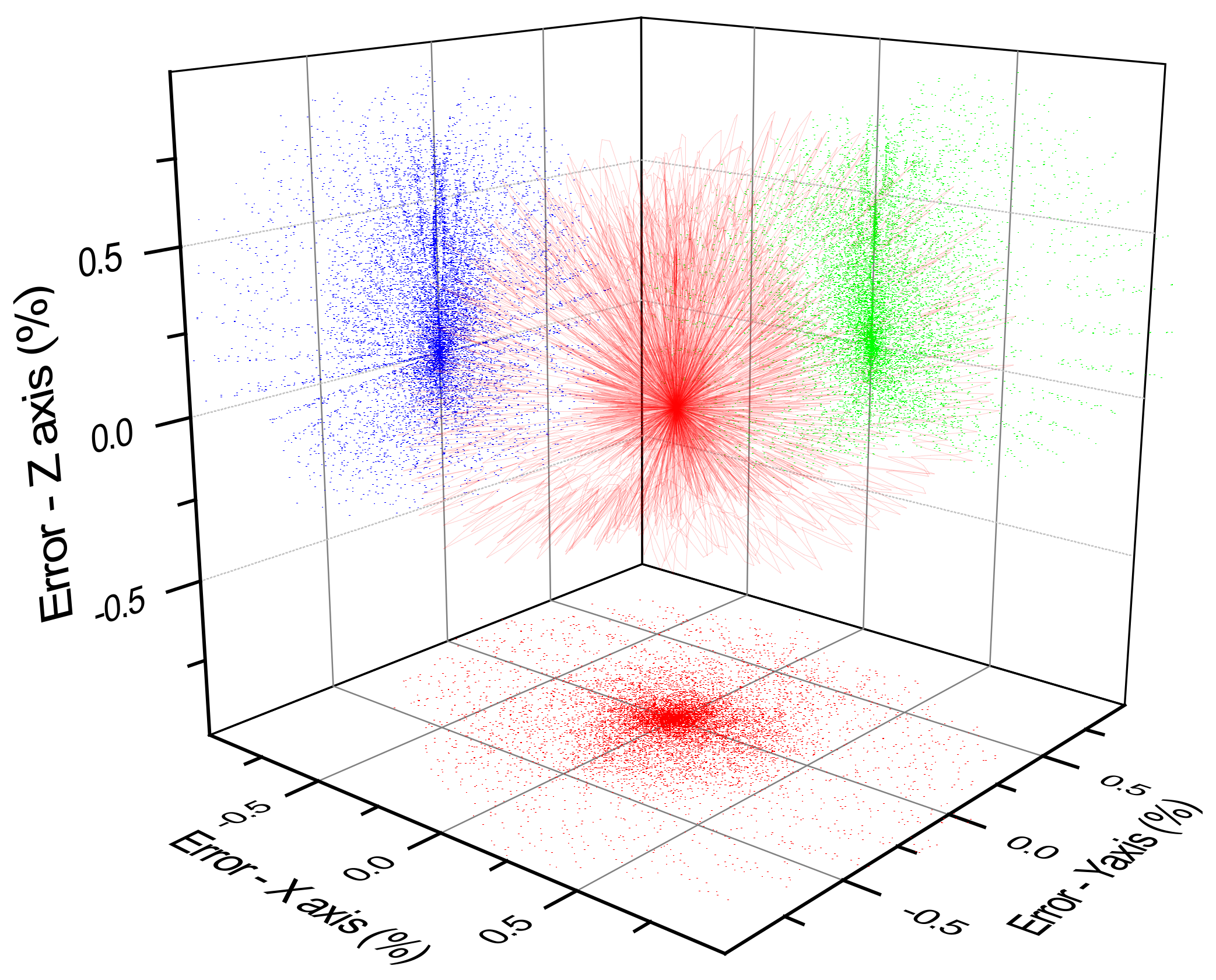
3.3. The Sensed Magnetic Field
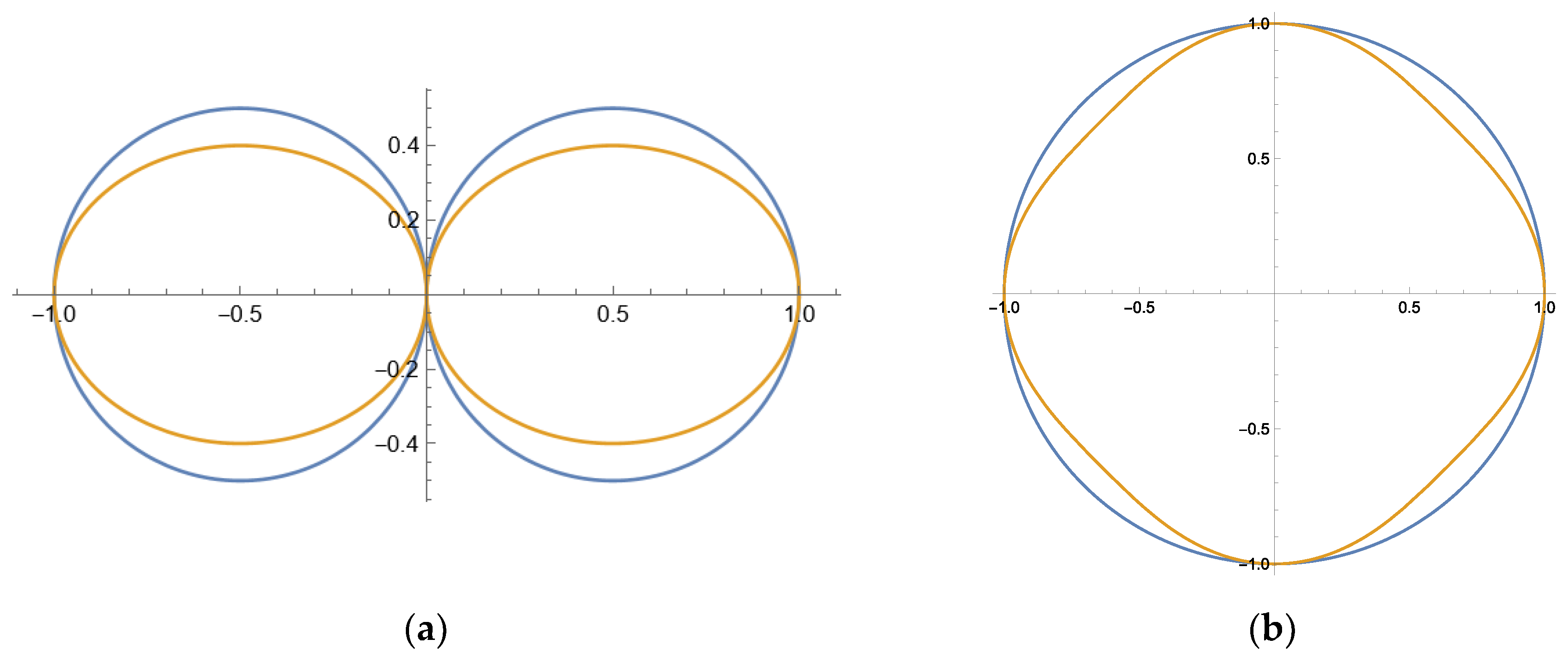
4. Discussion
Far-Field Pattern
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ripka, P. Review of fluxgate sensors. Sens. Actuators A 1992, 33, 29–141. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent Advances of Amorphous Wire CMOS IC Magneto-Impedance Sensors: Innovative High-Performance Micromagnetic Sensor Chip. J. Sens. 2015, 2015, 718069. [Google Scholar] [CrossRef]
- Murata, N.; Karo, H.; Sasada, I. Fundamental mode orthogonal fluxgate magnetometer applicable for measurements of DC and low-frequency magnetic fields. IEEE Sens. J. 2018, 99, 2705–2712. [Google Scholar] [CrossRef]
- Knobel, M.; Vázquez, M.; Kraus, L. Giant magnetoimpedance. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 15, pp. 497–563. [Google Scholar]
- Fodil, K.; Denoual, M.; Dolabdjian, C. Experimental and Analytical Investigation of a new 2D Magnetic Magnetic Imaging Method using magnetic nanoparticules. IEEE Trans. Magn. 2016, 52, 6500109. [Google Scholar] [CrossRef]
- Clem, T.R.; Kelis, G.J.; Lathrop, J.D.; Overway, D.J.; Wynn, W.M. Superconducting Magnetic Gradiometers for Mobile Applications with an Emphasis on Ordnance Detection. In SQUID Sensor: Fundamentals, Fabrication and Applications; Weinstock, H., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; Volume 329. [Google Scholar] [CrossRef]
- Sheinker, A.; Frumkis, L.; Ginzburg, B.; Salomonski, N.; Kaplan, B.-Z. Magnetic Anomaly Detection Using a Three-Axis Magnetometer. IEEE Trans. Magn. 2009, 45, 160–167. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.H.; Li, J.H.; Liu, S.; Miao, P.X.; Shi, Y.C.; Zhao, E.M. A brief review of magnetic anomaly detection. Meas. Sci. Technol. 2021, 32, 042002. [Google Scholar] [CrossRef]
- Dolabdjian, C.; Cordier, C. Analysis by systemic approach of magnetic dipole source location performances by using an IoT software gradiometer head. IEEE Sens. J. 2022, 22, 7709–7716. [Google Scholar] [CrossRef]
- Dufay, B.; Saez, S.; Dolabdjian, C.P.; Yelon, A.; Menard, D. Characterization of an optimized off-diagonal GMI-based magnetometer. IEEE Sens. J. 2013, 13, 379–388. [Google Scholar] [CrossRef]
- Esper, A.; Dufay, B.; Saez, S.; Dolabdjian, C. Theoretical and Experimental Investigation of Temperature-Compensated Off-Diagonal GMI Magnetometer and Its Long-Term Stability. IEEE Sens. J. 2020, 20, 9046–9055. [Google Scholar] [CrossRef]





| Characteristics | Units | |
|---|---|---|
| Sensitivity | 54,000 | V/T |
| White noise level | 15 | pT/√Hz |
| Bandwidth | 30,000 | Hz |
| 1/f noise corner | 5 | Hz |
| Dynamic range | ±60 | µT |
| Long-term stability | >5 | nT/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasnier, J.; Dolabdjian, C. Far-Field Spatial Response of Off-Diagonal GMI Wire Magnetometers. Application to Magnetic Field Sources Sensing. Magnetism 2024, 4, 47-53. https://doi.org/10.3390/magnetism4010004
Gasnier J, Dolabdjian C. Far-Field Spatial Response of Off-Diagonal GMI Wire Magnetometers. Application to Magnetic Field Sources Sensing. Magnetism. 2024; 4(1):47-53. https://doi.org/10.3390/magnetism4010004
Chicago/Turabian StyleGasnier, Julien, and Christophe Dolabdjian. 2024. "Far-Field Spatial Response of Off-Diagonal GMI Wire Magnetometers. Application to Magnetic Field Sources Sensing" Magnetism 4, no. 1: 47-53. https://doi.org/10.3390/magnetism4010004
APA StyleGasnier, J., & Dolabdjian, C. (2024). Far-Field Spatial Response of Off-Diagonal GMI Wire Magnetometers. Application to Magnetic Field Sources Sensing. Magnetism, 4(1), 47-53. https://doi.org/10.3390/magnetism4010004






