Effect of In-Plane Magnetic Field on Skyrmions in a Centrosymmetric Triangular-Lattice System with Symmetric Anisotropic Exchange Interaction
Abstract
1. Introduction
2. Model and Method
3. Results
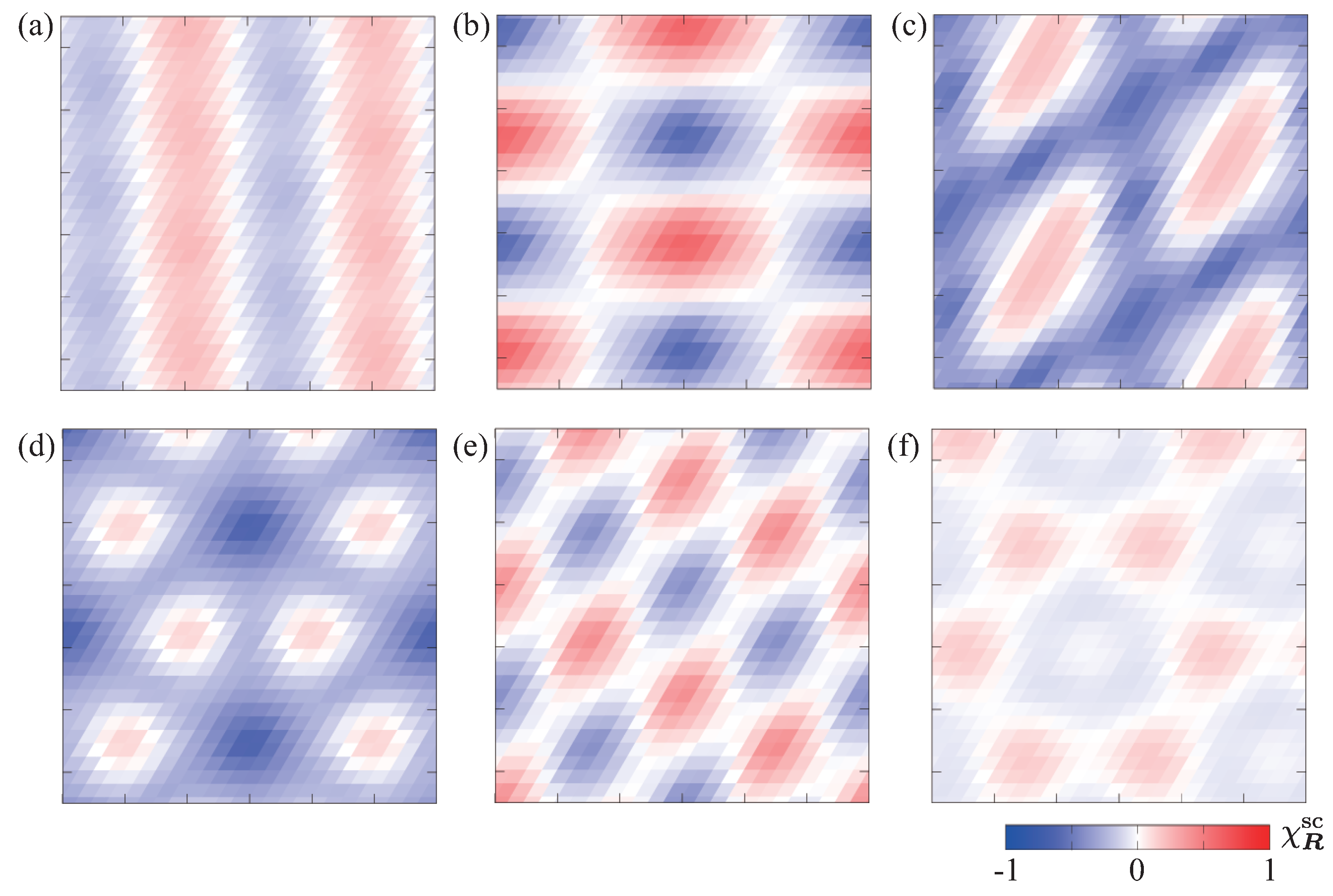
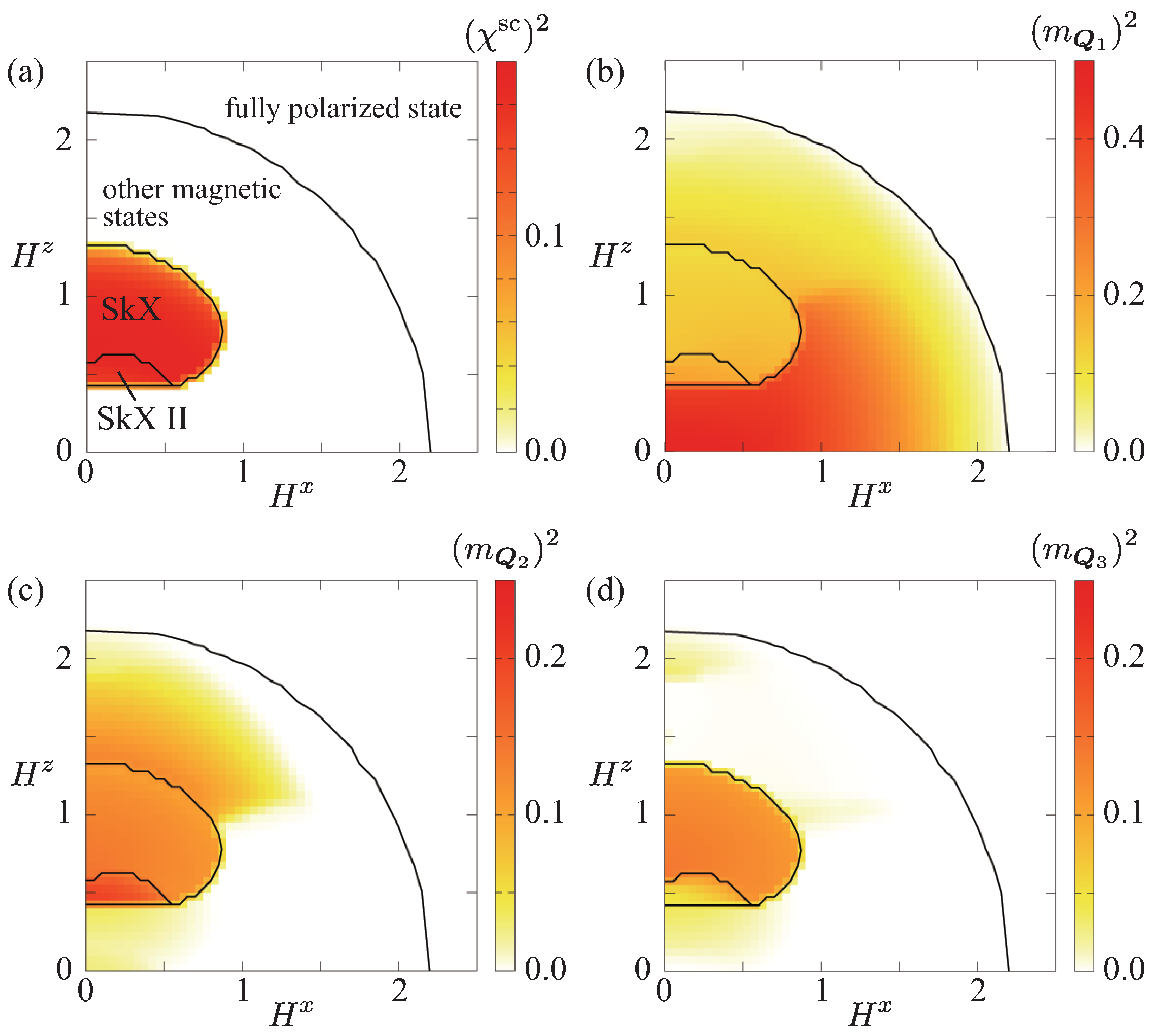
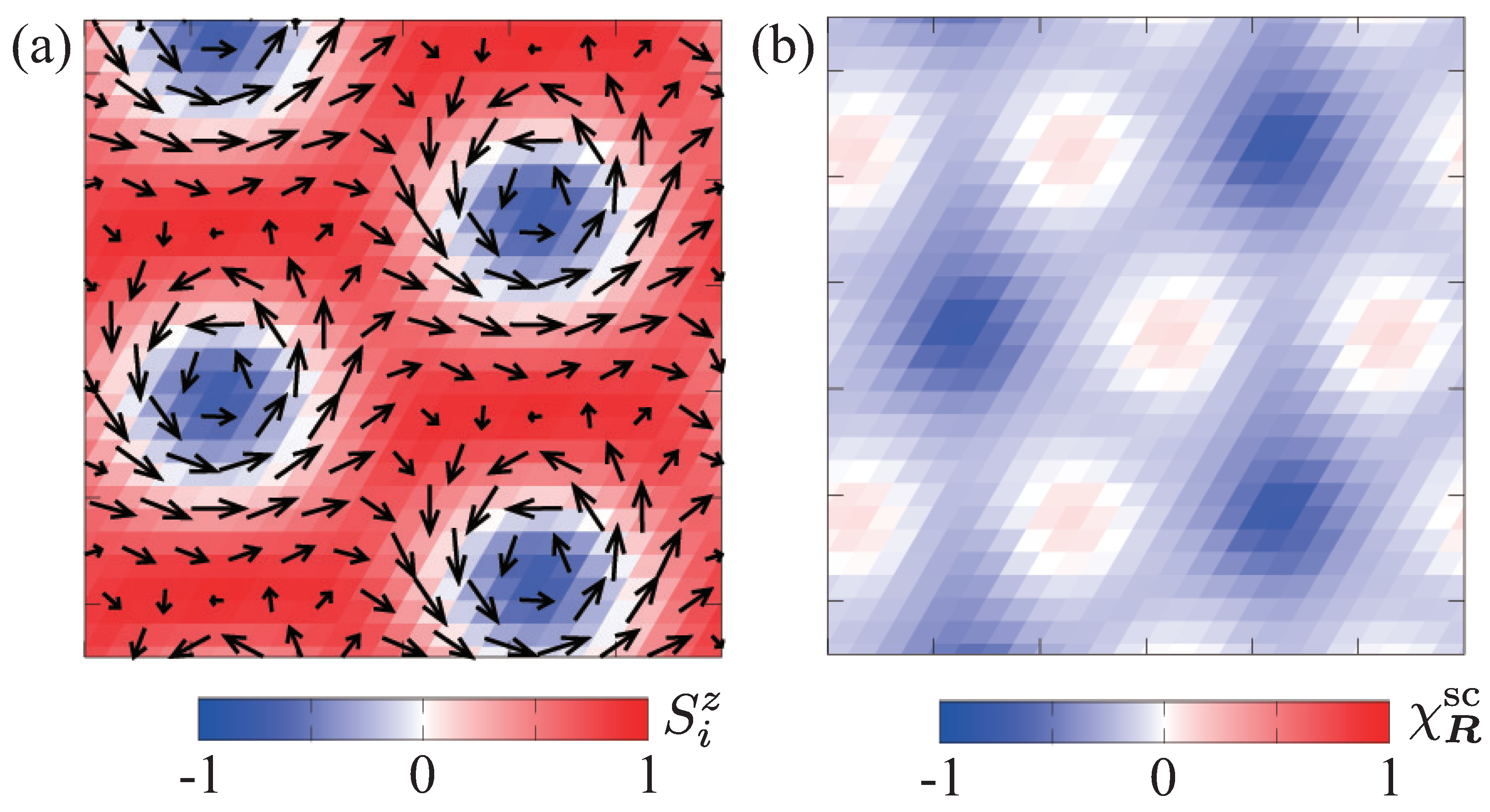
3.1. Out-of-Plane Field
3.2. In-Plane Field along the x-Direction
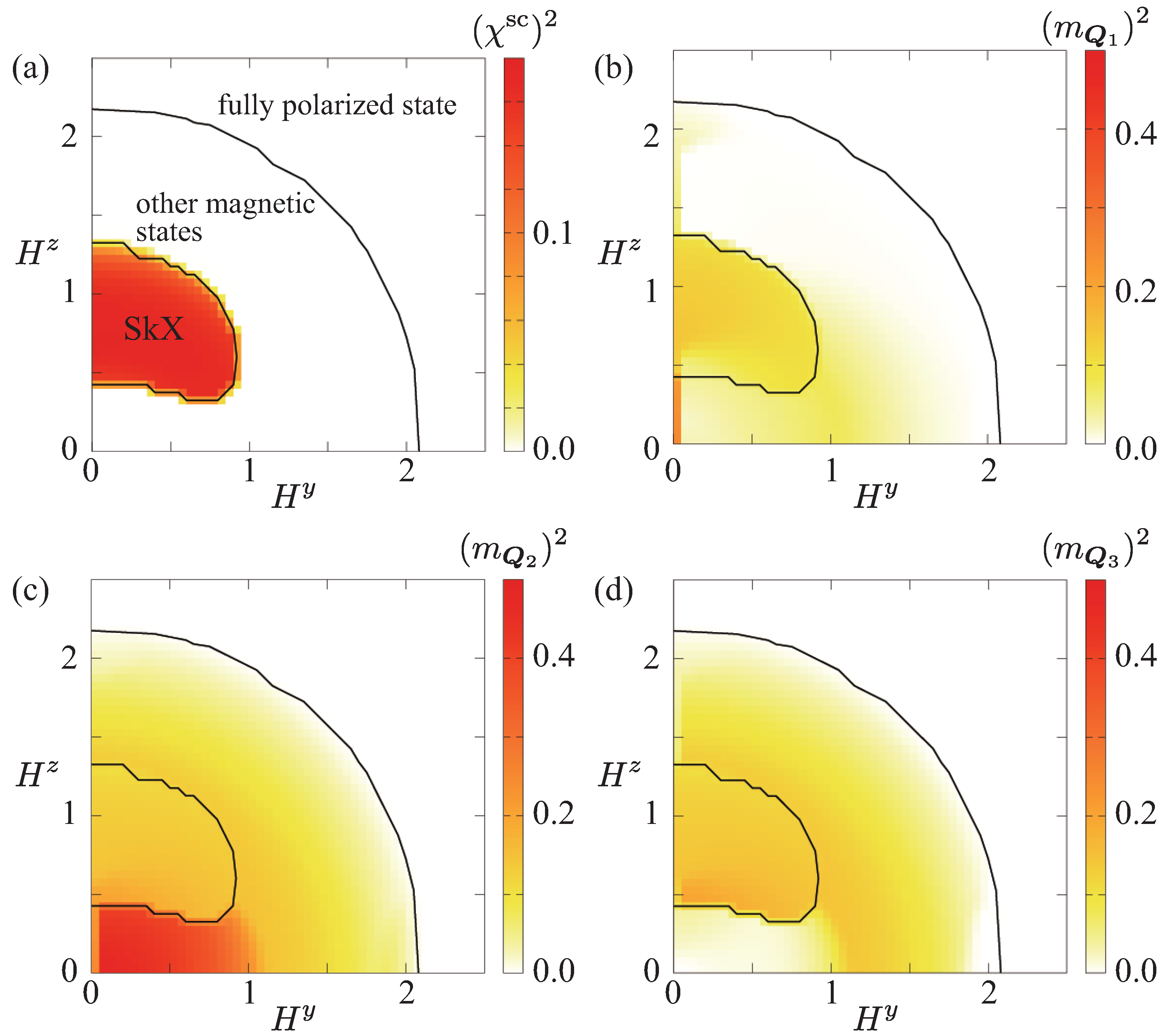
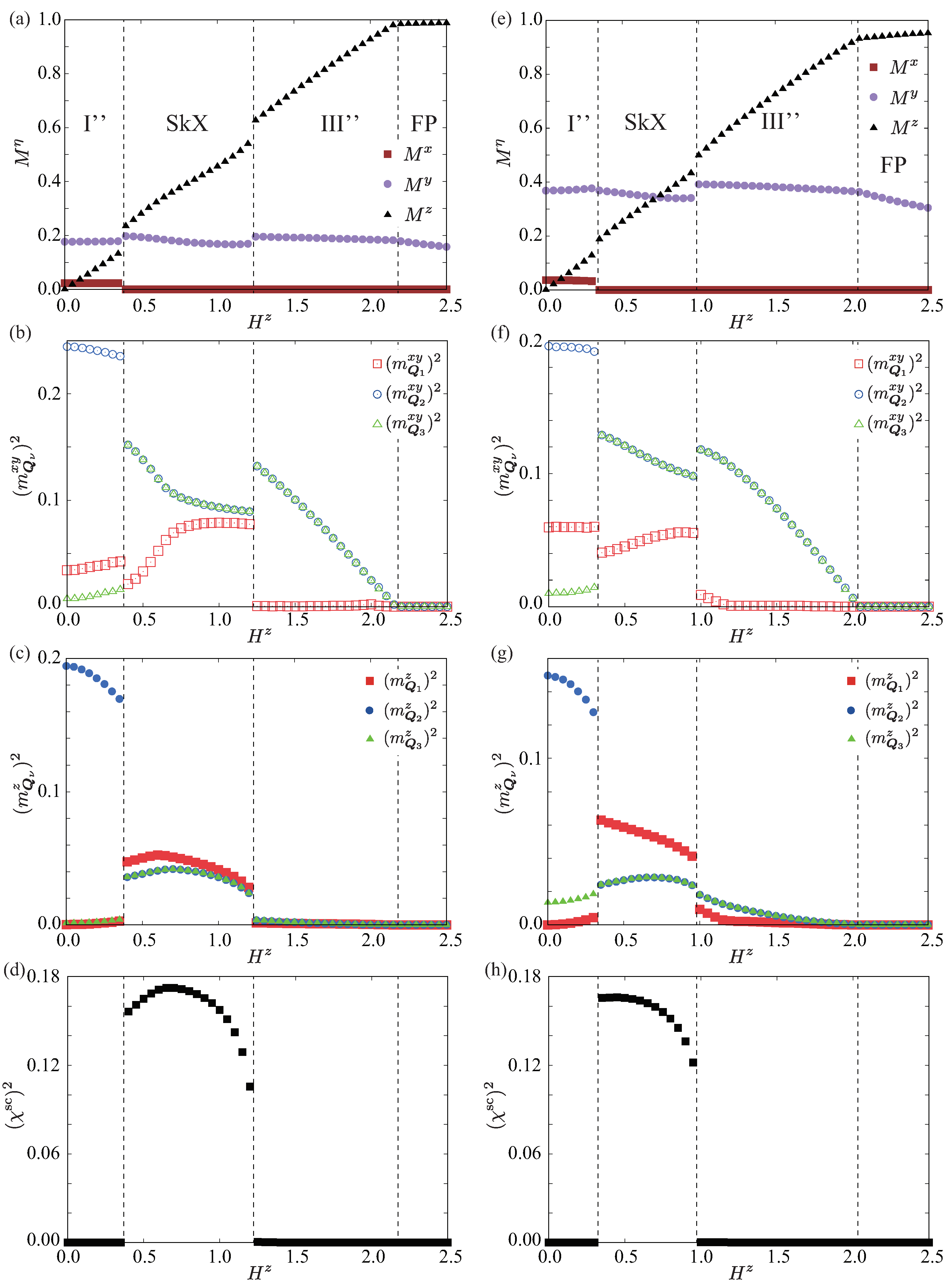
3.3. In-Plane Field along the y-Direction
4. Comparison with Other Mechanisms
5. Summary
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Katsura, H.; Nagaosa, N.; Balatsky, A.V. Spin Current and Magnetoelectric Effect in Noncollinear Magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef]
- Mostovoy, M. Ferroelectricity in Spiral Magnets. Phys. Rev. Lett. 2006, 96, 067601. [Google Scholar] [CrossRef] [PubMed]
- Cheong, S.W.; Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater. 2007, 6, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Levy, P.M.; Zhang, S.; Antropov, V. Identification of Transverse Spin Currents in Noncollinear Magnetic Structures. Phys. Rev. Lett. 2004, 93, 256602. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the Kagomé Lattice: Chiral Spin State Based A Ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Kanazawa, N.; Onose, Y.; Arima, T.; Okuyama, D.; Ohoyama, K.; Wakimoto, S.; Kakurai, K.; Ishiwata, S.; Tokura, Y. Large Topological Hall Effect in a Short-Period Helimagnet MnGe. Phys. Rev. Lett. 2011, 106, 156603. [Google Scholar] [CrossRef]
- Shiomi, Y.; Kanazawa, N.; Shibata, K.; Onose, Y.; Tokura, Y. Topological Nernst effect in a three-dimensional skyrmion-lattice phase. Phys. Rev. B 2013, 88, 064409. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I. Unconventional topological Hall effect in skyrmion crystals caused by the topology of the lattice. Phys. Rev. B 2017, 95, 094413. [Google Scholar] [CrossRef]
- Leroux, M.; Stolt, M.J.; Jin, S.; Pete, D.V.; Reichhardt, C.; Maiorov, B. Skyrmion lattice topological Hall effect near room temperature. Sci. Rep. 2018, 8, 15510. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.H.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef] [PubMed]
- Matsui, A.; Nomoto, T.; Arita, R. Skyrmion-size dependence of the topological Hall effect: A real-space calculation. Phys. Rev. B 2021, 104, 174432. [Google Scholar] [CrossRef]
- Park, H.; Heinonen, O.; Martin, I. First-principles study of magnetic states and the anomalous Hall conductivity of MNb3S6 (M = Co, Fe, Mn, and Ni). Phys. Rev. Mater. 2022, 6, 024201. [Google Scholar] [CrossRef]
- Oike, H.; Ebino, T.; Koretsune, T.; Kikkawa, A.; Hirschberger, M.; Taguchi, Y.; Tokura, Y.; Kagawa, F. Topological Nernst effect emerging from real-space gauge field and thermal fluctuations in a magnetic skyrmion lattice. Phys. Rev. B 2022, 106, 214425. [Google Scholar] [CrossRef]
- Takagi, H.; Takagi, R.; Minami, S.; Nomoto, T.; Ohishi, K.; Suzuki, M.T.; Yanagi, Y.; Hirayama, M.; Khanh, N.; Karube, K.; et al. Spontaneous topological Hall effect induced by non-coplanar antiferromagnetic order in intercalated van der Waals materials. Nat. Phys. 2023, 19, 961. [Google Scholar] [CrossRef]
- Cheon, S.; Lee, H.W.; Cheong, S.W. Nonreciprocal spin waves in a chiral antiferromagnet without the Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2018, 98, 184405. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M. Nonlinear nonreciprocal transport in antiferromagnets free from spin-orbit coupling. Phys. Rev. B 2022, 106, 014420. [Google Scholar] [CrossRef]
- Martin, I.; Batista, C.D. Itinerant Electron-Driven Chiral Magnetic Ordering and Spontaneous Quantum Hall Effect in Triangular Lattice Models. Phys. Rev. Lett. 2008, 101, 156402. [Google Scholar] [CrossRef]
- Akagi, Y.; Motome, Y. Spin Chirality Ordering and Anomalous Hall Effect in the Ferromagnetic Kondo Lattice Model on a Triangular Lattice. J. Phys. Soc. Jpn. 2010, 79, 083711. [Google Scholar] [CrossRef]
- Kumar, S.; van den Brink, J. Frustration-Induced Insulating Chiral Spin State in Itinerant Triangular-Lattice Magnets. Phys. Rev. Lett. 2010, 105, 216405. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Multiple-Q instability by (d-2)-dimensional connections of Fermi surfaces. Phys. Rev. B 2014, 90, 060402. [Google Scholar] [CrossRef]
- Ido, K.; Misawa, T. Many-body Chern insulator in the Kondo lattice model on a triangular lattice. arXiv 2023, arXiv:2310.07094. [Google Scholar]
- Shindou, R.; Nagaosa, N. Orbital Ferromagnetism and Anomalous Hall Effect in Antiferromagnets on the Distorted fcc Lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef]
- Ozawa, R.; Hayami, S.; Motome, Y. Zero-Field Skyrmions with a High Topological Number in Itinerant Magnets. Phys. Rev. Lett. 2017, 118, 147205. [Google Scholar] [CrossRef]
- Hayami, S.; Ozawa, R.; Motome, Y. Effective bilinear-biquadratic model for noncoplanar ordering in itinerant magnets. Phys. Rev. B 2017, 95, 224424. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Skyrmion Crystal from RKKY Interaction Mediated by 2D Electron Gas. Phys. Rev. Lett. 2020, 124, 207201. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef] [PubMed]
- Eto, R.; Pohle, R.; Mochizuki, M. Low-Energy Excitations of Skyrmion Crystals in a Centrosymmetric Kondo-Lattice Magnet: Decoupled Spin-Charge Excitations and Nonreciprocity. Phys. Rev. Lett. 2022, 129, 017201. [Google Scholar] [CrossRef]
- Wang, Z.; Batista, C.D. Skyrmion crystals in the triangular Kondo lattice model. SciPost Phys. 2023, 15, 161. [Google Scholar] [CrossRef]
- Sharma, V.; Wang, Z.; Batista, C.D. Machine learning assisted derivation of minimal low-energy models for metallic magnets. Npj Comput. Mater. 2023, 9, 192. [Google Scholar] [CrossRef]
- Miyazaki, Y. Equivariant neural networks for spin dynamics simulations of itinerant magnets. Mach. Learn. Sci. Technol. 2023, 4, 045006. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Hirschberger, M.; Spitz, L.; Nomoto, T.; Kurumaji, T.; Gao, S.; Masell, J.; Nakajima, T.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; et al. Topological Nernst Effect of the Two-Dimensional Skyrmion Lattice. Phys. Rev. Lett. 2020, 125, 076602. [Google Scholar] [CrossRef]
- Sampathkumaran, E.V. A report of (topological) Hall anomaly two decades ago in Gd2PdSi3, and its relevance to the history of the field of Topological Hall Effect due to magnetic skyrmions. arXiv 2019, arXiv:1910.09194. [Google Scholar]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3 (R = Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Hao, L.; Yang, J.; Noordhoek, K.; Pandey, S.; Zhou, H.; Liu, J. Anomalous magnetoresistance in centrosymmetric skyrmion-lattice magnet Gd2PdSi3. New J. Phys. 2020, 22, 083056. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
- Paddison, J.A.M.; Rai, B.K.; May, A.F.; Calder, S.; Stone, M.B.; Frontzek, M.D.; Christianson, A.D. Magnetic Interactions of the Centrosymmetric Skyrmion Material Gd2PdSi3. Phys. Rev. Lett. 2022, 129, 137202. [Google Scholar] [CrossRef] [PubMed]
- Bouaziz, J.; Mendive-Tapia, E.; Blügel, S.; Staunton, J.B. Fermi-Surface Origin of Skyrmion Lattices in Centrosymmetric Rare-Earth Intermetallics. Phys. Rev. Lett. 2022, 128, 157206. [Google Scholar] [CrossRef] [PubMed]
- Ju, J.; Saito, H.; Kurumaji, T.; Hirschberger, M.; Kikkawa, A.; Taguchi, Y.; Arima, T.H.; Tokura, Y.; Nakajima, T. Polarized neutron scattering study of the centrosymmetric skyrmion host material Gd2PdSi3. Phys. Rev. B 2023, 107, 024405. [Google Scholar] [CrossRef]
- Nomoto, T.; Arita, R. Ab initio exploration of short-pitch skyrmion materials: Role of orbital frustration. J. Appl. Phys. 2023, 133. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagome lattice. Nat. Commun. 2019, 10, 5831. [Google Scholar] [CrossRef]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Nakamura, S.; Kabeya, N.; Kobayashi, M.; Araki, K.; Katoh, K.; Ochiai, A. Magnetic phases of the frustrated ferromagnetic spin-trimer system Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 2023, 107, 014422. [Google Scholar] [CrossRef]
- Ogunbunmi, M.O.; Nair, H.S.; Strydom, A.M. Magnetic frustration-driven ground state properties of rare-earth magnetic ions on a breathing kagome lattice: A review of the Gd3Ru4 Al12 structure type magnets. Crit. Rev. Solid State Mater. Sci. 2023, 48, 480–501. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Hayami, S.; Kato, Y. Widely-sweeping magnetic field–temperature phase diagrams for skyrmion-hosting centrosymmetric tetragonal magnets. J. Magn. Magn. Mater. 2023, 571, 170547. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.; Schulz, S.; Kliemt, K.; Chulkov, E.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. arXiv 2023, arXiv:2306.01370. [Google Scholar] [CrossRef]
- Canepa, F.; Napoletano, M.; Palenzona, A.; Moze, O.; Kockelmann, W. Ferromagnetic and incommensurate antiferromagnetic order in a multi-sublattice itinerant magnet: Y3Co8Sn4. J. Phys. Condens. Matter 2004, 17, 373. [Google Scholar] [CrossRef]
- Takagi, R.; White, J.; Hayami, S.; Arita, R.; Honecker, D.; Rønnow, H.; Tokura, Y.; Seki, S. Multiple-q noncollinear magnetism in an itinerant hexagonal magnet. Sci. Adv. 2018, 4, eaau3402. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Adams, T.; Mühlbauer, S.; Pfleiderer, C.; Jonietz, F.; Bauer, A.; Neubauer, A.; Georgii, R.; Böni, P.; Keiderling, U.; Everschor, K.; et al. Long-Range Crystalline Nature of the Skyrmion Lattice in MnSi. Phys. Rev. Lett. 2011, 107, 217206. [Google Scholar] [CrossRef]
- Morikawa, D.; Shibata, K.; Kanazawa, N.; Yu, X.Z.; Tokura, Y. Crystal chirality and skyrmion helicity in MnSi and (Fe, Co)Si as determined by transmission electron microscopy. Phys. Rev. B 2013, 88, 024408. [Google Scholar] [CrossRef]
- Bauer, A.; Garst, M.; Pfleiderer, C. Specific Heat of the Skyrmion Lattice Phase and Field-Induced Tricritical Point in MnSi. Phys. Rev. Lett. 2013, 110, 177207. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Yokouchi, T.; Kanazawa, N.; Tsukazaki, A.; Kozuka, Y.; Kikkawa, A.; Taguchi, Y.; Kawasaki, M.; Ichikawa, M.; Kagawa, F.; Tokura, Y. Formation of in-plane skyrmions in epitaxial MnSi thin films as revealed by planar Hall effect. J. Phys. Soc. Jpn. 2015, 84, 104708. [Google Scholar] [CrossRef]
- Chacon, A.; Bauer, A.; Adams, T.; Rucker, F.; Brandl, G.; Georgii, R.; Garst, M.; Pfleiderer, C. Uniaxial Pressure Dependence of Magnetic Order in MnSi. Phys. Rev. Lett. 2015, 115, 267202. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Kikkawa, A.; Morikawa, D.; Shibata, K.; Tokunaga, Y.; Taguchi, Y.; Tokura, Y. Variation of skyrmion forms and their stability in MnSi thin plates. Phys. Rev. B 2015, 91, 054411. [Google Scholar] [CrossRef]
- Reiner, M.; Bauer, A.; Leitner, M.; Gigl, T.; Anwand, W.; Butterling, M.; Wagner, A.; Kudejova, P.; Pfleiderer, C.; Hugenschmidt, C. Positron spectroscopy of point defects in the skyrmion-lattice compound MnSi. Sci. Rep. 2016, 6, 29109. [Google Scholar] [CrossRef] [PubMed]
- Mühlbauer, S.; Kindervater, J.; Adams, T.; Bauer, A.; Keiderling, U.; Pfleiderer, C. Kinetic small angle neutron scattering of the skyrmion lattice in MnSi. New J. Phys. 2016, 18, 075017. [Google Scholar] [CrossRef]
- Nakajima, T.; Oike, H.; Kikkawa, A.; Gilbert, E.P.; Booth, N.; Kakurai, K.; Taguchi, Y.; Tokura, Y.; Kagawa, F.; Arima, T.H. Skyrmion lattice structural transition in MnSi. Sci. Adv. 2017, 3, e1602562. [Google Scholar] [CrossRef] [PubMed]
- Meynell, S.A.; Wilson, M.N.; Krycka, K.L.; Kirby, B.J.; Fritzsche, H.; Monchesky, T.L. Neutron study of in-plane skyrmions in MnSi thin films. Phys. Rev. B 2017, 96, 054402. [Google Scholar] [CrossRef]
- Luo, Y.; Lin, S.Z.; Fobes, D.M.; Liu, Z.; Bauer, E.D.; Betts, J.B.; Migliori, A.; Thompson, J.D.; Janoschek, M.; Maiorov, B. Anisotropic magnetocrystalline coupling of the skyrmion lattice in MnSi. Phys. Rev. B 2018, 97, 104423. [Google Scholar] [CrossRef]
- Bannenberg, L.J.; Sadykov, R.; Dalgliesh, R.M.; Goodway, C.; Schlagel, D.L.; Lograsso, T.A.; Falus, P.; Lelièvre-Berna, E.; Leonov, A.O.; Pappas, C. Skyrmions and spirals in MnSi under hydrostatic pressure. Phys. Rev. B 2019, 100, 054447. [Google Scholar] [CrossRef]
- Leishman, A.W.D.; Menezes, R.M.; Longbons, G.; Bauer, E.D.; Janoschek, M.; Honecker, D.; DeBeer-Schmitt, L.; White, J.S.; Sokolova, A.; Milošević, M.V.; et al. Topological energy barrier for skyrmion lattice formation in MnSi. Phys. Rev. B 2020, 102, 104416. [Google Scholar] [CrossRef]
- Dhital, C.; DeBeer-Schmitt, L.; Young, D.P.; DiTusa, J.F. Unpinning the skyrmion lattice in MnSi: Effect of substitutional disorder. Phys. Rev. B 2019, 99, 024428. [Google Scholar] [CrossRef]
- Chai, Y.; Lu, P.; Du, H.; Shen, J.; Ma, Y.; Zhai, K.; Wang, L.; Shi, Y.; Li, H.; Wang, W.; et al. Probe of skyrmion phases and dynamics in MnSi via the magnetoelectric effect in a composite configuration. Phys. Rev. B 2021, 104, L100413. [Google Scholar] [CrossRef]
- Kindervater, J.; Stasinopoulos, I.; Bauer, A.; Haslbeck, F.X.; Rucker, F.; Chacon, A.; Mühlbauer, S.; Franz, C.; Garst, M.; Grundler, D.; et al. Weak Crystallization of Fluctuating Skyrmion Textures in MnSi. Phys. Rev. X 2019, 9, 041059. [Google Scholar] [CrossRef]
- Soda, M.; Forgan, E.M.; Blackburn, E.; Campillo, E.; Ryukhtin, V.; Hoffmann, I.; Kikkawa, A.; Taguchi, Y.; Yoshizawa, H.; Kawano-Furukawa, H. Asymmetric slow dynamics of the skyrmion lattice in MnSi. Nat. Phys. 2023, 19, 1476–1481. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Adams, T.; Mühlbauer, S.; Neubauer, A.; Münzer, W.; Jonietz, F.; Georgii, R.; Pedersen, B.; Böni, P.; Rosch, A.; Pfleiderer, C. Skyrmion lattice domains in Fe1−xCoxSi. J. Phys. Conf. Ser. 2010, 200, 032001. [Google Scholar] [CrossRef]
- Münzer, W.; Neubauer, A.; Adams, T.; Mühlbauer, S.; Franz, C.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 2010, 81, 041203. [Google Scholar] [CrossRef]
- Bauer, A.; Garst, M.; Pfleiderer, C. History dependence of the magnetic properties of single-crystal Fe1−xCoxSi. Phys. Rev. B 2016, 93, 235144. [Google Scholar] [CrossRef]
- Dhital, C.; DiTusa, J.F. Entropic signatures of the skyrmion lattice phase in MnSi1−xAlx and Fe1−yCoySi. Phys. Rev. B 2020, 102, 224408. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Nakamura, S.; Sakakibara, T.; Hedo, M.; Nakama, T.; et al. Giant Hall resistivity and magnetoresistance in cubic chiral antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2018, 87, 023701. [Google Scholar] [CrossRef]
- Kaneko, K.; Frontzek, M.D.; Matsuda, M.; Nakao, A.; Munakata, K.; Ohhara, T.; Kakihana, M.; Haga, Y.; Hedo, M.; Nakama, T.; et al. Unique Helical Magnetic Order and Field-Induced Phase in Trillium Lattice Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 013702. [Google Scholar] [CrossRef]
- Tabata, C.; Matsumura, T.; Nakao, H.; Michimura, S.; Kakihana, M.; Inami, T.; Kaneko, K.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic Field Induced Triple-q Magnetic Order in Trillium Lattice Antiferromagnet EuPtSi Studied by Resonant X-ray Scattering. J. Phys. Soc. Jpn. 2019, 88, 093704. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Takeuchi, T.; Harima, H.; Hedo, M.; Nakama, T.; et al. Unique Magnetic Phases in the Skyrmion Lattice and Fermi Surface Properties in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 094705. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ganesan, V. A-phase, field-induced tricritical point, and universal magnetocaloric scaling in EuPtSi. Phys. Rev. B 2019, 100, 125113. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic field versus temperature phase diagram for H‖[001] in the trillium lattice antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 053703. [Google Scholar] [CrossRef]
- Sakakibara, T.; Nakamura, S.; Kittaka, S.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Fluctuation-Induced First-Order Transition and Tricritical Point in EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 093701. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Angle Dependence of the Magnetic Phase Diagram in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2020, 89, 093703. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Sakakibara, T.; Nakamura, S.; Kittaka, S.; Kakihana, M.; Hedo, M.; Nakama, T.; Onuki, Y. Magnetic Phase Transitions of the 4f Skyrmion Compound EuPtSi Studied by Magnetization Measurements. J. Phys. Soc. Jpn. 2021, 90, 064701. [Google Scholar] [CrossRef]
- Goetsch, R.J.; Anand, V.K.; Johnston, D.C. Antiferromagnetism in EuNiGe3. Phys. Rev. B 2013, 87, 064406. [Google Scholar] [CrossRef]
- Fabrèges, X.; Gukasov, A.; Bonville, P.; Maurya, A.; Thamizhavel, A.; Dhar, S.K. Exploring metamagnetism of single crystalline EuNiGe3 by neutron scattering. Phys. Rev. B 2016, 93, 214414. [Google Scholar] [CrossRef]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef]
- Matsumura, T.; Kurauchi, K.; Tsukagoshi, M.; Higa, N.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Distorted triangular skyrmion lattice in a noncentrosymmetric tetragonal magnet. arXiv 2023, arXiv:2306.14767. [Google Scholar]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Néel- and Bloch-Type Magnetic Vortices in Rashba Metals. Phys. Rev. Lett. 2018, 121, 137202. [Google Scholar] [CrossRef] [PubMed]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Shekhtman, L.; Aharony, A.; Entin-Wohlman, O. Bond-dependent symmetric and antisymmetric superexchange interactions in La2CuO4. Phys. Rev. B 1993, 47, 174–182. [Google Scholar] [CrossRef]
- Khomskii, D.; Mostovoy, M. Orbital ordering and frustrations. J. Phys. A 2003, 36, 9197. [Google Scholar] [CrossRef]
- Jackeli, G.; Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef]
- Li, Y.D.; Wang, X.; Chen, G. Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets. Phys. Rev. B 2016, 94, 035107. [Google Scholar] [CrossRef]
- Maksimov, P.A.; Zhu, Z.; White, S.R.; Chernyshev, A.L. Anisotropic-Exchange Magnets on a Triangular Lattice: Spin Waves, Accidental Degeneracies, and Dual Spin Liquids. Phys. Rev. X 2019, 9, 021017. [Google Scholar] [CrossRef]
- Becker, M.; Hermanns, M.; Bauer, B.; Garst, M.; Trebst, S. Spin-orbit physics of j = Mott insulators on the triangular lattice. Phys. Rev. B 2015, 91, 155135. [Google Scholar] [CrossRef]
- Rousochatzakis, I.; Rössler, U.K.; van den Brink, J.; Daghofer, M. Kitaev anisotropy induces mesoscopic Z2 vortex crystals in frustrated hexagonal antiferromagnets. Phys. Rev. B 2016, 93, 104417. [Google Scholar] [CrossRef]
- Liu, C.; Yu, R.; Wang, X. Semiclassical ground-state phase diagram and multi-Q phase of a spin-orbit-coupled model on triangular lattice. Phys. Rev. B 2016, 94, 174424. [Google Scholar] [CrossRef]
- Chern, G.W.; Sizyuk, Y.; Price, C.; Perkins, N.B. Kitaev-Heisenberg model in a magnetic field: Order-by-disorder and commensurate-incommensurate transitions. Phys. Rev. B 2017, 95, 144427. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Kamiya, Y.; Batista, C.D. Magnetic Vortex Crystals in Frustrated Mott Insulator. Phys. Rev. X 2014, 4, 011023. [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Chandragiri, V.; Iyer, K.K.; Sampathkumaran, E. Magnetic behavior of Gd3Ru4Al12, a layered compound with distorted kagomé net. J. Phys. Condens. Matter 2016, 28, 286002. [Google Scholar] [CrossRef]
- Nakamura, S.; Kabeya, N.; Kobayashi, M.; Araki, K.; Katoh, K.; Ochiai, A. Spin trimer formation in the metallic compound Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 2018, 98, 054410. [Google Scholar] [CrossRef]
- Matsumura, T.; Ozono, Y.; Nakamura, S.; Kabeya, N.; Ochiai, A. Helical ordering of spin trimers in a distorted kagome lattice of Gd3Ru4Al12 studied by resonant x-ray diffraction. J. Phys. Soc. Jpn. 2019, 88, 023704. [Google Scholar] [CrossRef]




| Phase | Remark | |||||||
|---|---|---|---|---|---|---|---|---|
| Phase I | – | ✓ | ✓ | ✓ | – | ✓ | – | |
| Phase II | – | ✓ | ✓ | ✓ | – | ✓ | – | |
| SkX II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| SkX | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Phase III | – | ✓ | – | ✓ | – | – | – | |
| Phase IV | – | ✓ | – | ✓ | – | ✓ | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Effect of In-Plane Magnetic Field on Skyrmions in a Centrosymmetric Triangular-Lattice System with Symmetric Anisotropic Exchange Interaction. Magnetism 2024, 4, 54-72. https://doi.org/10.3390/magnetism4010005
Hayami S. Effect of In-Plane Magnetic Field on Skyrmions in a Centrosymmetric Triangular-Lattice System with Symmetric Anisotropic Exchange Interaction. Magnetism. 2024; 4(1):54-72. https://doi.org/10.3390/magnetism4010005
Chicago/Turabian StyleHayami, Satoru. 2024. "Effect of In-Plane Magnetic Field on Skyrmions in a Centrosymmetric Triangular-Lattice System with Symmetric Anisotropic Exchange Interaction" Magnetism 4, no. 1: 54-72. https://doi.org/10.3390/magnetism4010005
APA StyleHayami, S. (2024). Effect of In-Plane Magnetic Field on Skyrmions in a Centrosymmetric Triangular-Lattice System with Symmetric Anisotropic Exchange Interaction. Magnetism, 4(1), 54-72. https://doi.org/10.3390/magnetism4010005






