Effect of Laminated Core Body Size on Motor Magnetic Properties
Abstract
1. Introduction
2. Experimental Procedure
2.1. Toroidal Core Samples
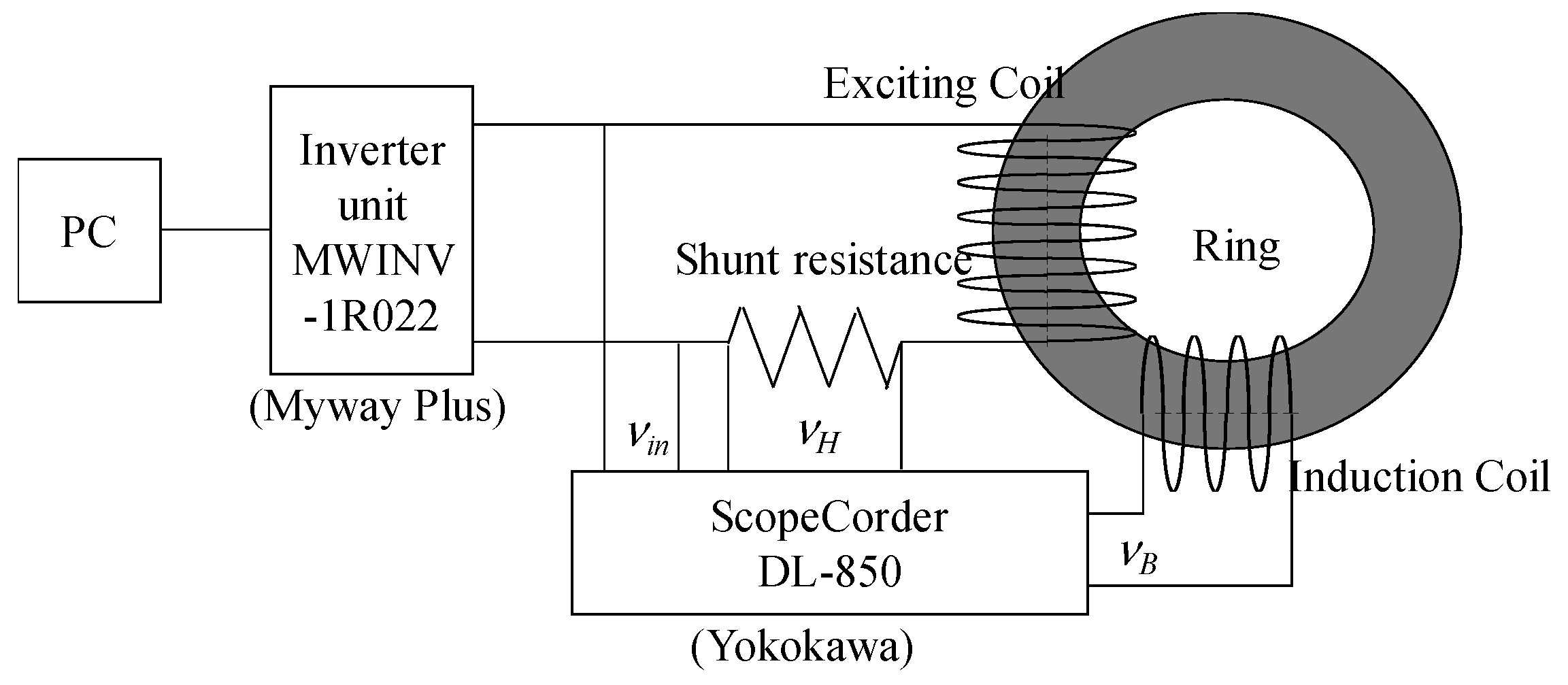
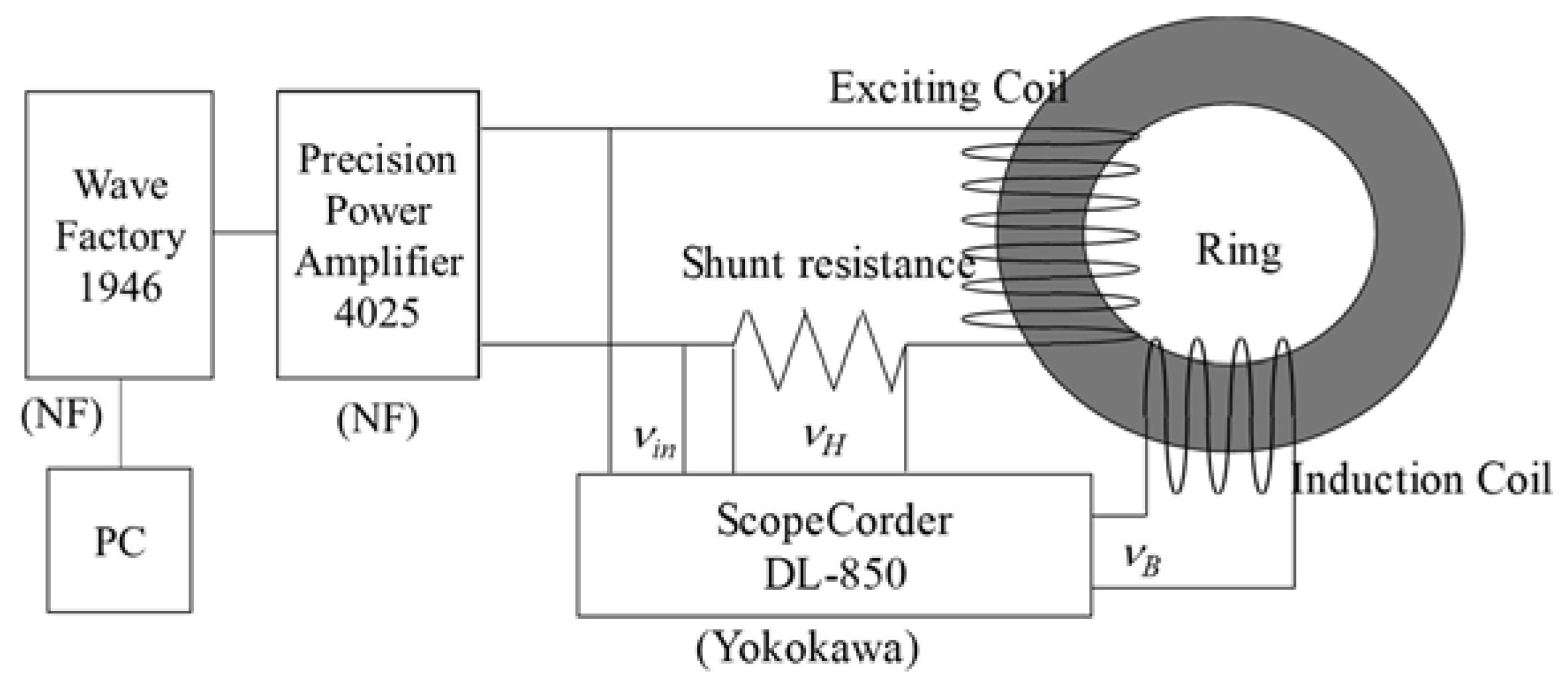
2.2. Measurement System
3. Results and Discussion
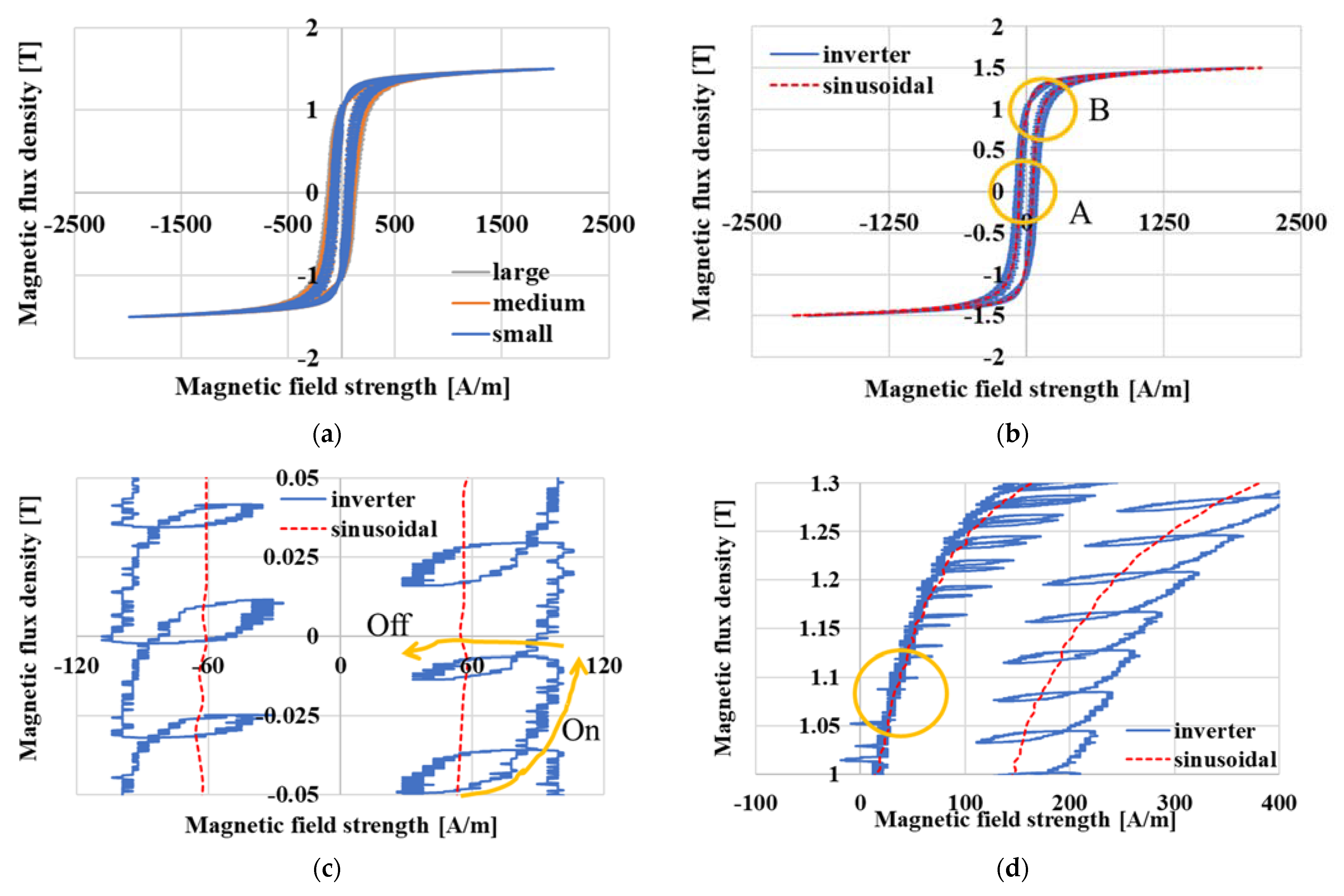
3.1. Magnetic Properties
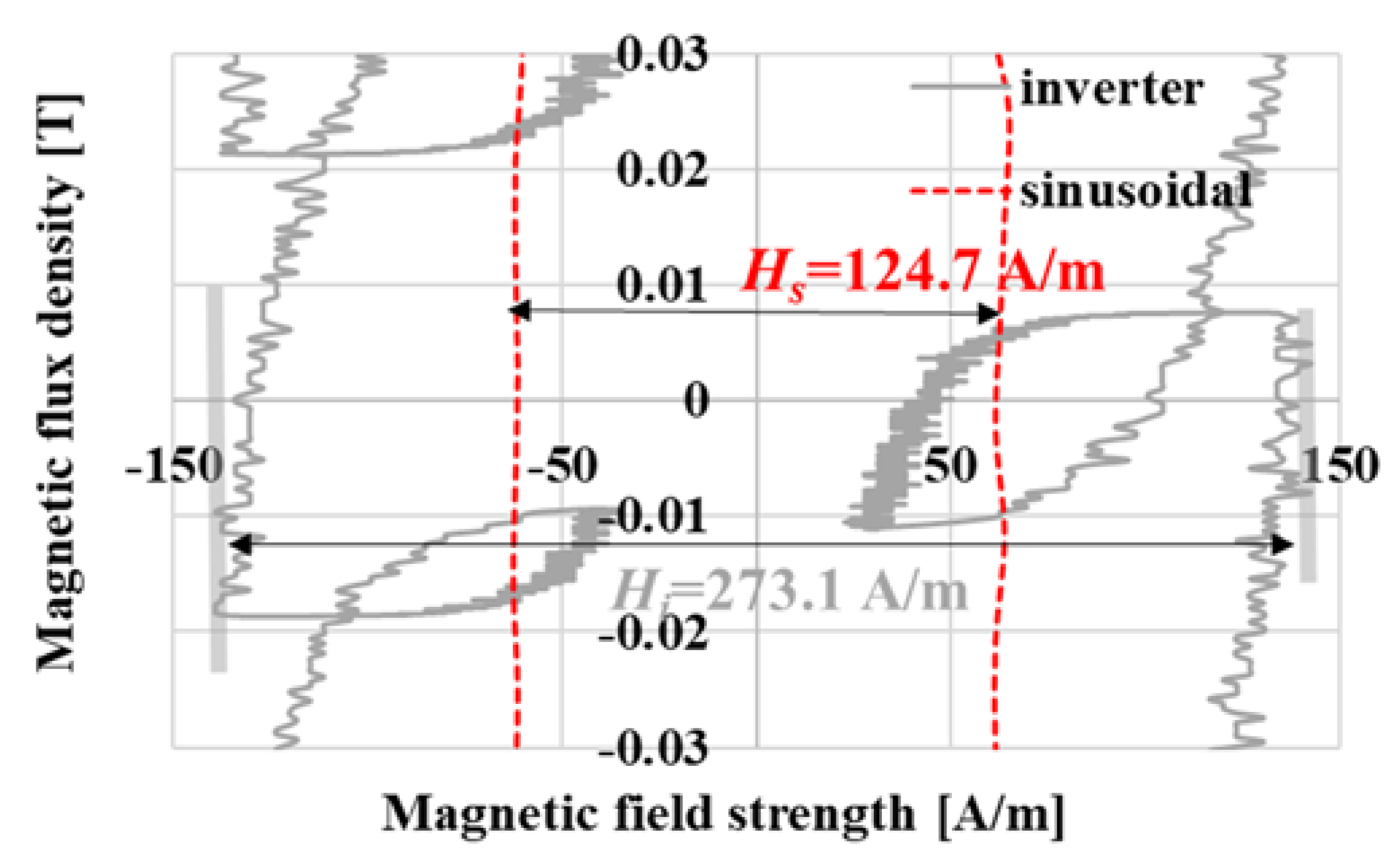
3.2. Major Loops
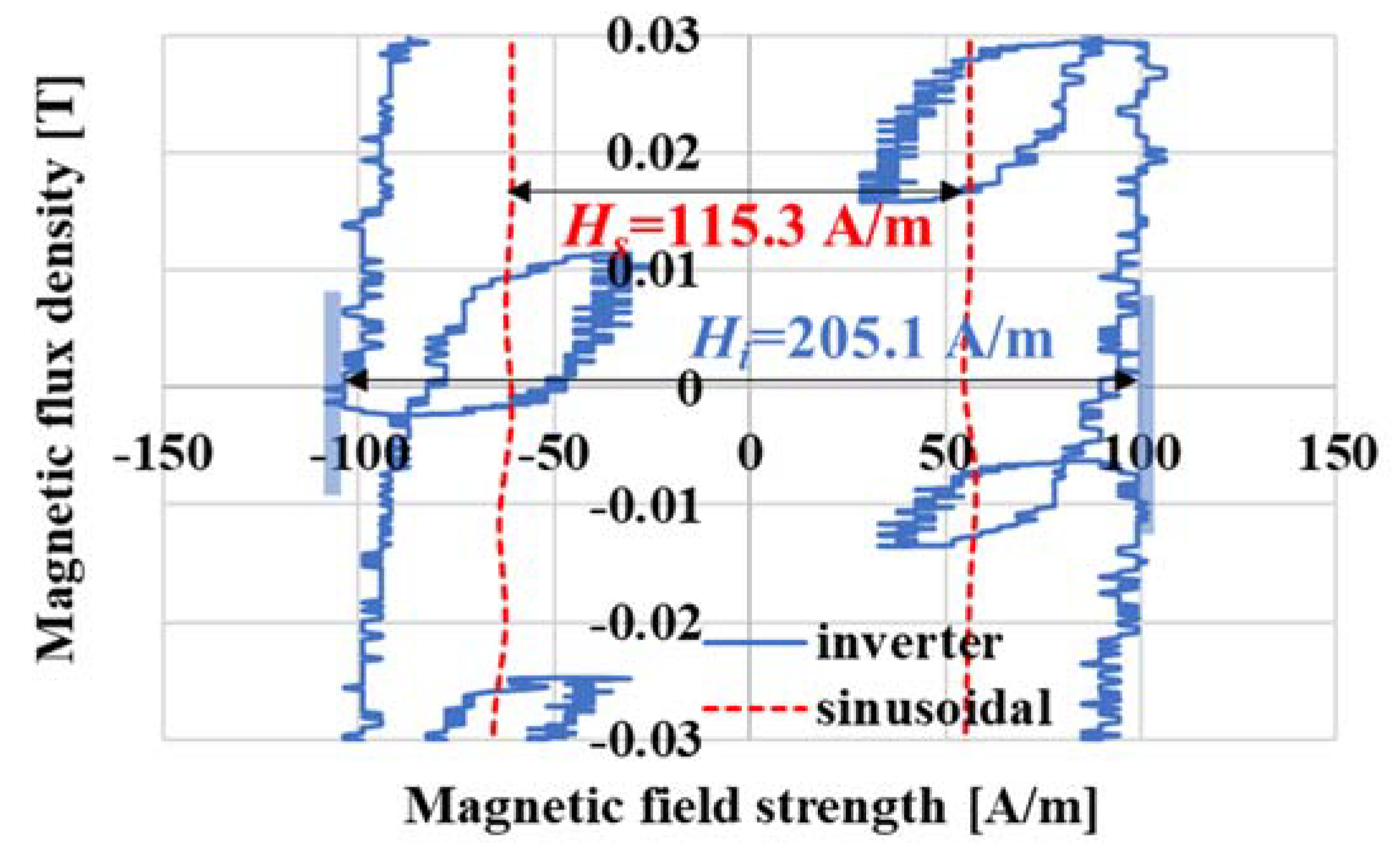
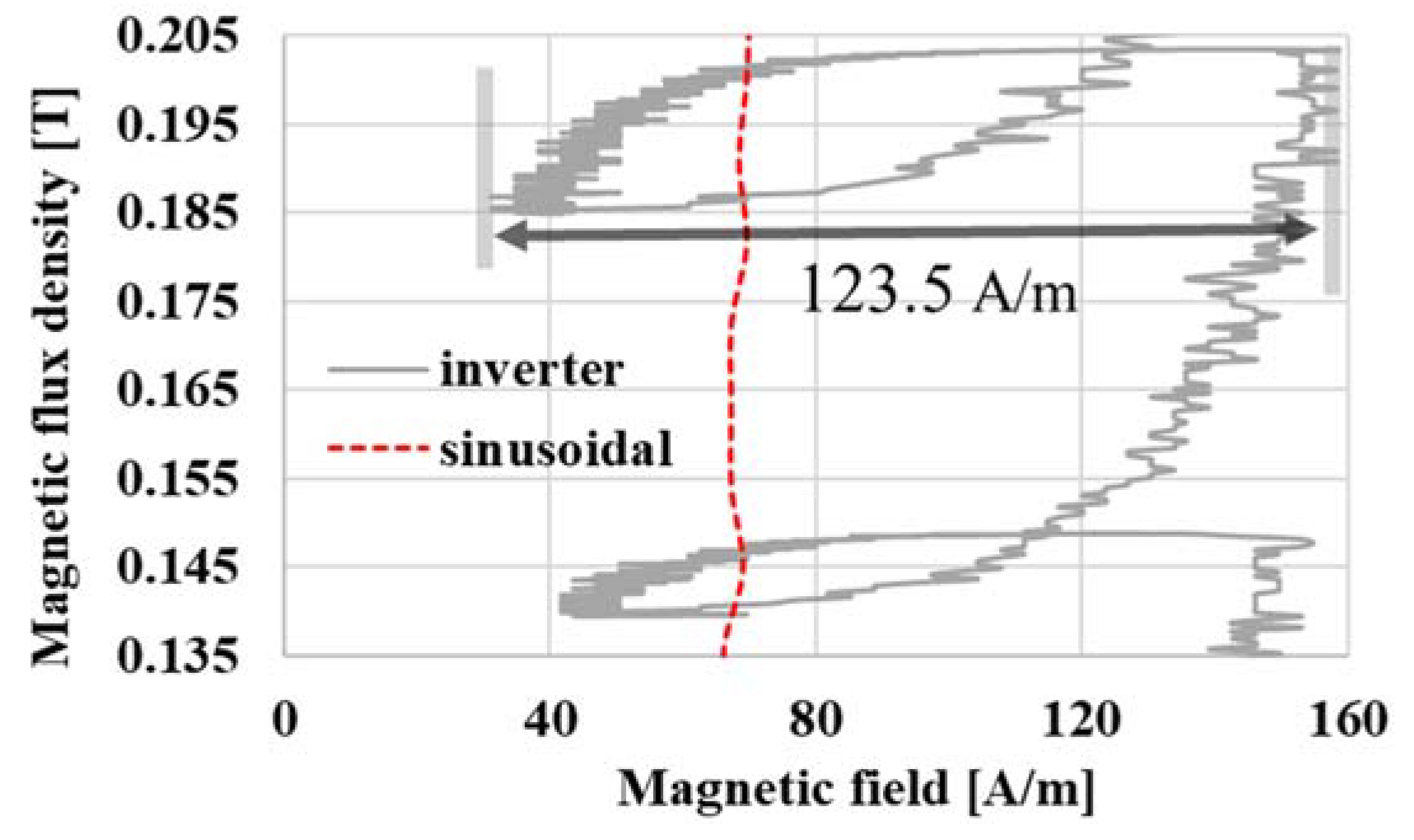
3.3. Minor Loops
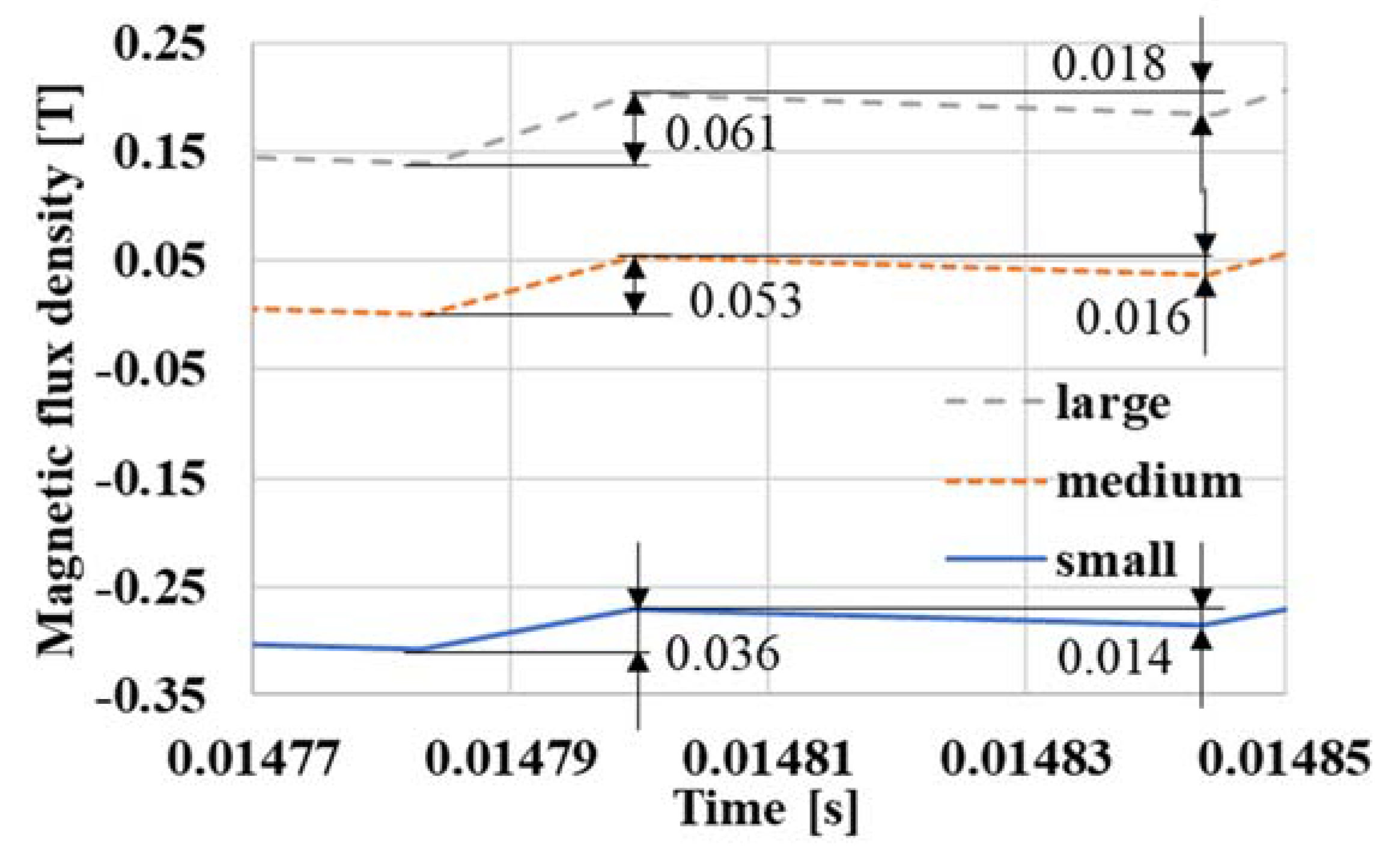
3.4. dB/dt Waveform Analysis
3.5. B Waveform Analysis
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. 2022. Available online: https://www.ipcc.ch/report/ar6/wg2/ (accessed on 20 April 2023).
- IPCC Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. 2022. Available online: https://www.ipcc.ch/report/ar6/wg3/ (accessed on 20 April 2023).
- European Commission. 2030 Climate Target Plan. 2020. Available online: https://climate.ec.europa.eu/eu-action/european-green-deal/2030-climate-target-plan_en (accessed on 20 April 2023).
- European Commission. 2050 Long-Term Strategy. 2021. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2050-long-term-strategy_en (accessed on 20 April 2023).
- Fuji Keizai Group. The Pulse-Taking of the Near Future and the Present Conditions about the Amount of Use Electricity of the Electricity Usage Apparatus; Fuji Keizai: Tokyo, Japan, 2009; pp. 1–53. (In Japanese) [Google Scholar]
- The Agency of Natural Resource and Energy. Japan’s Energy White Paper; Energy Forum: Tokyo, Japan, 2012; p. 88. (In Japanese)
- IEA. World Energy Outlook 2017; IEA Publications: Paris, France, 2017.
- Croucher, M. Energy efficiency: Is re-distribution worth the gains? Energy Policy 2012, 45, 304–307. [Google Scholar] [CrossRef]
- Pop, I.G.; Văduva, S.; Talpoș, M.-F. Energetic Sustainability and the Environment: A Transdisciplinary, Economic–Ecological Approach. Sustainability 2017, 9, 873. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D. Energy Costs of Energy Savings in Buildings: A Review. Sustainability 2012, 4, 1711–1732. [Google Scholar] [CrossRef]
- Yang, S.-H.; Pyo, H.-J.; Jung, D.-H.; Kim, W.-H. A Study on Optimal Design Process of Dual Rotor Axial-Flux Permanent Magnet Synchronous Motors. Machines 2023, 11, 445. [Google Scholar] [CrossRef]
- Deepak, K.; Frikha, M.A.; Benômar, Y.; El Baghdadi, M.; Hegazy, O. In-Wheel Motor Drive Systems for Electric Vehicles: State of the Art, Challenges, and Future Trends. Energies 2023, 16, 3121. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Sun, W.; Guo, L.; Wang, H. Design of Permanent Magnet-Assisted Synchronous Reluctance Motor with Low Torque Ripple. World Electr. Veh. J. 2023, 14, 82. [Google Scholar] [CrossRef]
- Paramonov, A.; Oshurbekov, S.; Kazakbaev, V.; Prakht, V.; Dmitrievskii, V. Investigation of the Effect of the Voltage Drop and Cable Length on the Success of Starting the Line-Start Permanent Magnet Motor in the Drive of a Centrifugal Pump Unit. Mathematics 2023, 11, 646. [Google Scholar] [CrossRef]
- Bian, Y.; Wen, X.; Fan, T.; Li, H.; Liu, Z. Data-Driven-Model-Based Full-Region Optimal Mapping Method of Permanent Magnet Synchronous Motors in Wide Temperature Range. Machines 2023, 11, 324. [Google Scholar] [CrossRef]
- Yun, K.; Eguchi, S. Magnetic Properties of Different Core Size with Inverter Excitation. IEEJ MAG-19-032 2019, 32, 31–34. (In Japanese) [Google Scholar]
- Yun, K.; Eguchi, S. Magnetic Properties of Different Core Size with Inverter Excitation—Part 2. IEEJ MAG-19-160 2019, 32, 13–15. (In Japanese) [Google Scholar]
- Asai, Y.; Yun, K. Influence of Different Core Size on Magnetic Properties. IEEJ MAG-21-055 2021, 32, 5–8. (In Japanese) [Google Scholar]
- Yun, K.; Fujisaki, K. Iron Loss Characteristics of Estimated On-Voltage of Power Semiconductor by PWM Shaped Voltage Excitation. IEEJ Trans. Fundam. Mater. 2015, 135, 605–610. [Google Scholar] [CrossRef]
- Yun, K. Magnetic Properties of Electrical Steel Sheets with Motor Control Excitation. J. Electron. Mater. 2019, 48, 1472–1479. [Google Scholar] [CrossRef]
- Fernandez, M.; Robles, E.; Aretxabaleta, I.; Kortabarria, I.; Martín, J.L. Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation. Machines 2023, 11, 404. [Google Scholar] [CrossRef]
- Lin, H.; Xu, J. Performance Evaluation of SiC-Based Two-Level VSIs with Generalized Carrier-Based PWM Strategies in Motor Drive Applications. Electronics 2022, 11, 4136. [Google Scholar] [CrossRef]
- Thao, N.G.M.; Zhong, S.; Fujisaki, K.; Iwamoto, F.; Kimura, T.; Yamada, T. Experimental Assessment of Motor Core Loss, Inverter Loss and Ringing Phenomenon Under SiC-MOSFET Inverter Excitation. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1634–1640. [Google Scholar] [CrossRef]
- Ibrahim, I.; Silva, R.; Mohammadi, M.H.; Ghorbanian, V.; Lowther, D.A. Surrogate Models for Design and Optimization of Inverter-Fed Synchronous Motor Drives. IEEE Trans. Magn. 2021, 57, 8203805. [Google Scholar] [CrossRef]
- Mecke, R. Multilevel Inverter with New Wide-Bandgap SiC and GaN Power Switches. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021; pp. 1–6. [Google Scholar] [CrossRef]






| Small | Medium | Large | |
|---|---|---|---|
| Outer diameter [mm] | 50 | 90 | 127 |
| Inner diameter [mm] | 40 | 80 | 117 |
| Exciting coil [turns] | 200 | 200 | 200 |
| Detection coil [turns] | 101 | 101 | 101 |
| Magnetic path length [mm] | 141 | 267 | 383 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, K. Effect of Laminated Core Body Size on Motor Magnetic Properties. Magnetism 2023, 3, 158-168. https://doi.org/10.3390/magnetism3020013
Yun K. Effect of Laminated Core Body Size on Motor Magnetic Properties. Magnetism. 2023; 3(2):158-168. https://doi.org/10.3390/magnetism3020013
Chicago/Turabian StyleYun, Kyyoul. 2023. "Effect of Laminated Core Body Size on Motor Magnetic Properties" Magnetism 3, no. 2: 158-168. https://doi.org/10.3390/magnetism3020013
APA StyleYun, K. (2023). Effect of Laminated Core Body Size on Motor Magnetic Properties. Magnetism, 3(2), 158-168. https://doi.org/10.3390/magnetism3020013






