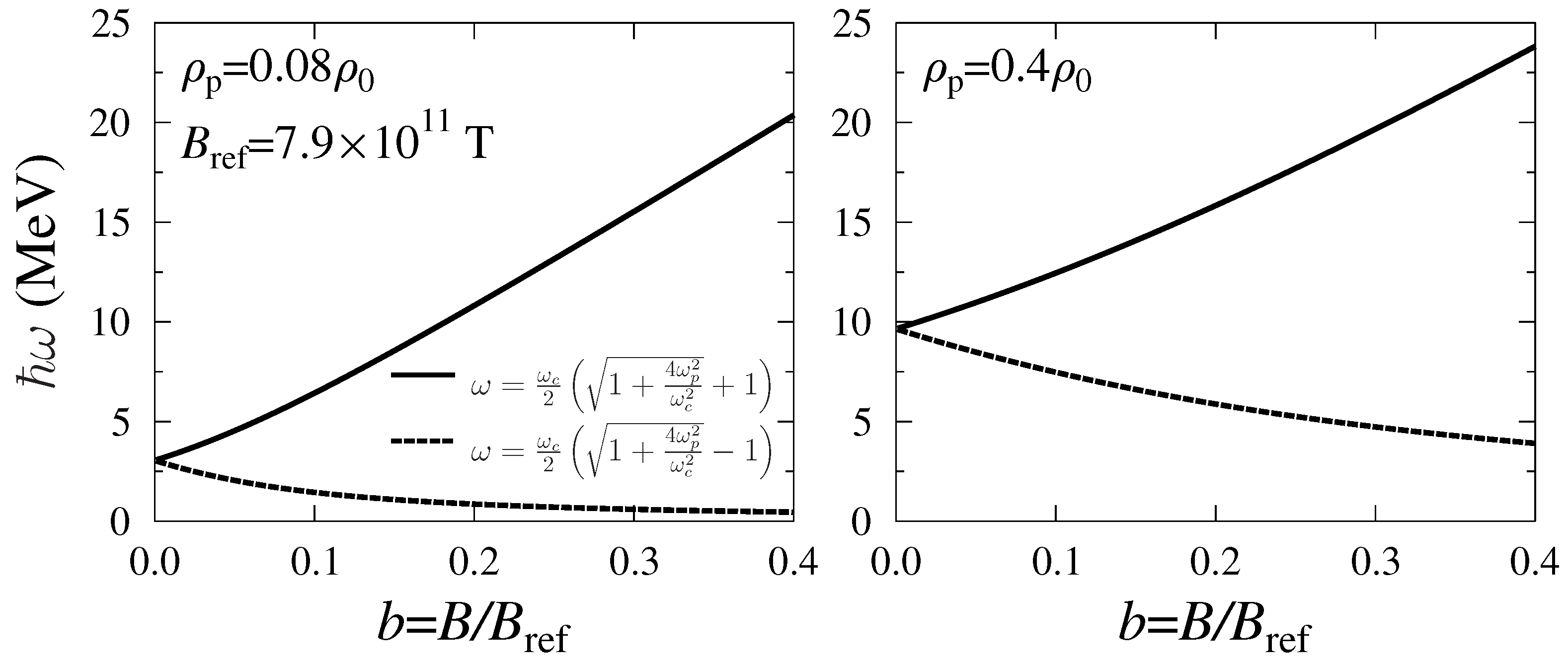Hydromagnetic Waves in Cold Nuclear Matter

Abstract

I consider a proton–neutron fluid mixture placed in an ultra-strong external static magnetic field and derive the spin-independent, small-amplitude disturbances in infinitely extended systems. As a theoretical framework I adopt a hydrodynamical model for the proton and neutron fluids moving in a Skyrme mean-field derived from the time-dependent Hartree Fock formulation of the many-body nuclear problem. From the mass, momentum balance, and Maxwell equations, I set up a system of equations governing the electromagnetic field and the continuum-mechanical fields of the mixture. Next, the hydromagnetic equations are linearized, and the occurrence of small-amplitude distortions of the velocity field is analyzed for various orientations of the constant external magnetic induction with respect to the wave propagation vector. The derivation of the above equations is carried out for the inviscid case.

1. Introduction

Static magnetic effects in nuclei are primarily determined by the fact that their constituents, i.e., protons and neutrons, possess their own magnetic moments. Due to the disproportion between the nuclear mass and the electron mass, the magnetic moments of nucleons and nuclei are smaller by the same proportion with respect to the orbital and spin magnetic moments of an atomic electron shell. In this respect, recall the tiny value of the nuclear magneton, ${\mu }_N=3.1524512326\left(45\right)\times {10}^{-18}$ MeV/G. Consequently, in the absence of an external field or probe of magnetic nature other than the magnetic field of the electron shell, nuclear magnetism can be manifested in a subtle way such as is the case of nuclear hyperfine structure [1]. In more recent times and in connection with the investigation of the properties of dense matter, primarily motivated by the quest for a putative ferromagnetic state of superdense matter, it was pointed out that the magnetization of asymmetric nuclear matter [2,3,4], and, in particular, neutron matter [5,6,7,8] due to magnetic fields in excess of ${10}^{17}$ G, is likely to affect the nuclear equation of state (EOS) of magnetic stars.

On the other hand, the manifestation of dynamic magnetic properties in nuclei is well-documented for collective excitations characterized by significative probabilities of M1-transitions [9,10].

It is well-known that, in astrophysical environments, the magnetic white dwarf pulsars can develop fields with strengths in excess of ${10}^{12}$ Gauss (G) [11] and ${10}^{14}$ G for magnetars [12]. An extremely rapid mechanism of magnetic field amplification during the merging of a binary neutron star system was reported in [13]. According to these authors, the existing neutron star magnetic fields (∼${10}^{12}$ G) become amplified within the first millisecond after the merger, i.e., long before the collapse to a black hole can proceed, up to values of ${10}^{15}$ G, though, as they pointed out, it is highly probable that much stronger fields are generated during this violent process. On the other hand, massive stellar magnetized objects that undergo gravitational collapse tend to convert the huge quantity of available energy into the generation of fantastic magnetic fields as high as B∼${10}^{28}$ G [14]. For more details regarding the occurrence of huge magnetic fields developed in the astrophysical context, the interested reader may consult [15].

One should also recall that, under laboratory conditions, magnetic fields over a large range of values are produced. For example the ephemere magnetic fields, produced at CERN in proton–proton and nucleus–nucleus collisions at ultra-high energies, are estimated to attain values as high as $B\approx {10}^{21}$ G, corresponding to a collision time of $t_0\approx 0.1\mathrm{fm}/c$ (see [16] and references therein). Such strengths are already surpassing the critical magnetic field, which causes changes in the structure of the QCD vacuum and, therefore, are of no relevance for our investigation. On the other hand, the highest magnetic field, currently measured under terrestrial laboratory conditions, is significantly lower. Very recently, the newly developed megagauss generator system, operating at the Institute for Solid State Physics (University of Tokyo), generated a magnetic field strength of $1.2\times {10}^7$ G for around 100 microseconds, a value that dwarfs almost any artificial magnetic field ever recorded on Earth [17].

It was pointed out by Hannes Alfvén that in a conducting fluid subjected to a constant magnetic field $H_0$, the electric currents produced by the mechanical displacements of charges will produce a mechanical stress that alters the dynamical behavior of the fluid [18]. More precisely, a new type of wave (Alfvén wave) is generated and propagated along the direction of the imposed magnetic field with a speed of $v_{\mathrm{A}}$∼$H_0$. In Alfvén’s view, the magnetic field lines are pictured as elastic strings in a dynamic process, and therefore the square of the intrinsic magnetic field plays a role analogous to the elastic shear modulus. Note that the velocity of shear waves in elastic media is $v_S=\sqrt{\mu /\rho }$, where $\mu$ is the shear modulus and $\rho$ is the body’s density. Thus, for a region of the sun where the magnetic induction is $B_0$ = 15 G and the density is $\rho =$ 5 kg/${\mathrm{m}}^3$, the velocity amounts to $v_{\mathrm{A}}$∼60 cm/s. As a first application in the astrophysical context, Alfvén proposed a scenario for the generation of strong magnetic fields on the spots of the sun by surmising the transmission of a magnetic field disturbance $\delta \mathit{H}$, produced in the sun’s center, towards the surface via transverse hydromagnetic incompressional waves [19]. These waves propagate along the lines of the sun’s general magnetic field ${\mathit{H}}_0$. The existence of low-frequency transverse waves across a finite conductivity liquid placed in a constant magnetic field, was verified in a laboratory experiment by Lundquist using a cylindrical geometry [20]. Another Swedish scientist extended the framework put forward by Alfvén to compressible liquids such that longitudinal waves associated with compressions of the frozen-in magnetic field were predicted [21]. Some years later, Alfvén put forward the challenging idea that, in a manner similar to the sun, transverse hydromagnetic waves are generated by the perturbation of the nucleus intrinsic magnetic field [22]. In his short note, he commented that, for a nucleus with electric conductivity assumed to be infinite, for what he called “reasonable values” of the external magnetic field strength and the nuclear mass number A, the eigenfrequency of the lowest hydromagnetic mode, macroscopically pictured as a torsional wave along the direction of the magnetic field, is in the order of a few keV. In recent times, Bastrukov et al. revisited the problem raised by Alfvén, developed a simple nuclear-fluid collective model, and concluded that energies in the range of the giant dipole resonance (GDR) are obtained for the hydromagnetic resonance, provided the magnetic field falls in the interval $3\times {10}^{17}\le B\le 9\times {10}^{17}$ G [23].

The hydromagnetic oscillations of a fluid sphere were considered mainly in connection with self-gravitating bodies (stars in which there is a prevailing magnetic field) (see [24] and references therein). In view of the bounding character of the gravitational interaction, an important issue in this context concerns the stability of such excitation modes. In finite nuclear systems, where gravitation is not important, the stability is dictated, in turn, by the balance between nuclear and Coulomb forces.

In recent years, there has been renewed interest in the topic of collective excitations in exotic nuclear matter, as can be encountered in the inner crust of neutron stars and supernovas [25]. Previous exploratory theoretical investigations on the shell structure of nuclei in such an environment concluded that a magnetic field of the strength scale B∼${10}^{16}$–${10}^{17}$ G can significantly shift the nuclear magic numbers of the iron region towards smaller mass numbers [26]. For magnetic fields of this order of magnitude, covariant density functional theory predicts a significative change in nuclear masses and radii [27]. The implementation of advanced microscopic techniques, such as the Hartree–Fock–Bogoliubov+QRPA encounters serious difficulties due to the nontrivial shapes acquired by neutron-rich nuclear clusters immersed in a superfluid ocean of neutrons. An important problem raised by the authors of the aforementioned studies concerns the validity of the Wigner cell approximation. A suggestion to treat nuclear matter wave phenomena in neutron stars by resorting to continuum mechanics of neutron-rich liquid crystals was made in [28].

Below, I investigate the occurrence of hydromagnetic waves in infinite nuclear matter, portrayed as a normal fluid mixture composed of protons and neutrons in a very strong magnetic field.

2. Fluid-Dynamical Description of a Neutron–Proton Fluid Mixture Placed in an External Uniform Magnetic Field

The foundations of nuclear hydrodynamics applied to the study of the Giant Dipole Resonance (GDR) can be found, for example, in [29,30]. This framework was subsequently extended to the case when the particles of the mixture interact via Skyrme forces [31,32].

By introducing the constituent densities ${\rho }_{p,n}$ and velocities ${\stackrel{\prime }{\mathbf{\chi }}}_{p,n}$, the kinetic energy of the fluid mixture reads

$$T=\frac{1}{2}m\int dr({\rho }_p{\stackrel{\prime }{\mathbf{\chi }}}_p^2+{\rho }_n{\stackrel{\prime }{\mathbf{\chi }}}_n^2).$$

(1)

The nucleons are assumed to move in a mean-field described by a Skyrme parametrized energy density, ${\mathcal{H}}_{\mathrm{Sky}}$, expressed in a compact form in terms of the total and the $q=n,p$ components of the local densities, $\rho ,{\rho }_q$, kinetic energy densities, $\tau ,{\tau }_q$, as well the mass–current densities $\mathit{j},{\mathit{j}}_q=\frac{m}{\hslash }{\rho }_q{\stackrel{\prime }{\mathbf{\chi }}}_q$ [33],

$$\begin{array}{ccc}\hfill {\mathcal{H}}_{\mathrm{Sky}}& & =\frac{{\hslash }^2}{2m}({\tau }_p+{\tau }_n)+B_1{\rho }^2+B_2({\rho }_p^2+{\rho }_n^2)\hfill \\ & & +B_3(\rho \tau -{\mathit{j}}^2)+B_4({\rho }_p{\tau }_p-{\mathit{j}}_p^2+{\rho }_n{\tau }_n-{\mathit{j}}_n^2)\hfill \\ & & +\left[B_7{\rho }^2+B_8({\rho }_p^2+{\rho }_n^2)\right]{\rho }^{\alpha }.\hfill \end{array}$$

(2)

The terms ∼${\rho }^2,{\rho }_q^2$ result from the central short-range component of the Skyrme interaction, whereas the term on the last line of (2) originates from the density-dependent short-range of the force. In the above choice of the Skyrme energy density, spin-dependent (spin-orbit and tensor spin-gradient) terms are dropped out, since magnetic spin-waves are not addressed in the present paper. The gradient terms in the densities are also neglected since, in the ground state, the fluid mixture is assumed to be homogeneous. The kinetic energy density, ∼${\tau }_q$, is treated within the Thomas–Fermi approximation [34]. Note that the Galilean invariance of the Skyrme interaction is accounted for by terms of the type $\rho \tau -j^2$. The terms ∼$\rho \tau ,{\rho }_q{\tau }_q$ have their roots in the nonlocal part of the short-range interaction.

Next, the mean-field one-body potential ${\mathcal{U}}_q$ is derived by taking the functional derivative of the energy density with respect to the q-th constituent density,

$${\mathcal{U}}_q\equiv \frac{\delta {\mathcal{H}}_{\mathrm{Sky}}}{\delta {\rho }_q\left(\mathit{r}\right)}=\frac{\partial {\mathcal{H}}_{\mathrm{Sky}}}{\partial {\rho }_q}-\nabla ·\frac{\partial {\mathcal{H}}_{\mathrm{Sky}}}{\partial \nabla {\rho }_q}+\Delta \frac{\partial {\mathcal{H}}_{\mathrm{Sky}}}{\partial \Delta {\rho }_q}.$$

(3)

The internal energy can be then written as

$$U=\int d\mathit{r}{\mathcal{H}}_{\mathrm{Sky}}\left(\mathit{r}\right).$$

(4)

In this paper, I consider an external static magnetic field, ${\mathit{B}}_0$, that starts to act at time $t=0$ upon the neutron and proton fluids. The interaction of the charged component of the fluid mixture with the external electromagnetic field of strength $(\mathit{E},\mathit{B})$ reads [35]

$$W_{\mathrm{em}}=e\int d\mathit{r}{\rho }_p{\mathbf{\chi }}_p·\left(\mathit{E}+{\stackrel{\prime }{\mathbf{\chi }}}_p\times \mathit{B}\right),$$

(5)

where ${\mathbf{\chi }}_p$ is the proton fluid displacement field, which is trivially related to the proton fluid velocity field,

$${\stackrel{\prime }{\mathbf{\chi }}}_p(\mathit{r},t)=\frac{\partial {\mathbf{\chi }}_p(\mathit{r},t)}{\partial t}.$$

(6)

In order to derive the dynamical equations governing the continuum-mechanical system combining the proton and neutron fluids, I apply the Hamilton principle to the four-fold action integral [36]

$$\delta S=\delta \int dt(T-U+W_{\mathrm{em}}+C)=0.$$

(7)

The last term in the above integral is related to the mass balance in the mixture and is added to the Lagrangian by means of undetermined multipliers ${\lambda }_{p,n}$,

$$C=\int d\mathit{r}\sum _q\left[\frac{\partial }{\partial t}\left({\lambda }_q{\rho }_q\right)+\nabla ·\left({\lambda }_q{\rho }_q{\stackrel{\prime }{\mathbf{\chi }}}_q\right)-{\lambda }_q\frac{\partial {\rho }_q}{\partial t}-{\lambda }_q\nabla ·\left({\rho }_q{\stackrel{\prime }{\mathbf{\chi }}}_q\right)\right].$$

(8)

As shown in a previous paper [37], the particles of the fluid mixture are subjected to a virtual variation with respect to the dynamical variables ${\rho }_q$ and ${\stackrel{\prime }{\mathbf{\chi }}}_q$. As a result, the Lagrange equations for the proton and neutron fluid velocities yield

$$\begin{array}{ccc}\hfill m{\stackrel{″}{\mathbf{\chi }}}_p& =& e\left[\mathit{E}+{\stackrel{\prime }{\mathbf{\chi }}}_p\times \mathit{B}-{\mathbf{\chi }}_p\times (\mathbf{\nabla }\times \mathit{E})\right]-\mathbf{\nabla }{\mathcal{U}}_p,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill m{\stackrel{″}{\mathbf{\chi }}}_n& =& -\mathbf{\nabla }{\mathcal{U}}_n,\hfill \end{array}$$

(10)

provided the quadratic terms in the velocities are neglected.

The hydrodynamical equations established above are supplemented with the equations relating the electromagnetic fields to the charge and current distributions of the fluid mixture (Maxwell equations):

$$\nabla ·\mathit{E}=\frac{e}{{\epsilon }_0}{\rho }_p;\nabla ·\mathit{B}=0;\mathbf{\nabla }\times \mathit{E}=-\frac{\partial \mathit{B}}{\partial t};\frac{1}{{\mu }_0}\mathbf{\nabla }\times \mathit{B}=e{\rho }_p{\stackrel{\prime }{\mathbf{\chi }}}_p+{\epsilon }_0\frac{\partial \mathit{E}}{\partial t},$$

(11)

In the nonperturbed state, the following relations are satisfied

$$\rho ={\rho }_p+{\rho }_n={\rho }_0;{\stackrel{\prime }{\mathbf{\chi }}}_p={\stackrel{\prime }{\mathbf{\chi }}}_n=0.$$

(12)

3. Hydromagnetic Waves in Cold Neutron–Proton Mixtures

At $t=0$, the $p-n$ “plasma” is perturbed, and consequently, the density, mean-field potential, velocity, and electric and magnetic fields are varied,

$${\rho }_q⟶{\rho }_q^0+\delta {\rho }_q,{\mathcal{U}}_q⟶{\mathcal{U}}_q^0+\delta {\mathcal{U}}_q{\stackrel{\prime }{\mathbf{\chi }}}_q⟶{\mathit{v}}_q,\mathit{E}⟶\delta \mathit{E},\mathit{B}⟶{\mathit{B}}_0+\delta \mathit{B}.$$

(13)

where ${\rho }_q$ denotes the equilibrium densities and $\delta {\rho }_q\ll {\rho }_q$. Since I neglect the contributions generating nonlocal effects, e.g., $\mathbf{\nabla }{\rho }_q^0,\mathbf{\nabla }{\mathcal{U}}_q^0=0$, as well as the second-order terms, and since small perturbations are assumed, a linear dependence of the one-body potentials on the proton and neutron density fluctuations is left,

$$\delta {\mathcal{U}}_q=G_{qq}^{\left(1\right)}\delta {\rho }_q+G_{q{q}^{\prime }}^{\left(1\right)}\delta {\rho }_{q^{\prime }},$$

(14)

where the G-coefficients in the Skyrme parametrization are given in Section 3 of ref. [32].

The linearized hydrodynamic Equations (9) of the $p-n$ “plasma” are

$$\begin{array}{ccc}\hfill \frac{\partial {\mathit{v}}_p}{\partial t}& =& -\frac{1}{m}\nabla \delta {\mathcal{U}}_p+\frac{e}{m}(\delta \mathit{E}+{\mathit{v}}_p\times {\mathit{B}}_0),\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \frac{\partial {\mathit{v}}_n}{\partial t}& =& -\frac{1}{m}\nabla {\delta \mathcal{U}}_n.\hfill \end{array}$$

(16)

The above two equations, expressing the momentum balance, are supplemented with the equations ensuring the mass balance of the proton and neutron fluids,

$$\begin{array}{ccc}\hfill \frac{\partial \delta {\rho }_{p,n}}{\partial t}& =& -{\rho }_{p,n}^0\nabla ·{\mathit{v}}_{p,n}.\hfill \end{array}$$

(17)

The Maxwell equations for the fluctuated fields are obtained by substituting the transformations (13) in (11),

$$\begin{array}{ccc}& & \mathbf{\nabla }·\delta \mathit{E}=\frac{e}{{\epsilon }_0}\delta {\rho }_p,\mathbf{\nabla }·\delta \mathit{B}=0\hfill \\ & & \mathbf{\nabla }\times \delta \mathit{E}=-\frac{\partial }{\partial t}\delta \mathit{B},\mathbf{\nabla }\times \delta \mathit{B}={\mu }_{0}e{\rho }_p^0{\mathit{v}}_p+\frac{1}{c^2}\frac{\partial \delta \mathit{E}}{\partial t}.\hfill \end{array}$$

(18)

Since the external magnetic field is prone to the induction of charged currents flowing on closed loops (vortical currents), it is reasonable to appeal to the incompressibility approximation, i.e., I assume that the total density remains constant during the excitation of hydromagnetic modes,

$${\rho }_p+{\rho }_n={\rho }_0,$$

(19)

and therefore $\delta {\rho }_p=-\delta {\rho }_n$. Due to this constraint, 10 independent variables are left: $\delta {\rho }_p$, ${\mathit{v}}_p$, $\delta \mathit{E}$, and $\delta \mathit{B}$ ($\delta {\rho }_n$ and ${\mathit{v}}_n$ are therefore not independent). Assuming that these variables posses plane wave solutions, i.e., $\sim exp\left[i(\mathit{k}·\mathit{r}-\omega t)\right]$, the time derivative and gradient operators are subjected to the substitution $\partial /\partial t⟶-i\omega$, $\mathbf{\nabla }⟶i\mathit{k}$. Thus, the continuity Equation (17), the Euler equation for the proton fluid (15), and the Maxwell Equation (18) are recasted in the form of a coupled system of algebraic equations

$$\delta {\rho }_p=\frac{{\rho }_p^0}{\omega }\mathit{k}·{\mathit{v}}_p;$$

(20)

$${\mathit{v}}_p=\frac{ie}{m\omega }\left(\delta \mathit{E}+{\mathit{v}}_p\times \delta \mathit{B}\right)+\frac{c_{\mathrm{s}}^2}{{\omega }^2}\mathit{k}(\mathit{k}·{\mathit{v}}_p);$$

(21)

$$i\mathit{k}·\delta \mathit{E}=\frac{e}{{\epsilon }_0}\delta {\rho }_p;i\mathit{k}·\delta \mathit{B}=0;i\mathit{k}\times \delta \mathit{E}=i\omega \delta \mathit{B};i\mathit{k}\times \delta \mathit{B}={\mu }_{0}e{\rho }_p^0{\mathit{v}}_p-\frac{i\omega }{c^2}\delta \mathit{E}.$$

(22)

Above, I introduced the square of the speed of sound in nuclear matter

$$c_{\mathrm{s}}^2=\frac{{\rho }_p^0}{m}(G_{pp}-G_{pn}).$$

(23)

I also introduce the proton plasma frequency

$${\omega }_p=\sqrt{\frac{e^2{\rho }_p^0}{m{ϵ}_0}},$$

(24)

and the cyclotron frequency

$${\omega }_{\mathrm{c}}=\frac{e{B}_0}{m}={\omega }_p\frac{v_{\mathrm{A}}}{c},$$

(25)

where $v_{\mathrm{A}}=B_0/\sqrt{m{\mu }_0{\rho }_p^0}$ is the Alfύen velocity, obtained from the above system of algebraic equations:

$$\left(1-\frac{{\omega }_p^2}{{\omega }^2-k^2{c}^2}\right){\mathit{v}}_p-\frac{1}{{\omega }^2}\left(c_{\mathrm{s}}^2-\frac{c^2{\omega }_p^2}{{\omega }^2-k^2{c}^2}\right)\mathit{k}(\mathit{k}·{\mathit{v}}_p)-\frac{ie}{m\omega }{\mathit{v}}_p\times {\mathit{B}}_0=0.$$

(26)

Let us consider a configuration with ${\mathit{B}}_0$ aligned to the z-axis and

$$\mathit{k}=k_{\perp }({\mathit{e}}_{x}cos\varphi +{\mathit{e}}_{y}sin\varphi )+k_{\perp }{\mathit{e}}_z.$$

(27)

First, I choose the orientation with k aligned to ${\mathit{B}}_0$ ($\mathit{k}\Vert {\mathit{B}}_0$); thus, $k_{\perp }=0$, $k_z=k$, the motion in the $x-y$ plane is separated from the motion along the z-axis, and therefore, two dispersion relations are obtained,

$${\left(1-\frac{{\omega }_p^2}{{\omega }^2-k^2{c}^2}\right)}^2-{\left(\frac{{\omega }_{\mathrm{c}}}{\omega }\right)}^2=0,$$

(28)

and

$$1-\frac{{\omega }_p^2}{{\omega }^2-k^2{c}^2}+\frac{k^2}{{\omega }^2}\left(\frac{c^2{\omega }_p^2}{{\omega }^2-k^2{c}^2}-c_{\mathrm{s}}^2\right)=0.$$

(29)

Let us focus on the first equation, (28), which encodes the effect of the magnetic field inducing the rotatory motion in the $x-y$ plane. In this case, there are two branches resulting from a cubic equation, i.e.,

$${\omega }^3\mp {\omega }^2{\omega }_{\mathrm{c}}-\omega ({\omega }_p^2+k^2{c}^2)\pm {\omega }_{\mathrm{c}}{k}^2{c}^2=0.$$

(30)

I note in passing that due to the long-range interactions exhibited by the plasmon term, the relationship between $\omega$ and k is nonlinear [38]. For $k\to 0$, there are two branches:

$$\omega =\frac{{\omega }_c}{2}\left(\sqrt{1+\frac{4{\omega }_p^2}{{\omega }_c^2}}\pm 1\right).$$

(31)

In this case, for $B_0>0$, the plasmon oscillation bifurcates into a magnetic wave ($\omega \to {\omega }_c$ when $B_0\to \infty$) and a wave decaying with an increasing magnetic field (see Figure 1).

For a large momentum ($k\to \infty$) or high frequency, the undamped mode tends toward the cyclotron (magnetic) branch, regardless of $B_0$.

For the second dispersion relation, i.e., Equation (29), corresponding to the orientation $\mathit{k}\Vert {\mathit{B}}_0$, the motion along the z-axis is described by

$${\omega }^4-({\omega }_p^2+k^2{c}_{\mathrm{s}}^2){\omega }^2+k^2{c}^2{\omega }_p^2=0.$$

(32)

In the low-k regime, this equation provides approximately a combination of the plasma and acoustic modes (plasma–acoustic wave),

$${\omega }^2\approx {\omega }_p^2+k^2{c}_{\mathrm{s}}^2.$$

(33)

The high-$\omega$ behavior is ruled by a a pure acoustic mode

$${\omega }^2\approx k^2{c}_{\mathrm{s}}^2.$$

(34)

As a second orientation, I consider $\mathit{k}\perp {\mathit{B}}_0$; thus, $k_z=0$ and $k_{\perp }=k$ is chosen. Consequently, the motion along the z-axis separates in the form of vacuum propagation of an electromagnetic wave altered by the presence of the electrically charged proton “plasma”,

$${\omega }^2={\omega }_p^2+k^2{c}^2.$$

(35)

This relation points out to the fact that such transverse waves propagate at frequencies of $\omega >{\omega }_p$. Inside the frequency range $0<\omega <{\omega }_p$, this mode is confined to a stop band, as occurs in plasma physics [39].

For $\mathit{k}\perp {\mathit{B}}_0$, the motion in the $x-y$ plane is described by the dispersion relation

$${\left(1-\frac{{\omega }_p^2}{{\omega }^2-k^2{c}^2}\right)}^2+\frac{k^2}{{\omega }^2}\left(1-\frac{{\omega }_p^2}{{\omega }^2-k^2{c}^2}\right)\left(\frac{c^2{\omega }_p^2}{{\omega }^2-k^2{c}^2}-c_{\mathrm{s}}^2\right)-\frac{{\omega }_c^2}{{\omega }^2}=0.$$

(36)

For $k\to 0$, one speaks of a magneto–plasma wave, i.e.,

$${\omega }^2\approx {\omega }_c^2+{\omega }_p^2.$$

(37)

At the other extreme ($k\to \infty$), one deals with a magneto–acoustic wave

$${\omega }^2\approx {\omega }_c^2+k^2{c}_{\mathrm{s}}^2.$$

(38)

The case of low frequencies is governed by

$${\omega }^2\approx {\left(1+\frac{{\omega }_p^2}{k^2{c}^2}\right)}^{-2}\left[{\omega }_c^2+\left(1+\frac{{\omega }_p^2}{k^2{c}^2}\right)(k^2{c}_{\mathrm{s}}^2+{\omega }_p^2)\right]\stackrel{k\to \infty }{⟶}{\omega }_c^2+{\omega }_p^2+k^2{c}_{\mathrm{s}}^2,$$

(39)

whereas for high frequencies,

$${\omega }^2={\omega }_c^2+2{\omega }_p^2+k^2{c}^2,$$

(40)

one deals with a combination of magnetic, plasma, and electromagnetic modes.

4. Discussion

To date, the subject of hydromagnetic waves in nuclear matter has received scarce attention in the literature. However, the presence of condensed baryon matter in intense magnetic fields produced in the astrophysical context (supernovae, neutron stars) or in relativistic heavy-ion reactions, as revealed in many publications from previous years, requires the investigation of nuclear magnetohydrodynamical phenomena.

In this paper, using the framework of nuclear hydrodynamics for two boundless fluids moving in a Skyrme nuclear mean-field and excited by an external static ultra-intense magnetic field, I described the generation of small-amplitude waves for various geometrical configurations. The conditions allowing the generation of magnetic waves in nuclear matter were derived and showed that this mode arises in combination with plasma and acoustic modes. It is important to point out that, in the case of an increasing $B_0$, the wave propagating along the direction of the imposed magnetic field with a speed approaching $v_{\mathrm{A}}$ could be ascribed to an Alfvén wave type.

I should also remind the reader that the isospin effect is incorporated in the speed of sound $c_{\mathrm{s}}$. It is transparent from Equation (23) that, due to the dependence on the coefficients $G_{pp}$ and $G_{pn}$, expressed according to [32], in terms of the strengths $B_2$, $B_4$, and $B_8$, pertaining to components of the Skyrme force (2) with isovector content, the isospin effect is visible in hydromagnetic modes containing an acoustic component.

Note that, in the past, the possibility of exciting hydromagnetic modes in spherical nuclei was discussed under very restrictive assumptions [22,23]: restriction to a single, incompressible nucleon fluid (note that, in the present approach, both fluid components are compressible), ignoring the displacement current in the last Maxwell Equation (18), and neglecting the nuclear interaction. The present investigation can be straightforwardly extended to finite systems, the only additional requirement being the selection of appropriate boundary conditions.

It was inferred in the previous section that, in infinite nuclear matter, a strong magnetic field, i.e., $B_0>{10}^{10}$ T (${10}^{14}$ G), gives rise to a significant modification of the dispersion relation for standard plasma and sound oscillations and the dominance of magnetic (Alfvén) perturbations at large $B_0$ values. On the other hand, the previously mentioned exploratory investigations on magnetic-field-induced shifts in nuclear masses [26], excitation of Alfvén modes in spherical nuclei [23], or the alteration of nuclear matter properties [6], point to higher values of the magnetic field where nuclear properties are affected, i.e., $B_0$∼${10}^{16}$–${10}^{17}$ G. Such high fields are suspected to arise during the merging of a binary neutron star system. The generation of wave motion in nuclear matter by such intense magnetic fields contributes, once friction is included in the hydrodynamical approach [40,41], to the heating of these astrophysical objects, and therefore affects, in a non-negligible manner, the merging process.

The present framework can be straightforwardly extended to include friction effects. It is well-known that the inclusion of viscosity (controlled by the width $\Gamma$, a quantity that can be fixed by the experiment for electric giant resonances) provides a time scale for the decay of the collective mode, i.e., ${\tau }_{\mathrm{dec}}$∼${\Gamma }^{-1}$. Making the reasonable guess that the nature of viscosity is the same in finite or infinite nuclear matter and for approximately the same range of energies and noting from previous work [37] that 0.42 MeV $\le \hslash \Gamma \le$ 2.25 MeV, the decay time for hydromagnetic modes should be, at most, ∼${10}^{-20}$ s.

Another open issue concerns the inclusion of spin-degrees of freedom and the role played, in realistic circumstances, by the surrounding electrons. Simple arguments points to a suppression of the nuclear hydromagnetic effect due to screening. However to assess the screening effect as well the generation of additional spin-dependent hydromagnetic modes in a coherent manner, a more elaborate version of the present continuum mechanical framework is needed. A fluid viscous mixture with 6 components (protons + neutrons + electron spin-up and spin-down fluids) could be envisaged with the price of dealing with complicate couplings in the equations of motion.