Mössbauer Synchrotron and X-ray Studies of Ultrathin YFeO3 Films
Abstract
1. Introduction
2. Sample Preparation
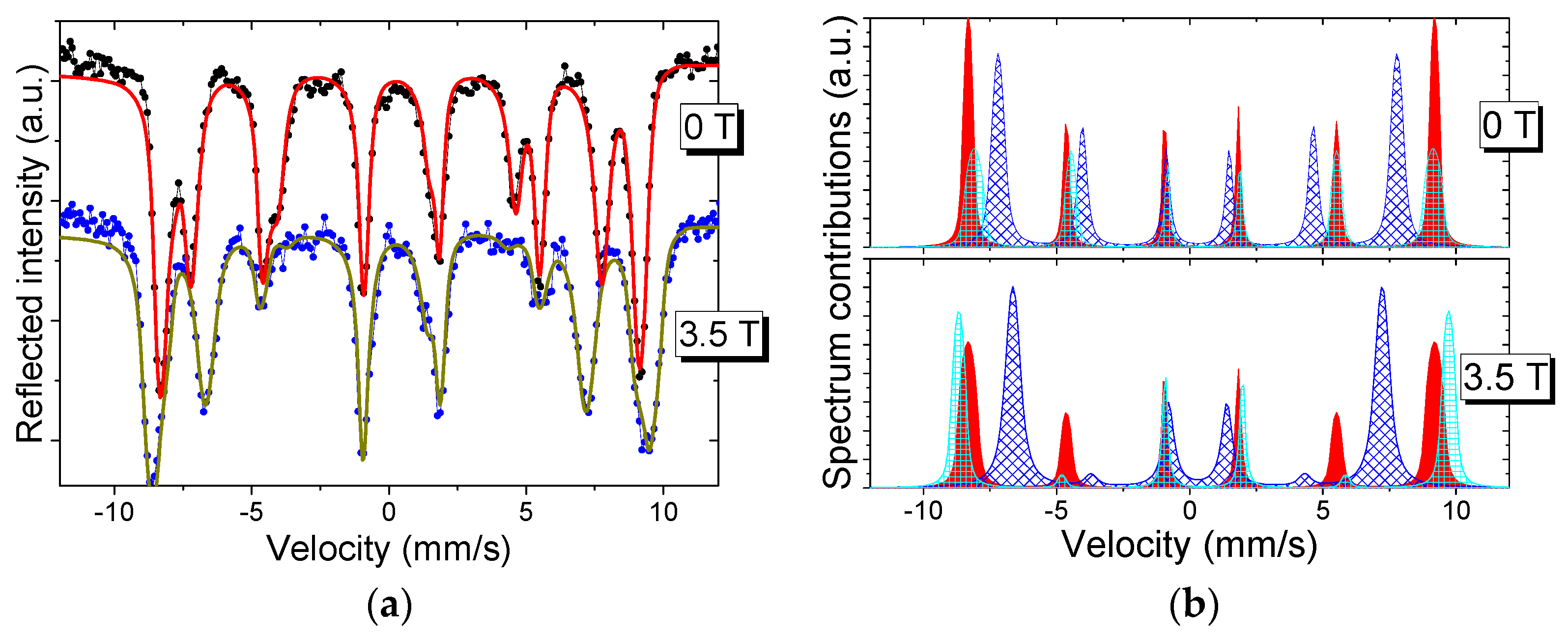
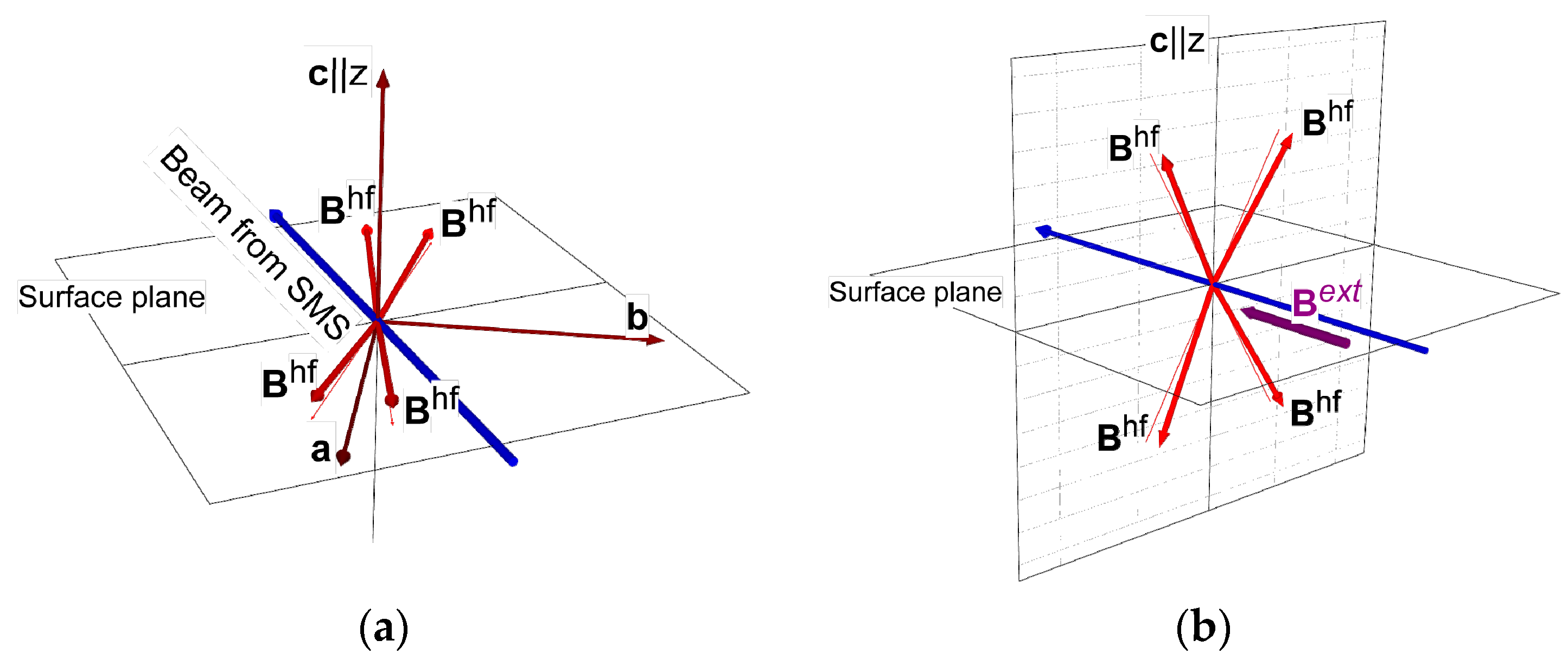
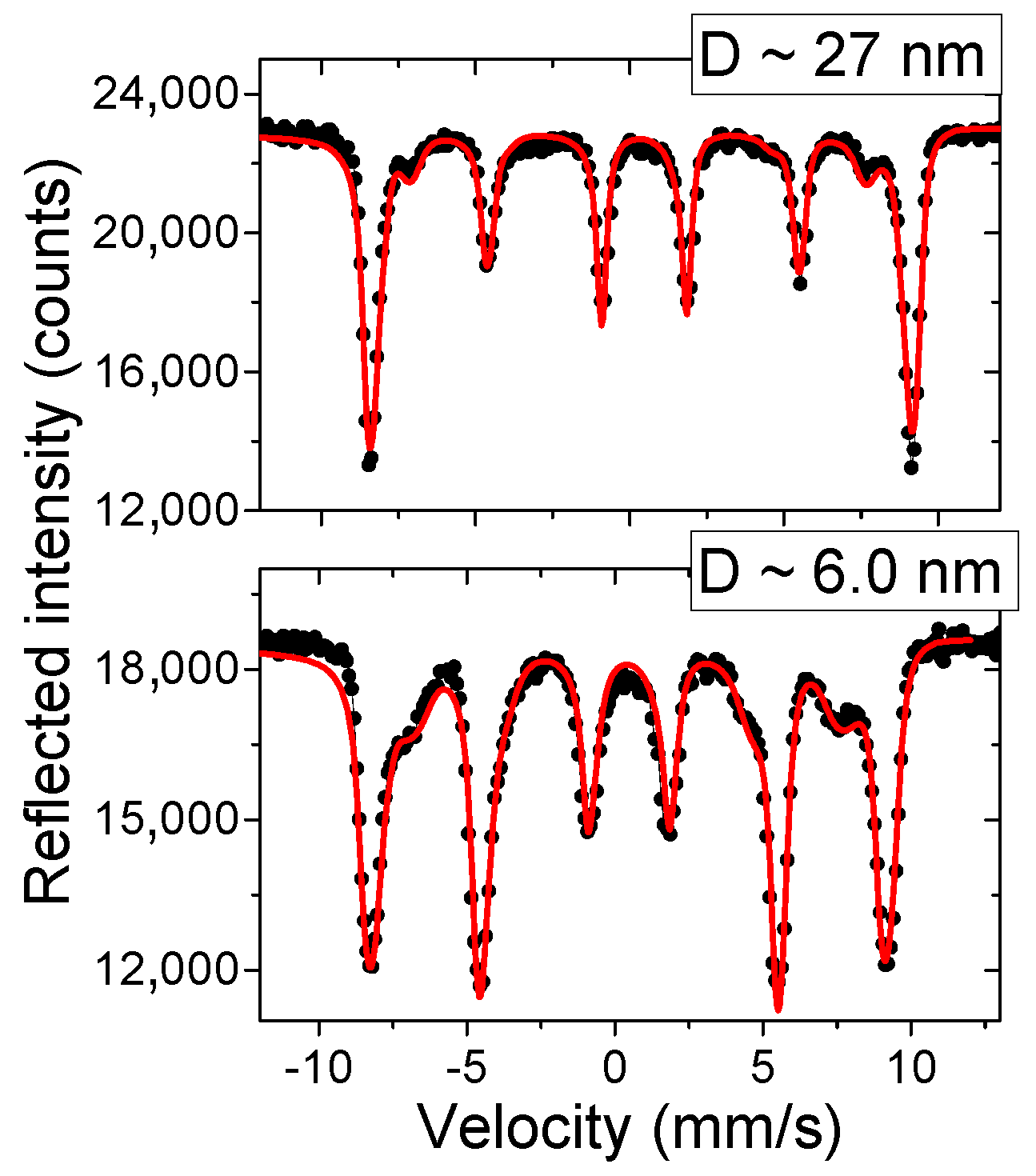
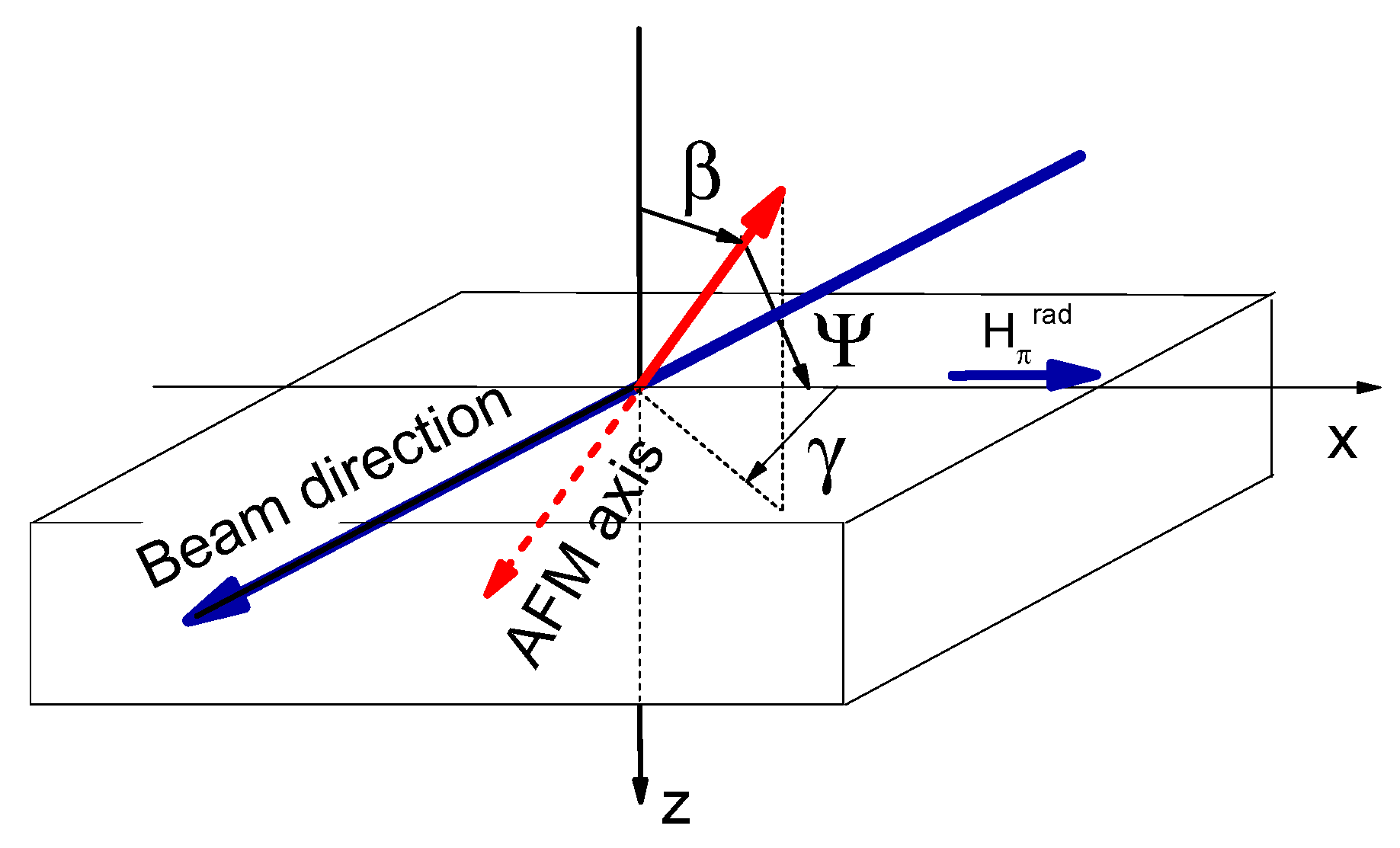
3. Mössbauer Reflectivity Spectra
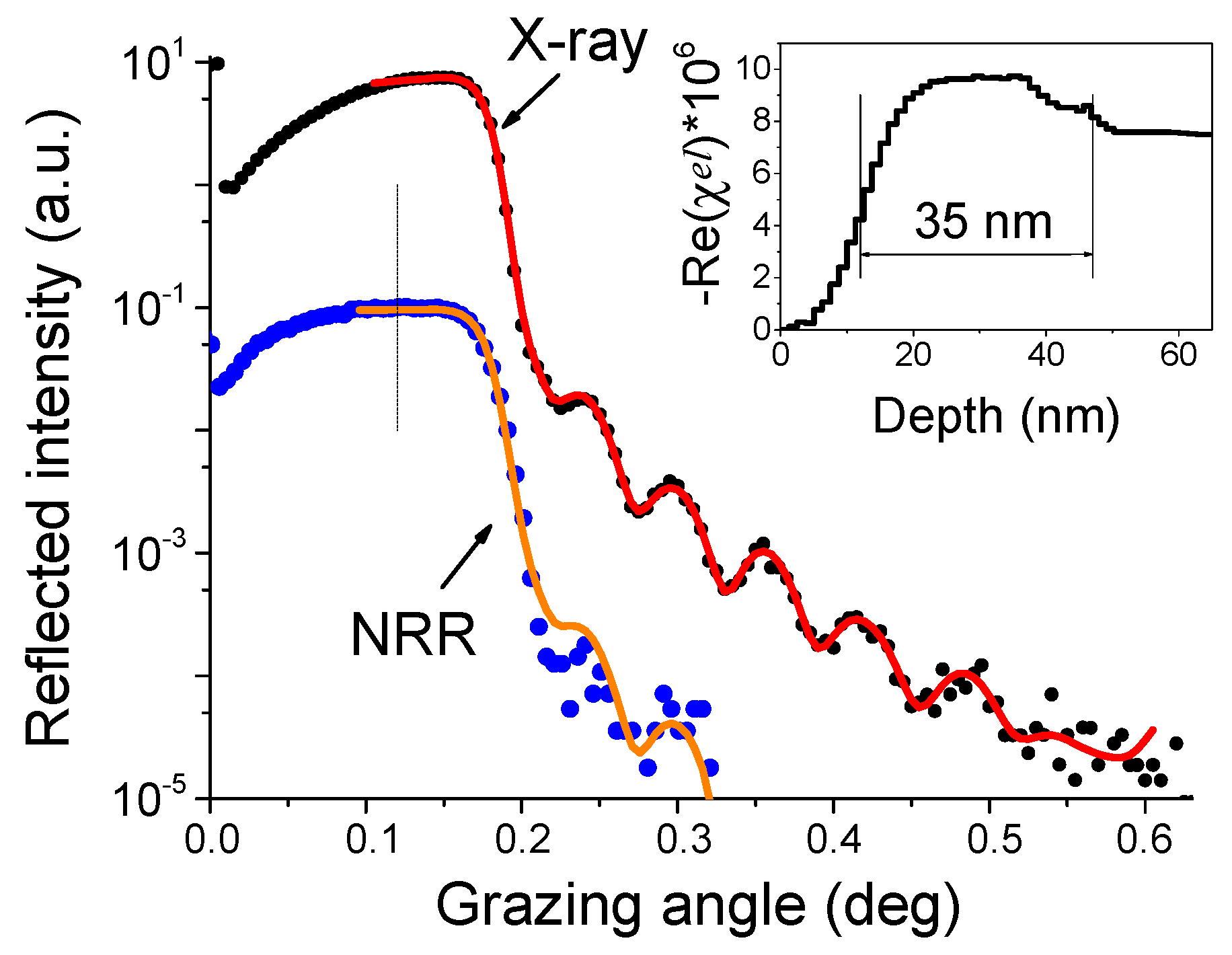
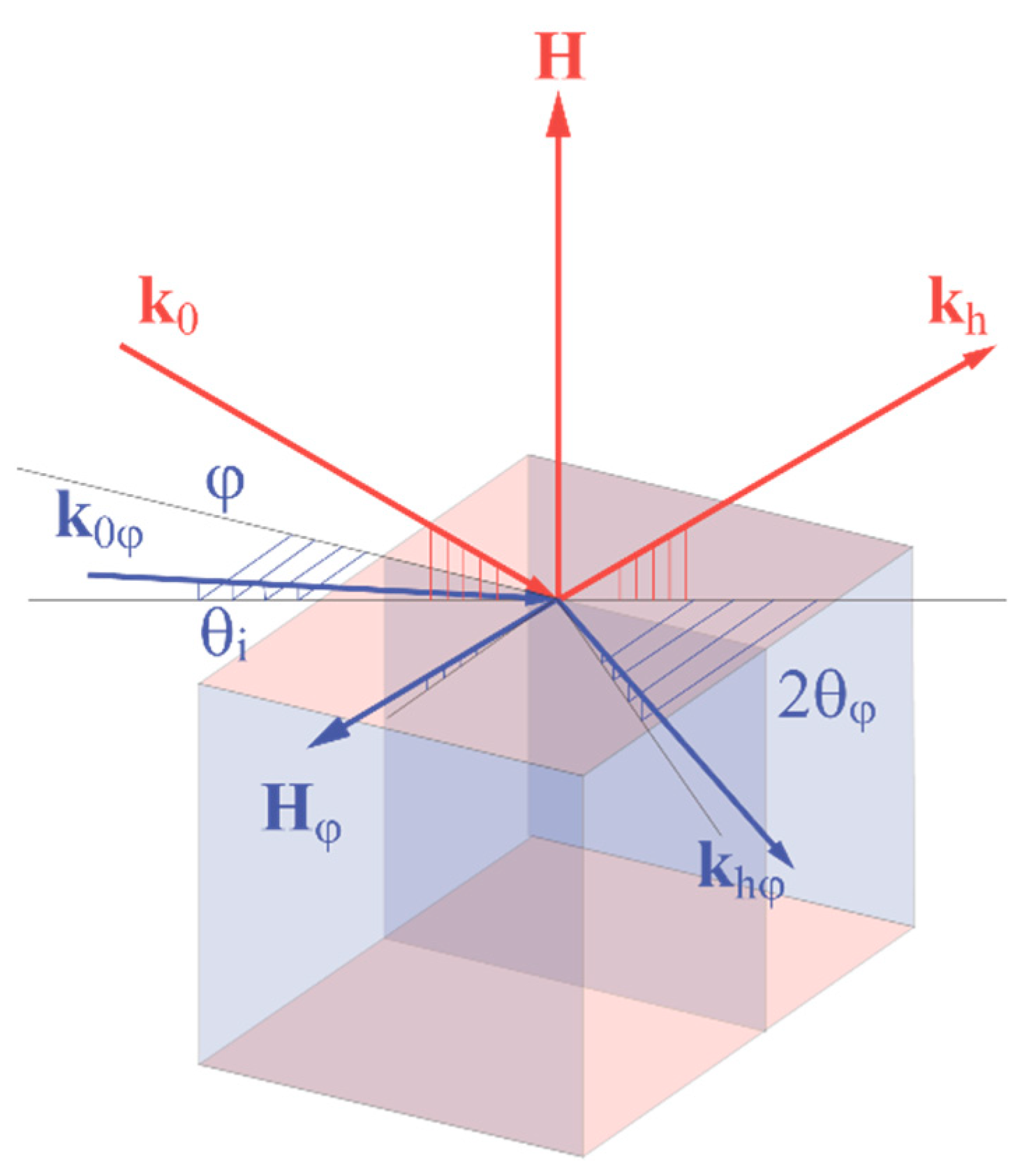
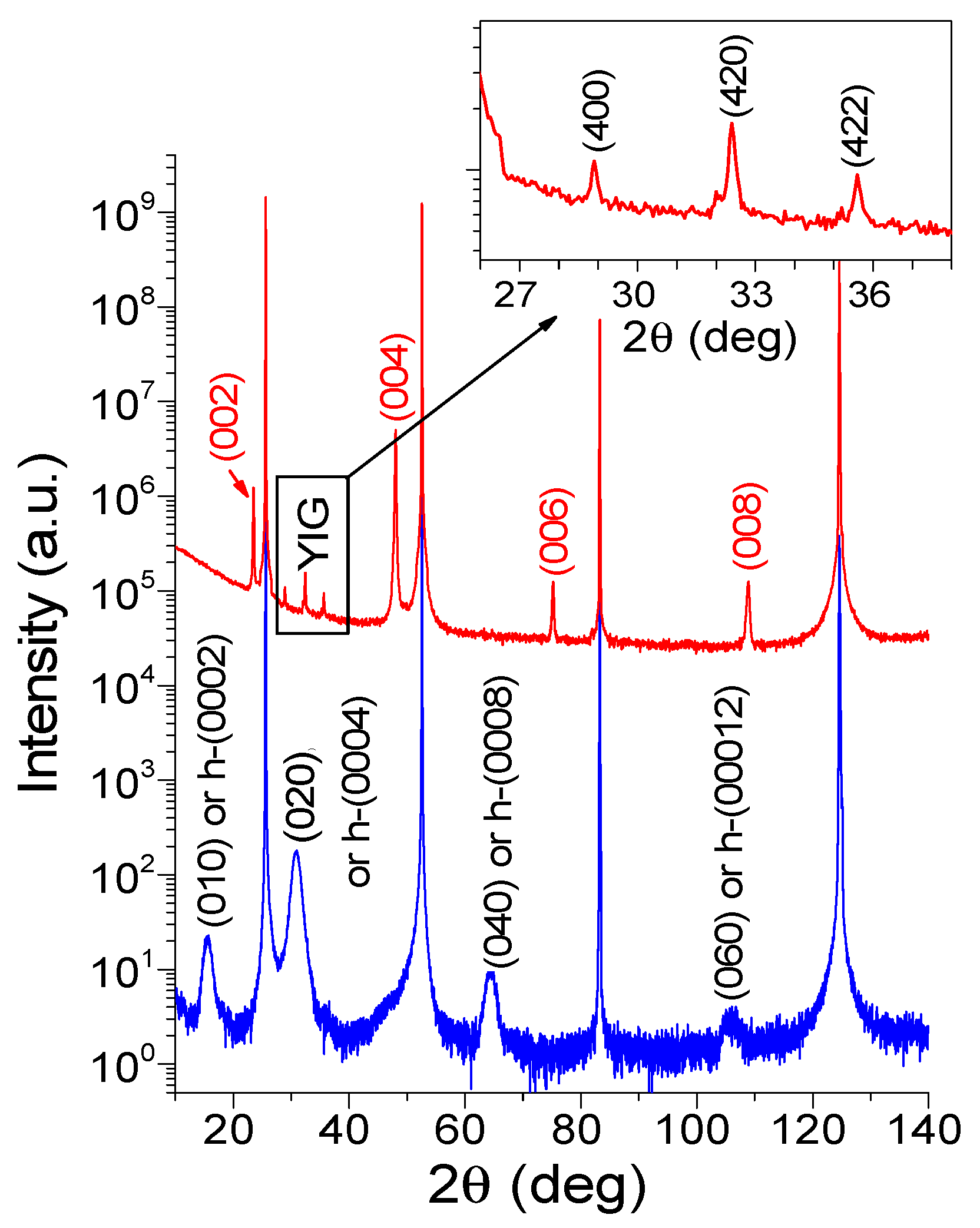
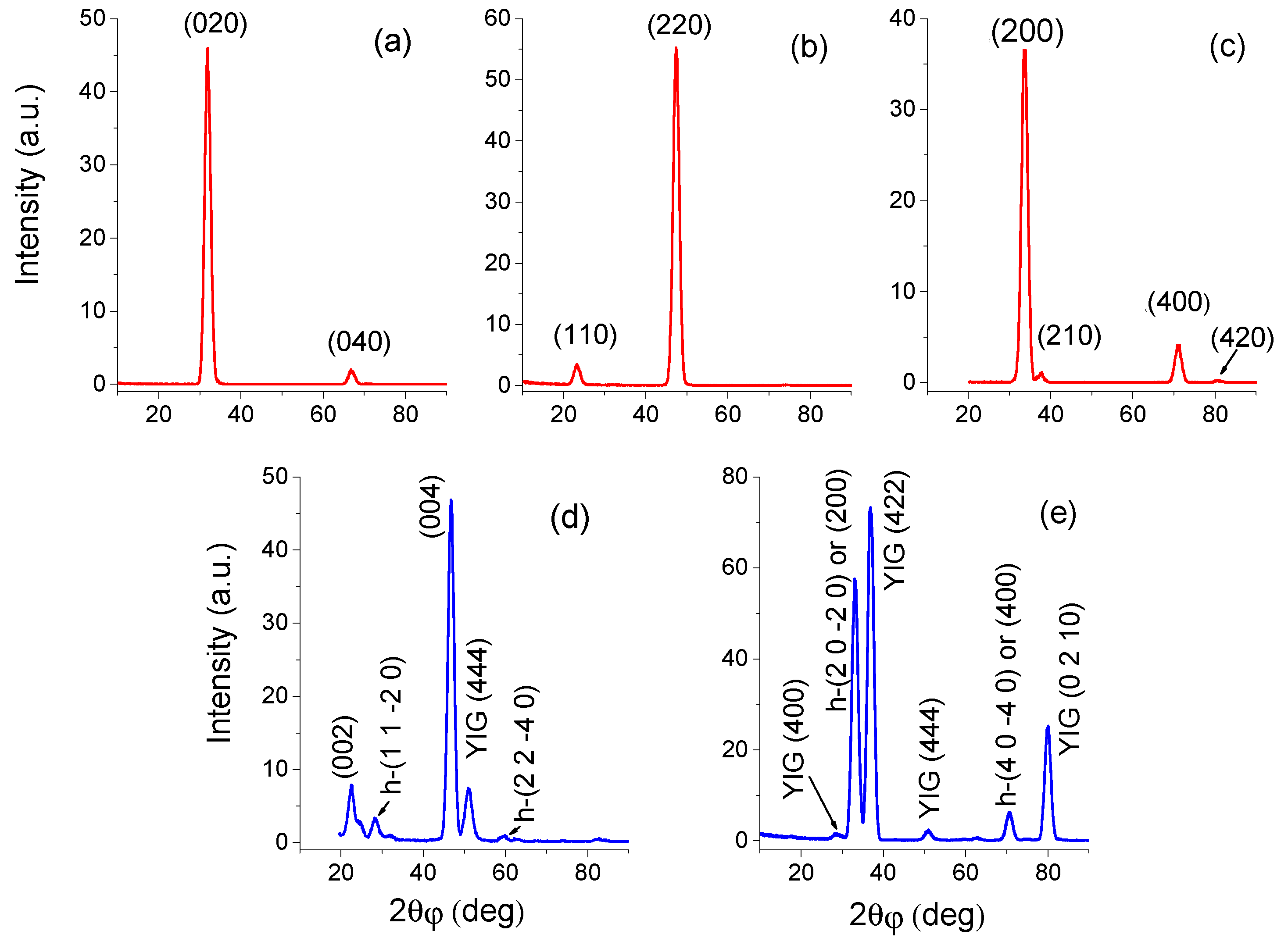
4. X-ray Diffraction Study
5. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, J.-H.; Jeng, Y.K.; Park, J.H.; Oak, M.-A.; Jang, H.M.; Son, J.Y.; Scott, J.F. Spin-Canting-Induced Improper Ferroelectricity and Spontaneous Magnetization Reversal in SmFeO3. Phys. Rev. Lett. 2011, 107, 117201. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.A.; Selim, M.S.; Arman, M.M. Novel multiferroic La0.95Sb0.05FeO3 orthoferrite. Mater. Chem. Phys. 2011, 129, 705–712. [Google Scholar] [CrossRef]
- Shang, M.; Zhang, C.; Zhang, T.; Yuan, L.; Ge, L.; Yuan, H.; Feng, S. The multiferroic perovskite YFeO3. Appl. Phys. Lett. 2013, 102, 062903. [Google Scholar] [CrossRef]
- Rosales-González, O.; Sánchez-De Jesús, F.; Cortés-Escobedo, C.A.; Bolarín-Miró, A.M. Crystal structure and multiferroic behavior of perovskite YFeO3. Ceram. Int. 2018, 44, 15298–15303. [Google Scholar] [CrossRef]
- Arman, M.M.; El-Dek, S.I. Enhancement in dielectric and optical properties of La1−xCexFeO3 nanoparticles. J. Mater. Res. Technol. 2019, 8, 5396–5404. [Google Scholar] [CrossRef]
- Solórzano, M.; Durán, A.; López, R.; Mata, J.; Falconi, R. Structural characterization, dielectric, and magnetic properties of Ti-doped YFeO3 multiferroic compound. J. Mater. Sci. Mater. Electron. 2020, 31, 14478–14486. [Google Scholar] [CrossRef]
- Didosyan, Y.S.; Hauser, H.; Nicolics, J.; Haberl, F. Application of orthoferrites for light spot position measurements. J. Appl. Phys. 2000, 87, 7079–7081. [Google Scholar] [CrossRef]
- Didosyan, Y.S.; Hauser, H. Observation of Bloch lines in yttrium orthoferrite. Phys. Lett. A 1998, 238, 395–397. [Google Scholar] [CrossRef]
- Didosyan, Y.S.; Barash, V.Y.; Bovarin, N.A.; Hauser, H.; Fulmek, P. Magnetic field sensor by orthoferrites. Sens. Actuators A Phys. 1997, 59, 56–60. [Google Scholar] [CrossRef]
- Ripka, P.; Vértesy, G. Sensors based on soft magnetic materials Panel discussion. J. Magn. Magn. Mater. 2000, 215–216, 795–799. [Google Scholar] [CrossRef]
- Tang, P.; Sun, H.; Chen, H.; Cao, F. Hydrothermal processing-assisted synthesis of nanocrystalline YFeO3 and its visible-light photocatalytic activity. Curr. Nanosci. 2012, 8, 64–67. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, J.; Wang, X.; Feng, F.; Zhang, Y.; Tang, Y. Synthesis YFeO3 by salt-assisted solution combustion method and its photocatalytic activity. J. Ceram. Soc. Jpn. 2014, 122, 146–150. [Google Scholar] [CrossRef]
- Cheng, Z.X.; Shen, H.; Xu, J.Y.; Liu, P.; Zhang, S.J.; Wang, J.L.; Wang, X.L.; Dou, S.X. Magnetocapacitance effect in nonmultiferroic YFeO3 single crystal. J. Appl. Phys. 2012, 111, 034103. [Google Scholar] [CrossRef]
- Popkov, V.I.; Almjasheva, O.V.; Semenova, A.S.; Kellerman, D.G.; Nevedomskiy, V.N.; Gusarov, V.V. Magnetic properties of YFeO3 nanocrystals obtained by different soft-chemical methods. J. Mater. Sci. Mater. Electron. 2017, 28, 7163–7170. [Google Scholar] [CrossRef]
- Raut, S.; Babu, P.D.; Sharma, R.K.; Pattanayak, R.; Panigrahi, S. Grain boundary-dominated electrical conduction and anomalous optical-phonon behaviour near the Neel temperature in YFeO3 ceramics. J. Appl. Phys. 2018, 123, 174101. [Google Scholar] [CrossRef]
- Jacobs, I.S.; Burne, H.F.; Levinson, L.M. Field-Induced Spin Reorientation in YFeO3 and YCrO3. J. Appl. Phys. 1971, 42, 1631–1632. [Google Scholar] [CrossRef]
- Durbin, G.W.; Johnson, C.E.; Thomas, M.F. Direct observation of field-induced spin reorientation in YFeO3 by the Mossbauer effect. J. Phys. C Solid State Phys. 1975, 8, 3051–3057. [Google Scholar] [CrossRef]
- Schmool, D.; Keller, N.; Guyot, M.; Krishnan, R.; Tessier, M. Evidence of very high coercive fields in orthoferrite phases of PLD grown thin films. J. Magn. Magn. Mater. 1999, 195, 291–298. [Google Scholar] [CrossRef]
- Maiti, R.; Basu, S.; Chakravorty, D. Synthesis of nanocrystalline YFeO3 and its magnetic properties. J. Magn. Magn. Mater. 2009, 321, 3274–3277. [Google Scholar] [CrossRef]
- Wang, M.; Wang, T.; Song, S.; Tan, M. Structure-Controllable Synthesis of Multiferroic YFeO3 Nanopowders and Their Optical and Magnetic Properties. Materials 2017, 10, 626. [Google Scholar] [CrossRef]
- Wang, M.; Wang, T.; Song, S.; Ravi, M.; Liu, R.; Ji, S. Effect of calcination temperature on structural, magnetic and optical properties of multiferroic YFeO3 nanopowders synthesized by a low temperature solid-state reaction. Ceram. Int. 2017, 43, 10270–10276. [Google Scholar] [CrossRef]
- Nguyen, N.A.; Almjasheva, O.V.; Mittova, I.Y.; Stognei, O.V.; Soldatenko, S.A. Synthesis and magnetic properties of YFeO3 nanocrystals. Inorg. Mater. 2009, 45, 1304–1308. [Google Scholar]
- Racu, A.V.; Ursu, D.H.; Kuliukova, O.V.; Logofatu, C.; Leca, A.; Miclau, M. Direct low temperature hydrothermal synthesis of YFeO3 microcrystals. Mater. Lett. 2015, 140, 107–110. [Google Scholar] [CrossRef]
- Zhang, R.-L.; Chen, C.-L.; Jin, K.X.; Niu, L.W.; Xing, H.; Luo, B.C. Dielectric behavior of hexagonal and orthorhombic YFeO3 prepared by modified sol-gel method. J. Electroceram. 2014, 32, 187–191. [Google Scholar] [CrossRef]
- Bolarín-Miró, A.M.; Sánchez-De Jesús, F.; Cortés-Escobedo, C.A.; Valenzuela, R.; Ammar, S. Structure and magnetic properties of GdxY1−xFeO3 obtained by mechanosynthesis. J. Alloy. Compd. 2014, 586, S90–S94. [Google Scholar] [CrossRef]
- Lazarević, Z.; Jovalekić, Č.; Gilić, M.; Ivanovski, V.; Umićević, A.; Sekulić, D.; Romčević, N. Yttrium orthoferrite powder obtained by the mechanochemical synthesis. Sci. Sinter. 2017, 49, 277–284. [Google Scholar] [CrossRef]
- Potapkin, V.; Chumakov, A.I.; Smirnov, G.V.; Celse, J.-P.; Rüffer, R.; McCammon, C.; Dubrovinsky, L. The 57Fe Synchrotron Mössbauer Source at the ESRF. J. Synchrotron Rad. 2012, 19, 559–569. [Google Scholar] [CrossRef]
- Rüffer, R.; Chumakov, A.I. Nuclear resonance beamline at ESRF. Hyperfine Interact. 1996, 97, 589–604. [Google Scholar] [CrossRef]
- Mathur, S.; Veith, M.; Rapalaviciute, R.; Shen, H.; Goya, G.F.; Filho, W.L.M.; Berquo, T.S. Molecule derived synthesis of nanocrystalline YFeO3 and investigations on its weak ferromagnetic behavior. Chem. Mater. 2004, 16, 1906–1913. [Google Scholar] [CrossRef]
- Varouti, E.; Devlin, E.; Sanakis, Y.; Pissas, M.; Christides, C.; Tomara, G.N.; Karahaliou, P.K.; Georga, S.N.; Krontiras, C.A. A systematic Mössbauer spectroscopy study of Y3Fe5O12 samples displaying different magnetic ac-susceptibility and electric permittivity spectra. J. Magn. Magn. Mater. 2019, 495, 165881. [Google Scholar] [CrossRef]
- Andreeva, M.A. Nuclear resonant reflectivity data evaluation with the REFTIM program. Hyperfine Interact. 2008, 185, 17–21. [Google Scholar] [CrossRef]
- REFTIM, Version 7.4. Available online: http://www.esrf.eu/Instrumentation/software/data-analysis/OurSoftware/REFTIM-1 (accessed on 12 January 2016).
- Jacob, K.T.; Rajitha, G. Nonstoichiometry, defects and thermodynamic properties of YFeO3, YFe2O4 and Y3Fe5O12. Solid State Ion. 2012, 224, 32–40. [Google Scholar] [CrossRef]
- Widatallah, H.M.; Johnson, C.; Al-Harthi, S.H.; Gismelseed, A.M.; Al-Rawas, A.D.; Stewart, S.J.; Elzain, M.E.; Al-Omari, I.A.; Yousif, A.A. A structural and Mössbauer study of Y3Fe5O12 nanoparticles prepared with high energy ball milling and subsequent sintering. Hyperfine Interact. 2008, 183, 87–92. [Google Scholar] [CrossRef]
- Wadgane, S.R.; Shirsath, S.E.; Gaikwad, A.S.; Satpute, S.; Kadam, A.B.; Kadam, R.H. Ferro- and magneto-electric characteristics in YFeO3−Y3Fe5O12 nanocomposites. J. Magn. Magn. Mater. 2018, 457, 103–109. [Google Scholar] [CrossRef]
- Ismael, M.; Elhaddad, E.; Taffa, D.; Wark, M. Synthesis of Phase Pure Hexagonal YFeO3 Perovskite as Efficient Visible Light Active Photocatalyst. Catalysts 2017, 7, 326. [Google Scholar] [CrossRef]
- Andreeva, M.A.; Baulin, R.A.; Chumakov, A.I.; Rüffer, R.; Smirnov, G.V.; Babanov, Y.A.; Devyaterikov, D.I.; Milyaev, M.A.; Ponomarev, D.A.; Romashev, L.N.; et al. Nuclear resonance reflectivity from [57Fe/Cr]30 multilayer with the Synchrotron Mössbauer Source. J. Synchrotron Rad. 2018, 25, 473–483. [Google Scholar] [CrossRef]
- Treves, D. Magnetic studies of some orthoferrites. Phys. Rev. 1962, 125, 1843–1853. [Google Scholar] [CrossRef]
- White, R.L. Review of Recent Work on the Magnetic and Spectroscopic Properties of the Rare-Earth Orthoferrites. J. Appl. Phys. 1969, 40, 1061–1069. [Google Scholar] [CrossRef]
- Andreeva, M.A.; Baulin, R.A. Reflectivity spectra as absorption ones—Is it correct? arXiv 2022, arXiv:2203.12649. [Google Scholar]
- Izyurov, V.I.; Andreeva, M.A.; Baulin, R.A.; Nosov, A.P.; Gribov, I.V.; Kondratiev, O.A.; Subbotin, I.A.; Pashaev, E.M. Dependence of the Neel temperature on the thickness of ultrathin YFeO3 films. Phys. Met. Metallogr. 2022; in press. [Google Scholar]
- Kurchatov Complex for Synchrotron and Neutron Investigations. Available online: http://kcsni.nrcki.ru/en.shtml (accessed on 1 February 2022).
- Imamov, R.M.; Kondrashkina, E.A.; Aleksandrov, P.A.; Grabchak, V.P.; Uvarov, O.V. X-ray diffraction under total external reflection conditions applied for investigation of silicon subsurface layers implanted by heavy metals ions. Poverkhnost’ Fiz. Khimiya Mekhanika 1987, 3, 41–47. [Google Scholar]
- Kondrashkina, E.A.; Stepanov, S.A.; Schmidbauer, M.; Opitz, R.; Köhler, R.; Rhan, H. High-resolution grazing-incidence X-ray diffraction for characterization of defects in crystal surface layers. J. Appl. Phys. 1997, 81, 175–183. [Google Scholar] [CrossRef]
- Du Boulay, D.; Maslen, E.N.; Streltsov, V.A.; Ishizawa, N. A synchrotron X-ray study of the electron density in YFeO3. Acta Crystallogr. Sect. B Struct. Sci. 1995, 51, 921–929. [Google Scholar] [CrossRef]
- Wang, X.-L.; Hubbard, C.R.; Alexander, K.B.; Becher, P.F.; Fernandez-Baca, J.A.; Spooner, S. Neutron Diffraction Measurements of the Residual Stresses in Al2O3-ZrO2 (CeO2) Ceramic Composites. J. Am. Ceram. Soc. 1994, 77, 1569–1575. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Available online: https://www.ch.cam.ac.uk/computing/software/vesta (accessed on 29 June 2022).
- Wie, C.R.; Tombrello, T.A.; Vreeland, T., Jr. Dynamical X-ray diffraction from nonuniform crystalline films: Application to X-ray rocking curve analysis. J. Appl. Phys. 1986, 59, 3743–3746. [Google Scholar] [CrossRef]
- Materials Explorer. Available online: https://materialsproject.org/materials/mp-24999/ (accessed on 10 October 2021).
- Finger, L.W.; Hazen, R.M. Crystal structure and isothermal compression of Fe2O3, Cr2O3, and V2O3 to 50 kbars. J. Appl. Phys. 1980, 51, 5362–5367. [Google Scholar] [CrossRef]
- Salazar-Rodriguez, R.; Aliaga-Guerra, D.; Taddei, K.M. X-ray diffraction, Mössbauer spectroscopy, neutron diffraction, optical absorption and ab-initio calculation of magnetic process in orthorhombic YFexCr(1−x)O3 (0 ≤ x ≤ 1) compounds. Hyperfine Interact. 2019, 240, 82. [Google Scholar] [CrossRef]
- Coutinho, P.V.; Cunha, F.; Barrozo, P. Structural, vibrational and magnetic properties of the orthoferrites LaFeO3 and YFeO3: A comparative study. Solid State Commun. 2017, 252, 59–63. [Google Scholar] [CrossRef]
- Shukla, R.; Sayed, F.N.; Grover, V.; Deshpande, S.K.; Guleria, A.; Tyagi, A.K. Quest for Lead Free Relaxors in YIn1−xFexO3 (0.0 ≤ x ≤ 1.0) System: Role of Synthesis and Structure. Inorg. Chem. 2014, 53, 10101–10111. [Google Scholar] [CrossRef]
- Derras, M.; Hamdad, N. New approach for the spin effect on the ground state properties of the cubic and hexagonal YFeO3 perovskite oxide: GGA+U based on the DFT+U description. Results Phys. 2013, 3, 61–69. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreeva, M.; Baulin, R.; Nosov, A.; Gribov, I.; Izyurov, V.; Kondratev, O.; Subbotin, I.; Pashaev, E. Mössbauer Synchrotron and X-ray Studies of Ultrathin YFeO3 Films. Magnetism 2022, 2, 328-339. https://doi.org/10.3390/magnetism2040023
Andreeva M, Baulin R, Nosov A, Gribov I, Izyurov V, Kondratev O, Subbotin I, Pashaev E. Mössbauer Synchrotron and X-ray Studies of Ultrathin YFeO3 Films. Magnetism. 2022; 2(4):328-339. https://doi.org/10.3390/magnetism2040023
Chicago/Turabian StyleAndreeva, Marina, Roman Baulin, Aleksandr Nosov, Igor Gribov, Vladimir Izyurov, Oleg Kondratev, Ilia Subbotin, and Elkhan Pashaev. 2022. "Mössbauer Synchrotron and X-ray Studies of Ultrathin YFeO3 Films" Magnetism 2, no. 4: 328-339. https://doi.org/10.3390/magnetism2040023
APA StyleAndreeva, M., Baulin, R., Nosov, A., Gribov, I., Izyurov, V., Kondratev, O., Subbotin, I., & Pashaev, E. (2022). Mössbauer Synchrotron and X-ray Studies of Ultrathin YFeO3 Films. Magnetism, 2(4), 328-339. https://doi.org/10.3390/magnetism2040023






