Abstract
In this article, the stress/stress sensing capability of FeSiB thin films is demonstrated and discussed. The sensing relies on the change in permeability by the application of stress, compressive and tensile, and the application of DC magnetic field. This susceptibility/permeability was tested by the exciting field (AC) being in the same direction with the applied stress. The susceptibility was shown to exhibit a maximal value at a given applied stress, the critical stress. Moreover, this maximal amplitude and position was changing with the application of an external DC magnetic field. For the DC field applied in the direction of the exciting field (AC) and longitudinal to the stress, the critical stress was shifted toward negative values and for the DC field applied perpendicularly, the critical stress was shifted toward larger positive values. This was experimentally demonstrated, and a model was constructed for a better understanding.
1. Introduction
The magnetic properties of amorphous soft magnetic material can be used for magnetic sensors [1]. Typical commercial magnetic field sensors are based on the Giant Magneto Impedance (GMI) effect (Z(H) − Z(Hmax)/Z(Hmax), with Z being the impedance, H the magnetic field and Hmax the largest applied field. This can sense magnetic field down to µ0H = 10−12 T [1]. To produce this effect, an AC current is flowing through the material. In this case, depending on the frequency, the current density is concentrated close to the material edge (skin). The current density has a characteristic depth δ, called skin depth, that can be expressed, for a semi-infinite planar interface as [2]:
where µ0 = 4π10−7 H/m is the vacuum permeability, µr is the material relative permeability, γ is the material electric conductivity and f is the AC current frequency. Large permeability is reducing the skin depth, and the impedance of the conductor becomes higher; and the low permeability is increasing the skin depth, resulting in lower impedance. The application of an external magnetic field can then reduce the magnetic permeability µr(H). The GMI effect consists of the change in the measured impedance due to the application of a DC magnetic field [3,4].
Change in material permeability can also be achieved by applying another type of external stimulus. Especially, in the stress impedance (SI) effect, a strain or stress σ is applied to the magnetic material and a change in the magnetic permeability µr(H, σ) also changes the measured impedance [5,6,7]: Z(σ) − Z(σmax)/Z(σmax), with Z the impedance, σ the magnetic field and σmax the largest applied stress [8].
The SI effect has been used to successfully demonstrate strain sensing devices based with wires, ribbons and also thin films [5,9,10,11,12,13,14,15]. They showed generally much higher gauge factors than devices, using conventional effects (resistive, semiconductor). Beside general investigations as a strain gauge, also more specific applications, such as for structural health monitoring, pressure sensors, or force sensors have been proposed [15,16]. In a recent work, an amorphous FeSiB material was used to demonstrate the application for stress sensor [17]. A thin layer of this material was sputtered on top of a silicon beam. When stress was applied to the beam, the bending of the beam results in compressive stress, or tensile stress, in the magnetic layer, depending on the curvature of the beam. An external magnetic field was applied along the beam direction or perpendicularly. This revealed the complete map of the magneto elastic effect on the magnetic permeability. To complete this work, a theoretical description of the system should be provided.
Some models of the GMI are presented in the literature [18,19,20,21,22], including the effect of the stress on the GMI [23] to optimize the GMI because a low magnetostriction constant was experimentally yielding to a large GMI measurement [24]. Although those models were matching the experimental data, few models can be found for the susceptibility change with stress, and most of them are modeling only the case with an applied stress perpendicular to the anisotropy axis, and without external field [25,26].
In the present article, calculation of susceptibility is performed to understand the effect for many possible cases (compressive and tensile stress, different magnetic field directions) and to be able to predict permeability behavior with field and stress. Such results can be used to optimize sensors based on the magnetic susceptibility change.
2. Materials and Methods
Sample production and mechanical test were described in [17] and are briefly summarized here: the magnetic material, Ti/Fe79Si7B14/Ti, was sputtered using a magnetron system (QAM-4-S, ULVAC, Inc., Tokyo, Japan) on a 300 µm thick Si wafer and the thicknesses were 20/500/20 nm, respectively. The titanium acted as adhesion layer and surface protection. The samples were cut in rectangle with length l = 40.4 mm and width w = 7.7 mm. A three-point bending test was applied to the sample and the applied force was recorded using a load cell (Xforce P, ZwickRoell Corporation, Ulm, Germany) with maximal force of 5 N. A coil was wrapped around the sample with the coil axis being parallel to the sample length. The coil was connected to an impedance analyzer (PSM1735, Newton4th Ltd., Leicester, the UK) for inductance measurements, at a frequency of 20 kHz. An electromagnet was used to generate an external magnetic field, along or perpendicular to the sample axis, with an amplitude of up to µ0H = 40 mT.
Magnetic characterizations, the M versus H loop, were performed in a BHV-50H Vibrating Sample Magnetometer (VSM) from Riken Denshi Co. (Tokyo, Japan). The applied field ranged from −1000 Oe to 1000 Oe (approximately − 80 kA/m to + 80 kA/m in S.I. units). From the magnetic loop the relative permeability was estimated as µr(H) = 1+ (dM(H)/dH).
3. Experimental Results
The inductance change is presented in Figure 1 for the external field in the direction of the sample and in Figure 2 for the external field applied perpendicularly [17].
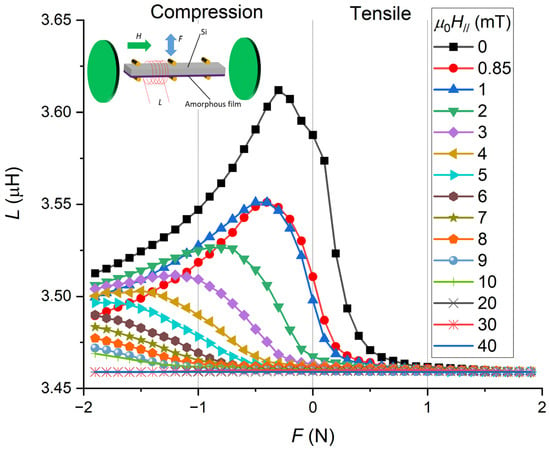
Figure 1.
Measurement of the coil inductance versus the applied force with the applied longitudinal field.
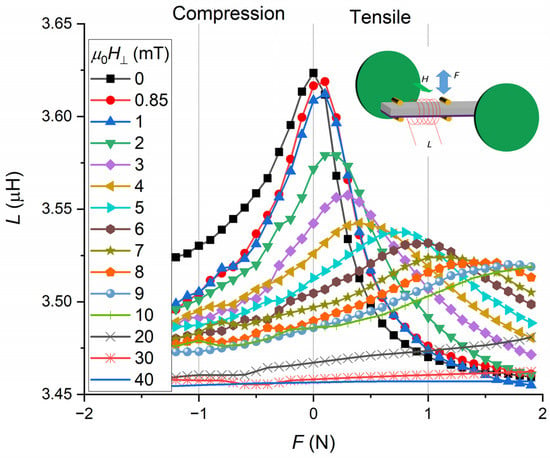
Figure 2.
Measurement of the coil inductance versus the applied force with the applied orthogonal field.
Figure 1 presents the result of the inductance measurement of the coil, for the case where the applied field was in the sample axis. For the case where there was no applied field, H// = 0, the compressive stress affected the inductance differently when compared to the tensile one. The curve was not symmetric with respect to the force. The curve was maximum at a critical force Fc, and the decrease was smooth for the force on the compression side and sharp on the tensile side of the curve. At a large applied force, F > 1 N, the inductance became constant at a value of L ~ 3.46 µH. As the magnetic field H//was increased, the initial inductance measured at zero force was decreasing to the same inductance value of L ~ 3.46 µH. In fact, the longitudinal field was (i) shifting the inductance versus force curve toward compressive force and (ii) reducing the inductance amplitude. Eventually, at larger fields, the inductances versus force curves were constant with values of L ~ 3.46 µH in the force measurement range.
After this set of measurements, performed in the longitudinal magnetic field configuration, the electromagnet was rotated to apply the magnetic field perpendicular to the sample axis. Figure 2 presents the result of the inductance measurement of the coil, for the case where the applied field was perpendicular to the sample axis. In this perpendicular configuration and for HꞱ = 0, the curve was different than the previous experiments in the longitudinal configuration and H// = 0. The experiments were performed first, by applying force (compression and tensile) in the longitudinal configuration, then the experiments were performed by applying force (compression and tensile) after setting the configuration into the perpendicular configuration. Therefore, the sample has first experienced many stimuli (tensile and compressive stresses, plus longitudinal) large enough to affect the magnetic state. So, the state of these two curves, H// = 0 and HꞱ = 0 has no reason to be exactly the same because of history. It is believed that there was a little hysteresis, but the shape of the curve remained very similar to the previous case: smooth for the force on the compression side and sharp on the tensile side of the curve. The effect of the field HꞱ was different from the effect of H//: the inductance peaks were shifting toward tensile force here. The inductances were reduced in both cases by the application of the magnetic field.
Figure 3a shows the result of the VSM measurement, and the magnetic loop is presented. Magnetic saturation was MS ~ 1.1 MA/m and a coercive field Hc was ~ 400 A/m. The relative permeability was then extracted and plotted here versus the applied magnetic field in Figure 3a. This result was compared with the inductance measurement of the coil around the sample with the applied magnetic field and without an applied mechanical force.
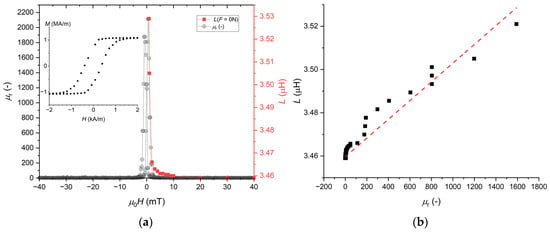
Figure 3.
(a) Permeability obtained from the VSM (black circle) and coil inductance (red square) measured on a sample without a magnetic field; the inset shows the magnetic loop M versus H; (b) Approximation of the relationship between the measured inductance to the permeability.
High inductances were observed at high permeability values and lowest inductances are observed at lowest permeability values. In fact, when the magnetic field was larger than µ0H = 10 mT, the permeability has a low value of µr = 1; this was corresponding to a low and constant value of inductance L ~ 3.46 µH. This value L ~ 3.46 µH was then used to refer to the saturation of the sample. The inductance of a coil is usually expressed as L = kµr with the coefficient k being related to the number of turns of the coil, and the geometry of the coil and the sample [27,28]. The positive and negative sides of the µr(H) curve, Figure 3a, were then averaged as µr(Hi) = (µr(+Hi) + µr(−Hi))/2 and plotted versus the coil inductances measured at the corresponding field L(Hi). Figure 3b is showing the value of permeability plotted versus the inductance at the same magnetic field Hi amplitude: µr(Hi) versus L(Hi).
A linear approximation of the relationship between permeability and inductance can be extracted as L = (4.33 × 10−5) × µr + 3.46. This line was also plotted in Figure 3b.
Figure 1 and Figure 2 were presenting the inductance curve versus the applied force in the case of longitudinal DC field (H//) and orthogonal DC field (HꞱ), respectively. The curves were presenting inductance peaks which can be characterized by the position of the peak, i.e., the critical force Fc, and the peak amplitude ΔLmax. This value of the peak amplitude ΔLmax was extracted by subtraction of the saturation value of 3.46 µH: ΔLmax = max(L) − 3.46 µH. This peak amplitude is an indicator of the permeability according to the relationship highlighted in Figure 3b as ΔL ~ Δµr.
Figure 4 shows the critical force Fc and the peak amplitude ΔLmax for all the tested configurations. The magnetic field direction was clearly changing the position of the inductance peak. Longitudinal field (H//) was reducing the critical force (dFc/dH < 0) and the orthogonal field (HꞱ) was increasing the critical force (dFc/dH > 0). In both cases, a linear tendency was observed. The peak amplitudes ΔLmax were reduced by the magnetic field: with H//, the decrease was faster than with HꞱ. The tendency of ΔLmax with applied fields was nonlinear.
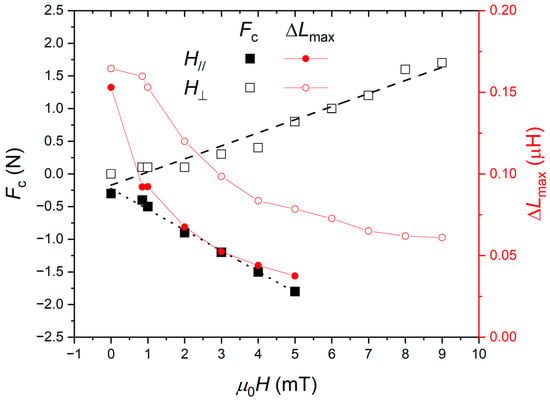
Figure 4.
Experimental peak parameters: critical force Fc and maximal coil inductance change ΔLmax versus the applied force. Data for the longitudinal (H//) and orthogonal (HꞱ) configuration.
4. Modeling
In this section, a model built to understand these experimental observations is described. According to the result of Figure 3b, the coil inductances can be interpreted by the magnetic state of the material. In this model, the magnetic states will be calculated as a function of stress and magnetic field. From these calculated magnetic states, the susceptibilities χ will be derived. Susceptibilities and permeabilities of materials with such large permeabilities will be supposed to be similar as for µr ~ 103, then χ = µr − 1 ~ µr.
First, the coupling between the magnetization and the applied magnetic fields has to be expressed. For this coupling, there are two contributions: one from the AC exciting field hac, created by the coil, and the second one is from the applied DC magnetic field H.
In the following, we will assume that the AC exciting field has a small amplitude compared to the field; hac << H. The coupling between an applied magnetic field and a magnetization vector, with an amplitude Ms, is expressed by the Zeeman energy. The Zeeman energies are expressed for the two contributions as:
and:
It can be noticed that these Zeeman energies are minimized when the magnetization and the field are collinear.
Secondly, the coupling between the magnetization and the magnetic anisotropy has to be taken into account. In the following, we will assume two contributions: one from the intrinsic magneto crystalline anisotropy (small for this amorphous material) and a second one from the extrinsic magneto elastic coupling. For the magneto crystalline anisotropy, the energy is expressed, assuming a uniaxial anisotropy in the y-direction, as:
where Ka is the first-order magnetic anisotropy constant and θ is the angle between the magnetization vector and the anisotropy axis. This energy term minimization would require that θ = 0, hence, the magnetization should be in the anisotropy direction.
When stress σ is applied to the magnetostrictive material, the corresponding magnetoelastic anisotropy can also be expressed by Equation (4), with the corresponding constant Kσ being expressed here as:
In this Equation (5), λs is the magnetostriction constant of the material.
The final state of the magnetization, under magnetic field H, is obtained by minimizing the sum of all these energetic contributions. For instance, in the case where the uniaxial magnetic anisotropy and the applied field are orthogonal, the total magnetic interaction energy E is expressed, as:
By defining the anisotropy field Ha as:
the two magnetization components, ML (longitudinal, along with the field direction) and MT (transverse to the field direction), can be expressed, for field H < Ha, as:
For field H > Ha the two components are then reduced to ML = MS and MT = 0. These two curves are plotted in Figure 5a. For H < Ha, ML is linearly increasing up to MS and remained ML = MS for H > Ha. For H < Ha, MT is decreasing from MS down to 0 and remained MT = 0 for H > Ha.
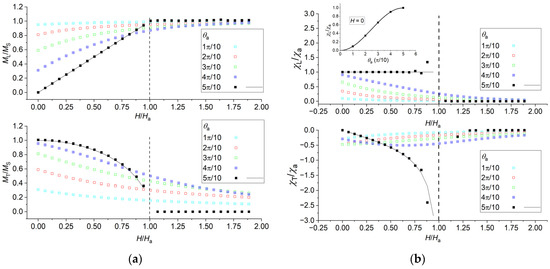
Figure 5.
(a) Relative magnetization components (ML/MS and MT/MS) versus H/Ha for different magnetic anisotropy direction θa; (b) Relative susceptibility components (χL/χa and χT/χa) versus H/Ha for different magnetic anisotropy direction θa. The full lines are theoretical values (Equation (8) for ML and MT, Equation (9) for χL and Equation (10) for χT) and square are numerical results from model.
The corresponding relative susceptibility (dM/dH) components, χL and χT, are directly obtained for field H < Ha from Equation (8) as:
and:
For field H > Ha the two components are then reduced to χL = 0 and χT = 0. These susceptibilities can be normalized according to the constant χa = MS/Ha.
These two curves are plotted in Figure 5b. It can be pointed out that, at H = Ha, there was no susceptibility calculated. In fact, plotting the angle dependency of E for different values of field H could reveal this particularity, as explained in detail in Appendix A.
5. Calculated Results of the Model
The model was used in COMSOL software to calculate the magnetization direction and then the susceptibility. This AC susceptibility was then calculated from the dependency of the magnetization with the AC field hac. It was assumed that hac is in the sample’s main axis, the x-direction (longitudinal direction). The longitudinal direction is then referred below to as the x-direction and the orthogonal (perpendicular) direction as the y-direction. The susceptibility was extracted from the x-component of the magnetization as χL = dMx/dhac. This susceptibility was then calculated with the two types of external stimuli: applied DC field H and stress σ. Especially, the DC field can be in the x-direction (longitudinal configuration: H//) or in the y-direction (orthogonal configuration, HꞱ). In addition, the stress was supposed to be applied in the x-direction. Both tensile stress (positive values) and compressive stress (negative values) were considered. Susceptibilities are then plotted in the normalized unit (χL/χa) and the same for the applied field (H/Ha) and stress (Kσ/Ka) to provide a general overview of the phenomenon. A summary of direction of physical quantities is presented in Table 1.

Table 1.
Physical quantity of the model.
5.1. Without Magnetostriction
Figure 5a is presenting the curves ML/MS and MT/MS versus different anisotropy angles θa. The component ML is linear with the applied field H < Ha and is constant for the applied field H > Ha for θa = π/2. The corresponding susceptibility, presented in Figure 5b, is constant for H < Ha as χL = χa and for H > Ha as χL = 0. For other angles, the longitudinal component ML is continuously increasing with H with an asymptotic behavior tending to the value MS. The corresponding susceptibility χL is observed to continuously decrease with H tending toward the value 0. The inset of Figure 5b) is presenting the effect of θa on χL at H = 0: this is following the law χL = χasin2(θa).
5.2. With Magnetostriction
5.2.1. No External Field
Figure 6 is presenting the curves χL/χa versus the anisotropy ratio Kσ/Ka: defined as the ratio between the magnetoelastic anisotropy (Equation (5)) and magnetic anisotropy constant, with an angle θa between these two anisotropy directions. The magnetostriction constant was supposed to be λs = 30 ppm. Firstly, it can be observed that at angle θa = π/2, a peak appeared in the tensile stress part (σ > 0) at the exact value Kσ = +Ka. This situation is similar to the magnetic field H = Ha applied perpendicularly to the anisotropy axis, as discussed previously, where the energy is independent of the magnetization angle (Appendix A and Appendix B), yielding to largest susceptibility. At angle θa = 0, a sharp peak appeared in the compressive stress part (σ < 0) at the exact value Kσ = −Ka because the total energy angular dependence would disappear.
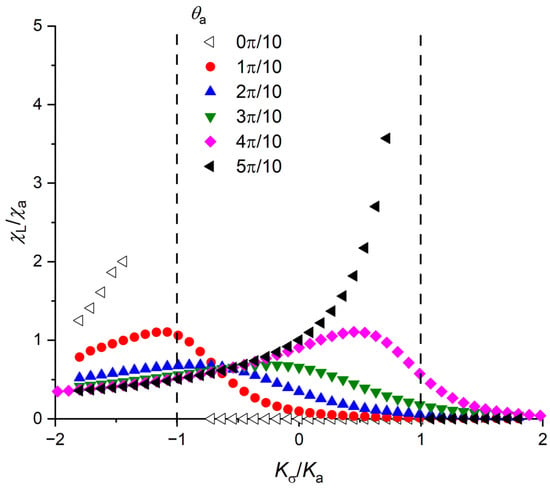
Figure 6.
Relative susceptibility components (χL/χa) versus anisotropy ratio Kσ/Ka with λs = 30 ppm, for different angle θa between these two anisotropies: from 0 (same direction) to π/2 (perpendicular).
In the case θa = π/2, the value Kσ = +Ka was corresponding to 3σλs = 2Ka, defining the critical stress [25,26,29,30] as σc = 2Ka/3λs. The part of the curve with θa = π/2 and σ < σc was a smooth increasing curve, whereas for σ > σc the curve became constant: the magnetic moments were now aligned with the stress. When the angle θa was reduced, the discontinuity disappeared and a continuous curve is observed until the angle was θa = 0 where the curve was again discontinuous at stress value corresponding to Kσ = −Ka. For the intermediate angles, a bump appeared at an intermediate stress value (−Ka ≤ Kσ ≤ Ka). However, by reducing the angle toward θa = 0, the global shape of the curve remained: below the critical stress (σ < σc) the curve was smoothly increasing and over the critical stress (σ > σc), the curve was more sharply decreasing.
The calculation was performed for different values of magnetostriction constant λs when no DC magnetic field was applied (HDC = 0). The corresponding curves are plotted in Figure 7. It can be observed that the stress has no influence on the susceptibility for magnetostriction constant λs = 0. In this case, the susceptibility remains constant. For magnetostriction constant λs > 0, the susceptibility is then dependent on the amplitude of λs. For the lowest value, λs = 5 ppm, the susceptibility is increasing linearly with the applied stress in the range considered here. For the largest value λs = 30 ppm, the simulation was performed over a wider range of stress, revealing more about the behavior of the susceptibility curve: for large compression and large tensile stresses, the susceptibilities were very low whereas, at the critical stress σc, the curve is exhibiting a maximum value.
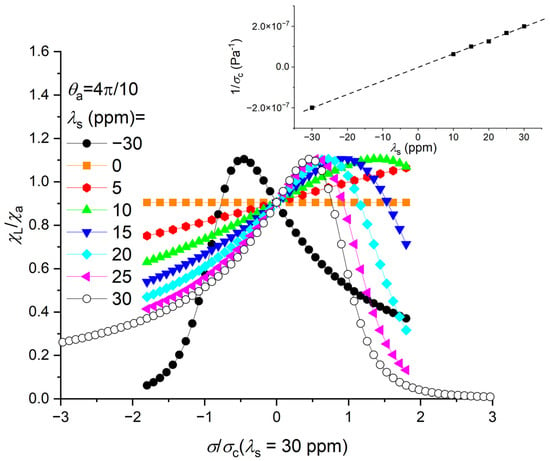
Figure 7.
Relative susceptibility components (χL/χa) versus stress σ for different magnetostriction constant λs. The inset shows the inverse of the critical stress σc versus magnetostriction constant λs and dashed line is a guideline.
As the value of λs was increased, the critical stress σc was shifted to relatively smaller tensile stress. The inverse value of the extracted critical stress σc from these curves was linearly increased when the value of λs was increased. The susceptibility was defined, in the case of θa = π/2, by Equation (7), as χL = MS/Ha, where Ha was defined in Equation (9). The susceptibility is χa = µ0Ms2/(2Ka) and if Ka is low, then is χa large. Adding the magnetostrictive term Kσ, then the effective anisotropy constant can be expressed as Ka − Kσ (Appendix B). The largest susceptibility appeared at Ka − Kσ = 0, at the critical stress σc [25,26,29,30]. The critical stress depends on the magnetostriction constant as σc = 2Ka/3λs ≅ 1/λs. For positive magnetostriction constant (λs > 0), the critical stress σc is positive (tensile) and for negative magnetostriction constant (λs < 0), the critical stress σc is negative (compression). The effect of positive and negative stress was also investigated here for value λs = 30 ppm and value λs = −30 ppm, as seen in Figure 7. The resulting curves were found to be symmetric to each other. The critical stress σc occurred at opposite values. This behavior was also observed in the literature [30,31]. For instance, Figure 8 shows an example of two materials permeability versus stress curves, one having a positive (λs > 0) and the other material with a negative magnetostriction constant (λs < 0). The two constants were not exactly opposite so the critical strains (εc = Eσc, with E the material Young’s modulus) were not opposite too. Nonetheless, the shapes of the two curves were in agreement with our calculations.
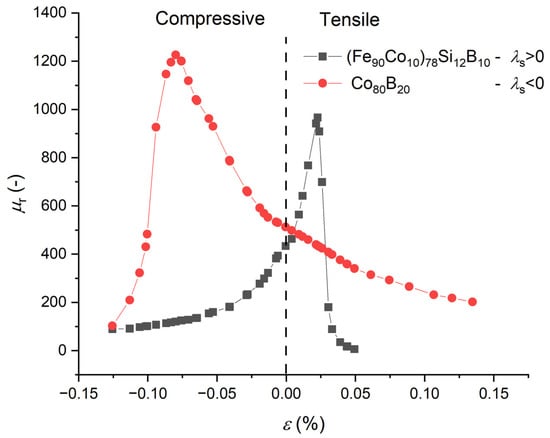
Figure 8.
Permeability (µr ~ χ) versus strain (ε = Eσ, with E the material Young’s modulus of the materials) for a Fe-based material with positive λs and a Co-based material with negative λs [30].
5.2.2. With External Field
Finally, the results of the calculation, including the effect of the external magnetic field, are presented in this section. First, the effect of the longitudinal field is plotted in Figure 9. This curve is showing the susceptibility versus the applied stress and magnetic field applied in the same direction. The curves are observed to shift towards negative stress. These simulated curves are in agreement with the experimental curves presented in Figure 1. Magnetization is, without stress and field, directed along the magnetic anisotropy. As a stress is applied, the effective anisotropy is changing, as discussed in the previous: compressive stress is reinforcing a perpendicular anisotropy, and the whereas the tensile stress is lowering a perpendicular anisotropy. The effect of longitudinal field is similar to the tensile stress and the longitudinal magnetization component, and therefore the longitudinal susceptibility, are then affected (Figure A2 and Figure A4).
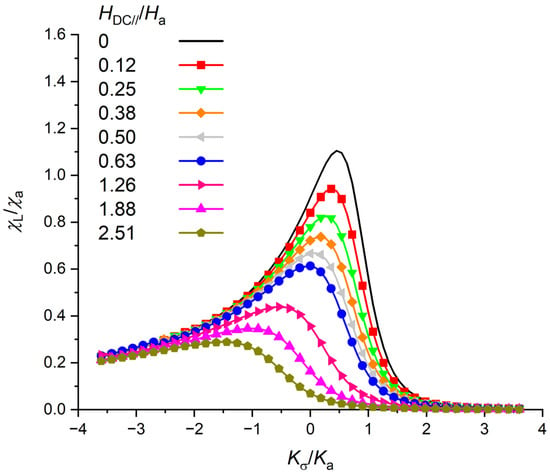
Figure 9.
Relative susceptibility components (χL/χa) versus anisotropy ratio Kσ/Ka with λs = 30 ppm for different longitudinal field.
The second configuration for the application of the external field, the perpendicular configuration, is presented in Figure 10. In this case, the effect was the opposite: the curves were shifted toward positive stress. The effect of perpendicular field is similar to the compressive stress which reinforced the effect of the magnetic anisotropy. The longitudinal magnetization component and therefore the longitudinal susceptibility are then affected (Figure A3 and Figure A4).
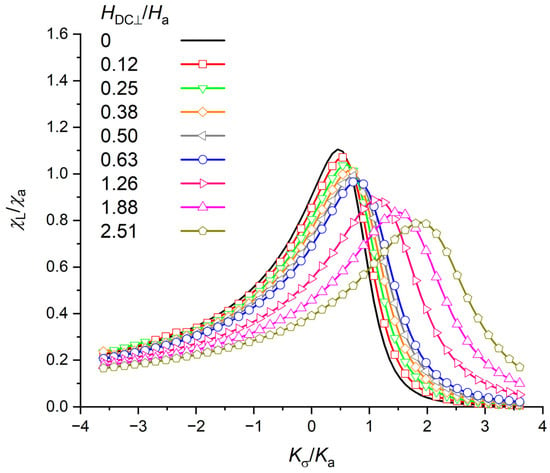
Figure 10.
Relative susceptibility components (χL/χa) versus anisotropy ratio Kσ/Ka with λs = 30 ppm for different orthogonal field.
Figure 11 is presenting the peak parameters extracted from these simulated susceptibility curves for comparison with the experimental results, presented in Figure 4. The behavior of the critical stress, in the longitudinal and perpendicular configurations, are matching the behavior of the critical force experimentally found for the same configuration in Figure 4: longitudinal field was linearly reducing the critical stress whereas the perpendicular field was linearly increasing this critical stress. From Figure 11, the slope of the critical stress σc versus applied field was extracted, by fitting the curve by linear fit method, for the case of longitudinal field (H//) and for the case of perpendicular field (HꞱ). The results are presented in Table 2. The slope of the critical stress, in the longitudinal field configuration was of −1.72 whereas it was 1.27 in the perpendicular field configuration. The longitudinal value was 1.35 times larger than the perpendicular one (in absolute value). Experimentally, inductances were measured for the force applied during the bending test. This force is somehow believed to be proportional to the stress in the magnetic thin film. The change in the critical force measured under field is then proportional to the change in critical stress with magnetic field. From the experimental critical force, shown Figure 4, the same linear fit was performed to Fc(H) − Fc(H = 0); the experimental offset was subtracted. The linear fit results are also presented in Table 2: in the longitudinal field configuration the slope was of −0.29 N/mT whereas it was 0.16 N/mT in the perpendicular field configuration. The experimental longitudinal slope value was 1.77 times larger than the perpendicular one (in absolute value). These two values, 1.35 (exp.) and 1.77 (sim.), are in relatively good agreement.
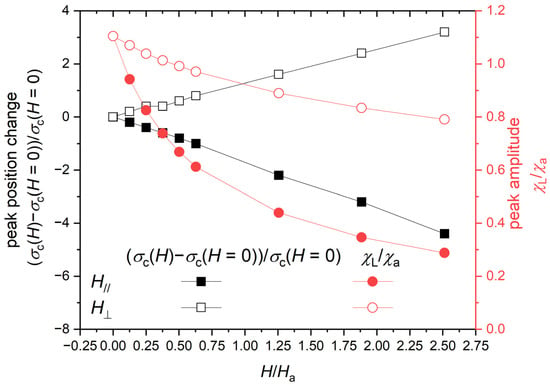
Figure 11.
Peak parameters: critical stress σc and maximal susceptibility change versus the applied magnetic field.

Table 2.
Fitting parameters for the critical stress and Force versus fields (H//and HꞱ).
The behavior of the simulated susceptibility peak amplitudes was also similar to the experimental results: the applied field was reducing the amplitude of the peak for the two configurations, although the decrease was faster in the case of the longitudinal configuration. To quantify these, a decay function: y = A*exp(−H/Hdecay) was arbitrary selected to represented the behavior of the susceptibility peak amplitudes decrease with applied fields (H//and HꞱ). The curves ΔLmax(H), obtained from Figure 4 for H//and HꞱ, were fitted using this function. The results are given in Table 2. The decay coefficients Hdecay obtained from the fitted curves of ΔLmax(H//) and ΔLmax(HꞱ) were then 1.32 mT−1 and 3.67 mT−1, respectively. Hence, the experimental longitudinal coefficient value was 2.78-times smaller than the perpendicular one. The simulated χL(H//)/χa and χL(HꞱ)/χa versus H/Ha were fitted using the same decay function. The results are given in Table 2 as well. The decay coefficients Hdecay obtained from the fitted curves of χL(H//)/χa and χL(HꞱ)/χa were then 0.68 and 1.48, respectively. Hence the simulated longitudinal coefficient value was 2.18-times smaller than the perpendicular one. These two values, 2.78 (exp.) and 2.18 (sim.), are in relatively good agreement.
Finally, the important parameters, for the stress sensor application [32], of such susceptibility versus stress curves are presented in Figure 12. The chosen conditions were selected to better understand the magnetization behavior in such materials, due to field and stress was classical material (FeSiB) for GMI and SI, but not optimized for the best condition. Stress-impedance sensors would have larger sensibility by several thermal/stress and magnetic treatments [3,33]. The model presented above might help to predict these parameters and to adapt and optimize the material’s magnetic behavior, as a high value of susceptibility is needed to increase the sensitivity. The sensitivity direction can be selected to have a positive slope or negative slope by selecting the magnetostriction constant (Figure 7). In addition, the sensibility can be linear over a large range of stress by selecting a low amplitude magnetostriction constant, as seen in Figure 7.
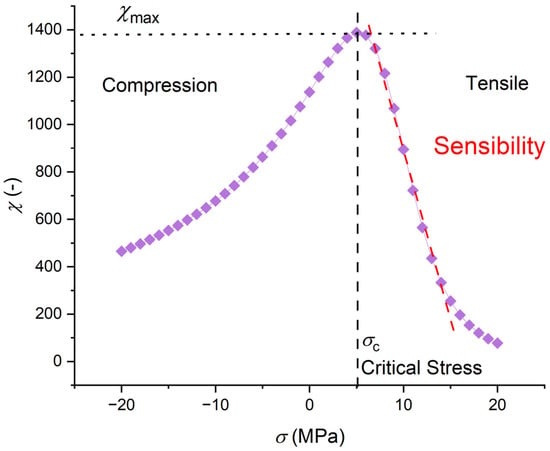
Figure 12.
Stress sensor sensibility, calculated with MS = 1 MA/m, Ha ~ 800 A/m, (χa = 1250) and with λs = 30 ppm and angle θa = 4π/10.
If the shape of the µr (~χ) versus stress σ (~ε) was directly controlled by the sign of the magnetostriction constant λs, the position of the peak depends on the anisotropy stress direction as seen in Figure 6, which was observed in [6]. Moreover, this susceptibility peak can be shifted with a magnetic field, although this was decreasing the peak amplitude.
6. Conclusions
In this article, magneto elastic susceptibility was studied. Experimental data reported that when a force (stress) was applied in the same direction as the exciting field (AC field), for a critical force, the susceptibility was maximal. Under a longitudinal applied magnetic field, this critical force was reduced, even getting negative, and on the other hand, with the application of a perpendicular field, this critical force was shifted to larger values. In both cases, the observed peak amplitudes were reduced.
From these observations, a model of this magnetic behavior was constructed. This model assumed the magnetization rotation under the application of stress and magnetic field, and magnetic anisotropy. By setting the magnetostriction constant positive around λs = 30 ppm, the shape of the susceptibility can be retrieved. Moreover, this model was successful to demonstrate similar behavior of the magnetic field effect on the susceptibility.
It is believed that this model is useful to provide a guideline in the conception of a stress sensor using the magneto elastic behavior of film based on the FeSiB type series; for stress impedance sensors or for coil-type sensors, as they are both sensitive to the magnetic state of the material under applied stress.
This can be used for both Fe-based (λs > 0) and Co-based (λs < 0) amorphous films. It can also help to predict the critical stress value, where the best sensitivity of the sensor can be found.
Author Contributions
Conceptualization, G.D., H.K. and J.F.; methodology, G.D., H.K., J.F. and F.N.; software, G.D.; investigation, K.M., G.D. and H.K.; writing—original draft preparation, G.D.; writing—review and editing, J.F., H.K., F.N., K.O. and F.N.; supervision, J.F. and F.N.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Tohoku University Frontier Research in Duo grant, Japan Keirin Autorace foundation (JKA) and Ensemble Continuation Grant 2022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
These curves are presented in Figure A1. The curves corresponding to the case H > Ha are clearly showing that the magnetization angle would be locked at an angle θ = π/2: the field is strong enough to orientate the magnetization in the field direction. The curves corresponding to the case H < Ha are showing a minimum between 0 and π/2: the magnetization is at an intermediate angle between the anisotropy axis and field direction. The curve corresponding to the case H = Ha shows a broader minimum. This means that the magnetization can rotate more easily; the rotational susceptibility is then larger.
The Taylor expansion of E, Equation (6), around the angle θ = π/2, is:
Then, by rearranging the terms and using Ha = 2K/µ0Ms, we obtain:
By setting the field value as H = Ha, the energy expression is finally simplified as:
This Expression (A3) shows that if the field is applied perpendicularly to the Easy Axis, and with amplitude as H = Ha, then the angular dependency vanished. These Taylor expansions, Equation (A1), are plotted for field values around Ha, showing the inversion of curvature as H is crossing the value H = Ha which is a flat curve.
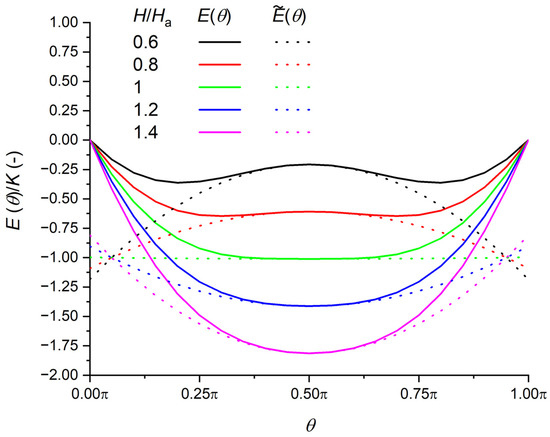
Figure A1.
Angular dependence of the energy. Solid lines were constructed by using Equation (6) and dotted lines were based on the Taylor expansion, Equation (A3).
This was the simple case where a uniaxial magnetic anisotropy exists with θa = π/2, at other angles, the magnetization curves were smoother and the susceptibility could be calculated for many field values. In the following, the effect of stress is considered along with the fields.
Appendix B
In the case of two uniaxial anisotropies, the treatment is provided in [34] and adapted below. Considering the anisotropy constants KA (magneto crystalline) and Kσ = 3σλs/2 (magneto elastic term) with perpendicular directions, then the total energy can be written as:
If KA = Kσ, the total energy is then independent of the angle. The first derivative of this energy is:
In addition, the second derivative of this energy is:
From Equation (A5), the minimum can be found at θ = 0 and/or π/2; to determine whether the total energy is a minimum at these angles, the Equation (A6) must be positive. So, a condition on (KA − Kσ) appeared: if KA > Kσ, then the minimum is for angle θ = 0 (then M is along the magneto crystalline direction) and if KA < Kσ, then the minimum is for angle θ = π/2 (then M is along the stress direction). The term in sin2(θ), after adding the magneto elastic term, behaves with an effective constant KA − Kσ. For tensile stress (σ > 0), the effective term in sin2(θ) is reduced whereas for compressive stress (σ < 0), the term in sin2(θ) is enhanced. Tensile stress is reducing the magneto crystalline anisotropy and compressive stress is reinforcing it.
Appendix C
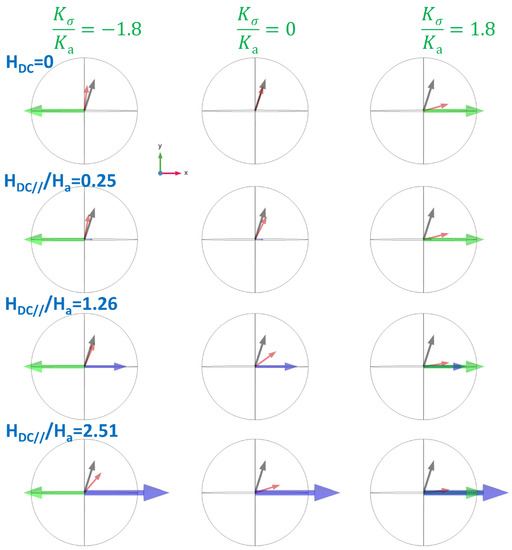
Figure A2.
Snapshots of the magnetic state of the Magnetization (in red) at a given magnetic anisotropy (in black), for different stress (in green) and different longitudinal applied field (in blue).
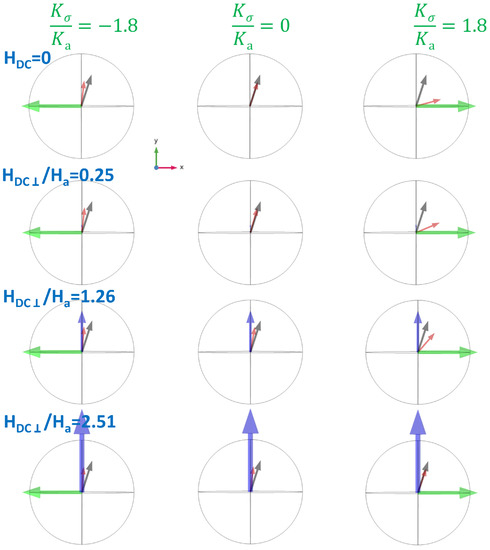
Figure A3.
Snapshots of the magnetic state of the Magnetization (in red) at a given magnetic anisotropy (in black), for different stress (in green) and different perpendicular applied field (in blue).
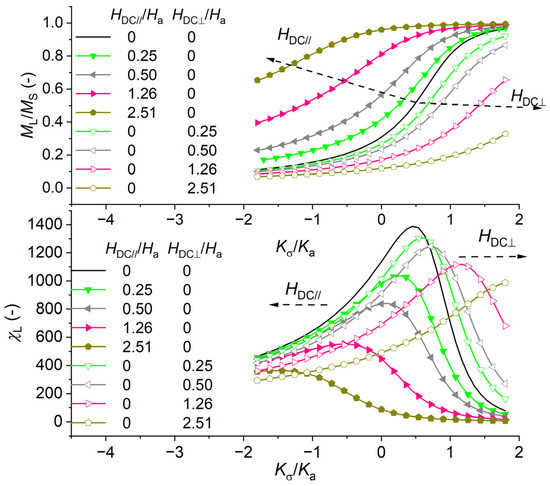
Figure A4.
Relative longitudinal magnetization component (ML/MS) versus stress for different for different applied field (top) and corresponding relative longitudinal susceptibility component χL versus stress for different for different applied field (bottom).
References
- Khan, M.A.; Sun, J.; Li, B.; Przybysz, A.; Kosel, J. Magnetic sensors-A review and recent technologies. Eng. Res. Express 2021, 3, 022005. [Google Scholar] [CrossRef]
- Wheeler, H.A. Formulas for the skin-effect. Proc. IRE 1942, 30, 412–424. [Google Scholar] [CrossRef]
- Garcia, D.A.; Munoz, J.L.; Kurlyandskaya, G.; Vasquez, M.; Ali, M.; Gibbs, M.R.J. Induced anisotropy, magnetic domain structure and magnetoimpedance effect in CoFeB amorphous thin films. J. Magn. Magn. Mater. 1999, 191, 339–344. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. MagnetoImpedance in Multilayer films. Sens. Actuators 2000, 81, 71–77. [Google Scholar] [CrossRef]
- Fosalau, C.; Damian, C.; Zet, C. A high performance strain gage based on the stress impedance effect in magnetic amorphous wire. Sens. Actuators A Phys. 2013, 191, 105–110. [Google Scholar] [CrossRef]
- Hashi, S.; Sora, D.; Ishiyama, K. strain and vibration sensor based on inverse magnetostriction of amorphous magnetostrictive films. IEEE Magn. Lett. 2019, 10, 8110604. [Google Scholar] [CrossRef]
- Froemel, J.; Akita, S.; Tanaka, S. Simple Device to Measure Pressure Using the Stress Impedance Effect of Amorphous Soft Magnetic Thin Layer. Micromachines 2020, 11, 649. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhokov, A.P.; Gonzalez, J. Torsional stress impedance and magneto-impedance in (Co0.95Fe0.05)72.5Si12.5B15 amorphous wire with helical induced anisotropy. J. Phys. D Appl. Phys. 1999, 32, 3140–3145. [Google Scholar] [CrossRef]
- Shen, L.P.; Uchimiya, T.; Mohri, K.; Kita, E.; Bushida, K. Sensitive stress-impedance micro sensor using amorphous magnetostrictive wire. IEEE Trans. Magn. 1997, 33, 3355–3357. [Google Scholar] [CrossRef]
- Mohri, K.; Uchimiya, T.; Shen, L.P.; Cai, C.M.; Panina, L.V.; Honkura, Y.; Yamamoto, M. Amorphous wire and CMOS IC-based sensitive micromagnetic sensors utilizing magnetoimpedance (MI) and stress-impedance (SI) effects. IEEE Trans. Magn. 2002, 38, 3063–3068. [Google Scholar] [CrossRef]
- Tejedor, M.; Hernando, B.; Sanchez, M.; Prida, V.; Vasquez, M. Magneto-impedance effect in amorphous ribbons for stress sensor applications. Sens. Actuators A Phys. 2000, 81, 98–101. [Google Scholar] [CrossRef]
- Garcia-Arribas, A.; Combarro, L.; Goiriena-Goikoetxea, M.; Kurlyandskaya, G.V.; Svalov, A.V.; Fernandez, E.; Orue, L.; Feuchtwanger, J. Thin-film Magnetoimpedance Structures onto Flexible Substrates as Deformation Sensors. IEEE Trans. Magn. 2017, 53, 2000605. [Google Scholar] [CrossRef]
- Suwa, Y.; Agatsuma, S.; Hashi, S.; Ishiyama, K. Study on impedance change of strain sensor using magnetostrictive film. J. Magn. Soc. Jpn. 2010, 34, 342–346. [Google Scholar] [CrossRef]
- Chen, J.A.; Ding, W.; Zhou, Y.; Cao, Y.; Zhou, Z.M.; Zhang, Z.M. Stress-Impedance effects in sandwiched FeCuNbCrSiB/Cu/FeCuNbCrSiB films. Mater. Lett. 2006, 60, 2554–2557. [Google Scholar] [CrossRef]
- Vincent; Rodriguez, M.; Leong, Z.; Morley, N.A. Design and Development of Magnetostrictive Actuators and Sensors for Structural Health Monitoring. Sensors 2020, 20, 711. [Google Scholar] [CrossRef] [PubMed]
- Froemel, J.; Diguet, G.; Muroyama, M. Micromechanical Force Sensor Using the Stress–Impedance Effect of Soft Magnetic FeCuNbSiB. Sensors 2021, 21, 7578. [Google Scholar] [CrossRef]
- Kurita, H.; Diguet, G.; Froemel, J.; Narita, F. Stress sensor performance of sputtering Fe-Si-B alloy thin coating under tensile and bending loads. Sens. Actuators A Phys. 2022, 343, 113652. [Google Scholar] [CrossRef]
- Usov, N.A.; Antonov, N.A.; Lagar’kov, A.N. Theory of giant magneto-impedance effect in amorphous wires with different types of magnetic anisotropy. J. Magn. Magn. Mater. 1998, 185, 159–173. [Google Scholar] [CrossRef]
- Machado, F.L.A.; Rezende, S.M. A theoretical model for the giant magnetoimpendace in ribbons of amorphous soft-ferromagnetic alloys. J. Appl. Phys. 1996, 79, 6558. [Google Scholar] [CrossRef]
- Jin, F.; Li, J.; Zhou, L.; Peng, J.; Chen, H. Simulation of Giant Magnetic Impedance effect in Co-based Amorphous films with demagnetizing field. IEEE Trans. Magn. 2015, 51, 7100404. [Google Scholar] [CrossRef]
- Chen, H.; Britel, M.R.; Zhukova, V.; Zhukov, A.; Dominguez, L.; Chizik, A.B.; Blanco, J.M.; Gonzalez, J. Influence of AC magnetic field amplitude on the surface magnetoimpedance tensor in amorphous wire with helical magnetic anisotropy. IEEE Trans. Magn. 2004, 40, 3368–3377. [Google Scholar] [CrossRef]
- Kraus, L. Theory of giant magneto-impedance in the planar conductor with uniaxial magnetic anisotropy. J. Magn. Magn. Mater. 1999, 195, 764–778. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, W.L.; Zhang, W.X.; Jiang, H.C.; Yang, S.A. Simulation of stress impedance effect in magnetoelastic films. J. Magn. Magn. Mater. 2005, 288, 326–330. [Google Scholar] [CrossRef]
- Sartorelli, M.L.; Knobel, M. Giant magneto-impedance and its relaxation in Co-Fe-Si-B amorphous ribbons. Appl. Phys. Lett. 1997, 71, 2208. [Google Scholar] [CrossRef]
- Spano, M.L.; Hathaway, K.B.; Savage, H.T. Magnetostriction and magnetic anisotropy of field annealed Metglas 2605 alloys via M-H loop measurements under stress. J. Appl. Phys. 1982, 53, 2667. [Google Scholar] [CrossRef]
- Livingston, J. Magnetomechanical properties of amorphous metals. Phys. Status Solidi A 1982, 70, 591–596. [Google Scholar] [CrossRef]
- He, D.F.; Shiwa, M. A magnetic sensor with amorphous wire. Sensors 2014, 14, 10644–10649. [Google Scholar] [CrossRef]
- Mendoza Zelis, P. Magnetostrictive bimagnetic trilayer ribbons for temperature sensing. J. Appl. Phys. 2006, 101, 034507. [Google Scholar] [CrossRef]
- Shin, K.H.; Inoue, M.; Arai, K.I. Elastically coupled magneto-electric elements with highly magnetostrictive amorphous films and PZT subtrates. Smart Mater. Struct. 2000, 9, 357–361. [Google Scholar] [CrossRef]
- Ludwig, A.; Frommberger, M.; Tewes, M.; Quandt, E. High-frequency magnetoelastic multilayer thin films and applications. IEEE Trans. Magn. 2003, 39, 3062. [Google Scholar] [CrossRef]
- Appino, C.; Fiorillo, F.; Maraner, A. initial susceptibility versus applied stress in amorphous alloys with positive and negative magnetostriction. IEEE Trans. Magn. 1993, 29, 3469–3471. [Google Scholar] [CrossRef]
- Kubo, Y.; Hashi, S.; Yokoi, H.; Arai, K.; Ishiyama, K. Development of strain and vibration sensor using magnetostriction of magnetic thin film. IEEE Trans. Sens. Micromach. 2018, 138, 153–158. (In Japanese) [Google Scholar] [CrossRef]
- Ding, Q.; Li, J.; Zhang, R.; He, A.; Dong, Y.; Sun, Y.; Zheng, J.; Li, X.; Liu, X. Effect of transverse magnetic field annealing on the magnetic properties and microstructure of FeSiBNbCuP nanocrystalline alloys. J. Magn. Magn. Mater. 2022, 560, 169628. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Magnetic anisotropy. In Introduction to Magnetic Materials, 2nd ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).