Definition
This entry examines Lorenz’s error growth models with quadratic and cubic hypotheses, highlighting their mathematical connections to the non-dissipative Lorenz 1963 model. The quadratic error growth model is the logistic ordinary differential equation (ODE) with a quadratic nonlinear term, while the cubic model is derived by replacing the quadratic term with a cubic one. A variable transformation shows that the cubic model can be converted to the same form as the logistic ODE. The relationship between the continuous logistic ODE and its discrete version, the logistic map, illustrates chaotic behaviors, demonstrating computational chaos with large time steps. A variant of the logistic ODE is proposed to show how finite predictability horizons can be determined, emphasizing the continuous dependence on initial conditions (CDIC) related to stable and unstable asymptotic values. This review also presents the mathematical relationship between the logistic ODE and the non-dissipative Lorenz 1963 model.
1. Introduction
The study offers a concise overview of the mathematical framework for Lorenz error growth models (Lorenz 1969a [1]) and their connections to other relevant systems (e.g., the non-dissipative Lorenz model, Shen 2018, 2020 [2,3]). In the 1960s, Lorenz utilized the first-order ordinary differential equations (ODEs) incorporating quadratic or cubic nonlinear terms to study root mean square (RMS) errors, aiding in the estimation of doubling times and thus predictability horizons (Lorenz 1969a, b [1,4]; Shen et al., 2024 [5]). The model with the quadratic term is commonly referred to as the logistic ODE. In contrast, the error growth model with a cubic term can be transformed into the logistic ODE (with a quadratic term). It is important to distinguish this error growth model from Lorenz’s widely recognized 1969 multiscale model in meteorology (Lorenz 1969c [6]; Shen et al., 2024 [5]).
Since the 1960s, the logistic ODE, the continuous form of the logistic equation, has been extensively used to assess RMS forecast errors in ensemble forecasts (e.g., Lorenz 1969a, 1982, 1996 [1,7,8]; Nicolis 1992 [9]; Kalnay 2003 [10]; Zhang et al. 2019 [11]). Historically, the logistic ODE has also been used to analyze population growth, assuming that the growth rate of a population is proportional to both the existing population and the available resources (represented by the growth rate in Equation (1)). The logistic ODE-based model offers a more realistic portrayal of population growth compared to simple exponential models. This model has also been adapted to study the dynamics of recovered individuals during the COVID-19 pandemic (Postnikov, 2020 [12]; Paxson and Shen 2022 [13]).
The logistic map, a discrete form of the logistic equation, stands as the most straightforward model for demonstrating chaos, as recognized in the works of Lorenz (1964, 1969d) [14,15], May (1976) [16], and Li and Yorke (1975) [17]. This map exhibits both periodic and chaotic behaviors, heavily influenced by a system parameter that acts as a forcing term. Initially introduced by Lorenz in 1964, the map was used to describe the transition from regular to irregular solutions in dynamic systems. Robert May (1976) [16] utilized this map to investigate population dynamics in biological contexts, while Li and Yorke (1975) [17] employed it to demonstrate the concept of “Period Three Implies Chaos”, where the term “chaos” was initially introduced to describe irregular solutions. Consequently, the logistic map has become an influential tool in studying chaos and complexity within dynamical systems and was recognized by Stewart (2013) [18] as one of the 17 equations that changed the world.
This article explores both the continuous and discrete versions of the logistic equation, providing a mathematical perspective on Lorenz models. It highlights a crucial, yet often overlooked, aspect of continuous dependence on initial conditions (CDIC). This concept is demonstrated by showing how the predictability horizon, as derived from the logistic ODE, can be extended progressively by refining the initial conditions. The structure of the study is as follows: After presenting the equations for the Logistic ODE, this entry analyzes its error growth rates and its linkage to the Logistic map. The Logistic ODE and map are employed to illustrate CDIC and irregular solutions, respectively. This entry also explores the connection between the logistic ODE and the non-dissipative Lorenz model (Lorenz 1963 [19]; Shen 2020, 2023 [3,20]), and finally discusses the finite predictability horizons in a variant of the logistic ODE. Concluding remarks are presented at the end.
2. Lorenz’s Equations
This section initially presents the equations for Lorenz’s error growth models and analyze both nonlinear and linear relative growth rates. This section proceeds to discuss the CDIC within the logistic ODE and showcase chaotic solutions using the logistic map. Furthermore, this section derives relationships between the logistic ODE and the non-dissipative Lorenz model and evaluate the solutions of a variant of the logistic ODE aimed at establishing a finite predictability horizon.
2.1. Lorenz’s Error Growth Models
Here, this subsection provides a brief summary of Lorenz’s error growth models proposed in 1969 (Lorenz 1969a [1] ). The first and most popular of these models is a first-order ODE featuring a linear term and a quadratic term, presented as follows:
Traditionally, the dependent variable u represents the root mean square (RMS) difference or errors (Lorenz 1982 [7]). The above equation is indeed the logistic ODE. Give the initial condition (IC) , the corresponding solution to Equation (1) is:
which is known as the S-shaped sigmoid function. Figure 1 displays the sigmoid function. To facilitate discussions, and are used.
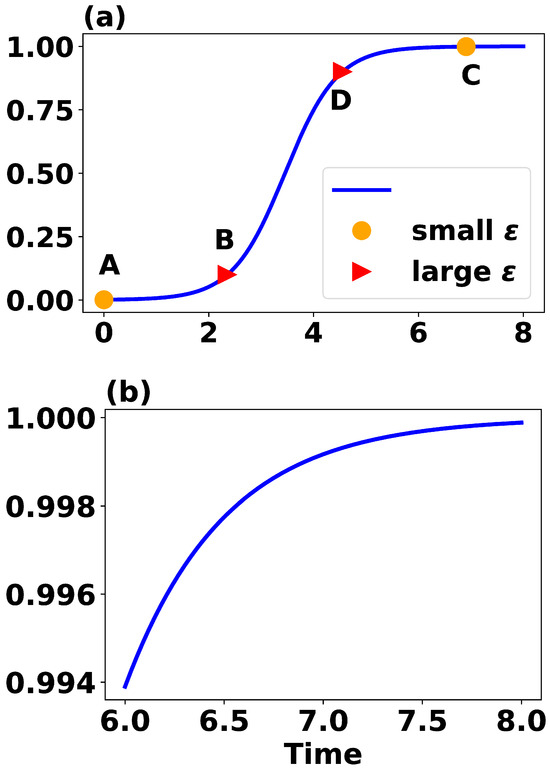
Figure 1.
The solution of u to the logistic ODE in Equation (1). (a) Four points, A, B, C, and D, indicate locations for the values of u = 0.001, 0.1, 0.9, and 0.999, respectively. (b) The bottom panel indicates that it requires more than 4 time units for u to increase from 0.994 to 1.
By comparison, the second of Lorenz’s error growth models incorporates a cubic term, instead of a quadratic term, which can be expressed as follows:
A major difference between Equations (1) and (3) is that the number of critical points is different. Their discrete versions (i.e., quadratic and cubic maps) may produce different results, which is beyond the scope of this study (Shen et al., 2023 [21]). However, by choosing
it can be shown that Equation (3) can be transformed into the same form as Equation (1). This analysis indicates the mathematical relationship between the error growth models with quadratic and cubic hypotheses. However, a direct comparison of Equations (1) and (3) indicates the same saturated value but different initial relative growth rates. If one would like to have the same initial relative growth rate for both the quadratic and cubic hypotheses, two different saturated values should be used. Below, this report focuses on the analysis of the logistic ODE, its solutions, linear and nonlinear growth rates, and its relationship to the logistic map and the non-dissipative Lorenz 1963 model.
2.2. Nonlinear and Linear Relative Growth Rates
Predictability horizons have been a key area of study in real-world weather and climate forecasts and nonlinear chaotic dynamics. Common methods for assessing predictability horizons include (1) analyzing growth rates, (2) performing stability analysis of critical points, and (3) calculating Lyapunov exponents (e.g., Shen 2014, 2019 [22,23]), which indicate the long-term average rate of divergence among nearby trajectories. Here, leveraging its analytical solution, differences between nonlinear and linear growth rates and discuss their connections to Lyapunov exponents are illustrated. The growth rate from Equation (1) can be computed as follows:
The left hand side of Equation (5) defines a relative growth rate. By substituting the analytical solution of Equation (2) into the right-hand side of Equation (5), the temporal evolution of growth rates is depicted in Figure 2a. Here, a numerical solution of growth rates using a finite difference method is also provided for comparison. Both analytical and numerical calculations show good agreement.
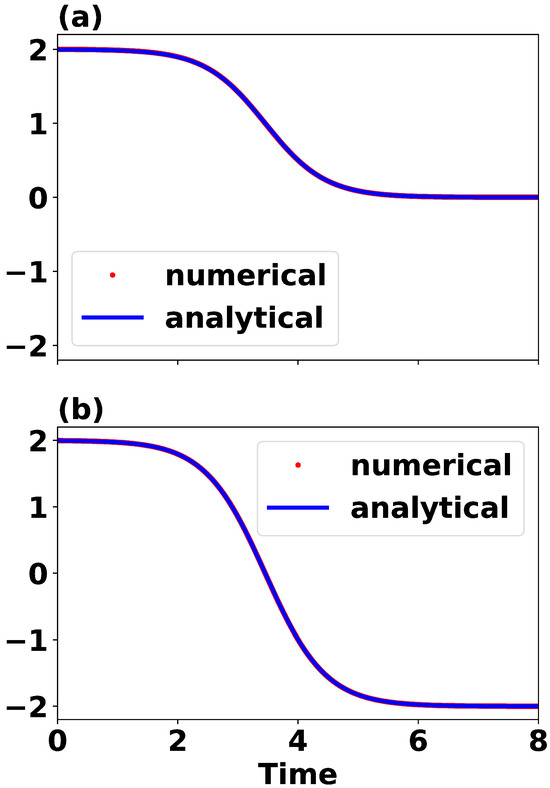
Figure 2.
(a) Nonlinear and (b) linear growth rates of the solution to the logistic ODE.
Starting from small positive initial values, the evolution of growth rates unfolds through three distinct phases:
- (1)
- An initial linear increase driven by the equation’s linear term;
- (2)
- A reduction in growth rate moderated by the equation’s nonlinear component as the error expands; and
- (3)
- A leveling off at a constant error level.
These stages—linear increase, moderated growth, and saturation—are consistently observed in various real-world and idealized models (e.g., Shen 2020 [3]). Both initial growth rates (e.g., doubling times) and saturated RMS errors are utilized to determine predictability horizons (e.g., Lorenz 1969a [1]; Zhang et al., 2019 [11]). The results are referred to as nonlinear growth rates.
Below, to contrast with the nonlinear growth rates, this report presents the linear growth rates. Initially, the variation equation is written as follows:
which describes how perturbations evolve along a trajectory. The above equation leads to the following expression for the linear growth rate:
Similar to the method used for calculating nonlinear growth rates, by inserting the analytical solution from Equation (2) into the right-hand side of Equation (7), this entry displays the temporal evolution of linear growth rates in Figure 2b. Here, results display a transition from an unstable point with local, positive, nearly constant growth rates to a stable point with local, negative, nearly constant growth rates (Paxson and Shen 2022 [13]). The observed dynamics, characterized by what is known as heteroclinic behavior (e.g., Balmforth, 1995 [24]), align with the stability analysis of the two critical points at and . As discussed below in the context of the relationship between the logistic ODE and the non-dissipative Lorenz model, this characteristic is indeed associated with a homoclinic orbit that connects unstable and stable manifolds within a two-dimensional phase space.
The linear growth rates discussed above are compared by calculations using two nearby trajectories. From the analytical solution in Equation (2), this study computes two solutions, designated as control and parallel runs:
subject to the initial conditions and , respectively. Hence, the parallel run represents the solution to the system with a tiny initial perturbation () from the control run. Therefore, the growth rates can be computed using the following formula:
As shown in Figure 2b, these numerical results align with those obtained using the variation equation in Equation (7), confirming that Equation (7) accurately represents the local divergence rate of two nearby trajectories. Consequently, the long-term average of the linear growth rates is negative, consistent with the calculation of the Lyapunov exponent.
This section discusses both nonlinear and linear growth rates within the logistic ODE framework. Initially, their time evolutions are similar during the linear phase, yet differ during the nonlinear phase. A thorough analysis comparing these two types of growth rates and their impact on predictability estimates is outside the scope of this report. Readers interested in this subject may refer to the works of Chen et al. (2006) [25], Ding and Li (2007) [26], and Ding et al. (2017) [27].
2.3. The Logistic ODE and Continuous Dependence on ICs (CDIC)
A chaotic system is characterized by two key features: one or more positive (global) Lyapunov exponents (LE) and solution boundedness. The global Lyapunov exponent represents the long-term average of local growth rates. Upon calculating an initial growth rate (for a linear system) and the Lyapunov exponent (for a nonlinear system), predictability horizons can be estimated using the following ODE:
In this equation, X denotes error, and represents either the initial color red relative growth rate or LE.
As illustrated in Strogatz (2015) [28] on page 330, the formula for estimating predictability is expressed as:
where denotes the deviation between two initially nearby trajectories, is the initial discrepancy, and is the Lyapunov exponent. This is a solution to Equation (11). Assuming as the threshold beyond which predictions are deemed unreliable, the time scale of predictability () is effectively inverse to the Lyapunov exponent:
However, global, finite-time, and local Lyapunov exponents exhibit differences, which have been extensively explored in our papers since 2011 (e.g., Shen 2014, 2019 [21,22]). As emphasized by Shen et al. (2021) [29] and supported by other references, a global positive exponent may correlate with time-varying local Lyapunov exponents (i.e., time-varying local growth rates), indicating the dependence of distinct predictability limits on initial conditions (Slingo and Palmer 2011 [30]; Nese 1989 [31]; Zeng et al., 1993 [32]). As a result, while the presence of a global Lyapunov exponent may suggest finite predictability in chaotic systems, its averaged properties cannot effectively establish an upper bound on predictability.
As a result, since Equation (11) with does not account for time-varying growth rates (i.e., sensitive dependence of solutions on initial condition, SDIC), results produced by the system should be interpreted with caution. This interpretation is supported by personal communication via emails with Prof. Strogatz on 3 February 2022 [33].
It is important to note that the above solution (and its corresponding ODE, Equation (11)) includes an unstable asymptotic value at , meaning when . As discussed in Section 2.6, this characteristic suggests a continuous increase in the predictability horizon by reducing initial errors. Therefore, the validity of Equation (11) in demonstrating finite predictability is questionable.
Although an in-depth discussion of the above method for chaotic systems exceeds the scope of this study, our focus remains on the application of the logistic ODE to estimate predictability horizons.
The solution to the logistic equation is an S-shaped sigmoid function. The zero state (backward in time) and saturation value (forward in time) are only asymptotically reachable. Such a feature suggests that predictability horizons can be extended continuously by reducing initial errors or applying larger thresholds. A simple illustration is provided here.
In Figure 1, four points, A, B, C, and D, indicate locations for the values of 0.001, 0.1, 0.9, and 0.999, respectively. Points A and B can be considered as initial conditions for errors, while points C and D may serve as upper thresholds. Consequently, the time span between an initial value and a threshold defines a predictability horizon.
Given the same initial error at point A (or B), the durations to reach points C and D vary, illustrating how predictability horizons depend on chosen thresholds. Conversely, with the same threshold at point C (or D), the intervals from A to C and from B to C are different, indicating that predictability horizons also depend on the magnitude of the initial conditions. This characteristic relates to the continuous dependence of solutions on the initial condition (CDIC). Therefore, in scenarios using either Equation (1) or the simplified ODE in Equation (11), the CDIC feature implies that predictability horizons may be incrementally extended through continual refinement of initial conditions.
2.4. The Logistic Map and Chaotic Solutions
While the Logistic ODE generates regular solutions, its discrete counterpart has yielded intriguing outcomes (Lorenz 1964 [14]; May 1976 [16]; Li and Yorke 1975 [17]). The following discussions explore the relationship between the continuous and discrete versions. By employing a forward finite difference scheme, one can transform Equation (1) into:
yielding:
By defining a new variable and a new parameter
Equation (13) becomes:
which is the logistic map. Table 1 lists both the logistic ODE and logistic map.

Table 1.
Comparative analysis of the logistic ODE, logistic map, and non-dissipative Lorenz model (LM). The text discusses how the first model serves as a basis for deriving the second and third equations.
Figure 3 presents solutions for three different values of 1.8, 2.0, and 2.6 using Equation (13). While the steady-state solution in the first panel is also reflected by the continuous version of the logistic equation, the periodic and irregular solutions observed in the second and third panels are absent from the logistic ODE. The appearance of the periodic solution in the second panel is termed period doubling. As the parameter increases up to 3, period doubling recurs repeatedly. At 2.56994567 (i.e., 3.56994567), the period doublings become infinite, yielding a chaotic solution (Wikipedia: https://en.wikipedia.org/wiki/Logistic_map#Period-doubling_route_to_chaos (accessed on 1 May 2024) ).
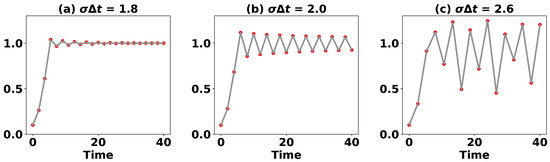
Figure 3.
Solutions of the logistic map in Equation (13). The three panels display a steady-state, periodic, and irregular solution, respectively.
2.5. The Logistic ODE and the Non-Dissipative Lorenz Model (NLM)
As previously mentioned, the solution to the logistic ODE is the sigmoid function, which starts at zero and approaches a saturated value (namely, the one in this case). By examining the relationship between the sigmoid function and the hyperbolic tangent function, and revealing the derivative of the hyperbolic tangent function as a solitary wave solution, this study explores the derivation of the Z-component of the non-dissipative Lorenz 1963 model from the logistic ODE (Shen 2018; 2020 [2,3]).
Squaring a term on the right-hand side of Equation (1) yields:
The above equation suggests that the introduction of the following new variable
leads to
It can be shown that the solution to the above equation is a hyperbolic tangent function:
Second, based on Equation (18), one can define a variable Z as the derivative of the solution w:
which is a hyperbolic secant squared function. Through straightforward derivations, a second-order ODE for Z can be obtained, as follows:
which can be rewritten as follows:
The above is mathematically identical to the KdV-SIR equation (e.g., Equation (17) of Paxson and Shen 2022 [13]), producing a solitary wave solution with an amplitude maximum of . From Equation (17)b of Paxson and Shen (2022) [13], the solution to Equation (22) is written as follows:
A solitary wave is described by one peak with long tails, indicated by:
Figure 4 displays the solitary wave solution in Equation (23) and its relationship to the hyperbolic tangent and sigmoid functions. The above establishes a connection between the S-shaped solution in the logistic ODE and the solitary/homoclinic solutions within the non-dissipative Lorenz model. Note that the non-dissipative Lorenz model, with additional constants different from the constraint conditions in Equation (24), includes two types of oscillatory solutions and two homoclinic orbits (Shen 2018, 2020 [2,3]). Currently, the study has not made efforts to derive an error growth model for all of the solutions within the non-dissipative Lorenz model.
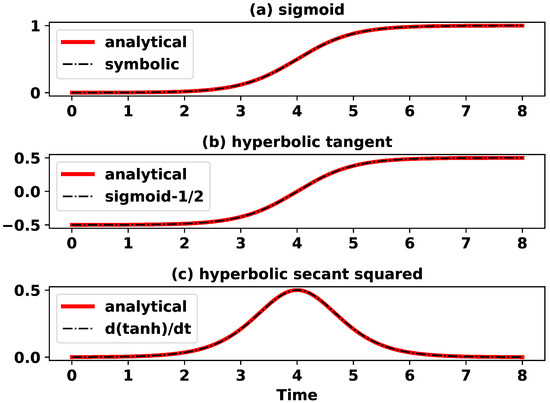
Figure 4.
Panels (a–c) display the sigmoid, hyperbolic tangent, and hyperbolic secant squared functions, respectively, indicating the relationship between the Lorenz error growth model (i.e., the Logistic ODE) and the non-dissipative Lorenz 1963 model. See main texts for details. The solution in panel (a) is = 1/(1 + ((t − 4))) with for a comparison.
In Table 2, various second-order ODEs contain common features, including a second derivative, a linear term, and a quadratic term characterized by two coefficients (such as a and b with ). As these equations involve one independent variable and one dependent variable, systems with such coefficient pairings can be transformed to become equivalent. As a result, Equation (22) is precisely equivalent to the Z-component of the non-dissipative Lorenz 1963 model. It is observed that the X-component of the non-dissipative Lorenz 1963 model, which includes a cubic term, is mathematically identical to the inviscid Pedlosky model (Pedlosky 1971 [34]). By introducing a new variable Q (where ), the inviscid Pedlosky model can be transformed to match the form of Equation (21). Table 1 provides a summary of the logistic ODE, logistic map, and the non-dissipative Lorenz 1963 model.

Table 2.
A nonlinear second-order ODE representing four different physical solutions. This ODE appears as the Korteweg-de Vries (KdV) equation in the traveling wave coordinate, the non-dissipative Lorenz 1963 [19] (L63) model, the KdV-SIR equation, and the inviscid Pedlosky model. It is used to study solitary waves, homoclinic orbits, epidemic waves, and nonlinear baroclinic waves, respectively. For the inviscid Pedlosky model, which is mathematically identical to the X component of the non-dissipative L63 model (e.g., Shen 2021 [35]), the second order ODE of a new variable Q () is the same as the Z component of the non-dissipative L63 model. is a constant. (Table reproduced from Paxson and Shen (2022) [13]. With permission from copyright owner International Journal of Bifurcation and Chaos).
2.6. A Variant of the Logistic ODE for a Finite Predictability Horizon
From the original logistic ODE in Equation (1), two critical points at and indicate two asymptotic values: an unstable asymptotic value at and a stable asymptotic value at . As a result of the asymptotic features, approaching the zero value (backward in time) and the saturated value (forward in time), it is evident that the predictability horizon can be continuously extended by reducing the initial errors or adjusting the thresholds. Thus, how can one construct an error growth model to reveal a finite interval between the initial errors and the thresholds? To do so, both values must be chosen differently from the asymptotic values. For example, from Figure 1, a threshold value of 0.6 can be selected, which is away from the stable asymptotic value of 1. Additionally, as shown in Figure 4, the unstable asymptotic value can be shifted to a negative value, ensuring that zero error occurs at a finite time. This concept is further discussed below.
Consider the following ODE (Dalcher and Kalnay, 1987 [36]; Kalnay 2003) [10]:
subject to the initial condition
where , b, and are constants. Relative to Equation (1), Equation (25) introduces an additional parameter b, which is essential for establishing a finite predictability horizon, as detailed below. As discussed below, the above ODE introduces a new term b that not only changes growth rates but also shifts the unstable asymptotic value to become negative.
The solution to the above ODE and initial condition is written as follows:
where
The solution possesses the following features:
- (1)
- When , . This is a stable asymptotic value.
- (2)
- When , . This represents an unstable asymptotic value, which is less than zero.
- (3)
- When , . This solution is the same as Equation (2) within the original logistic ODE.
These results are also consistent with the critical point analysis, showing critical points at and . Based on the discussion for the logistic ODE in Section 2.2, the variation equation for the revised logistic ODE indicates local growth rate of and near the critical points and , respectively.
The above results are also presented in Figure 5 under the initial condition . Figure 5a shows solutions for three different values of b: , , and . The solution with closely aligns with the solution in Equation (2). From the figure and the solution in Equation (27), the parameter affects growth rates. Additionally, the parameter b alters the unstable asymptotic value. Consequently, the time intervals between the initial value and vary, with larger values of b resulting in shorter time intervals (Figure 5b). This indicates that the revised logistic ODE in Equation (25) with a non-zero b can effectively illustrate the finite time interval.
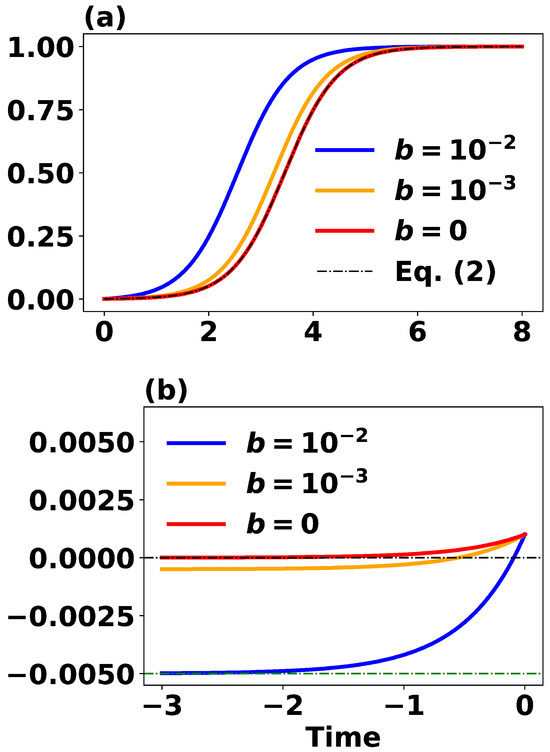
Figure 5.
Solutions of the modified logistic ODE in Equation (25) with an additional parameter b under the initial condition . (a) Solutions for three different values of b. The solution with closely matches the solution of the original logistic ODE in Equation (2). (b) Time intervals between the initial value and for three solutions curves, used for illustrating the impact by continuously reducing the initial error to . The value signifies the error inherent in the current technology, while represents the error in an ideal scenario.
3. Concluding Remarks
This report offers a concise mathematical analysis of Lorenz’s error growth models (Lorenz 1969a) [1] and their connection to the non-dissipative Lorenz 1963 model (Lorenz 1963 [19]; Shen 2018 [2]). Each of the error growth models, comprising first-order ordinary differential equations (ODEs) with either quadratic or cubic nonlinearities, demonstrates fundamental mathematical links: the first model is indeed the logistic ODE, while the second can be reformulated into the first, illustrating a mathematical relationship. However, a direct comparison of Equations (1) and (3) indicates different initial relative growth rates. Therefore, to maintain the same initial relative growth rate for both the quadratic and cubic hypotheses, one must use two different saturated values. The classical logistic ODE and related variants have been utilized to characterize errors in advanced numerical weather prediction models. Our findings suggest that predictability horizons are influenced by the scale of initial errors, defined thresholds, and system parameters such as b in Equation (25). In fact, the introduction of parameter b, compared to the original logistic equation, effectively determines a finite predictability horizon.
The empirical nature of these error growth models presents challenges in establishing mathematical and physical consistency with real-world data. Lorenz himself acknowledged in 1982 that the inclusion of the nonlinear quadratic term in the error growth model is reasonable, but not readily verifiable (Lorenz 1982 [7]). Over the past decades, significant efforts have continued to justify this nonlinear quadratic term (e.g., Nicolis 1992 [9]; Shen 2020 [3]). This study first reiterated the connections among the sigmoid, hyperbolic tangent, and hyperbolic secant squared functions, and progressively provided the links between the logistic ODE and the non-dissipative Lorenz 1963 model. While both are idealized, the Lorenz 1963 model is fundamentally derived from the Rayleigh Benard convection partial differential equations. To the best of our knowledge, this is the first attempt to integrate Lorenz’s error growth model with his 1963 model.
The logistic map is recognized as one of the simplest equations for demonstrating chaos, with its effectiveness in modeling irregular behaviors validated over many years (e.g., Lorenz 1964, 1969d [14,15]; May 1976 [16]; Li and Yorke 1975 [17]). This report, by comparing the logistic ODE and logistic map, suggests that the irregular responses observed in the logistic map can be interpreted as computational chaos manifesting in the logistic ODE under large integration time steps (Lorenz 1989) [37].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Python code available upon request.
Acknowledgments
The author thanks students of Math340 for valuable feedback.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef]
- Shen, B.-W. On periodic solutions in the non-dissipative Lorenz model: The role of the nonlinear feedback loop. Tellus A 2018, 70, 1471912. [Google Scholar] [CrossRef]
- Shen, B.-W. Homoclinic Orbits and Solitary Waves within the non-dissipative Lorenz Model and KdV Equation. Int. J. Bifurc. Chaos 2020, 30, 2050257. [Google Scholar] [CrossRef]
- Lorenz, E.N. Studies of Atmospheric Predictability. [Part 1] [Part 2] [Part 3] [Part 4] Final Report, February, Statistical Forecasting Project; Air Force Research Laboratories, Office of Aerospace Research, USAF: Bedford, MA, USA, 1969; p. 145. [Google Scholar]
- Shen, B.-W.; Pielke, R.A.; Zeng, X. Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz’s Predictability Studies in the 1960s. Atmosphere, 2024; in press. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric predictability experiments with a large numerical model. Tellus 1982, 34, 505–513. [Google Scholar] [CrossRef]
- Lorenz, E.N. Predictability—A problem Partly Solved. In Proceedings of the Seminar on Predictability, Reading, UK, 4–8 September 1995; ECMWF: Reading, UK, 1996; Volume 1. [Google Scholar]
- Nicolis, C. Probabilistic aspects of error growth in atmospheric dynamics. Q. J. R. Meteorol. Soc. 1992, 118, 553–568. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge: New York, NY, USA, 2003; p. 369. [Google Scholar]
- Zhang, F.; Sun, Y.Q.; Magnusson, L.; Buizza, R.; Lin, S.-J.; Chen, J.-H.; Emanuel, K. What is the predictability limit of midlatitude weather? J. Atmos. 2019, 76, 1077–1091. [Google Scholar] [CrossRef]
- Postnikov, E.B. Estimation of COVID-19 dynamics “on a back-of-envelope”: Does the simplest SIR model provide quantitative parameters and predictions? Chaos Solitons Fractals 2020, 135, 109841. [Google Scholar] [CrossRef]
- Paxson, W.; Shen, B.-W. A KdV-SIR Equation and Its Analytical Solutions for Solitary Epidemic Waves. Int. J. Bifurc. Chaos 2022, 32, 13. [Google Scholar] [CrossRef]
- Lorenz, E.N. The problem of deducing the climate from the governing equations. Tellus 1964, 16, 1–11. [Google Scholar] [CrossRef]
- Lorenz, E.N. How much better can weather prediction become? MIT Technol. Rev. 1969, 1969, 39–49. [Google Scholar]
- May, R.M. Simple Mathematical Models with very Complicated Dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Li, T.-Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Stewart, I. Seventeen Equations That Changed the World; Profile Book: London, UK, 2013; p. 342. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Shen, B.-W. A Review of Lorenz’s Models from 1960 to 2008. Int. J. Bifurc. Chaos 2023, 33, 2330024. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A.; Zeng, X. 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Special Issue on Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere 2023, 14, 1279. [Google Scholar] [CrossRef]
- Shen, B.-W. Nonlinear feedback in a five-dimensional Lorenz model. J. Atmos. Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Shen, B.-W. Aggregated negative feedback in a generalized Lorenz model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef]
- Balmforth, N.J. Solitary waves and homoclinic orbits. Annu. Rev. Fluid Mech. 1995, 27, 335–373. [Google Scholar] [CrossRef]
- Chen, B.; Li, J.; Ding, R. Nonlinear local Lyapunov exponent and atmospheric predictability research. Sci. China Ser. Earth Sci. 2006, 49, 1111–1120. [Google Scholar] [CrossRef]
- Ding, R.; Li, J. Nonlinear finite-time Lyapunov exponent and predictability. Phys. Lett. 2007, 364, 396–400. [Google Scholar] [CrossRef]
- Ding, R.; Li, J.; Li, B. Determining the spectrum of the nonlinear local Lyapunov exponents in a multidimensional chaotic system. Adv. Atmos. Sci. 2017, 34, 1027–1034. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos. With Applications to Physics, Biology, Chemistry, and Engineering. Westpress View; CRC Press: Boulder, CO, USA, 2015; p. 513. [Google Scholar]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is weather chaotic? coexistence of chaos and order within a generalized Lorenz model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. [Google Scholar] [CrossRef]
- Slingo, J.; Palmer, T. Uncertainty in weather and climate prediction. Philos. Trans. R. Soc. 2011, 369A, 4751–4767. [Google Scholar] [CrossRef] [PubMed]
- Nese, J.M. Quantifying local predictability in phase space. Physica D 1989, 35, 237–250. [Google Scholar] [CrossRef]
- Zeng, X.; Pielke, R.A.; Eykholt, R. Chaos theory and its applications to the atmosphere. Bull. Am. Meteor. Soc. 1993, 74, 631–644. [Google Scholar] [CrossRef]
- Shen, B.-W. (San Diego State University, San Diego, CA, USA); Strogatz, S. (Cornell University, Ithaca, NY, USA). Personal communication, 2022.
- Pedlosky, J. Finite-amplitude baroclinic waves with small dissipation. J. Atmos. Sci. 1971, 28, 587–597. [Google Scholar] [CrossRef]
- Shen, B.-W. Solitary Waves, Homoclinic Orbits, and Nonlinear Oscillations within the non-dissipative Lorenz Model, the inviscid Pedlosky Model, and the KdV Equation. In Springer Proceedings in Complexity, Proceedings of the 13th Chaos International Conference CHAOS 2020, Florence, Italy, 9–12 June 2020; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Dalcher, A.; Kalnay, E. Error growth and predictability in operational ECMWF forecasts. Tellus 1987, 39A, 474491. [Google Scholar]
- Lorenz, E.N. Computational chaos: A prelude to computational instability. Physica 1989, 35D, 299–317. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).