Complexities of Lighting Measurement and Calculation
Abstract
1. Introduction
2. From Candlelight to Candela
3. Photometry Instruments
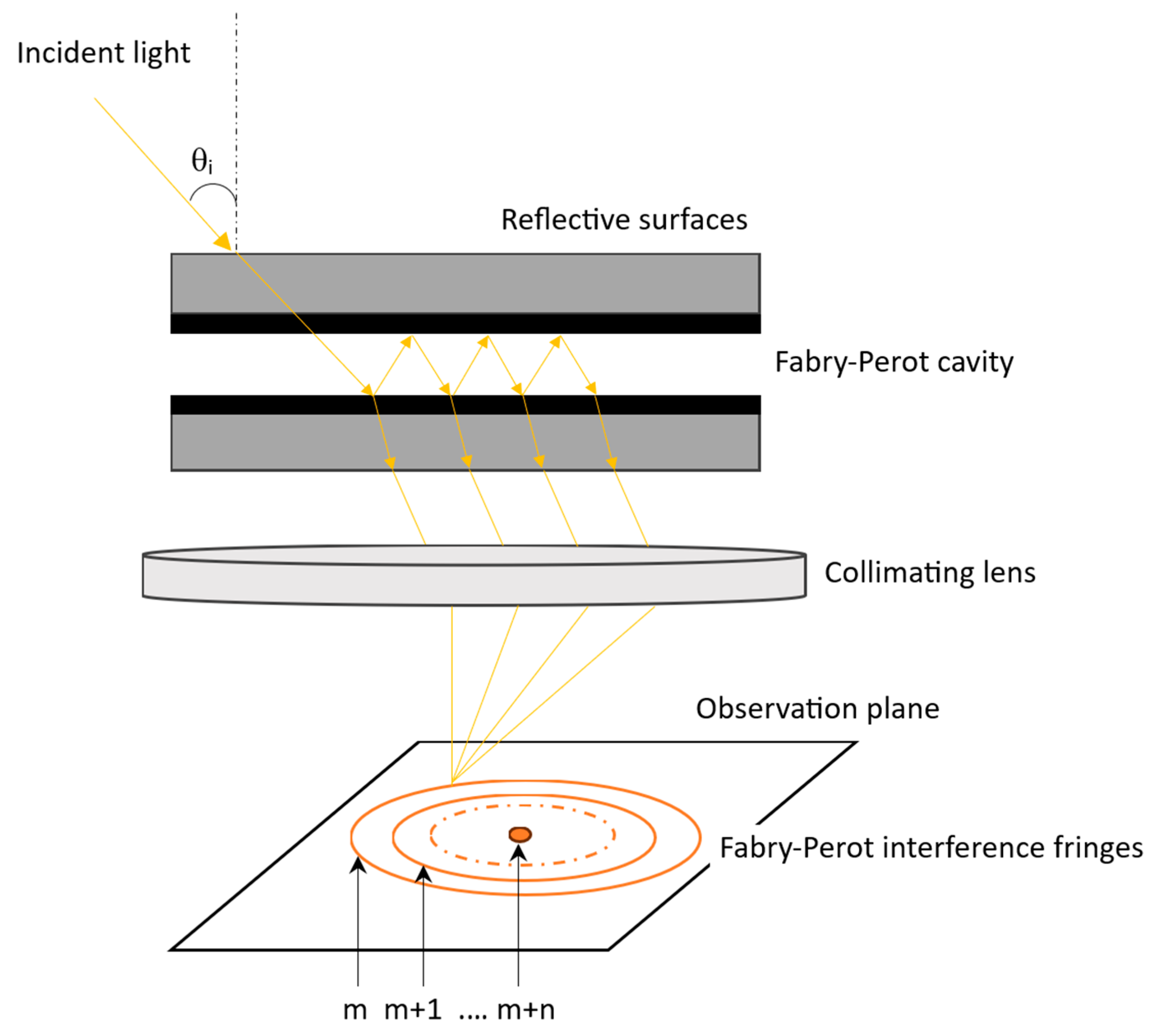
3.1. Etalons in Light Measurement
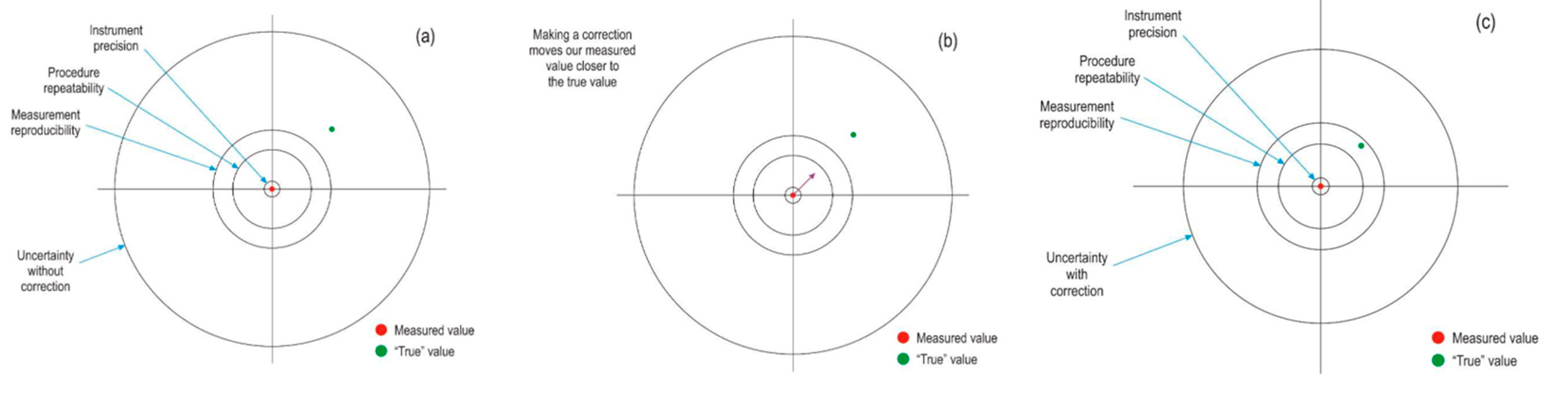
3.2. Instruments for Quantitative and Qualitative Lighting Analysis
4. Radiometric, Photometric, and Quantum Parameters
4.1. Radiometric Units
4.2. Photometric Units
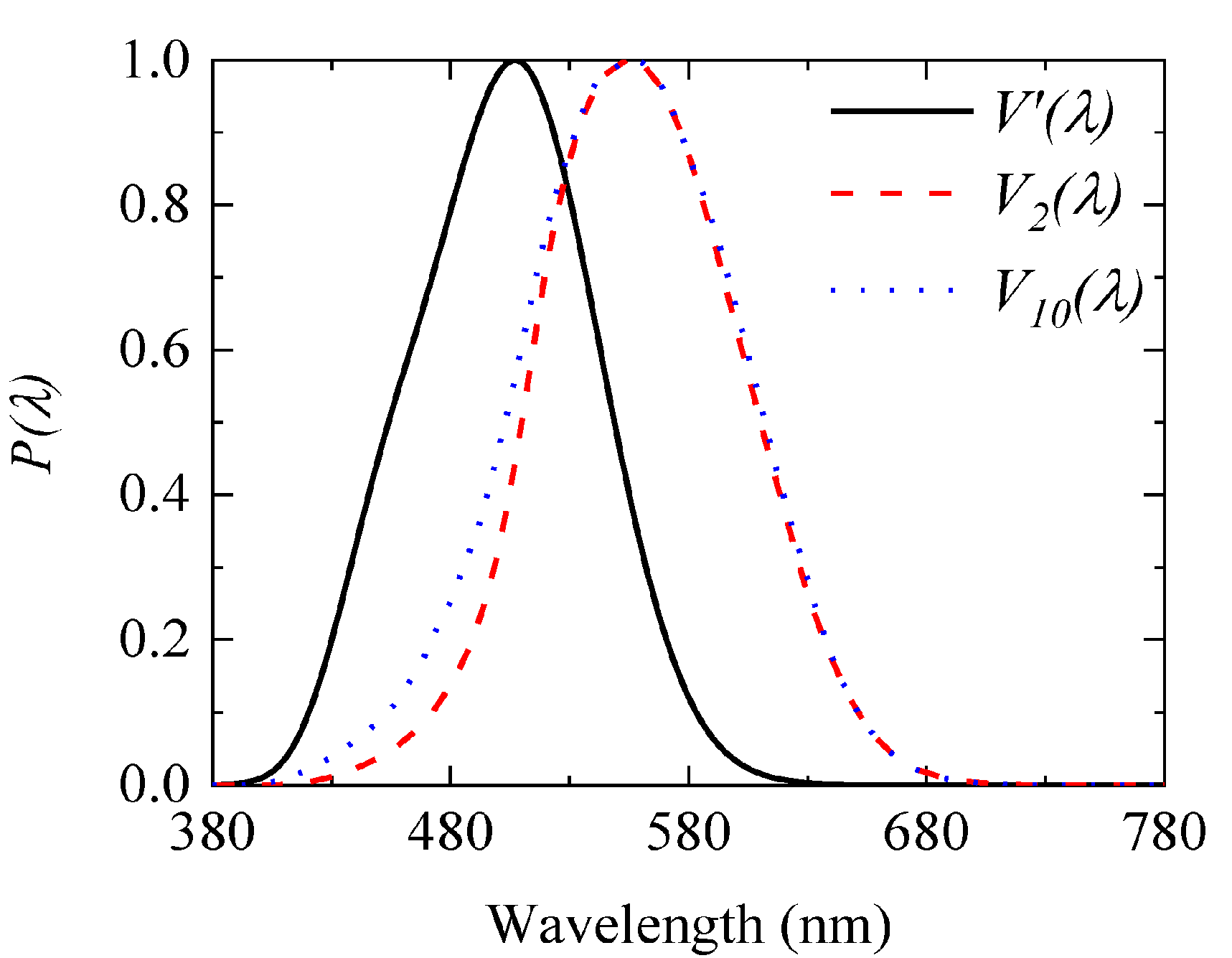
- V(λ) is the relative spectral luminous efficacy function (defined by the CIE spectral sensitivity function), which has a maximum value of 1 corresponding to the wavelength of 555 nm for daylight (photopic) vision and to 507 nm for night (scotopic) vision, V′(λ)—Figure 4. The values of V(λ) for visible wavelengths were statistically established by CIE (International Commission on Illumination) for the average eye, first for a standard photometric observer with a viewing angle of 2 degrees (in 1932), then for a 10-degree observer (1964). Lighting researchers and practitioners prefer to use the original CIE spectral luminous efficacy function V2(λ) (2-degree standard observer) [48], because it describes the cone vision within the fovea (cones being the color receptors of the eye and having the fastest response kinetics to altered lighting—20 ms [49]). For calculation, reference values of V(λ), V′(λ) and conversion factors are given in Table 5.
- Km is the maximum luminous efficacy of radiation, equal to 683 lm/W for photopic vision (at 555 nm) and 1700 lm/W for scotopic vision (at 507 nm). However, the difference between these two values of Km does not reflect the relative magnitude of the luminous response (or perceived brightness) for the two types of vision. As seen from Table 5, they only reflect the definition of light levels and the normalization convention of the two functions at the peak wavelengths. This standard value of 683 lm/W for the maximum luminous efficacy of radiant power was formally introduced in 1979 during the 16th General Conference on Weights and Measures (see Table 2), when the photometric quantities in the International System of Units (SI) were redefined in terms of physical constants. There marked a key moment in the integration of photometric and radiometric systems, ensuring consistency in the science and engineering of light.
- The use of spectral weighing functions with radiometric quantities.
- The law of arithmetic additivity for photometric quantities.
- The choice and definition of the photometric base unit, including the setting of its magnitude [23].
4.3. Quantum Units
4.4. Example of Conversion from Radiometric to Photometric Quantities
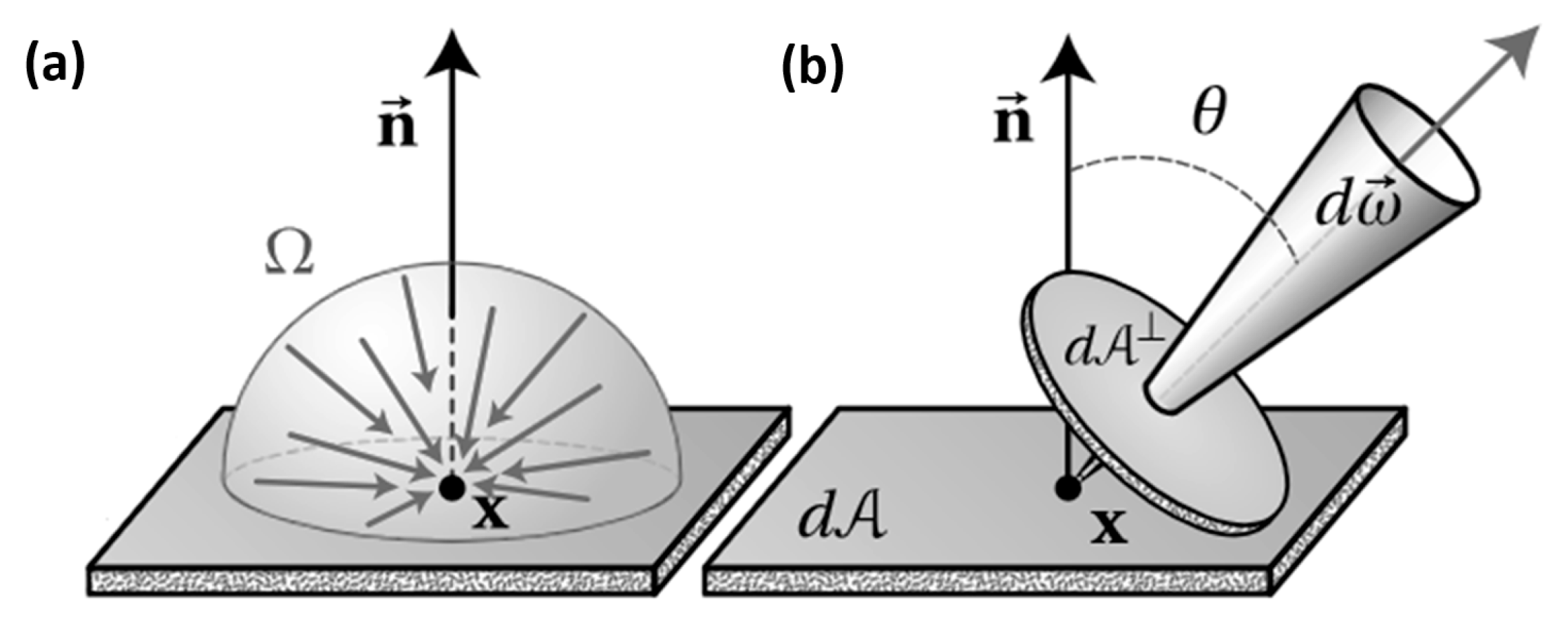
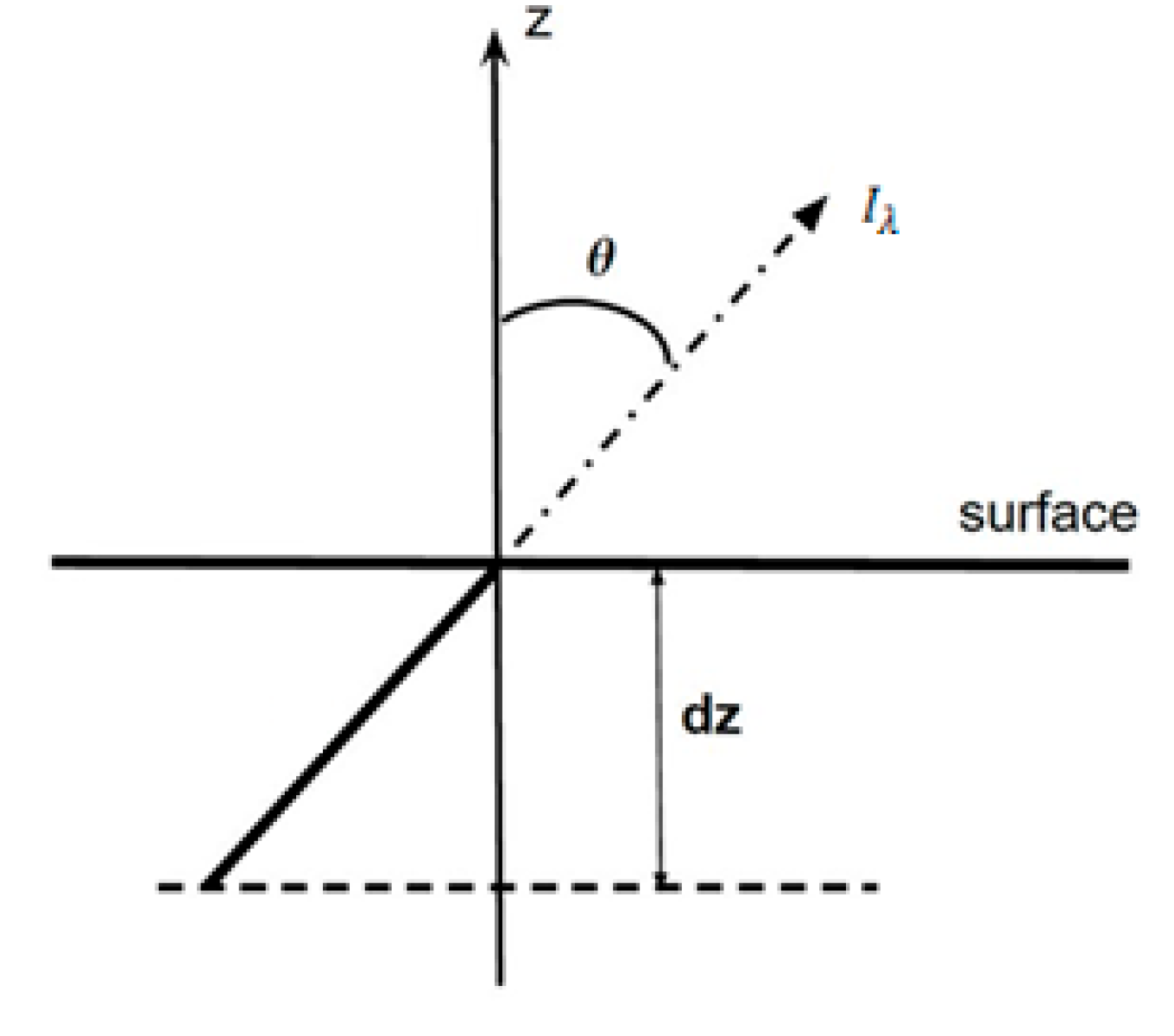
4.5. Radiative Transfer and Light Propagation in Media
5. Actinic Effects of Light
- −
- To assess the effectiveness of lighting on circadian regulation, the melanopic equivalent daylight illuminance (M-EDI) has to be calculated:
- −
- To assess how light affects sleep–wake cycles and overall circadian health, the circadian stimulus (CS) model has to be applied:
- −
- To assess the spectral composition of a light source relative to daylight (widely used in human-centric lighting design), melanopic daylight efficacy ratio has to be calculated:
- −
- To assess the impact of light on the circadian system based on the spectral composition of the light source, melanopic ratio has to be determined:
6. Lighting Audit
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chitu, C.; Dumitran, A.; Manole, C.; Antohe, S. The Light-an integrated approach to the phenomenon. Procedia-Soc. Behav. Sci. 2011, 15, 277–283. [Google Scholar] [CrossRef]
- Khan, S.A. Medieval Arab contributions to optics. Dig. Middle East Stud. 2016, 25, 19–35. [Google Scholar] [CrossRef]
- Dijksterhuis, F.J. Conjunctions in Paris: Interactions Between Rømer and Huygens. Centaurus 2012, 54, 58–76. [Google Scholar] [CrossRef]
- Aldersey-Williams, H. Dutch Light: Christiaan Huygens and the Making of Science in Europe; Pan Macmillan: London, UK, 2020. [Google Scholar]
- Klem-Musatov, K.; Hoeber, H.C.; Moser, T.J.; Pelissier, M.A. Classical and Modern Diffraction Theory; Society of Exploration Geophysicists: Tulsa, OK, USA, 2016; Volume 29, Chapter 1; p. 117. [Google Scholar]
- Birch, T. Hypothesis Explaining the Properties of Light. In The History of the Royal Society; A. Millar: London, UK, 1757; Volume 3, pp. 247–305. [Google Scholar]
- Gage, J. Kulturgeschichte der Farbe: Von der Antike bis zur Gegenwart; Moses, M., Opstelten, B., Trans., Eds.; Ravensburger Buchverlag: Ravensburg, Germany, 1994. [Google Scholar]
- Wong, S.G. The composition of light in Newton’s Opticks. Prose Stud. 1993, 16, 119–147. [Google Scholar] [CrossRef]
- Lipson, A.; Lipson, S.G.; Lipson, H. Optical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Engheta, N. 150 years of Maxwell’s equations. Science 2015, 349, 136–137. [Google Scholar] [CrossRef]
- Mochrie, S.; De Grandi, C. Maxwell’s Equations and Then There Was Light. In Introductory Physics for the Life Sciences; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Sarkar, T.K.; Dyab, W.; Palma, M.S. What did Maxwell do to prove light was electromagnetic in nature and the concept of his displacement current. In Proceedings of the 2012 IEEE International Conference on Wireless Information Technology and Systems (ICWITS), Maui, HI, USA, 11–16 November 2012; pp. 1–4. [Google Scholar]
- Milonni, P.W.; Boyd, R.W. Momentum of light in a dielectric medium. Adv. Opt. Photonics 2010, 2, 519–553. [Google Scholar] [CrossRef]
- Chiatti, L. On Some Forgotten Formulas of L. de Broglie and the Nature of Thermal Time. Entropy 2024, 26, 692. [Google Scholar] [CrossRef]
- Elbaz, C. Wave-particle duality in Einstein-de Broglie programs. J. Mod. Phys. 2014, 5, 2192–2199. [Google Scholar] [CrossRef]
- Drezet, A. Whence Nonlocality? Removing Spooky Action-at-a-Distance from the de Broglie Bohm Pilot-Wave Theory Using a Time-Symmetric Version of the de Broglie Double Solution. Symmetry 2024, 16, 8. [Google Scholar] [CrossRef]
- Bertenshaw, D.R. Light and Photometry, the Path to Standardisation; Die Vierte Wand; Initiative TheaterMuseum Berlin e.V.: Berlin, Germany, May 2019; Volume 009, pp. 152–163. [Google Scholar]
- Palaz, A. A Treatise on Industrial Photometry with Special Application to Electric Lighting, 2nd ed.; Patterson, G.W., Trans., D., Eds.; Van Nostrand Company: London, UK, 1896. [Google Scholar]
- Raju, M.P.; T’Ien, J.S. Modelling of candle burning with a self-trimmed wick. Combust. Theory Model. 2008, 12, 367–388. [Google Scholar] [CrossRef]
- Paterson, C.C. XXXIV. The proposed international unit of candle power. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1909, 18, 263–274. [Google Scholar] [CrossRef]
- Saha, S.; Jaiswal, V.K.; Sharma, P.; Aswal, D.K. Evolution of SI base unit candela: Quantifying the light perception of human eye. Mapan 2020, 35, 563–573. [Google Scholar] [CrossRef]
- Higgs, P. Candle-power of the electric light. Minutes Proc. Inst. Civ. Eng. 1882, 68, 117–122. [Google Scholar] [CrossRef]
- Zwinkels, J.C.; Ikonen, E.; Fox, N.P.; Ulm, G.; Rastello, M.L. Photometry, radiometry and ‘the candela’: Evolution in the classical and quantum world. Metrologia 2010, 47, R15. [Google Scholar] [CrossRef]
- Zong, Y. From candle to candela. Nat. Phys. 2016, 12, 614. [Google Scholar] [CrossRef]
- Sperling, A.; Kück, S. The SI Unit Candela. Ann. Der Phys. 2019, 531, 1800305. [Google Scholar] [CrossRef]
- Islam, M.R.; Ali, M.M.; Lai, M.-H.; Lim, K.-S.; Ahmad, H. Chronology of Fabry-Perot Interferometer Fiber-Optic Sensors and Their Applications: A Review. Sensors 2014, 14, 7451–7488. [Google Scholar] [CrossRef]
- Wei, C.; Li, L. Ultrasonic/Acoustic Methods for Process Monitoring. In Handbook of Laser Micro- and Nano-Engineering; Sugioka, K., Ed.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; p. 12. [Google Scholar]
- González-García, A.; Pottiez, O.; Grajales-Coutiño, R.; Ibarra-Escamilla, B.; Kuzin, E.A. Optical pulse compression and amplitude noise reduction using a non-linear optical loop mirror including a distributed Gires–Tournois etalon. Opt. Laser Technol. 2010, 42, 1103–1111. [Google Scholar] [CrossRef]
- Amiel, Y.; Nedvedski, R.; Mandelbaum, Y.; Tischler, Y.R.; Tischler, H. Super-Spectral-Resolution Raman spectroscopy using angle-tuning of a Fabry-Pérot etalon with application to diamond characterization. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 325, 125038. [Google Scholar] [CrossRef]
- Gu, S.; Hou, X.; Li, N.; Yi, W.; Ding, Z.; Chen, J.; Hu, G.; Dou, X. First comparative analysis of the simultaneous horizontal wind observations by collocated meteor radar and FPI at low latitude through 892.0-nm airglow emission. Remote Sens. 2021, 13, 4337. [Google Scholar] [CrossRef]
- Bertenshaw, D.R. The standardisation of light and photometry–A historical review. Light. Res. Technol. 2020, 52, 816–848. [Google Scholar] [CrossRef]
- Available online: https://www.radiantvisionsystems.com/products/imaging-colorimeters-photometers/prometric-y-imaging-photometers (accessed on 1 December 2024).
- Available online: https://labsphere.com/wp-content/uploads/2021/09/Integrating-Sphere-Radiometry-and-Photometry.pdf (accessed on 2 December 2024).
- Pavlov, D.; Ivanov, D. Methods to Improve Quantitative and Qualitative Indicators of Lighting in Classrooms. In Proceedings of the 2022 14th Electrical Engineering Faculty Conference (BulEF), Varna, Bulgaria, 14–17 September 2022; IEEE: New York, NY, USA, 2022; pp. 1–4. [Google Scholar]
- Panahiazar, S.; Matkan, M. Qualitative and quantitative analysis of natural light in the dome of San Lorenzo, Turin. Front. Arch. Res. 2018, 7, 25–36. [Google Scholar] [CrossRef]
- Tabaka, P.; Wtorkiewicz, J. Analysis of the Spectral Sensitivity of Luxmeters and Light Sensors of Smartphones in Terms of Their Influence on the Results of Illuminance Measurements—Example Cases. Energies 2022, 15, 5847. [Google Scholar] [CrossRef]
- Wolfe, W. Spectrometers. In Fundamentals and Basic Optical Instruments; CRC Press: Boca Raton, FL, USA, 2017; pp. 405–446. [Google Scholar]
- Meunier, B.; Cosmas, J.; Ali, K.; Jawad, N.; Eappen, G.; Zhang, X.; Zhao, H.; Li, W.; Zhang, H. Visible light positioning with lens compensation for non-Lambertian emission. IEEE Trans. Broadcast. 2023, 69, 289–302. [Google Scholar] [CrossRef]
- Spieringhs, R.M.; Phung, T.H.; Audenaert, J.; Hanselaer, P. Exploring the Applicability of the Unified Glare Rating for an Outdoor Non-Uniform Residential Luminaire. Sustainability 2022, 14, 13199. [Google Scholar] [CrossRef]
- Andrews, S.S. Color. In Light and Waves: A Conceptual Exploration of Physics; Springer International Publishing: Cham, Switzerland, 2023; pp. 249–271. [Google Scholar]
- Dang, R.; Guo, W.; Luo, T. Correlated colour temperature index of lighting source for polychrome artworks in museums. Build. Environ. 2020, 185, 107287. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, F.; Yan, N.; Wu, Y. State of the art in defect detection based on machine vision. Int. J. Precis. Eng. Manuf.-Green Technol. 2022, 9, 661–691. [Google Scholar] [CrossRef]
- Available online: https://www.flusmeter.com/what-factors-affect-the-measurement-results-of-a-light-meter (accessed on 7 October 2025).
- ISO/IEC 17025:2017; General Requirements for the Competence of Testing and Calibration Laboratories. International Organization for Standardization: Geneva, Switzerland, 2017.
- CIE 198-SP2:2018; Determination of Measurement Uncertainties in Photometry Supplement 2: Spectral measurements and derivative quantities. CIE: Vienna, Austria, 2018; ISBN 978-3-902842-11-4.
- CIE TN 009:2019; The Use of “Accuracy” and Related Terms in the Specifications of Testing and Measurement Equipment, Technical Note. CIE: Vienna, Austria, 2019.
- Castro, P.J.; Payne, T.; Frey, V.C.; Kinateder, K.K.; Godar, T.J. Calculating photometric uncertainty. In Proceedings of the AMOS Technical Conference, Maui, HI, USA, 15–18 September 2020. [Google Scholar]
- Song, W.; Durmus, D. Evaluating Energy Efficiency and Colorimetric Quality of Electric Light Sources Using Alternative Spectral Sensitivity Functions. Buildings 2022, 12, 2220. [Google Scholar] [CrossRef]
- Lamb, T. Why rods and cones? Eye 2016, 30, 179–185. [Google Scholar] [CrossRef]
- Ding, J.; Yao, Q.; Jiang, L. Comparisons of Scotopic/Photopic Ratios Using 2- and 10-Degree Spectral Sensitivity Curves. Appl. Sci. 2019, 9, 4471. [Google Scholar] [CrossRef]
- Available online: https://cie.co.at/datatable/cie-spectral-luminous-efficiency-photopic-vision (accessed on 10 January 2024).
- Available online: https://cie.co.at/datatable/cie-spectral-luminous-efficiency-scotopic-vision (accessed on 10 January 2024).
- Jarosz, W.; Schönefeld, V.; Kobbelt, L.; Jensen, H.W. Theory, analysis and applications of 2D global illumination. ACM Trans. Graph. (TOG) 2012, 31, 1–21. [Google Scholar] [CrossRef]
- Salguero-Andújar, F.; Cabeza-Lainez, J.-M. New Computational Geometry Methods Applied to Solve Complex Problems of Radiative Transfer. Mathematics 2020, 8, 2176. [Google Scholar] [CrossRef]
- Zhang, Z.; Lou, C.; Kalaycı, N.; Cai, W. Entropy and exergy analyses of a direct absorption solar collector: A detailed thermodynamic model. Int. J. Heat Mass Transf. 2025, 239, 126566. [Google Scholar] [CrossRef]
- Wünsch, R. Radiation transport methods in star formation simulations. Front. Astron. Space Sci. 2024, 11, 1346812. [Google Scholar] [CrossRef]
- Ramley, I.; Alzayed, H.M.; Al-Hadeethi, Y.; Chen, M.; Barasheed, A.Z. An Overview of Underwater Optical Wireless Communication Channel Simulations with a Focus on the Monte Carlo Method. Mathematics 2024, 12, 3904. [Google Scholar] [CrossRef]
- Capilla, M.T.; Talavera, C.F.; Ginestar, D.; Verdú, G. A study of the radiative transfer equation using a spherical harmonics-nodal collocation method. J. Quant. Spectrosc. Radiat. Transf. 2017, 189, 25–36. [Google Scholar] [CrossRef]
- Wei, J.; Shi, Y.; Ren, Y.; Li, Q.; Qiao, Z.; Cao, J.; Ayantobo, O.O.; Yin, J.; Wang, G. Application of Ground-Based Microwave Radiometer in Retrieving Meteorological Characteristics of Tibet Plateau. Remote Sens. 2021, 13, 2527. [Google Scholar] [CrossRef]
- Lambert, J.; Paletou, F.; Josselin, E.; Glorian, J.M. Numerical radiative transfer with state-of-the-art iterative methods made easy. Eur. J. Phys. 2015, 37, 015603. [Google Scholar] [CrossRef]
- Warburg, O. Über die Geschwindigkeit der photochemischen Kohlensäurezersetzung in lebenden Zellen. Biochem. Z. 1928, 30, 540–541. [Google Scholar]
- BIPM. The International System of Units (SI), 9th ed.; V3.01; BIPM: Sèvres, France, August 2024. [Google Scholar]
- BIPM. Principles Governing Photometry, 2nd ed.; BIPM: Sèvres, France, 2019. [Google Scholar]
- BIPM. SI Brochure, 9th Edition (2019)—Appendix 3 v1.02, Units for Photochemical and Photobiological Quantities; BIPM: Sèvres, France, 2021. [Google Scholar]
- Sliney, D.H. Radiometric quantities and units used in photobiology and photochemistry: Recommendations of the Commission Internationale de l’Eclairage (International Commission on Illumination). Photochem. Photobiol. 2007, 83, 425–432. [Google Scholar] [CrossRef]
- Noor, M.C.; Saradj, F.M.; Yazdanfar, S.A. Analytical evolution of measurement methods for light’s non-visual effects. Results Eng. 2023, 17, 100922. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Dai, Q. Comparative analysis of circadian lighting models: Melanopic illuminance vs. circadian stimulus. Opt. Express 2024, 32, 29494–29513. [Google Scholar] [CrossRef]
- Esposito, T.; Houser, K. Correlated color temperature is not a suitable proxy for the biological potency of light. Sci. Rep. 2022, 12, 20223. [Google Scholar] [CrossRef]
- ISO/CIE TR 21783:2022 (First edition, 2022); Light and Lighting—Integrative Lighting—Non-visual Effects. ISO/CIE: Geneva, Switzerland, 2022.
- IEC 60081:1997/AMD6:2017; Edition 5.0, Amendment 6. Double-capped Fluorescent Lamps—Performance Specifications. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- IEC 60969:2016; Edition 2.0. Self-ballasted Compact Fluorescent Lamps for General Lighting Services—Performance Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2016.
- IEC 62031:2018; Edition 2.0. LED Modules for General Lighting—Safety Specifications. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- Rabani, J.; Mamane, H.; Pousty, D.; Bolton, J.R. Practical chemical actinometry—A review. Photochem. Photobiol. 2021, 97, 873–902. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.m4mining.eu/wp-content/uploads/2024/10/D3.1-UAS-integrated-with-multi-sensor-payload-ready-to-fly.pdf (accessed on 7 February 2025).
- Zeng, C.; King, D.J.; Richardson, M.; Shan, B. Fusion of Multispectral Imagery and Spectrometer Data in UAV Remote Sensing. Remote Sens. 2017, 9, 696. [Google Scholar] [CrossRef]
- Available online: https://www.energy.gov/sites/prod/files/2020/03/f72/ssl-mp-ratios_lda_feb2020.pdf (accessed on 8 February 2025).
- Kotsenos, A.; Madias, E.N.; Topalis, F.; Doulos, L. Circadian Stimulus Calculators as Environmental Building Design Tools: Early Results of a Critical Review. IOP Conf. Ser. Earth Environ. Sci. 2022, 1123, 012035. [Google Scholar] [CrossRef]
- Available online: https://www.starbeamlighting.com/lighting-regulations-and-compliance-for-commercial-buildings/ (accessed on 8 February 2025).

| Candle | Height of Flame [mm] | Hourly Consumption [g] | Value in Carcels |
|---|---|---|---|
| French | 52.2 | 12 | 0.136 |
| British | 46 | 7.8 | 0.120 |
| German Veriens | 50 | 7.5 | 0.134 |
| German Munich | 55 | 10.4 | 0.153 |
| Notion | Adopted by | Year | Definition |
|---|---|---|---|
| Candle-power | Great Britain | 1860 | The light produced in a specific direction by a pure Spermaceti Candle weighing 1/6 lb and burning at a rate of 120 grains per hour. |
| International candle | Laboratoire Central de l’Electricité (Paris) | 1909 | The light output of a Carcel burner consuming 42 g/h of rapeseed oil. |
| International candle | CIE | 1921 | The luminous intensity of a light source in terms of a standardized carbon filament incandescent lamp. |
| The candela | CIPM *, CIE | 1948 | The luminous intensity of a light source that radiated 1/683 watt per steradian at a wavelength of 555 nm (green light), which is the peak sensitivity of the human eye. |
| Candela | CGPM ** | 1967 | The luminous intensity, in the perpendicular direction, of a surface of 1/600,000 m2 of a blackbody at the temperature of freezing platinum under a pressure of 101,325 N/m2 (based on blackbody radiation). |
| Candela | CGPM | 1979 | The luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 × 1012 Hz and that has a radiant intensity in that direction of 1/683 W per steradian (based on radiant intensity of a monochromatic radiation). |
| Candela | CGPM | 2019 | The luminous intensity in a given direction. It is defined by taking the fixed numerical value of the luminous efficacy of monochromatic radiation of frequency 540 × 1012 Hz, Kcd to be 683, when expressed in the unit [lm/W], which is equal to [cd·sr/W], or [cd·sr·kg−1·m−2·s3], where the kilogram, meter, and second are defined in terms of h, c, and ΔνCs (based on a defining constant). |
| Instrument | Output Parameter | Basis Equation | Mathematical Considerations | |
|---|---|---|---|---|
| Quantitative | Lux meter | Illuminance (lux) | E = ϕ/A | [36]. |
| Spectroradiometer | Spectral power distribution (W/m2) | S(λ) = dϕ/dλ | [37]. | |
| Integrating sphere | Total luminous flux (lm) | ϕ = E × A | (derived from the principles in [33]). fb is baffle correction factor obtained experimentally by measuring a reference source with and without the baffle (i.e., the ratio of the corresponding detector responses) or by means of ray-tracing simulations, ρ is average sphere wall reflectance, Ap—port area, As—total sphere’s internal surface area. | |
| Goniophotometer | Angular light distribution (°) | I(α) = dϕ/dΩ | Because the definition of luminous intensity assumes ideal Lambertian emission, real sources that deviate from this distribution require [38] | |
| Luminance meter | Luminance (cd/m2) | L= Iα/(A × cosα) | The standard luminance definition is exact for Lambertian emitters. For non-Lambertian sources, angular corrections are applied: . | |
| Qualitative | Luminance distribution meter (with glare evaluation software) | Glare indices (UGR, DGI, fTI, etc.) | Measurement uncertainty arises mainly from instrument calibration affecting luminance, specifically, background and source luminance (Lb and Ls) distribution capture that influence Ω and environmental conditions (e.g., lens distortion, stray light) that affect the Guth position index p [39] | |
| Colorimeter | CCT, RGB values, XYZ coordinates | Is based on CIE 1931 XYZ color space account for human color perception, approximating the eye’s response to different wavelengths. The obtained values can be further converted into CIE Lab or RGB color spaces for different applications [40]. | ||
| Spectroradiometer (with CRI/TM-30 evaluation software) | CRI, TM-30 | CRI and TM-30 values are calculated from the measured spectral power distribution (SPD) of the light source. Their accuracy depends on the instrument’s spectral resolution, calibration, and on the algorithm used for the calculation. As human color perception is non-linear, the color difference (ΔE) equation is used to determine perceptible color differences in various lighting environments [41]. | ||
| Hemispherical photography | Light distribution patterns | Image processing algorithms | Distortion and calibration errors often occur, as wide-angle lenses introduce geometric distortions that must be corrected [42]. |
| Instrument | Common Application | Primary Error Sources | Limitations |
|---|---|---|---|
| Lux meter | General lighting audits, workspace compliance | Spectral mismatch error (V(λ) approximation), cosine error | Inaccurate under non-standard spectra (e.g., LED); angle sensitivity |
| Spectroradiometer | Light source spectrum characterization, CRI/CCT analysis (product display lighting, architectural lighting) | Stray light, thermal drift, wavelength calibration inaccuracy Reference data inaccuracies, non-linear perception modeling | Requires stable environment and calibration Incorrect perception if using outdated color samples |
| Integrating sphere | Calibration of photometric instruments, luminous flux measurement, reflectance and transmittance testing | Port losses, non-uniform reflectance, baffle misalignment | Large dimensions, sensitive to geometry, needs correction factors |
| Goniophotometer | Beam angle distribution, automotive headlamp design | Positioning errors, mechanical backlash, detector alignment | Large dimensions, time-intensive setup |
| Luminance meter | Display testing, road visibility and safety, brightness uniformity, office lighting, indoor workspaces | Angular error, vignetting, stray light, inconsistent background luminance | Sensitive to measurement distance and viewing geometry. High sensitivity with small changes in environment |
| Colorimeter | Ambiental lighting design, rapid color checks | Filter drift, limited spectral resolution, ambient light contamination | Low precision compared to spectroradiometers |
| Hemispherical photography | Solar radiation and daylighting analysis, light distribution and luminance mapping, architectural and horticultural visualizations, lighting simulation and assessment in 3D environments | Lens distortion, exposure miscalibration, sensor vignetting | Requires complex correction algorithms; error-prone under dynamic light |
| Wavelength λ [nm] | Spectral Luminous Efficacy for Photopic Vision V(λ) | Photopic Conversion Factor [lm/W] | Spectral Luminous Efficacy for Scotopic Vision V′(λ) | Scotopic Conversion Factor [lm/W] |
|---|---|---|---|---|
| 380 | 0.000039 | 0.027 | 0.000589 | 1.001 |
| 390 | 0.000120 | 0.082 | 0.002209 | 3.755 |
| 400 | 0.000396 | 0.270 | 0.009290 | 15.793 |
| 410 | 0.001210 | 0.826 | 0.034840 | 59.228 |
| 420 | 0.004000 | 2.732 | 0.096600 | 164.220 |
| 430 | 0.011600 | 7.923 | 0.199800 | 339.660 |
| 440 | 0.023000 | 15.709 | 0.328100 | 557.770 |
| 450 | 0.038000 | 25.954 | 0.455000 | 773.500 |
| 460 | 0.060000 | 40.980 | 0.567000 | 963.900 |
| 470 | 0.090980 | 62.139 | 0.676000 | 1149.200 |
| 480 | 0.139020 | 94.951 | 0.793000 | 1348.100 |
| 490 | 0.208020 | 142.078 | 0.904000 | 1536.800 |
| 500 | 0.323000 | 220.609 | 0.982000 | 1669.400 |
| 507 | 0.444310 | 303.464 | 1.000000 | 1700.000 |
| 510 | 0.503000 | 343.549 | 0.997000 | 1694.900 |
| 520 | 0.710000 | 484.930 | 0.935000 | 1589.500 |
| 530 | 0.862000 | 588.746 | 0.811000 | 1378.700 |
| 540 | 0.954000 | 651.582 | 0.655000 | 1105.000 |
| 550 | 0.994950 | 679.551 | 0.481000 | 817.700 |
| 555 | 1.000000 | 683.000 | 0.402000 | 683.000 |
| 560 | 0.995000 | 679.585 | 0.328800 | 558.960 |
| 570 | 0.952000 | 650.216 | 0.207600 | 352.920 |
| 580 | 0.870000 | 594.210 | 0.121200 | 206.040 |
| 590 | 0.757000 | 517.031 | 0.065500 | 111.350 |
| 600 | 0.631000 | 430.973 | 0.033150 | 56.355 |
| 610 | 0.503000 | 343.549 | 0.015930 | 27.081 |
| 620 | 0.381000 | 260.223 | 0.007370 | 12.529 |
| 630 | 0.265000 | 180.995 | 0.003335 | 5.670 |
| 640 | 0.175000 | 119.525 | 0.001497 | 2.545 |
| 650 | 0.107000 | 73.081 | 0.000677 | 1.151 |
| 660 | 0.061000 | 41.663 | 0.000313 | 0.532 |
| 670 | 0.032000 | 21.856 | 0.000148 | 0.252 |
| 680 | 0.017000 | 11.611 | 0.000072 | 0.122 |
| 690 | 0.008210 | 5.607 | 0.000035 | 0.060 |
| 700 | 0.004102 | 2.802 | 0.000018 | 0.030 |
| Radiometric (Energetic) Units | Photometric Units | Quantum Units | |||
|---|---|---|---|---|---|
| Quantity | Symbol and SI Unit | Quantity | Symbol and SI Unit | Quantity | Symbol and SI Unit |
| Radiant energy | Qe [J] | Luminous energy | Ql [lm·s] | Photon energy | E [J] |
| Radiant flux | Φe [W] | Luminous flux | Φ [lm] | Photon flux | Q [photons/s] |
| Radiant intensity | Ie [W/sr] | Luminous intensity | I [cd] | - | - |
| Radiance | Le [W/m2·sr] | Luminance | L [cd/m2] | - | - |
| Irradiance or radiant flux density | Ee [W/m2] | Illuminance or luminous flux density | E [lx] | Photon irradiance | Eq [photons/(m2·s)] |
| Method | Mathematical Approach | Specific Applications | Advantages | Limitations |
|---|---|---|---|---|
| Two-Stream Approximation | Reduces angular dependence to two directions (upward and downward) | Climate models, remote sensing | Captures bulk radiation behavior | Poor accuracy for highly anisotropic scattering |
| Diffusion Approximation | Treats radiation as diffusive transport | Cloud physics, biomedical optics | Converts RTE into a simpler diffusion equation | Inaccurate for optically thin layers |
| Rayleigh & Mie Scattering Approximations | Approximates scattering behavior for different particle sizes (Rayleigh and Mie—small and large particles) | Cloud optics, aerosol modeling, atmospheric physics | Captures dominant scattering effects | Rayleigh fails for large particles, Mie requires more complex phase functions |
| P-N Approximation (Spherical Harmonics) | Expands radiation intensity as a series of spherical harmonics | Optical transport, planetary atmospheres | Higher orders improve accuracy | Computationally expensive for higher-order terms |
| Monte Carlo Method | Simulates photon trajectories stochastically | Remote sensing, biomedical optics, astrophysics | Very accurate, handles complex geometries | Computationally expensive, slow for large simulations |
| Beer’s Law Approximation | Assumes exponential attenuation of direct radiation | Optical filters, thin clouds, atmospheric transmittance | Simple and fast, widely used | Ignores multiple scattering, only valid for direct light |
| k-Distribution Method | Reorders absorption coefficients by probability distribution | Climate models, gas absorption calculations | More accurate than band averaging, improves spectral resolution | Requires precomputed spectral data |
| Eddington Approximation (2-Stream Eddington Method) | Assumes isotropic intensity in forward and backward directions and linear angular dependence | Radiative transfer in atmospheres, cloud modeling | Improves accuracy over basic 2-stream | Less accurate for highly anisotropic scattering |
| Planck Mean Approximation | Averages absorption coefficient using a blackbody weighting function | Combustion modeling, atmospheric gas absorption | Simplifies spectral integration, useful for gas-phase radiative transfer | Less accurate in nonlocal thermodynamic equilibrium conditions, ignores spectral variations |
| Rosseland Mean Approximation | Uses Rosseland mean opacity, averaging absorption over spectrum | Astrophysical plasmas, high-energy radiation transport | Converts RTE into a simple diffusion equation, reducing computation | Fails in optically thin media, assumes local thermodynamic equilibrium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serea, E.; Donciu, C.; Temneanu, M.C. Complexities of Lighting Measurement and Calculation. Metrology 2025, 5, 61. https://doi.org/10.3390/metrology5040061
Serea E, Donciu C, Temneanu MC. Complexities of Lighting Measurement and Calculation. Metrology. 2025; 5(4):61. https://doi.org/10.3390/metrology5040061
Chicago/Turabian StyleSerea, Elena, Codrin Donciu, and Marinel Costel Temneanu. 2025. "Complexities of Lighting Measurement and Calculation" Metrology 5, no. 4: 61. https://doi.org/10.3390/metrology5040061
APA StyleSerea, E., Donciu, C., & Temneanu, M. C. (2025). Complexities of Lighting Measurement and Calculation. Metrology, 5(4), 61. https://doi.org/10.3390/metrology5040061






