Metrology for Virtual Measuring Instruments Illustrated by Three Applications

Abstract

In the course of digitalization, the importance of modeling and simulating real-world processes in a computer is rapidly increasing. Simulations are now in everyday use in many areas. For example, simulations are used to gain a better understanding of the real experiment, to plan new experiments, or to analyze existing experiments. Simulations are now also increasingly being used as an essential component of a real measurement, usually as part of an inverse problem. To ensure confidence in the results of such virtual measurements, traceability and methods for evaluating uncertainty are needed. In this paper, the challenges and benefits inherent to virtual metrology techniques are shown using three examples from different metrological fields: the virtual coordinate measuring machine, the tilted-wave interferometer, and the virtual flow meter.

1. Introduction

In the course of digitalization, the importance of modeling and simulating real-world processes in a computer is rapidly increasing. Simulations are now in everyday use in many areas. They are, for example, used to gain a better understanding of the real experiment [1,2,3,4,5,6,7,8,9,10] or to substitute parts of it [11,12,13]. Furthermore, simulations are used to evaluate measurement uncertainty [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. In some applications, simulations form an essential component of a real measurement, usually as part of an inverse problem [11,34,35,36,37,38,39,40,41,42,43,44].

The importance of virtual metrology is also stated in the Strategic Research Agendas of the European Metrology Networks (EMNs) for Mathematics and Statistics (MATHMET) and for Advanced Manufacturing [45,46]. According to [45], simulations have been established in science as a third pillar alongside theory and experiment […] as they provide a deep insight into the measurement process, allow improvement and development of measurement methods, design novel measurement devices, facilitate the evaluation of uncertainties and are necessary to evaluate indirect measurements. In [46], it is stated that extremely powerful distributed computational facilities promote the separation between the experimental measurement and the derivation of results, […] which allows evaluating the measurement task-specific uncertainty. […] The systematic availability of product metadata and the capability of evaluating them […] enable to correct/optimize production facilities with potentially large savings and improved environmental friendliness.

Whenever simulations are used to imitate real measuring equipment, this implementation of the measurement principle in a computer can be described as “virtual measuring device”or “virtual instrument” [47,48,49]. In this paper, these terms are used interchangeably, both referring to the implementation of the model equations in software. The terms ”virtual measurement” or “virtual experiment”, on the other hand, are used in this paper for the virtual model of a real measurement, i.e., its counterpart in a computer [16,50]. To ensure confidence in the results of such virtual measurements, traceability and methods for evaluating uncertainty are needed. This includes also the verification of the numerical models and the validation of simulation results, see e.g., ref. [51,52,53,54,55].

According to [45], virtual metrology should be on the same quality level as metrology. Hence, the development of virtual measuring devices should be closely linked to real experiments. This means that, in the long-term, the same metrological procedures that are used to ensure reliability and trustworthiness for real measurements should also be applied to virtual ones, including the calibration of virtual devices, the comparison of virtual devices, and the traceability chain to a virtual/real standard [45].

In [46], a statement of the EMN Vice-chair Alessandro Balsamo is cited: Virtual instruments indicating measured values and the associated uncertainties will be commonly used and become the new standard in the future. For this, according to [46], an implementation of metrology systems and infrastructure following FAIR principles for rapid, reliable, and secure access to holistic metrology data for absolute confidence in decision making at all points in the manufacturing workflow is needed.

At the Physikalisch-Technische Bundesanstalt (PTB), the national metrology institute of Germany, the internal competence center “Metrology for virtual measuring instruments (VirtMet)” [56] was installed to bundle the existing expertise in this field and promote interdisciplinary exchange. In the following chapters, the challenges and benefits inherent to virtual metrology techniques are shown using three examples from different metrological fields within the competence center: the virtual coordinate measuring machine (VCMM), the tilted-wave interferometer (TWI), and the virtual flow meter.

2. The Virtual Coordinate Measuring Machine (VCMM)

In dimensional metrology and its application in industrial quality control and quality assurance, the determination of measurement uncertainty is of crucial importance for the assessment of compliance with defined tolerances [57] for production according to e.g., ISO 1101 [58]. The parts’ spectrum of geometric features that need to be measured comprises a wide variety of geometric properties and the measured objects can range from the sub-millimeter scale to several meters. Hence, for all characteristics, individual, so-called task-specific measurement uncertainties have to be determined. Considering the wealth of geometries used in modern-day product design and production, this challenging task can only be tackled by the classical methods of type A and type B described in the Guide to the Expression of Uncertainty in Measurement (GUM) [59] in very rare and simple cases. As a consequence, the use of virtual metrology techniques such as Monte Carlo simulations (MCS) following GUM Supplement 1 [60] has long been investigated. With the development of the VCMM [14,23,61,62,63] as a digital-metrological twin (D-MT) [64] of a coordinate measuring machine (CMM) and its availability for use by accredited calibration laboratories and industry alike, a powerful method for the measurement uncertainty evaluation is available.

2.1. Application for Uncertainty Evaluation

The VCMM is developed, maintained, and regularly expanded by PTB as an institution independent of CMM manufacturers. The software kernel can be integrated into the CMM’s commercial application software, which can exchange information through common interfaces during the run-time of the VCMM. The measurement uncertainty is determined in a six-step process. The first two steps correspond to the procedure of a regular measurement using a CMM:

• The CMM captures the measuring points of all features to be inspected on the workpiece.
• The evaluation software of the CMM calculates the corresponding measurands from the measured point cloud of the features.

• Afterwards, four additional VCMM-specific steps are required to calculate the corresponding measurement uncertainties:

3.

The VCMM generates new 3D point coordinates based on the measured coordinates, which are slightly distorted due to systematic and random measurement deviations.

4.

The coordinates generated in this way are fed to the same evaluation algorithm as the real measured coordinates, and a further measured value is obtained for the feature, which is generated by simulating possible and realistic measurement errors.

5.

Steps 3 and 4 are repeated n times until sufficient statistical stability of the measurement uncertainty calculation is achieved.

6.

After n repetitions, the uncertainties for all measurands are derived from the distribution and the mean values of the simulated measurement results.

The mathematical and physical models of the VCMM are divided into individual modules (Figure 1) dedicated to the uncertainty contributions of the measuring device, the environmental conditions, and the workpiece itself. They are taken into account as constant (unchanging) contributions covering measurement errors that are not changed during the simulation, unknown residual systematics that are varied prior to each simulation run, or random contributions varied for each individual measurement point. While the current models are validated for coordinate measurements of prismatic geometries using spherical probing elements (i.e., styli), as part of the project ADAM [65], additional modules are developed to expand the spectrum of applications toward the increased utilization of optical sensors [22,50] and the emerging need for measurements of industrial freeform geometries [66,67] on CMM.

2.2. Traceability

The prerequisite for the applicability of the VCMM is that the used CMM, the environmental conditions, the measured workpiece, and the measurement process itself are described by suitable models to cover the influences on the measurement uncertainty [51,52]. Furthermore, the models have to be verified for the measurement task, which can be achieved by round robins using measurement standards calibrated through independent procedures.

For the immediate use of the VCMM, it has to be parametrized to resemble the current state of the CMM, the measurement conditions, as well as the measured object. In addition to these requirements, the input parameters to the models must be determined using calibrated measurement standards or calibrated sensors to establish traceability to the international system of units SI [62,68,69,70].

Since not all parameters vary on the same time scale, there are different times and means to obtain them. While geometric errors of the CMM, i.e., the deviation of the CMM mechanics, in general, only change on long time scales if the rated operation conditions are obeyed, uncertainty contributions of the probing system and the used stylus configuration may change from one measurement task to another. For typical CMM applications, the geometric errors and probing errors are checked by comparing measurements of a step gauge or a reference to the manufacturer’s specifications following the procedures in ISO 10360-2 [71] and ISO 10360-5 [72]. In order to be sufficient for the consideration of the relevant uncertainty contributions for the VCMM, additional measurements have to be carried out. In the case of the geometric errors, error mapping using either two-dimensional measurement standards, such as hole plates [61] or laser interferometers [69,73], can be applied, where typical intervals for re-parametrization can range from a few months to up to two years depending on the mechanical quality of the CMM and the environmental stability. The characteristics of the probing system and the stylus configuration is typically evaluated by repeated measurements using independent reference spheres. These measurements are frequently repeated when changes to the probing system or the stylus setup are made.

Furthermore, influences of the surface of the probed workpiece are closely tied to the production and surface finishing process, and thus, their parametrization needs be carried out for the individual feature during the measurement process.

2.3. Other Benefits

While the VCMM’s main purpose is to enable CMM users from accredited calibration laboratories and industrial quality control to reliably and efficiently determine the task-specific measurement uncertainty, it should be noted that it can also provide aid and support to metrologists in other fields of their work.

Although the typical application procedure uses 3D point coordinates from a measurement, the VCMM software (e.g., the current Build 2.0.0.2872) can be used to select the most suitable CMM and measurement strategy in preparation of the measurements. Therefore, the calculations can be performed using the ideal geometry data, e.g., from computer-aided design (CAD) models, and knowledge about the production process of the workpiece. Paired with parametrized CMM information, an estimate of the achievable measurement uncertainty can be computed to decide if the CMM and the selected strategy is sufficient to test the characteristics with respect to the specified tolerance or if a different CMM or an improved measurement strategy needs to be utilized.

In addition to the support in planning individual measurements, the well-parametrized VCMM can be applied to standardized measurement tasks, e.g., measurements of a stepgauge as described in [71] or typical quality control tasks, to perform a sensitivity analysis and identify improvement scenarios for the metrological conditions. As a result of comparing the relative outcomes of VCMM uncertainty estimates considering only specific uncertainty contributions from each of the modules, conclusions about the largest contributor to the measurement uncertainty can be drawn. Due to the limited number of Monte Carlo simulations used for the sensitivity analysis, the absolute value of the uncertainty contribution may not be accurate; however, the relative importance can provide valuable information.

The example of a CMM (see Figure 2) shows that in a well-controlled laboratory, the dominant influences are the geometric errors of the CMM and the tactile probing process, while this may significantly change for other CMMs in different environmental conditions, such as those close to industrial production lines.

Overall, this sensitivity analysis helps users and decision makers to improve their measurement conditions in the most efficient way possible, directing efforts to address the most significant influences on the measurement uncertainty at the highest priority. In light of the digital transformation in manufacturing, virtual metrology tools as the VCMM can thus be of great benefit for factories of the future applications.

3. The Tilted-Wave Interferometer (TWI)

An example of modern optical metrology is the TWI [11,34,36,74,75,76]. This interferometer constitutes a measurement system that is utilized for the purpose of determining the form of optical aspheres and freeform surfaces.

The measurement system combines model-based evaluation procedures with a special interferometer setup, in which the surface under test is illuminated by several tilted wavefronts in four different groups of tilted wavefronts. Consequently, the absence of a comprehensive model of the entire apparatus precludes the acquisition of any measurement outcomes. This characteristic makes the present application example very special, and it is sometimes referred to as a “device with an embedded virtual experiment”. The concept involves the simulation of measurement data based on the assumed form of the surface. Subsequent comparison of these simulated data with the measurement data, in conjunction with the discrepancy between the two, enables the solution of an inverse problem. Thereby, the form of the surface under test is reconstructed. It is important to note that the utilization of simulated data necessitates the adaptation of the model of the interferometer to the actual instrument. The objective of this is to achieve the most accurate representation in the computer. To this end, highly accurate spherical reference surfaces of well-known form are measured at numerous positions within the interferometer. The results are then compared to the simulated measurement data. Subsequently, an additional inverse problem is addressed, aiming to adjust the model parameters while minimizing the discrepancy between the measurement data and the simulated data. It must be noted that, in addition to the necessity to solve inverse problems, the datasets measured and simulated for solving the inverse problems are very large, and especially for the model adjustment, many parameters have to be adapted.

In this particular metrology application, simulations are not only part of the reconstruction process, but virtual experiments also play a central role to estimate measurement uncertainty. For example, they are utilized to investigate the primary influencing parameters [10,27] and conduct sensitivity analyses [77,78]. Additionally, virtual experiments are used to undertake investigations regarding the design of experiments [4,79,80,81]. The objective of the latter is to optimize the experimental design, thereby enhancing the outcomes. To illustrate this, simulations of the measurements are, e.g., utilized to determine a measurement position within the interferometer for the surface to be measured. In contrast to the measurement of simple surfaces such as spheres with classical interferometers, there are numerous possible specimen positions for measuring surfaces in a TWI. In a classical interferometer, a spherical surface is measured in the so-called null test position [82,83], in which the rays hit the surface perpendicularly. To determine a suitable surface position in the TWI, the surface is placed in a model of the interferometer near the null test position of the best-fit sphere of the surface, and then a position sweep is performed by simulating the measurement data for several positions around this initial position. The outcomes of this simulation include the determination of the measurability of the surface, the identification of the areas of the surface that can be measured, and the determination of the form and size of the sub-interferograms (also called patches) that are to be observed during the measurement process. Additionally, the simulations provide insights into the overlapping areas between these patches. In Figure 3, examples of the simulated interferogram patterns on the camera for two different measurement positions for the same asphere are shown. The camera images were generated with SimOptDevice, a flexible library for opto-mechanical virtual experiments developed at PTB [84]. The figure shows for each asphere position the four different camera images that are expected when activating the four different groups of tilted wavefronts in the interferometer. From these data, the experienced user can decide which position to choose to receive highly accurate measurement results. For example, it is more convenient to choose a position with an even distribution of patches of approximately equivalent size across the surface area to be measured as shown in the figure on the left (asphere position 1). The asphere position used to generate the camera images shown in Figure 3 on the right (asphere position 2) is less appropriate because numerous very tiny patches are generated, which do not even cover a closed area of the surface.

Besides this visual inspection, more analytical criteria may be investigated using virtual experiments for the purpose of finding an optimized design of experiment. For instance, the Jacobian describing the partial derivatives of the surface under test with regard to the parameters that are used for form reconstruction can be analyzed and used to find an optimized measurement position by calculating the covariance matrix from the Jacobian [79]. This is merely one illustration of the utilization of virtual experiments to optimize experimental designs within a TWI. Other investigations include the determination of the optimal position of the camera within the setup, or the determination of the measurement strategy (e.g., choosing the sample rate or data point distribution for solving the inverse problems) to improve the reconstruction result, to name just a few examples.

Other applications of simulations for this measuring device are the development and testing of new methods for data evaluation and the optimization of procedures within the measuring process. An example of the latter is the development of alignment strategies for the surface under test within the experimental setup. This is an important task in order to reduce measurement uncertainty, as positioning errors in TWI measurements are a major source of uncertainty [4,85]. To reduce this influence, the position of the surface under test within the measurement setup must be accurately aligned with the position selected in the model. The development of such alignment strategies with the help of simulations was demonstrated in [86]. Here, simulations were used to investigate the sensitivity of the measurement data for the specimen close to the Cat’s Eye reference position (a reference position typically used in interferometry [87,88]) to alignment errors. With the results of such simulations, an alignment procedure was developed and tested with the experimental setup [86].

The TWI is an example of a measurement principle with high complexity. The examples given above show that in such applications, simulations and virtual experiments facilitate comprehension of the processes occurring within the measurement device, thereby enhancing the discernment of measurement effects. Virtual metrology therefore enables the systematic investigation of complex measurement systems.

For measurement systems with an embedded virtual experiment, such as the TWI, the development of uncertainty methods is part of today’s research [89]. Also in this context, simulations and virtual experiments play a central role. Recently, an approximative Bayesian approach was developed to tackle the inverse problem of the TWI. It is based on a statistical model derived from the computational model of the interferometer [27]. In this example, a proof-of-concept study for a Bayesian uncertainty evaluation framework was proposed. It was applied to the TWI, taking into account some key influencing factors to demonstrate the performance of the methodology [27]. Such methods to estimate uncertainty for the TWI, and for other applications, will be further investigated and extended within the ViDiT project [89].

One advantage of a device with an “embedded virtual experiment” is the ability to validate the virtual experiment with real measurements and to compare the results (or characteristic parts of them) with reference measurements [11,90]. Since the measurement result of such instruments includes the virtual measurement, such a comparison of the measurement result with the result of reference measurements helps to validate the virtual measurements. In addition, other typical validation methods can be used, e.g., systematic introduction of errors in the real experiment and comparison of the behavior with the behavior when the errors are introduced in a virtual experiment.

4. The Virtual Flow Meter

In flow metrology, virtual experiments can be used to simulate how the flow measurement is influenced by disturbed flow conditions [20,91,92,93,94,95,96,97,98,99,100,101,102,103,104]. For this, the flow field is simulated with computational fluid dynamics (CFD) in a first step. In a second step, the measurement principle of the considered flow meter is applied to the calculated flow field. This virtually determined flow rate measurement can then be compared with the actual flow rate, providing an estimate of the error of the flow meter under the considered disturbed flow condition. Of course, the error of a flow meter under disturbed conditions can also be determined by measurements. However, they are often costly and time-consuming and, thus, limited to specific geometries only. In contrast, virtual experiments allow for the consideration of a lot of different configurations, covering a wide range of possible velocity distributions and secondary flow motions. Furthermore, the influence of uncertainties in the input parameters on the resulting prediction and uncertainty of the flow rate can be investigated systematically.

In Weissenbrunner et al. [13], a surrogate model is developed, which allows for the prediction of velocity profiles downstream of practically relevant elbow configurations. The model is based on 263 CFD simulations covering single and double elbows in- and out-of-plane with curvature radii and distances between the elbows ranging from 0.5 to 10 and 0 to 5.5 pipe diameters, respectively. Furthermore, Reynolds number and pipe wall roughness can be changed without performing additional simulations. By incorporating the measurement principle, the model allows for the prediction of the error of the respective flow meter. The results are also implemented in a graphical user interface (GUI) [105], which illustrates the predicted flow profile for the chosen configuration as well as the predicted error of the chosen measurement device.

However, before this method can generally be used in practical applications to correct the flow rates measured under these conditions, one needs to assure first that the predictions of the surrogate model fully reflect the real experimental setup and that the virtual measurements take into account all contributions of uncertainty. This means that, besides the uncertainties of all input parameters, also the uncertainty of the virtual experiment needs to be determined.

In Straka et al. [12], an approach for calculating the simulation uncertainty of virtual flow meters is presented. Their paper shows that it is not enough to determine the different discretization and approximation errors of the numerical model and sum them up to an overall calculation uncertainty; modeling errors also need to be taken into account. However, in complex models, there is usually an interaction between numerical and modeling errors. Hence, it is hardly possible to determine the uncertainty of the virtual model by determining the different error contributions separately and summing them up. In this case, the simulation uncertainty can only be determined by validating the simulation results by comparison with experimental data. Using an ultrasonic clamp-on meter applied to a double bend out-of-plane as an example, the paper determines the simulation uncertainty for a variety of different turbulence models. For the Spalart–Allmaras model [106], which was used in the surrogate model of Weissenbrunner et al. [13], a value of $2.10 \times {10}^{-2}$ is stated for the simulation uncertainty of the considered double bend out-of-plane configuration (for $z/D\in \left[2.45, 35.49\right]$ and $\mathrm{Re}=5 \times {10}^4$). On the contrary, the calculation uncertainty is approximately one order of magnitude lower ($2.96 \times {10}^{-3}$), see [12] for details.

Figure 4 illustrates how the results of [12,13] can be combined for four example configurations, see

Table 1. Definition of the four different test cases (two single elbow (SE) and two double elbow out-of-plane (DE) configurations) and their respective errors as predicted by [105]. Curvature radius $R_c$, distance between two elbows (only for DE) $d_l$, downstream distance z, and wall roughness $k_s$ are given in dimensionless form normalized with the inner pipe diameter D. The given Reynolds numbers $\mathrm{Re} = 1.12 \times {10}^5$ and $\mathrm{Re} = 1.34 \times {10}^6$ are calculated from the prescribed velocities $v = 0.5 \mathrm{m}/\mathrm{s}$ and $v = 6 \mathrm{m}/\mathrm{s}$, taking the inner pipe diameter D as well as the properties of water at ${25 }^{\circ }\mathrm{C}$ into account.

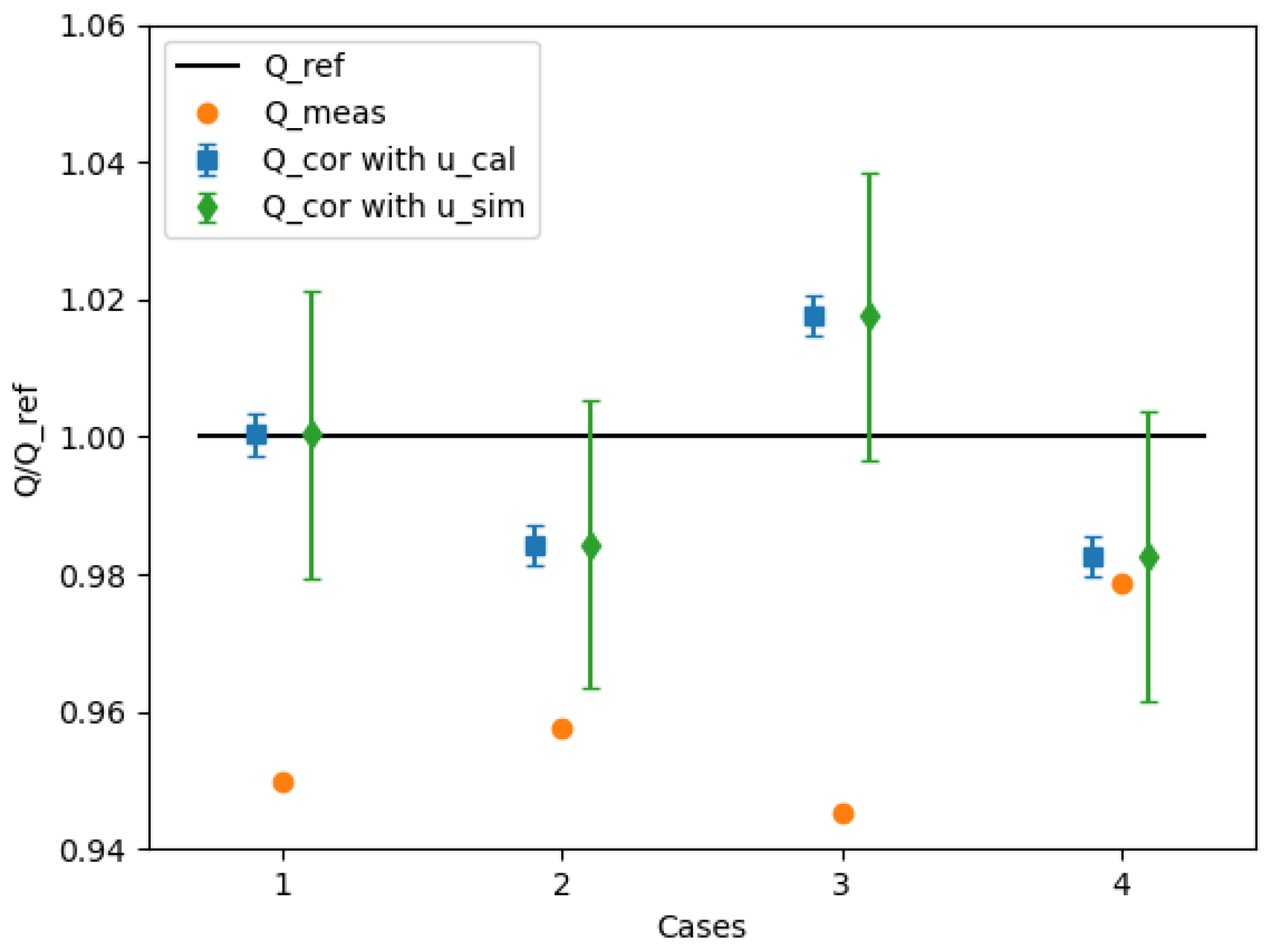
Test Case	1	2	3	4
Flow case	SE	SE	DE	DE
Curvature radius	$R_c/D=1.4$	$R_c/D=1.4$	$R_c/D=1.4$	$R_c/D=1.4$
Distance betw. elbows	–	–	$d_l/D=5$	$d_l/D=5$
Downstream distance	$z/D=5$	$z/D=10$	$z/D=5$	$z/D=20$
Installation angle	$\alpha ={45}^{\circ }$	$\alpha ={45}^{\circ }$	$\alpha ={45}^{\circ }$	$\alpha ={45}^{\circ }$
Reynolds number	$\mathrm{Re}=1.34\times {10}^6$	$\mathrm{Re}=1.12\times {10}^5$	$\mathrm{Re}=1.12\times {10}^5$	$\mathrm{Re}=1.34\times {10}^6$
Wall roughness	$k_s/D=0$	$k_s/D=0$	$k_s/D=0$	$k_s/D=0$
Predicted error	$-5.05\%$	$-2.72\%$	$-7.11\%$	$-0.39\%$

for a definition of the cases. In the example, an ultrasonic flow meter with a ${45}^{\circ }$ V-path configuration was chosen as the measurement principle.

Starting from measured data (orange dots in Figure 4), the flow rates can be corrected according to the error predictions of [105], which are also given in Table 1. One observes that these corrected values (blue squares/green diamonds) are closer to the reference flow rate (black line—for sake of simplicity, we assume that the error of measuring the reference flow rate is negligible) than the original data. However, they are still not exactly the same. In the next step, we include the uncertainty of the virtual model according to [12] (here, it is assumed that the results derived for a double-elbow out-of-plane configuration and a Reynolds number of $\mathrm{Re} = 5 \times {10}^4$ can be transferred to the other test cases as well). If in this case only the calculation uncertainty is taken into account (blue error bars), the predictions still do not include the reference flow rate in most cases. On the other hand, if the simulation uncertainty is used instead (green error bars), the predictions now all include the reference value. Please note that the simulation uncertainty does not include the error caused by approximating the CFD data with a surrogate model. According to [13], this error is less than 0.4 % and, hence, negligible compared to the simulation uncertainty (which is mainly caused by the error of the CFD model).

In the example above, it has been assumed that the measurements are exact and that there are no uncertainties associated with them. In practice, however, additional uncertainties are introduced by missing information in the description of the measurement setup and by the execution of the measurements. For the flow meter, examples include missing information on the exact geometry of the pipe system (e.g., the curvature radius), uncertainties in the operating conditions (e.g., the temperature of the fluid), lack of documentation on the installation angle of the flow meter, or only approximate knowledge of the roughness of the pipe. All these uncertainties must be taken into account. In real measurement campaigns, these uncertainties can either be quantified by additional measurements (e.g., dimensional measurements of the geometry) or be provided by certificates. In some cases, when all the previously mentioned information is missing, they can only be estimated or bounded using the knowledge and experience of experts.

In Weissenbrunner [105], uncertainties in the geometry, in the downstream position of the measurement, the installation angle, the Reynolds number, and in the wall roughness can be included. To derive a reliable prediction of the flow rate from the virtual flow meter, these uncertainties must be combined with the errors and uncertainties associated with the modeling and with the uncertainties of the measurement itself. In Bayazit et al. [33], a framework is presented, which allows the uncertainties of the measurement to be combined with the uncertainties of the parameters going into the virtual model. In particular, the existing approaches as documented in the GUM [59] were implemented and adjusted to include virtual experiments, resulting in a generalized framework for the uncertainty evaluation of virtual flow meters. This framework will be further extended within the ViDiT project [89] to allow for the inclusion of modeling errors.

5. Discussion

In this paper, the use of virtual metrology methods has been shown using three exemplary approaches from different metrological fields, tailored to different purposes, and targeting different user groups. They are designed applying a wide range of approaches and techniques, and thus are emblematic for emphasizing the various opportunities created by virtual metrology.

The examples in this paper show that modern metrology even goes so far that virtual metrology contributes directly to the measurement process and is necessary to determine the measurand in the first place. One example of this is the TWI, where simulations are part of the reconstruction process. Another example is the virtual flow meter, where simulations replace expensive and time-consuming measurement campaigns to determine the measurand.

In addition, virtual metrology offers the possibility of determining the measurement uncertainty, especially in cases where other methods of uncertainty determination are not applicable or are too cost-intensive, as shown in all three examples above.

The examples presented also demonstrate the power of virtual metrology in performing systematic investigations of complex measurement systems, optimizing experimental designs and performing sensitivity analyses to identify the main sources of uncertainty. With these tools, metrologists are supported in selecting the most suitable measurement equipment and strategies. Furthermore, virtual metrology enables them to develop and test new methods for data evaluation or to optimize certain procedures within the measurement process. These methods help users and decision makers to improve their measurement conditions as efficiently as possible and to prioritize efforts on the most important influences on measurement uncertainty. In light of the digital transformation in manufacturing, virtual metrology tools can therefore be of great benefit to the factory of the future.

Although the aforementioned methods are key enabling technologies in light of the digital transformation in metrology, which provide numerous benefits, their trustworthy implementation and reliable use come with some challenges to be addressed.

It is of fundamental importance for the use in applications, such as those described in Section 2, Section 3 and Section 4, that in the conceptualization and design phase of the software, all relevant sources of errors and uncertainties that contribute to the measurement process are properly identified. In order to derive one or more suitable models, decisions on the degree of generalization have to be made to fit the use case. This, in turn, leads to a balance between highly individual, tailor-made models with highest possible accuracy on the one hand, and more widely applicable or cost-efficient models sacrificing accuracy on the other hand.

Once models for virtual metrology have been implemented, the software needs to be validated before use. In most cases, this is achieved by comparison to reference datasets, reference algorithms, or inter-comparisons with suitable measurement procedures and calibrated measurement standards. While these requirements are predominantly important during the development and deployment phase of the virtual metrology software, additional needs have to be considered during their operation. In case of digital-metrological twins (D-MT), such as the VCMM, the time scales on which model parameters are updated have to be aligned with the temporal variations of influence conditions of the real-world experiment. For virtual metrology tools that are utilized to evaluate the measurement uncertainty, a major contribution to their applicability is the development of models and uncertainty propagation in compliance with the GUM [59] as well as establishing traceability. This can be achieved through validated algorithms and strategies for the parametrization of the models using calibrated measurement standards and sensors.

In order to be used in industrial process chains rather than tailor-made research applications, great care has to be taken to ensure reliable long-term operation of the virtual metrology tools. On the one hand, there is a constant need for model maintenance and revalidation during operation due to environmental changes and component aging. In the case of the TWI application, for example, the model correction procedure must be repeated regularly to ensure that the model best reflects the behavior of the measurement system. The necessary interval for this procedure depends on the stability of the environmental conditions. Whether the model is still valid must be checked regularly by taking measurements on calibrated reference surfaces. On the other hand, this means that any changes of the software need to be well documented and tested on reference cases prior to the release of updates. Different versions’ outcomes should be compared using well-defined theoretical datasets as well as real measurement data. Furthermore, major changes in the underlying models of the computations most likely require a thorough re-validation process. In the case of the VCMM, all minor changes are complemented by a number of test scenarios and the comparison to a set of the same measurement tasks with different software versions prior to official releases to industrial customers. Furthermore, major changes and augmentations of the models and the handling of measurement data are re-validated in round robins using several CMMs from different manufactures and accuracy classes operated in different environmental conditions. For these measurements, independently calibrated measurement standards and workpieces are used to cover the targeted industrial applications. It should also be noted that reports on the results of (re-)validations should be made available to users, auditors, and accreditation bodies to ensure trust in the methods.

In light of the digital transformation in all areas of economy and society, virtual metrology tools such as the VCMM, the TWI, and the virtual flow meter can thus be of great benefit for a wealth of applications.