Incremental Capacity and Voltammetry of Batteries, and Implications for Electrochemical Impedance Spectroscopy
Abstract
1. Introduction
2. Experimental Methods
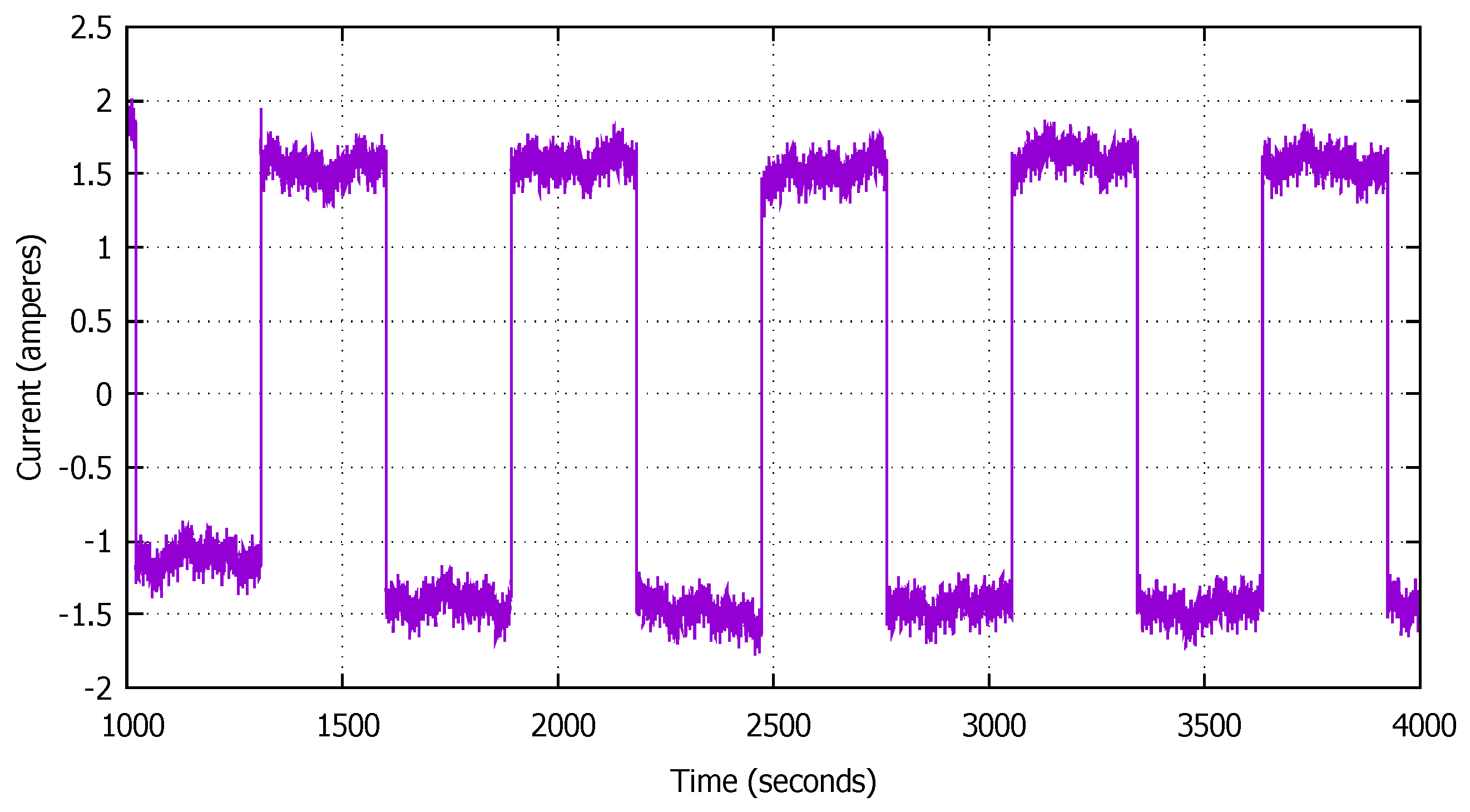
2.1. Battery Cycling and Incremental Capacity and Voltammetric Analysis
2.1.1. Data Processing
2.1.2. Connecting Incremental Capacity and Voltammetry
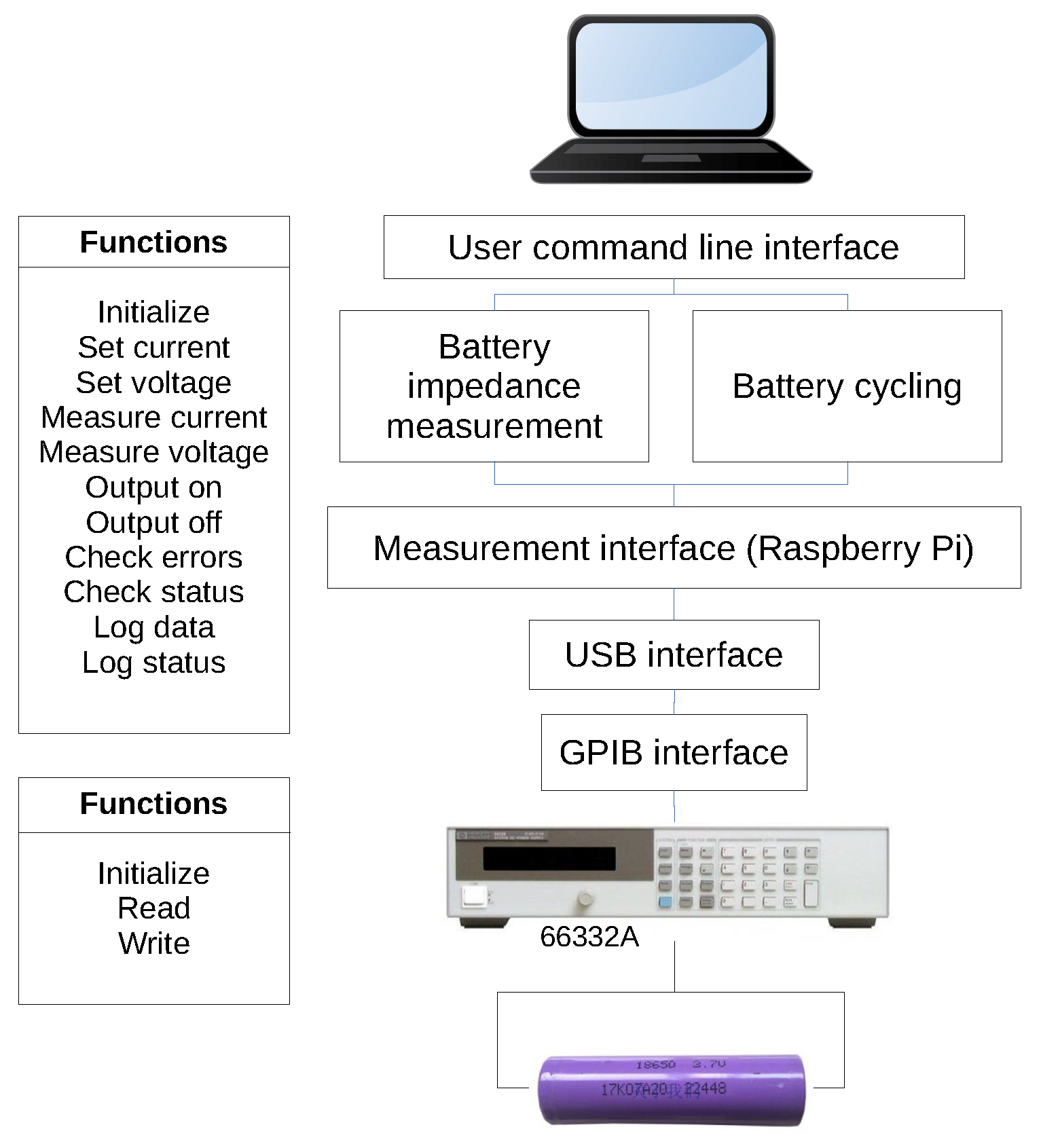
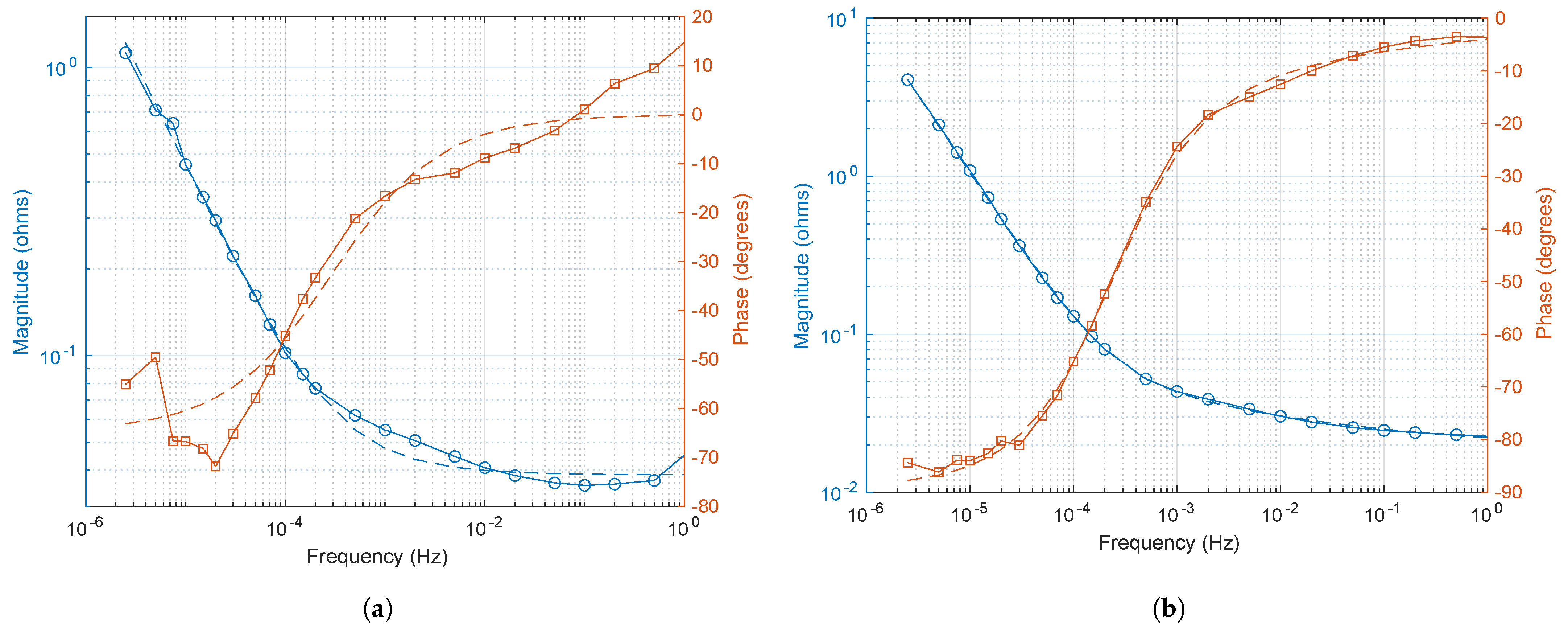
2.2. EIS Measurement
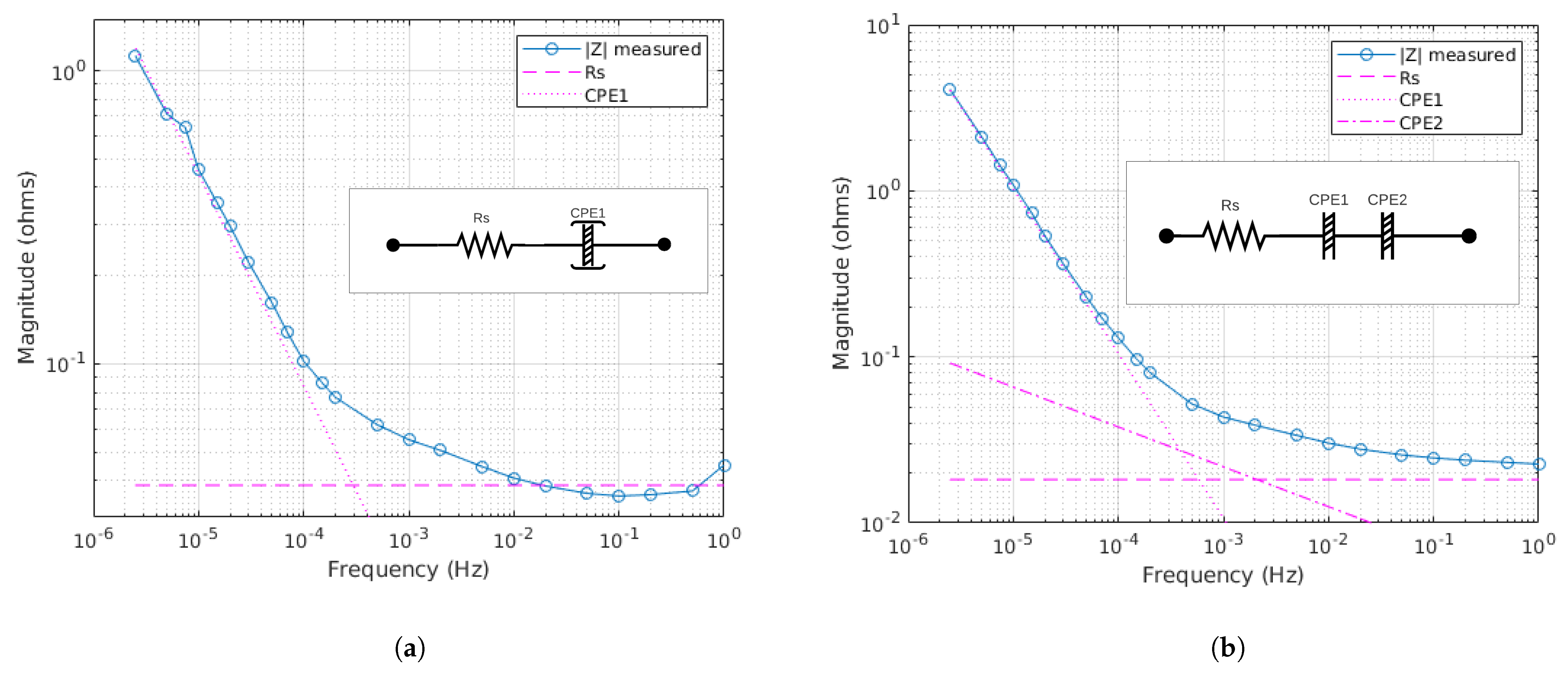
2.3. ECM Fitting
3. Results and Discussion
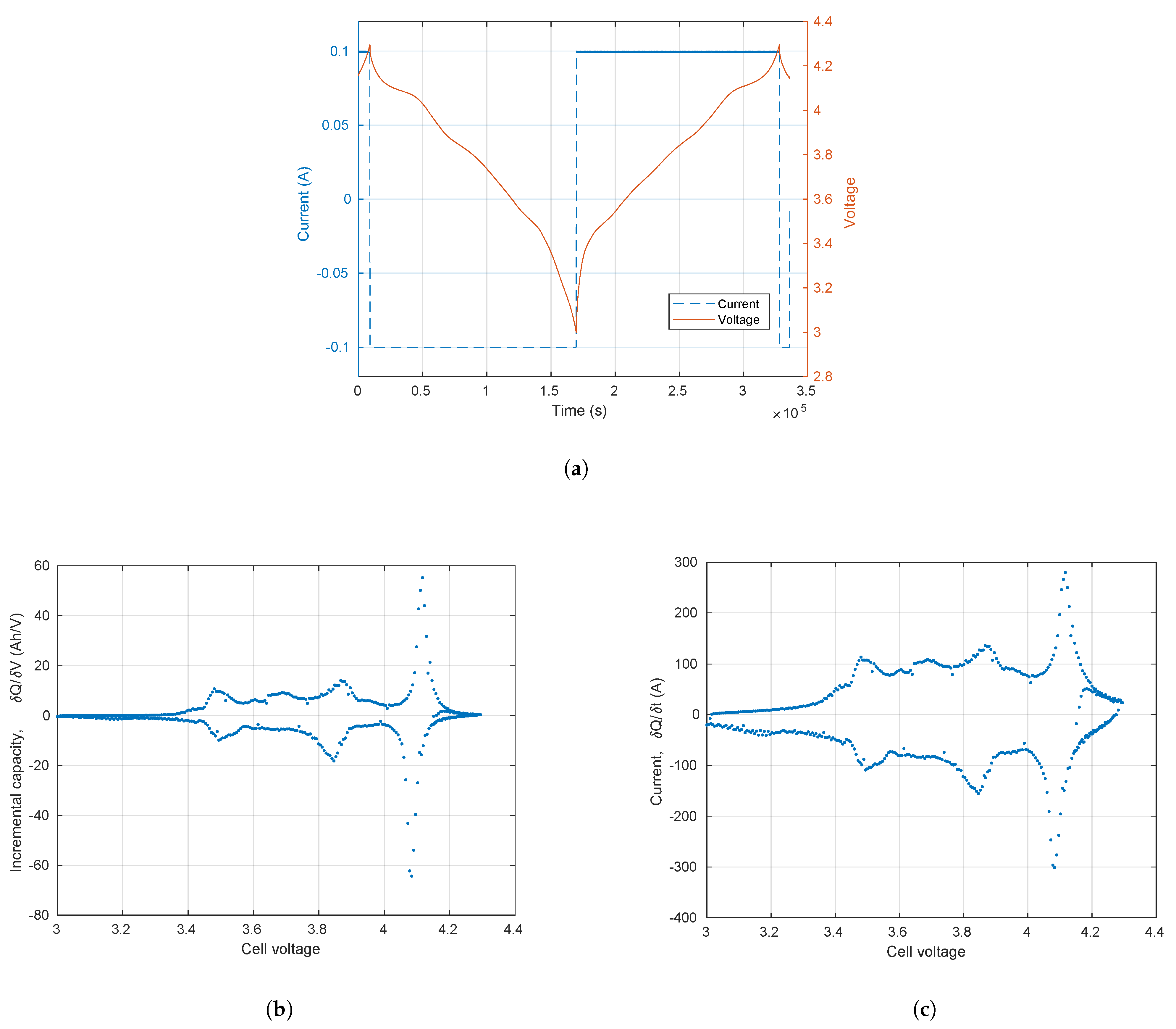
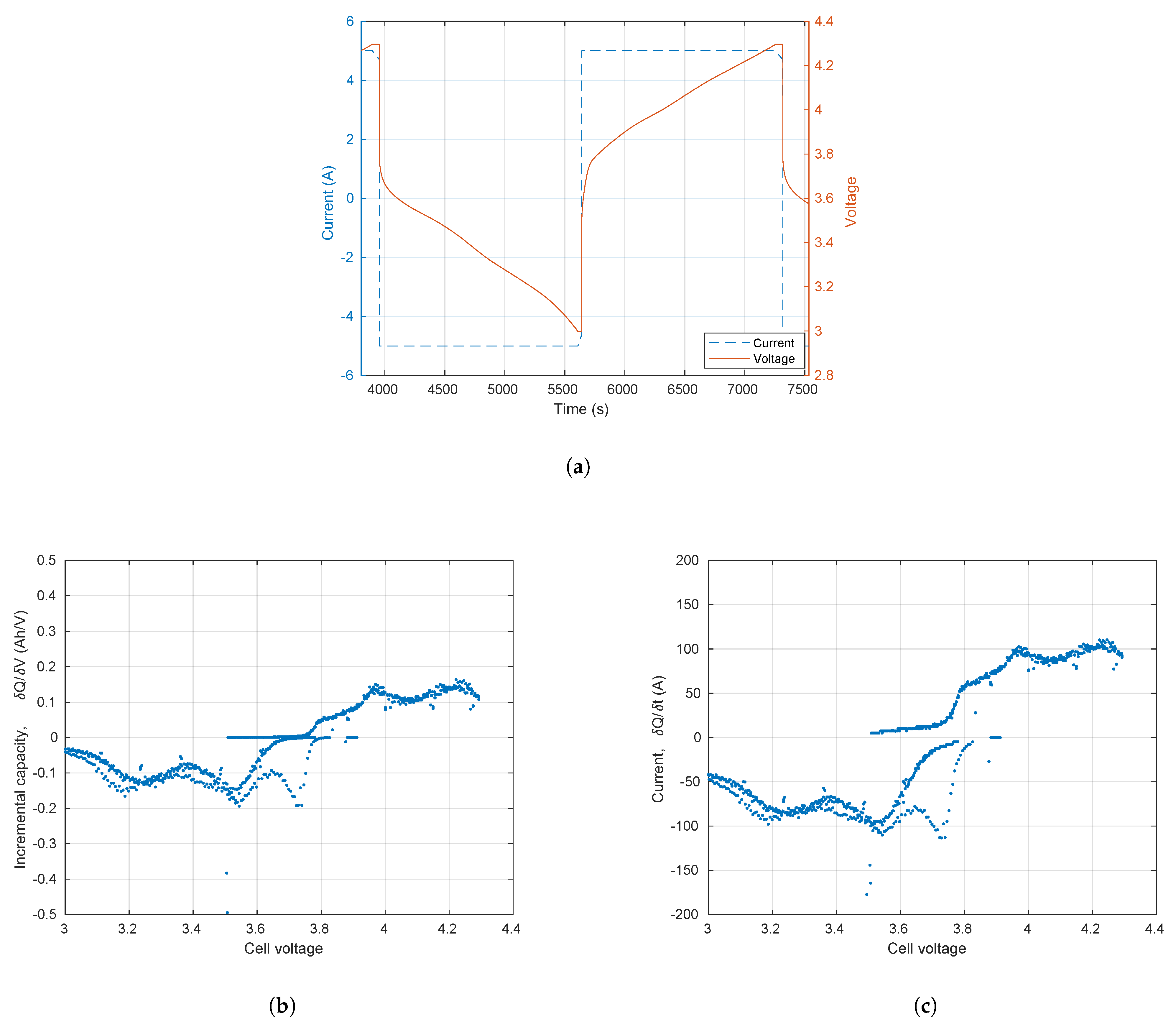
3.1. Incremental Capacity and Voltammetry
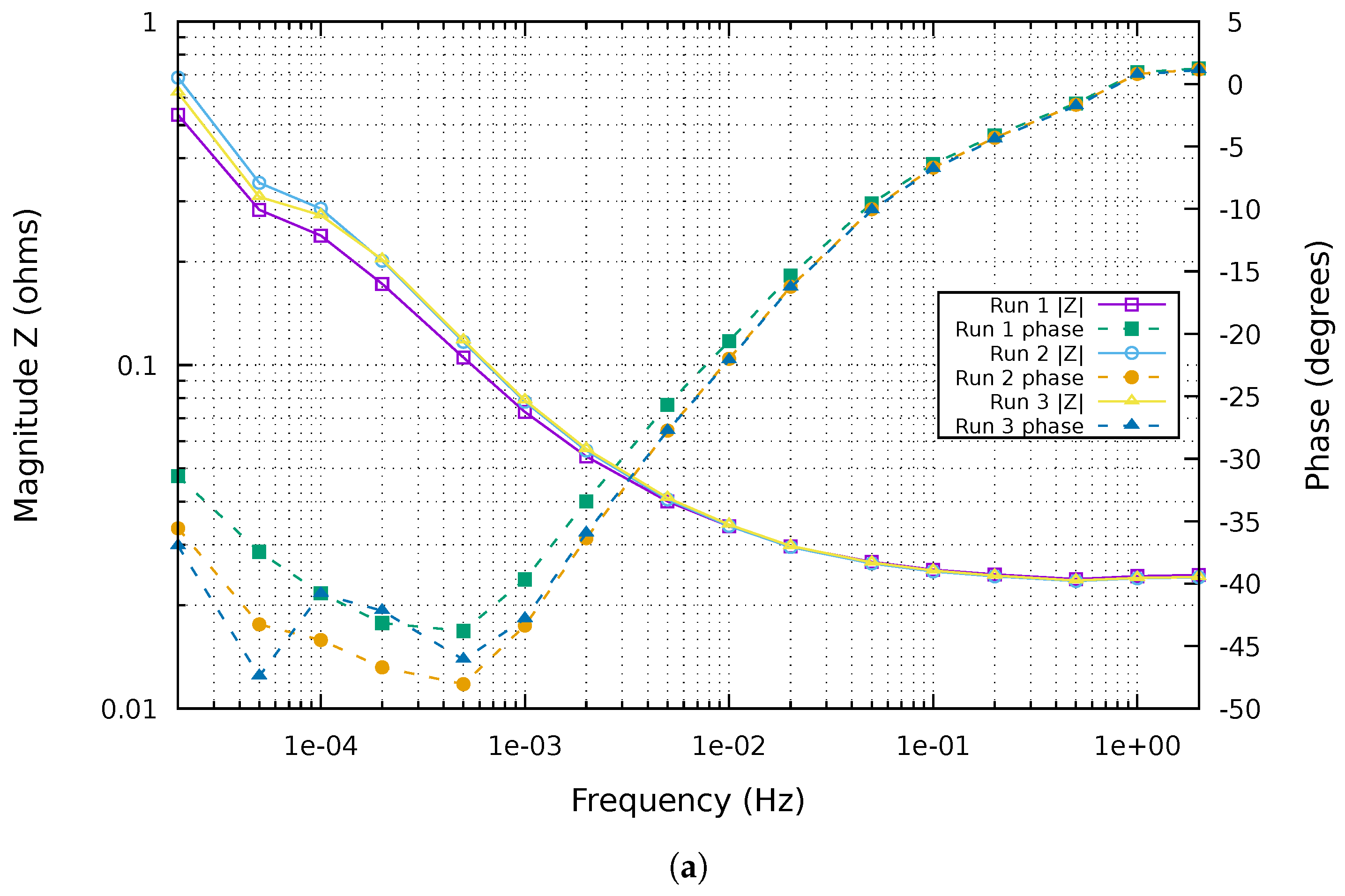
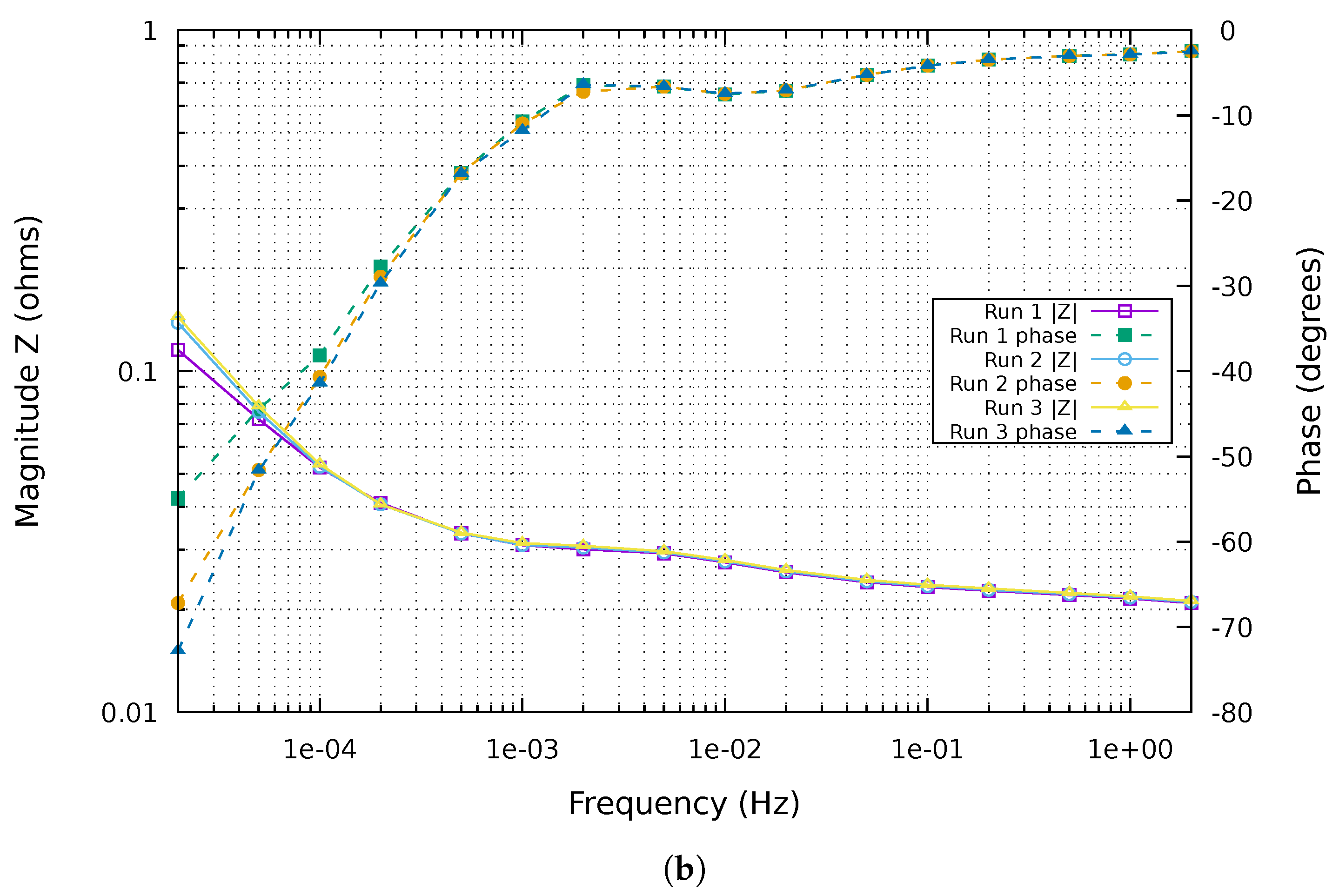
3.2. Conditions for Reliable EIS and ECM Fitting
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CC-CV | Constant current-constant voltage |
| CPE | Constant-phase element |
| CV | Cyclic voltammetry |
| DVA | Differential voltage analysis |
| ECM | Equivalent-circuit model |
| EIS | Electrochemical impedance spectroscopy |
| ELF | Extra-low frequency |
| ICA | Incremental capacity analysis |
| NCA | Lithium nickel cobalt aluminum |
| RMSE | Root mean square error |
References
- Atkins, P.W.; De Paula, J. Atkins’ Physical Chemistry, 8th ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2006. [Google Scholar]
- Anonymous. Linear Sweep and Cyclic Voltammetry: The Principles. 2013. Available online: https://www.ceb.cam.ac.uk/research/groups/rg-eme/Edu/linear-sweep-and-cyclic-voltametry-the-principles (accessed on 21 May 2025).
- Marken, F.; Neudeck, A.; Bond, A.M. Cyclic voltammetry. In Electroanalytical Methods: Guide to Experiments and Applications; Scholtz, F., Ed.; Springer: Berlin, Germany; New York, NY, USA, 2002. [Google Scholar]
- Yu, D.Y.W.; Fietzek, C.; Weydanz, W.; Donoue, K.; Inoue, T.; Kurokawa, H.; Fujitani, S. Study of LiFePO4 by Cyclic Voltammetry. J. Electrochem. Soc. 2007, 154, A253. [Google Scholar] [CrossRef]
- Kurzweil, P.; Scheuerpflug, W.; Frenzel, B.; Schell, C.; Schottenbauer, J. Differential Capacity as a Tool for SOC and SOH Estimation of Lithium Ion Batteries Using Charge/Discharge Curves, Cyclic Voltammetry, Impedance Spectroscopy, and Heat Events: A Tutorial. Energies 2022, 15, 4520. [Google Scholar] [CrossRef]
- Ovejas, V.; Cuadras, A. Battery Aging Impedance Spectroscopy and Incremental Capacity Analysis. In Proceedings of the 10th International Workshop on Impedance Spectroscopy (IWIS): Chair of Measurement and Sensor Technology, Chemnitz, Germany, 26–29 September 2017. [Google Scholar]
- Anseán, D.; García, V.M.; González, M.; Blanco-Viejo, C.; Viera, J.C.; Pulido, Y.F.; Sánchez, L. Lithium-Ion Battery Degradation Indicators Via Incremental Capacity Analysis. IEEE Trans. Ind. Appl. 2019, 55, 2992–3002. [Google Scholar] [CrossRef]
- Vennam, G.; Sahoo, A.; Ahmed, S. A survey on lithium-ion battery internal and external degradation modeling and state of health estimation. J. Energy Storage 2022, 52, 104720. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Lu, D.D.C.; Wang, G.; He, T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Westerhoff, U.; Kurbach, K.; Lienesch, F.; Kurrat, M. Analysis of Lithium-Ion Battery Models Based on Electrochemical Impedance Spectroscopy. Energy Technol. 2016, 4, 1620–1630. [Google Scholar] [CrossRef]
- Poihipi, E.; Scott, J.; Dunn, C. Distinguishability of Battery Equivalent-Circuit Models Containing CPEs: Updating the Work of Berthier, Diard, & Michel. J. Electroanal. Chem. 2022, 911, 116201. [Google Scholar] [CrossRef]
- Talaie, E.; Bonnick, P.; Sun, X.; Pang, Q.; Liang, X.; Nazar, L.F. Methods and Protocols for Electrochemical Energy Storage Materials Research. Chem. Mater. 2017, 29, 90–105. [Google Scholar] [CrossRef]
- Mauracher, P.; Karden, E. Dynamic modelling of lead/acid batteries using impedance spectroscopy for parameter identification. J. Power Sources 1997, 67, 69–84. [Google Scholar] [CrossRef]
- Scott, J.; Hasan, R. New Results for Battery Impedance at Very Low Frequencies. IEEE Access 2019, 7, 106925–106930. [Google Scholar] [CrossRef]
- Hasan, R.; Scott, J. Extending Randles’s Battery Model to Predict Impedance, Charge–Voltage, and Runtime Characteristics. IEEE Access 2020, 8, 85321–85328. [Google Scholar] [CrossRef]
- Dunn, C.; Scott, J. Achieving Reliable and Repeatable Electrochemical Impedance Spectroscopy of Rechargeable Batteries at Extra-Low Frequencies. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Kim, T.; Choi, W.; Shin, H.C.; Choi, J.Y.; Kim, J.M.; Park, M.S.; Yoon, W.S. Applications of Voltammetry in Lithium Ion Battery Research. J. Electrochem. Sci. Technol 2020, 11, 14–25. [Google Scholar] [CrossRef]
- Farrow, V. Characterisation of Rechargeable Batteries: Addressing Fractional Ultralow-Frequency Devices. Master’s Thesis, University of Waikato, Hamilton, New Zealand, 2020. [Google Scholar]
- Scott, J.; Parker, A. Distortion analysis using SPICE. J. Audio Eng. Soc. 1995, 43, 1029–1040. [Google Scholar]
- Randles, J.E.B. Kinetics of rapid electrode reactions. Discuss. Faraday Soc. 1947, 1, 11. [Google Scholar] [CrossRef]
- Lasia, A. Dispersion of Impedances at Solid Electrodes. In Electrochemical Impedance Spectroscopy and Its Applications; Springer: New York, NY, USA, 2014; pp. 177–201. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielect. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Jacquelin, J. The Phasance Concept. Curr. Top. Electrochem. 1997, 4, 127–136. [Google Scholar]
- Choi, W.; Shin, H.C.; Kim, J.M.; Choi, J.Y.; Yoon, W.S. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-ion Batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, C.; Wen, G. Equivalent circuit model analysis on electrochemical impedance spectroscopy of lithium metal batteries. J. Power Sources 2015, 294, 67–74. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Press, W.H. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Jiang, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Gao, Y.; Guo, Q. Recognition of battery aging variations for LiFePO4 batteries in 2nd use applications combining incremental capacity analysis and statistical approaches. J. Power Sources 2017, 360, 180–188. [Google Scholar] [CrossRef]
- Kalogiannis, T.; Stroe, D.I.; Nyborg, J.; Nørregaard, K.; Christensen, A.E.; Schaltz, E. Incremental Capacity Analysis of a Lithium-Ion Battery Pack for Different Charging Rates. ECS Trans. 2017, 77, 403–412. [Google Scholar] [CrossRef]
- Krupp, A.; Ferg, E.; Schuldt, F.; Derendorf, K.; Agert, C. Incremental Capacity Analysis as a State of Health Estimation Method for Lithium-Ion Battery Modules with Series-Connected Cells. Batteries 2020, 7, 2. [Google Scholar] [CrossRef]
- Maures, M.; Zhang, Y.; Martin, C.; Delétage, J.Y.; Vinassa, J.M.; Briat, O. Impact of temperature on calendar ageing of Lithium-ion battery using incremental capacity analysis. Microelectron. Reliab. 2019, 100–101, 113364. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Briat, O.; Delétage, J.Y.; Martin, C.; Chadourne, N.; Vinassa, J.M. Efficient state of health estimation of Li-ion battery under several ageing types for aeronautic applications. Microelectron. Reliab. 2018, 88–90, 1231–1235. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Norregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental Capacity Analysis Applied on Electric Vehicles for Battery State-of-Health Estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Plattard, T.; Barnel, N.; Assaud, L.; Franger, S.; Duffault, J.M. Combining a Fatigue Model and an Incremental Capacity Analysis on a Commercial NMC/Graphite Cell under Constant Current Cycling with and without Calendar Aging. Batteries 2019, 5, 36. [Google Scholar] [CrossRef]
- Huang, M. Incremental Capacity Analysis-Based Impact Study of Diverse Usage Patterns on Lithium-Ion Battery Aging in Electrified Vehicles. Batteries 2019, 5, 59. [Google Scholar] [CrossRef]
- Kim, N.; Shamim, N.; Crawford, A.; Viswanathan, V.V.; Sivakumar, B.M.; Huang, Q.; Reed, D.; Sprenkle, V.; Choi, D. Comparison of Li-ion battery chemistries under grid duty cycles. J. Power Sources 2022, 546, 231949. [Google Scholar] [CrossRef]
| ECM | RMSE | |||||
|---|---|---|---|---|---|---|
| bzdcp66 with 10 mA square wave (negligible working current) | ||||||
| R-CPE | 38.53 | 0.7200 | 2397 | 0.1456 | ||
| R-CPE-CPE | 36.64 | 0.7445 | 3141 | 747.1 | 0.2731 | 0.1439 |
| bzdcp66 with 500 mA square wave (working current) | ||||||
| R-CPE | 26.80 | 0.9053 | 6160 | 0.1479 | ||
| R-CPE-CPE | 18.25 | 0.9913 | 14,250 | 155.3 | 0.2402 | 0.0296 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunn, C.; Scott, J.; Wilson, M.; Mucalo, M.; Cree, M. Incremental Capacity and Voltammetry of Batteries, and Implications for Electrochemical Impedance Spectroscopy. Metrology 2025, 5, 31. https://doi.org/10.3390/metrology5020031
Dunn C, Scott J, Wilson M, Mucalo M, Cree M. Incremental Capacity and Voltammetry of Batteries, and Implications for Electrochemical Impedance Spectroscopy. Metrology. 2025; 5(2):31. https://doi.org/10.3390/metrology5020031
Chicago/Turabian StyleDunn, Christopher, Jonathan Scott, Marcus Wilson, Michael Mucalo, and Michael Cree. 2025. "Incremental Capacity and Voltammetry of Batteries, and Implications for Electrochemical Impedance Spectroscopy" Metrology 5, no. 2: 31. https://doi.org/10.3390/metrology5020031
APA StyleDunn, C., Scott, J., Wilson, M., Mucalo, M., & Cree, M. (2025). Incremental Capacity and Voltammetry of Batteries, and Implications for Electrochemical Impedance Spectroscopy. Metrology, 5(2), 31. https://doi.org/10.3390/metrology5020031







