An Advanced Synchronized Time Digital Grid Twin Testbed for Relay Misoperation Analysis of Electrical Fault Type Detection Algorithms
Abstract
1. Introduction
2. The Set-Default Relay Method vs. the Boundary Admittance Method
2.1. The Set-Default Relay Method
2.2. The Boundary Admittance Method
3. Materials and Methods
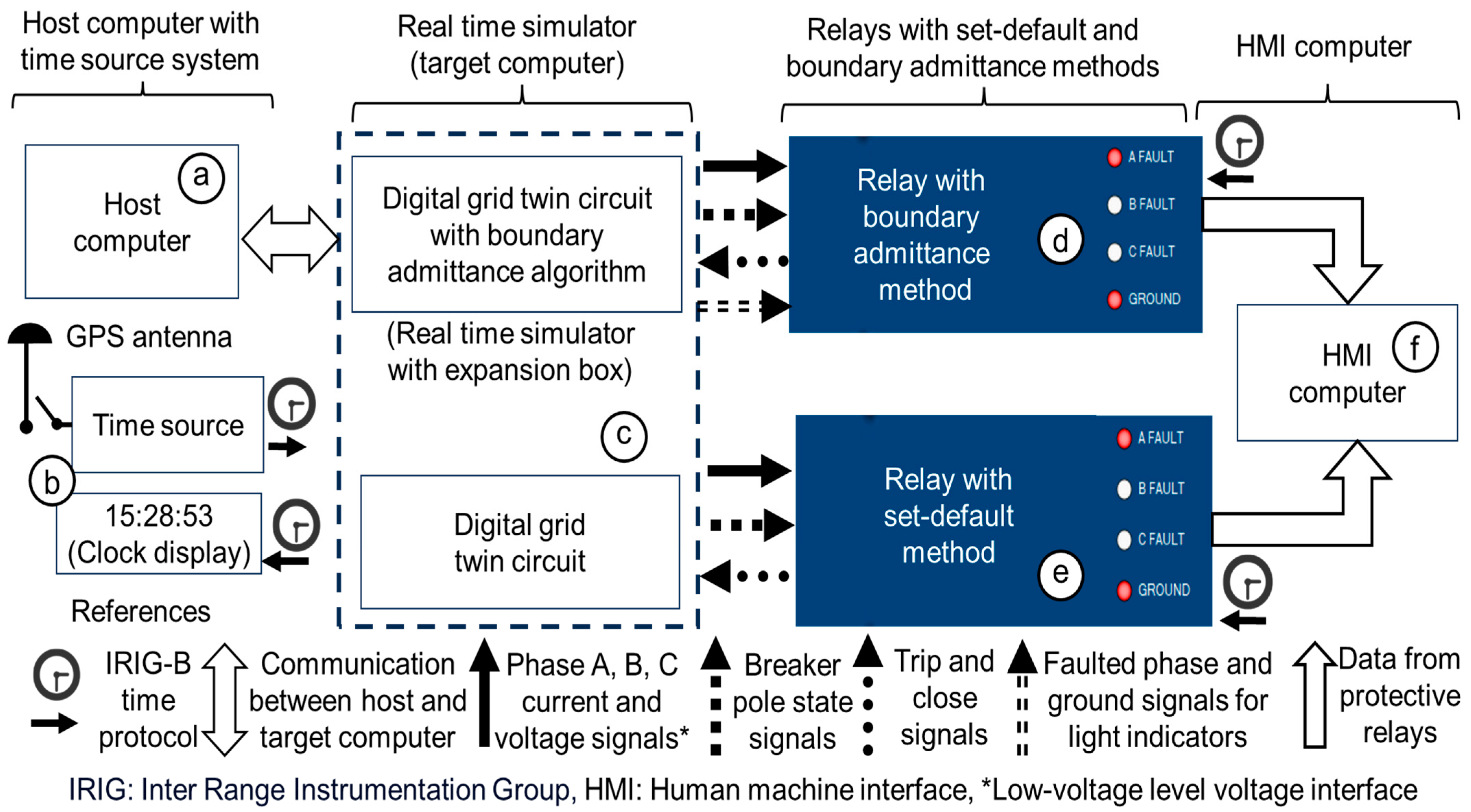
3.1. The Advanced Synchronized Time Digital Grid Twin Testbed with Paired Relays
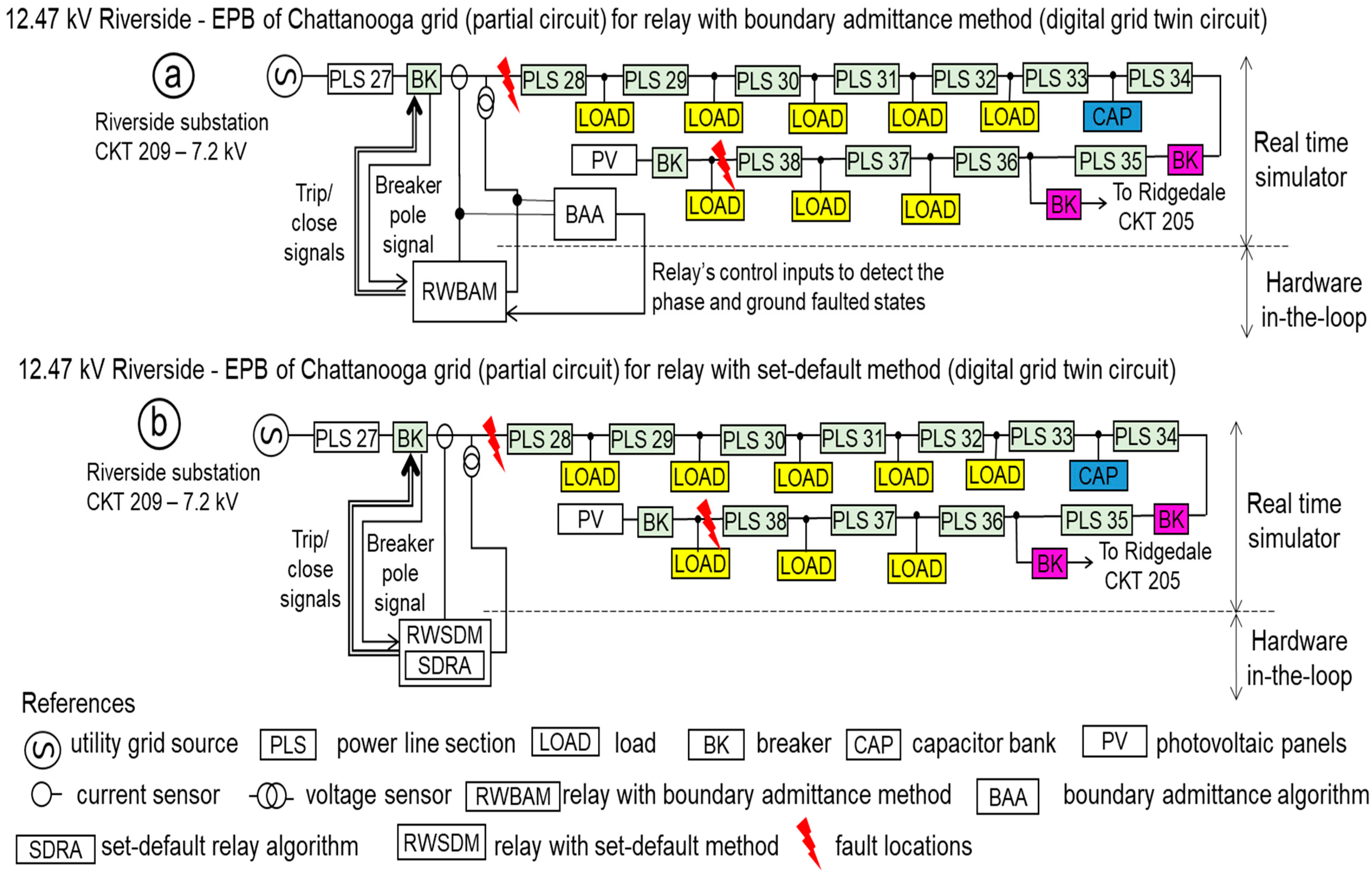
3.2. A Single-Line Diagram of the Digital Grid Twin
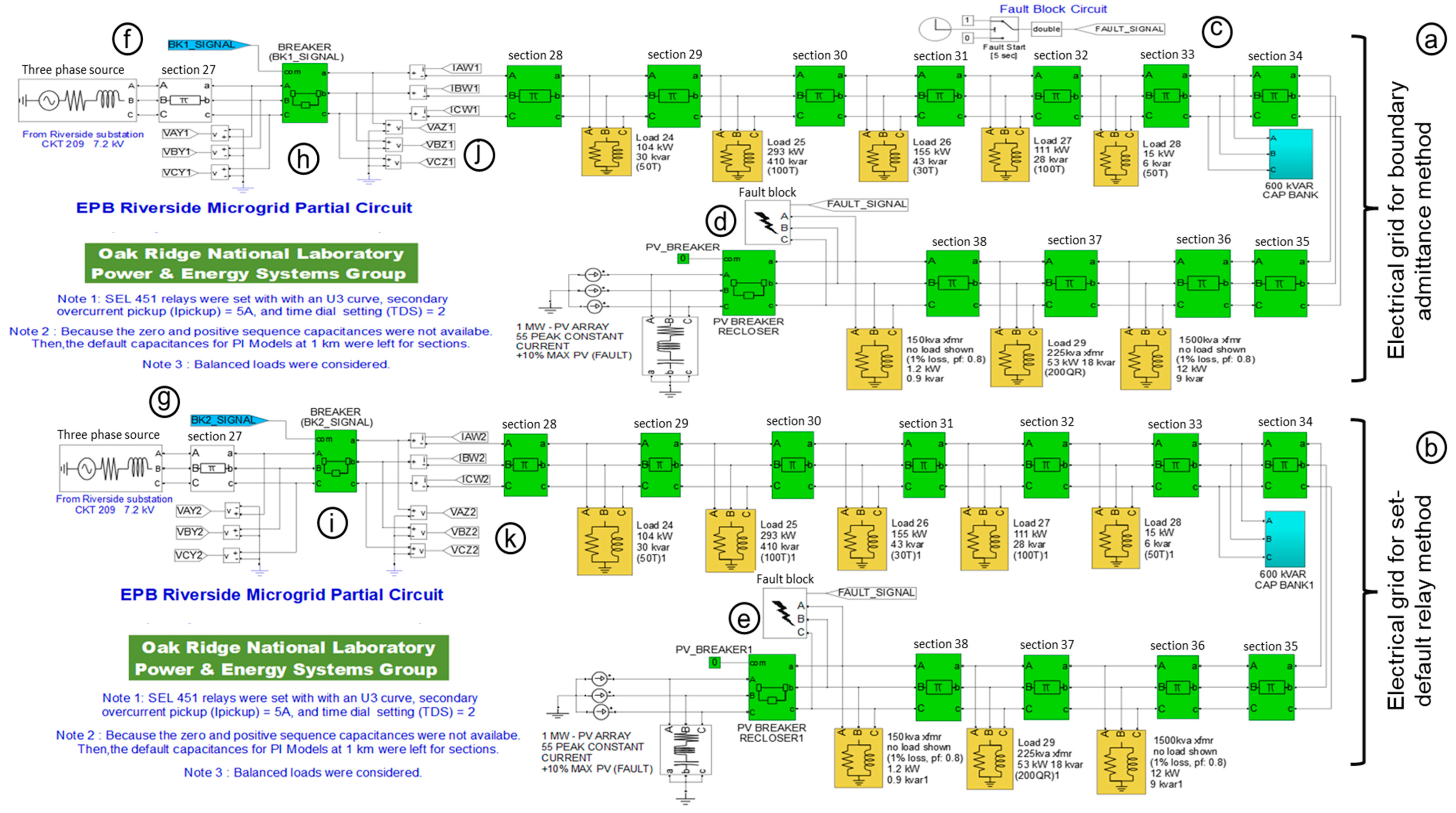
3.3. A Three-Line Diagram of the Digital Grid Twin
3.4. Twin Relay Settings
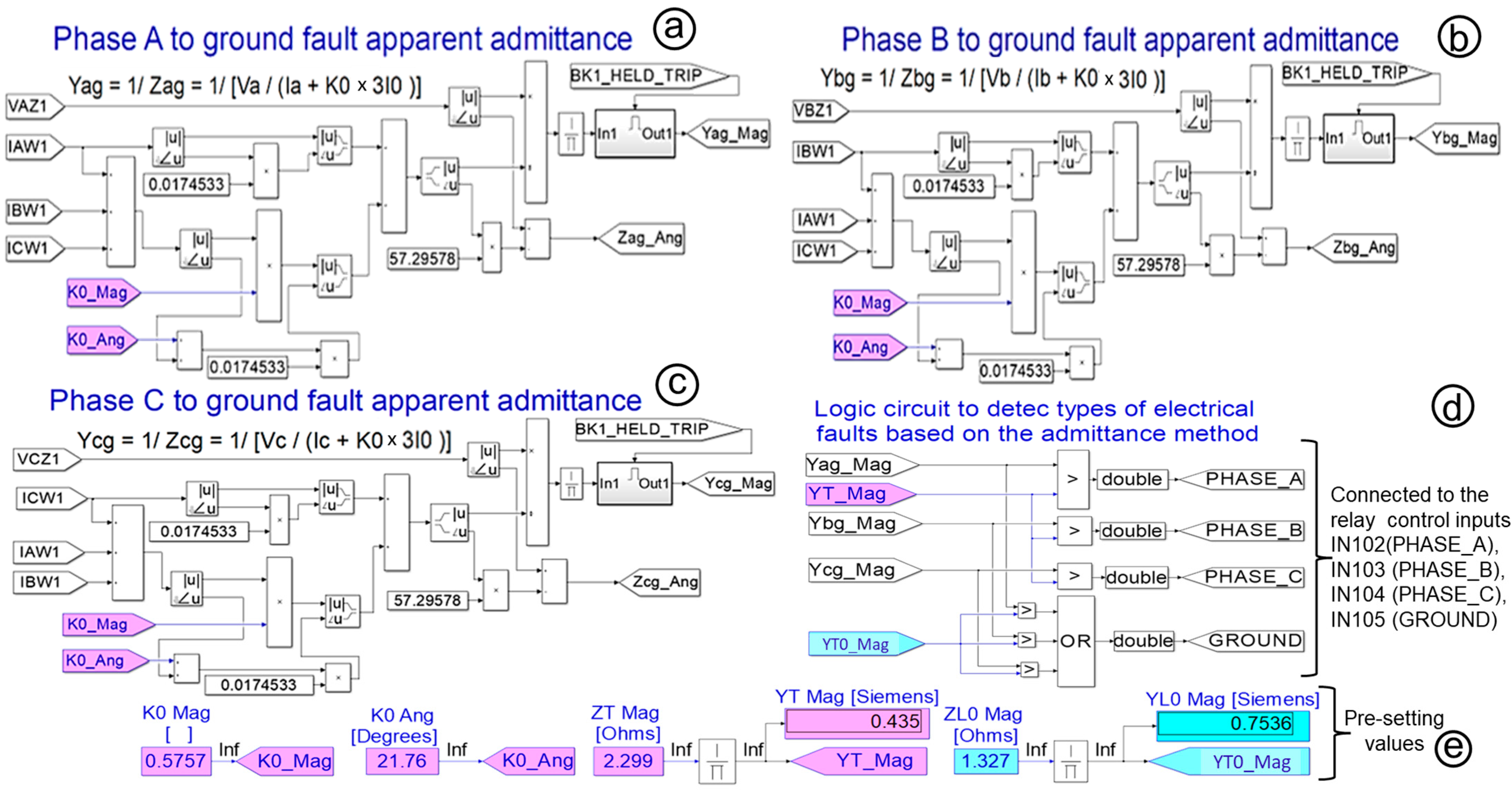
3.5. The Algorithm, Logic Circuit, and Boundaries
4. Results
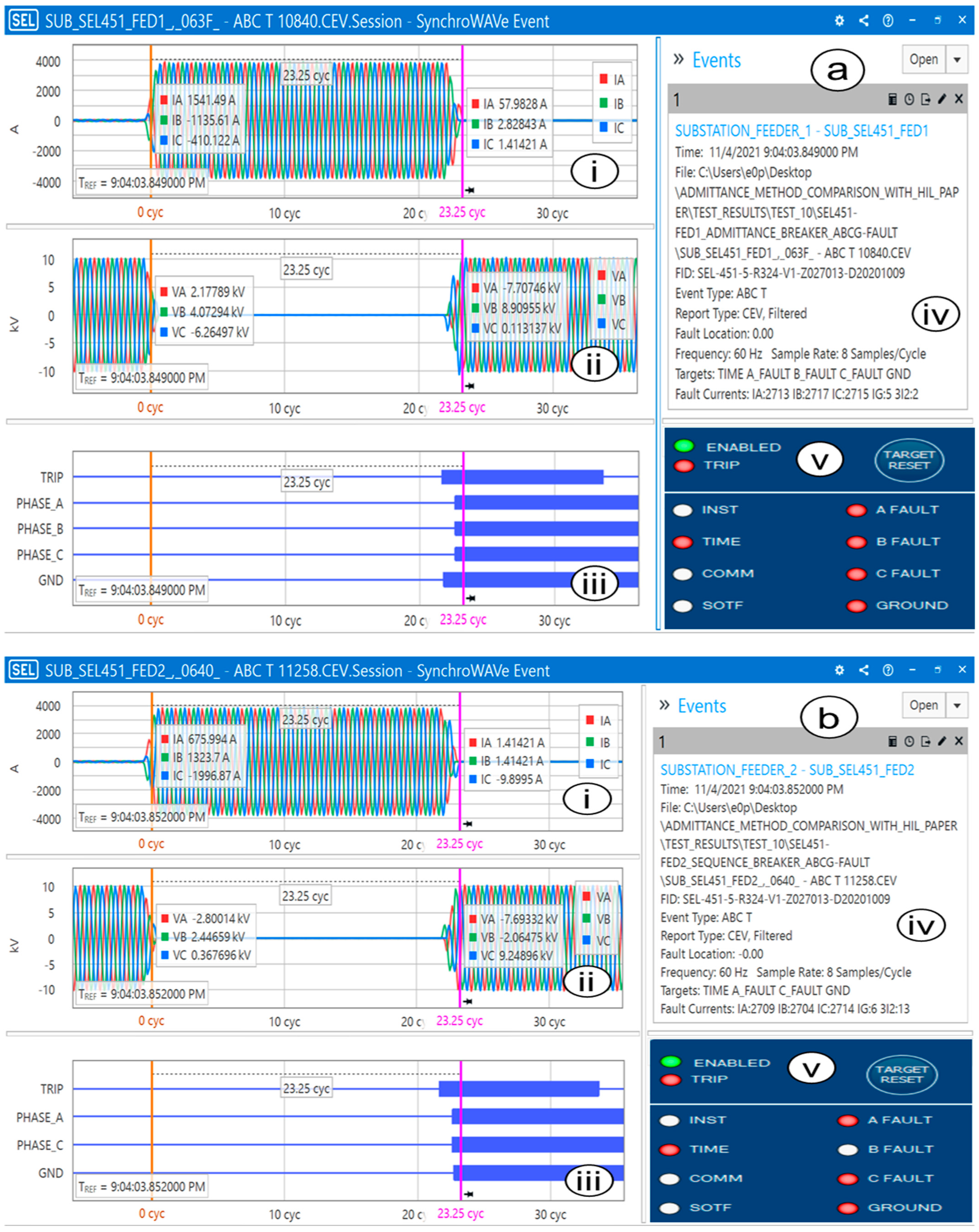
4.1. Events and Tests
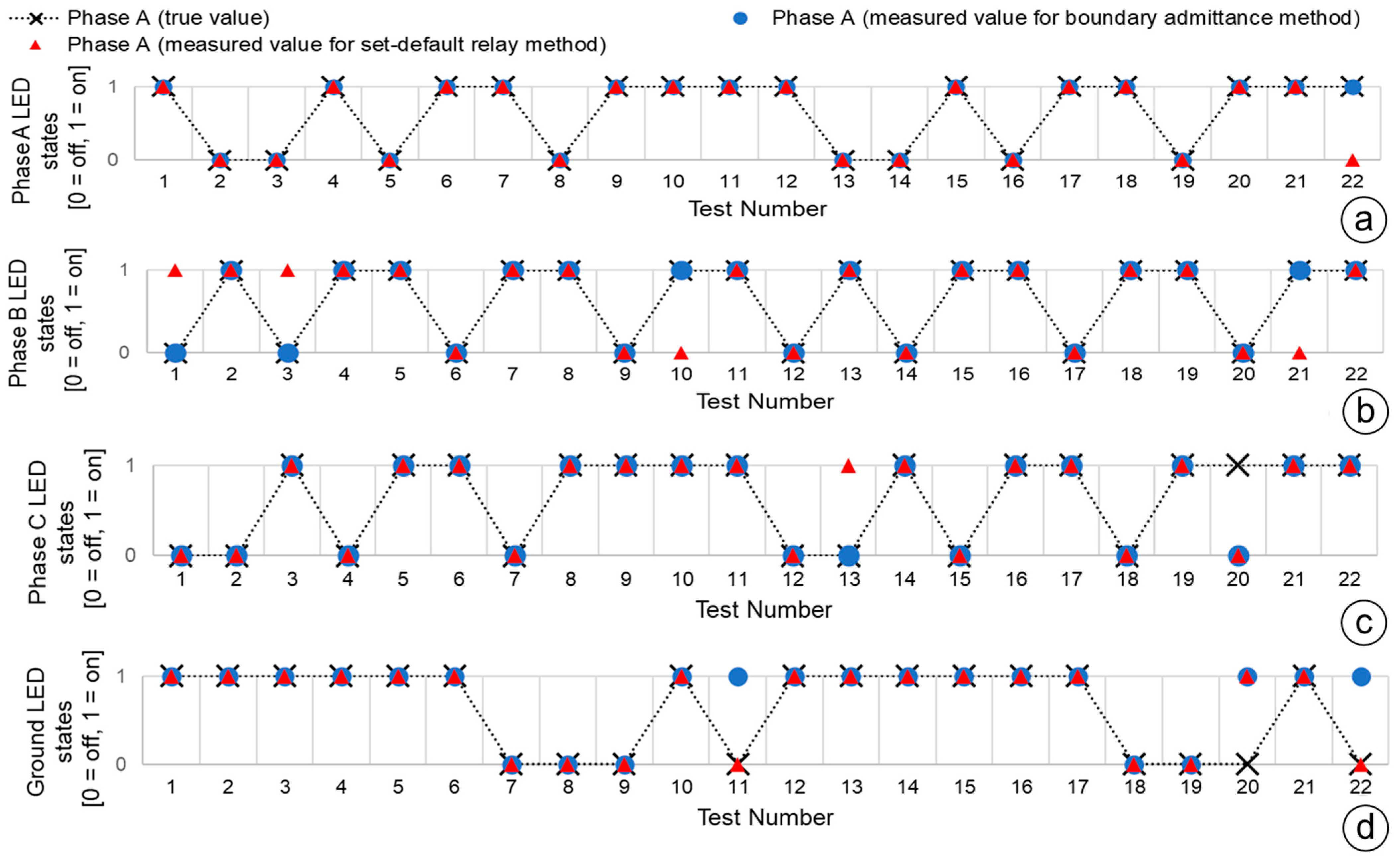
4.2. Analysis of the Measured Phase and Ground LED States
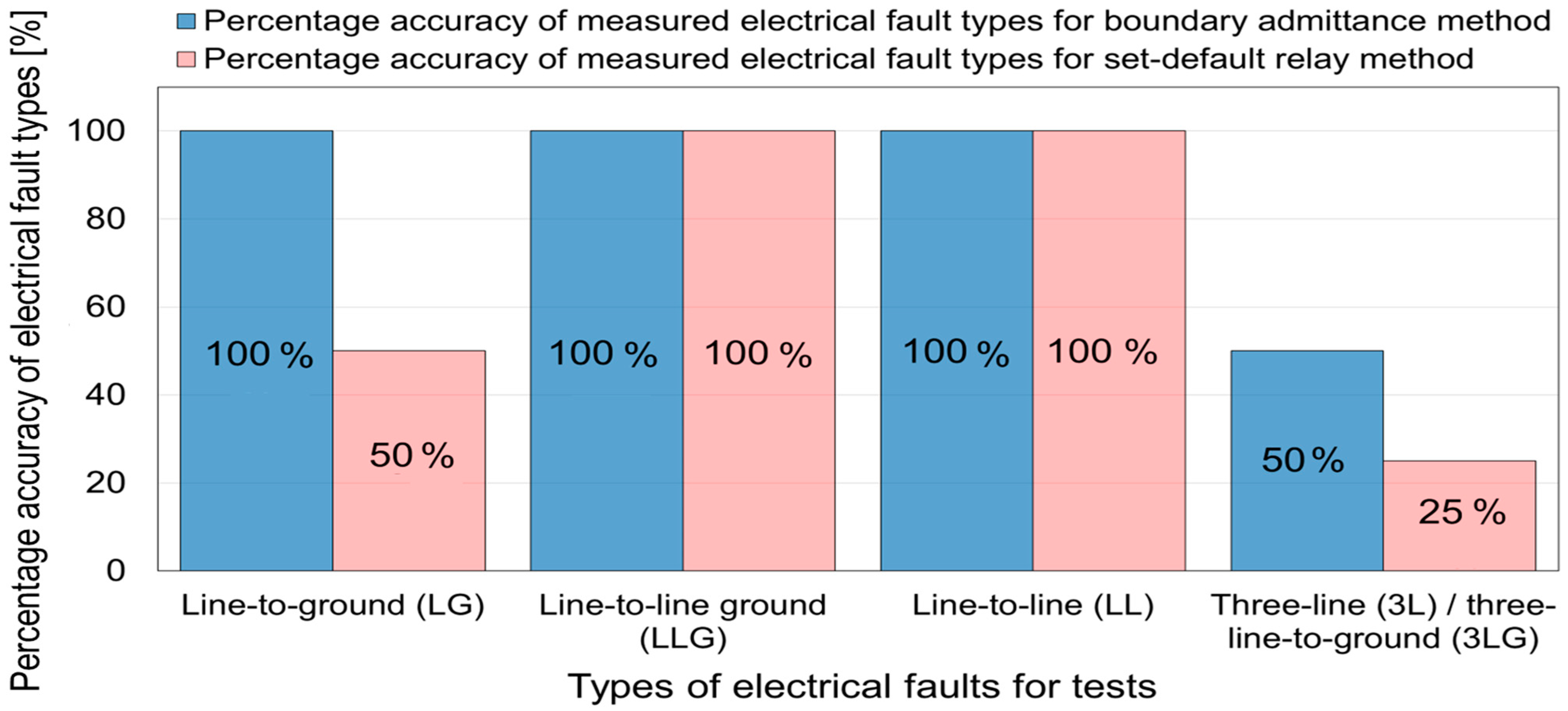
4.3. Analysis of the Measured Electrical Fault Types
5. Discussion
- Main novelty: The ASTDGT testbed method was created to evaluate external relay algorithms because no specific standards are available for testing external relay algorithms; therefore, the ASTDGT testbed’s main contribution was focused on comparing the test results for the boundary admittance method (external algorithm) to those for the set-default relay method (internal algorithm) to assess an external relay algorithm for detecting electrical fault types.
- A platform with complex grids and high sampling frequencies: The ASTDGT testbed (Figure 3) has a digital grid twin circuit (Figure 6) created with an RTS and a time step of 50 us (sampling frequency of 20 kHz). The digital grid twin circuit is formed of breakers, power line sections, capacitor banks, and source models from MATLAB/Simulink (Figure 6), offering a realistic simulation approach for electrical fault scenarios and relays with high sampling frequencies greater than 3 kHz. Thus, the ASTDGT testbed presents a better simulation approach than commercial relay test systems [36,37,38], which are formed with one three-phase voltage/current source that cannot implement complex electrical grids and has a frequency limitation of 3 kHz [42].
- A digital grid twin to commission relays with synchronized time stamps: The ASTDGT testbed (Figure 3) can commission internal and external relay algorithms at the same time with multiple relays. In this case, two identical relays were used to evaluate the set-default relay method (internal algorithm) and the boundary admittance method (external algorithm) using a digital grid twin circuit (Figure 6) and a synchronized time source system (Figure 3) to evaluate the event behavior for both relays with the same time stamps.
- The application of time domain external relay algorithms: The ASTDGT implements the boundary admittance algorithm (Figure 3c), formed of an external relay algorithm (Figure 7) in an RTS. The implementation of this external relay algorithm using an RTS could be a great tool for integration with relays in the field in the future, considering RTSs are based on a time domain process with a time step of 50 us, which could speed the relay’s decisions up in some critical situations, such as the operation of breakers for inverter-based DERs.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jagadeesan Nair, V.; Venkataramanan, V.; Haider, R.; Annaswamy, A.M. A Hierarchical Local Electricity Market for a DER-Rich Grid Edge. IEEE Trans. Smart Grid 2022, 14, 1353–1366. [Google Scholar] [CrossRef]
- Memon, A.A.; Karimi, M.; Kauhaniemi, K. Evaluation of New Grid Codes for Converter-Based DERs from the Perspective of AC Microgrid Protection. IEEE Access 2022, 10, 127005–127030. [Google Scholar] [CrossRef]
- Chapagain, P.; Culler, M.; Ishchenko, D.; Valdes, A. Stability Impact of IEEE 1547 Operational Mode Changes under High DER Penetration in the Presence of Cyber Adversary. In Proceedings of the 2021 IEEE Green Technologies Conference, Denver, CO, USA, 7–9 April 2021; pp. 67–74. [Google Scholar] [CrossRef]
- Ravi, A.; Bai, L.; Cecchi, V.; Ding, F. Stochastic Strategic Participation of Active Distribution Networks with High-Penetration DERs in Wholesale Electricity Markets. IEEE Trans. Smart Grid 2022, 14, 1515–1527. [Google Scholar] [CrossRef]
- PRC-004.6; Protection System Misoperation Identification and Correction. North American Electric Reliability Corporation: Atlanta, GA, USA, 2019; pp. 1–32. Available online: https://www.nerc.com/pa/Stand/Reliability%20Standards/PRC-004-6.pdf (accessed on 17 July 2024).
- Bian, J.J.; Slone, A.D.; Tatro, P.J. Protection system misoperation analysis. In Proceedings of the 2014 IEEE PES General Meeting, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. Available online: https://ieeexplore.ieee.org/document/6939488 (accessed on 21 June 2024).
- Welton, D.; Knapek, W. Important Considerations for Testing and Commissioning Digital Protective Relays: Avoid Misoperations. IEEE Ind. Appl. Mag. 2019, 25, 24–28. Available online: https://ieeexplore.ieee.org/document/8691670 (accessed on 21 June 2024). [CrossRef]
- Hosseini, M.; Stephen, B.; McArthur, S.D.; Helm, J. Current Based Trip Coil Analysis of Circuit Breakers for Fault Diagnosis. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe, Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Biswas, S.S.; Srivastava, A.K.; Whitehead, D. A Real-Time Data-Driven Algorithm for Health Diagnosis and Prognosis of a Circuit Breaker Trip Assembly. IEEE Trans. Ind. Electron. 2014, 62, 3822–3831. [Google Scholar] [CrossRef]
- Kasztenny, B.; Mynam, M.V.; Fischer, N. Sequence Component Applications in Protective Relays—Advantages, Limitations, and Solutions. In Proceedings of the 46th Annual Western Protective Relay Conference, Spokane, WA, USA, 22–24 October 2019; pp. 1–23. Available online: https://selinc.com/api/download/125781/ (accessed on 17 July 2024).
- Costello, D.; Zimmerman, K. Determining the Faulted Phase. In Proceedings of the 63rd Annual Conference for Protective Relay Engineers, College Station, TX, USA, 29 March–1 April 2010; pp. 1–20. Available online: https://selinc.com/api/download/6381/ (accessed on 17 July 2024).
- Zimmerman, B.; Costello, D. Impedance-Based Fault Location Experience. SEL J. Reliab. Power 2010, 1, 1–28. Available online: https://selinc.com/api/download/4912 (accessed on 17 July 2024).
- C37.113-2015; IEEE Guide for Protective Relay Applications to Transmission Lines. IEEE: Piscataway, NJ, USA, 2016. Available online: https://standards.ieee.org/standard/C37_113-2015.html (accessed on 21 June 2024).
- Fentie, D.D. Understanding the Dynamic Mho Distance Characteristic. In Proceedings of the 69th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 4–7 April 2016; pp. 1–15. [Google Scholar] [CrossRef]
- C37.2-2008; IEEE Standard Electrical Power System Device Function Numbers, Acronyms, and Contact Designations. IEEE: Piscataway, NJ, USA, 2008. Available online: https://standards.ieee.org/standard/C37_2-2008.html (accessed on 17 July 2024).
- Godoy, E.; Celaya, A.; Altuve, H.J.; Fischer, N.; Guzmán, A. Tutorial on Single-Pole Tripping and Reclosing. In Proceedings of the 39th Annual Western Protective Relay Conference, Spokane, WA, USA, 16–18 October 2012; pp. 1–21. [Google Scholar]
- Haleem, A.M.; Sharma, M.; Sajan, K.; Babu, K.D. A Comparative Review of Fault Location/Identification Methods in Distribution Networks. In Proceedings of the 2018 1st International Conference on Advanced Research in Engineering Sciences, Dubai, United Arab Emirates, 7–9 January 2018; pp. 1–6. [Google Scholar] [CrossRef]
- SEL-451-5 Protection, Automation, and Bay Control System Instruction Manual. 2017. Available online: https://selinc.com/products/451/docs/ (accessed on 17 July 2024).
- Wang, L. The Fault Causes of Overhead Lines in Distribution Network. MATEC Web Conf. 2016, 61, 02017. [Google Scholar] [CrossRef]
- Liu, P.; Huang, C. Detecting Single-Phase-to-Ground Fault Event and Identifying Faulty Feeder in Neutral Inefectively Grounded Distribution System. IEEE Trans. Power Deliv. 2017, 33, 2265–2273. [Google Scholar] [CrossRef]
- SPAJ 142 C Overcurrent and Earth-Fault Relay, User’s Manual and Technical Description, ABB. 2002. Available online: https://library.e.abb.com/public/b3cb5ff579b5707dc2256bf1002cfb67/FM_SPAJ142C_EN_BAC.pdf (accessed on 17 July 2024).
- Piesciorovsky, E.C.; Smith, T.; Ollis, T.B. Protection schemes used in North American microgrids. Int. Trans. Electr. Energy Syst. 2020, 30, e12461. [Google Scholar] [CrossRef]
- Bo, Z.; Caunce, B.; Redfern, M.; Dong, X. Under Voltage Accelerated Protection of Single Source Distribution Systems. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; pp. 2066–2071. [Google Scholar] [CrossRef]
- Liang, X.; Wallace, S.A.; Nguyen, D. Rule-Based Data-Driven Analytics for Wide-Area Fault Detection Using Synchrophasor Data. IEEE Trans. Ind. Appl. 2016, 53, 1789–1798. [Google Scholar] [CrossRef]
- Alstom Grid Worldwide Contact Centre. Distance Protection. In Network Protection & Automation Guide; Alstom Grid: Paris, France, 2022; Chapter 11; pp. 171–191. [Google Scholar]
- Wilkinson, S.B.; Mathews, C.A. Dynamic Characteristics of Mho Distance Relays, GE Power Management, GER-3742. Available online: https://www.gegridsolutions.com/products/applications/ger3742.pdf (accessed on 17 July 2024).
- Roberts, J.; Guzman, A. Schweitzer III EO, Z = V/I Does Not Make a Distance Relay. In Proceedings of the 48th Annual Georgia Tech Protective Relaying Conference, Atlanta, GA, USA, 9–21 October 1994; pp. 1–20. Available online: https://selinc.com/api/download/2429?id=2429 (accessed on 17 July 2024).
- Piesciorovsky, E.C.; Morales Rodriguez, M.E. Assessment of the Phase-to-Ground Fault Apparent Admittance Method with Phase/Ground Boundaries to Detect Types of Electrical Faults for Protective Relays Using Signature Library and Simulated Events. Int. Trans. Electr. Energy Syst. 2022, 2022, 1951836. [Google Scholar] [CrossRef]
- Jeong, D.-Y.; Baek, M.-S.; Lim, T.-B.; Kim, Y.-W.; Kim, S.-H.; Lee, Y.-T.; Jung, W.-S.; Lee, I.-B. Digital Twin: Technology Evolution Stages and Implementation Layers With Technology Elements. IEEE Access 2022, 10, 52609–52620. [Google Scholar] [CrossRef]
- Jamakatel, P.; Eberhardt, M.; Kerber, F. Development of a Toolchain for Automated Optical 3D Metrology Tasks. Metrology 2022, 2, 274–292. [Google Scholar] [CrossRef]
- Scholz, G.; Fortmeier, I.; Marschall, M.; Stavridis, M.; Schulz, M.; Elster, C. Experimental Design for Virtual Experiments in Tilted-Wave Interferometry. Metrology 2022, 2, 84–97. [Google Scholar] [CrossRef]
- Vlaeyen, M.; Haitjema, H.; Dewulf, W. Uncertainty-Based Autonomous Path Planning for Laser Line Scanners. Metrology 2022, 2, 479–494. [Google Scholar] [CrossRef]
- Straka, M.; Weissenbrunner, A.; Koglin, C.; Höhne, C.; Schmelter, S. Simulation Uncertainty for a Virtual Ultrasonic Flow Meter. Metrology 2022, 2, 335–359. [Google Scholar] [CrossRef]
- Lindqvist, R.P.; Strand, D.; Nilsson, M.; Collins, V.; Torstensson, J.; Kressin, J.; Spensieri, D.; Archenti, A. 3D Model-Based Large-Volume Metrology Supporting Smart Manufacturing and Digital Twin Concepts. Metrology 2023, 3, 29–64. [Google Scholar] [CrossRef]
- Barbie, A.; Hasselbring, W. From Digital Twins to Digital Twin Prototypes: Concepts, Formalization, and Applications. IEEE Access 2024, 12, 75337–75365. [Google Scholar] [CrossRef]
- F6000 Family of Power System Simulators User Guide, Doble Engineering Company, 2001, 72A-1589 Rev. C. Available online: https://www.trs-rentelco.com/Specs-Manuals/Doble-F6000-Series-Users-Guide-5121.pdf (accessed on 17 July 2024).
- CMC 356 User Manual, Omicron® Electronics. 2020. Available online: https://pesvs.com.au/wp-content/uploads/2022/05/CMC-356-User-Manual.pdf (accessed on 17 July 2024).
- MTS-5100 Protective Relay Test System User Manual, Manta Test Systems, First Edition. 2012. Available online: https://www.doble.com/wp-content/uploads/MTS-5100_User_Manual.pdf (accessed on 17 July 2024).
- Percentage Accuracy Calculator Weblink, Calculator Academy Team. Available online: https://calculator.academy/percentage-accuracy-calculator/ (accessed on 17 July 2024).
- Piesciorovsky, E.C.; Borges Hink, R.; Werth, A.; Hahn, G.; Lee, A.; Polsky, Y. Assessment and Commissioning of Electrical Substation Grid Testbed with a Real-Time Simulator and Protective Relays/Power Meters in the Loop. Energies 2023, 16, 4407. [Google Scholar] [CrossRef]
- Piesciorovsky, E.C.; Smith, T.; Mukherjee, S.K.; Marshall, M.W. A generic method for interfacing IEDs using low voltage interfaces to real-time simulators with hardware in the loop. Electr. Power Syst. Res. 2021, 199, 107431. [Google Scholar] [CrossRef]
- Piesciorovsky, E.C.; Karnowski, T. Variable Frequency Response Testbed to Validate Protective Relays up to 20 kHz. Electr. Power Syst. Res. 2021, 194, 107071. [Google Scholar] [CrossRef]
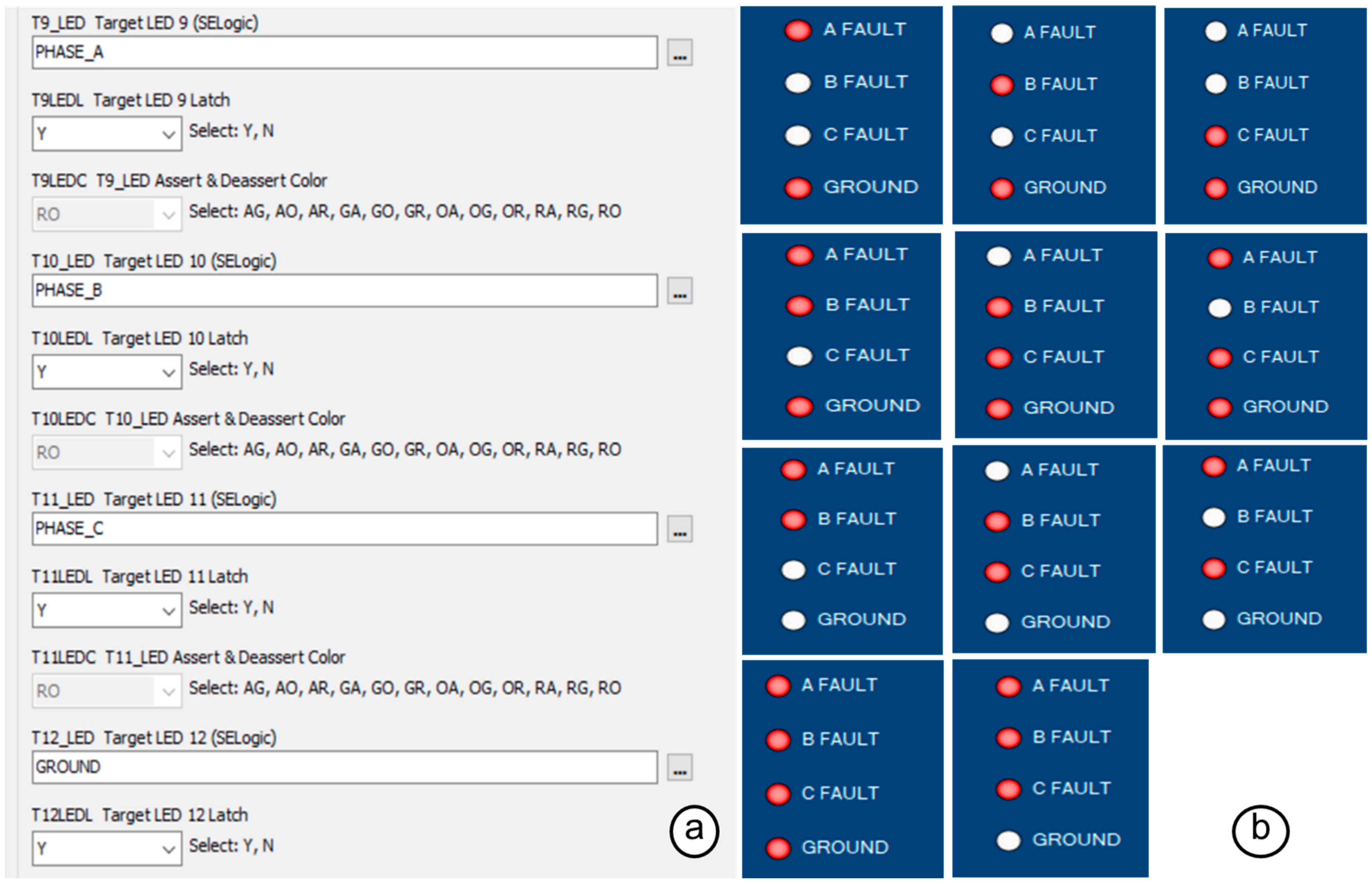



| Relay Front Panel Location and Setting Identification | Relay Target LED Settings | ||
|---|---|---|---|
| Relay front panel location | Relay setting identification | Set-default (internal algorithm) relay method | Boundary admittance (external algorithm) method |
| A FAULT | T9_LED | PHASE_A | IN102 |
| B FAULT | T10_LED | PHASE_B | IN103 |
| C FAULT | T11_LED | PHASE_C | IN104 |
| GROUND | T12_LED | GROUND | IN105 |
| 1—Computation of Total Resistance and Reactance from Power Line Sections 28–38 | 2—Computation of Total Admittance | 3—Computation of Boundaries | |||
|---|---|---|---|---|---|
| RT1 | XT1 | RT = 2 RT1 + RT0 | XT = 2 XT1 + XT0 | |YT| | |Ypg| > |YT| |
| 0.3044 Ω | 0.3900 Ω | 1.1518 Ω | 1.9904 Ω | 0.435 S | |Ypg| > 0.435 S |
| RT0 | XT0 | |YT0| | |Ypg| > |YT0 | | ||
| 0.5430 Ω | 1.2104 Ω | 0.7536 S | |Ypg| > 0.7536 S | ||
| Test No. | Test Name (Method_Fault Location_Fault Type) | Measured Values | True Values | |||||
|---|---|---|---|---|---|---|---|---|
| Relay Event No. | Electrical Fault on Relay’s LED | Results | Electrical Fault in MATLAB Fault Block | |||||
| FAULT A | FAULT B | FAULT C | GND | |||||
| 1 | BOUNDARY ADMITTANCE METHOD_BREAKER_AG | 10,814 | X | X | AG | AG | ||
| SET-DEFAULT RELAY METHOD_BREAKER_AG | 11,232 | X | X | X | ABG | |||
| 2 | BOUNDARY ADMITTANCE METHOD_BREAKER_BG | 10,815 | X | X | BG | BG | ||
| SET-DEFAULT RELAY METHOD_BREAKER_BG | 11,233 | X | X | BG | ||||
| 3 | BOUNDARY ADMITTANCE METHOD_BREAKER_CG | 10,816 | X | X | CG | CG | ||
| SET-DEFAULT RELAY METHOD_BREAKER_CG | 11,234 | X | X | X | BCG | |||
| 4 | BOUNDARY ADMITTANCE METHOD_BREAKER_ABG | 10,817 | X | X | X | ABG | ABG | |
| SET-DEFAULT RELAY METHOD_BREAKER_ABG | 11,235 | X | X | X | ABG | |||
| 5 | BOUNDARY ADMITTANCE METHOD_BREAKER_BCG | 10,818 | X | X | X | BCG | BCG | |
| SET-DEFAULT RELAY METHOD_BREAKER_BCG | 11,236 | X | X | X | BCG | |||
| 6 | BOUNDARY ADMITTANCE METHOD_BREAKER_ACG | 10,819 | X | X | X | ACG | ACG | |
| SET-DEFAULT RELAY METHOD_BREAKER_ACG | 11,237 | X | X | X | ACG | |||
| 7 | BOUNDARY ADMITTANCE METHOD_BREAKER_AB | 10,820 | X | X | AB | AB | ||
| SET-DEFAULT RELAY METHOD_BREAKER_AB | 11,238 | X | X | AB | ||||
| 8 | BOUNDARY ADMITTANCE METHOD_BREAKER_BC | 10,821 | X | X | BC | BC | ||
| SET-DEFAULT RELAY METHOD_BREAKER_BC | 11,239 | X | X | BC | ||||
| 9 | BOUNDARY ADMITTANCE METHOD_BREAKER_AC | 10,822 | X | X | AC | AC | ||
| SET-DEFAULT RELAY METHOD_BREAKER_AC | 11,240 | X | X | AC | ||||
| 10 | BOUNDARY ADMITTANCE METHOD_BREAKER_ABCG | 10,840 | X | X | X | X | ABCG | ABCG |
| SET-DEFAULT RELAY METHOD_BREAKER_ABCG | 11,258 | X | X | X | ACG | |||
| 11 | BOUNDARY ADMITTANCE METHOD_BREAKER_ABC | 10,841 | X | X | X | X | ABCG | ABC |
| SET-DEFAULT RELAY METHOD_BREAKER_ABC | 11,259 | X | X | X | ABC | |||
| 12 | BOUNDARY ADMITTANCE METHOD_SECTION38_AG | 10,847 | X | X | AG | AG | ||
| SET-DEFAULT RELAY METHOD_SECTION38_AG | 11,275 | X | X | AG | ||||
| 13 | BOUNDARY ADMITTANCE METHOD_SECTION38_BG | 10,848 | X | X | BG | BG | ||
| SET-DEFAULT RELAY METHOD_SECTION38_BG | 11,276 | X | X | X | BCG | |||
| 14 | BOUNDARY ADMITTANCE METHOD_SECTION38_CG | 10,849 | X | X | CG | CG | ||
| SET-DEFAULT RELAY METHOD_SECTION38_CG | 11,277 | X | X | CG | ||||
| 15 | BOUNDARY ADMITTANCE METHOD_SECTION38_ABG | 10,851 | X | X | X | ABG | ABG | |
| SET-DEFAULT RELAY METHOD_SECTION38_ABG | 11,279 | X | X | X | ABG | |||
| 16 | BOUNDARY ADMITTANCE METHOD_SECTION38_BCG | 10,852 | X | X | X | BCG | BCG | |
| SET-DEFAULT RELAY METHOD_SECTION38_BCG | 11,280 | X | X | X | BCG | |||
| 17 | BOUNDARY ADMITTANCE METHOD_SECTION38_ACG | 10,853 | X | X | X | ACG | ACG | |
| SET-DEFAULT RELAY METHOD_SECTION38_ACG | 11,281 | X | X | X | ACG | |||
| 18 | BOUNDARY ADMITTANCE METHOD_SECTION38_AB | 10,854 | X | X | AB | AB | ||
| SET-DEFAULT RELAY METHOD_SECTION38_AB | 11,282 | X | X | AB | ||||
| 19 | BOUNDARY ADMITTANCE METHOD_SECTION38_BC | 10,855 | X | X | BC | BC | ||
| SET-DEFAULT RELAY METHOD_SECTION38_BC | 11,283 | X | X | BC | ||||
| 20 | BOUNDARY ADMITTANCE METHOD_SECTION38_AC | 10,856 | X | X | AC | AC | ||
| SET-DEFAULT RELAY METHOD_SECTION38_AC | 11,284 | X | X | AC | ||||
| 21 | BOUNDARY ADMITTANCE METHOD_SECTION38_ABCG | 10,857 | X | X | X | X | ABCG | ABCG |
| SET-DEFAULT RELAY METHOD_SECTION38_ABCG | 11,285 | X | X | X | ACG | |||
| 22 | BOUNDARY ADMITTANCE METHOD_SECTION38_ABC | 10,858 | X | X | X | X | ABCG | ABC |
| SET-DEFAULT RELAY METHOD_SECTION38_ABC | 11,286 | X | X | BC | ||||
| LEDs (Phase/Ground) | A | B | C | GND |
|---|---|---|---|---|
| Figures | Figure 9a | Figure 9b | Figure 9c | Figure 9d |
| TV LEDn: Number of true values for the boundary admittance and set-default relay methods at the phase and ground LEDs | 22 | 22 | 22 | 22 |
| MV BAM LEDn: Number of measured values matching true values for the boundary admittance method at the phase and ground LEDs | 22 | 22 | 21 | 19 |
| MV SDRM LEDn: Number of measured values matching true values for the set-default relay method at the phase and ground LEDs | 21 | 18 | 20 | 21 |
| Electrical Fault Types | ||||
|---|---|---|---|---|
| LG | LLG | LL | 3L/3LG | |
| TV EFTm: Number of true electrical fault type values | 6 | 6 | 6 | 4 |
| MV BAM EFTm: Number of measured electrical fault type values matching true electrical fault type values for the boundary admittance method | 6 | 6 | 6 | 2 |
| MV SDRM EFTm: Number of measured electrical fault type values matching the true electrical fault type values for the set-default relay method | 3 | 6 | 6 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piesciorovsky, E.C.; Reno, M.J.; Ferrari Maglia, M.; Summers, A.K. An Advanced Synchronized Time Digital Grid Twin Testbed for Relay Misoperation Analysis of Electrical Fault Type Detection Algorithms. Metrology 2024, 4, 374-397. https://doi.org/10.3390/metrology4030023
Piesciorovsky EC, Reno MJ, Ferrari Maglia M, Summers AK. An Advanced Synchronized Time Digital Grid Twin Testbed for Relay Misoperation Analysis of Electrical Fault Type Detection Algorithms. Metrology. 2024; 4(3):374-397. https://doi.org/10.3390/metrology4030023
Chicago/Turabian StylePiesciorovsky, Emilio C., Mathew J. Reno, Maximiliano Ferrari Maglia, and Adam K. Summers. 2024. "An Advanced Synchronized Time Digital Grid Twin Testbed for Relay Misoperation Analysis of Electrical Fault Type Detection Algorithms" Metrology 4, no. 3: 374-397. https://doi.org/10.3390/metrology4030023
APA StylePiesciorovsky, E. C., Reno, M. J., Ferrari Maglia, M., & Summers, A. K. (2024). An Advanced Synchronized Time Digital Grid Twin Testbed for Relay Misoperation Analysis of Electrical Fault Type Detection Algorithms. Metrology, 4(3), 374-397. https://doi.org/10.3390/metrology4030023






