Improving Experimental Design through Uncertainty Analysis
Abstract
:1. Introduction
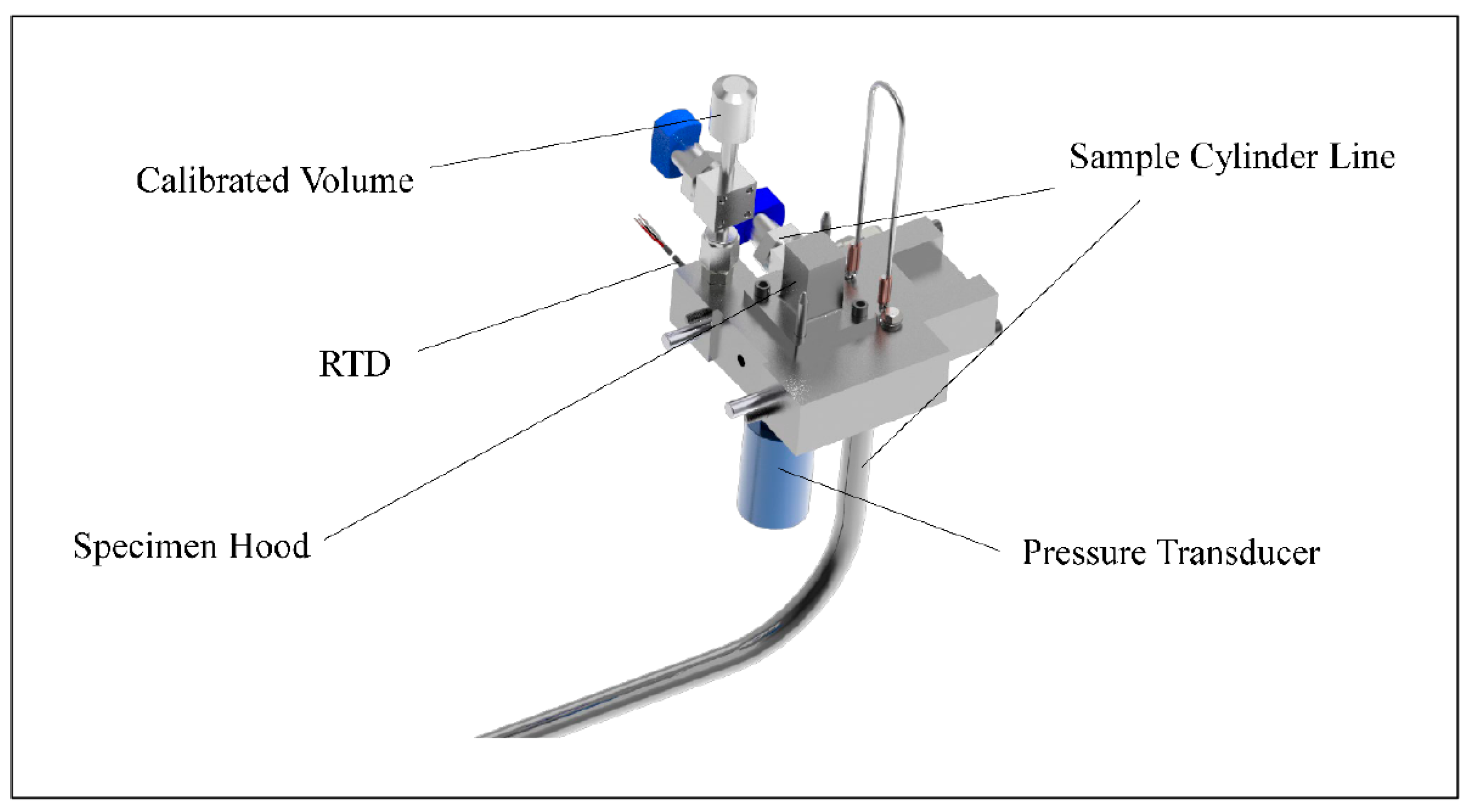
2. Materials and Methods
3. Results and Discussion
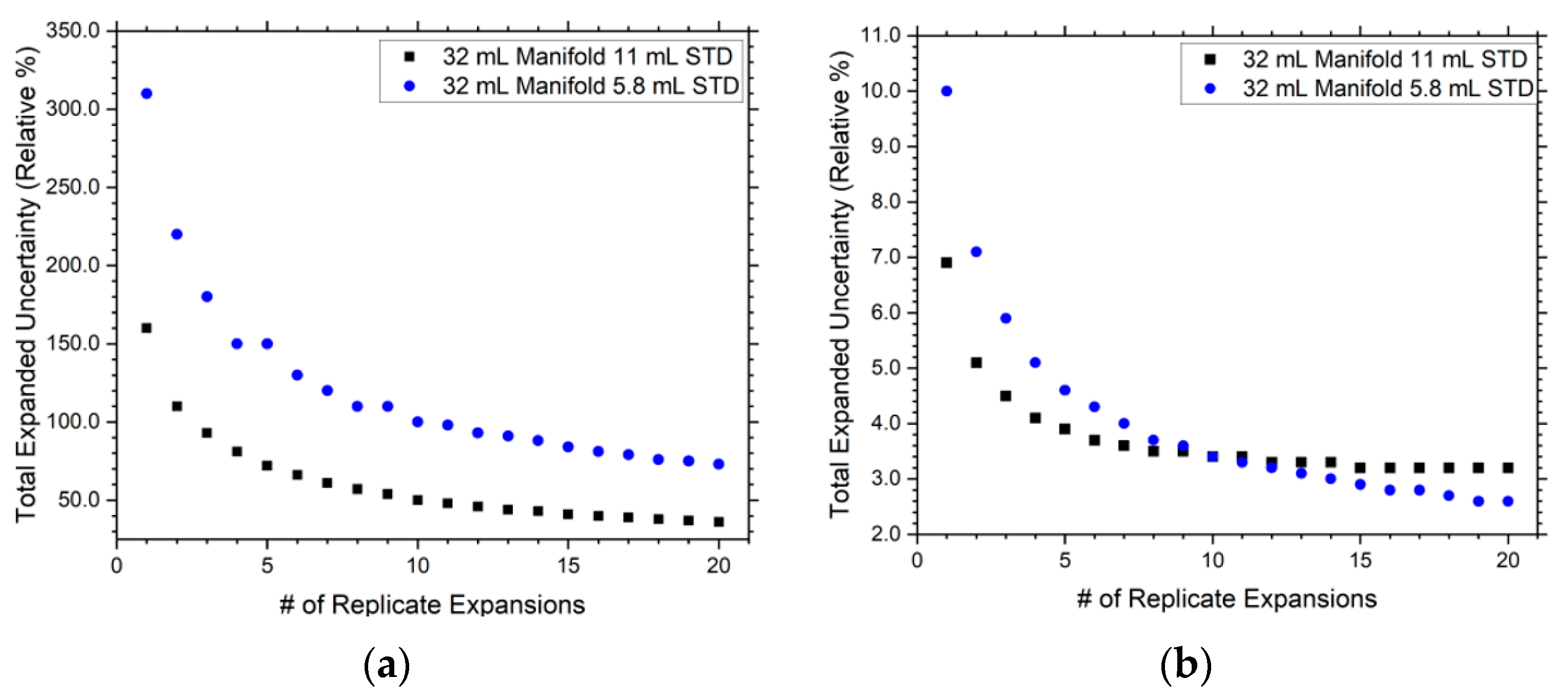
3.1. 32 mL Manifold Design
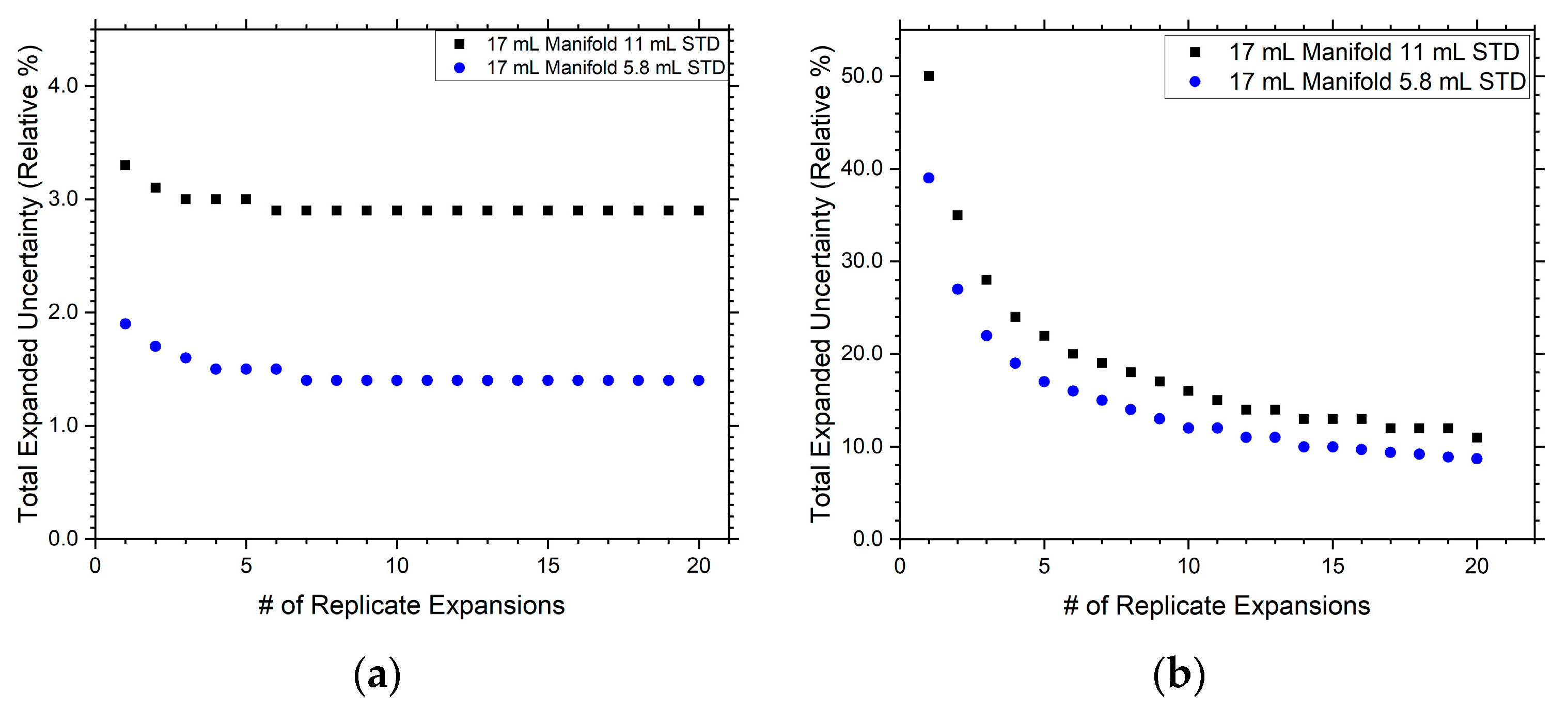
3.2. 17 mL Manifold Design
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carmack, W.; Chichester, H.; Porter, D.; Wootan, D. Metallography and fuel cladding chemical interaction in fast flux test facility irradiated metallic U-10Zr MFF-3 and MFF-5 fuel pins. J. Nucl. Mater. 2016, 473, 167–177. [Google Scholar] [CrossRef]
- Porter, D.; Tsai, H. Full-length U–xPu–10Zr (x = 0, 8, 19wt.) FFTF. J. Nucl. Mater. 2012, 427, 46–57. [Google Scholar] [CrossRef]
- Wachs, D.M.; Capriotti, L.; Porter, D. Behavior of metallic fast reactor fuels during an overpower transient. J. Nucl. Mater. 2021, 557, 153304. [Google Scholar] [CrossRef]
- Guide to the Expression of Uncertainty in Measurement; Technical Report; BIPM: Sèvres, France; IEC: Geneva, Switzerland; IFCC: Portland, Oregon; ISO: Geneva, Switzerland; IUPAC: Zürich, Switzerland; IUPAP: Italy, France; OML: Oklahoma City, OK, USA, 1995.
- Laugier, A.; Garai, J. Derivation of the Ideal Gas Law. J. Chem. Educ. 2007, 84, 1832. [Google Scholar] [CrossRef]
- Winkler, A. A new accurate calibration method for thermal desorption spectra. J. Vac. Sci. Technol. A 1984, 2, 1393–1394. [Google Scholar] [CrossRef]
- Dobrozemsky, R. Calibration of vacuum systems by gas quantities. Vacuum 1990, 41, 2109–2111. [Google Scholar] [CrossRef]
- Wuthrich, C.; Coulibaly, M. The determination of volume ratios by gas depletion through multiple expansions. Vacuum 2006, 81, 453–458. [Google Scholar] [CrossRef]
- Arri, E.; Cabiati, F.; D’Emilio, S.; Gonella, L. On the application of the guide to the expression of uncertainty in measurement to measuring instruments. Measurement 1995, 16, 51–57. [Google Scholar] [CrossRef]
- Kacker, R.; Sommer, K.D.; Kessel, R. Evolution of modern approaches to express uncertainty in measurement. Metrologia 2007, 44, 513–529. [Google Scholar] [CrossRef]
- Kessel, R.; Berglund, M.; Wellum, R. Application of consistency checking to evaluation of uncertainty in multiple replicate measurements. Accredit. Qual. Assur. 2008, 13, 293–298. [Google Scholar] [CrossRef]
- Kessel, R.; Kacker, R.; Berglund, M. Coefficient of contribution to the combined standard uncertainty. Metrologia 2006, 43, S189–S195. [Google Scholar] [CrossRef]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
| Rodlet Volume (mL) | 11.85 mL Volume Standard | 5.81 mL Volume Standard |
|---|---|---|
| 2.50 | 3.2% | 2.6% |
| 0.25 | 12% | 21% |
| 0.12 | 21% | 42% |
| 0.07 | 36% | 73% |
| Rodlet Volume (mL) | 11.85 mL Volume Standard | 5.81 mL Volume Standard | ||
|---|---|---|---|---|
| Index | χ2 | Index | χ2 | |
| 2.50 | 82.9% | 1.5 × 10−6 | 26.9% | 7.2 × 10−6 |
| 0.250 | 5.3% | 7.1 × 10−4 | 0.4% | 6.6 × 10−4 |
| 0.123 | 11.9% | 4.8 × 10−4 | 0.1% | 9.1 × 10−3 |
| 0.070 | 0.6% | 2.3 × 10−3 | 0.0% | 9.1 × 10−3 |
| Rodlet Volume (mL) | Volume STD 5.81 mL | Volume STD 11.85 mL |
|---|---|---|
| 2.50 | 1.4% | 2.9% |
| 0.250 | 2.8% | 4.2% |
| 0.123 | 5.1% | 6.9% |
| 0.070 | 8.7% | 11% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobbs, I.M.; Charboneau, J.A.; Jacobsen, T.L. Improving Experimental Design through Uncertainty Analysis. Metrology 2023, 3, 246-253. https://doi.org/10.3390/metrology3030014
Hobbs IM, Charboneau JA, Jacobsen TL. Improving Experimental Design through Uncertainty Analysis. Metrology. 2023; 3(3):246-253. https://doi.org/10.3390/metrology3030014
Chicago/Turabian StyleHobbs, Ian M., Joey A. Charboneau, and Todd L. Jacobsen. 2023. "Improving Experimental Design through Uncertainty Analysis" Metrology 3, no. 3: 246-253. https://doi.org/10.3390/metrology3030014
APA StyleHobbs, I. M., Charboneau, J. A., & Jacobsen, T. L. (2023). Improving Experimental Design through Uncertainty Analysis. Metrology, 3(3), 246-253. https://doi.org/10.3390/metrology3030014






