Doric Foot and Metrological Implications of the Ancient Theatre of Makyneia, Western Greece

Abstract

Understanding the length and subdivisions of ancient length units is necessary for Archaeology, Architecture, and engineering, among other fields. These metrological units derive from anthropocentric concepts (fathom, cubit, foot, finger, etc.) and hence their metrological characteristics are variable and unknown for various ancient civilizations. The Roman length units are well determined, but the ancient Greek units are not. A rule sculpted in a metrological relief recently permitted the recognition of the Doric foot as having a length of 327 mm, but the broader use and divisions of this length unit remain unknown. In this article we present evidence of use of the Doric foot from the modeling of an ancient, atypical small theatre of the 4th–3rd century B.C., at Makyneia, on the western Greece mainland. It was found that this structure was designed using the Doric foot and its division in 24 (or even 12) digits. This result from a small provincial town indicates that the Doric foot was in broad use in architectural and engineering works of the ancient Greek World, and this result may be used to solve various problems of that era.

1. Introduction

Engineering works and other activities (sculptures, coins, etc.) in antiquity were based on units of length, which depended on the region and the period. In some cases, changes of length (and eventually of other metrological units) followed political and social changes; for example, sociopolitical changes in ancient Athens were followed by new length measurement systems [1]; in more recent times, soon after the 1789 French Revolution, new metrological units were also adopted. For these reasons, Metrology is an important field in the study of antiquity.

The precise dimensions of some of the ancient units are well-known; for example, the Roman foot (pes, equal to 296 mm) and the Roman mile (equal to 1.481 km) are precisely known as numerous engineering measuring tools (rules) and numerous milestones in roads have been found [1]. In one case there has been found a sculpted marble surface (relief) in Leptis Magna, Libya, North Africa, depicting the Punic, the Egyptian and the Roman length units and their subdivisions, thus permitting their comparison [2] (Figure 1); this was due to Libya being under Roman control, as well as also being under the influence of the Punic (Carthage) culture from the west and Egyptian culture from the east.

For some other regions and periods associated with having has an important ancient civilization, for example ancient Greece, contrarily, length units are very poorly known. Notably, there is not even consensus for the units underlying the construction of the Parthenon! A reason is that the term “ancient Greece” covers different cultures, changing in time and space, due to political changes. The information on the length units used in ancient Greece is limited. There is a report by Pliny that the Roman foot equals 24/25 of the Attic foot (Pliny, HN 2.21), but no match with building data is evident. There are a few elaborate buildings that provide some evidence that some of their dimensions are a multiple of a Doric foot of 327 mm [3], but no direct evidence for this length unit existed until recently [1]. On the contrary, there is evidence that the Doric foot was in the range 326–328 mm [4]. This variation seems small for the antiquity, but it is critical for the analogies and design of elaborate temples with columns such as the Parthenon and the ancient Greek temples of Sicily.

2. Length Units in Ancient Greece

Ancient length units in Greece and in most other ancient civilizations were anthropocentric, derived from the length of a foot (“pous”), a cubit (“pechus”, typically one and half foot, measured from the elbow to the edge of the longest finger), finger (“daktylos”), a subdivision of the foot, usually 16 or 24 (or 12) fingers per foot. Then, there was fathom (“orgya”, from the length between horizontally stretched hands of a person), typically 6 feet, and stadion, probably equal to 600 feet. The length of such units was variable, and this is responsible for the apparent variety of units used in ancient Greece and other ancient civilizations. It is generally believed that there existed three classes of length units in ancient Greece, with foot units ranging between 294–296 mm, 325–328 mm and 348–350 mm [1]. A Doric foot of 327 mm is, however, usually assumed by various scholars [3], but evidence of physical, standardized ancient Greek length units is limited to three findings:

(i) Metrological relief in the British Ashmolean Museum

This is a so-called metrological relief, part of the decoration of a temple, currently exhibited in the British Ashmolean Museum. This metrological relief, of unknown origin, is dated between 449–420 B.C. and shows a person with horizontally stretched hands to indicate a fathom, plus the print of a foot. The dimensions of its sculptures indicate a unit length of 523 mm, equal to the royal cubit of Egypt, and on this evidence, it is assumed that it comes from the island of Samos (East Aegean Sea), known for its connection with Egypt (see [5]).

(ii) Metrological relief from Salamis, Piraeus Museum, near Athens

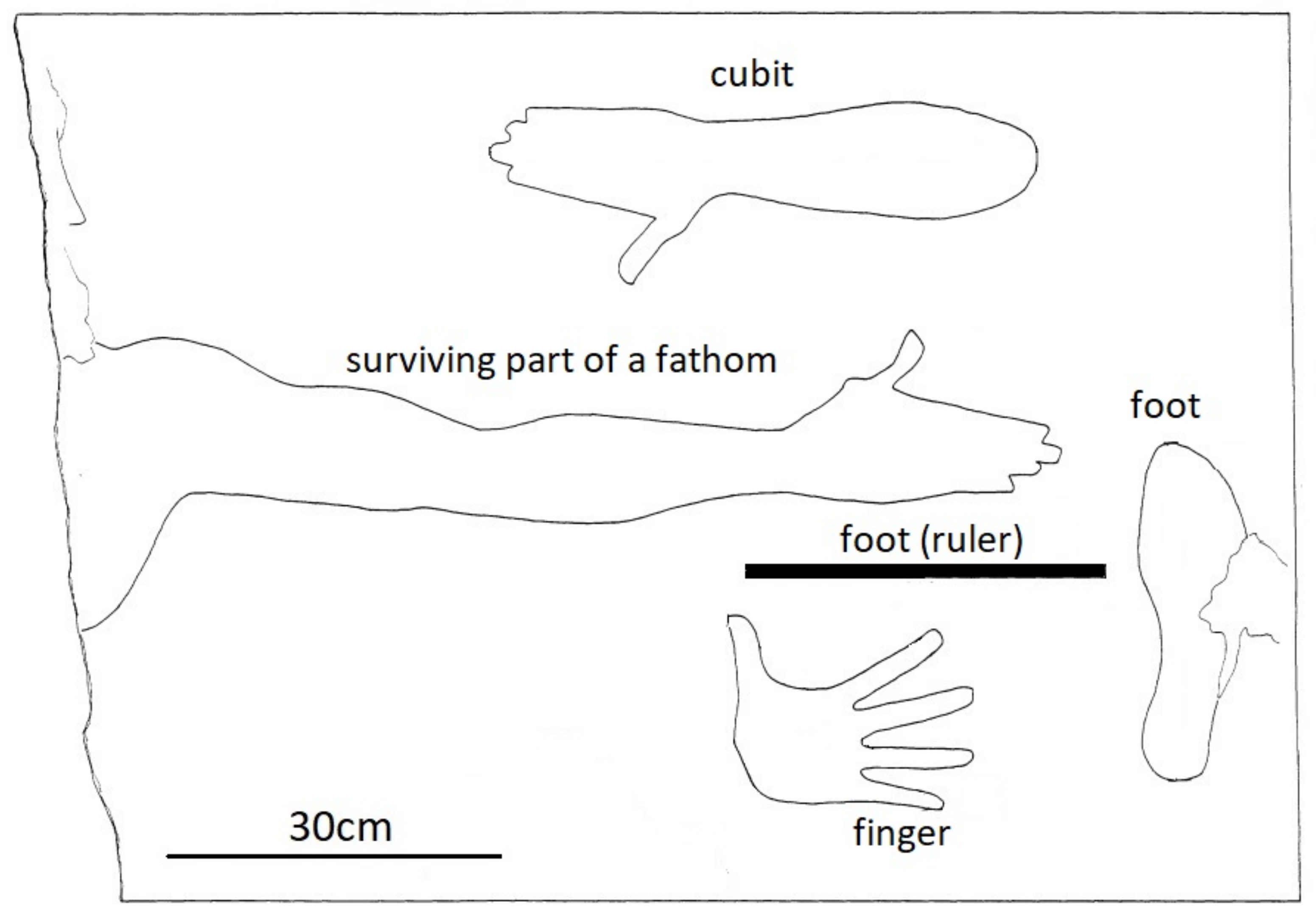
This is a sculpted marble slab, known as the “Salamis metrological relief” found in the 1980s in Salamis, an island very close to Athens, more widely known due to a famous naval battle in antiquity, during the invasion of Persians to ancient Greece. The surviving part of this relief shows part of a man standing erect with hands extended horizontally to indicate a fathom, prints of a cubit and of a foot, as well as an open fist to indicate fingers to represent the subdivision of a foot. The extraordinary point in this relief is that, apart from anthropomorphic length units, it also includes the length of a measuring rod (Figure 2; [6]). This finding, however, was not without surprises.

The first surprise concerned the length of the Doric foot. The archaeologist who identified this relief measured the length of this rod as 322 mm [6], which was much shorter than the assumed length of the Doric foot, which was 327 mm. However, a more recent study indicated that the edges of the curving are not normal to the slab surface but inclined, so that 322 mm is measured at the bottom of the curving and 327.5 mm at its perimeter on the slab surface. This was indeed the first direct evidence of a Doric foot [1], previously inferred only from the dimensions of a few elaborate monuments [1,4].

The second surprise concerned the length of the “short foot”. Instead of a length in the range of 294–296 mm, a foot with a length of 301–302 mm was derived from the Salamis relief. This led Slapsak [7] to suggest the absence of scale in the presentation of some features of the relief.

(iii) Wooden rule from a wreckage

A ruler and a gnomon (L-shaped instrument to design 90° angles), both wooden, were found in a shipwreck. This ship had a cargo of schist stones from the island of Euboea (central-west Aegean Sea, Greece) and Cyprus, and had sunk, circa 400 B.C., off the shore of Israel. In the ruler, probably an architect’s instrument, the lengths of 333 mm and 327.5 mm were recognized [8].

3. The Makyneia Theatre and Evidence of Broad Use of the Doric Foot in Architecture

Although a Doric foot of (327 ± 0.5) mm is documented from the Salamis metrological relief, it was a question whether this unit has been widely used in ancient Greek Architecture, or it was confined to a few elaborate buildings.

An answer to this problem is given by the analysis of the small ancient theatre of Makyneia, a small town in the south-western modern Greek mainland, about 200 km west of Athens ([9]; for location see https://topostext.org/place/384217UMak, last accessed on 18 August 2022).

Ancient Greek theatres had a formal typology. Actors were playing on a quasi-semicircular stage (“orchestra” in ancient Greek), bounded from one side by the scene and by the other side by a quasi-semi-circular sitting space, known as “koilon” (literary hollow) or “cavea” in Latin. The sitting place (koilon) was formed by rows of seats following segments of homocentric circles at an elevation systematically increasing away from the stage. The lowermost row of seats, proximal to the stage, usually with different dimensions and construction, was allocated to priests of the adjacent temple, and to high authorities [3,9,10].

Apart from the typical theatres, there were a few other atypical ones, usually with koilon formed by three rectangular segments leading to a nearly rectangular orchestra (stage), or a combination of rectangular and circular segments [9]. The Makyneia theatre is a characteristic example, with a circular koilon limited to an angle of 90°, (hence contrasting with typical theatres with an angle between 140° and 220°), and a linear segment with a single row of seats. Two views of this theatre are shown in Figure 3.

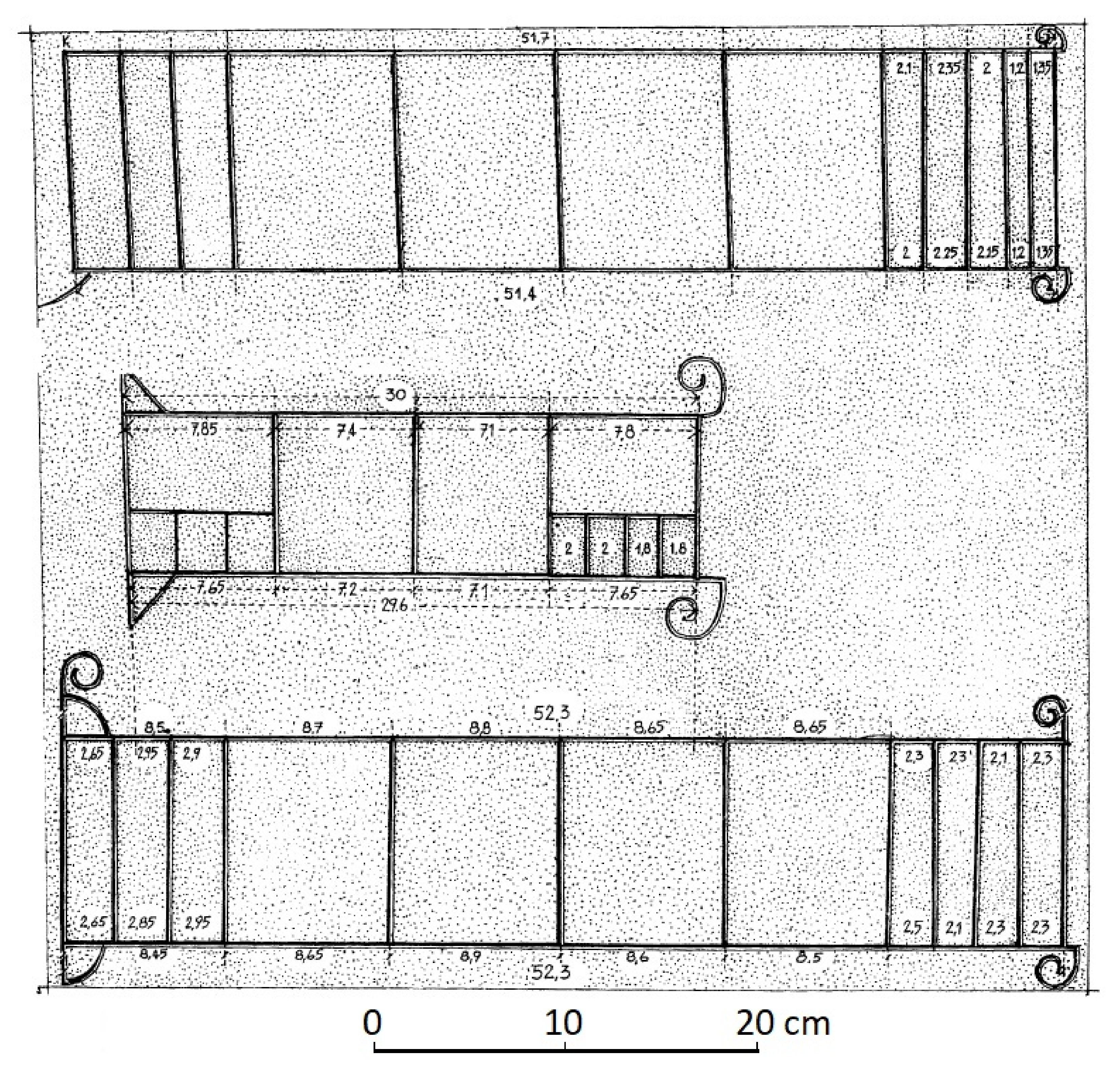
The circular part of the theatre was curved in the cliff of a hill, just beneath the town fortifications and seats were made with large hewn blocks of consolidated sandstone, arranged along parts of concentric circles. In total, 14 rows of seats are still visible, but the blocks forming them were slightly to badly displaced or titled as a result of the erosion of their foundations, especially in upper rows (Figure 3a,b). For this reason, no detailed reconstruction of the plan of the theatre is possible. Furthermore, the dating of the theatre remains imprecise, and it is essentially assigned to the 4th–3rd century B.C. [11].

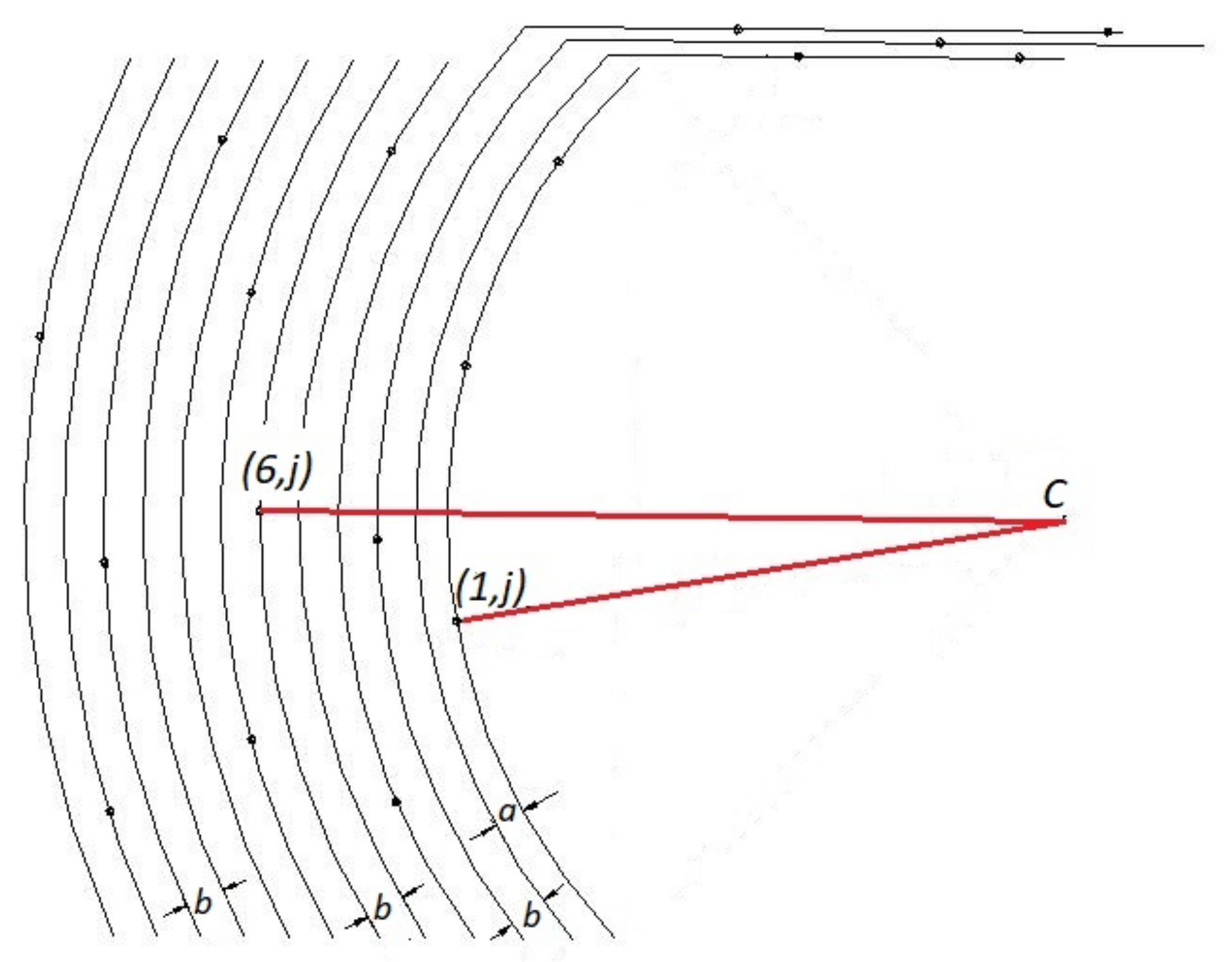
In order to document the design of this theatre, it was assumed that the inner edges of hewn blocks in situ or nearly in situ, forming the rows of seats, are nearly randomly displaced from their original position. As a consequence, the plan of the reconstructed koilon can be derived from the modeling of all blocks as tangent to concentric circles with equal spacing. Slabs essentially displaced from their initial position were not taken into consideration in this analysis. This approach offers more accuracy than the modeling of the whole koilon from a few blocks apparently remaining in situ. The details of the modeling are explained in the Appendix A.

The overall output is that the curvilinear part of the theatre was designed on the basis of homocentric cycles, confined to an angle of 90°. These rows were equidistant, except for the lowermost one, which was slightly narrower since there was no need for circulation of spectators on this row [1].

4. Metrological Implications of the Makyneia Theatre

From the adjusted values of the design characteristics of the theatre, summarized in

Table A1. Design parameters of the Makyneia theatre (adjusted values).

Design Parameter	Estimated Value (m)
R1	10.910 ± 0.030
a	0.548 ± 0.009
b	0.692 ± 0.001

, it can be derived that the basic design element of the theatre was the radius R₂ of the second row of seats, which, within the error limits of the observations and calculations, corresponds to 35 Doric feet (R₂ = 11.358 m ≈ 35 ∙ 0.327 m). Similarly, the lowermost radius R₁ corresponds to 33.33 Doric feet (R₁ = 10.910 m ≈ 33.33 ∙ 0.327 m). The fact that one third of a foot was used, indicates a division of the foot into 24 and not 16 fingers, with each finger being 327/24 = 13.62 mm wide. A division in 12 fingers is also possible. The spacing of the rows of seats from the second row corresponds to two feet and three fingers (b = 692 mm ≈ 3 ∙ 327 mm + 3 ∙ 13.92 mm). These calculations are clearly approximate, and are accurate to within a few mm as the Makyneia theatre was a large-scale structure without very accurate setting up, as would be the case in ancient temples with columns, while the basic unit could fluctuate within a tolerance margin of 0.5 mm.

The Makyneia theatre is the first engineering structure, beyond temples and certain votive or other elaborate monuments, which was designed using the Doric foot. A subdivision in 24 fingers (or even 12 fingers, [4]) is inferred. Particularly since Makyneia was a small town with limited influence from main cultural centers, the above metrological evidence indicates that the Doric foot was widely adopted in the large-scale engineering and architectural projects of the ancient Greek World.

5. Conclusions

The analysis of survey data covering the remains of a small, ancient, atypical Greek theatre revealed that it was designed using the Doric foot, having a length of 327 mm. This metrological unit was assumed to have played a major role in ancient Greek architecture by various investigators [3], but clear evidence for its very existence was provided only from a so-called metrological relief showing both anthropocentric units and a rule (Figure 2). The evidence from the small provincial town of Makyneia indicates for the first time a rather broad use of this standardized unit in ancient Greek architecture and civil engineering. Ideally, this type of study, the metrological analysis of ancient remains from modeling which compensate for measurement errors and not from isolated measurements, which are contaminated by measurement errors, should be expanded to various other structures. Still, limitations in work permits for the study of important ancient remains is an issue in various countries.

The above discussion also reveals that metrological data can be used even to constrain the origin of ancient findings exhibited in museums, as is the case with metrological relief in the British Ashmolean Museum, assumed to come from Samos [5] and perhaps their dating. This new evidence may also be used to constrain the theatre of Makyneia, the dating of which remains imprecise [11].

The variability in ancient length units is important not only for understanding ancient Architecture and ancient History, but for many other fields; for example, the understanding of seismic displacements produced by historical earthquakes (e.g., [12]).