Optimization of the Processing Time of Cross-Correlation Spectra for Frequency Measurements of Noisy Signals
Abstract
:1. Introduction
2. Fundamentals
2.1. Cross-Correlation
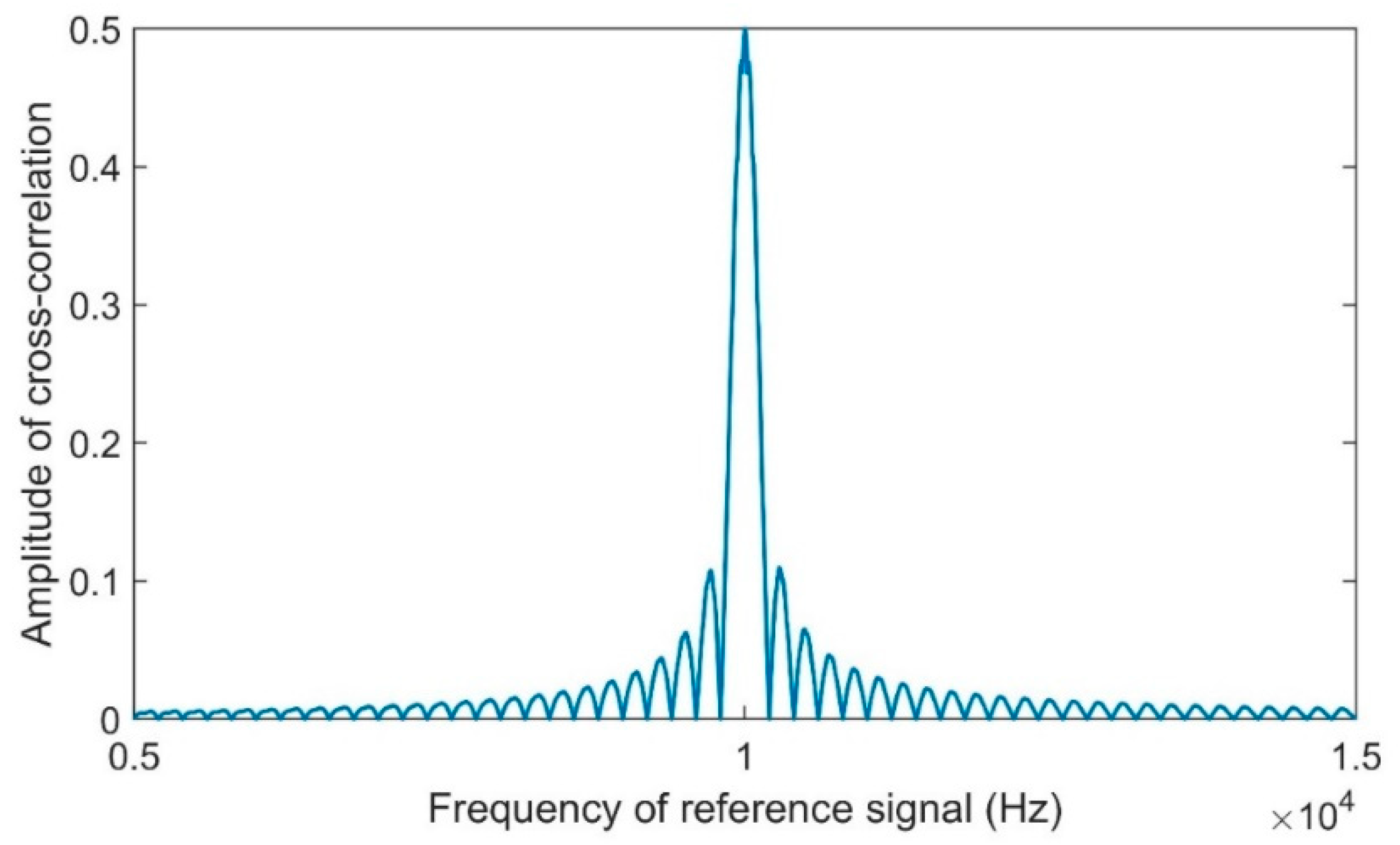
2.2. Cross-Correlation Spectrum
- 1.
- The CCS’s frequency range and the frequency resolution are set by the user. is set to 0;
- 2.
- is initialized to ();
- 3.
- The sine function is generated according to Equation (17);
- 4.
- The cross-correlation function between the and the measuring signal is calculated;
- 5.
- The cross-correlation spectrum’s value for the current frequency is determined by identifying the amplitude of the cross-correlation function . In [13], it is accomplished by finding the function’s maximum value;
- 6.
- The frequency is increased by , i.e., ;
- 7.
- The steps from 3–6 are repeated, until has been determined.
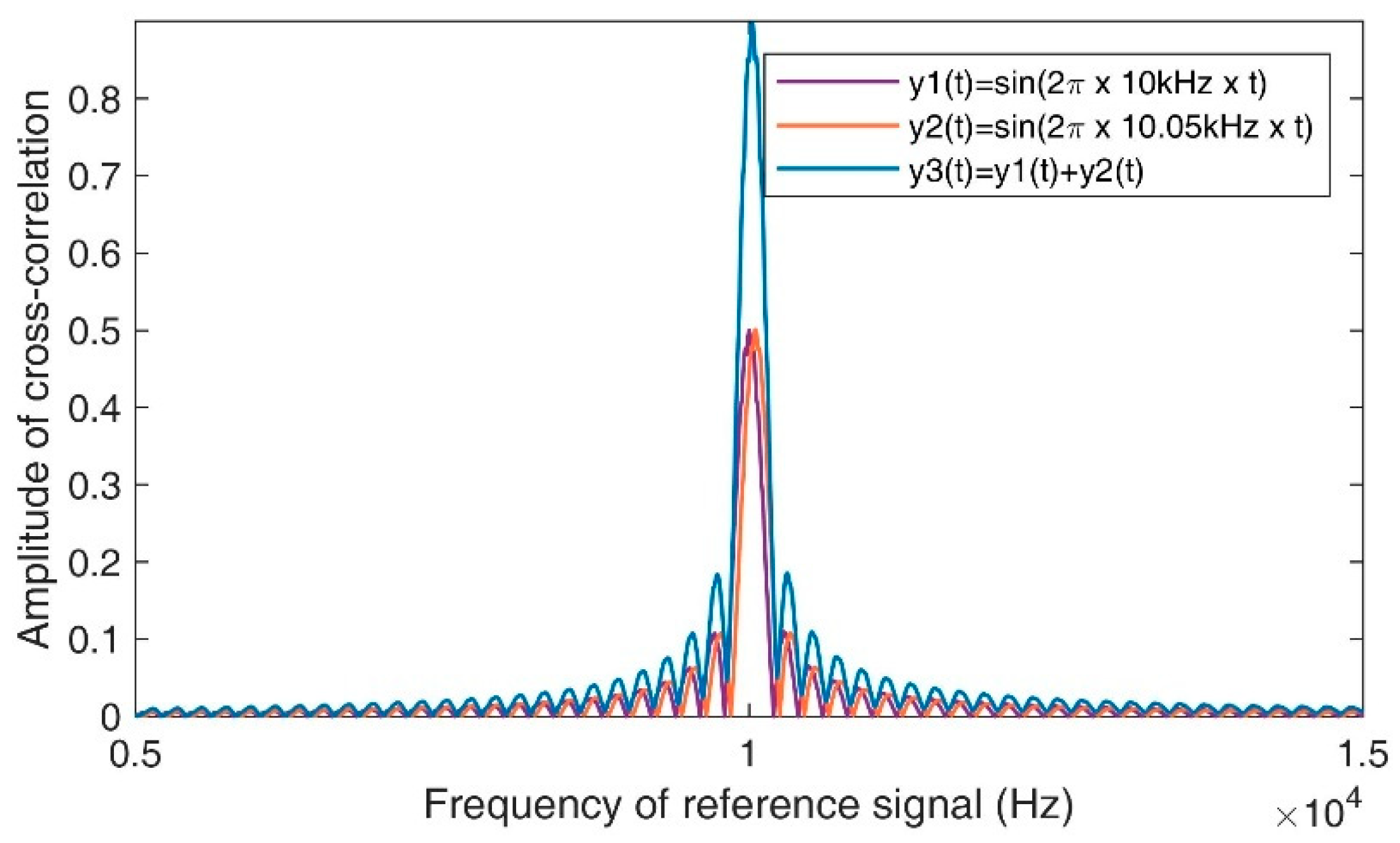
3. New Version of Cross-Correlation Spectrum
3.1. Theory
3.2. Simulations
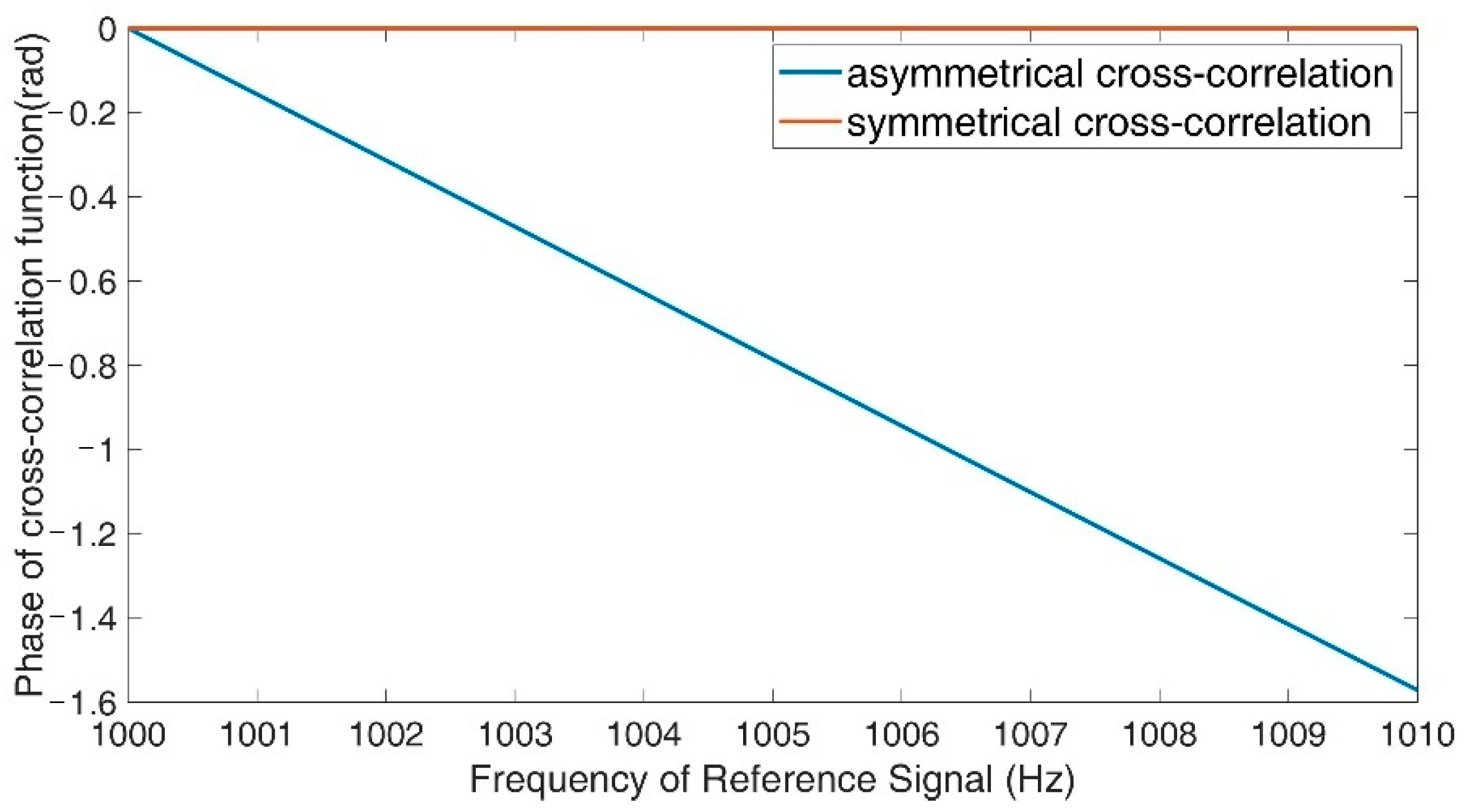
4. Phase Measurement Using Cross Correlation
5. Frequency and Phase Measurement Method
6. Application Example
6.1. Self-Mixing Interferometry

6.2. Experiments on SMI-Signals
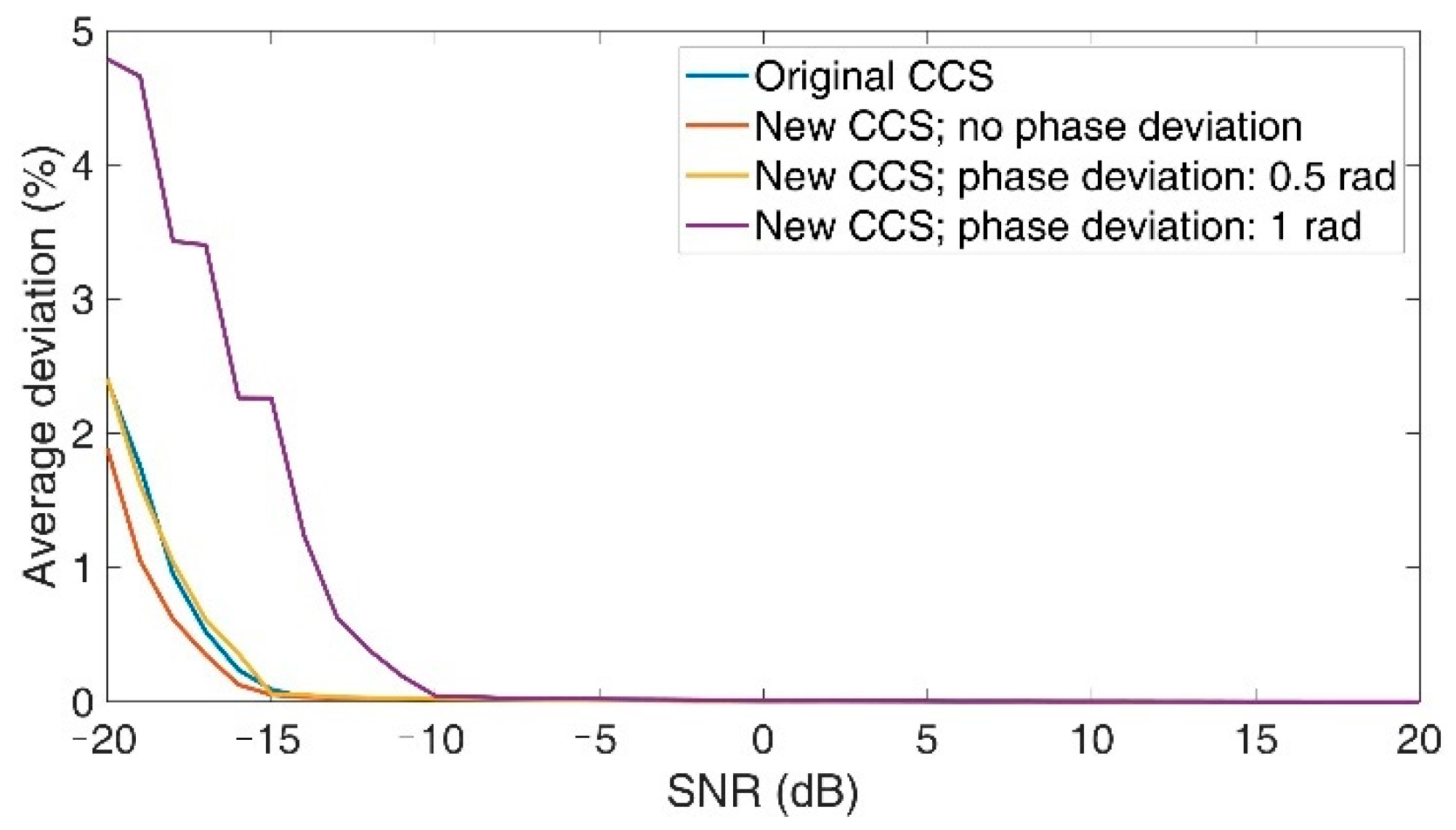
7. Discussions
- Creating reference signals with different frequencies can require a lot of processing time, which could be reduced by improved algorithms;
- Depending on the application’s requirement, the spectrum’s resolution could vary in different frequency ranges. While a lower resolution is initially used, critical frequency ranges could be assigned higher resolutions. This way, an optimum between accuracy and computational effort could be achieved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lopez, J.D.S.; Rico, F.N.M.; Petranovskii, V.; García, J.A.; Gaxiola, R.I.Y.; Sergiyenko, O.; Tyrsa, V.; Hipolito, J.I.N.; Briseno, M.V. Effect of phase in fast frequency measurements for sensors embedded in robotic systems. Int. J. Adv. Robot. Syst. 2019, 16, 1–7. [Google Scholar]
- Murrieta-Rico, F.N.; Petranovskii, V.; Dalván, D.H.; Sergiyenko, O.; Antúnez-García, J.; Yocupicio-Gaxiola, R.I.; de Dios Sanchez-Lopez, J. Phase effect in frequency measurements of a quartz crystal using the pulse coincidence principle. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics, Delft, The Netherlands, 17–19 June 2020; pp. 185–190. [Google Scholar]
- Deng, W.; Yang, T.; Jin, L.; Yan, C.; Huang, H.; Chu, X.; Wang, Z.; Xiong, D.; Tian, G.; Gao, Y.; et al. Cowpea-structured PVDF/ZnO nanofibers based flexible self-powered piezoelectric bending motion sensor towards remote control of gestures. Nano Energy 2019, 55, 516–525. [Google Scholar] [CrossRef]
- Ju, F.; Wang, Y.; Zhang, Z.; Wang, Y.; Yun, Y.; Guo, H.; Chen, B. A miniature piezoelectric spiral tactile sensor for tissue hardness palpation with catheter robot in minimally invasive surgery. Smart Mater. Struct. 2019, 28, 025033. [Google Scholar] [CrossRef]
- Liu, H.; Pang, G.K.H. Accelerometer for mobile robot positioning. IEEE Trans. Ind. Appl. 2001, 37, 812–819. [Google Scholar] [CrossRef]
- Karns, A.M. Development of a Laser Doppler Velocimetry System for Supersonic Jet Turbulence Measurements. Master’s Thesis, The Pennsylvania State University, State College, PA, USA, 2014. [Google Scholar]
- Sun, H.; Liu, J.G.; Zhang, Q.; Kennel, R.M. Self-mixing interferometry for rotational speed measurement of servo drives. Appl. Opt. 2016, 55, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Sondkar, S.Y.; Dudhane, S.; Abhyankar, H.K. Frequency Measurement Methods by Signal Processing Techniques. Procedia Eng. 2012, 38, 2590–2594. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Liu, J.; Kennel, R. Frequency Measurement Method of Signals with Low Signal-to-Noise-Ratio Using Cross-Correlation. Machines 2021, 9, 123. [Google Scholar] [CrossRef]
- Tan, C.; Yue, Z.M.; Wang, J.C. Frequency measurement approach based on linear model for increasing low SNR sinusoidal signal frequency measurement precision. IET Sci. Meas. Technol. 2019, 13, 1268–1276. [Google Scholar] [CrossRef]
- Najmi, A.H.; Sadowsky, J. The Continuous Wavelet Transform and Variable Resolution Time-Frequency Analysis. Johns Hopkins Apl. Tech. Dig. 1997, 18, 134–139. [Google Scholar]
- Khan, N.A.; Jafri, M.N.; Qazi, S.A. Improved resolution short time Fourier transform. In Proceedings of the 2011 7th International Conference on Emerging Technologies, Piscataway, NJ, USA, 5–6 September 2011. [Google Scholar]
- Liu, Y.; Jiang, Z.; Wang, G.; Xiang, J. Synchrosqueezing transform based general linear chirplet transform of instantaneous rotational frequency estimation for rotating machines with speed variation. In Proceedings of the 2020 Asia-Pacific International Symposium on Advanced Reliability and Maintenance Modeling (APARM), Vancouver, BC, Canada, 20–23 August 2020; pp. 1–5. [Google Scholar]
- Liu, J. Eigenkalibrierende Meßverfahren und deren Anwendungen bei den Messungen elektrischer Größen; Fortschritt-Berichte VDI: Düsseldorf, Germany, 2000; Line 8, Nr. 830. [Google Scholar]
- Wang, H.; Ruan, Y.; Yu, Y.; Guo, Q.; Xi, J.; Tong, J. A New Algorithm for Displacement Measurement Using Self-Mixing Interferometry with Modulated Injection Current. In Proceedings of the 2011 7th International Conference on Emerging Technologies, Islamabad, Pakistan, 5–6 September 2011; Volume 8. [Google Scholar]
- Sun, H. Optimization of Velocity and Displacement Measurement with Optical Encoder and Laser Self-Mixing Interferometry. Ph.D. Thesis, Technical University Munich, München, Germany, 2020. [Google Scholar]
- Liu, Y.; Liu, J.; Kennel, R. Rotational speed measurement using self-mixing interferometry. Appl. Opt. 2021, 60, 5074–5080. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Liu, J.G.; Kennel, R.M. Improving the accuracy of laser self-mixing interferometry for velocity measurement. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 236–241. [Google Scholar] [CrossRef]
- Kliese, R.; Rakić, A.D. Spectral broadening caused by dynamic speckle in self-mixing velocimetry sensors. Opt. Express 2012, 20, 18757–18771. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mowla, A.; Nikolic, M.; Taimre, T.; Tucker, J.; Lim, Y.; Bertling, K.; Rakic, A. Effect of the optical system on the Doppler spectrum in laser-feedback interferometry. Appl. Opt. 2015, 54, 18–26. [Google Scholar] [CrossRef] [PubMed]








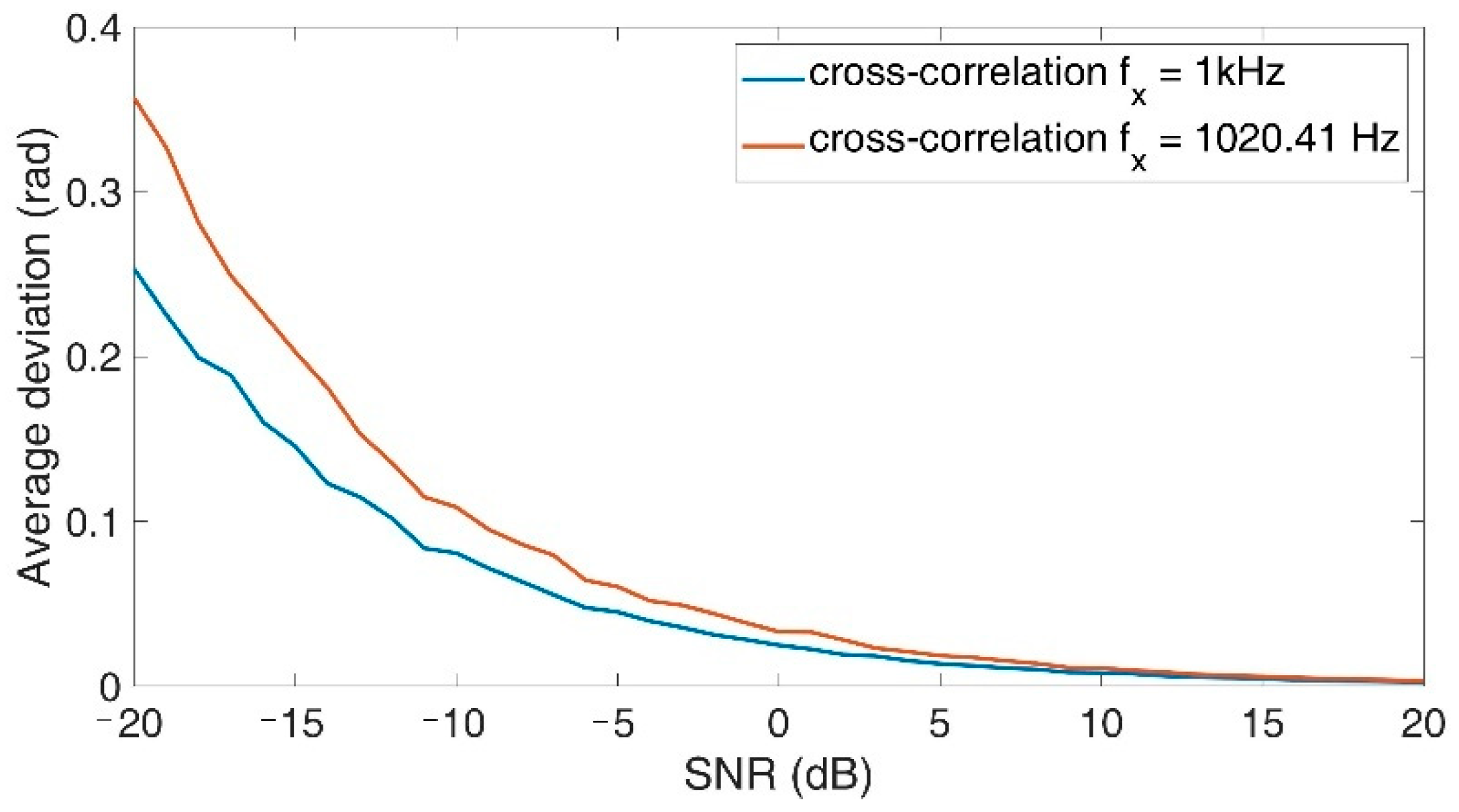

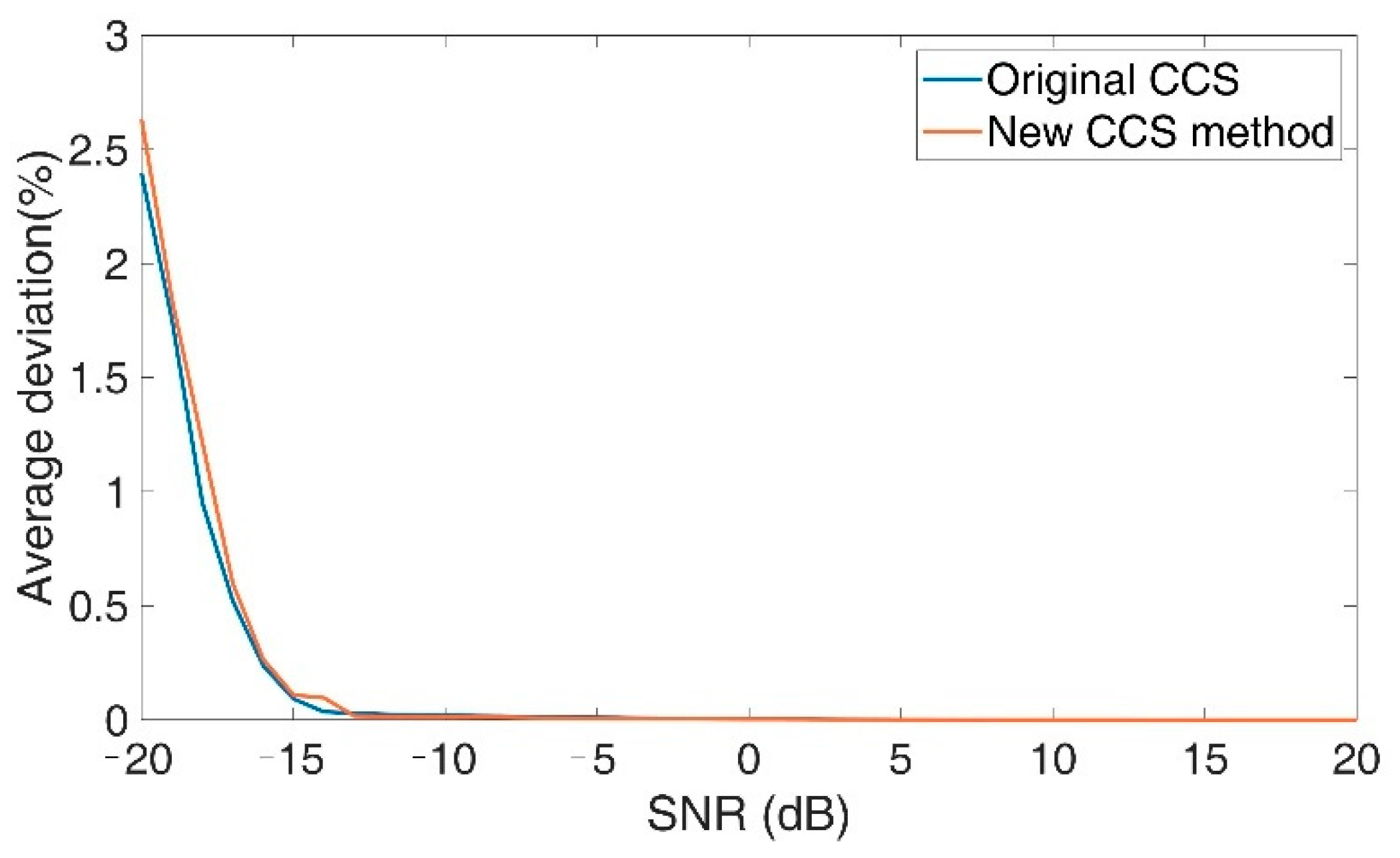




| Phase Difference | Behavior of Accuracy |
|---|---|
| Increasing phase difference leads to accuracy deterioration | |
| Increasing phase difference leads to accuracy improvement | |
| Increasing phase difference leads to accuracy deterioration | |
| Increasing phase difference leads to accuracy improvement |
| Original CCS | New CCS Method |
|---|---|
| 286.93 ms | 30.82 ms |
| Rotational Speed in RPM | Linearity of Method in [19] | Linearity with Original CCS | Linearity with New CCS Method |
|---|---|---|---|
| 5 | −0.21 | −0.24% | +0.23% |
| 10 | −0.18 | −0.20% | +0.20% |
| 20 | −0.10 | −0.06% | +0.08% |
| 30 | +0.01 | 0.03% | −0.00% |
| 40 | +0.10 | 0.09% | −0.10% |
| 50 | +0.14 | 0.11% | −0.10% |
| 75 | +0.31 | 0.35% | −0.27% |
| 100 | +0.21 | 0.40% | +0.32% |
| 125 | −0.26 | −0.21% | +0.14% |
| 150 | −0.12 | −0.16% | +0.10% |
| 175 | +0.18 | 0.03% | +0.02% |
| 200 | −0.21 | −0.12% | +0.18% |
| Rotational Speed (RPM) | NRMSE of Method in [19] | NRMSE with Original CCS (%) | NRMSE with New CCS (%) |
|---|---|---|---|
| 5 | 0.16 | 0.16 | 0.18 |
| 10 | 0.06 | 0.06 | 0.07 |
| 20 | 0.05 | 0.08 | 0.09 |
| 30 | 0.08 | 0.14 | 0.13 |
| 40 | 0.15 | 0.18 | 0.21 |
| 50 | 0.13 | 0.13 | 0.12 |
| 75 | 0.07 | 0.04 | 0.05 |
| 100 | 0.06 | 0.06 | 0.07 |
| 125 | 0.06 | 0.06 | 0.09 |
| 150 | 0.07 | 0.08 | 0.08 |
| 175 | 0.05 | 0.06 | 0.07 |
| 200 | 0.06 | 0.03 | 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, J.; Kennel, R. Optimization of the Processing Time of Cross-Correlation Spectra for Frequency Measurements of Noisy Signals. Metrology 2022, 2, 293-310. https://doi.org/10.3390/metrology2020018
Liu Y, Liu J, Kennel R. Optimization of the Processing Time of Cross-Correlation Spectra for Frequency Measurements of Noisy Signals. Metrology. 2022; 2(2):293-310. https://doi.org/10.3390/metrology2020018
Chicago/Turabian StyleLiu, Yang, Jigou Liu, and Ralph Kennel. 2022. "Optimization of the Processing Time of Cross-Correlation Spectra for Frequency Measurements of Noisy Signals" Metrology 2, no. 2: 293-310. https://doi.org/10.3390/metrology2020018
APA StyleLiu, Y., Liu, J., & Kennel, R. (2022). Optimization of the Processing Time of Cross-Correlation Spectra for Frequency Measurements of Noisy Signals. Metrology, 2(2), 293-310. https://doi.org/10.3390/metrology2020018







