The Difference in Wave Dynamics between SARS-CoV-2 Pre-Omicron and Omicron Variant Waves
Abstract
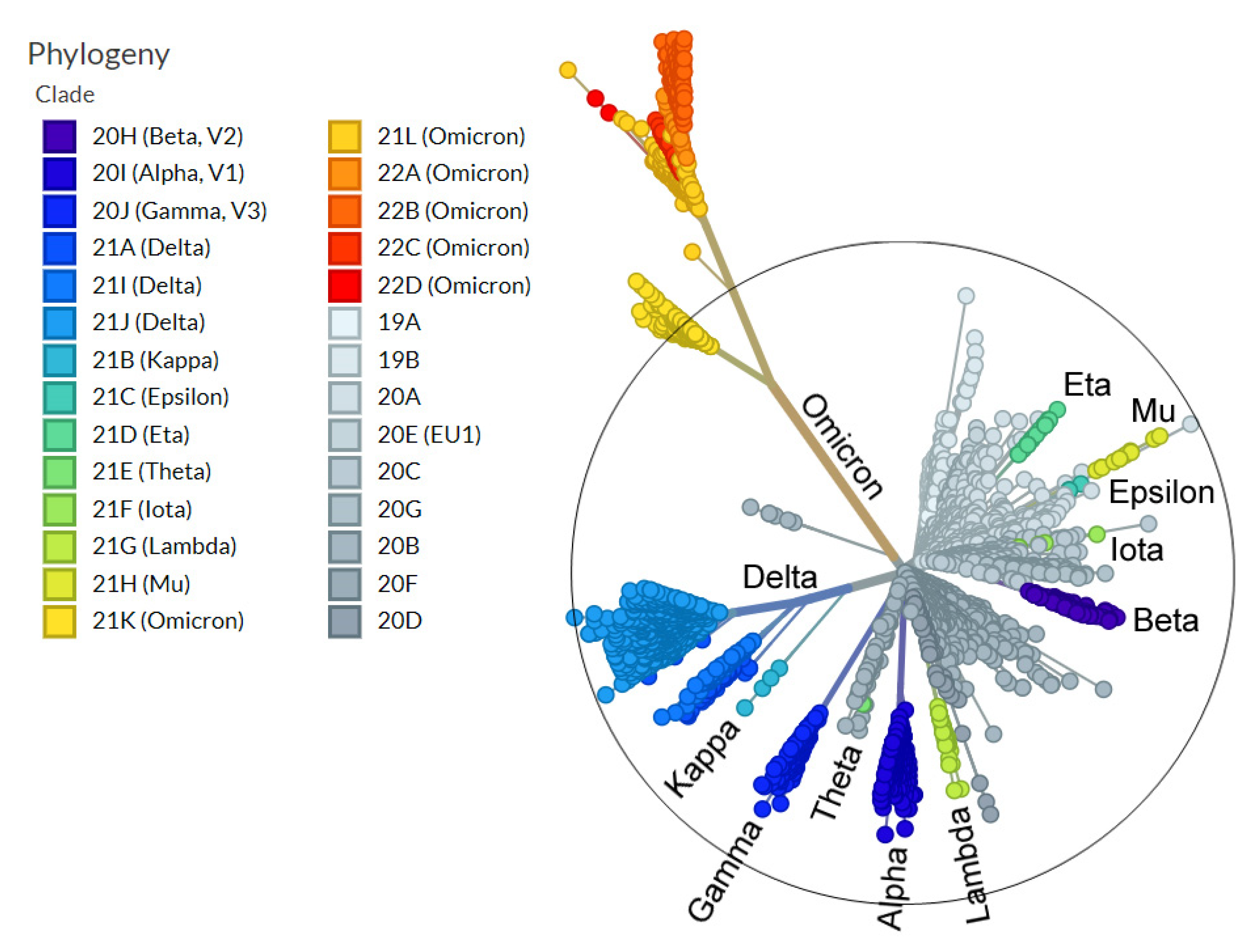
1. Introduction
2. Materials and Methods
2.1. Data of Daily Incidence
2.2. Data Processing
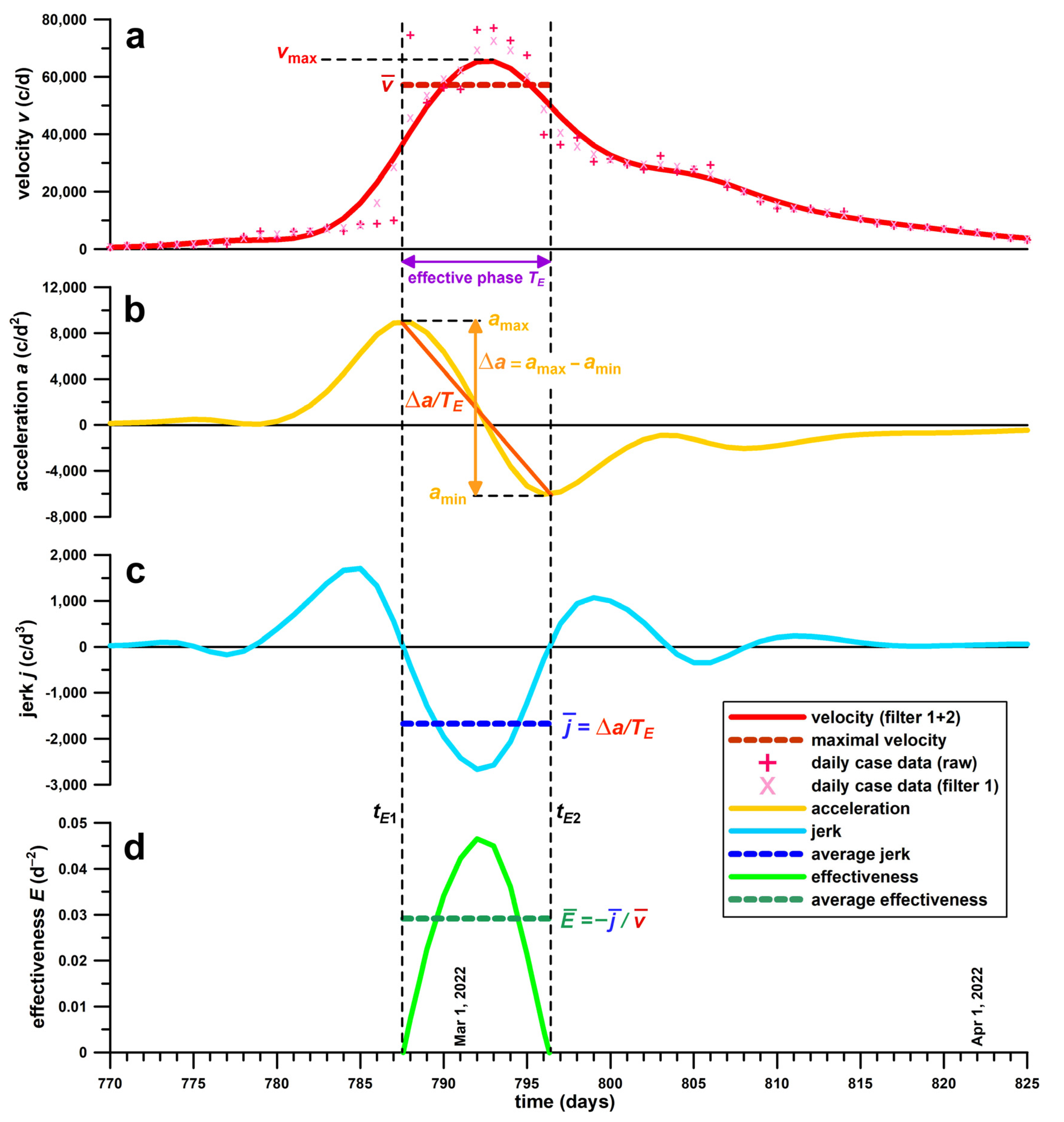
2.3. Explanation and Definition of Effectiveness Parameters, and Their Practical Application in the Public Health Context
- (1)
- The effectiveness E, sensu stricto, refers to the rate of change of acceleration, that is, how quickly the positive acceleration peak, amax, becomes negative, amin (Δa/TE; Figure 1). As the gradient Δa/TE is case number dependent (velocity dependent), it has to be normalised to the average velocity during the effective phase TE. The greater E, the more effectively an epidemic wave is managed.
- (2)
- The duration of the effective phase, TE, refers to the interruption of the acceleration. Outside the effective phase, any control measures are ineffective, as the acceleration increases before the effective phase; and the deceleration decreases after the effective phase. A shorter effective phase TE, means that an epidemic wave is managed more effectively. This phenomenon can be explained easily from two waves with the same Δa, but different TE. Thus, the shorter TE, the greater is E.
- (3)
- The ratio ρ of E to TE addresses the following relationship: both E and TE are functions of the width of a wave [16]. The wider the wave in terms of daily case numbers, the smaller is E and the longer is TE. As E and TE are inversely related to each other, a greater E and a shorter TE result in a greater ratio ρ. The ratio ρ therefore combines the two individual effectiveness parameters of E and TE in a single one, referring to the magnitude of effectiveness E per unit time, i.e., per a single day. The greater ρ, the more effectively an epidemic wave is managed.
- (4)
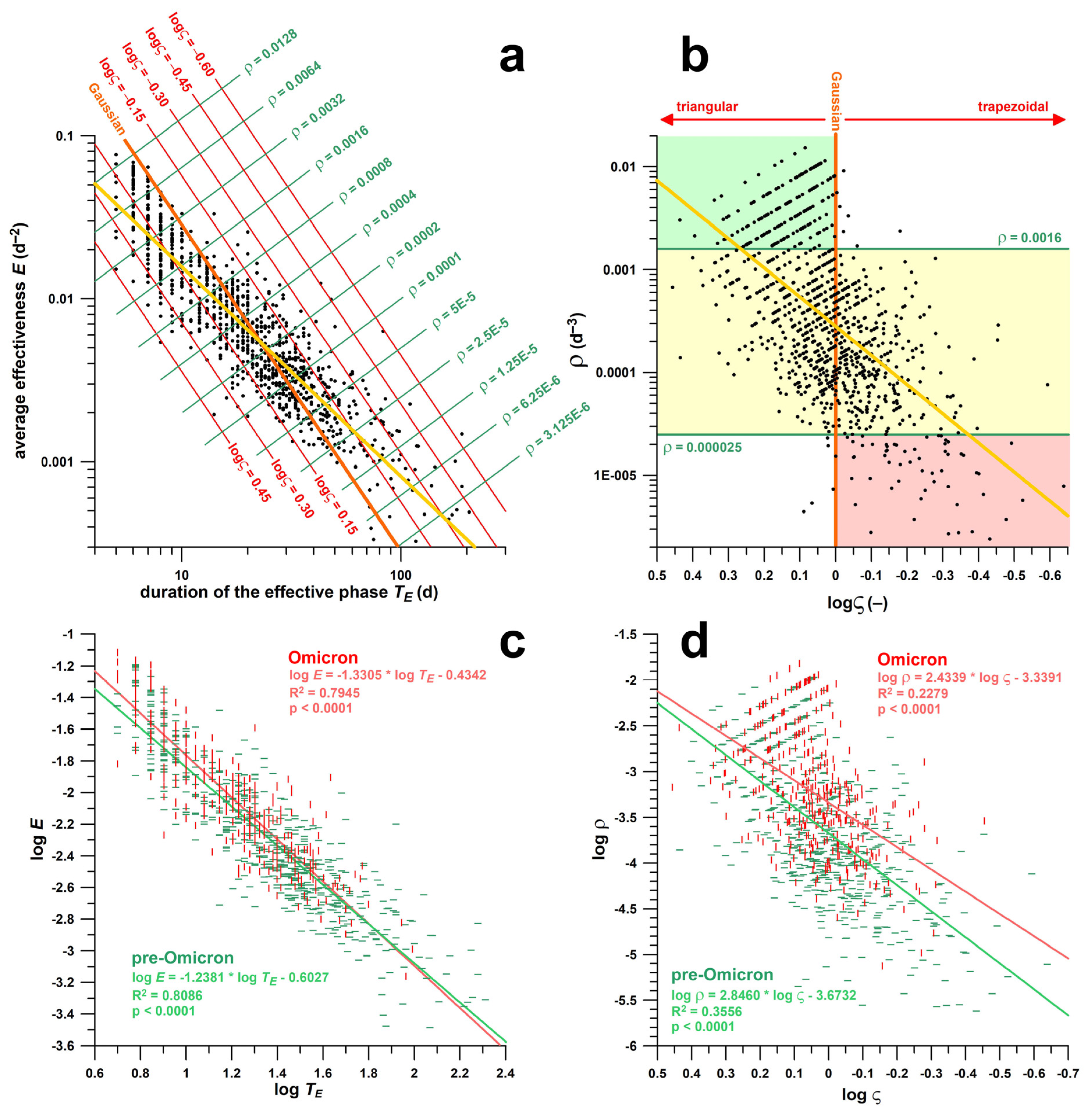
- As mentioned before, both E and TE are functions of the width of a wave s [16], specifically in Gaussian wave profiles E = c1 s−2 and TE = c2 s, (where c1 and c2 are constants), and therefore the product of E and TE is proportional to a constant, namely: E·TE ∝ s−1. Any deviation from this constant indicates that the shape of the wave is no longer Gaussian. The ratio ς, mentioned above, and defined as ς = C E−0.5 TE−1, (where C is a constant [16]) addresses this problem. The shape factor logς defines the peak pattern of the velocity profile. If logς > 0, the velocity peak is triangular, if logς < 0, the peak is trapezoidal (with a plateau), and if logς = 0, the peak is round (Gaussian function). The greater logς > 0, the more triangular or pointed the velocity peak is, and the more effectively an epidemic wave is managed. A triangular shape indicates rapid change from increasing to declining daily case data, whereas a trapezoidal plateau shows that a wave is struggling with achieving a sustained decline of daily case data.
2.4. Wave Definition
2.5. Statistics
2.5.1. Correlations
2.5.2. Regressions
- -
- apparently increasing trend:
- -
- H0: the effect (gradient of the trend) is smaller than or equal to zero
- -
- H1: the effect is greater than zero
- -
- apparently decreasing trend:
- -
- H0: the effect is greater than or equal to zero
- -
- H1: the effect is smaller than zero
2.5.3. Comparison of Pre-Omicron and Omicron Wave Data
2.5.4. Influence of Geographic and Socioeconomic Data
3. Results
3.1. Wave Data
3.2. Correlation Analysis of Effectiveness Parameters
3.3. Regression Analysis of Effectiveness Parameters and Peak Daily Case Data against Time
3.3.1. Data of All Waves
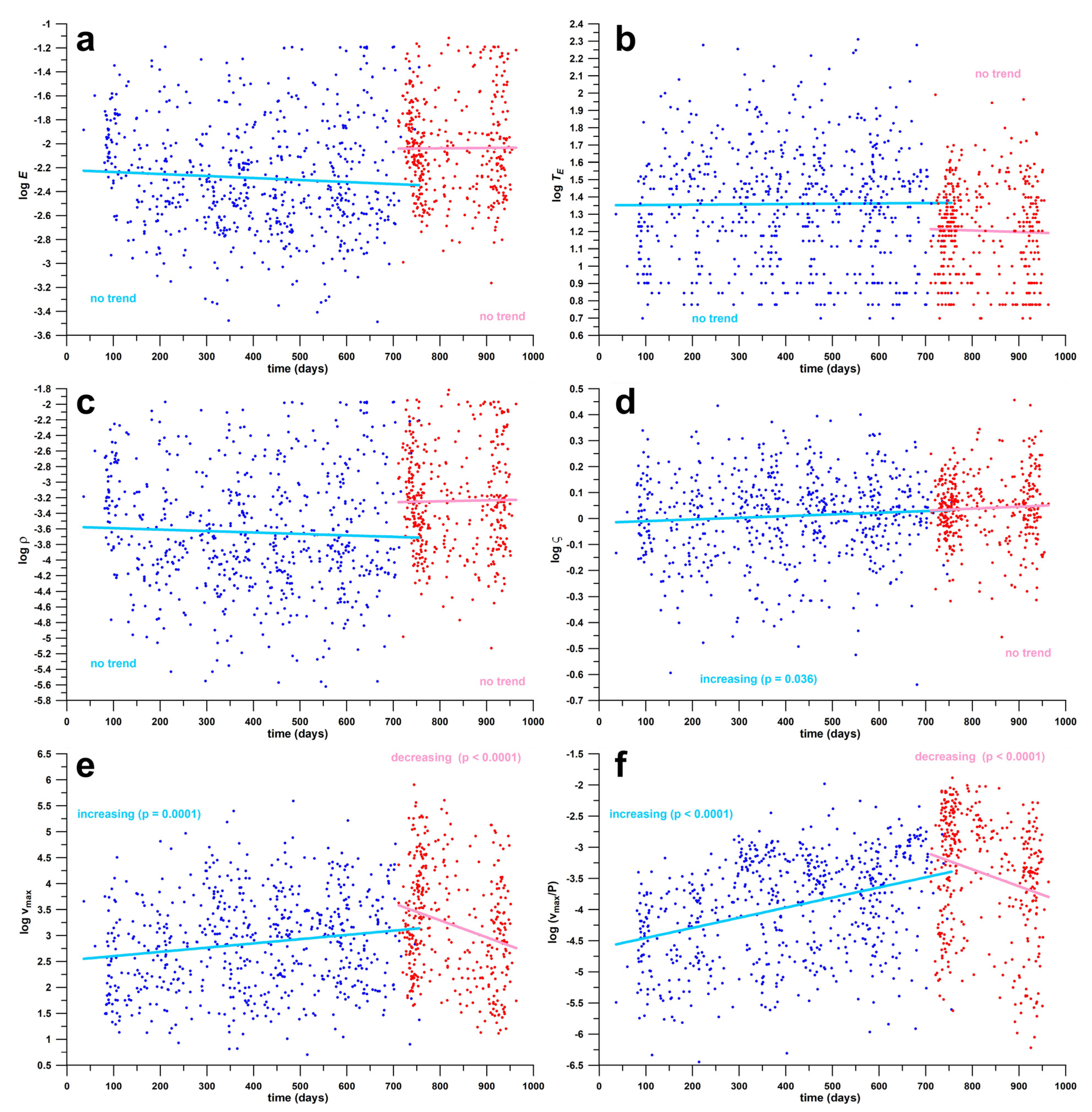
3.3.2. Pre-Omicron and Omicron Waves Separated
3.4. Comparison of Pre-Omicron and Omicron Data
3.5. Relationship of Epidemiological Parameters with Geographical and Socioeconomic Data
3.5.1. Data of All Waves
3.5.2. Pre-Omicron Wave Data
3.5.3. Omicron Wave Data
4. Discussion
- (1)
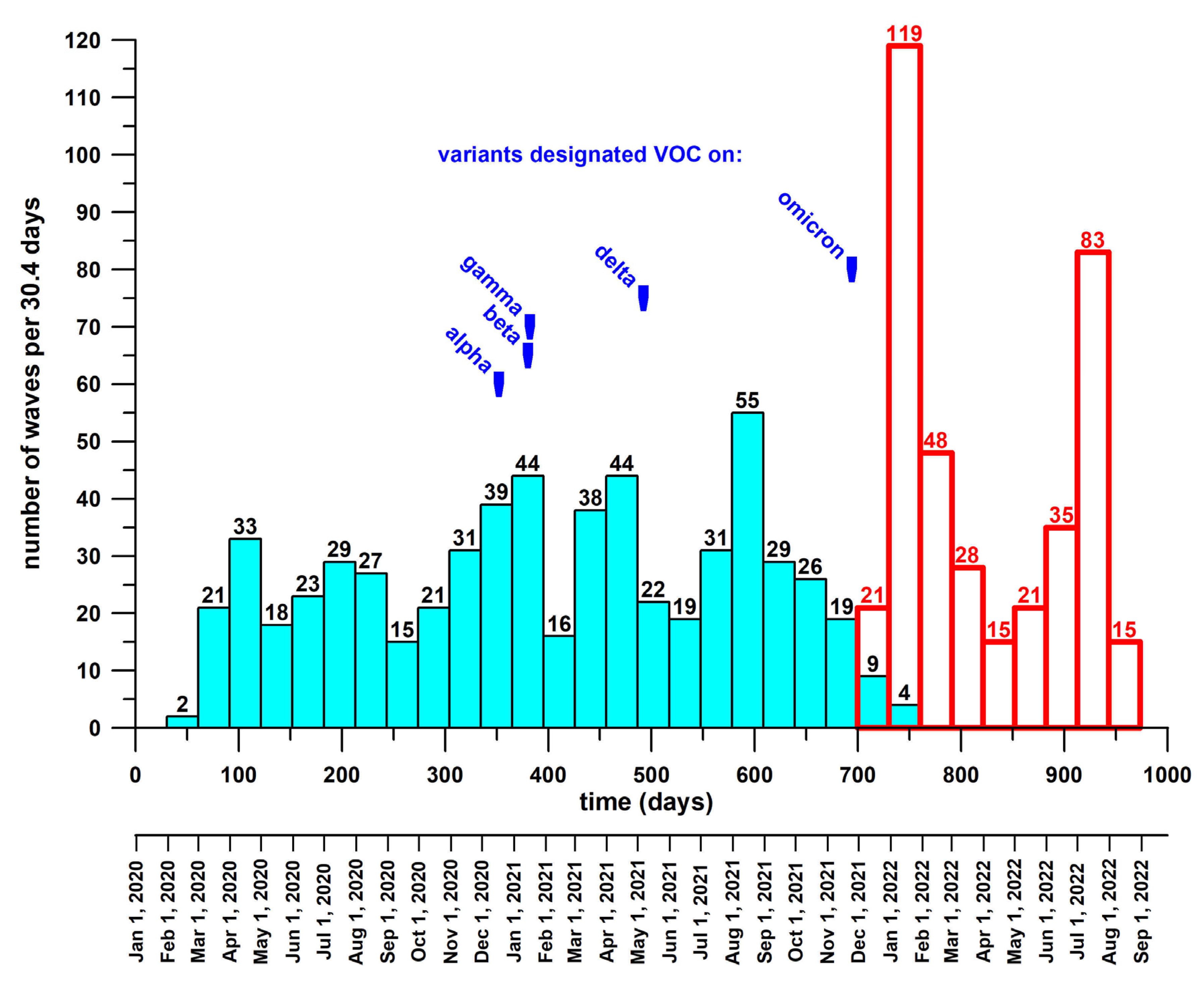
- the average number of Omicron waves per month (42.78) was greater than the one of pre-Omicron waves per month (25.62) (Figure 4);
- (2)
- (3)
- Omicron waves generated more cases (vmax and vmax/P) than pre-Omicron waves; the pre-Omicron trend showed increasing numbers over time, whereas the Omicron trend showed decreasing numbers (Figure 7e,f);
- (4)
- (1)
- The type of control measure; if there were no further influences, then the control measure is expected to succeed, and the effectiveness would correlate with the severity and complexity of the control measures, resulting in maximum coherence.
- (2)
- The compliance of the citizens [30], which can be enforced by restrictions but suffers when disagreeing with enforcement.
- (3)
- Socioeconomic status: citizens of richer countries are better educated and thus less likely to follow orders [16].
- (4)
- Geographical factors: smaller countries with less population manage the waves more efficiently, specifically small islands [16].
- (5)
- Timely introduction of control measures: if, e.g., a lockdown is introduced one serial interval before the end of the effective phase, then it was implemented too late and cannot contribute to the flattening of the curve anymore [17] which at this point is already completed.
- (6)
- Epidemiological factors, related to microorganisms (e.g., contagiousness), herd immunity, vaccines, etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shahhosseini, N.; Babuadze, G.; Wong, G.; Kobinger, G.P. Mutation Signatures and In Silico Docking of Novel SARS-CoV-2 Variants of Concern. Microorganisms 2021, 9, 926. [Google Scholar] [CrossRef] [PubMed]
- Quarleri, J.; Galvan, V.; Delpino, M.V. Omicron variant of the SARS-CoV-2: A quest to define the consequences of its high mutational load. GeroScience 2022, 44, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Gowrisankar, A.; Priyanka, T.M.; Banerjee, S. Omicron: A mysterious variant of concern. Eur. Phys. J. Plus 2022, 137, 100. [Google Scholar] [CrossRef] [PubMed]
- Elliott, P.; Eales, O.; Bodinier, B.; Tang, D.; Wang, H.; Jonnerby, J.; Haw, D.; Elliott, J.; Whitaker, M.; Walters, C.E.; et al. Dynamics of a national Omicron SARS-CoV-2 epidemic during January 2022 in England. Nat. Commun. 2022, 13, 4500. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention (CDC). Variants of the Virus. Available online: https://www.cdc.gov/coronavirus/2019-ncov/variants/index.html (accessed on 15 October 2022).
- Willyard, C. What the Omicron wave is revealing about human immunity. Nature 2022, 602, 22–25. [Google Scholar] [CrossRef] [PubMed]
- Backer, J.A.; Eggink, D.; Andeweg, S.P.; Veldhuijzen, I.K.; van Maarseveen, N.; Vermaas, K.; Vlaemynck, B.; Schepers, R.; Hof, S.V.D.; Reusken, C.B.; et al. Shorter serial intervals in SARS-CoV-2 cases with Omicron BA.1 variant compared with Delta variant, the Netherlands, 13 to 26 December 2021. Eur. Surveill. 2022, 27, 2200042. [Google Scholar] [CrossRef] [PubMed]
- Kremer, C.; Braeye, T.; Proesmans, K.; André, E.; Torneri, A.; Hens, N. Serial Intervals for SARS-CoV-2 Omicron and Delta Variants, Belgium, November 19-December 31, 2021. Emerg. Infect. Dis. 2022, 28, 1699–1702. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Kang, L.; Guo, Z.; Liu, J.; Liu, M.; Liang, W. Incubation Period of COVID-19 Caused by Unique SARS-CoV-2 Strains: A Systematic Review and Meta-analysis. JAMA Netw Open. 2022, 5, e2228008. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.M.; Nakayama, J.Y.; O’Hegarty, M.; McGowan, A.; Teran, R.A.; Bart, S.M.; Mosack, K.; Roberts, N.; Campos, B.; Paegle, A.; et al. SARS-CoV-2 B.1.1.529 (Omicron) Variant Transmission Within Households—Four U.S. Jurisdictions, November 2021–February 2022. MMWR Morb. Mortal. Wkly. Rep. 2022, 71, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Hadfield, J.; Megill, C.; Bell, S.M.; Huddleston, J.; Potter, B.; Callender, C.; Sagulenko, P.; Bedford, T.; Neher, R.A. Nextstrain: Real-time tracking of pathogen evolution. Bioinformatics 2018, 34, 4121–4123. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Deng, X.; Fang, L.; Sun, K.; Wu, Y.; Che, T.; Zou, J.; Cai, J.; Liu, H.; Wang, Y.; et al. Epidemiological characteristics and transmission dynamics of the outbreak caused by the SARS-CoV-2 Omicron variant in Shanghai, China: A descriptive study. Lancet Reg. Health—West. Pac. 2022, 29, 100592. [Google Scholar] [CrossRef] [PubMed]
- Hay, J.A.; Kissler, S.M.; Fauver, J.R.; Mack, C.; Tai, C.G.; Samant, R.M.; Connelly, S.; Anderson, D.J.; Khullar, G.; MacKay, M.; et al. Viral dynamics and duration of PCR positivity of the SARS-CoV-2 Omicron variant. medRxiv 2022. [Google Scholar] [CrossRef]
- Our World in Data. Available online: https://ourworldindata.org/explorers/coronavirus-data-explorer (accessed on 28 August 2022).
- COVID-19 Data. Available online: https://github.com/owid/covid-19-data/tree/master/public/data (accessed on 28 August 2022).
- Fuss, F.K.; Weizman, Y.; Tan, A.M. COVID-19 Pandemic: How Effective Are Preventive Control Measures and Is a Complete Lockdown Justified? A Comparison of Countries and States. COVID 2022, 2, 18–46. [Google Scholar] [CrossRef]
- Fuss, F.K.; Weizman, Y.; Tan, A.M. Which Preventive Control Measure Initiated the ‘Flattening of the Curve’: A Comparison of Austria and Victoria during the 2nd Wave of the COVID-19 Pandemic. Wien. Klin. Wochenschr. (Cent. Eur. J. Med. ) 2022, 134, 831–841. [Google Scholar] [CrossRef] [PubMed]
- BBC News. South Korea Says It Has a Second Wave of Coronavirus Infections—But What Does That Really Mean? Available online: https://www.abc.net.au/news/2020-06-24/coronavirus-covid-19-countries-second-wave-explainer-south-korea/12385882 (accessed on 24 October 2022).
- Zhang, S.X.; Arroyo Marioli, F.; Gao, R.; Wang, S. A Second Wave? What Do People Mean by COVID Waves?—A Working Definition of Epidemic Waves. Risk Manag. Healthc Policy 2021, 14, 3775–3782. [Google Scholar] [CrossRef] [PubMed]
- McGrath, R.E.; Meyer, G.J. When effect sizes disagree: The case of r and d. Psychol. Meth. 2006, 11, 386–401. [Google Scholar] [CrossRef] [PubMed]
- List of Countries and Dependencies by Population. Available online: https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_population (accessed on 1 August 2022).
- List of Countries and Dependencies by Area. Available online: https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_area (accessed on 1 August 2022).
- List_of_Countries_by_GDP. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_GDP_(nominal) (accessed on 1 August 2022).
- Education Index. Available online: https://en.wikipedia.org/wiki/Education_Index (accessed on 1 August 2022).
- Wald, A. The fitting of straight lines if both variables are subject to error. Ann. Math. Stat. 1940, 11, 282–300. [Google Scholar] [CrossRef]
- Fuss, F.K.; Düking, P.; Weizman, Y. Discovery of a Sweet Spot on the Foot with a Smart Wearable Soccer Boot Sensor That Maximizes the Chances of Scoring a Curved Kick in Soccer. Front. Physiol. 2018, 9, 63. [Google Scholar] [CrossRef] [PubMed]
- Farr, W. Causes of Death in England and Wales. Second Annual Report of the Registrar General of Births, Deaths and Marriages in England; Clowes and Sons: London, UK, 1840; Available online: https://babel.hathitrust.org/cgi/pt?id=njp.32101064041955&view=1up&seq=1 (accessed on 16 October 2022).
- Pacheco-Barrios, K.; Cardenas-Rojas, A.; Giannoni-Luza, S.; Fregni, F. COVID-19 pandemic and Farr’s law: A global comparison and prediction of outbreak acceleration and deceleration rates. PLoS ONE 2020, 15, e0239175. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Murphy, K.; Williamson, H.; Sargeant, E.; McCarthy, M. Why people comply with COVID-19 social distancing restrictions: Self-interest or duty? Aust. N. Z. J. Criminol. 2020, 53, 477–496. [Google Scholar] [CrossRef]

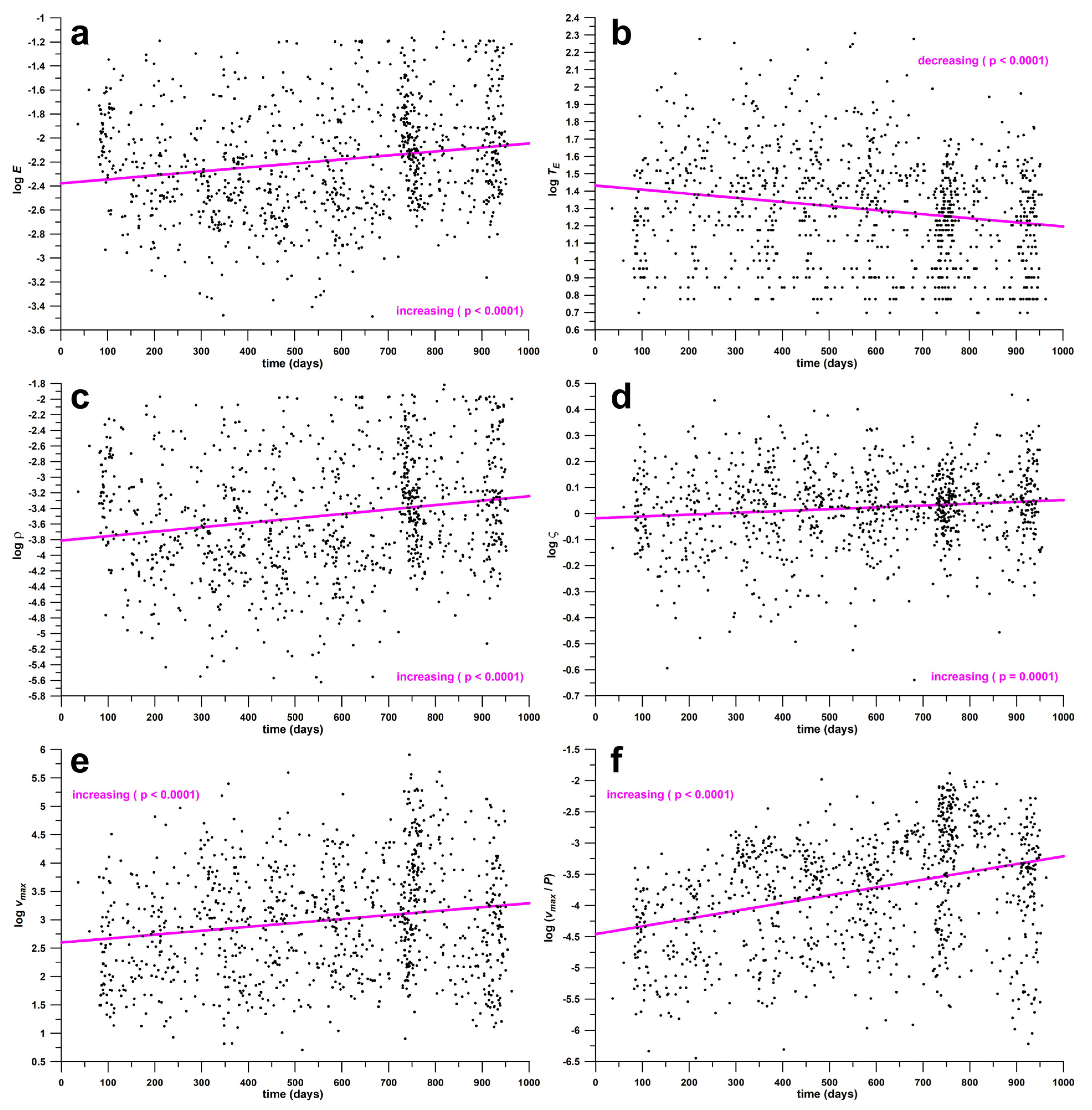

| All Waves | R2 | r | Effect | p-Value | Standard Error |
|---|---|---|---|---|---|
| log TE | 0.0358 | 0.1927 | small | p < 0.0001 | 0.3124 |
| log E | 0.0351 | 0.1907 | small | p < 0.0001 | 0.4446 |
| log ρ | 0.0371 | 0.1964 | small | p < 0.0001 | 0.7382 |
| log ς | 0.0141 | 0.1195 | small | p = 0.0001 | 0.1489 |
| log (vmax/P) | 0.1213 | 0.3715 | medium | p < 0.0001 | 0.8719 |
| log vmax | 0.0320 | 0.1818 | small | p < 0.0001 | 0.9794 |
| pre-Omicron waves | R2 | r | effect | p-value | standard error |
| log TE | 0.0001 | 0.0104 | very small | p > 0.05 | 0.3329 |
| log E | 0.0044 | 0.0664 | very small | p > 0.05 | 0.4573 |
| log ρ | 0.0019 | 0.0439 | very small | p > 0.05 | 0.7708 |
| log ς | 0.0053 | 0.0727 | very small | p = 0.036 | 0.1613 |
| log (vmax/P) | 0.1305 | 0.3873 | medium | p < 0.0001 | 0.7614 |
| log vmax | 0.0262 | 0.1642 | small | p = 0.0001 | 0.9051 |
| Omicron waves | R2 | r | effect | p-value | standard error |
| log TE | 0.0007 | 0.0267 | very small | p > 0.05 | 0.2669 |
| log E | 0 | 0.0058 | very small | p > 0.05 | 0.3985 |
| log ρ | 0.0002 | 0.0146 | very small | p > 0.05 | 0.6478 |
| log ς | 0.0022 | 0.0472 | very small | p > 0.055 | 0.1269 |
| log (vmax/P) | 0.0517 | 0.2334 | small | p < 0.0001 | 0.9336 |
| log vmax | 0.0622 | 0.2575 | medium | p < 0.0001 | 1.0193 |
| Parameters | Median Pre-Omicron | Median Omicron | U | p | r | Effect | Interpretation: Omicron Waves Have a … Median |
|---|---|---|---|---|---|---|---|
| log TE | 1.380 | 1.255 | 85,359 | <0.0001 | 0.279 | medium | smaller |
| log E | −2.334 | −2.120 | 79,591 | <0.0001 | 0.328 | medium | greater |
| log ρ | −3.722 | −3.368 | 81,110 | <0.0001 | 0.315 | medium | greater |
| log ς | 0.025 | 0.043 | 107,037 | 0.0108 | 0.096 | very small | greater |
| log vmax | 2.963 | 3.283 | 96,037 | <0.0001 | 0.189 | small | greater |
| log (vmax/P) | −3.845 | −3.229 | 73,844 | <0.0001 | 0.376 | large | greater |
| P | Cut-Off | n1, Low P | n2, High P | Median, Low P | Median, High P | U | p | r | Effect | Interpretation |
|---|---|---|---|---|---|---|---|---|---|---|
| log TE | 6.539 | 337 | 666 | 1.23 | 1.352 | 88,571 | <0.0001 | 0.211 | small | more P, longer duration |
| log E | 6.539 | 337 | 666 | −2.061 | −2.305 | 81,296 | <0.0001 | 0.276 | medium | more P, less effective |
| log ρ | 6.539 | 337 | 666 | −3.254 | −3.668 | 83,755 | <0.0001 | 0.254 | medium | more P, less effective |
| log ς | 6.966 | 519 | 483 | 0.042 | 0.022 | 112,511 | 0.0051 | 0.102 | small | more P, less triangular |
| log (vmax/P) | 7.067 | 594 | 409 | −3.319 | −4.204 | 52,960 | <0.0001 | 0.564 | large | more P, less relative cases |
| A | cut-off | n1, small A | n2, large A | median, small A | median, large A | U | p | r | effect | interpretation |
| log TE | 4.584 | 339 | 663 | 1.204 | 1.362 | 86,818.5 | <0.0001 | 0.227 | small | more A, longer duration |
| log E | 4.627 | 352 | 651 | −2.063 | −2.319 | 82,163 | <0.0001 | 0.283 | medium | more A, less effective |
| log ρ | 4.627 | 352 | 652 | −3.246 | −3.685 | 84,149 | <0.0001 | 0.267 | medium | more A, less effective |
| log ς | 4.916 | 429 | 575 | 0.045 | 0.025 | 111,384.5 | 0.0085 | 0.097 | very small | more A, less triangular |
| log (vmax/P) | 4.96 | 460 | 542 | −3.242 | −3.976 | 69,799.5 | <0.0001 | 0.44 | large | more A, less relative cases |
| G | cut-off | n1, low G | n2, high G | median, low G | median, high G | U | p | r | effect | interpretation |
| log TE | −1.966 | 336 | 663 | 1.279 | 1.322 | 99,292 | 0.005 | 0.109 | small | more G, longer duration |
| log E | −1.947 | 663 | 336 | 0.007 | 0.005 | 88,280 | <0.0001 | 0.207 | small | more G, less effective |
| log ρ | −1.844 | 416 | 583 | −3.418 | −3.667 | 101,392 | <0.0001 | 0.164 | small | more G, less effective |
| log ς | −1.757 | 511 | 489 | 0.023 | 0.039 | 115,093.5 | 0.0308 | 0.079 | very small | more G, more triangular |
| log (vmax/P) | −1.947 | 336 | 665 | −4.568 | −3.312 | 35,558 | <0.0001 | 0.682 | large | more G, more relative cases |
| I | cut-off | n1, low I | n2, high I | median, low I | median, high I | U | p | r | effect | interpretation |
| log TE | 0.638 | 338 | 586 | 1.255 | 1.362 | 79,376.5 | <0.0001 | 0.198 | small | more I, longer duration |
| log E | 0.638 | 338 | 586 | −2.058 | −2.334 | 68,536.5 | <0.0001 | 0.308 | medium | more I, less effective |
| log ρ | 0.638 | 338 | 671 | −3.312 | −3.643 | 87,807.5 | <0.0001 | 0.226 | small | more I, less effective |
| log ς | 0.805 | 658 | 262 | 0.025 | 0.046 | 73,681.5 | 0.0006 | 0.145 | small | more I, more triangular |
| log (vmax/P) | 0.64 | 335 | 671 | −4.54 | −3.315 | 36,844.5 | <0.0001 | 0.672 | large | more I, more relative cases |
| D | cut-off | n1, low D | n2, high D | median, low D | median, high D | U | p | r | effect | interpretation |
| log TE | in-significant | |||||||||
| log E | 1.912 | 487 | 513 | −2.177 | −2.23 | 135,079.5 | 0.0257 | 0.081 | very small | more D, less effective |
| log ρ | 1.903 | 484 | 515 | −3.471 | −3.56 | 115,667 | 0.0488 | 0.072 | very small | more D, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 1.974 | 539 | 463 | −3.814 | −3.409 | 100,923.5 | <0.0001 | 0.191 | small | more D, more relative cases |
| P | Cut-Off | n1, Low P | n2, High P | Median, Low P | Median, High P | U | p | r | Effect | Interpretation |
|---|---|---|---|---|---|---|---|---|---|---|
| log TE | 6.96 | 302 | 314 | 1.301 | 1.447 | 36,495.5 | <0.0001 | 0.23 | small | more P, longer duration |
| log E | 6.63 | 207 | 409 | −2.15 | −2.432 | 29,834 | <0.0001 | 0.295 | medium | more P, less effective |
| log ρ | 6.96 | 302 | 314 | −3.518 | −3.885 | 34,911 | <0.0001 | 0.264 | medium | more P, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 7.067 | 357 | 260 | −3.566 | −4.338 | 24,561 | <0.0001 | 0.471 | large | more P, less relative cases |
| A | cut-off | n1, small A | n2, large A | median, small A | median, large A | U | p | r | effect | interpretation |
| log TE | 4.682 | 210 | 406 | 1.255 | 1.447 | 30,755.5 | <0.0001 | 0.279 | medium | more A, longer duration |
| log E | 4.628 | 206 | 410 | −2.123 | −2.45 | 27,597 | <0.0001 | 0.347 | medium | more A, less effective |
| log ρ | 4.682 | 210 | 406 | −3.359 | −3.883 | 28,867 | <0.0001 | 0.323 | medium | more A, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 4.959 | 276 | 341 | −3.404 | −4.122 | 25,696 | <0.0001 | 0.454 | large | more A, less relative cases |
| G | cut-off | n1, low G | n2, high G | median, low G | median, high G | U | p | r | effect | interpretation |
| log TE | in-significant | |||||||||
| log E | −1.99 | 207 | 409 | −2.286 | −2.4 | 35,805 | 0.0017 | 0.154 | small | more G, less effective |
| log ρ | −1.916 | 227 | 389 | −3.676 | −3.802 | 38,788 | 0.0117 | 0.121 | small | more G, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 1.99 | 208 | 409 | −4.649 | −3.514 | 14,107 | <0.0001 | 0.668 | large | more G, more relative cases |
| I | cut-off | n1, low I | n2, high I | median, low I | median, high I | U | p | r | effect | interpretation |
| log TE | 0.618 | 205 | 368 | 1.342 | 1.431 | 31,044 | 0.0004 | 0.177 | small | more I, longer duration |
| log E | 0.618 | 205 | 413 | −2.241 | −2.412 | 32,901.5 | <0.0001 | 0.223 | small | more I, less effective |
| log ρ | 0.604 | 199 | 373 | −3.58 | −3.87 | 28,214.5 | <0.0001 | 0.24 | small | more I, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 0.632 | 207 | 407 | −4.639 | −3.503 | 14,265.5 | <0.0001 | 0.661 | large | more I, more relative cases |
| D | cut-off | n1, low D | n2, high D | median, low D | median, high D | U | p | r | effect | interpretation |
| log TE | 2.105 | 410 | 206 | 1.431 | 1.301 | 36,743 | 0.0085 | 0.13 | small | more D, SHORTER duration |
| log E | 2.105 | 410 | 206 | −2.424 | −2.216 | 36,434.5 | 0.0054 | 0.137 | small | more D, MORE effective |
| log ρ | 2.073 | 404 | 213 | −3.818 | −3.559 | 37,706 | 0.0114 | 0.124 | small | more D, MORE effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 1.833 | 250 | 367 | −3.99 | −3.687 | 36,395 | <0.0001 | 0.207 | small | more D, more relative cases |
| P | Cut-Off | n1, Low P | n2, High P | Median, low P | Median, High P | U | p | r | Effect | Interpretation |
|---|---|---|---|---|---|---|---|---|---|---|
| log TE | 7.226 | 258 | 127 | 1.176 | 1.301 | 12,861.5 | 0.0006 | 0.215 | small | more P, longer duration |
| log E | 7.226 | 258 | 127 | −2.028 | −2.168 | 13,078.5 | 0.0013 | 0.202 | small | more P, less effective |
| log ρ | 7.226 | 258 | 127 | −3.2 | −3.477 | 12,871.5 | 0.0006 | 0.214 | small | more P, less effective |
| log ς | 7.226 | 258 | 127 | 0.051 | 0.031 | 14,016.5 | 0.0214 | 0.144 | small | more P, less triangular |
| log (vmax/P) | 6.349 | 125 | 261 | −2.792 | −3.493 | 8522 | <0.0001 | 0.478 | large | more P, less relative cases |
| A | cut-off | n1, small A | n2, large A | median, small A | median, large A | U | p | r | effect | interpretation |
| log TE | in-significant | |||||||||
| log E | 4.482 | 135 | 250 | −1.988 | −2.115 | 14,278.5 | 0.0128 | 0.154 | small | more A, less effective |
| log ρ | 4.482 | 135 | 250 | −3.168 | −3.39 | 14,425.5 | 0.0188 | 0.145 | small | more A, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 4.952 | 182 | 203 | −2.868 | −3.583 | 10,426.5 | <0.0001 | 0.436 | large | more A, less relative cases |
| G | cut-off | n1, low G | n2, high G | median, low G | median, high G | U | p | r | effect | interpretation |
| log TE | −1.66 | 212 | 174 | 1.19 | 1.279 | 13,957.5 | <0.0001 | 0.243 | medium | more G, longer duration |
| log E | −1.66 | 212 | 174 | −1.968 | −2.23 | 11,065 | <0.0001 | 0.4 | large | more G, less effective |
| log ρ | −1.707 | 209 | 177 | −3.173 | −3.54 | 12,165 | <0.0001 | 0.342 | medium | more G, less effective |
| log ς | −1.4 | 267 | 119 | 0.031 | 0.064 | 13,004 | 0.0044 | 0.181 | small | more G, more triangular |
| log (vmax/P) | −1.648 | 218 | 168 | −3.74 | −2.742 | 5889 | <0.0001 | 0.678 | large | more G, more relative cases |
| I | cut-off | n1, low I | n2, high I | median, low I | median, high I | U | p | r | effect | interpretation |
| log TE | 0.659 | 130 | 218 | 1.097 | 1.279 | 9323.5 | <0.0001 | 0.342 | medium | more I, longer duration |
| log E | 0.659 | 130 | 218 | −1.838 | −2.177 | 7005 | <0.0001 | 0.506 | large | more I, less effective |
| log ρ | 0.659 | 130 | 218 | −2.943 | −3.482 | 7819 | <0.0001 | 0.448 | large | more I, less effective |
| log ς | 0.731 | 203 | 145 | 0.025 | 0.067 | 11,584 | 0.0007 | 0.213 | small | more I, more triangular |
| log (vmax/P) | 0.765 | 223 | 163 | −3.688 | −2.672 | 5432.5 | <0.0001 | 0.701 | large | more I, more relative cases |
| D | cut-off | n1, low D | n2, high D | median, low D | median, high D | U | p | r | effect | interpretation |
| log TE | 1.903 | 187 | 199 | 1.204 | 1.255 | 15,896.5 | 0.0135 | 0.146 | small | more D, longer duration |
| log E | 1.903 | 187 | 198 | −2.017 | −2.123 | 15,072.5 | 0.0016 | 0.186 | small | more D, less effective |
| log ρ | 1.903 | 187 | 198 | −3.251 | −3.378 | 15,401.5 | 0.0044 | 0.168 | small | more D, less effective |
| log ς | in-significant | |||||||||
| log (vmax/P) | 1.974 | 207 | 179 | −3.4 | −3.019 | 14,878 | 0.0008 | 0.197 | small | more D, more relative cases |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuss, F.K.; Weizman, Y.; Tan, A.M. The Difference in Wave Dynamics between SARS-CoV-2 Pre-Omicron and Omicron Variant Waves. COVID 2023, 3, 28-50. https://doi.org/10.3390/covid3010002
Fuss FK, Weizman Y, Tan AM. The Difference in Wave Dynamics between SARS-CoV-2 Pre-Omicron and Omicron Variant Waves. COVID. 2023; 3(1):28-50. https://doi.org/10.3390/covid3010002
Chicago/Turabian StyleFuss, Franz Konstantin, Yehuda Weizman, and Adin Ming Tan. 2023. "The Difference in Wave Dynamics between SARS-CoV-2 Pre-Omicron and Omicron Variant Waves" COVID 3, no. 1: 28-50. https://doi.org/10.3390/covid3010002
APA StyleFuss, F. K., Weizman, Y., & Tan, A. M. (2023). The Difference in Wave Dynamics between SARS-CoV-2 Pre-Omicron and Omicron Variant Waves. COVID, 3(1), 28-50. https://doi.org/10.3390/covid3010002







