The proposed technique mimics the real-world dependencies for COVID-19 confinement. The process includes considering the demographic factors of specific locations impacting the COVID-19 spread.
The demographic factors such as population, facilities, public willingness to vaccination, isolation, and socio-economic factors vary from state to state. These factors would impact the COVID-19 spread from state to state. Based on this information, a COVID-19 game is built to control the infection rates of different states in the US. However, the demographic factors do not consider the mobility between states which creates interdependencies between states for COVID-19 spread. To include the individual location’s demographics and the dependencies between locations, we propose the Graph-Learning based iterative technique in modeling a solution for COVID-19 spread.
3.1. Overview of the Proposed Solution
Further, to create inter-dependencies, we take each state’s demographic factors and game theory strategic solution to create nodes representing each state, as shown in step 2 of
Figure 1. These nodes are connected using mobility information, to form a graph database. A graph learning algorithm is developed to identify the high impacting connection in virus spread. In this work, graph learning refers to learning the mobility and infection rates from the graph (demographic topology) and the ability to formulate a control solution from them. The high impacting connections are removed, and each state’s infection rates are updated and given as input to the COVID-19 game theory. The process occurs iteratively, between game theory-based confinement and graph learning algorithm until the virus spread is confined up to 50%.
The connection between states is completely broken with the stay-at-home [
43] and quarantine [
44] orders where people are not allowed to cross their states or provinces. However, in a real-world scenario, the connection between states may not be completely broken, for such cases, the proposed technique has a mobility factor, where 0 indicates a strict travel ban, whereas 1 indicates no travel restrictions and the intermediate values (0–1) indicate looser restrictions, i.e., the weight of the edges is modified in our technique to restrict the mobility, if not completely broken for better confinement of the disease.
At the end of the solution, each state gets assigned a control strategy that best fits them, based on the demographic conditions. The control strategy is the optimal solution to the proposed technique, which can decrease the disease spread, i.e., the infection rate 50% under limited cost, is considered to be the optimal strategy in confining the disease.
3.2. Modeling of SARS-2 COVID-19 Epidemic
As outlined in the overview, we proposed a compartmental SEIRV/D model [
13] to analyze the spread of the SARS-2 COVID-19 disease. SEIRV/D is widely used to model infectious diseases [
13] mathematically. We employ this model based on the fact that COVID-19 has an incubation period, i.e., a person who is exposed might not be infected immediately, and a person who is recovered from the disease can be reinfected, COVID-19 may also lead to the death of an infected person. The only case a person can be prevented from being re-infected by the COVID-19 infection is to get vaccinated. Hence, the SEIRV/D model is considered in this work, in contrast to the SEIR or SIR models.
In SEIRV/D, S represents the number of susceptible people, E represents the number of people who are exposed, I represents the number of people infected, R represents the number of people recovered from the disease, V is the number of people who are vaccinated against the disease and D represents the number of people dead by the disease.
As represented in
Figure 2, at the beginning of the disease, the whole population is Susceptible (
S) to the disease, then a certain fraction of people get Exposed (
E) to the disease. The infection has an incubation period, in which, from the exposed population, a certain fraction of people will be Infected (
I) by the disease. Among the infected people, a certain fraction of people will be Recovered (
R) but can get reinfected, and a certain fraction of the infected will be Dead (
D). In each time instance, a certain fraction of people are Vaccinated (
V), who are assumed to be excluded from the epidemic spread.
At any given point of time the total population can be divided into
,
,
,
,
and
elements. So the total population
of any effected area, can be represented as sum of all these factors.
In the above equations,
N is the total population, ∧ is the susceptible rate of the population to the disease,
represents the population exposure rate to the disease,
is the transmission rate of the disease,
is the recovery rate of the infected population,
represents the mortality rate of the infected population,
represents the rate of people vaccinated against the disease who are in the susceptible status. Moreover,
represents the rate of people vaccinated against the disease and in the recovered status. The explanation of these symbols are also provided in
Table 2 and
Table 3.
Thus, the population is divided into the above-mentioned compartments and the people are progressed between the compartments in the SEIRV/D order, as shown in
Figure 2.
3.3. COVID-19 Confinement with Game Theory
Game Theory is the process of modeling the strategic changes between two or more players. That is building-specific strategies for the players and cost functions for each player to enforce the strategy. The players in the gameplay as opponents, known as attackers and defenders, and each trying to win the game. The attacker tries to maximize their gain with minimal attacker cost, while the defender tries to maximize their gain and minimize their defender cost. Each player formulates certain strategies, supporting their chance of winning. By measuring the impact of the strategies and their costs, game theory produces the game’s outcome.
We consider two players for the COVID-19 game, an attacker and a defender. The attacker tries to increase the number of people infected by the disease, and the defender tries to decrease the number of people infected by the disease. Usually, one player’s gain would be another player’s loss, and there will be a Nash Equilibrium attained by the gain, which will be equal to zero. However, with the COVID-19 game, Nash equilibrium can not be achieved, that is, the attacker’s gain will usually be higher than the defender’s loss. This is because the defender cannot recover the infected people at the same rate as the attacker infects them. So this game is a Non-Zero Sum game.
Figure 3 shows the workflow of our proposed game-theoretic framework for COVID-19 confinement.
The
Table 4, represents the attacker’s and defender’s strategies used in the COVID-19 game.
The attacker’s enforced strategies try to speed up the infection rate, such as reduced incubation, mutation of the virus, and creating red zones. A reduced incubation strategy decreases the virus’s incubation period, and thereby, the exposed person can transmit the virus immediately. Evolution or mutations of the virus make the traditional defense strategies (including vaccines in some scenarios) less effective and force the defender to employ more costly techniques. Red Zones are certain areas such as malls, gyms, movie theatres, recreational centers, and clubs where there will be more people in a close space, so the attacker has the chance to infect more people. To enforce these techniques the attacker needs to pay a certain cost. Thus, the payoff for each attacker strategy is defined as follows:
In the above equations, is the number of people susceptible to the disease; is the number of people infected with the disease; represents the attacker’s cost of reduced incubation; represents the attacker’s cost of evolution; represents the attacker’s cost of red zones; and , , represent the cost functions of reduced incubation, evolution, and red zone attacker strategies, respectively.
The defender’s strategies are targeted to decrease the infection rate, to minimize the number of people infected. The defender’s strategies are masking, social distancing, and contact tracing. With the masking technique, the susceptible people are advised to follow masking, and people who are infected will be masked mandatorily; with this, the spread of infection can be controlled. In the social distancing strategy, the susceptible people are advised to follow social distancing, and those who are infected will be asked to follow strict social distancing. In the contact tracing strategy, the infected people and the people they met after being infected are traced and isolated. The costs associated with each of these strategies are modeled as follows:
In the above equations,
is the number of people susceptible to the disease in the above equations;
is the number of people infected with the disease;
represents the cost of mandatory masking;
represents the defender cost of masking;
represents the cost of strict social distancing;
represents the cost of social distancing;
represent the cost of contact tracing; and
,
,
represent the cost functions of masking, social distancing, and contact tracing strategies, respectively. The total defender payoff can be defined as follows:
where
represents the percentage of strategy masking being enforced;
represents the masking strategy cost;
represents the percentage of strategy social distancing being enforced;
represents the social distancing strategy cost;
represents the percentage of strategy contact tracing being enforced; and
represents the contact tracing strategy cost.
In this work, the defender is the government or public health agencies that try to control the spread of COVID-19. Thus, the defender (government) allocates this budget based on total funds available for different activities to curb the pandemic, such as costs for paying front-line workers, testing, vaccination, building hospitals, boosting facilities during the pandemic, and providing PPE kits. We assume that the total defender’s payoff is less than the allocated defender budget to minimize the economic impacts. However, the maximum cost defender can pay for enforcing the strategies is equal to the maximum amount available in the budget.
3.4. Optimal Strategy for COVID-19 Using Game Theory
We build an attacker-defender game, enforce different strategies, and observe the COVID-19 spread pattern using the SEIRV/D epidemic model. To be specific to the state, we consider demographic information of each state such as population, public awareness, socio-economic factors, economic costs, and willingness to vaccination. These factors would impact the COVID-19 spread from state to state. We consider all these factors in formulating a new term
, the demographic factor.
is defined as follows:
In Equation (
13),
is the demographic factor which is the sum of factors
,
,
, that vary from state to state and must be considered to observe their effect in COVID-19 spread.
x,
y, and
z are the rates of each of these factors’ impact. We assume that
x +
y +
z + ⋯= 1. Demographic factors such as economic costs, socio-economic factors of the state, and medical infrastructure available of each state are considered to handle an epidemic.
We redefine the equation of the number of people infected
from the
epidemic model by adding the demographic factor
.
is updated because demographic factors such as economic costs, medical infrastructure, etc, can influence the disease spread. All the other factors
,
,
,
, and
are dependent on
. So, by changing
, we are indirectly changing other epidemic modeling terms. The redefined
in terms of
is shown in the following equation.
In Equation (
14),
is the transmission rate of the disease,
is the demographic factor of each state, and
is the recovery rate of the people infected by the disease.
The epidemic
model is dependent on variables such as, ∧,
,
,
,
and
. Nevertheless, the optimal solution for the game is modeled based on
variations, so the COVID-19 game can be defined as follows:
To obtain an optimal control strategy from the COVID-19 game, the following steps must be followed as shown in Algorithm 1. The inputs to the game are COVID-19 spread factors such as
and the demographic factor
. The COVID-19 spread is observed at different time instances by varying
and the impact they create on S, E, I, R, V, and D terms. At each time interval, the infection is tried to confine by using certain defender strategies. The impact of each strategy is estimated in terms of, the amount of decrease in the infection rate they can achieve and how much they cost. After comparing these factors of each defender strategy, a strategy that can achieve the least infection rate at a minimum cost is considered as game theory optimal control policy and assigned to the state.
| Algorithm 1: Optimal Game Theory Strategy. |
- 1:
Input: Susceptible rate (), Infection rate (), Recovery rate (), mortality rate , demographic impact factor , Budget B - 2:
define : - 3:
for : do - 4:
- 5:
- 6:
- 7:
- 8:
- 9:
- 10:
- 11:
- 12:
- 13:
if m or ct or sd > B - 14:
break - 15:
else - 16:
- 17:
- 18:
end if - 19:
end for - 20:
- 21:
return - 22:
Output:
|
Algorithm 1 represents the workflow of the COVID-19 game using game theory. represents the game theory function and are inputs to the game. Where ∧ is the susceptible rate of the population to the disease, represents the population exposure rate to the disease, is the transmission rate of the disease, is the recovery rate of the infected population, and represents the mortality rate of the infected population.
For different time instances
t, the disease spread is observed. So, in Algorithm 1, the time
t is in a for a loop. The variables
,
,
,
,
and
are updated over different time values (instances). The updated variables are stored in susceptible
s, exposed
e, infected
i, recovered
r, vaccinated
v, and dead
d terms. Our goal is to make the defender win by selecting a defender strategy that can control the COVID-19 infection rate. All the defender strategies are analyzed to determine which can decrease the COVID-19 infection rate and the cost they require to achieve it. The total cost of a strategy is calculated by multiplying the percentage of its application and the cost for it. So for masking
m, the total cost is defined as, the percentage of masking
times the cost of masking
, For contact tracing
, the total cost is defined as the percentage of contact tracing
times the cost of contact tracing
. Moreover, for social distancing
, the total cost is defined as the percentage of social distancing
times the cost of social distancing
. The cost functions
,
and
are taken from Equations (
10) and (
11).
The budget B is the total defender budget. All the strategies should abide by this budget to play the COVID-19 game. If the defender strategy cost is more than the budget B, the COVID-19 game will be terminated. If the defender strategies fall under the budget B, the COVID-19 game is played to obtained the confined infection rate and the optimal control strategy specific to each demography.
The function min accesses each defender strategy and produces an optimal control strategy as an output to the game. Where, is a function of the masking strategy m and its controlled infection number . The is a function of the contract tracing strategy , and its controlled infection number . The is a function of social distancing strategy , and its controlled infection number . The selected control strategy and corresponding confined infection rate are given as outputs to the COVID-19 game . The selected control strategy is stored in variable and its corresponding confined infection rate is stored in the variable .
We currently have many variations of COVID-19; the disease is mutating with spread patterns. So for the ever-changing disease, we cannot formulate a single solution and use it for variations. We need a dynamic solution, which is adaptable to different COVID-19 mutations. To study if our model produces a suitable solution for COVID-19 variants, we vary the game’s input parameters and observe the game’s output effectiveness. So we vary game input variables such as ∧, , , , , and with three different values for each variable, considered as best-case scenario to worst-case scenario. We even vary because there could be changes in the demographic conditions.
As shown in Algorithm 2, three different values are considered for each of the following variables, susceptible rate
,
,
, disease exposure rate
,
,
, transmission rate
,
,
, recovery rate
,
,
, mortality rate
,
,
and factors that represent demographic conditions
,
,
. The values are taken from the New York Times [
45] daily COVID-19 reports of each state and their demographic factors. For each state, these variables are iterated using loop and given as input to the game theory function
, represented as
. For
j in the range of 3,
,
,
,
,
,
are iterated with their initialized values. As shown in Algorithm 2, for each case, game theory
plays the COVID-19 game and control strategy as output. The output control strategy to confine the disease is stored in the
variable. Moreover,
values are appended to a form a list of solutions represented as
. Here,
n represents the list of all states in US.
contains output to the COVID-19 game for different states in US with varied demographic and infection conditions.
| Algorithm 2: Game-Theory Optimal Strategics for Variants. |
- 1:
Input: , , , , , - 2:
- 3:
- 4:
- 5:
- 6:
- 7:
- 8:
for - 9:
for : do - 10:
- 11:
- 12:
- 13:
- 14:
- 15:
- 16:
{// Algorithm 1) - 17:
- 18:
end for - 19:
end for - 20:
Output:
|
3.5. Graph Theory
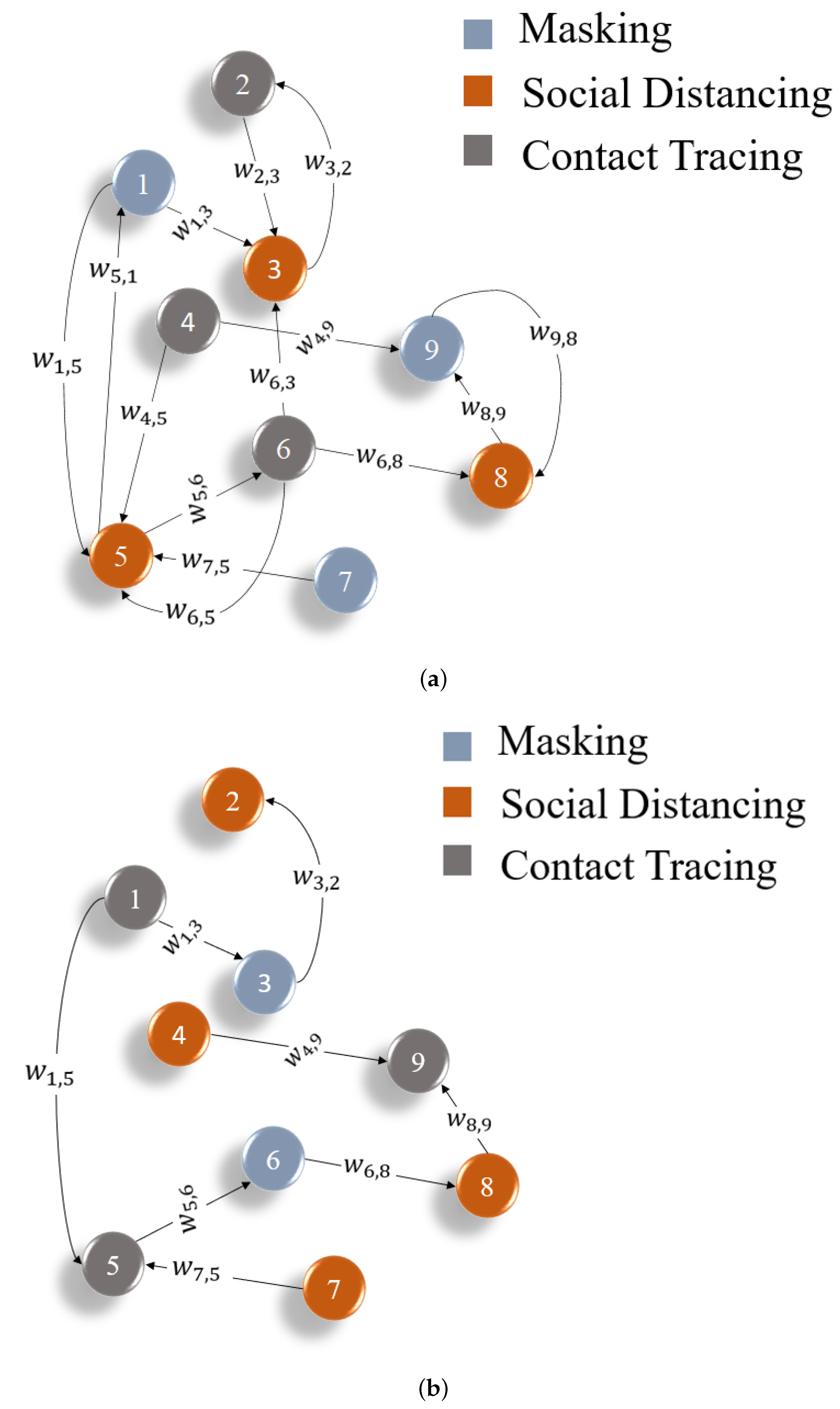
A graph is defined as a function containing nodes and edges . Nodes are connected with the help of edges. We can create directed and undirected graphs. Directed graphs are known to represent the flow from one node to another using arrows, whereas, in undirected graphs, there are no arrows rather straight lines connecting nodes . The relationships between the nodes are based on the weights of the edges . While replicating the real-world conditions between states, huge amounts of interlinked data are collected, and graph modeling techniques are employed to model it.
In our database, states are represented by the nodes which are populated with different features such as
,
,
,
,
, the number of infected specific to the state, and the day on which we are observing the disease from the start. The edge weights are represented by the mobility rates incoming and outgoing from each state. We represent our graph database as
. In
Figure 4a, we can observe an example graph connecting different nodes with respect to weights. We have incoming and outgoing weights from one node to another. The graph is a basic representation of the structure of a graph database. The COVID-19 graph database has connections between all states with incoming and outgoing mobility between states as weights. To theoretically demonstrate the workflow of proposed method, consider the nodes (2, 3) where
represents the weight from 2 to 3 and
represents the weight from 3 to 2.
As shown in
Figure 1, we build our graph database with inputs from the Game Theory solution and mobility rates. After applying the graph algorithm, we update these factors with new mobility and optimal infected cases. The connection between states which contribute to high infection spread is removed. This iterative process continues until the number of infected is less than 50% from the original value. The
Table 5, gives insights to important terminology used to create graph database and graph algorithm.
Algorithm 3 provides information on how to create a graph database. Where
represents the nodes of the graph, similar to the numbers
as shown in
Figure 4a. In the COVID-19 graph database, the nodes are different states in the US. These nodes are populated with features such as the susceptible rate ∧, disease exposure rate
, transmission rate
, recovery rate
, mortality rate
, and factor that represents demographic conditions
, the optimal strategic output of game theory
, specific to each state. To populate different nodes (states)
is iterated using a for a loop. These features are added for each node (state)
in graph
. These features are represented as
, where, F is the variable that represents different features.
| Algorithm 3: Creating COVID-19 Graph Database. |
- 1:
Input: Susceptible rate (), Infection rate (), Recovery rate (), Mortality rate , Demographic impact factor , Budget B - 2:
define : - 3:
for : do - 4:
- 5:
- 6:
- 7:
- 8:
- 9:
- 10:
- 11:
for : do - 12:
- 13:
end for - 14:
end for - 15:
return - 16:
Output:
|
In Algorithm 3, the feature susceptible rate ∧ of each state is added to the corresponding node in the graph and is represented using . The feature disease exposure rate of each state is added to the corresponding node in the graph and it is represented using . The feature transmission rate of each state is added to the corresponding node in the graph and is represented using . The feature recovery rate of each state is added to the corresponding node in the graph and it is represented using . The feature mortality rate of each state is added to the corresponding node in the graph and it is represented using . The feature demographic factor of each state is added to the corresponding node in the graph and it is represented using . The feature, optimal strategic output of game theory of each state is added to the corresponding node in the graph and is represented using . In a conventional database, these features are like the columns of a table. The states are connected using weights W, all the external states are considered as Traffic, except the state itself, which is represented as , and they are connected using mobility W. The query interprets the creation of connection between states. Where contains the information of the graph’s weights. interprets the creation of connection, represents the connection between state and external states (traffic). The output o Algorithm 3 is a COVID-19 graph database , obtained by iteratively populating nodes of each state and connecting them.
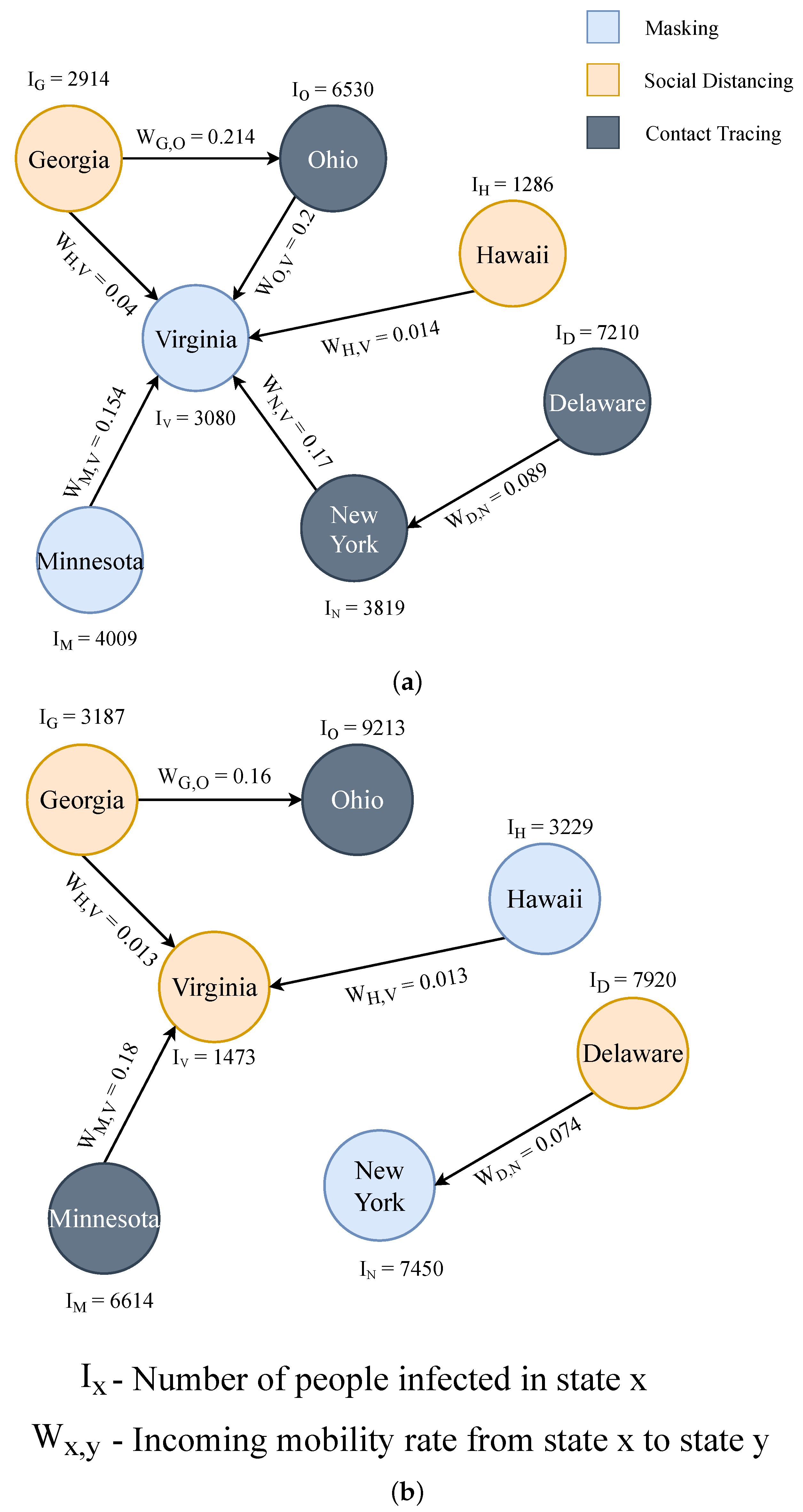
Algorithm 4 describes the functionality of the graph algorithm built to restrict mobility in the COVID-19 graph database. The graph database is built to recreate the real-world conditions between states regarding the demographics and mobility of intra- and inter-states. A graph database is created for each state, and interconnections are made between them using mobility rates. For example, we consider Virginia state for applying the graph algorithm. For simplicity Virginia is represented as
. The goal of the algorithm is to reduce the total optimal infection rate of Virginia state
by
. Virginia state’s total optimal infection rate
represents the total infection rate induced due to external mobility (incoming traffic from other states). The total optimal infection rate
is defined as the sum of infection rates induced by all other incoming states into Virginia. Individual infection rates induced from other states are represented as
,
,
,.....
.
| Algorithm 4: Graph Algorithm for Optimal Solution with Mobility Restrictions. |
- 1:
Input: , - 2:
- 3:
- 4:
- 5:
- 6:
- 7:
for - 8:
if and - 9:
break - 10:
else - 11:
- 12:
- 13:
- 14:
- 15:
- 16:
- 17:
- 18:
- 19:
- 20:
end if - 21:
end for - 22:
Output:
|
We have n different states incoming to Virginia. Each state comes in with a different mobility rate and the infection rate of that state is represented as .The infection induced by each incoming state is defined as the product of mobility rates between Virginia state and the incoming state and the infection rate of that incoming state . The impact factor is calculated for all the n states and compared. The link between VA and the state with the highest impact factor is removed by making the mobility factor of that state equal to zero (). Based on the updated mobility, the graph representing the connection between all states in US is updated by eliminating the link between states. As the graph is updated, the conditions of COVID-19 spread is different, so the infection rate of the state VA is evaluated. If it is lower than 50% of the initial infection rate, it is considered the optimal solution, and the corresponding strategy is considered the optimal strategy. The algorithm is stopped by breaking the loop, but if the infection rate of the state VA is higher than 50% then the algorithm is iterated until it finally becomes less than 50%.
When the infection rate of the state VA is higher than 50%, the graph is updated which reflects in updating the variables , , , , . Which updates the game output and updates the Optimal Strategy for the game. A new graph is made based on the new variables and new Optimal Solutions. The high-impact mobility link is identified and removed for the new graph with updated mobilities and other states’ infection rates. If now the infection rate of VA is less than 50% the process is stopped, or it is again iterated as shown in Algorithm 3 until the desired condition is reached.