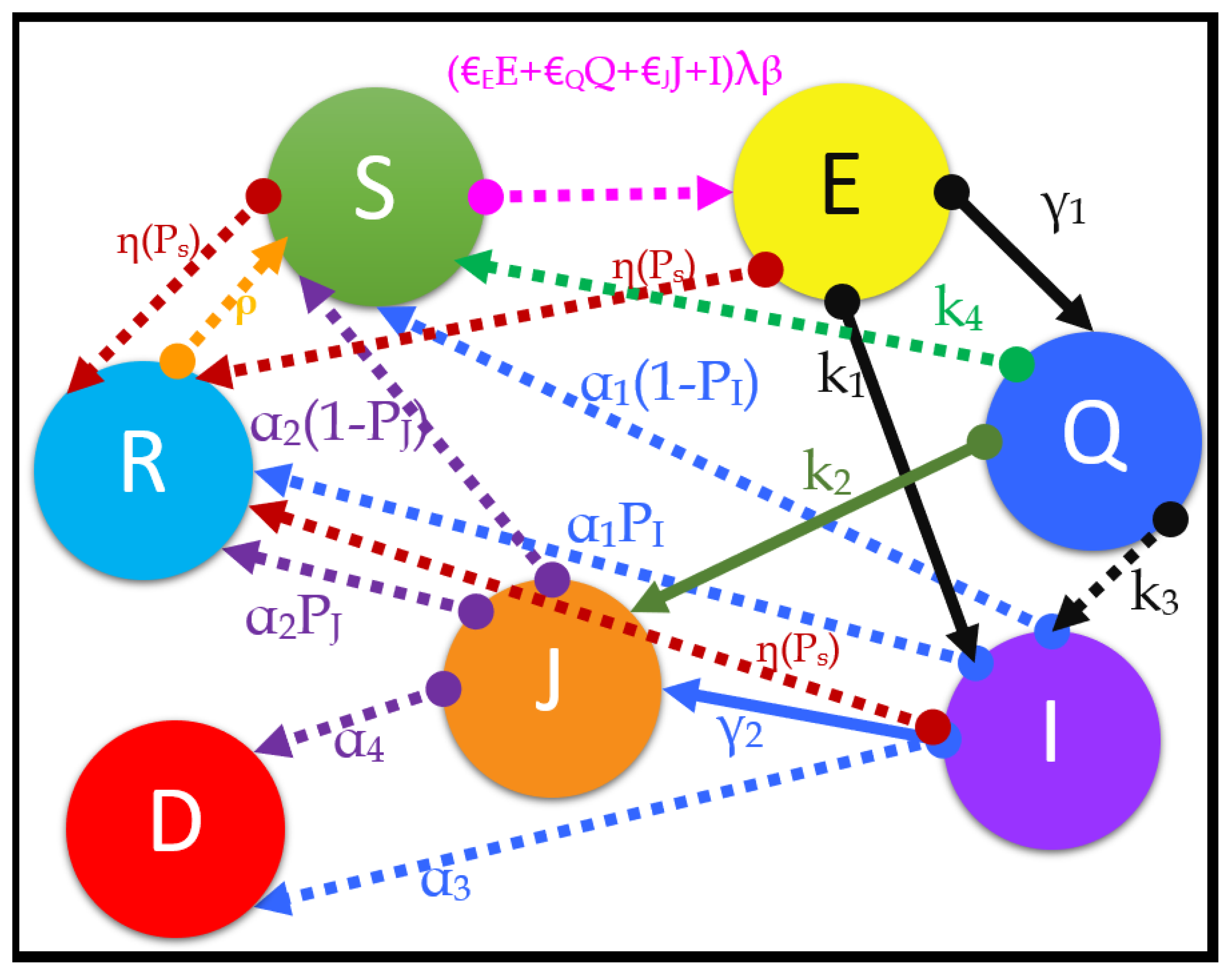
We introduce a modified model known as the susceptible, transmitted, quarantined, non-diagnosed infected, hospitalized diagnosed infected, recovered, dead, susceptible (SEQIJRDS) model, which is formed by using the SEIS model, SEIR model, and SEQIJR model given in [
26], and by
introducing a new class known as “Dead”. We introduce the Dead class since the rate and number of deaths are important parameters when making decisions about health interventions, and we identify it separately without identifying it in the "Removed" class, as in [
26], which includes both dead and fully recovered patients in the same removed class. It should be noted that
we use the R class to identify the population that is fully immunized against infection. Further, note that class
I contains infected and clinically non-diagnosed patients, while class
J contains infected and clinically diagnosed patients. These are compartment models for which the total population (
N) under consideration is divided into compartments, and there is a rate of moving from one compartment into another. The compartments and the associated movements are given in
Figure 1.
The model can be described as follows by referring to the compartment model shown in
Figure 1. We define a transmitted group (
E) as the people who have come into direct contact with a person who is more likely to become infected by the virus (probable infectives: transmitted person, transmitted and quarantined person, already infected person), and who the virus has been transmitted to from the probable infectives. It should be noted that the transmitted group (
E) does not have symptoms of the virus and is not infected with the virus. That is because a person who has contracted the virus needs to pass an incubation period (period between exposure to infection) in order to become infected [
26]. First, a susceptible person can come into contact with the virus from multiple sources, such as directly from the infected non-diagnosed class (
I), from the hospitalized infected group (
J) due to the imperfect isolation (rate of
), from the quarantined population (
Q) due to the imperfect quarantine (rate of
), or from the transmitted population (
E) itself (rate of
) multiplied by the transmission probability (
) and relative transmissibility (
), as is evident from the pink dotted arrow line in
Figure 1. A susceptible person can also become a recovered person by the vaccination process directly, as seen from the brown dotted line extending from
S to
R in
Figure 1. Once transmitted, the transmitted person is either quarantined (at a rate of
) or becomes a non-diagnosed infected person (at a rate of
), as is evident from the thick black lines in
Figure 1, or enters the recovered group by vaccination, as is evident from the dotted brown line from
E to
R in
Figure 1. Quarantining is the process of identifying and isolating a transmitted individual from making further contact with society for a quarantine period (
T), so as to prevent the further propagation of the virus from the transmitted person. Quarantined members are closely examined for the development of symptoms, and tests are conducted to check whether the quarantined person is infected or not. At the end of the quarantine period, when a quarantined patient is diagnosed with the virus, such a patient will directly go into class
J without going to class
I (at a rate of
), as will occur in a practical scenario, evidently from the thick henna-green color arrow from
Q to
J in
Figure 1. That is because quarantined people are observed for the development of symptoms, polymerase chain reaction (PCR) tests are conducted at the end of the quarantine period, and it is less likely that a quarantined person (
Q) can become an infected person who is not diagnosed, and ending in class
I. However, in rare cases, a quarantined patient can become infected without being diagnosed (at a rate of
) and go to class
I, as seen from the dotted black line in
Figure 1 from
Q to
I. The rest of the quarantined population (
Q) at the end of the quarantine period will go back to the susceptible class (
S) without becoming infected (at a rate of
), as shown by the dotted green arrow in
Figure 1 from
Q to
S. Here, we assume that the tests are conducted at the end of the quarantine period only, such that all people who entered the quarantine group
T days (quarantine period) before the present day will be removed from the quarantine population either as infected people (
I or
J) or as susceptible people (
S). Then, a non-diagnosed patient in class
I will either die, entering class
D (at a rate of
, as evident from blue dotted arrow line from
I to
D in
Figure 1), or develop natural immunity by recovering (at a rate of
, as evident from the blue dotted line from
I to
R in
Figure 1), or develop immunity by vaccination and move into class
R (at a rate of
, as evident from the brown dotted line from
I to
R in
Figure 1), or be clinically diagnosed and move into class
J (at a rate of
, as evident from thick blue color arrow from
I to
J in
Figure 1), or become a susceptible person again, and enter class
S (at a rate of
, as evident from blue dotted arrow from
I to
S in
Figure 1). A clinically diagnosed patient in class
J can either die to enter class
D (at a rate of
, as evident from the purple dotted arrow from
J to
D in
Figure 1), or develop natural immunity to enter class
R (at a rate of
, as evident from the purple dotted arrow from
J to
R in
Figure 1), or become susceptible (
S) again (at a rate of
, as seen in the purple dotted arrow from
J to
S in
Figure 1). According to health guidelines, clinically diagnosed patients in class
J and quarantined patients in class
Q are not vaccinated until they exit the compartment. As is evident from
Figure 1, the brown dotted arrow lines show the movement of people who develop full immunity to the virus by the vaccination process from each of the compartments
S,
E, and
I. Note that susceptible people can re-emerge from classes
Q,
I,
J, and
R, as is evident from the arrows corresponding to the rates
in
Figure 1.
We solve the system of first-order differential equations using the MATLAB R2021a software tool. The statistical analysis of the historical data was performed using Microsoft Excel 2016 to deduce the rates and probabilities.
2.6.4. Deriving the Basic Reproduction Number
The basic reproduction number (
) is the number of secondary infections that can be produced by a single person on average [
43]. Two classes,
E and
I, are mainly involved in infecting (exposing people which can result in infection) other people, whereas classes
Q and
J can be assumed to be partially infecting under non-perfect quarantine and non-perfect hospital isolation conditions. In such a scenario, the infecting classes’ equations can be written as given in Equations (
10)–(
13).
At the disease-free equilibrium state,
and all other compartments are zero. The next generation matrix method can be used to find the basic reproduction number as given in [
2,
43]. The gains to the
E class,
Q class,
I class, and
J class are
,
,
, and
, respectively. Further, the losses to the
E class,
Q class,
I class, and
J class are
,
,
, and
, respectively. Accordingly,
F and
V matrices can be obtained, as shown in the matrices in Equations (
14) and (
15), respectively.
The equation for the basic reproduction number can be written as
, where
is the spectral radius and
is the next-generation matrix. Hence, the basic reproduction number
can be calculated as given in Equation (
16).
The result derived for the implies useful information about the epidemiological model parameters. It shows clearly that the transmission probability , the relative transmissibility , the fractional exposing factor from transmitted people , the fractional exposing factor due to imperfect quarantine , and the fractional exposing factor due to imperfect hospital isolation , as direct factors, contribute to the increment of the basic reproduction number. The increment of the natural death rate of infected people in the society , the recovery rate of the hospitalized infected group , the death rate of the hospitalized group , the recovery rate of the non-hospitalized infected people , and the fractional rate of quarantined people becoming susceptible will cause the reproduction number to decrease. The effect of on the basic reproduction number is indeterminate, as these terms appear in both the numerator and denominator of the derived expression for R0 in Equation (16). Further, by increasing the overall vaccination rate (η) and the overall efficacy of vaccination (Ps), the basic reproduction number can be reduced.
Each of the variables of the epidemiological model can be modeled as given in the following subsections.
2.6.5. The Transmission Probability
Transmission probability is one of the main factors which governs the rate of the virus’ spread, as it is the rate at which the virus is transmitted to the susceptible population. We model
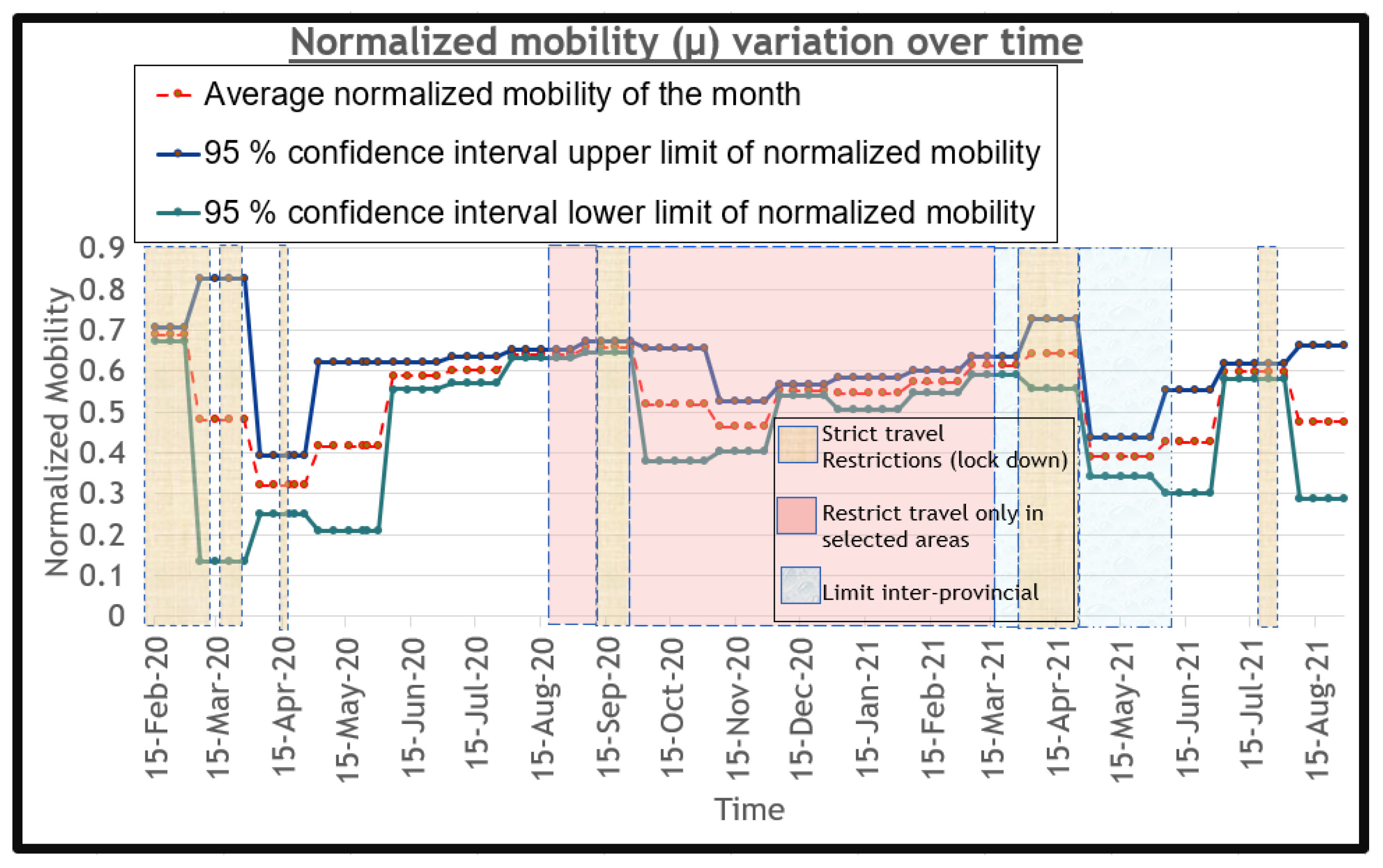
as a function of human behavior since it depends highly on how people behave. Therefore, the transmission probability depends on the normalized average mobility (
) of the population and exposure-preventative measures (
M) such as mask use, social distancing, and hand sanitizing. Both
and
M depend on the government policies and behavior adherence to policies of the general public. We model
as given by Equation (
17).
We define
in Equation (
17) as the base transmission probability, which is the transmission probability under the highest mobility (
) and lowest preventative measures (
M). In other terms,
is the worst-case transmission probability. We derive
using model fitting for historical data, so that this becomes a learned parameter. Normalized average mobility (
) in Equation (
17) is a parameter having a value of
1 under the highest mobility and a value of
0 for the least mobility. In order to obtain this parameter, the mobility of the people at a given time under different sectors should be averaged and mapped to a normalized value between 0 and 1, as described in
Section 2.6.7. In Equation (
17),
M is a normalized parameter which has a value of
0 under the highest possible exposure-prevention measures, and has a value of
1 at no preventative measures. The value of the parameter
M is critical, since it determines the rate of the propagation of the disease. At a given time, the value of
M can be calculated considering mask use, as given in Equation (
18).
In Equation (
18),
is the filtration efficiency of a particular type of mask and
is the fraction of the population which wears the
ith type of mask. Not wearing a mask is identical to wearing a mask with 0.00 filtration efficiency (FE). In situations which a fraction of the population does not wear a mask, such cases should be substituted in Equation (
18) with 0.00 FE, along with the corresponding mask fraction for not wearing a mask. Using Equation (
18), we can obtain
M for the universal N95 mask-use case, which assumes that the whole population wears a mask which prevents contact with the disease by a probability of 0.95 [
44] (e.g., by a whole population wearing an N95 or equivalent mask, where
,
,
). Yet, it cannot be guaranteed that a whole population will wear a mask and follow health guidelines. There are hard-working people who are unwilling to wear a mask or cannot wear masks due to their difficult working conditions. In addition to N95 masks, people can wear other masks such as surgical or cloth masks, having maximum filtration efficiencies of 0.88 and 0.23, respectively [
45]. So, our simulations will consider different cases of the parameter
M and also study other parameters under the average case for
M. In summary, when the mobility of the population increases (
increases) and exposure-preventative measures decrease (
M increases), the transmission probability (
) will increase, and vice versa.
2.6.8. Overall Vaccination Rate— and Overall Vaccination Efficacy—
The population of Sri Lanka is 21,514,267, according to [
49]. Vaccines are given to all humans of ages greater than 15. The population percentage of such a group of people is 74.8% [
50]. Therefore, the eligible population for vaccination is around 16.09 million. In order for a vaccine to be accepted by the WHO, it needs to have an efficacy of at least 50% [
51]. Therefore, all COVID-19 vaccines have an efficacy greater than 50%. However, based on the vaccine type that is given and the dose, this efficacy can vary. Pfizer has an efficacy of 57% for the first dose and of 95% for the second dose, Moderna has an efficacy of 92.1% for the first dose and 94.5% for the second dose, AstraZeneca has an efficacy of 63.9% for the first dose and 70% for the second dose, and Sinopharm has an efficacy of 63% for the first dose and 79% for the second dose, as shown in [
52,
53,
54]. Further, Sputnik V has an efficacy of 79.4% for the first dose and 92% for the second dose, according to [
55,
56], and the Covishield vaccine has an efficacy of 49% for the first dose and 70% for the second dose, according to [
57,
58].
First, we will determine the overall vaccination rate (
) 3 weeks before the present date. Vaccination data was collected from the epidemiology unit of Sri Lanka.
Table 3 shows the cumulative vaccination values at the end of each month for each of the doses.
As evident from
Table 3, 12.34 million people (76.7% of the eligible population) have been given the first dose, and 7.29 million people (45.3% of the eligible population) have been given the second dose by the end of August 2021. The vaccination process began in March and only a few have been vaccinated in April, due to the Sinhala and Hindu new year vacation period, as is evident from
Table 3. Since the vaccination rates among different types of vaccines are different, and their corresponding efficacy for a given dose is also different, we have to find the parameter of the overall vaccination efficacy for all the vaccines.
Now, let us derive the overall vaccination rate
at any given time. For this, we need to shift the time axis of vaccination by 3 weeks for both doses for all the vaccines. Since we make calculations at the end of each month, for convenience, we shift the time axis by 1 month, not 3 weeks.
Table 4 shows the variations of the average vaccination fraction per day of both doses for each month for each type of the vaccine, and for all vaccines with time axis shifted by 1 month.
As seen from
Table 4, the AstraZeneca vaccine was given mainly at the start of the vaccination program. However, towards the end of May, Sinopharm vaccination began, and then continued as the dominant vaccine with the highest rate of vaccination. The overall vaccination rate (
) can be directly obtained from the row showing the overall vaccination rate in
Table 4.
Now, let us determine the overall vaccination efficacy (
). For that, let us define the parameter
as the vaccination rate for a specific type of vaccine for a given dose, and
as the efficacy for a specific type of vaccine for a given dose. The
for each of the vaccines for a given dose should be found using
Table 4. Using these values and the corresponding efficacy (
) of each vaccine type for a given dose, the overall efficacy (
) for the SEQIJRDS model can be calculated as given in Equation (
21).
The set of vaccines used in Equation (
21) are Pfizer, Sinopharm, Sputnik V, Moderna, Astrazenaca. This
value will be used to solve the differential equations in the proposed SEQIJRDS model. Accordingly, by substituting, in Equation (
21), the individual vaccination rates for each doses of a given vaccine type obtained from
Table 4, and for the individual efficacy of each vaccine for a given dose, we obtain
for the months of April, May, June, July, August, and September of the year 2021, respectively.