Abstract
In this in silico study, different pharmaceutical co-crystals based on (hydroxy)chloroquine with macrolide antibiotics (azithromycin, clarithromycin, or erythromycin A) were analyzed for the first time. These findings present a new molecular perspective and therefore suggest that the combination of (hydroxy)chloroquine/azithromycin, in the stoichiometric ratio of 1:1, as model co-crystal systems has less toxicity and is the most effective for inhibiting the new severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2).
1. Introduction
Recently, enormous efforts have widely focused on facing a new coronavirus, the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), a disease designated as COVID-19 [1]. The World Health Organization (WHO) declared the COVID-19 outbreak as a new pandemic on 11 March 2020 [2]. In order to contribute to the front line of the fight against this disease, researchers worldwide are moving to an investigation of an effective treatment regimen (based mainly on known drugs) against infection caused by the SARS-CoV-2 virus [1,2,3,4,5]. Most recently, the combination of drugs, for example, (hydroxy)chloroquine with azithromycin (AZ), has been used as a strategy and has also been clinically tested to treat the SARS-CoV-2 outbreak [6,7,8,9,10,11]. The possible benefits of this therapeutic option are still being debated [8,9,10,11]. It is additionally expected, however, that computational screening can aid in accelerating the discovery as well as the development of new and more effective drugs against SARS-CoV-2 [1]. To the best of our knowledge, no study reports the benefits of using pharmaceutical co-crystals to treat patients with infection caused by the SARS-CoV-2 virus. However, a simple consultation of the literature suggests that pharmaceutical co-crystal research has become a prevalent theme in the last few years [12,13,14,15,16,17,18]. In particular, pharmaceutic co-crystals are usually defined as multicomponent crystals that incorporate two or more drugs [13,14,18]. These co-crystals exhibit different and improved physical–chemical properties, and thus, they are widely considered good candidates for diverse therapeutic applications [14]. Further, a large variety of synthetic strategies has been successfully developed to obtain controlled pharmaceutical co-crystals with different structures. Notable examples include solid-state grinding, solution- and melt-crystallization, solvent evaporation, and so on [12,14,15,16,17]. Therefore, from this perspective, we believe that a computational model of co-crystal systems is essential to gain further insight into their biological activity, aiding directly in the emergence of new experimental research to confront COVID-19.
In this paper, we have selected (hydroxy)chloroquine (denoted as HQ and CQ, respectively) with macrolide antibiotics (such as AZ, clarithromycin (CL), or erythromycin A (ER)) in the stoichiometric ratio of 1:1, as a co-crystal model system for a computational screening study. First of all, these compounds were selected because of some preliminary clinical studies [6,7,8,9,10,11]. However, more recent results, which were released after the conclusion of this research, suggest the ineffectiveness of the use of CQ and HCQ in the treatment and prevention of COVID-19 [19]. Despite this fact, it is also important to emphasize that information on the mechanism of action of co-crystals as a new therapeutical option, especially from a computational point of view, is of course scarce in the literature. This is probably related to the difficulty of structurally treating these compounds in the active site of the target biomolecule. In addition, in this case, we observe that this study also represents advances in the computational treatment of such systems. Hence, this work can reveal the interaction profile and affinity of these co-crystals at short and long ranges, serving as a guide for future studies in this field. Second, AZ and CL are well-known semi-synthetic derivatives of ER, the first and most-known macrolide antibiotic to be isolated in 1952 [20,21,22]. These macrolide antibiotics are mainly used to treat patients with certain infections of the respiratory tract [20]. Further, it is well-known that the combination of AZ with antimalarial drugs (e.g., (hydroxy)chloroquine), shows some crucial benefits for the treatment of malaria [23]. A third relevant aspect of this study is that both (hydroxy)chloroquine and macrolide antibiotics usually crystallize in a monoclinic structure according to the CSD (Cambridge Structural Database [24], which is fundamental for the construction of these co-crystal model systems. Therefore, from this perspective, we have developed the first theoretical model of co-crystals applied in the treatment of SARS-CoV-2. We believe that this strategy can bring additional benefits to the use of this therapy as well as contributing to a better understanding of a molecular point of view.
Finally, our molecular target, the SARS-CoV-2 main proteinase (Mpro), is a key enzyme responsible for the processing of viral polyproteins [25,26,27]. Together with the papain-like proteases, Mpro is essential for the processing of polyproteins translated from viral RNA [28,29]. In a structural analysis, the Mpro enzyme consists of three domains. Located in a cleft between domains I and II, the Mpro active site presents a catalytic dyad formed by the conserved Cys145 and His41 amino acid residues. CQ and HCQ are well-known due to their antimalarial activity, but have possible effectiveness against COVID-19. HCQ inhibits terminal glycosylation of ACE2, the receptor for cell entry. ACE2 in the non-glycosylated state may less efficiently interact with the SARS-CoV-2 spike protein, making the viral entry difficult [30]. In this work, we evaluated the antimalarials CQ and HCQ in combination with other macrolide antibiotics, in the single crystal and co-crystal formats. This study can allow us to have a deeper understanding of the affinity of these co-crystals for the molecular target, in comparison with single crystals of antibiotics.
2. Computational Details
Six co-crystal model systems were prepared in this study, as shown in Figure 1, based on the combination of HCQ and CQ with the AZ, CL or ER antibiotics in the stoichiometric ratio of 1:1. As a strategy, the unit cell of these compounds was replicated for the investigated set of single and co-crystals, that is, their structural parameters were maintained as similar as possible. All of these model systems were then optimized (as the starting point for docking studies), and their structural and vibrational properties were fully evaluated at the PM6 theoretical level, using the Gaussian 09 package [31]. In order to better describe the electronic/optical properties of these model systems, we also employed the Kohn–Sham time-dependent density functional theory (TDDFT) using the B3LYP functional with the 6-31+G(d,p) basis set. In addition to the partial charges of the atoms, we calculated the natural bond orbitals (NBOs).
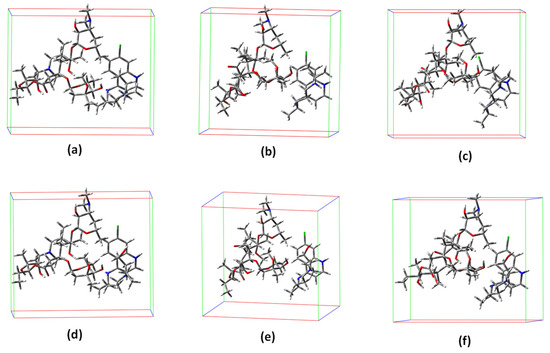
Figure 1.
Representation of optimized co-crystal structures in this study. (a) CQ/AZ; (b) CQ/CL; (c) CQ/ER; (d) HQ/AZ; (e) HQ/CL; and (f) HQ/ER.
In the docking studies, the affinity of the single and co-crystals in the Mpro active site was investigated. The compounds were then docked inside the crystallographic structure of viral protein Mpro (PDB code 6LU7; resolution = 2.16 Å) [32], using the Molegro Virtual Docker program (MVD®) [33], taking into account the same procedures employed previously [34,35,36]. According to our calculation protocol, the radius was about 20 Å, where the residues of the catalytic triad were kept flexible. Due to the nature of the docking methods, the calculations were carried out, generating approximately 50 poses (such as conformation and orientation) for each ligand studied.
In the MVD program, the MolDock score algorithm method used as a scoring function is based on the piecewise linear potential, which is fundamentally a simplified potential whose parameters are in turn fitted to protein–ligand structures, binding data scoring functions, and further extended in the Generic Evolutionary Method for molecular docking, including a new hydrogen bonding term as well as new charge schemes [33]. Along this line, the docking scoring function values, Escore, are usually defined by Equation (1):
wherein:
Note that EPLP represents ‘‘piecewise linear potential’’, which consists of two different parameter sets, as described: one for the approximation of the steric term (i.e., Van der Waals) among atoms, as well as the other potential for hydrogen bonding. As can be seen, the second term is, of course, related to the electrostatic interactions among overloaded atoms. Typically, it is a Coulomb potential with a dielectric constant dependent on the distance (which can be approximately described as D(r) = 4r). Hence, the numerical value of 332.0 is then responsible for the electrostatic energy unit to be given in kilocalories per molecule [33].
Eintra is defined as the internal energy of each ligand. That is:
Note that the first part of the equation (double summation) is among all pairs of atoms in the ligand, except those connected by two bonds. Thus, in this equation, the second term denotes the torsional energy, where θ is the bond’s torsional angle. Hence, if several torsions could be determined, then each torsional energy is considered an average among them. The last term of this equation, Eclash, has (not taking into account infeasible ligand conformations) a penalty incurred of about 1.000 for those exhibiting a distance between two heavy atoms (e.g., with more than two bonds apart) smaller than 2.0 Å [33]. Thus, in the MVD program, the docking search algorithm is based on the whole the interactive optimization technique (inspired by Darwinian evolution theory), which implies a new hybrid search algorithm conveniently called guided differential evolution. As such, this hybrid combines a differential evolution optimization technique with a cavity prediction algorithm during the search process. As a result, this approach provides a simple, fast, and accurate description of potential binding modes (poses) [33,37,38].
Additionally, taking into account the experimental inexistence of acute toxicity data for the compounds employed in this study and in order to estimate the theoretical values of the lethal dose (denoted as LD50), a rat model-based admetSAR predictor was used. This admetSAR approach is freely available online at http://lmmd.ecust.edu.cn:8000/ (accessed on 15 August 2020).
Based on our docking and ADMET results, we carried out molecular dynamics (MD) simulation using the GROMOS54A7 all-atom force field [39] using GROMACS 5.1 software [39,40]. The co-crystal-Mpro complex was then inserted into a 12 Å water box with the SPC solvation model, and sodium and chlorine ions were added as strategy for charge neutralization under periodic boundary conditions. In this study, the long-range electrostatic interactions were calculated assuming the Particle Mesh Ewald method with a cut-off of 12 Å and a time step of 1 fs. Initially, the system was minimized over 5000 cycles using the steepest descent algorithm and was then submitted to a production simulation of 60 ns at 300 K and 1 bar pressure. Finally, all trajectories were later analyzed using Visual Molecular Dynamics (VMD, version 1.9.3) [41].
3. Results and Discussion
We started this study by analyzing frequency calculations for these co-crystals and the thermochemical parameters obtained (at 298.15 K and 1.00 atm) from them using the standard relations in the gas phase, given in Table 1. As such, the comparison of the difference between the total electronic energy (ΔE), used to predict the stability of the co-crystals designed, presented in Table 1, suggests that the HQ/ER is the co-crystal that is more stable. In both HQ/AZ and CQ/AZ co-crystals, it is the least stable in their respective series. Thus, the stability order obtained for the computed co-crystals is HQ/ER > HQ/CL > CQ/ER > CQ/CL > HQ/AZ > CQ/AZ, i.e., suggesting that HQ-based co-crystals are more stable than their CQ counterparts (see Table 1).

Table 1.
Analysis of thermodynamic parameters computed for the co-crystals at the PM6 theoretical level.
The typical calculated infrared (IR) spectrum is shown in Figure 2a–f. According to these results, we observed only positive modes, suggesting that the structures proposed in this study are well optimized and therefore represent a minimum energy. Further, the IR-active modes confirm that co-crystals were obtained with a monoclinic-like structure. These results are consistent with experimental observations for both (hydroxy)chloroquine and macrolide antibiotics [1,12,42,43]. As can be seen in Figure 3, the computed UV-vis absorption spectrum of these co-crystals revealed only one well-defined peak. As such, the more intense UV band located in the range of 617 nm to 771 nm for the HQ-based co-crystals (AZ to ER) is due to a predominant HOMO-to-LUMO+2 transition. In comparison, for the CQ-based co-crystals (AZ to ER) this UV band was located from 624 nm to 955 nm (which is due to a predominant HOMO-to-LUMO+3 transition for CQ/AZ, and both CQ/CL and CQ/ER was best assigned to HOMO-to-LUMO+2 transition).
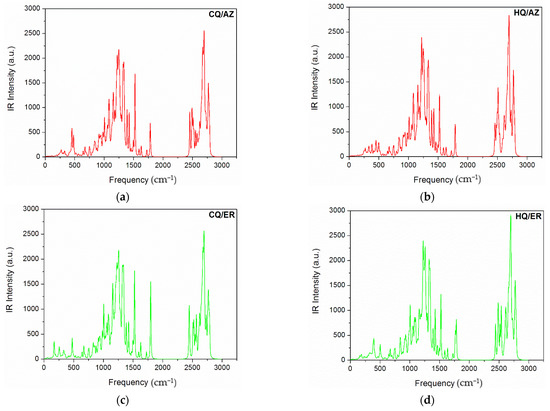
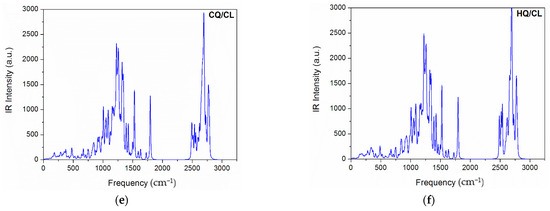
Figure 2.
Simulated IR spectra of the co-crystals formed between Chloroquine (graphs a,c,e) and Hydroxychloroquine (graphs b,d,f) with macrolide antibiotics at the PM6 theoretical level.
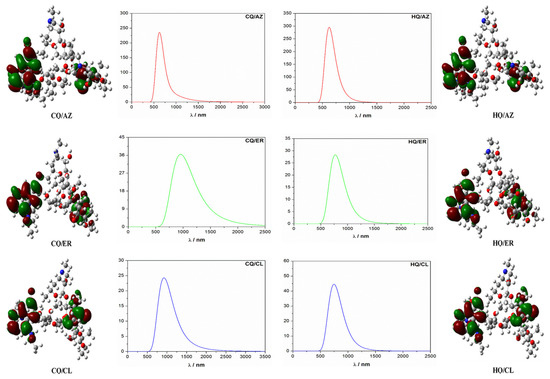
Figure 3.
Simulated UV-vis spectra and frontier molecular orbitals of the co-crystals using a contour value of 0.020. For each co-crystal, the HOMO orbitals are represented on the left and LUMO orbitals on the right in the same figure.
In all cases, we observed a red-shift UV-vis absorption spectrum of HQ-based and CQ-based co-crystals in the function of increasing structural polarization (summarized by the calculated dipole moment, as shown in Table 2). This was the main reason for the slight variation in the angles and bond lengths observed in the studied models (Figure 1).

Table 2.
Comparison of the dipole moment, HOMO–LUMO energy gap, exciton binding energy, hardness, softness, electronegativity, and electrophilicity values for the computed co-crystals at the TDDFT theoretical level.
Additionally, the calculated value of the HOMO–LUMO energy gap (Eg), exciton binding energy (EB), hardness (η), softness (S), electronegativity (x), and electrophilicity (ω) values for the computed co-crystals at the TDDFT theoretical level are given in Table 2. According to the Eg values, we noticed an increase in the order CQ/AZ < CQ/ER < HQ/ER = HQ/AZ < HQ/CL < CQ/CL. Our results also suggest better chemical stability for the CQ/CL co-crystal. In addition, these HQ-based and CQ-based co-crystals have EB values from 0.07 eV to 0.47 eV, which is typical of organic crystals containing aromatic groups [44].
Based on this analysis, supported by theory [45,46,47], we identified that HQ and CQ moieties are donor states, and the AZ, CL, or ER moieties are acceptor states. As such, the frontier molecular orbital analysis is illustrated in Figure 3 to view the energy and charge transfer process (denoted as ECT) that occurs in these co-crystals. In general, this process has a profound impact on the functional properties of these model systems. The electronic excitation and natural bond orbital (NBO) analysis was performed using the TDDFT theoretical level and hence can be used to measure ECT. Thus, in this perspective, the stabilization energy (E2) associated with the delocalization of electrons between the electron donor NBO (i) and the electron acceptor NBO (j) was evaluated according to the following equation [48,49].
where qi represents the orbital occupancy, εi and εj are diagonal elements (i.e., orbital energies), and Fij is the off-diagonal NBO Fock matrix element. From these calculations, we calculated the ECT for these co-crystals, as shown in Table 2. As expected, the HQ-based co-crystals had higher values of ECT than their CQ counterparts. Consequently, in this case, we identified that the ECT process was slower and hence can more easily induce symmetric structural polarization. For the CQ-based co-crystals, this result suggested a fast ECT process that can more likely induce an asymmetric structural polarization.
According to the above co-crystal structure analysis, the molecular docking calculations were performed to adjust the ligands in the Mpro active cavity, evaluating the affinity among them. For this study, a cavity prediction algorithm based on a 3D box was employed in order to generate the binding sites. Thus, the volume of the calculated active cavity was approximately 130.56 Å3.
In order to understand the interaction modes of these single and co-crystals within the SARS-CoV-2 Mpro active site, some parameters that contribute to affinity were investigated. Table 3 shows the intermolecular interaction energy values and theoretical toxicity prediction for the ligands under study.

Table 3.
Values of the parameters obtained by molecular docking calculations for the single and co-crystals within the SARS-CoV-2 Mpro active site through MVD® software and toxicity prediction through ADMET.
As shown in Table 3, all of the single and co-crystals studied interacted very well with the Mpro active site, with interaction energy values in the range of −141.7 to −280.7 kcal mol−1. We also observed that the co-crystal formed by HQ and AZ had the highest stabilizing interaction energy (−280.7 kcal mol−1), followed by the co-crystals HQ/ER (−275.7 kcal mol−1) and CQ/AZ (−275.3 kcal mol−1). The conformation of HQ/AZ in the Mpro active cavity is shown in Figure 4. Note that the single crystals of CQ and HQ had interaction energies of approximately −141.7 and −162.6 kcal mol−1, respectively. However, when combined with AZ, these single crystals gained stability and had lower interaction energies. In fact, the single crystal of AZ was much more stable than those of CQ and HQ when docked in the active site, and their combination with AZ led to increased affinity for the viral enzyme. Regarding the co-crystals formed by the combination with AZ, we observed the following energy differences: HQ to HQ/AZ (118.1 kcal mol−1) and CQ to CQ/AZ (133.6 kcal mol−1). Based on our computations, CQ/AZ was the co-crystal that showed the more significant energy difference, followed by HQ/AZ, suggesting the suitability of combining AZ with CQ and HQ, thus boosting their therapeutic effects (Table S1).
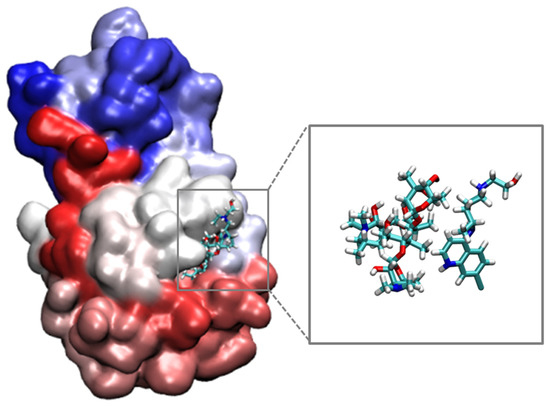
Figure 4.
Representation of the conformation of the most stabilizing HQ/AZ in the Mpro active site.
According to Table 3, the combination of HQ with ER also led to stabilizing interaction energies, from −162.6 kcal mol−1 for HQ to −275.7 kcal mol−1 for HQ/ER. This trend was also observed for CQ; its interaction energy was stabilized to 88.1 kcal mol−1 when combined with ER. Interestingly, the formation of the co-crystal HQ/ER was much more significant in energetic terms due to the larger energy difference between the single crystal and co-crystal, i.e., 113.1 kcal mol−1. In addition, with respect to the co-crystals formed by the combination with CL, we observed the following energy differences: HQ to HQ/CL (97.0 kcal mol−1) and CQ to CQ/CL (99.2 kcal mol−1). In general terms, all macrolide antibiotics led to the formation of low-energy co-crystals, indicating that such co-crystals can be easily obtained experimentally.
With respect to the interactions observed in the molecular docking, we observed that most compounds (single and co-crystals) interacted with important residues in the site, such as the residues H41, C145, and E166. In the active site, H41 and C145 constituted the dyad catalytic of Mpro, being key residues for the enzyme’s inhibition process. Furthermore, E166 is also an important species for keeping the active conformation of the enzyme [3,50,51]. As a result, the interactions of all compounds investigated can be visualized in Figure S1 and Figure 5.
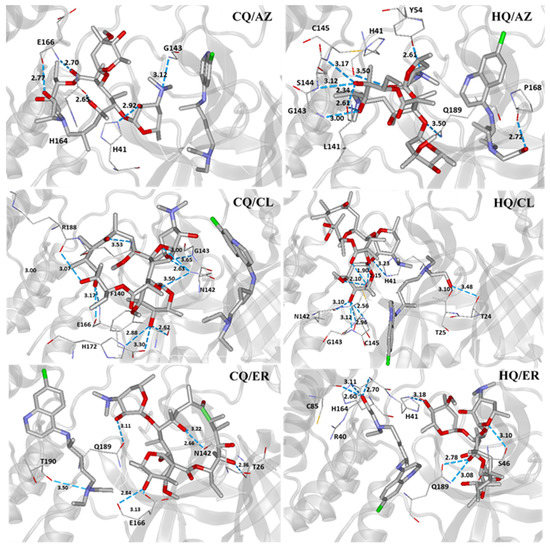
Figure 5.
Intermolecular interactions of the co-crystals in the viral Mpro active site.
Usually, the efficacy of a drug can be attributed to many factors. Along this line, the absorption–distribution–metabolism–excretion–toxicity (ADMET) evaluations involve sequential and iterative assessments of the efficacy, pharmacokinetics, pharmacodynamics, metabolic, and toxicological properties in the model of therapeutic agents, contributing to the design of safer and more efficient drugs [52]. The ADMET analysis was carried out in order to evaluate the toxicity of our compounds, single and co-crystals, under investigation. According to our results in Table 3, the LD50 value found for ER, 2.23 mol.kg−1, indicates more toxicity in relation to other single and co-crystal compounds. However, we observed that its combination with CQ and HQ led to co-crystals of lower toxicity, as well as more stabilizing interaction energies, making these efficient species candidates for COVID-19 treatment. In addition, when using CL combined with CQ and HQ, there was a slightly decreased toxicity and significant interactions of lower energies in the Mpro active site. The most remarkable results were found for the co-crystals formed by the combination with AZ. The data reinforce our previous findings, which indicate that the co-crystals of CQ and HQ combined with AZ significantly improved the affinity and decreased toxicity, thus making them more potent therapeutic agents against SARS-CoV-2.
Additionally, in this study, the dynamic behavior of the HQ/ER-Mpro complex was investigated. The co-crystal HQ/ER had a stabilizing interaction energy and lower toxicity, according to the docking and ADMET results, respectively. This system was chosen for a deeper investigation through Molecular Dynamics (MD) simulation. Initially, we observed that the complex reached thermodynamic equilibrium after 45 ns of MD simulation (see Figure 6). The extracted frame, which was considered the representative conformational structure of the co-crystal throughout the MD simulation, corresponds to the average of the Root Mean Square deviation (RMSD) value. By analyzing the results of the RMSD graph, we noticed that most of the deviations from HQ/ER were larger during most of the MD simulation, suggesting that the co-crystal requires a period of time to reach a stable accommodation in the active site. By analyzing the graph of the hydrogen bond (Figure 6), we found that the co-crystal HQ/ER performed up to six hydrogen bond type interactions. However, more effective interactions were observed by the end of simulation (after 45 ns), after the co-crystal was well-accommodated and with stable interactions in the site. According to the total energy graph (Figure 6), the energy oscillated during all simulation periods; however, this oscillation was constant, without very large variations. In addition, based on the Root Mean Square Fluctuation (RMSF; Figure 6), we observed an oscillation of the backbone, protein, and sidechain, during the MD simulation. Based on the graph, this oscillation suggests conformational changes in the protein structure, allowing for a stable accommodation of the co-crystal in the site during the simulation.
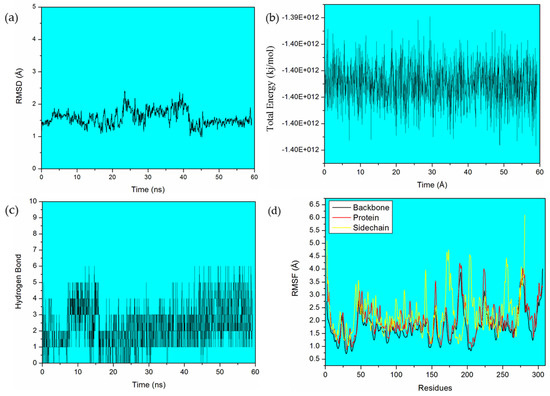
Figure 6.
(a) RMSD, (b) Total Energy, (c) Hydrogen Bond, and (d) RMSF graphs of a 60-ns simulation of the HQ/ER-Mpro complex.
It is important to emphasize that in silico research can contribute to a better physicochemical interpretation of a huge variety of biological processes at the molecular level, and in this direction, such strategies can contribute to accelerating the process of developing new drugs [53,54,55,56]. Usually, however, due to great structural complexity and high computational cost in the treatment of more realistic models, only a small part of the tar-get microorganism is used during these simulations. In other words, these results repre-sent only an initial effort of preclinical research. For this reason, only clinical trials can indeed confirm the effectiveness of such therapeutic options. Finally, from this perspective, we and other authors believe that in the future, the use of realistic models based on the complete structure of the target microorganism, as recently reported by Durrant et al. [57], will be dominant in this field of computational drug design. Undoubtedly, these advances will lead to a new era in computational drug design, providing better prediction power of how the structure will affect their biological activity under more realistic conditions, accelerating the discovery of new therapeutic options.
4. Conclusions
In summary, our theoretical findings are of great importance and provide a new molecular perspective on the effectiveness and toxicity of co-crystals formed between (hydroxy)chloroquine with macrolide antibiotics for the treatment of SARS-CoV-2 infection. Our findings also enable a new interpretation in for the intramolecular energy and charge transfer process in these co-crystals, which is critical to the rationalization of their functional properties, providing an innovative way to connect structural changes with electronic transfer kinetics. Overall, the co-crystals of CQ and HQ combined with AZ significantly improved the affinity and decreased toxicity, making them more potent therapeutic agents against SARS-CoV-2. However, it must be emphasized that the therapeutic potential benefits can only be determined in practice using rigorous clinical studies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/covid2030018/s1, Table S1: Cartesian coordinates (in Å) for co-crystals computed at PM6, Figure S1: Intermolecular interactions of single-crystals in the viral Mpro active site.
Author Contributions
A.A.d.C.: conceptualization, investigation, data curation, formal analysis, methodology, writing—original draft. L.C.A.: conceptualization, investigation, data curation, formal analysis, methodology, writing—original draft. E.F.F.d.C.: conceptualization, formal analysis, methodology, project administration, resources, supervision, writing—review and editing. T.C.R.: conceptualization, formal analysis, methodology, project administration, resources, supervision, writing—review and editing. F.A.L.P.: conceptualization, formal analysis, methodology, project administration, resources, supervision, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge the support from the Brazilian agencies CNPq, CAPES and FAPEMIG. We are also especially grateful for the computational facilities at UFLA. This work was supported by the Excellence project UHK.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Assis, L.C.; de Castro, A.A.; de Jesus, J.P.A.; Nepovimova, E.; Kuca, K.; Ramalho, T.C.; La Porta, F.A. Computational evidence for nitro derivatives of quinoline and quinoline N-oxide as low-cost alternative for the treatment of SARS-CoV-2 infection. Sci. Rep. 2021, 11, 6397. [Google Scholar] [CrossRef] [PubMed]
- Arabi, Y.M.; Murthy, S.; Webb, S. COVID-19: A novel coronavirus and a novel challenge for critical care. Intensive Care Med. 2020, 46, 833–836. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, D.; Sun, X.; Curth, U.; Drosten, C.; Sauerhering, L.; Becker, S.; Rox, K.; Hilgenfeld, R. Crystal structure of SARS-CoV-2 main protease provides a basis for design of improved α-ketoamide inhibitors. Science 2020, 368, eabb3405. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Hu, S.; Gao, J. Discovering drugs to treat coronavirus disease 2019 (COVID-19). Drug Discov. Ther. 2020, 14, 58–60. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, M.D.L.; de Oliveira, K.M.T. Comparative Computational Study of SARS-CoV-2 Receptors Antagonists from Already Approved Drugs 2020. ChemRxiv 2020. [Google Scholar] [CrossRef]
- Savarino, A.; Di Trani, L.; Donatelli, I.; Cauda, R.; Cassone, A. New insights into the antiviral effects of chloroquine. Lancet Infect. Dis. 2006, 6, 67–69. [Google Scholar] [CrossRef]
- Wang, M.; Cao, R.; Zhang, L.; Yang, X.; Liu, J.; Xu, M.; Shi, Z.; Hu, Z.; Zhong, W.; Xiao, G. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro. Cell Res. 2020, 30, 269–271. [Google Scholar] [CrossRef]
- Rosenberg, E.S.; Dufort, E.M.; Udo, T.; Wilberschied, L.A.; Kumar, J.; Tesoriero, J.; Weinberg, P.; Kirkwood, J.; Muse, A.; DeHovitz, J.; et al. Association of Treatment with Hydroxychloroquine or Azithromycin with In-Hospital Mortality in Patients with COVID-19 in New York State. JAMA 2020, 323, 2493–2502. [Google Scholar] [CrossRef] [PubMed]
- Fintelman-Rodrigues, N.; Sacramento, C.Q.; Lima, C.R.; da Silva, F.S.; Ferreira, A.C.; Mattos, M.; de Freitas, C.S.; Soares, V.C.; da Gomes Dias, S.S.; Temerozo, J.R.; et al. Atazanavir inhibits SARS-CoV-2 replication and pro-inflammatory cytokine production. bioRxiv 2020, 64, e00825-20. [Google Scholar]
- Geleris, J.; Sun, Y.; Platt, J.; Zucker, J.; Baldwin, M.; Hripcsak, G.; Labella, A.; Manson, D.K.; Kubin, C.; Barr, R.G.; et al. Observational Study of Hydroxychloroquine in Hospitalized Patients with COVID-19. N. Engl. J. Med. 2020, 382, 2411–2418. [Google Scholar] [CrossRef]
- Hung, I.F.-N.; Lung, K.-C.; Tso, E.Y.-K.; Liu, R.; Chung, T.W.-H.; Chu, M.-Y.; Ng, Y.-Y.; Lo, J.; Chan, J.; Tam, A.R.; et al. Triple combination of interferon beta-1b, lopinavir–ritonavir, and ribavirin in the treatment of patients admitted to hospital with COVID-19: An open-label, randomised, phase 2 trial. Lancet 2020, 395, 1695–1704. [Google Scholar] [CrossRef]
- Nikam, V.J.; Patil, S.B. Pharmaceutical cocrystals of nebivolol hydrochloride with enhanced solubility. J. Cryst. Growth 2020, 534, 125488. [Google Scholar] [CrossRef]
- Steed, J.W. The role of co-crystals in pharmaceutical design. Trends Pharmacol. Sci. 2013, 34, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Karimi-Jafari, M.; Padrela, L.; Walker, G.M.; Croker, D.M. Creating Cocrystals: A Review of Pharmaceutical Cocrystal Preparation Routes and Applications. Cryst. Growth Des. 2018, 18, 6370–6387. [Google Scholar] [CrossRef]
- Maheshwari, C.; Jayasankar, A.; Khan, N.A.; Amidon, G.E.; Rodríguez-Hornedo, N. Factors that influence the spontaneous formation of pharmaceutical cocrystals by simply mixing solid reactants. CrystEngComm 2009, 11, 493–500. [Google Scholar] [CrossRef]
- Leyssens, T.; Tumanova, N.; Robeyns, K.; Candoni, N.; Veesler, S. Solution cocrystallization, an effective tool to explore the variety of cocrystal systems: Caffeine/dicarboxylic acid cocrystals. CrystEngComm 2014, 16, 9603–9611. [Google Scholar] [CrossRef]
- Baird, J.A.; Van Eerdenbrugh, B.; Taylor, L.S. A classification system to assess the crystallization tendency of organic molecules from undercooled melts. J. Pharm. Sci. 2010, 99, 3787–3806. [Google Scholar] [CrossRef] [PubMed]
- Duggirala, N.K.; Perry, M.L.; Almarsson, Ö.; Zaworotko, M.J. Pharmaceutical cocrystals: Along the path to improved medicines. Chem. Commun. 2016, 52, 640–655. [Google Scholar] [CrossRef] [PubMed]
- Hennekens, C.H.; Rane, M.; Solano, J.; Alter, S.; Johnson, H.; Krishnaswamy, S.; Shih, R.; Maki, D.; DeMets, D.L. Updates on Hydroxychloroquine in Prevention and Treatment of COVID-19. Am. J. Med. 2022, 135, 7–9. [Google Scholar] [CrossRef] [PubMed]
- Kirst, H.A. Introduction to the Macrolide Antibiotics BT—Macrolide Antibiotics; Schönfeld, W., Kirst, H.A., Eds.; Birkhäuser Basel: Basel, Switzerland, 2002; pp. 1–13. ISBN 978-3-0348-8105-0. [Google Scholar]
- Mcguire, J.M.; Bunch, R.L.; Anderson, R.C.; Boaz, H.E.; Flynn, E.H.; Powell, H.M.; Smith, J.W. Ilotycin, a new antibiotic. Antibiot. Chemother. 1952, 2, 281–283. [Google Scholar]
- Chico, R.M.; Pittrof, R.; Greenwood, B.; Chandramohan, D. Azithromycin-chloroquine and the intermittent preventive treatment of malaria in pregnancy. Malar. J. 2008, 7, 255. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Allen, F.H. The Cambridge Structural Database: A quarter of a million crystal structures and rising. Acta Crystallogr. Sect. B 2002, 58, 380–388. [Google Scholar] [CrossRef] [PubMed]
- Arsic, B.; Awan, A.; Brennan, R.J.; Aguilar, J.A.; Ledder, R.; McBain, A.J.; Regan, A.C.; Barber, J. Theoretical and experimental investigation on clarithromycin, erythromycin A and azithromycin and descladinosyl derivatives of clarithromycin and azithromycin with 3-O substitution as anti-bacterial agents. Med. Chem. Commun. 2014, 5, 1347–1354. [Google Scholar] [CrossRef]
- Kumar, V.; Tan, K.-P.; Wang, Y.-M.; Lin, S.-W.; Liang, P.-H. Identification, synthesis and evaluation of SARS-CoV and MERS-CoV 3C-like protease inhibitors. Bioorg. Med. Chem. 2016, 24, 3035–3042. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Verschueren, K.H.G.; Anand, K.; Shen, J.; Yang, M.; Xu, Y.; Rao, Z.; Bigalke, J.; Heisen, B.; Mesters, J.R.; et al. pH-dependent Conformational Flexibility of the SARS-CoV Main Proteinase (Mpro) Dimer: Molecular Dynamics Simulations and Multiple X-ray Structure Analyses. J. Mol. Biol. 2005, 354, 25–40. [Google Scholar] [CrossRef]
- Anand, K.; Ziebuhr, J.; Wadhwani, P.; Mesters, J.R.; Hilgenfeld, R. (3CL pro) Structure: Basis for Design of Anti-SARS Drugs. Science 2003, 300, 1763–1767. [Google Scholar] [CrossRef] [PubMed]
- Hilgenfeld, R. From SARS to MERS: Crystallographic studies on coronaviral proteases enable antiviral drug design. FEBS J. 2014, 281, 4085–4096. [Google Scholar] [CrossRef] [PubMed]
- Báez-Santos, Y.M.; St. John, S.E.; Mesecar, A.D. The SARS-coronavirus papain-like protease: Structure, function and inhibition by designed antiviral compounds. Antivir. Res. 2015, 115, 21–38. [Google Scholar] [CrossRef]
- Yazdany, J.; Kim, A.H.J. Use of Hydroxychloroquine and Chloroquine during the COVID-19 Pandemic: What Every Clinician Should Know. Ann. Intern. Med. 2020, 172, 754–755. [Google Scholar] [CrossRef]
- Frisch, J.M.; Trucks, W.G.; Schlegel, B.H.; Scuseria, E.G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.H.; et al. Gaussian 09 (Revision A02); Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Jin, Z.; Du, X.; Xu, Y.; Deng, Y.; Liu, M.; Zhao, Y.; Zhang, B.; Li, X.; Zhang, L.; Peng, C.; et al. Structure of Mpro from SARS-CoV-2 and discovery of its inhibitors. Nature 2020, 582, 289–293. [Google Scholar] [CrossRef] [PubMed]
- Thomsen, R.; Christensen, M.H. MolDock: A New Technique for High-Accuracy Molecular Docking. J. Med. Chem. 2006, 49, 3315–3321. [Google Scholar] [CrossRef] [PubMed]
- Silva, T.C.; dos Pires, M.S.; de Castro, A.A.; da Cunha, E.F.F.; Caetano, M.S.; Ramalho, T.C. Molecular insight into the inhibition mechanism of plant and rat 4-hydroxyphenylpyruvate dioxygenase by molecular docking and DFT calculations. Med. Chem. Res. 2015, 24, 3958–3971. [Google Scholar] [CrossRef]
- Guimaraes, A.P.; Oliveira, A.A.; da Cunha, E.F.F.; Ramalho, T.C.; Franco, T.C.C. Analysis of Bacillus anthracis nucleoside hydrolase via in silico docking with inhibitors and molecular dynamics simulation. J. Mol. Model. 2011, 17, 2939–2951. [Google Scholar] [CrossRef] [PubMed]
- Matos, K.S.; Mancini, D.T.; da Cunha, E.F.F.; Kuca, K.; Franca, T.C.C.; Ramalho, T.C. Molecular Aspects of the Reactivation Process of Acetylcholinesterase Inhibited by Cyclosarin. J. Braz. Chem. Soc. 2011, 22, 1999–2004. [Google Scholar] [CrossRef]
- da Cunha, E.F.F.; Barbosa, E.F.; Oliveira, A.A.; Ramalho, T.C. Molecular Modeling of Mycobacterium Tuberculosis DNA Gyrase and its Molecular Docking Study with Gatifloxacin Inhibitors. J. Biomol. Struct. Dyn. 2010, 27, 619–625. [Google Scholar] [CrossRef] [PubMed]
- Souza, T.C.S.; Josa, D.; Ramalho, T.C.; Caetano, M.S.; da Cunha, E.F.F. Molecular modelling of Mycobacterium tuberculosis acetolactate synthase catalytic subunit and its molecular docking study with inhibitors. Mol. Simul. 2008, 34, 707–713. [Google Scholar] [CrossRef]
- Scott, W.R.P.; Hünenberger, P.H.; Tironi, I.G.; Mark, A.E.; Billeter, S.R.; Fennen, J.; Torda, A.E.; Huber, T.; Krüger, P.; van Gunsteren, W.F. The GROMOS Biomolecular Simulation Program Package. J. Phys. Chem. A 1999, 103, 3596–3607. [Google Scholar] [CrossRef]
- Deepa, G.; Sivakumar, K.C.; Sajeevan, T.P. Molecular simulation and in vitro evaluation of chitosan nanoparticles as drug delivery systems for the controlled release of anticancer drug cytarabine against solid tumours. 3 Biotech 2018, 8, 493. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Fernandes, R.F.; Stroppa, P.H.F.; Ferreira, G.R.; da Silva, A.D.; Edwards, H.G.M.; de Oliveira, L.F.C. Vibrational spectroscopic study of some quinoline derivatives. Vib. Spectrosc. 2016, 86, 128–133. [Google Scholar] [CrossRef]
- Adeli, E. Preparation and evaluation of azithromycin binary solid dispersions using various polyethylene glycols for the improvement of the drug solubility and dissolution rate. Braz. J. Pharm. Sci. 2016, 52, 1–13. [Google Scholar] [CrossRef]
- Dey, S. Plasmon Enhanced Hybrid Photovoltaics. In Imerging Research in Science and Engineering Based on Advanced Experimental and Computational Strategies. Engineering Materials; La Porta, F.A., Taft, C.A., Eds.; Springer: Cham, Switzerland, 2020; ISBN 978-3-030-31402-6. [Google Scholar]
- La Porta, F.A.; Ramalho, T.C.; Santiago, R.T.; Rocha, M.V.J.; da Cunha, E.F.F. Orbital Signatures as a Descriptor of Regioselectivity and Chemical Reactivity: The Role of the Frontier Orbitals on 1,3-Dipolar Cycloadditions. J. Phys. Chem. A 2011, 115, 824–833. [Google Scholar] [CrossRef] [PubMed]
- da Silva, R.R.; Ramalho, T.C.; Santos, J.M.; Figueroa-Villar, J.D. On the Limits of Highest-Occupied Molecular Orbital Driven Reactions: The Frontier Effective-for-Reaction Molecular Orbital Concept. J. Phys. Chem. A 2006, 110, 1031–1040. [Google Scholar] [CrossRef] [PubMed]
- Fukui, K.; Yonezawa, T.; Shingu, H. A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Carpenter, J.E.; Weinhold, F. Analysis of the geometry of the hydroxymethyl radical by the “different hybrids for different spins” natural bond orbital procedure. J. Mol. Struct. Theochem 1988, 169, 41–62. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Yang, S.; Chen, S.J.; Hsu, M.F.; Wu, J.D.; Tseng, C.T.K.; Liu, Y.F.; Chen, H.C.; Kuo, C.W.; Wu, C.S.; Chang, L.W.; et al. Synthesis, crystal structure, structure-activity relationships, and antiviral activity of a potent SARS coronavirus 3CL protease inhibitor. J. Med. Chem. 2006, 49, 4971–4980. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Liu, Y.; Zhang, W.; Wei, P.; Huang, C.; Pei, J.; Yuan, Y.; Lai, L. Isatin compounds as noncovalent SARS coronavirus 3C-like protease inhibitors. J. Med. Chem. 2006, 49, 3440–3443. [Google Scholar] [CrossRef] [PubMed]
- Cardoso Gajo, G.; Rodrigues Silva, D.; Barigye, S.J.; da Cunha, E.F.F. Multi-objective Optimization of Benzamide Derivatives as Rho Kinase Inhibitors. Mol. Inform. 2018, 37, 1700080. [Google Scholar] [CrossRef]
- La Porta, F.A.; Taft, C. Emerging Research in Science and Engineering Based on Advanced Experimental and Computational Strategies; Springer Nature: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-030-31402-6. [Google Scholar]
- La Porta, F.A.; Taft, C.A. (Eds.) Functional Properties of Advanced Engineering Materials and Biomolecules, 1st ed.; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-62225-1. [Google Scholar]
- Ramalho, T.C.; de Castro, A.A.; Silva, D.R.; Silva, M.C.; Franca, T.C.C.; Bennion, B.J.; Kuca, K. Computational Enzymology and Organophosphorus Degrading Enzymes: Promising Approaches toward Remediation Technologies of Warfare Agents and Pesticides. Curr. Med. Chem. 2016, 23, 1041–1061. [Google Scholar] [CrossRef] [PubMed]
- de Castro, A.A.; Prandi, I.G.; Kuca, K.; Ramalho, T.C. Organophosphorus degrading enzymes: Molecular basis and perspectives for enzymatic bioremediation of agrochemicals. Cienc. Agrotecnologia 2017, 41, 471–482. [Google Scholar]
- Durrant, J.D.; Kochanek, S.E.; Casalino, L.; Ieong, P.U.; Dommer, A.C.; Amaro, R.E. Mesoscale All-Atom Influenza Virus Simulations Suggest New Substrate Binding Mechanism. ACS Cent. Sci. 2020, 6, 189–196. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).