A Data Driven Analysis and Forecast of COVID-19 Dynamics during the Third Wave Using SIRD Model in Bangladesh
Abstract
:1. Introduction
2. Data Source
3. Methodology
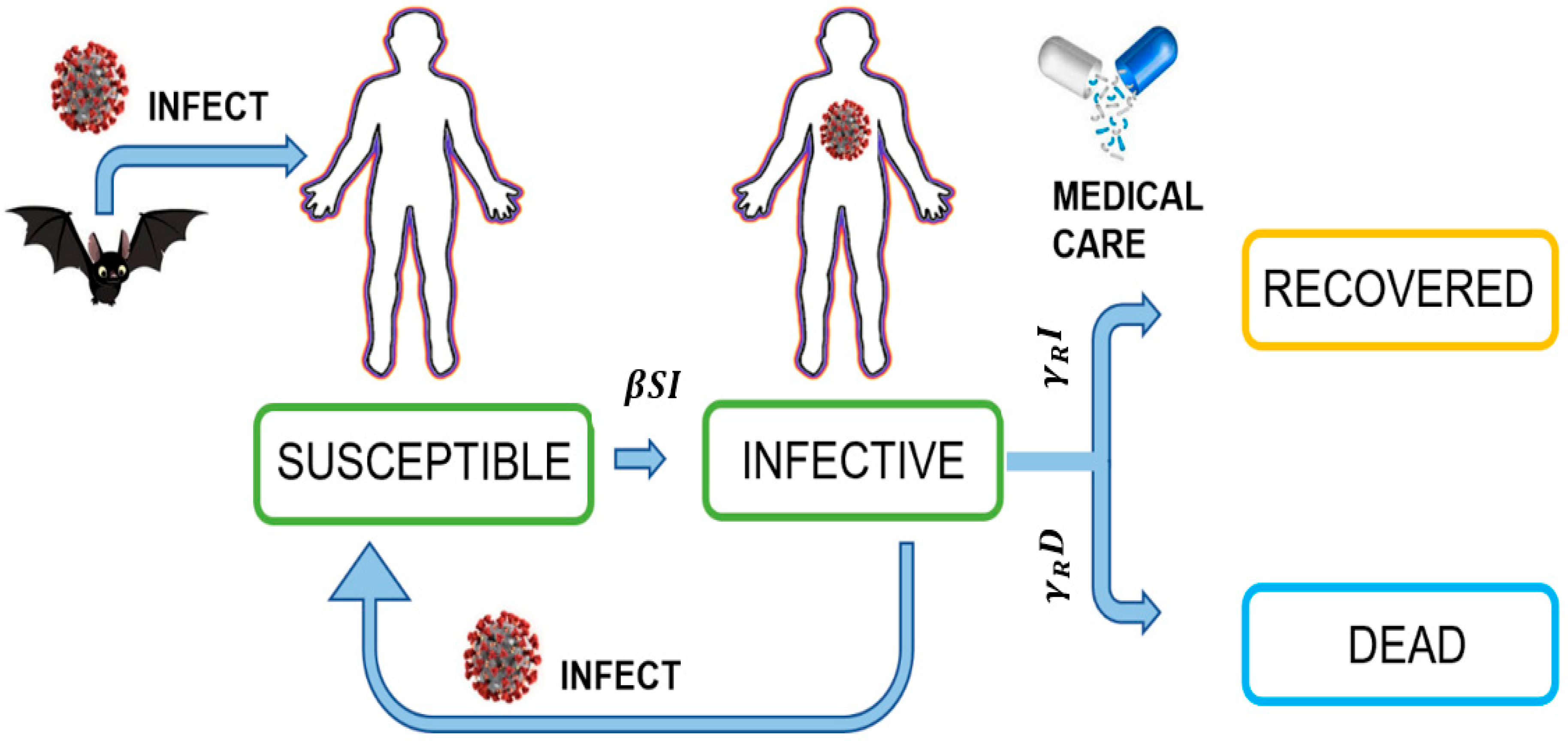
- Susceptible class —those who could become infected,
- Infected class —those who are infected with the virus at the time,
- Recovered class —those who have recovered from the infection.
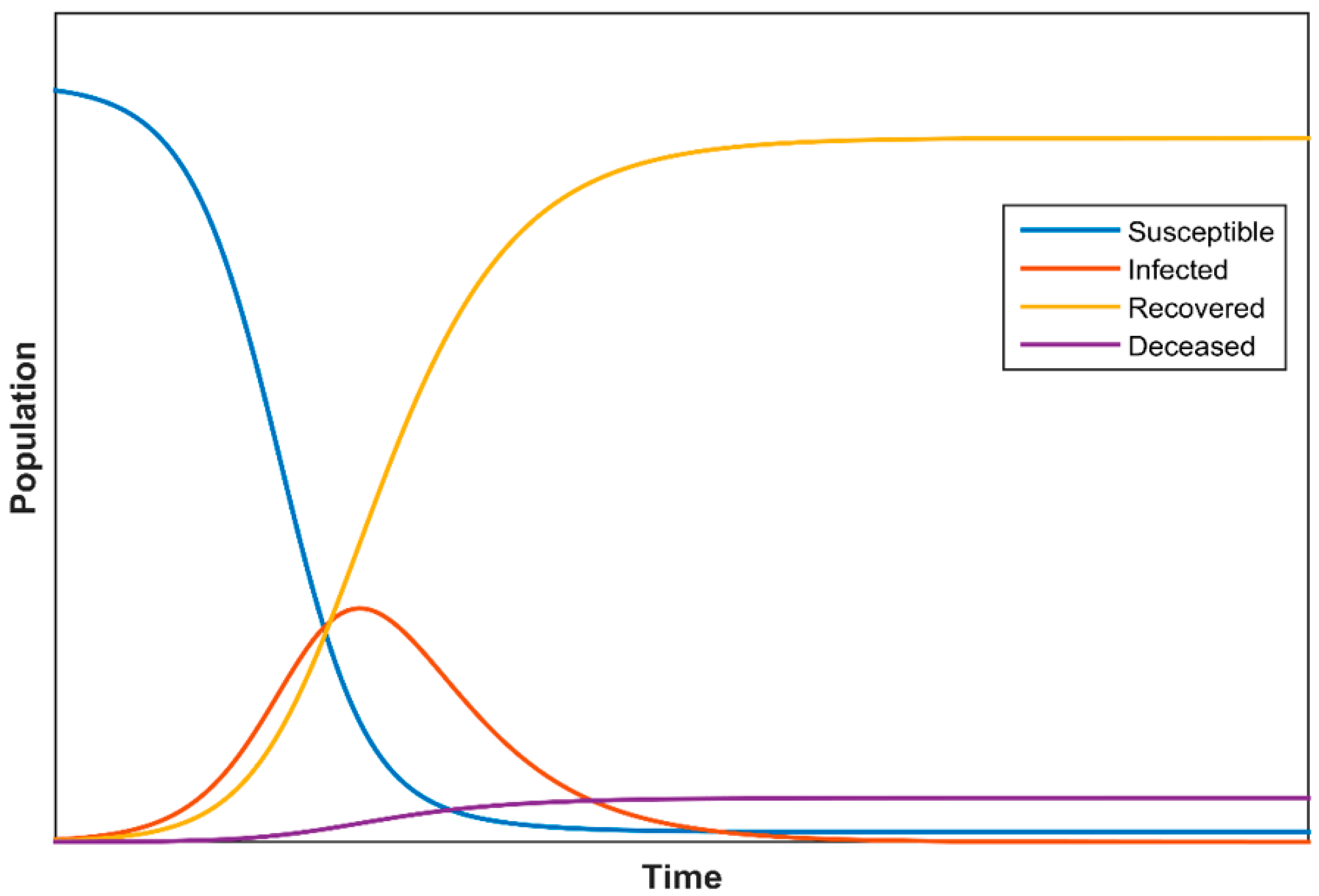
3.1. SIRD Model
- (i)
- The total population is closed.
- (ii)
- The susceptible and infected individuals are homogeneous in the population.
- (iii)
- The natural death or birth rate is not considered in this model. We only take into account the fatalities associated with COVID-19.
- (iv)
- The recovered population develops permanent immunity.
- (v)
- All variables and parameters regarding the model are non-negative.
3.2. Basic Reproduction Number
3.3. Regression Coefficient
3.4. Estimation of Parameters
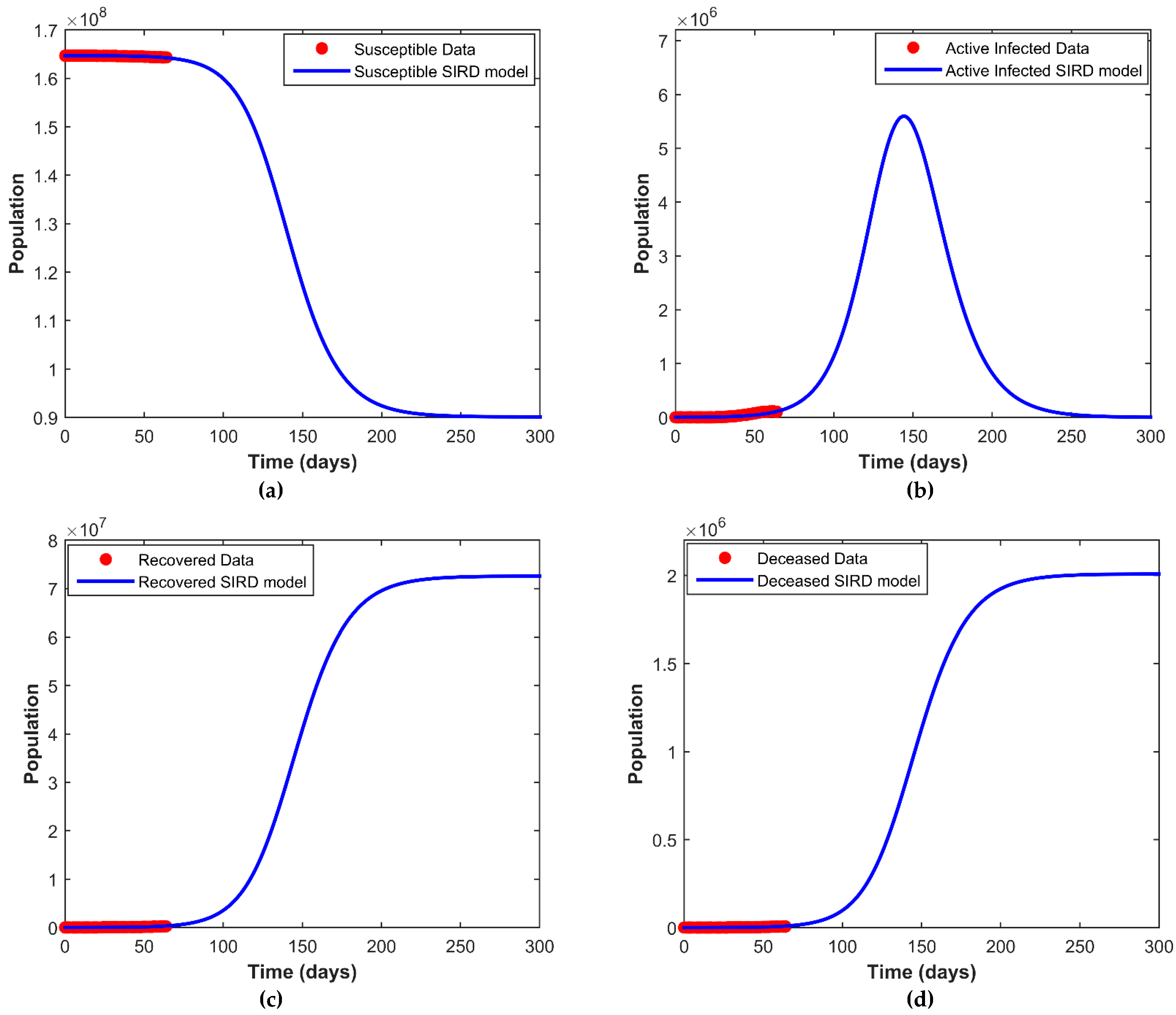
4. Results and Discussion
4.1. Interpretation of the Public Data
4.2. Fitting the SIRD Model to Data
4.3. Sensitivity Analysis
4.4. COVID-19 Forecast for Bangladesh
4.5. Study Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johns Hopkins University Center for Systems Science and Engineering. 2019 Novel Coronavirus COVID-19 (2019-nCoV) Data Repository by Johns Hopkins CSSE. 2020. Available online: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series (accessed on 2 August 2021).
- Directorate General of Health Services, Bangladesh. Available online: http://103.247.238.92/webportal/pages/covid19.php (accessed on 2 August 2021).
- The Humanitarian Data Exchange. Available online: https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases (accessed on 2 August 2021).
- Github. Our World in Data. Available online: https://ourworldindata.org/ (accessed on 2 August 2021).
- IECDR, Institute of Epidemiology Disease Control And Research. Available online: https://www.iedcr.gov.bd (accessed on 2 August 2021).
- IEDCR: 78% Covid Cases in June Caused by Delta Variant. Available online: https://www.dhakatribune.com/health/coronavirus/2021/07/04/iedcr-delta-variant-dominant-in-bangladesh (accessed on 28 July 2021).
- SARS-CoV-2 Delta Variant. Available online: https://en.wikipedia.org/wiki/SARS-CoV-2_Delta_variant (accessed on 28 July 2021).
- Bangladesh Battles Third Wave of COVID-19. Available online: https://www.devex.com/news/bangladesh-battles-third-wave-of-covid-19-100340 (accessed on 28 July 2021).
- Sedaghat, A.; Mosavi, A. Predicting Trends of Coronavirus Disease (COVID-19) Using SIRD and Gaussian-SIRD Models. Preprints 2020. [Google Scholar] [CrossRef]
- Korolev, I. Identification and estimation of the SEIRD epidemic model for COVID-19. J. Econom. 2021, 220, 63–85. [Google Scholar] [CrossRef] [PubMed]
- Sedaghat, A.; Oloomi, S.A.A.; Malayer, M.A.; Band, S.; Rezaei, N.; Mosavi, A.; Nadai, L. Coronavirus (COVID-19) Outbreak Prediction Using Epidemiological Models of Richards Gompertz Logistic Ratkowsky and SIRD. In Proceedings of the 2020 IEEE 3rd International Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 18–19 November 2020; pp. 289–298. [Google Scholar] [CrossRef]
- Sen, D.; Sen, D. Use of a Modified SIRD Model to Analyze COVID-19 Data. Ind. Eng. Chem. Res. 2021, 60, 4251–4260. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A Simulation of a COVID-19 Epidemic Based on a Deterministic SEIR Model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Victor Okhuese, A. Estimation of the Probability of Reinfection With COVID-19 by the Susceptible-Exposed-Infectious-Removed-Undetectable-Susceptible Model. JMIR Public Health Surveill 2020, 6, e19097. Available online: https://publichealth.jmir.org/2020/2/e19097 (accessed on 28 July 2021). [CrossRef]
- Sedaghat, A.; Alkhatib, F.; Mostafaeipour, N.; Abbas Oloomi, S.A. Prediction of COVID-19 Dynamics in Kuwait using SIRD Model. Integr. J. Med. Sci. 2020, 7, 170. Available online: https://mediterraneanjournals.com/index.php/ijms/article/view/170 (accessed on 27 July 2021). [CrossRef]
- De León, U.A.-P.; Pérez, Á.G.C.; Avila-Vales, E. A data driven analysis and forecast of an SEIARD epidemic model for COVID-19 in Mexico. Big Data Inf. Anal. 2020, 5, 14–28. [Google Scholar] [CrossRef]
- Gebremeskel, A.A.; Berhe, H.W.; Atsbaha, H.A. Mathematical modelling and analysis of COVID-19 epidemic and predicting its future situation in Ethiopia. Results Phys. 2021, 22, 103853. [Google Scholar] [CrossRef] [PubMed]
- Martínez, V. A Modified SIRD Model to Study the Evolution of the COVID-19 Pandemic in Spain. Symmetry 2021, 13, 723. [Google Scholar] [CrossRef]
- Caccavo, D. Chinese and Italian COVID-19 outbreaks can be correctly described by a modified SIRD model. medRxiv 2020. [Google Scholar] [CrossRef]
- Khan, M.H.R.; Hossain, A. COVID-19 Outbreak Situations in Bangladesh: An Empirical Analysis. medRxiv 2020. [Google Scholar] [CrossRef]
- Pabel Shahrear, S.M.; Rahman, S.; Nahid, M.M.H. Prediction and mathematical analysis of the outbreak of coronavirus (COVID-19) in Bangladesh. Results Appl. Math. 2021, 10, 100145. [Google Scholar] [CrossRef]
- Lounis, M.; dos Santos Azevedo, J. Application of a Generalized SEIR Model for COVID-19 in Algeria. Eur. J. Sustain. Dev. Res. 2021, 5, em0150. [Google Scholar] [CrossRef]
- Hassan, R.; Dosar, A.S.; Mondol, J.K.; Khan, T.H.; Noman, A.A.; Sayem, M.S.; Hasan, M.; Juyena, N.S. Prediction of Epidemics Trend of COVID-19 in Bangladesh. Front. Public Health 2020, 8, 559437. [Google Scholar] [CrossRef] [PubMed]
- Fargana, A.; Arifutzzaman, A.; Rakhimov, A.A. Spreading Analysis of COVID-19 Epidemic in Bangladesh by Dynamical Mathematical Modelling. Eur. J Med. Educ. Technol. 2021, 14, em2109. [Google Scholar] [CrossRef]
- Annas, S.; Pratama, M.I.; Rifandi, M.; Sanusi, W.; Side, S. Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia. Chaos Solitons Fractals 2020, 139, 110072. [Google Scholar] [CrossRef] [PubMed]
- Berhe, H.W.; Makinde, O.D.; Theuri, D.M. Parameter Estimation and Sensitivity Analysis of Dysentery Diarrhea Epidemic Model. J. Appl. Math. 2019, 2019, 8465747. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Sensitivity Analysis in a Dengue Epidemiological Model. Conf. Pap. Sci. 2013, 721406. [Google Scholar] [CrossRef]
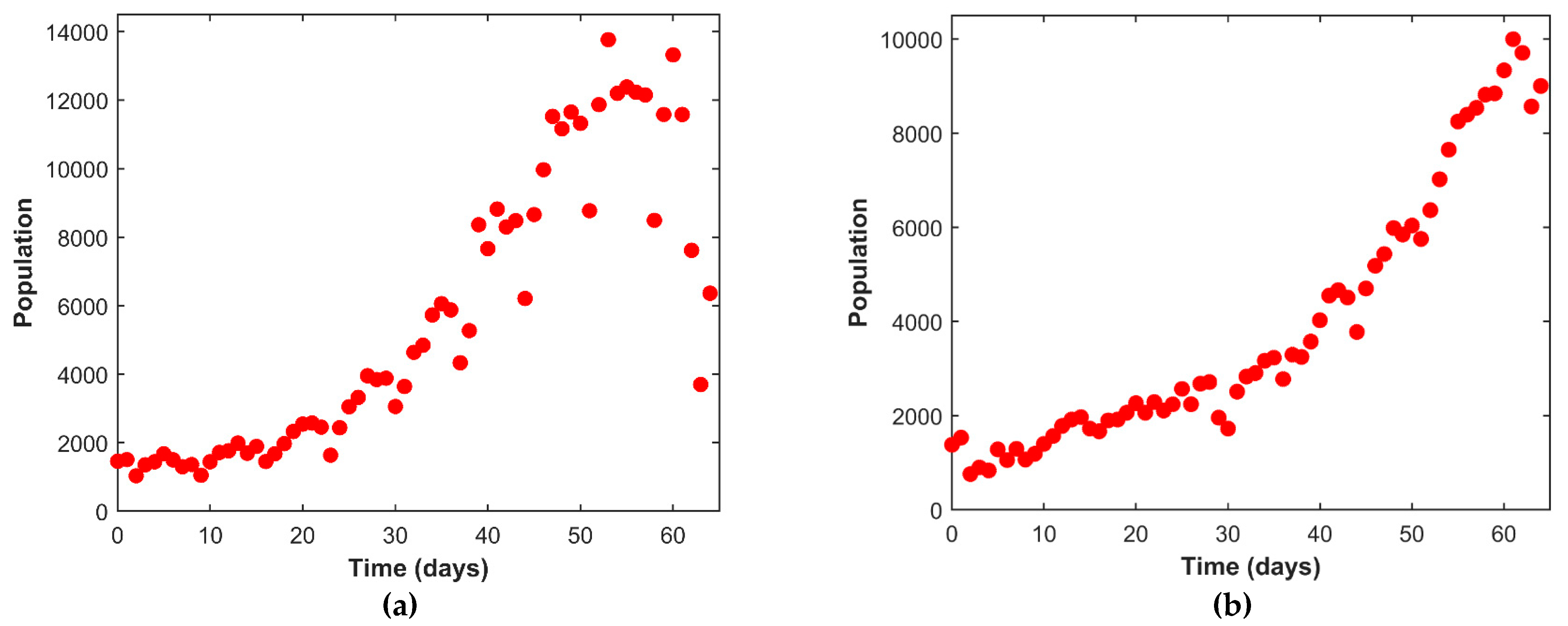
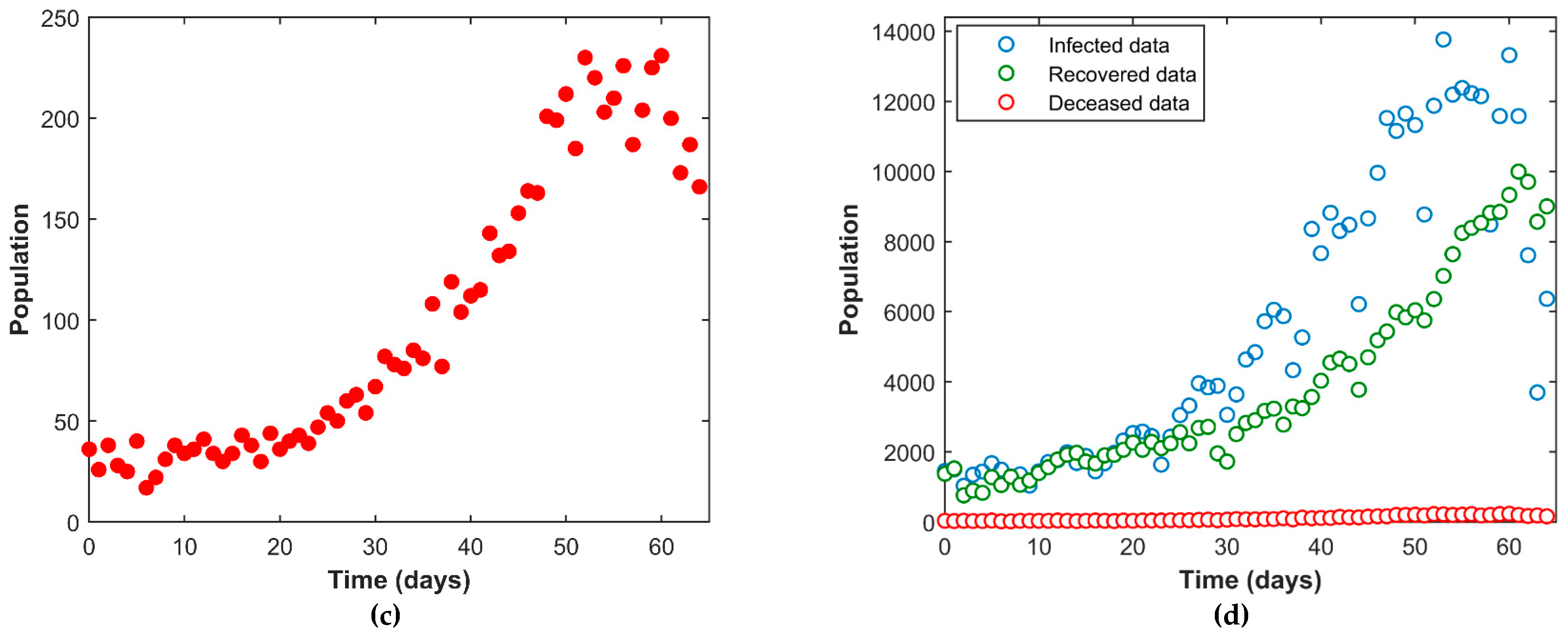
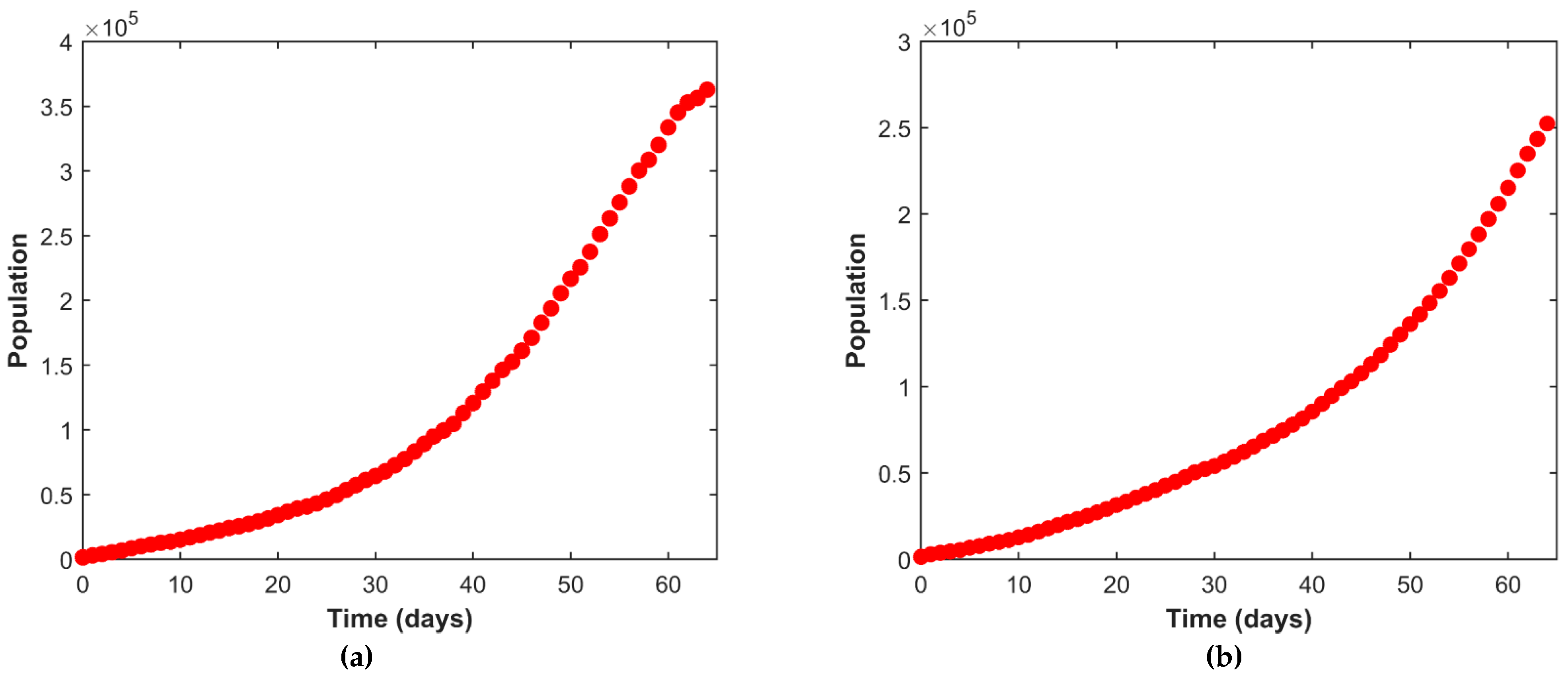
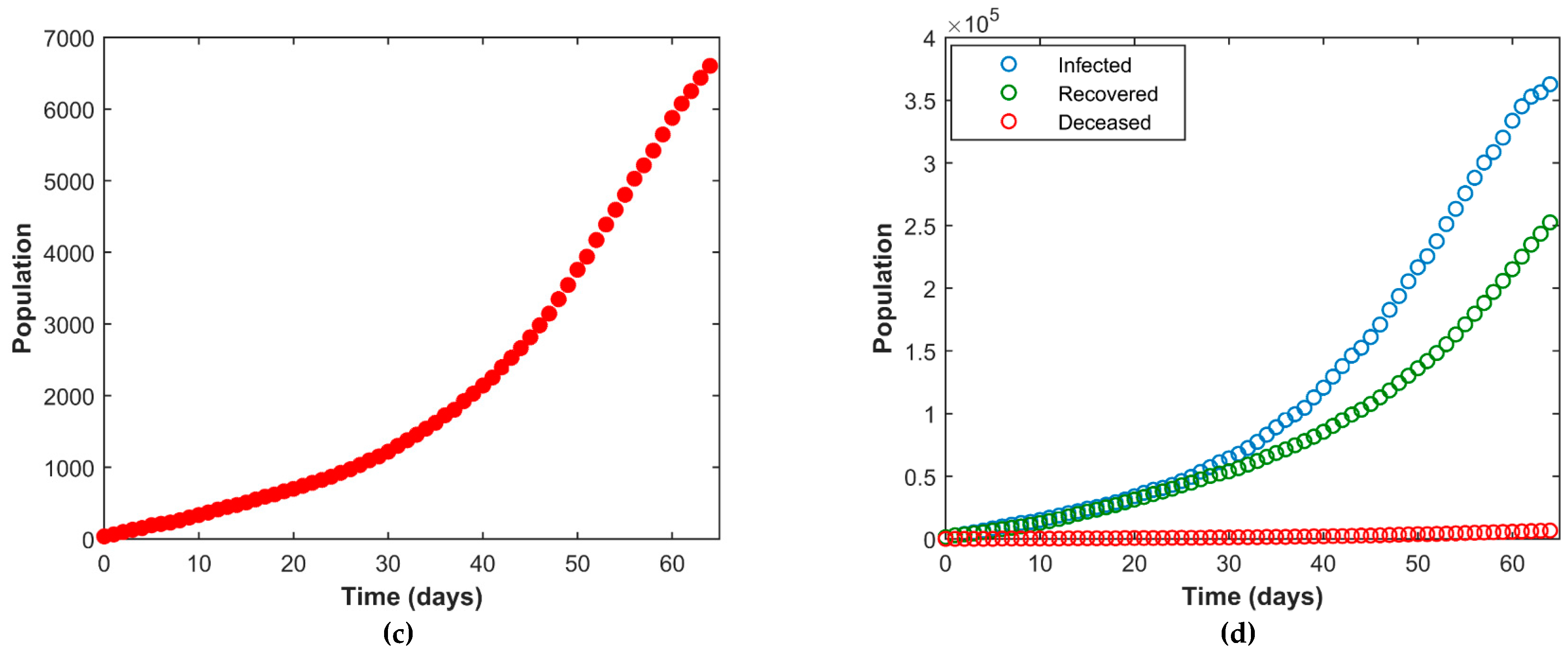
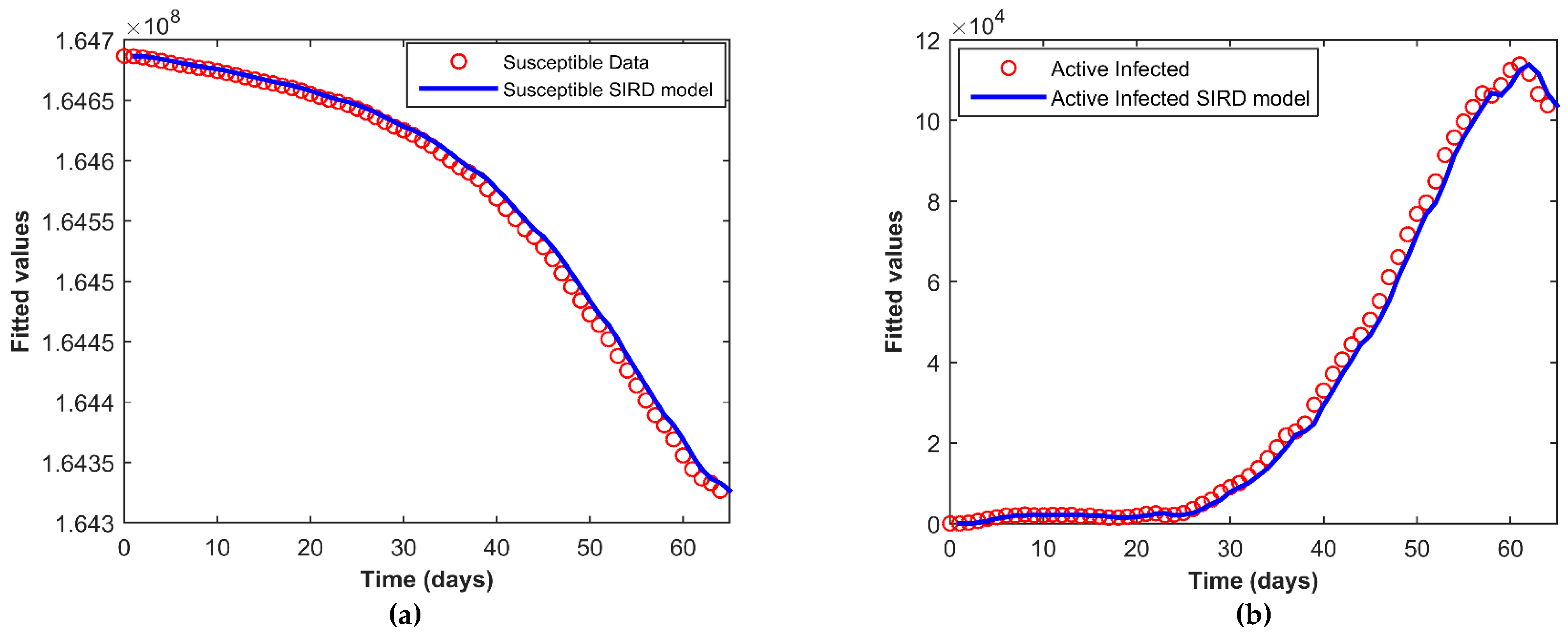
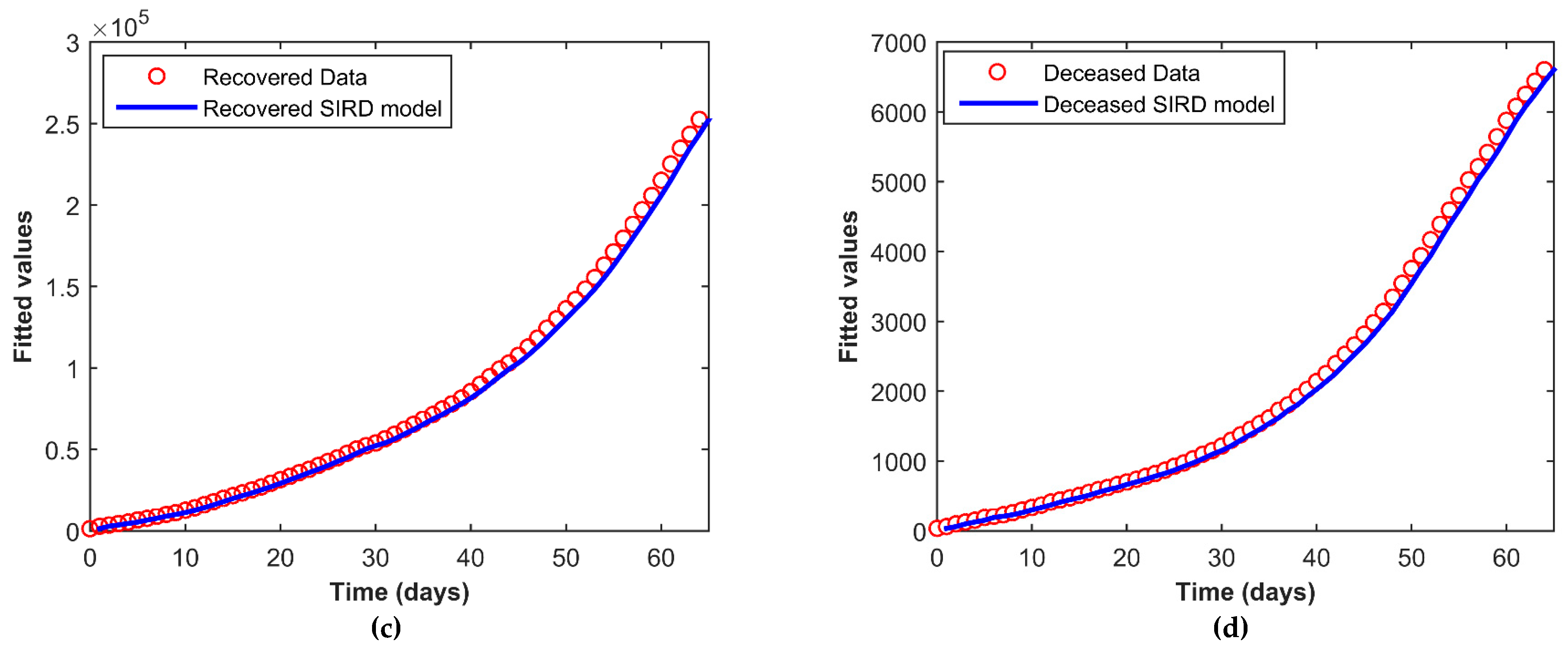
| Date | Cases | Recovered | Deceased | Date | Cases | Recovered | Deceased |
|---|---|---|---|---|---|---|---|
| 20 May | 1457 | 1378 | 36 | 22 June | 4846 | 2903 | 76 |
| 21 May | 1504 | 1529 | 26 | 23 June | 5727 | 3168 | 85 |
| 22 May | 1028 | 759 | 38 | 24 June | 6058 | 3230 | 81 |
| 23 May | 1354 | 899 | 28 | 25 June | 5869 | 2776 | 108 |
| 24 May | 1441 | 834 | 25 | 26 June | 4334 | 3295 | 77 |
| 25 May | 1675 | 1279 | 40 | 27 June | 5268 | 3249 | 119 |
| 26 May | 1497 | 1056 | 17 | 28 June | 8364 | 3570 | 104 |
| 27 May | 1292 | 1291 | 22 | 29 June | 7666 | 4027 | 112 |
| 28 May | 1358 | 1064 | 31 | 30 June | 8822 | 4550 | 115 |
| 29 May | 1043 | 1187 | 38 | 01 July | 8301 | 4663 | 143 |
| 30 May | 1444 | 1397 | 34 | 02 July | 8483 | 4509 | 132 |
| 31 May | 1710 | 1567 | 36 | 03 July | 6214 | 3777 | 134 |
| 01 June | 1765 | 1779 | 41 | 04 July | 8661 | 4698 | 153 |
| 02 June | 1988 | 1914 | 34 | 05 July | 9964 | 5185 | 164 |
| 03 June | 1687 | 1970 | 30 | 06 July | 11,525 | 5433 | 163 |
| 04 June | 1887 | 1723 | 34 | 07 July | 11,162 | 5987 | 201 |
| 05 June | 1447 | 1667 | 43 | 08 July | 11,651 | 5844 | 199 |
| 06 June | 1676 | 1897 | 38 | 09 July | 11,324 | 6038 | 212 |
| 07 June | 1970 | 1918 | 30 | 10 July | 8772 | 5755 | 185 |
| 08 June | 2322 | 2062 | 44 | 11 July | 11,874 | 6362 | 230 |
| 09 June | 2537 | 2267 | 36 | 12 July | 13,768 | 7020 | 220 |
| 10 June | 2576 | 2061 | 40 | 13 July | 12,198 | 7646 | 203 |
| 11 June | 2454 | 2286 | 43 | 14 July | 12,383 | 8245 | 210 |
| 12 June | 1637 | 2108 | 39 | 15 July | 12,236 | 8395 | 226 |
| 13 June | 2436 | 2242 | 47 | 16 July | 12,148 | 8536 | 187 |
| 14 June | 3050 | 2564 | 54 | 17 July | 8489 | 8820 | 204 |
| 15 June | 3319 | 2243 | 50 | 18 July | 11,578 | 8845 | 225 |
| 16 June | 3956 | 2679 | 60 | 19 July | 13,321 | 9335 | 231 |
| 17 June | 3840 | 2714 | 63 | 20 July | 11,579 | 9997 | 200 |
| 18 June | 3883 | 1955 | 54 | 21 July | 7614 | 9704 | 173 |
| 19 June | 3057 | 1725 | 67 | 22 July | 3697 | 8566 | 187 |
| 20 June | 3641 | 2509 | 82 | 23 July | 6364 | 9006 | 166 |
| 21 June | 4636 | 2827 | 78 |
| Notation | Description |
|---|---|
| Total population | |
| Susceptible population at time t | |
| Infected population at time t | |
| Recovered population at time t | |
| Deceased population at time t | |
| The rate of transmission from susceptible to infectious population | |
| The rate of recovery from infection | |
| The death rate induced by disease |
| Parameter | Regression Coefficient | |||||
|---|---|---|---|---|---|---|
| Parameter | Sensitivity Index |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faruk, O.; Kar, S. A Data Driven Analysis and Forecast of COVID-19 Dynamics during the Third Wave Using SIRD Model in Bangladesh. COVID 2021, 1, 503-517. https://doi.org/10.3390/covid1020043
Faruk O, Kar S. A Data Driven Analysis and Forecast of COVID-19 Dynamics during the Third Wave Using SIRD Model in Bangladesh. COVID. 2021; 1(2):503-517. https://doi.org/10.3390/covid1020043
Chicago/Turabian StyleFaruk, Omar, and Suman Kar. 2021. "A Data Driven Analysis and Forecast of COVID-19 Dynamics during the Third Wave Using SIRD Model in Bangladesh" COVID 1, no. 2: 503-517. https://doi.org/10.3390/covid1020043
APA StyleFaruk, O., & Kar, S. (2021). A Data Driven Analysis and Forecast of COVID-19 Dynamics during the Third Wave Using SIRD Model in Bangladesh. COVID, 1(2), 503-517. https://doi.org/10.3390/covid1020043







