Nano-Biomechanical Analysis of a Corticosteroid Drug for Targeted Delivery into the Alveolar Air—Water Interface Using Molecular Dynamics Simulation
Abstract
1. Introduction
2. Methodology of the Study
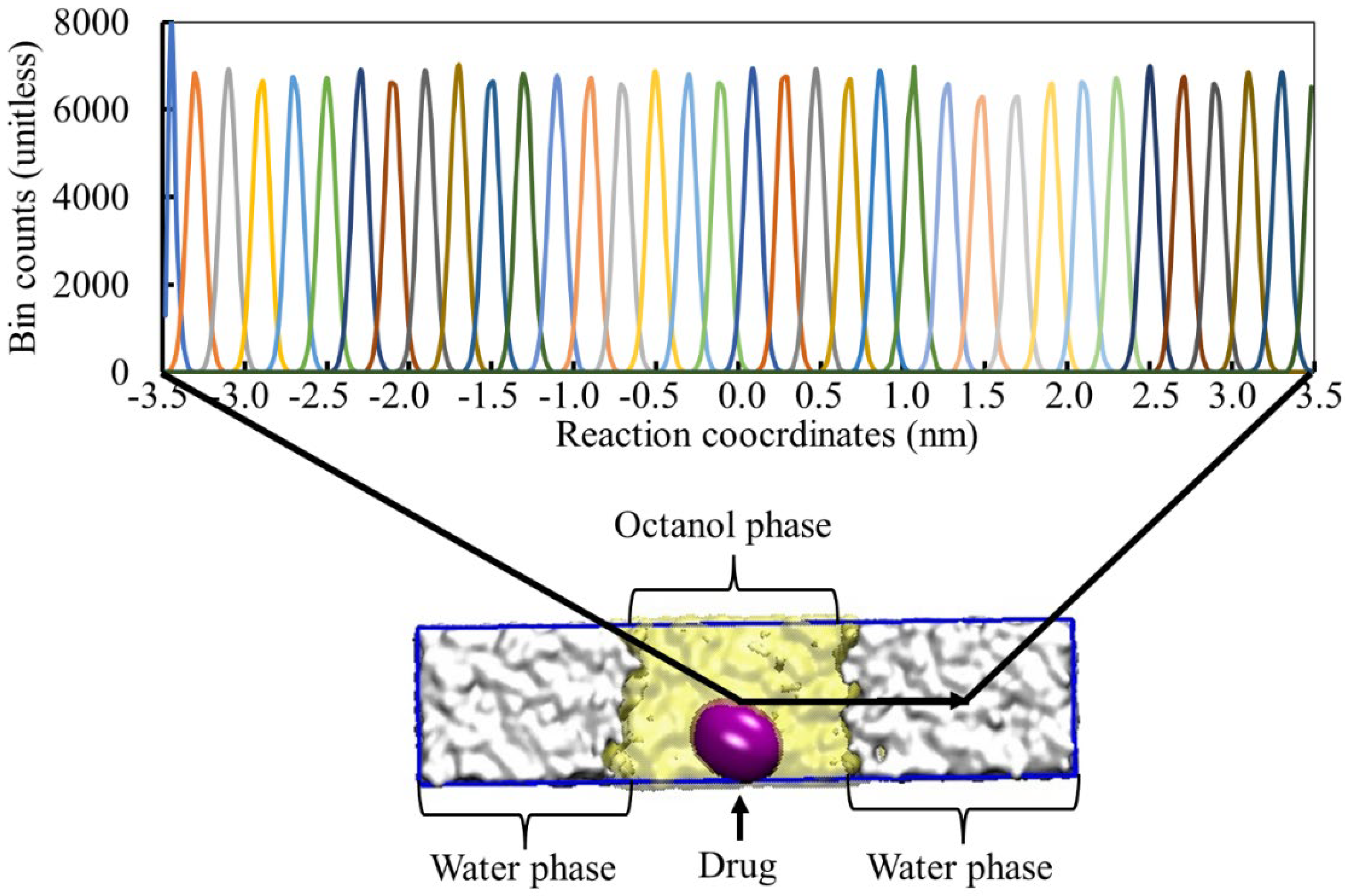
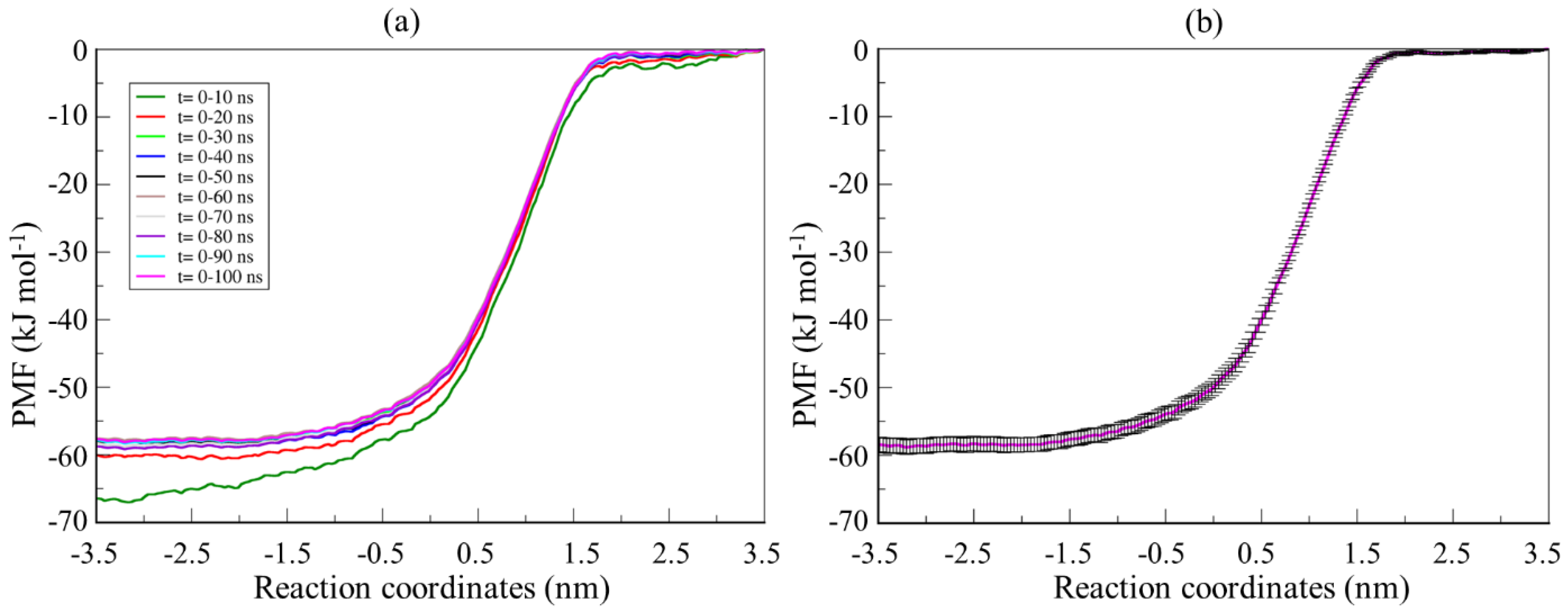
2.1. Drug Parameterization and Umbrella Sampling Simulation
2.2. System Simulation and Underlying Conditions
3. Results and Discussion
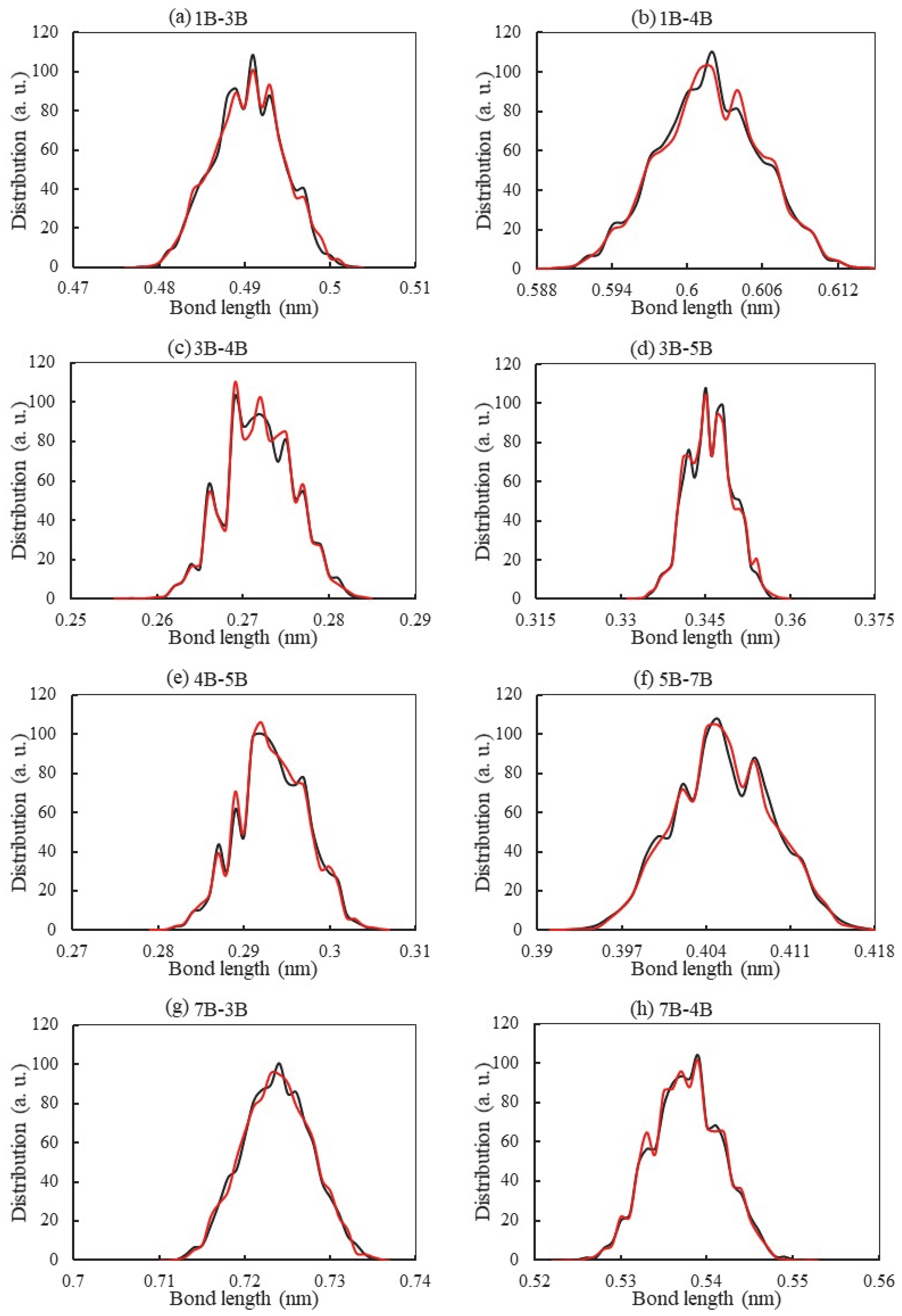
3.1. Bond Distribution Analysis of the Drug Molecules
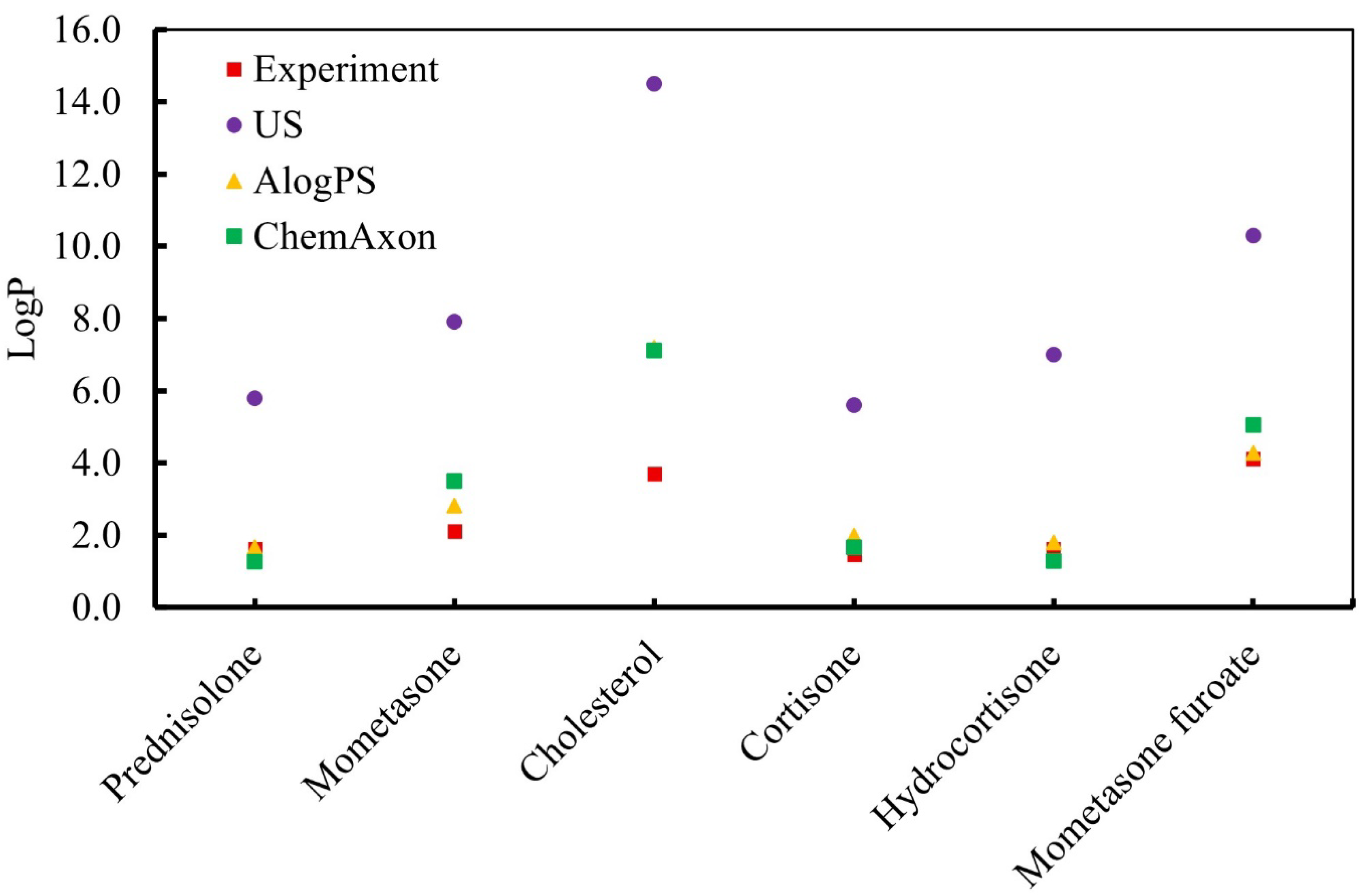
3.2. Calculation of the Partition Coefficient of the Drug Molecule
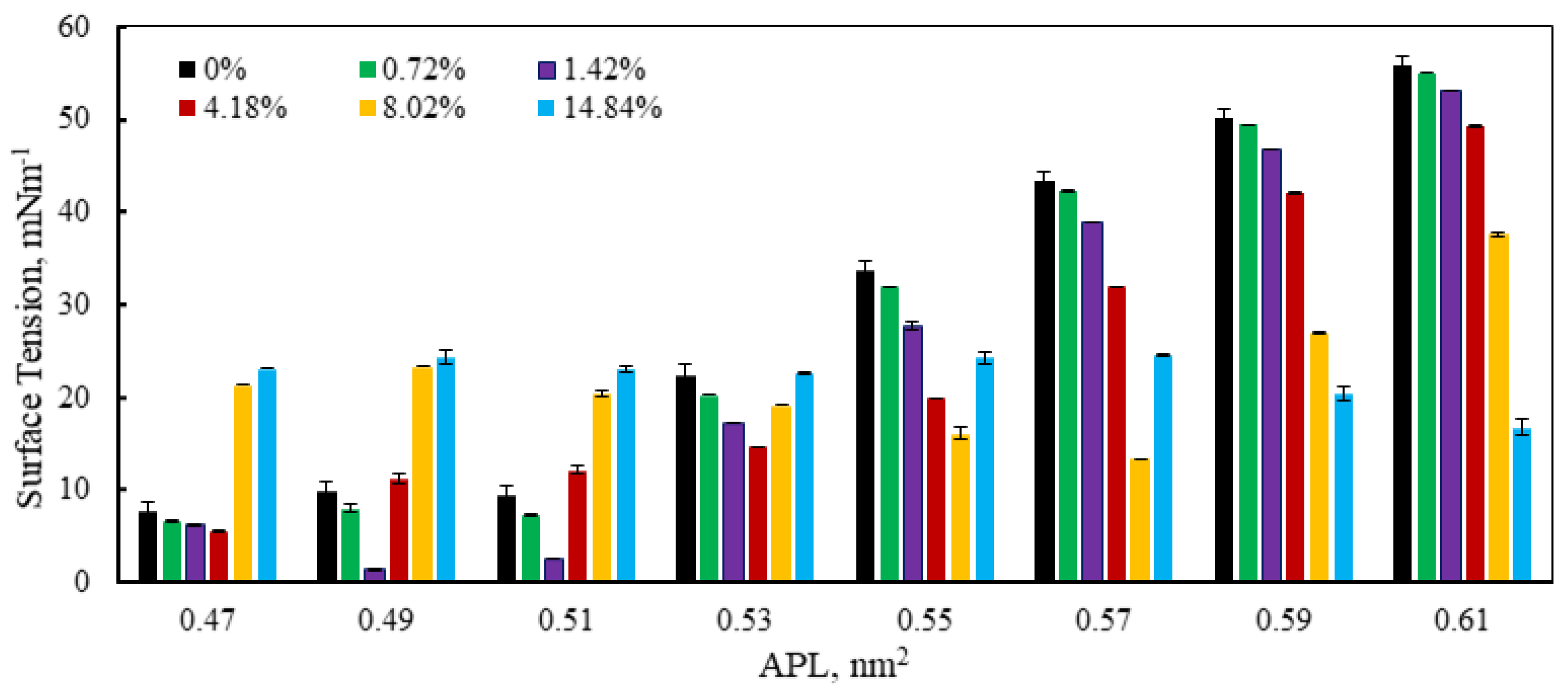
3.3. Monolayer Surface Tension Analysis
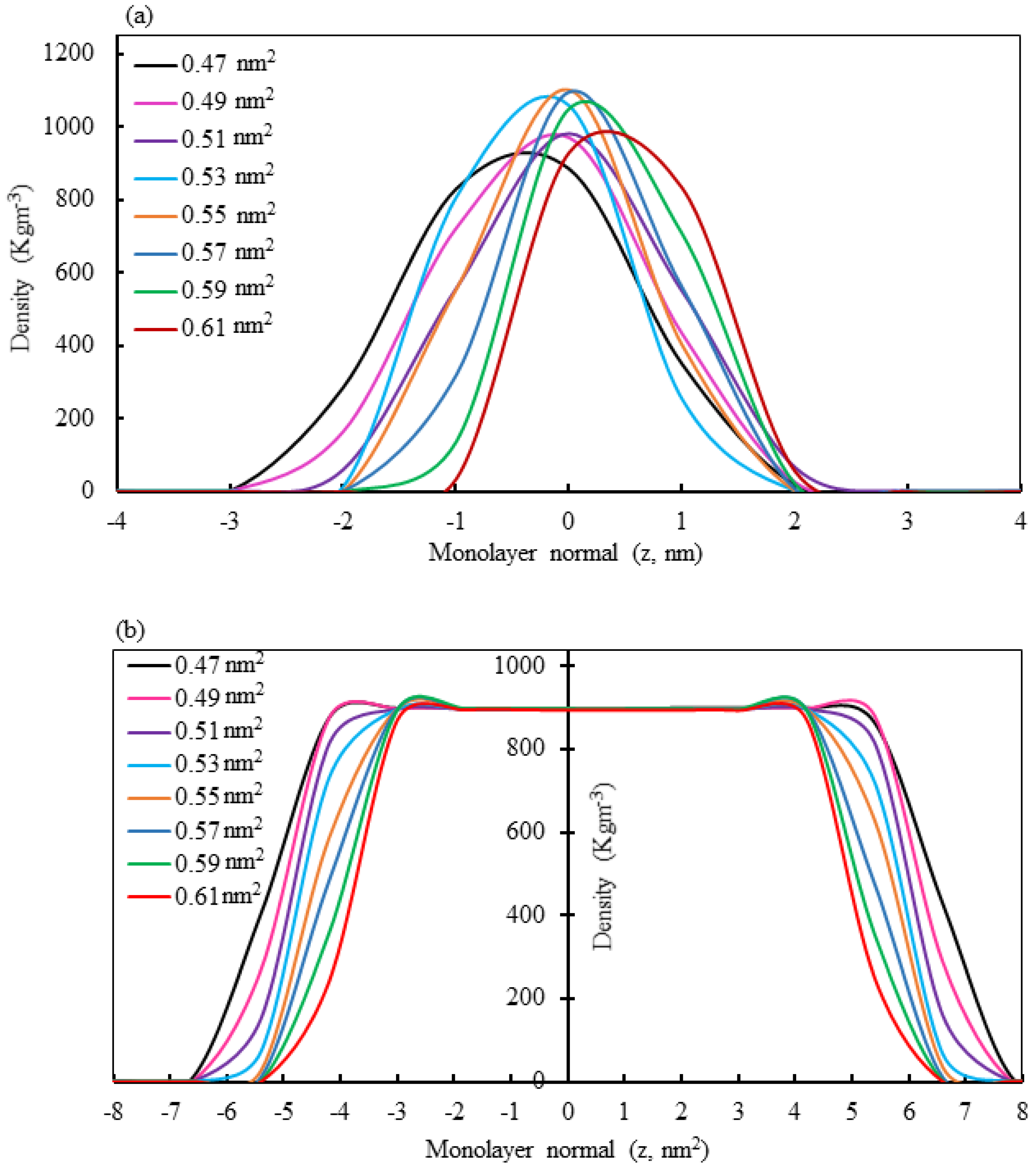
3.4. Monolayer Phase Analysis by Density Calculation
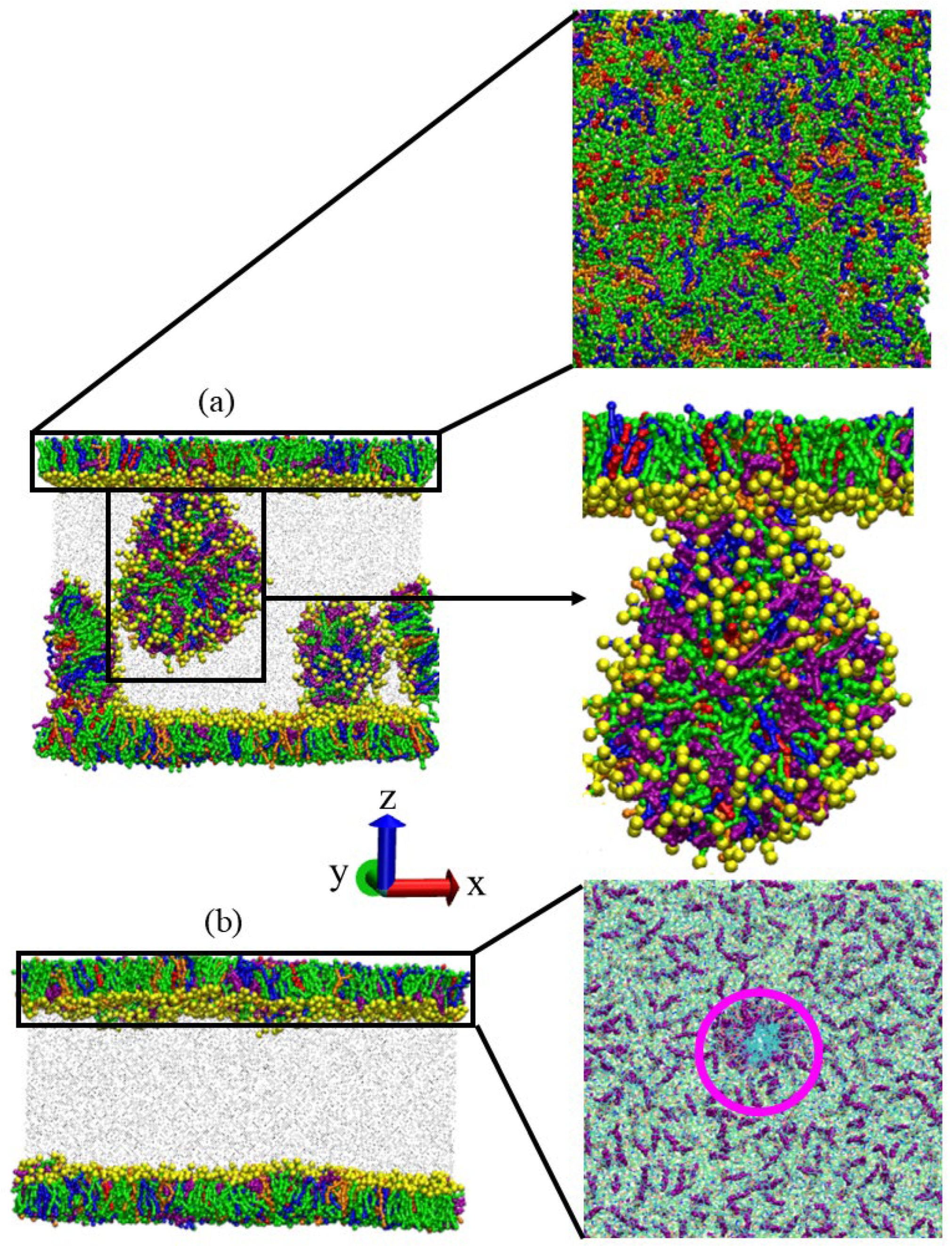
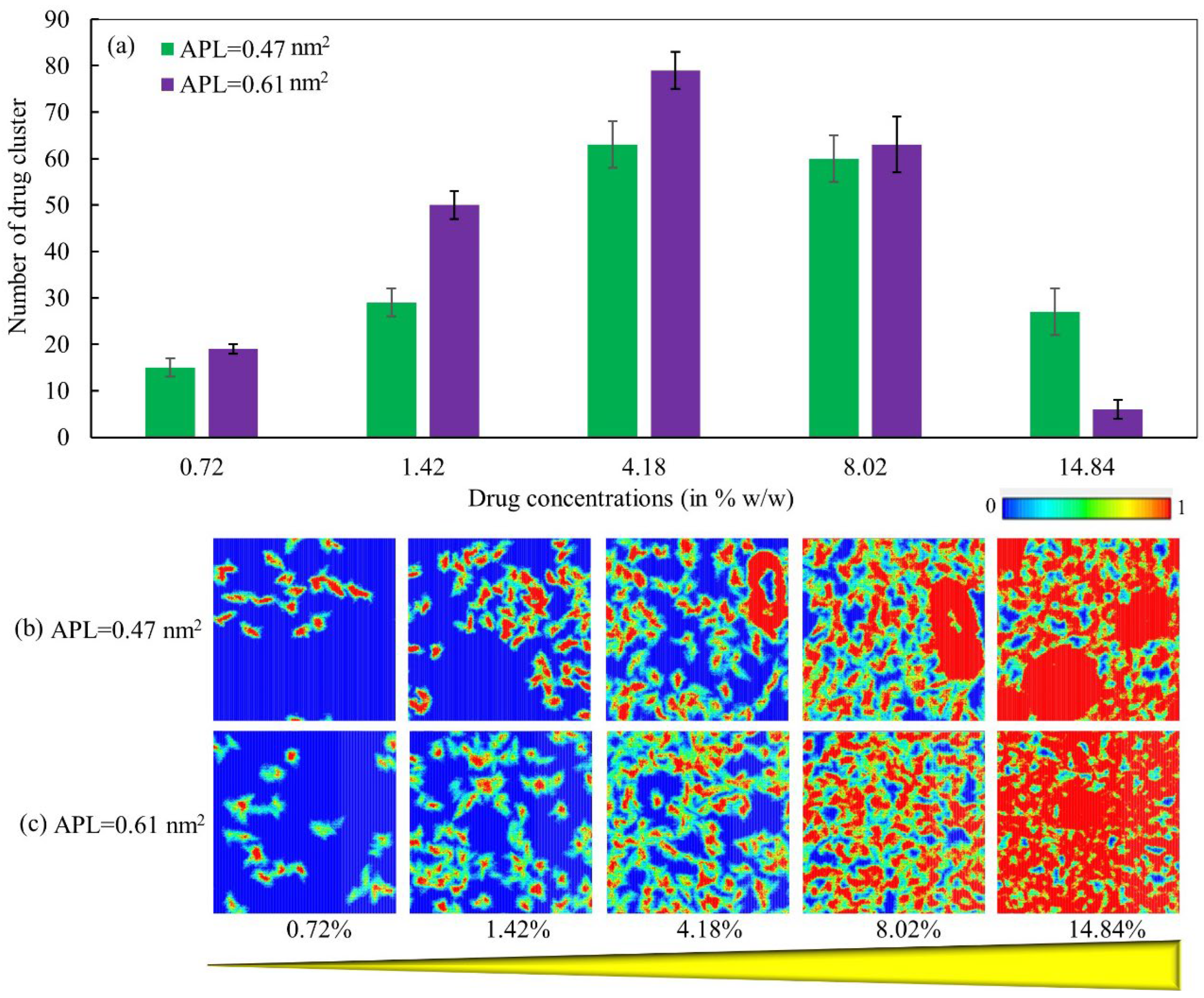
3.5. Drug Distribution by Clustering Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Chung, K.F.; Caramori, G.; Adcock, I.M. Inhaled corticosteroids as combination therapy with β-adrenergic agonists in airways disease: Present and future. Eur. J. Clin. Pharmacol. 2009, 65, 853–871. [Google Scholar] [CrossRef]
- Schäcke, H.; W.-Döcke, D.; Asadullah, K. Mechanisms involved in the side effects of glucocorticoids. Pharmacol. Ther. 2002, 96, 23–43. [Google Scholar] [CrossRef]
- Barnes, P.J. Inhaled glucocorticoids for asthma. N. Engl. J. Med. 1995, 332, 868–875. [Google Scholar] [CrossRef]
- Chrystyn, H. Methods to identify drug deposition in the lungs following inhalation. Br. J. Clin. Pharmacol. 2001, 51, 289–299. [Google Scholar] [CrossRef]
- Dani, C.; Corsini, I.; Burchielli, S.; Cangiamila, V.; Longini, M.; Paternostro, F.; Buonocore, G.; Rubaltelli, F.F. Natural surfactant combined with beclomethasone decreases oxidative lung injury in the preterm lamb. Pediatr. Pulmonol. 2009, 44, 1159–1167. [Google Scholar] [CrossRef]
- Raissy, H.H.; Kelly, H.W.; Harkins, M.; Szefler, S.J. Inhaled corticosteroids in lung diseases. Am. J. Respir. Crit. Care Med. 2013, 187, 798–803. [Google Scholar] [CrossRef] [PubMed]
- Pontremoli, C.; Barbero, N.; Viscardi, G.; Visentin, S. Insight into the interaction of inhaled corticosteroids with human serum albumin: A spectroscopic-based study. J. Pharm. Anal. 2018, 8, 37–44. [Google Scholar] [CrossRef]
- Heffler, E.; Madeira, L.N.G.; Ferrando, M.; Puggioni, F.; Racca, F.; Malvezzi, L.; Passalacqua, G.; Canonica, G.W. Inhaled corticosteroids safety and adverse effects in patients with asthma. J. Allergy Clin. Immunol. Pract. 2018, 6, 776–781. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; He, X.-O.; D’Urzo, A. A review on the safety and efficacy of inhaled corticosteroids in the management of asthma. Pulm. Ther. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Kelly, H.W. Comparison of inhaled corticosteroids: An update. Ann. Pharmacother. 2009, 43, 519–527. [Google Scholar] [CrossRef]
- Casale, T.B.; Corbridge, T.; Germain, G.; Laliberté, F.; MacKnight, S.D.; Boudreau, J.; Duh, M.S.; Deb, A. Real-world association between systemic corticosteroid exposure and complications in US patients with severe asthma. Allergy Asthma Clin. Immunol. 2024, 20, 1–13. [Google Scholar] [CrossRef]
- Gaucher, L.; Adda, L.; Séjourné, A.; Joachim, C.; Chaby, G.; Poulet, C.; Liabeuf, S.; Gras-Champel, V.; Masmoudi, K.; Moreira, A. Impact of the corticosteroid indication and administration route on overall survival and the tumor response after immune checkpoint inhibitor initiation. Ther. Adv. Med. Oncol. 2021, 13, 1–18. [Google Scholar] [CrossRef]
- Georgitis, J.W. The 1997 asthma management guidelines and therapeutic issues relating to the treatment of asthma. Chest 1999, 115, 210–217. [Google Scholar] [CrossRef]
- Barnes, P. Effect of corticosteroids on airway hyperresponsiveness. Am. Rev. Respir. Dis. 1990, 141, 70–76. [Google Scholar]
- Derendorf, H. Pharmacokinetic and pharmacodynamic properties of inhaled corticosteroids in relation to efficacy and safety. Respir. Med. 1997, 91, 22–28. [Google Scholar] [CrossRef] [PubMed]
- Wolthers, O.D.; Honour, J.W.; Path, F. Measures of hypothalamic-pituitary-adrenal function in patients with asthma treated with inhaled glucocorticoids: Clinical and research implications. J. Asthma 1999, 36, 477–486. [Google Scholar] [CrossRef] [PubMed]
- Parrow, A.; Larsson, P.; Augustijns, P.; Bergström, C.A. Molecular dynamics simulations on interindividual variability of intestinal fluids: Impact on drug solubilization. Mol. Pharm. 2020, 17, 3837–3844. [Google Scholar] [CrossRef]
- Ortiz-Collazos, S.; Estrada-López, E.D.; Pedreira, A.A.; Picciani, P.H.; Oliveira, O.N., Jr.; Pimentel, A.S. Interaction of levofloxacin with lung surfactant at the air-water interface. Colloids Surf. B Biointerfaces 2017, 158, 689–696. [Google Scholar] [CrossRef]
- Ortiz-Collazos, S.; Picciani, P.H.; Oliveira, O.N., Jr.; Pimentel, A.S.; Edler, K.J. Influence of levofloxacin and clarithromycin on the structure of DPPC monolayers. Biochim. Et Biophys. Acta (BBA)-Biomembr. 2019, 1861, 182994. [Google Scholar] [CrossRef]
- Ingólfsson, H.I.; Lopez, C.A.; Uusitalo, J.J.; de Jong, D.H.; Gopal, S.M.; Periole, X.; Marrink, S.J. The power of coarse graining in biomolecular simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 225–248. [Google Scholar] [CrossRef]
- Saunders, M.G.; Voth, G.A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef]
- Noid, W.G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 090901. [Google Scholar] [CrossRef]
- Voth, G.A. Coarse-Graining of Condensed Phase and Biomolecular Systems; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Souza, P.C.T.; Alessandri, R.; Barnoud, J.; Thallmair, S.; Faustino, I.; Grünewald, F.; Patmanidis, I.; Abdizadeh, H.; Bruininks, B.M.H.; Wassenaar, T.A. Martini 3: A general purpose force field for coarse-grained molecular dynamics. Nat. Methods 2021, 18, 382–388. [Google Scholar] [CrossRef]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef]
- Alessandri, R.; Grünewald, F.; Marrink, S.J. The martini model in materials science. Adv. Mater. 2021, 33, 2008635. [Google Scholar] [CrossRef] [PubMed]
- Alessandri, R.; Souza, P.C.T.; Thallmair, S.; Melo, M.N.; de Vries, A.H.; Marrink, S.J. Pitfalls of the Martini Model. J. Chem. Theory Comput. 2019, 15, 5448–5460. [Google Scholar] [CrossRef] [PubMed]
- Melo, M.; Ingólfsson, H.I.; Marrink, S.J. Parameters for Martini sterols and hopanoids based on a virtual-site description. J. Chem. Phys. 2015, 143, 243152. [Google Scholar] [CrossRef]
- Schmalhorst, P.S.; Deluweit, F.; Scherrers, R.; Heisenberg, C.P.; Sikora, M. Overcoming the Limitations of the MARTINI Force Field in Simulations of Polysaccharides. J. Chem. Theory Comput. 2017, 13, 5039–5053. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; de Vries, A.H.; Marrink, S.-J.; Pastor, R.W. A coarse-grained model for polyethylene oxide and polyethylene glycol: Conformation and hydrodynamics. J. Phys. Chem. B 2009, 113, 13186–13194. [Google Scholar] [CrossRef]
- Uusitalo, J.J.; Ingólfsson, H.I.; Akhshi, P.; Tieleman, D.P.; Marrink, S.J. Martini coarse-grained force field: Extension to DNA. J. Chem. Theory Comput. 2015, 11, 3932–3945. [Google Scholar] [CrossRef]
- Alessandri, R.; Barnoud, J.; Gertsen, A.S.; Patmanidis, I.; De Vries, A.H.; Souza, P.C.; Marrink, S.J. Martini 3 coarse-grained force field: Small molecules. Adv. Theory Simul. 2022, 5, 2100391. [Google Scholar] [CrossRef]
- Islam, M.Z.; Hossain, S.I.; Deplazes, E.; Saha, S.C. The steroid mometasone alters protein containing lung surfactant monolayers in a concentration-dependent manner. J. Mol. Graph. Model. 2022, 111, 108084. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Souza, L.M.; Souza, F.R.; Reynaud, F.; Pimentel, A.S. Tuning the hydrophobicity of a coarse grained model of 1, 2-dipalmitoyl-sn-glycero-3-phosphatidylcholine using the experimental octanol-water partition coefficient. J. Mol. Liq. 2020, 319, 114132. [Google Scholar] [CrossRef]
- Taddese, T.; Carbone, P. Effect of chain length on the partition properties of poly (ethylene oxide): Comparison between MARTINI coarse-grained and atomistic models. J. Phys. Chem. B 2017, 121, 1601–1609. [Google Scholar] [CrossRef]
- DeBolt, S.E.; Kollman, P.A. Investigation of structure, dynamics, and solvation in 1-octanol and its water-saturated solution: Molecular dynamics and free-energy perturbation studies. J. Am. Chem. Soc. 1995, 117, 5316–5340. [Google Scholar] [CrossRef]
- Jaidhan, B.; Rao, P.S.; Apparao, A. Energy minimization and conformation analysis of molecules using steepest descent method. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 3525–3528. [Google Scholar]
- Berendsen, H.J.; Postma, J.V.; van Gunsteren, W.F.; DiNola, A.; Haak, J. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Autilio, C.; Pérez-Gil, J. Understanding the principle biophysics concepts of pulmonary surfactant in health and disease. Arch. Dis. Child.-Fetal Neonatal Ed. 2019, 104, F443–F451. [Google Scholar] [CrossRef]
- Hossain, S.I.; Islam, M.Z.; Saha, S.C.; Deplazes, E. Drug Meets Monolayer: Understanding the Interactions of Sterol Drugs with Models of the Lung Surfactant Monolayer Using Molecular Dynamics Simulations. In Membrane Lipids: Methods and Protocols; Springer: New York, NY, USA, 2022; Volume 2402, pp. 103–121. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Cuendet, M.A.; van Gunsteren, W.F. On the calculation of velocity-dependent properties in molecular dynamics simulations using the leapfrog integration algorithm. J. Chem. Phys. 2007, 127, 184102. [Google Scholar] [CrossRef] [PubMed]
- Hub, J.S.; De Groot, B.L.; Van Der Spoel, D. g_wham-A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another Look at the Jackknife. In Breakthroughs in Statistics, Springer Series in Statistics; Springer: New York, NY, USA, 1992; Volume 2, pp. 569–593. [Google Scholar]
- Islam, M.Z.; Hossain, S.I.; Deplazes, E.; Luo, Z.; Saha, S.C. The concentration-dependent effect of hydrocortisone on the structure of model lung surfactant monolayer by using an in silico approach. RSC Adv. 2022, 12, 33313–33328. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A. Exploring QSAR. Fundamentals and applications in chemistry and biology. ACS Professional Reference Book. Am. Chem. Soc. 1995, 1, 557–1037. [Google Scholar]
- Fornasier, F.; Souza, L.M.; Souza, F.R.; Reynaud, F.; Pimentel, A.S. Lipophilicity of Coarse-Grained Cholesterol Models. J. Chem. Inf. Model. 2020, 60, 569–577. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.R.; Wand, C.R.; Vega, C.; Sanz, E.; Frenkel, D. Calculation of the water-octanol partition coefficient of cholesterol for SPC, TIP3P, and TIP4P water. J. Chem. Phys. 2018, 149, 224501. [Google Scholar] [CrossRef]
- Baluja, S.; Chavda, K.V. Prediction of solubility parameters of cholesterol in some organic solvents. Int. J. Pharm. Chem. Biol. Sci. 2015, 5. [Google Scholar]
- Wishart, D. DrugBank. 2006. Available online: https://go.drugbank.com/drugs/DB00764 (accessed on 15 March 2024).
- Wishart, D. DrugBank. 2006. Available online: https://go.drugbank.com/drugs/DB14512 (accessed on 15 March 2024).
- Tetko, I.V.; Gasteiger, J.; Todeschini, R.; Mauri, A.; Livingstone, D.; Ertl, P.; Palyulin, V.A.; Radchenko, E.V.; Zefirov, N.S.; Makarenko, A.S. Virtual computational chemistry laboratory–design and description. J. Comput. Aided Mol. Des. 2005, 19, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Chem Axon and Chemicalize. Available online: https://chemaxon.com/chemicalize (accessed on 22 April 2021).
- Estrada-López, E.D.; Murce, E.; Franca, M.P.; Pimentel, A.S. Prednisolone adsorption on lung surfactant models: Insights on the formation of nanoaggregates, monolayer collapse and prednisolone spreading. RSC Adv. 2017, 7, 5272–5281. [Google Scholar] [CrossRef]
- Daily, M.D.; Olsen, B.N.; Schlesinger, P.H.; Ory, D.S.; Baker, N.A. Improved coarse-grained modeling of cholesterol-containing lipid bilayers. J. Chem. Theory Comput. 2014, 10, 2137–2150. [Google Scholar] [CrossRef]
- Cleary, G.W.; Zatz, J.L. Interaction of hydrocortisone with model membranes containing phospholipid and cholesterol. J. Pharm. Sci. 1977, 66, 975–980. [Google Scholar] [CrossRef]
- Saad, S.M.; Neumann, A.W.; Acosta, E.J. A dynamic compression–relaxation model for lung surfactants. Colloids Surf. A Physicochem. Eng. Asp. 2010, 354, 34–44. [Google Scholar] [CrossRef]
- Wu, F.; Jin, X.; Guan, Z.; Lin, J.; Cai, C.; Wang, L.; Li, Y.; Lin, S.; Xu, P.; Gao, L. Membrane Nanopores Induced by Nanotoroids via an Insertion and Pore-Forming Pathway. Nano Lett. 2021, 21, 8545–8553. [Google Scholar] [CrossRef]
- Islam, M.Z.; Hossain, S.I.; Deplazes, E.; Saha, S.C. Concentration-dependent cortisone adsorption and interaction with model lung surfactant monolayer. Mol. Simul. 2022, 48, 1627–1638. [Google Scholar] [CrossRef]
- Islam, M.Z.; Krajewska, M.; Hossain, S.I.; Prochaska, K.; Anwar, A.; Deplazes, E.; Saha, S.C. Concentration-Dependent Effect of the Steroid Drug Prednisolone on a Lung Surfactant Monolayer. Langmuir 2022, 38, 4188–4199. [Google Scholar] [CrossRef] [PubMed]
- Majewski, J.; Kuhl, T.L.; Kjaer, K.; Gerstenberg, M.C.; Als-Nielsen, J.; Israelachvili, J.N.; Smith, G.S. X-ray Synchrotron Study of Packing and Protrusions of Polymer−Lipid Monolayers at the Air−Water Interface. J. Am. Chem. Soc. 1998, 120, 1469–1473. [Google Scholar] [CrossRef]
- Carotenuto, A.R.; Nguyen, N.; Cao, K.; Gaffney, A.; Waring, A.J.; Lee, K.Y.C.; Owen, D.; Fraldi, M.; Deseri, L.; Pocivavsek, L. Multiscale geometry and mechanics of lipid monolayer collapse. Curr. Top. Membr. 2021, 87, 1–45. [Google Scholar] [PubMed]
- Gopal, A.; Lee, K.Y.C. Morphology and collapse transitions in binary phospholipid monolayers. J. Phys. Chem. B 2001, 105, 10348–10354. [Google Scholar] [CrossRef]
- Baoukina, S.; Monticelli, L.; Marrink, S.J.; Tieleman, D.P. Pressure–Area Isotherm of a Lipid Monolayer from Molecular Dynamics Simulations. Langmuir 2007, 23, 12617–12623. [Google Scholar] [CrossRef]
- Baoukina, S.; Monticelli, L.; Risselada, H.J.; Marrink, S.J.; Tieleman, D.P. The molecular mechanism of lipid monolayer collapse. Proc. Natl. Acad. Sci. 2008, 105, 10803–10808. [Google Scholar] [CrossRef]
- Souza, F.; Souza, L.; Pimentel, A. Permeation of beta-defensin-3 encapsulated with polyethylene glycol in lung surfactant models at air-water interface. Colloids Surf. B Biointerfaces 2019, 182, 110357. [Google Scholar] [CrossRef] [PubMed]
- Labiris, N.R.; Dolovich, M.B. Pulmonary drug delivery. Part I: Physiological factors affecting therapeutic effectiveness of aerosolized medications. Br. J. Clin. Pharmacol. 2003, 56, 588–599. [Google Scholar] [CrossRef] [PubMed]
- Fadl, A.; Wang, J.; Zhang, Z. Metered-dose inhaler efficiency enhancement: A case study and novel design. Inhal. Toxicol. 2010, 22, 601–609. [Google Scholar] [CrossRef] [PubMed]
- Dolovich, M. New propellant-free technologies under investigation. J. Aerosol. Med. Pulm. Drug Deliv. 1999, 12, 9–17. [Google Scholar] [CrossRef] [PubMed]
- Ochs, M.; Nyengaard, J.R.; Jung, A.; Knudsen, L.; Voigt, M.; Wahlers, T.; Richter, J.; Gundersen, H.J.G. The number of alveoli in the human lung. Am. J. Respir. Crit. Care Med. 2004, 169, 120–124. [Google Scholar] [CrossRef]
- Hyde, D.; Tyler, N.; Putney, L.; Singh, P.; Gundersen, H. Total number and mean size of alveoli in mammalian lung estimated using fractionator sampling and unbiased estimates of the Euler characteristic of alveolar openings. Anat. Rec. Part A Discov. Mol. Cell. Evol. Biol. 2004, 277, 216–226. [Google Scholar] [CrossRef]
- Hess, B. Determining the shear viscosity of model liquids from molecular dynamics simulations. J. Chem. Phys. 2002, 116, 209–217. [Google Scholar] [CrossRef]
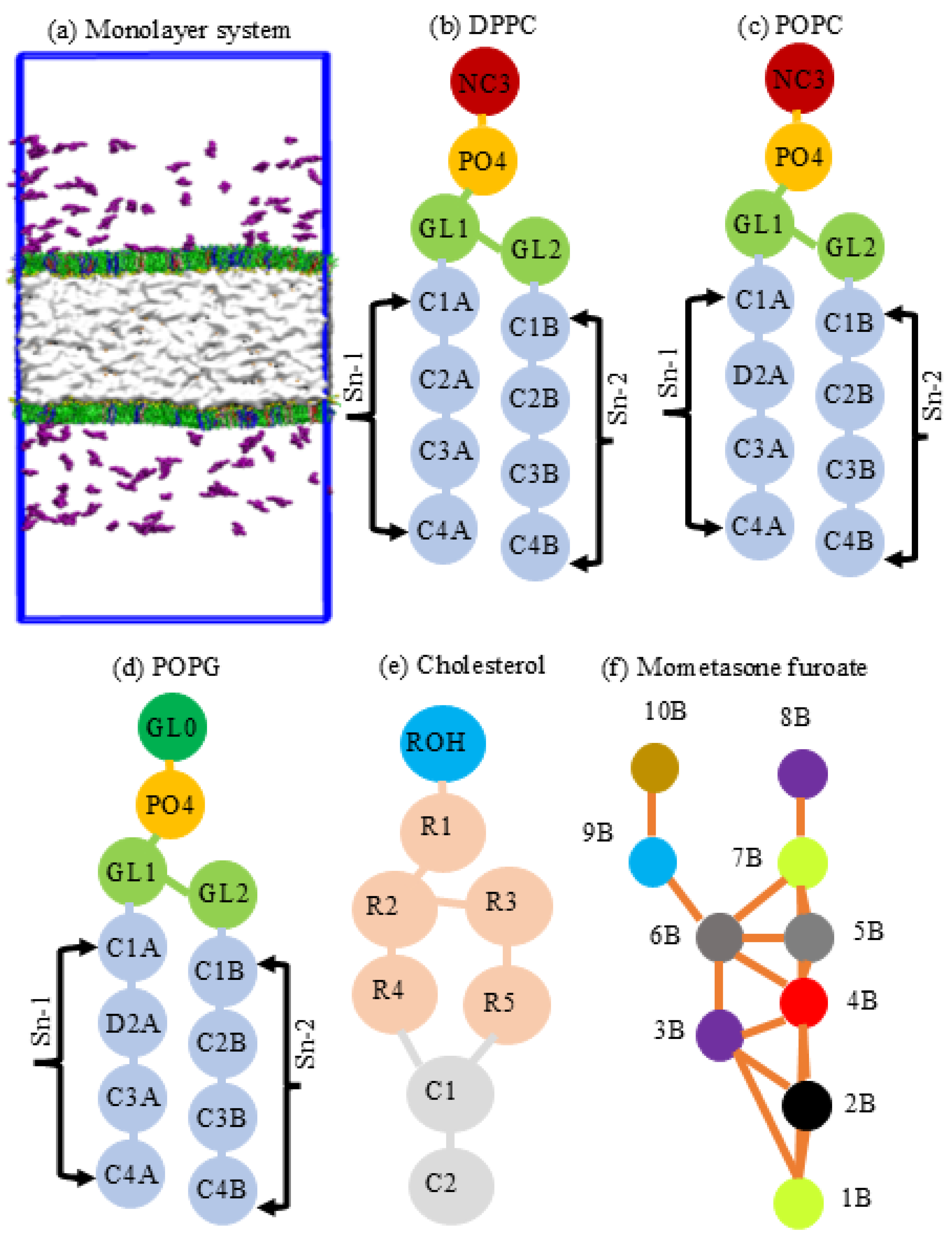
| Bead Name | Molecule Name | Bead Type | Group Moiety |
|---|---|---|---|
| 1B | RO1 | SNa | Cyclic ketone |
| 2B | R1 | SC4 | Cyclic diene |
| 3B | RCL1 | SC3 | Cyclic chloro-alkane |
| 4B | ROH | SP1 | Cyclic alcohol |
| 5B | R2 | SC2 | Cyclic alkane |
| 6B | R3 | SC2 | Cyclic alkane |
| 7B | RO2 | SNa | Cyclic ketone |
| 8B | RCL2 | C3 | Aliphatic chloride |
| 9B | ROO | Na | Aliphatic acetic acid |
| 10B | RO3 | SNa | propanol |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, Z.; Kaysar, K.B.; Hossain, S.; Hossain, A.; Saha, S.C.; Naas, T.T.; Kim, K.-Y. Nano-Biomechanical Analysis of a Corticosteroid Drug for Targeted Delivery into the Alveolar Air—Water Interface Using Molecular Dynamics Simulation. Micro 2025, 5, 44. https://doi.org/10.3390/micro5040044
Islam Z, Kaysar KB, Hossain S, Hossain A, Saha SC, Naas TT, Kim K-Y. Nano-Biomechanical Analysis of a Corticosteroid Drug for Targeted Delivery into the Alveolar Air—Water Interface Using Molecular Dynamics Simulation. Micro. 2025; 5(4):44. https://doi.org/10.3390/micro5040044
Chicago/Turabian StyleIslam, Zohurul, Khalid Bin Kaysar, Shakhawat Hossain, Akram Hossain, Suvash C. Saha, Toufik Tayeb Naas, and Kwang-Yong Kim. 2025. "Nano-Biomechanical Analysis of a Corticosteroid Drug for Targeted Delivery into the Alveolar Air—Water Interface Using Molecular Dynamics Simulation" Micro 5, no. 4: 44. https://doi.org/10.3390/micro5040044
APA StyleIslam, Z., Kaysar, K. B., Hossain, S., Hossain, A., Saha, S. C., Naas, T. T., & Kim, K.-Y. (2025). Nano-Biomechanical Analysis of a Corticosteroid Drug for Targeted Delivery into the Alveolar Air—Water Interface Using Molecular Dynamics Simulation. Micro, 5(4), 44. https://doi.org/10.3390/micro5040044









