Controlled Hydrogen Loading of Magnesium Thin Films in KOH—Effects on the Hydride Nucleation and Growth Regimes

Abstract

In this work, we propose a strategy to optimize electrochemical hydrogen loading in magnesium–palladium thin films, using 5 M KOH as an electrolyte. Mg thin films of thickness 26 nm were deposited on sapphire (0001) substrates and capped by a 32 nm Pd layer. By performing cyclic voltammetry with in situ optical microscopy, it appears that a loading potential of at least −1.2 V vs. Hg/HgO has to be achieved at the sample’s surface to trigger magnesium hydride formation. Loading potential effects are then further explored by hydrogenography, where different hydride formation mechanisms appear based on the actual potential. With a larger loading potential of −1.6 V vs. Hg/HgO, a magnesium hydride blocking layer is formed; in this case, Pd hydride temporarily forms in the capping layer as hydrogen diffuses towards the magnesium layer. Loading is optimized for a lower potential of −1.2 V vs. Hg/HgO, which leads to larger hydride precipitates and delays the blocking layer formation; in this case, Pd hydride only appears after the magnesium layer is completely hydrided.

1. Introduction

Magnesium is considered a superior option for solid-state hydrogen storage due to the high achievable gravimetric density of 7.6 wt.% upon magnesium hydride (MgH₂) formation [1] and because it is an inexpensive and easily available material. Despite these advantages, magnesium possesses significant drawbacks, especially the low diffusivity of hydrogen within the hydride phase [1,2]. This limitation can be partially overcome by employing nanostructured materials. Alongside the mechanical treatment of magnesium as bulk solid and powder [3,4], nanostructured materials can be achieved through thin film technologies, providing improved H kinetics [5], regarding both hydrogen diffusivity and hydride formation. Hence, controlled hydrogen loading in magnesium thin films has been successfully used to study hydrogen’s vertical [6,7,8] and lateral [9] diffusion, to investigate the system’s optical properties [10] and to study hydride formation and growth mechanisms [11,12,13,14,15,16], also in relation to the film’s thickness [17,18].

The Mg-H-phase diagram presents two main stable phases: the α phase corresponding to the solid solution of hydrogen in hcp magnesium, and the hydride-phase MgH₂ with a rutile crystal structure; other crystal structures for MgH₂ can be observed at high pressures [19]. The solubility of hydrogen in $\alpha$-Mg depends on temperature and pressure, but it is generally very low. The highest values are around 0.02 H/Mg and were observed at temperatures close to the Mg melting point [20]. Extrapolating from experimental values measured at 400–600 °C, at room temperature, we can expect a value of ~10⁻⁷ H/Mg [21,22]. However, experimental values may be higher due to the increased solubility at grain boundaries and other lattice defects. Above this very low solubility limit, the rutile hydride-phase MgH₂ forms in equilibrium with the $\alpha$-Mg solid solution. The stability of the hydride phase depends on the temperature and the hydrogen pressure according to the van ‘t Hoff equation [19]:

$$\ln \left({\displaystyle \frac{p_{eq}}{p_0}}\right)={\displaystyle \frac{\mathsf{\Delta }H}{RT}}-{\displaystyle \frac{\mathsf{\Delta }S}{R}}$$

(1)

where $p_{eq}$ is the pressure for hydride decomposition, $T$ is the temperature, $R$ is the gas constant, $\mathsf{\Delta }H$ is the enthalpy of formation and $\mathsf{\Delta }S$ is the entropy of formation. Several values have been calculated for these quantities [20], generally close to $\mathsf{\Delta }H=$ −74.5 kJ/mol and $\mathsf{\Delta }S$= −135 J/mol/K [21].

According to the literature, hydrogen is often introduced in magnesium samples from the gas phase by gradually increasing the gas pressure in a vacuum chamber. Given the small volume of the film compared to the volume of hydrogen introduced in the chamber, this method does not allow us to directly determine the hydrogen concentration in the sample by gravimetry or volumetry [23]. Thus, the hydrogen concentration is usually indirectly estimated, measuring the sample’s optical transmittance by applying the hydrogenography approach or measuring the resistance variation upon hydride formation [24,25]. Additionally, gas loading presents another limitation: by controlling the applied hydrogen pressure, one measures the chemical potential that is required to trigger the onset of hydride formation, but not necessarily the actual chemical potential during hydride growth for a fixed equilibrium hydrogen concentration in the sample. This can be misleading when there are potential barriers to the nucleation of the hydride, which require a higher driving force to initiate hydride formation. Consequently, with gas loading, it might not be possible to measure intermediate steps in the hydride formation, because once the nucleation barrier is surpassed, the whole sample will transform into the hydride phase before reaching an equilibrium condition due to the high availability of hydrogen in the gas atmosphere. Since one increases the applied hydrogen pressure at each loading step, the isotherms will always be inherently but artificially oriented upwards in the plateau region, even if one manages to measure several steps inside the pressure plateau. This is particularly problematic when the effects of hydrogen-induced stress and stress relaxation in thin films are considered, that result in a reduction in the chemical potential at a given hydrogen concentration [26].

Alternatively, electrochemical reactions can be conducted to introduce hydrogen atoms into metal thin films with defined amounts, allowing for a direct determination of the absorbed hydrogen concentration and an independent determination of the chemical potential at equilibrium [23]. Electrochemical loading of magnesium thin films is, however, challenging. Even if a protective Pd capping layer is added, the films tend to be corroded in standard acidic electrolytes such as Glycerin and Phosphoric acid [12]. Therefore, a different electrolyte has to be used: one alternative is 5 M or 6M KOH. While this electrolyte has been used in the past [9,13,27,28], its advantages and limitations are not yet studied. Recent studies on electrochemical hydrogenation relate to Mg-containing alloys for hydrogen storage and battery materials [29,30,31,32,33,34,35,36,37,38,39,40,41,42]. In these studies, the electrodes are not thin films but compressed powders, and the main focus is on the effect of different compositions of the alloying elements and different catalytic materials on hydrogen storage and kinetics.

This work explores the electrochemical boundary conditions and proposes routes to optimize the hydrogen loading in magnesium thin films in a 5 M KOH electrolyte. The main focus is to understand how controlled hydrogen loading can be achieved and to explore the advantages and disadvantages of the method, also in comparison with the more established gas-phase hydrogen loading method. With this purpose, cyclic voltammetry was combined with in situ optical microscopy and hydrogenography experiments on Mg-Pd thin films. The impact of different loading conditions on hydride nucleation and growth is addressed.

2. Materials and Methods

2.1. Sample Preparation

Magnesium thin films with a thickness of 26 nm were deposited on 1 cm² sapphire (0001) substrates by cathode argon–ion-beam sputtering. The magnesium layers were always covered with a palladium layer of 32 nm thickness, to prevent oxidation and to enhance hydrogen absorption. As previously introduced, the film thickness was chosen to benefit from faster hydrogenation kinetics and to allow the complete hydrogenation of the sample in a reasonable time frame. The layer thickness was calculated from the deposition time, by knowing the sputter rate for the different target materials. The sputter rate was quantified by depositing reference samples and measuring their thickness by X-ray reflectometry (XRR). The films are uniformly thick, given the small area of the substrate compared to the sputter cone. TEM investigations on Mg-Pd thin films deposited in similar conditions revealed a columnar grain microstructure with fiber texture [11]. The deposition system worked in ultra-high vacuum conditions, with a background pressure of $\sim 1\cdot {10}^{-10} \mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. The argon pressure during sputtering was $1.3\cdot {10}^{-4} \mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$, and the argon gas had a purity of 99.9999%. A low background pressure is necessary to avoid oxidation of the Mg layer during deposition; for the same reason, the magnesium and palladium targets could be alternated during the deposition without breaking the vacuum conditions. In addition, the magnesium target was eroded for 3 h before depositing the samples to remove the oxide layer that can form over time even in an ultra-high vacuum.

2.2. Hydrogenography

Hydrogen was loaded in the samples via electrochemical reactions in 5 M KOH, using an electrochemical cell in the three-electrode geometry, as shown in Figure 1a. Before loading, the electrolyte was bubbled with argon gas (purity 99.9999%) for 30 min to reduce its O₂ content. The sample acted as the working electrode (WE) and it was in direct contact with the electrolyte only through the Pd surface, exposing a circular area of $50 \mathrm{m}{\mathrm{m}}^2$. A platinum counter electrode (CE) of area $1 \mathrm{c}{\mathrm{m}}^2$ was connected to a voltage generator (Keithley 2601 SYSTEM Source Meter, Cleveland, OH, USA) to control the voltage at the sample’s surface. The voltage source was used in combination with a digital timer (company WEG, Jaraguá do Sul, Brazil) to create voltage steps in the electrolyte; during each loading step, H was adsorbed at the sample’s surface, which acts as a cathode. In subsequent steps, hydrogen diffused inside the sample to create a Mg-H solid solution and MgH₂. The potential at the sample’s surface was read and recorded against a Sensortechnik Meinsberg Hg/HgO reference electrode (RE) connected to a DAQ board (IOtech PersonalDaq/56, Spectrum Instrumentation, Grosshansdorf, Germany).

The potential at the sample’s surface is especially relevant because—once the equilibrium hydrogen distribution at a given H concentration is reached in the sample—it coincides with Nernst potential. The measured equilibrium potential $E_{eq}$ can, therefore, be converted into an equivalent hydrogen equilibrium pressure (the one that appears in Equation (1)), according to [27,43]:

$$E_{eq}\left(\mathrm{H}\mathrm{g}/\mathrm{H}\mathrm{g}\mathrm{O}\right)=-{\displaystyle \frac{RT}{nF}}\ln \left({\displaystyle \frac{p_{eq}}{p_0}}\right)-0.0592\cdot \mathrm{p}\mathrm{H}-E^0\left(\mathrm{H}\mathrm{g}/\mathrm{H}\mathrm{g}\mathrm{O}\right)=-{\displaystyle \frac{RT}{nF}}\ln \left({\displaystyle \frac{p_{eq}}{p_0}}\right)-0.954$$

(2)

where $n$ is the number of electrons involved in the hydrogen evolution reaction. In the rightmost equality we have used the present experimental data, i.e., $pH=14.70$ and $E^0\left(\mathrm{H}\mathrm{g}/\mathrm{H}\mathrm{g}\mathrm{O}\right)=0.085 \mathrm{V}$. According to this equation, we can expect an equilibrium potential of −0.78 V for magnesium hydride decomposition and of −0.89 V for palladium hydride decomposition.

The optical part of the setup, necessary for hydrogenography, is shown in Figure 1b. An optical Leica DM 2700 M microscope in transmission mode measured the optical transmittance $T$ of the sample, whose logarithm is proportional to the hydrogen concentration inside the sample according to Lambert–Beer’s law [25,44]:

$$\mathsf{\Delta } c_H={\displaystyle \frac{1}{\mathsf{ϵ}\mathrm{d}}} \mathrm{l}\mathrm{o}\mathrm{g}\left({\displaystyle \frac{T}{T_M}}\right)$$

(3)

where $d$ is the film’s thickness, $ϵ$ is the extinction coefficient and the transmittance $T$ after each loading step is compared to the initial value $T_M$ of the metal. The microscope is equipped with a white light source for transmittance measurement (LED LH113). Images of the films were acquired before each loading step and the recorded transmittance was compared to the initial value. Combining this information with the equilibrium potential reached after each loading step, which is proportional to the hydrogen chemical potential, the formation of magnesium hydride and its lateral distribution in the films can be observed by constructing isotherms. According to Equation (3), the optical transmittance change is mainly related to the formation of the hydride phase in magnesium. Because of the very low solubility of hydrogen in magnesium, the optical effect of the solid solution phase can be disregarded. With respect to the layered arrangement of the sample, hydride formation in the palladium layer also affects the optical transmittance. Both palladium and magnesium become more transparent to visible light with increasing hydrogen content [45], and, thus, their optical transmission images become brighter.

A batch of samples was studied by hydrogenography, changing the loading potential between −1.2 V and −1.6 V.

2.3. Cyclic Voltammetry

Cyclic voltammetry measurements with in situ optical microscopy were performed on the Mg-Pd films using a Gamry Interface 1010B potentiostat and the same electrochemical cell and optical setup employed for hydrogenography (see Figure 1). The potential was scanned at 20 mV/s between 0 and −1.5 V. The starting point was set at −0.2 V, corresponding to the open-circuit potential of the cell.

Using this technique, one can identify oxidation (reduction) electrochemical reactions that occur at the sample’s surface on increasing (decreasing) applied potential, giving rise to anodic (cathodic) current peaks.

3. Results

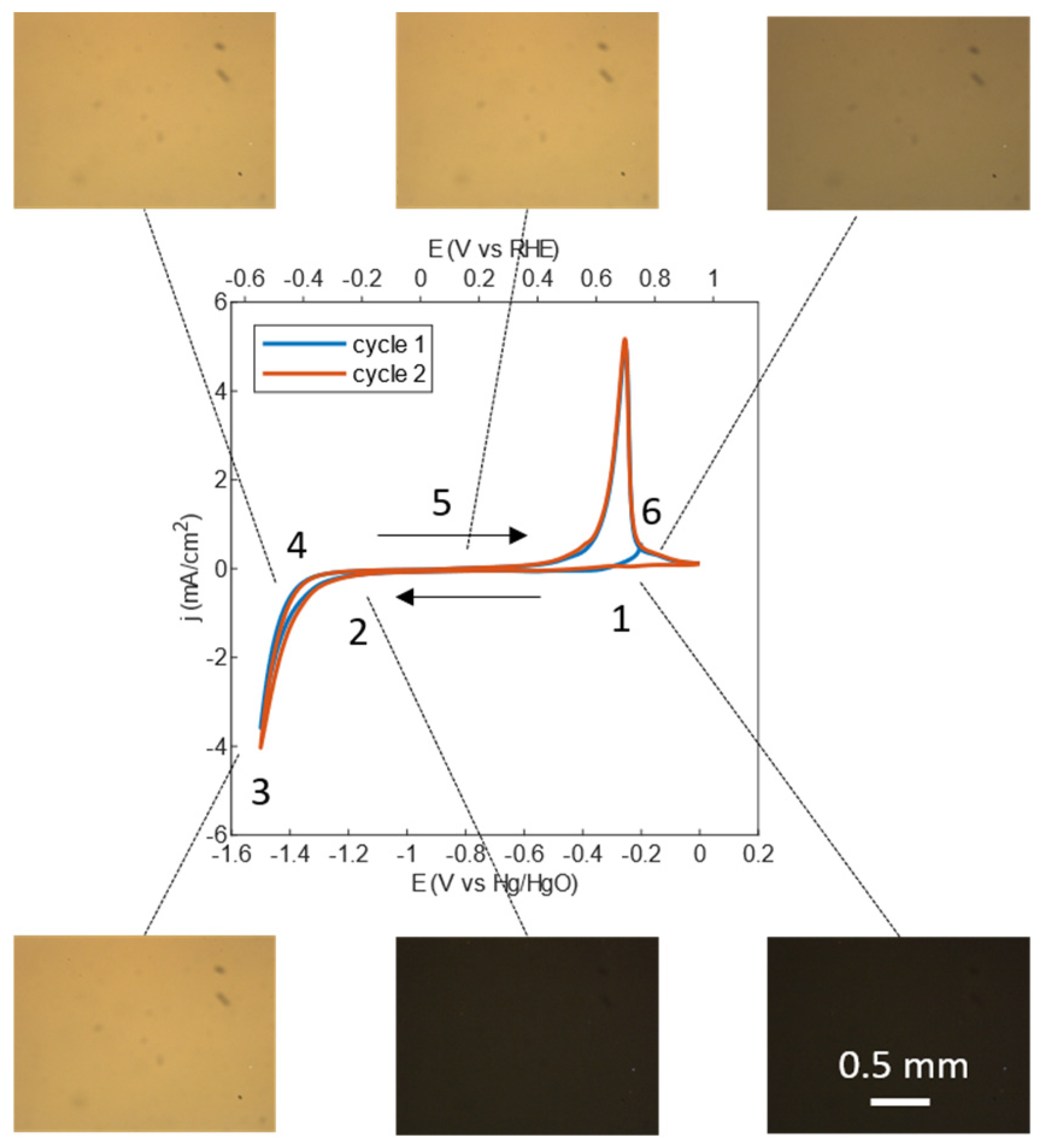
3.1. Cyclic Voltammetry Combined with In Situ Optical Microscopy

To optimize the electrochemical hydrogen loading of Pd-Mg thin films in 5 M KOH, we first needed to understand which electrochemical reactions take place at the sample’s surface and how they are related to the applied driving potential.

Figure 2 reports the CV results for an exemplary 32 nm Pd/26 nm Mg thin film along with optical images of the film. In total, two loading–unloading cycles were performed, and no exfoliation or detachment of the film was observed. The two voltammetry cycles in Figure 2 overlap. A cathodic current peak is observed for potentials below −1.2 V vs. Hg/HgO: this indicates a reduction reaction at the sample surface. This reaction is identified with ${\mathrm{P}\mathrm{d}+\mathrm{x}\mathrm{H}}_2\mathrm{O}+\mathrm{x}{\mathrm{e}}^{-}\to \mathrm{x}\mathrm{O}{\mathrm{H}}^{-}+\mathrm{P}\mathrm{d}{\mathrm{H}}_{\mathrm{x}}$, leading to water splitting and hydrogen absorption in the uppermost Pd layer [13,28]. Part of this hydrogen then diffuses inside the sample to create Mg hydride, as is confirmed by the recorded optical images becoming brighter (panels 2 $\to$ 3 of Figure 2, as opposed to the constant transmittance in panels 1 $\to$ 2). A brighter image is associated with a more transparent sample, which is an expected consequence of the metal-to-insulator transition related to Mg hydride formation. While scanning from −1.5 V to 0 V, the hydride is at first stable, as we can deduce from the constant optical transmittance in Figure 2, panels 4 $\to$ 5. A peak of anodic current appears between −0.4 and −0.2 V vs. Hg/HgO, indicating an oxidation reaction at the sample surface. This reaction is identified with water formation at the sample surface, according to $\mathrm{y}\mathrm{O}{\mathrm{H}}^{-}+\mathrm{P}\mathrm{d}{\mathrm{H}}_{\mathrm{x}}\to \mathrm{P}\mathrm{d}{\mathrm{H}}_{\mathrm{x}-\mathrm{y}}+\mathrm{y}{\mathrm{H}}_2\mathrm{O}+{\mathrm{y}\mathrm{e}}^{-}$ [13]. This reaction leads to H desorption from the sample surface, which is accompanied by the decomposition of part of the Mg hydride, as is confirmed by the decreasing optical transmittance in Figure 2, panels 5 $\to$ 6. It is worth noticing that in these conditions, KOH is not directly employed in the reactions for hydrogen production, which only involve splitting and the formation of water molecules. Excluding the changes described above, which are related to hydride formation and decomposition, the measured optical transmittance was constant within the forward and backward scan of both voltammetry cycles. After the first dehydrogenation, the transmittance did not return to the value for metallic magnesium because a fraction of the magnesium hydride was not decomposed in the short time scale of the experiment.

With a relatively fast scan rate of 20 mV/s, we have to apply an overpotential of at least −1.2 V vs. Hg/HgO to trigger hydrogen absorption and, consequently, hydride formation. A similar (or higher) overpotential was applied in hydrogenography experiments to achieve fast hydrogen absorption during short loading pulses of 5 s.

3.2. Potential Curves and Hydride Formation

Figure 3 shows the behavior of the potential measured against Hg/HgO during and after two different loading pulses, together with the film’s transmission images. Different loading conditions were tested, changing the applied potential between −1.2 V and −1.6 V. Here, representative results are reported, corresponding to the lowest and the highest applied potentials. The smallest value of −1.2 V was chosen based on the cyclic voltammetry results. The largest value of −1.6 V was chosen to minimize the formation of hydrogen bubbles at the sample’s surface. In fact, when a too-large potential is applied, not all the produced hydrogen can be absorbed by the sample, and part of it recombines, forming H₂ molecules and, consequently, hydrogen bubbles at the sample’s surface.

While the applied potential is different, the pulse duration in both cases is 5 s. The highlighted peaks in Figure 3 correspond to the time interval in which the external potential is applied directly between the sample and the counter electrode. Therefore, the measured potential, in this case, includes an overpotential that drives hydrogen absorption according to the reaction introduced in Section 3.1. After the voltage source is switched off, the potential (sometimes also referred to as electromotive force or EMF [46,47,48]) decreases with a different shape depending on the achieved loading potential. Figure 3a shows that a smaller loading potential of −1.2 V vs. Hg/HgO causes an exponential relaxation curve, while a larger loading potential of −1.6 V vs. Hg/HgO is related to a curve with two plateaus (Figure 3b). As will be shown in the following paragraph, these different shapes of the potential curves and different appearances of the film’s surface can be related to different hydride formation mechanisms.

Hydrogen absorption in the film is revealed by its optical transmission images becoming brighter after each loading step, as shown in Figure 3c,d. A brighter picture indicates that the film’s optical transmittance increases, as is expected as a consequence of MgH₂ formation (see Equation (3)). Figure 4 shows an example of a recorded equilibrium potential (EMF)–optical transmittance isotherm for 32 nm Pd/26 nm Mg films, which was constructed using 5 s loading steps at −1.2 V vs. Hg/HgO and at −1.6 V vs. Hg/HgO. We observe two potential plateaus in the curves: the first one is related to the formation of MgH₂ and the second one is related to the formation of PdH_x. As the loading curves are not expected to become completely flat for this type of sample, the equilibrium potential is approximated by taking the potential value after 10 min from the loading pulse. This results in apparently higher potential values for the sample loaded with −1.6 V pulses, because of the longer time necessary to achieve an equilibrium condition. To exclude electrolyte-related effects on the optical transmittance, caused, for example, by the interaction between the thin films and the K+ cations at the cathode, the results for electrochemical loading were compared to those of gas-phase loading at 1 mbar H₂ pressure. Both methods reveal a similar change in optical transmittance upon hydride formation, suggesting that possible optical effects related to the chosen electrolyte are minor compared to the transmittance changes caused by Mg and Pd hydride formation.

At first glance, this isotherm provides similar information to the pressure–transmission isotherms that are usually measured by the gas-phase loading of hydrogen in magnesium–palladium thin films. However, as stated in the introduction and detailed in the following paragraph, the potential curves recorded during each loading step convey more information than just the final plateau potential used to construct isotherms.

The measured potentials of −0.31 V and −0.35 V for magnesium hydride formation and −0.45 V for palladium hydride formation differ significantly from the ones calculated from Equation (2), respectively −0.78 V and −0.89 V. Even though the distance between the magnesium and palladium hydride plateaus is consistent with previous results [27], the measured equilibrium potentials are shifted upward by 0.45 V with respect to the expected values. This shift can be explained by oxygen gas dissolved in the electrolyte. In the presence of oxygen, the reactions previously introduced for hydrogen loading and unloading (see Section 3.1) are accompanied by a second redox system, namely ${\mathrm{O}}_2+2{\mathrm{H}}_2\mathrm{O}+4{\mathrm{e}}^{-}\leftrightarrow 4{\mathrm{O}\mathrm{H}}^{-}$ [49], whose equilibrium potential is +0.28 V vs. Hg/HgO in 5 M KOH. As a consequence, under open-circuit conditions, the measured potential is shifted upward with respect to the genuine equilibrium potential of the metal–hydrogen system [49]. Hence, this effect needs to be addressed and possibly avoided. To reduce the oxygen content, the electrolyte is usually bubbled with argon gas before and during hydrogen loading [49].

In this work, the electrolyte was only bubbled before the experiment because of the peculiar geometry of the hydrogenography cell. In fact, to combine electrochemical and optical measurements, the sample has to lie flat on top of the cell so that it can be observed with the optical microscope. Therefore, if the electrolyte were bubbled during hydrogen loading, argon bubbles would collect at the sample’s surface and interfere with the experiment. It is also important to notice that the potential shift caused by oxygen gas is maximum in open-circuit conditions, and it was reported to vanish when an oxidation or reduction current is present at the working electrode [49], as was the case during the loading steps and the cyclic voltammetry experiments. Regarding cyclic voltammetry, the shorter duration of the experiments, which were performed immediately after the bubbling of the electrolyte, also minimizes oxygen effects.

3.3. Dependence of the Potential Curves on the Loading Potential

The previous paragraph showed that the potential curves during Mg hydride formation exhibit different shapes based on the potential applied during the loading step (Figure 3). These effects are independent of the observed EMF shifts due to oxygen in the electrolyte. The different behaviors are accompanied by different optical appearances of the films during Mg hydride formation. Indeed, when a potential of −1.6 V vs. Hg/HgO is achieved during the loading step, the measured curve exhibits two plateaus during the relaxation to equilibrium (Figure 3b). The first plateau is observed around −0.45 V, the potential associated with Pd hydride formation in the presence of oxygen in the electrolyte. This loading potential is also linked to a spatially homogeneous variation in the brightness of the recorded images, indicating that the hydride precipitates are smaller than the microscope’s resolution limit of $2.11 \mathsf{\mu }\mathrm{m}$ (Figure 3d). With a smaller potential of −1.2 V vs. Hg/HgO during the loading step, the measured potential relaxed directly to the final equilibrium value of −0.32 V (Figure 3a), corresponding to MgH₂ formation. With this lower potential, some of the hydride precipitates were large enough to be observed with the optical microscope (Figure 3c).

We pointed out that the first plateau in Figure 3b is centered at the same potential of −0.45 V vs. Hg/HgO observed during Pd hydride formation (see Figure 4). Hence, it might be linked to H residing in the Pd layer during the process of equilibration of the H distribution in the sample and to intermediate Pd hydride formation. More details about hydride formation mechanisms and their relation to the applied loading potential will be introduced in the Discussion Section.

4. Discussion

Figure 3 shows how different loading potentials are related to different shapes of the EMF curves and different appearances of the film during hydride formation. A schematic representation of the proposed hydride formation mechanism for the two different loading potentials is shown in Figure 5.

For the larger loading potential of −1.6 V vs. Hg/HgO (Figure 5a), a first temporary plateau appears around −0.45 V, the potential value associated with the palladium hydride formation in our loading cell. This indicates that palladium hydride is briefly formed in the Pd capping layer, which is directly in contact with the electrolyte, before H atoms can diffuse into the Mg layer to create MgH₂. As MgH₂ is thermodynamically more stable than the Pd hydride, and as the amount of H atoms is limited, the Pd hydride has to decompose for MgH₂ to form.

The stability of the temporarily formed Pd hydride can also be enhanced by the presence of a MgH₂ blocking layer [11,12,50] at the interface between magnesium and palladium, hindering the diffusion of H atoms into the Mg layer. Hence, the formation of Pd hydride and the MgH₂ blocking layer are coupled processes triggered by the large driving force of H supplied to the sample.

In thin films, MgH₂ usually nucleates starting from the Mg-Pd interface [11,12,50]. The blocking effect occurs once MgH₂ completely covers the interface, because hydrogen diffusion is much slower in this phase compared to $\alpha$-Mg. In fact, the H diffusivity in MgH₂ was reported to be $D_H^{Mg{H}_2}=1.1\cdot {10}^{-20} {\mathrm{m}}^2 {\mathrm{s}}^{-1}$ at 305 K [51], while for the $\alpha$ phase, we expect values around ${10}^{-10}–{10}^{-11} {\mathrm{m}}^2{\mathrm{s}}^{-1}$ at room temperature [52,53,54].

As shown in previous works [12], the formation of a blocking layer depends on the driving force for hydride nucleation, which is proportional to the introduced H concentration step and, therefore, to the applied loading potential. In fact, the hydride nucleation site density depends on the driving force for nucleation, as illustrated in Figure 3. For the high potential of −1.6 V vs. Hg/HgO, the hydride nucleation site density is very high, thereby leading to coalescence of hydride nuclei and blocking layer formation. In this case, individual hydride domains cannot be distinguished in the optical transmission image (Figure 3d), and a homogeneous increase in transparency is observed. However, the blocking layer can be observed in Figure 3d because of the (final) lighter optical transmission image, and by the presence of the transient Pd hydride in the EMF curve. On the other hand, for a smaller driving force of −1.2 V vs. Hg/HgO, a low number density of hydride nuclei forms; these nuclei grow to larger half-spherical particles, separated by the remaining α-Mg-H phase. In this case, the formation of the blocking layer is delayed as it will take longer for the low-number-density hydride nuclei to finally coalesce and form a continuous layer, as represented in Figure 5b. In the meantime, H can still diffuse through the $\alpha$-Mg regions in between the hydride precipitates, resulting in a higher global diffusivity. This behavior is confirmed by the optical images showing large bright dots for the lower loading potential (Figure 3c). According to Lambert–Beer’s law (Equation (3)), this is due to a higher local H concentration and, because of the strong contrast, to MgH₂ precipitates. The mean MgH₂ precipitate diameter follows a lognormal distribution with an average value of $\left(5.98\pm 0.04\right) \mathsf{\mu }\mathrm{m}$. In line with this interpretation, the EMF curve no longer exhibits a Pd hydride plateau at −0.45 V for the lower loading voltage, since the hydrogen directly diffuses into the Mg layer.

Thus, the loading potential difference of ΔE = 0.4 V has drastic influences on the hydride precipitate distribution and the blocking layer formation in the Mg film, as they switch the MgH₂ growth mode from growth-controlled to nucleation-controlled.

After these considerations, the advantages of electrochemical loading in KOH, e.g., compared to gas-phase loading, become apparent. The first advantage is the possibility of measuring the potential at the sample’s surface in the time window that goes from the loading voltage pulse to the final equilibrium EMF for a fixed H concentration: in this sequence, the recorded EMF curves convey information on the actual thermodynamic path the system treads during hydride formation. Secondly, this path can be influenced by tuning the potential applied during the loading steps. In fact, it is shown that magnesium hydride formation can be optimized by reducing the applied voltage, and thus avoiding the formation of a MgH₂ blocking layer.

Despite these advantages, electrochemical loading of Mg thin films in 5 M KOH has some limitations. The main one is that not all the hydrogen created at the sample’s surface is eventually absorbed by the sample. Part of this hydrogen will desorb from the surface, creating H₂ bubbles, and, therefore, introducing an error in the calculated H concentration. The amount of desorbed H₂ depends on the induced concentration step at the sample’s surface; therefore, it can also be influenced by the loading voltage and time. In general, short pulses with a low loading potential will introduce a smaller error in the calculated H concentration. The second disadvantage is the error in the measured potentials introduced by oxygen dissolved in the electrolyte. This effect can be partially solved by electrolyte bubbling before and during hydrogen loading, but as shown above, that might not always be possible for every experimental setup.

In total, combining information from hydrogenography and cyclic voltammetry measurements, we are able to determine the optimal potential for fast electrochemical hydrogen loading in 5 M KOH. The experiments have shown that the optimal loading potential needs to be high enough to start the electrochemical reaction leading to H adsorption on the sample’s surface (see Figure 2). This sets a minimum potential value of about E = −1.2 V, to be achieved between the sample and Hg/HgO reference electrode by applying a proper voltage between the sample and platinum counter electrode. At the same time, the achieved potential needs to be low enough to limit the hydrogen supply to the sample and to delay the formation of a magnesium hydride blocking layer, so that one can benefit from a faster H diffusion regime for the longest time possible. Hence, there is a narrow range of loading potentials around −1.2 V vs. Hg/HgO for optimum loading conditions, in 5 M KOH. This method should be employed in the future to find the optimal loading voltage for different electrolytes.

5. Conclusions

In this study, we propose a way to optimize the electrochemical hydrogen loading of magnesium thin films in a 5 M KOH electrolyte. The first step consists of combining cyclic voltammetry measurements with in situ optical microscopy to identify the minimum potential vs. Hg/HgO that should be applied to introduce hydrogen into the sample. Given this constraint, the optimal potential value can be identified by observing the EMF curves during hydrogen absorption in the subsequent open-circuit condition. In this case, the formation of the hydride phase was optimized by lowering the applied potential and, therefore, avoiding the formation of a Mg hydride blocking layer.

This optimization process is not possible for the gas-phase loading method, as it relies on the main advantages offered by electrochemical loading in KOH, namely the following:

-

The ability to closely follow the time evolution of the chemical potential within each loading step, by measuring the EMF at the thin film sample’s surface. This is impossible to do with gas-phase loading and, as shown in this paper, carries information on the behavior of the system during hydride formation.

-

The ability to influence the behavior of the system within each loading step by acting on the applied loading voltage. It is here demonstrated how magnesium hydride formation can be optimized by choosing the appropriate loading voltage.

This combined method can be used to optimize the loading conditions for hydrogen storage systems based on MgH₂. A similar method may also be extended to other electrolytes and to other metals whose optical transmittance changes upon hydride formation, such as yttrium, lanthanum and other rare earth elements [55,56].