Electrochemical Characterization of Nanoporous Alumina-Based Membranes with Different Structure and Geometrical Parameters by Membrane Potential Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Membrane Potential Measurements
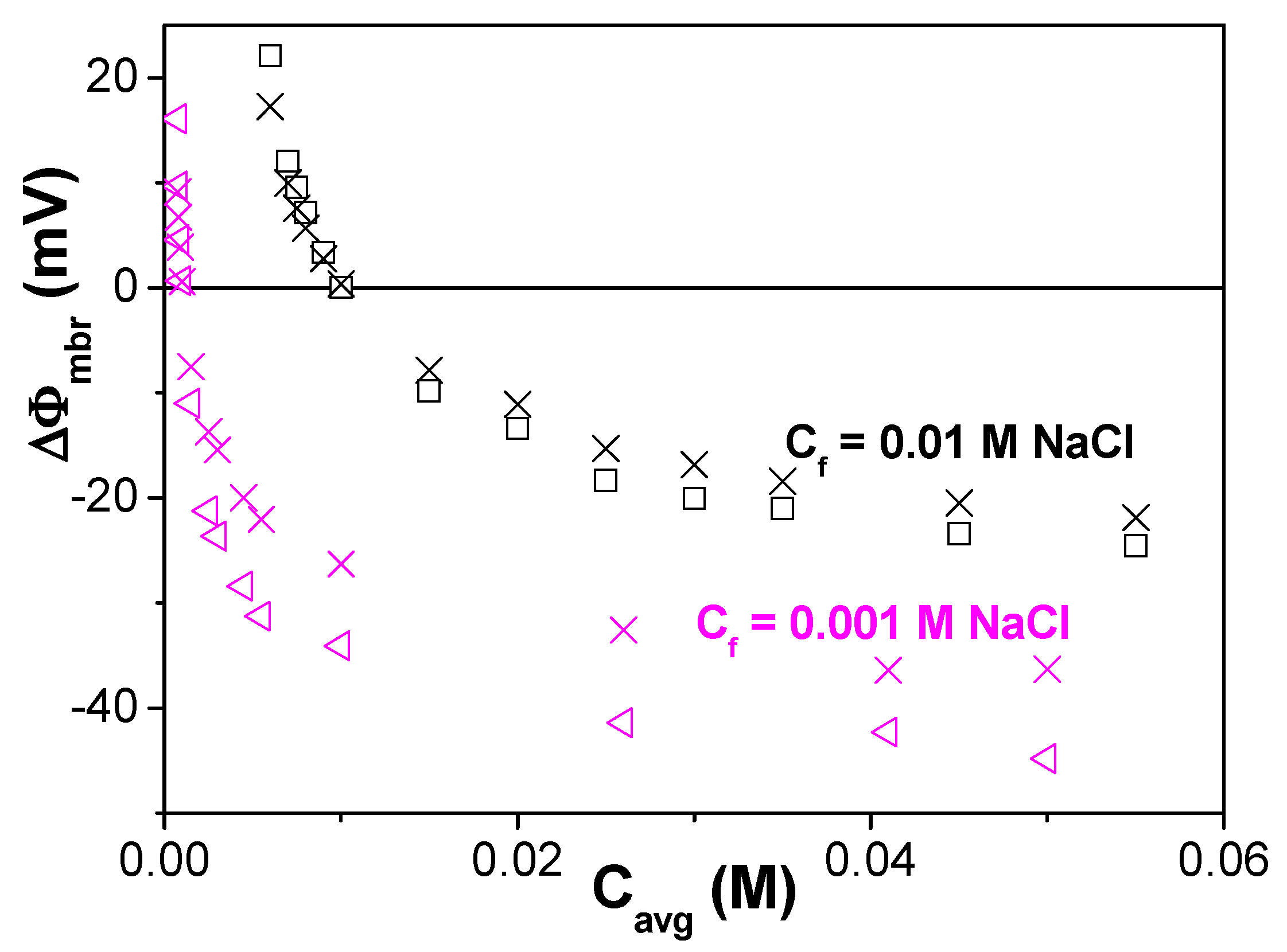
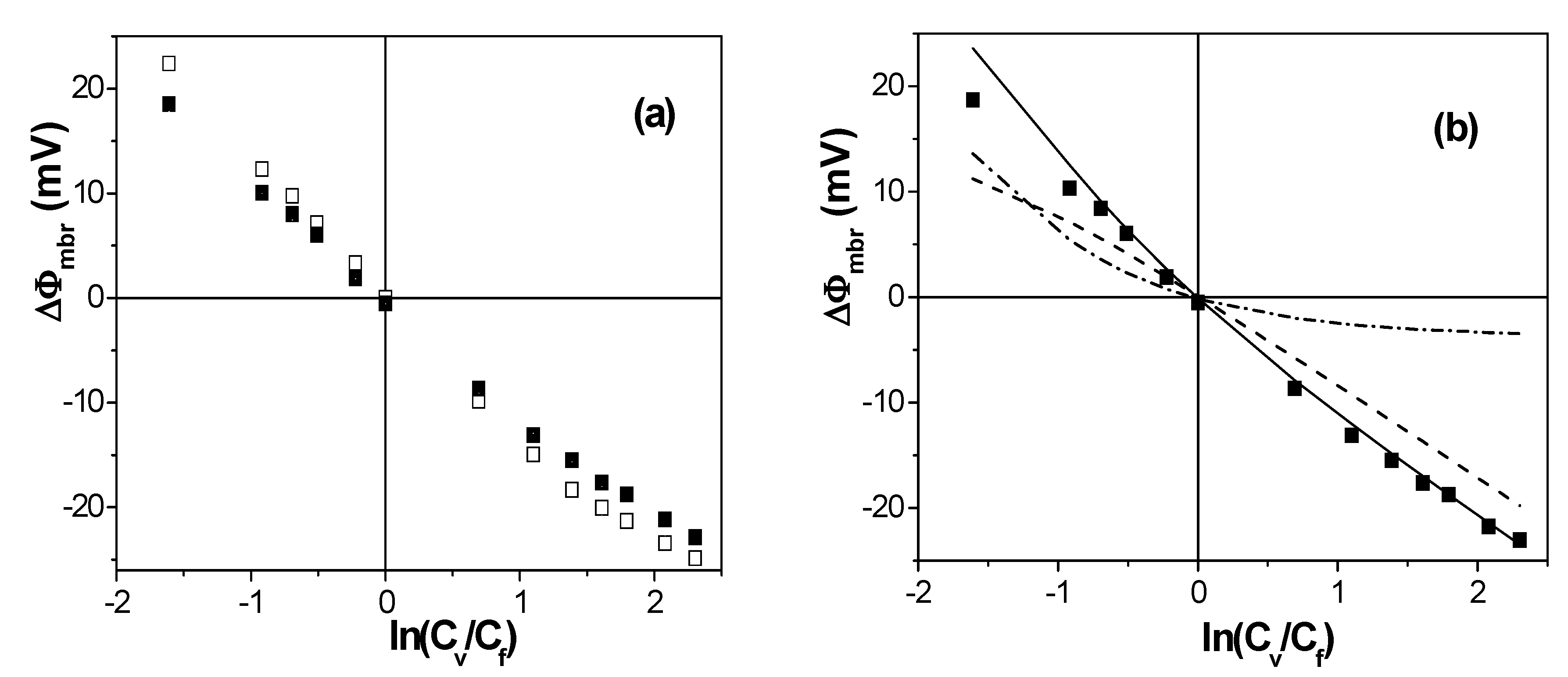
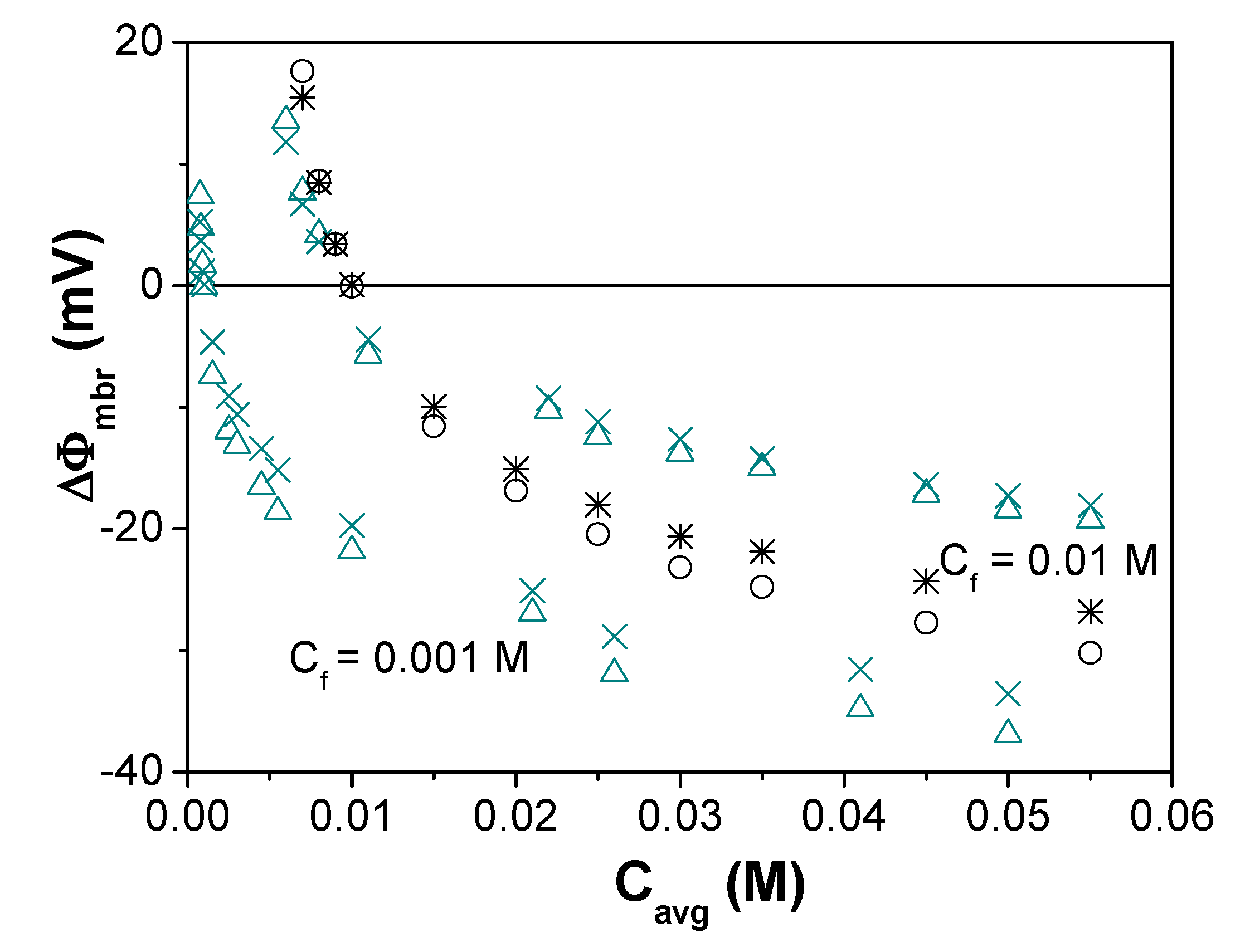
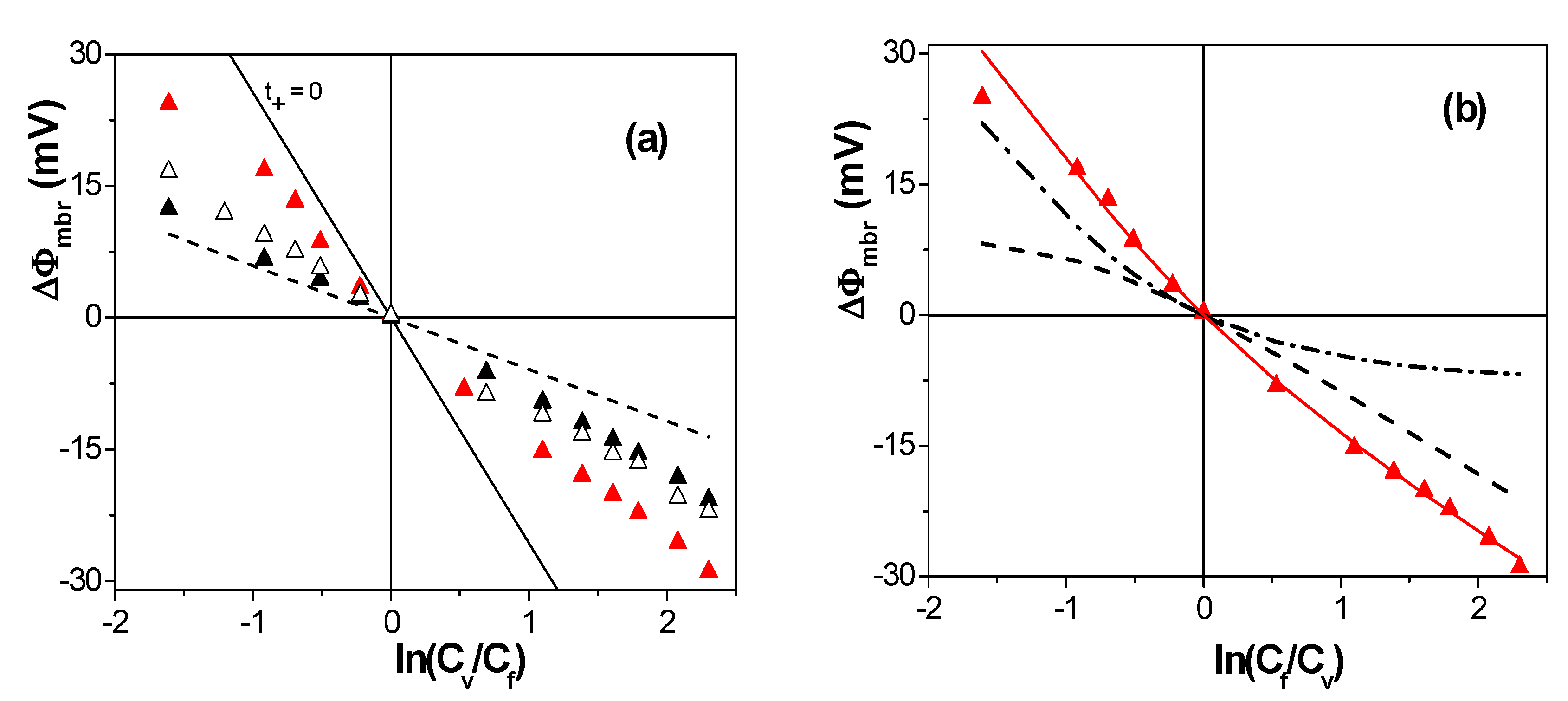
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bhave, R.R. Inorganic Membranes: Synthesis, Characteristics and Applications; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Ren, C.; Fang, H.; Gu, J.; Winnubst, L.; Chen, C. Preparation and characterization of hydropobic alumina planar membranes for water desalination. J. Europ. Cer. Soc. 2015, 35, 723–730. [Google Scholar] [CrossRef]
- Fraga, M.C.; Sanches, S.; Pereira, V.J.; Crespo, J.G.; Yuan, L.; Marcher, J.; Mártinez de Yuso, M.V.; Rodríguez-Castellón, E.; Benavente, J. Morphological, chemical surface and filtration characterization of a new silicom carbide membrane. J. Europ. Ceramic Soc. 2017, 37, 899–905. [Google Scholar] [CrossRef]
- Fard, A.K.; McKay, G.; Buekenhoudt, A.; Al Sulaiti, H.; Motmans, F.; Khraisheh, M.; Atieh, M. Inorganic Membranes: Preparation and Application for Water Treatment and Desalination. Materials 2018, 11, 74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedfort, G.; Zydney, A.L. The behaviour of suspensions and macromolecular solutions in crossflow microfiltration. J. Membr. Sci. 1996, 96, 1–58. [Google Scholar] [CrossRef]
- Tin, M.M.M.; Anioke, G.; Nakagoe, O.; Tanabe, S.; Kodamatani, H.; Nghiem, L.D.; Fujioka, T. Membrane fouling, chemical cleaning and separation performance assessment of a chlorine-resistant nanofiltration membrane for water recycling applications, Sep. Purif. Technol. 2017, 189, 170–175. [Google Scholar] [CrossRef] [Green Version]
- Masuda, H.; Fukuda, K. Ordered metal nanohole arrays made by a two-step replication of honeycomb structures of anodic alumina. Science 1995, 268, 1466–1468. [Google Scholar] [CrossRef] [PubMed]
- Voigt, K.; Heubner, C.; Lämmel, C.; Schneider, M.; Michaelis, A. Facile fabrication of nanostructured alumina membranes. Micropor. Mesopor. Mat. 2020, 302, 110207. [Google Scholar] [CrossRef]
- Ruíz-Clavijo, A.; Caballero-Calero, O.; Martín-González, M. Revisiting anodic alumina templates: From fabrication to applications. Nanoscale 2021, 13, 2227–2265. [Google Scholar] [CrossRef]
- Martín, R.; Manzano, C.V.; Martín-González, M. In-depth study of self-ordered porous alumina in the 140–400 nm pore diameter range. Micropor. Mesopor. Mat. 2012, 151, 311–316. [Google Scholar] [CrossRef]
- Holbein, J.; Steinhart, M.; Schiene-Fisher, C.; Benda, A.; Hof, M.; Hübner, C.G. Confined diffusion in ordered nanoporous alumina membranes. Small 2007, 3, 385–390. [Google Scholar] [CrossRef]
- Jiang, X.; Mishra, N.; Turner, J.N.; Spencer, M.G. Diffusivity of sub-1000 Da molecules in 40 299 nm silicon-based alumina membranes. Microfluid Nanofluid 2008, 5, 695–701. [Google Scholar] [CrossRef]
- Bluhm, E.A.; Schroeder, N.C.; Bauer, E.; Fife, J.N.; Chamberlin, R.M.; Abney, K.D.; Young, J.S.; Jarvinen, G.D. Surface Effects on Metal Ion Transport across Porous Alumina Membranes. 2. Trivalent Cations: Am, Tb, Eu, and Fe. Langmuir 2000, 16, 7056–7060. [Google Scholar] [CrossRef]
- Porta-i-Batalla, M.; Xifré-Pérez, E.; Eckstein, C.; Ferré-Borrull, J.; Marsal, L.F. 3D Nanoporous Anodic Alumina Structures for Sustained Drug Release. Nanomaterials 2017, 7, 227. [Google Scholar] [CrossRef] [PubMed]
- Law, C.S.; Lim, S.Y.; Abell, A.D.; Voelcker, N.H.; Santos, A. Nanoporous Anodic Alumina Photonic Crystals for Optical Chemo- and Biosensing: Fundamentals, Advances, and Perspectives. Nanomaterials 2018, 8, 788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weber, M.; Julbe, A.; Ayral, A.; Miele, P.; Bechelany, M. Atomic Layer Deposition for Membranes: Basics, Challenges, and Opportunities. Chem. Mater. 2018, 30, 7368–7390. [Google Scholar] [CrossRef]
- Cuevas, A.L.; Martínez de Yuso, M.V.; Vega, V.; González, A.S.; Prida, V.M.; Benavente, J. Influence of ALD Coating Layers on the Optical Properties of Nanoporous Alumina-Based Structures. Coatings 2019, 9, 43. [Google Scholar] [CrossRef] [Green Version]
- Petukhov, D.I.; Napolskii, K.S.; Eliseev, A.A. Permeability of anodic alumina membranes with branched channels. Nanotechnology 2012, 23, 335601. [Google Scholar] [CrossRef]
- Kumeria, T.; Santos, A.; Losic, D. Nanoporous anodic alumina platforms: Engineered surface chemistry and structure for optical sensing applications. Sensors 2014, 14, 11878–11918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, W.; Xu, Y.; Zhang, M.; Sun, P. A Nanoporous Alumina Membrane Based Electrochemical Biosensor for Histamine Determination with Biofunctionalized Magnetic Nanoparticles Concentration and Signal Amplification. Sensors 2016, 16, 1767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumeria, T.; Santos, A. Sensing and Biosensing Applications of Nanoporous Anodic Alumina. In Electrochemically Engineered Nanoporous Materials; Springer Series in Materials Science; Losic, D., Santos, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; p. 220. [Google Scholar] [CrossRef]
- Pol, L.; Acosta, K.; Ferré-Borrill, J.; Marsal, L.F. Aptamer-Based Nanoporous Anodic Alumina Interferometric Biosensor for Real-Time Thrombin Detection. Sensors 2019, 19, 4543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pol, L.; Eckstein, C.; Acosta, K.; Xifré-Pérez, E.; Ferré-Borrill, J.; Marsal, L.F. Real-time monitoring of biotinylated molecules detection dynamics in nanoporous anodic alumina for bio-sensing. Nanomaterials 2019, 9, 478. [Google Scholar] [CrossRef] [Green Version]
- Vera, R.; Gelde, L.; Anticó, E.; Martínez de Yuso, M.V.; Benavente, J.; Fontàs, C. Tuning physicochemical, electrochemical and transport characteristics of polymer inclusion membrane by varying the counter-anion of the ionic liquid Aliquat 336. J. Membr. Sci. 2017, 529, 87–94. [Google Scholar] [CrossRef]
- Benavente, J.; Romero, V.; Vázquez, M.I.; Anticó, E.; Fontàs, C. Electrochemical Characterization of a Polymer Inclusion Membrane Made of Cellulose Triacetate and Aliquat and Its Application to Sulfonamides separation. Separation 2018, 5, 5. [Google Scholar] [CrossRef] [Green Version]
- Algarra, M.; Cuevas, A.L.; Martínez de Yuso, M.D.V.; Benavente, J. Insights into the formation of an emissive CdTe-quantum-dots/cellulose hybrid film. J. Colloid Interface Sci. 2020, 579, 714–722. [Google Scholar] [CrossRef]
- Cañas, A.; Ariza, M.J.; Benavente, J. Characterization of active and porous sublayers of a composite reverse osmosis membrane by impedance spectroscopy, streaming and membrane potentials, salt diffusion and X-ray photoelectron spectroscopy. J. Membr. Sci. 2001, 183, 135–146. [Google Scholar] [CrossRef]
- Gelde, L.; Cuevas, A.L.; Benavente, J. Influence of pore-size/porosity on ion´s transport and static BSA-fouling for TiO2-covered nanoporous alumina membranes. Appl. Sci. 2021, 11, 5687. [Google Scholar] [CrossRef]
- González, A.S.; Vega, V.; Cuevas, A.L.; Martínez de Yuso, M.V.; Prida, V.M.; Benavente, J. Surface Modification of Nanoporous Anodic Alumina during Self-Catalytic Atomic Layer Deposition of Silicon Dioxide from (3-Aminopropyl)Triethoxysilane. Materials 2021, 14, 5052. [Google Scholar] [CrossRef] [PubMed]
- Benavente, J.; Jonsson, G. Effect of adsorption of charged macromolecules on streaming and membrane potential values measured with a microporous polysulfone membrane. Sep. Sci. Technol. 1997, 32, 1699–1710. [Google Scholar] [CrossRef]
- Benavente, J. Electrical characterization of membranes. In Monitoring and Visualizing Membrane-Based Processes; Güell, C., Ferrando, M., López, F., Eds.; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Liu, J.; Xiong, J.; Ju, X.; Gao, B.; Wang, L.; Sillanpää, M. Streaming potential for identification of foulants adsorption on PVDF membrane surface. J. Membr. Sci. 2018, 566, 428–434. [Google Scholar] [CrossRef]
- Teorell, T. Transport phenomena in membranes. Discuss. Faraday Soc. 1956, 21, 9–26. [Google Scholar] [CrossRef]
- Meyer, K.H.; Sievers, J.F. La perméabilité des membranes I. Théorie de la perméabilité ionique. Helv. Chim. Acta 1936, 19, 649–664. [Google Scholar] [CrossRef]
- Vázquez, M.I.; Romero, V.; Benavente, J.; Romero, R.; Hierrezuelo, J.; López-Romero, J.M.; Contreras-Cáceres, R. Characterization and stability of a bioactivated alumina nanomembrane for application in flow devices. Micropor. Mesopor. Mat. 2016, 226, 88–93. [Google Scholar] [CrossRef]
- Augustin, S.; Hennige, V.; Hörpel, G.; Hying, C. Ceramic but flexible: New ceramic membranes foils for fuel cells and batteries. Desalination 2002, 146, 23–28. [Google Scholar] [CrossRef]
- Romero, V.; Vega, V.; García, J.; Zierold, R.; Nielsch, K.; Prida, V.M.; Hernando, B.; Benavente, J. Changes in morphology and ionic transport induced by ALD SiO2 coating of nanoporous 309 alumina membranes. ACS Appl. Mater. Interfaces 2013, 5, 3556–3564. [Google Scholar] [CrossRef] [PubMed]
- Peláez, L.; Vázquez, M.I.; Benavente, J. Interfacial and fouling effects on diffusional permeability across a composite ceramic membrane. Ceramics Int. 2010, 36, 797–801. [Google Scholar] [CrossRef]
- Lakshminarayanaiah, N. Transport Phenomena in Membranes; Academic Press Inc.: New York, NY, USA, 1970; ISBN 9780124342507. [Google Scholar]
- Vázquez, M.I.; de Lara, R.; Benavente, J. Characterization of two microporous ceramic membranes with different geometrical parameters: Effect of protein adsorption on electrochemical parameters. J. Europ. Cer. Soc. 2007, 27, 4245–4250. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed.; Dover Publications, Incorporated: Mineola, NY, USA, 2012. [Google Scholar]
- Cuevas, A.L.; González, A.S.; Vega, V.; Prida, V.M.; Benavente, J. Optical and Electrochemical Characterization of Nanoporous Alumina Structures: Pore Size, Porosity, and Structure Effect. Appl. Sci. 2020, 10, 4864. [Google Scholar] [CrossRef]



| Membrane | Xef (M) | t+ | t− | Fit Error | P(-)% |
|---|---|---|---|---|---|
| CRF25 | +4.4 × 10−3 | 0.312 | 0.688 | 7.4% | 18.9 |
| CRF100 | +1.3 × 10−3 | 0.338 | 0.662 | 8.4% | 12.2 |
| CRF25(f) | +3.0 × 10−3 | 0.328 | 0.672 | 8.6% | 14.8 |
| Membrane | Xef (M) | t+ | t− | Fit Error | P(-)% |
|---|---|---|---|---|---|
| Sfw-NPAM | +6.5 × 10−3 | 0.287 | 0.713 | 3.1% | 25.5 |
| And-NPAM | +1.3 × 10−3 | 0.347 | 0.653 | 5.8% | 9.9 |
| And/BSA-NPAM | +0.3 × 10−3 | 0.338 | 0.662 | 6.8% | 12.2 |
| And/Theo1-NPAM | +5.8 × 10−3 | 0.310 | 0.670 | 5.4% | 19.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero, V.; Benavente, J. Electrochemical Characterization of Nanoporous Alumina-Based Membranes with Different Structure and Geometrical Parameters by Membrane Potential Analysis. Micro 2022, 2, 475-487. https://doi.org/10.3390/micro2030029
Romero V, Benavente J. Electrochemical Characterization of Nanoporous Alumina-Based Membranes with Different Structure and Geometrical Parameters by Membrane Potential Analysis. Micro. 2022; 2(3):475-487. https://doi.org/10.3390/micro2030029
Chicago/Turabian StyleRomero, Virginia, and Juana Benavente. 2022. "Electrochemical Characterization of Nanoporous Alumina-Based Membranes with Different Structure and Geometrical Parameters by Membrane Potential Analysis" Micro 2, no. 3: 475-487. https://doi.org/10.3390/micro2030029
APA StyleRomero, V., & Benavente, J. (2022). Electrochemical Characterization of Nanoporous Alumina-Based Membranes with Different Structure and Geometrical Parameters by Membrane Potential Analysis. Micro, 2(3), 475-487. https://doi.org/10.3390/micro2030029





