Abstract
This article presents a mini-review of the available data on the thermodynamics of the complexation of amino acids and peptides with some nucleic bases in a buffer medium. Data on changes in thermodynamic parameters (binding constants, Gibbs energy, enthalpy, entropy) during the complexation of nucleic bases with amino acids and peptides as a function of physicochemical properties are given at T = 298.15 K. The effects of complexation on the volumetric properties of nucleic bases, including apparent molar volumes, standard molar volumes, and limiting molar expansibility, over a temperature range of 288.15 to 313.15 K are considered in detail. Differences in the behavior of amino acids and peptides caused by different modes of coordination with nucleic bases are noted. These manifest in the stoichiometry of the formed complexes, the relationship with the acid dissociation constants of carboxyl and amino groups, enthalpy–entropy compensation in the complexation process, the temperature dependence of the transfer volumes, and the effect of hydrophobicity on volumetric characteristics.
1. Introduction
Interactions among proteins and nucleic acids (as well as between their fragments) underlie many biological processes, including viral peptide capsid interactions with cells and DNA within cell nuclei. The clarification of the mechanism and patterns of such interactions provides insight into fundamental biological processes at the molecular level. In addition, the clarification of the mechanisms of inhibition of these interactions is of practical interest for the development of therapeutic agents with increased specificity for viruses.
Both experimental and theoretical research methods are widely used to study the mechanisms of such processes. Experimental results have an advantage over computer modeling data, as they fully consider solvation effects and the transformations that occur due to intermolecular interactions in liquid media. Variations in solvation effects may include changes in the packing density of the hydration shells of solutes, the creation and destruction of H-bonds between solute and water molecules, and solvent electrostriction and its alteration due to the movement of water molecules from hydration shells into the bulk of the solvent, resulting from the overlapping of the hydration shells of solutes. The theoretical modeling of these interactions provides information on the reaction centers that ensure interaction and the structure of the resulting complexes. This is very valuable information, but it is clearly insufficient to identify patterns in interactions depending on the chemical structure. To establish patterns, it is convenient to use specially chosen series of biomolecule fragments with controlled changes in composition and structure: for proteins—amino acids and peptides; for nucleic acids—nucleic acid bases. In the present work, we adopted a thermodynamic approach for the analysis of the patterns of interaction of peptides with nucleic acid bases in aqueous solution based on the generalization of available data on the thermodynamic parameters of multicomponent systems containing these reagents. Necessary data on the ionic state of peptides and amino acids, as well as available data on the structures of the resulting complexes, are also used to correctly interpret changes in thermodynamic quantities.
2. Description of Datasets
This work summarizes data obtained previously via calorimetry and UV spectroscopy in [1,2,3,4,5,6] on the thermodynamic parameters of the complex formation of uracil and cytosine with heterocyclic amino acids (histidine, His; phenylalanine, Phe; tryptophan, Trp) and peptides (L-alanyl-L-alanine, AlaAla; glycyl-glycine, GlyGly; glycyl-L-tyrosine, GlyTyr; L-alanyl-L-tyrosine, AlaTyr; glycyl-L-phenylalanine, GlyPhe; L-alanyl-L-glutamine, AlaGln; glycyl-L-glutamic acid, GlyGlu; γ-L-glutamyl-L-cysteinyl-glycine, γ-GluCysGly) in a phosphate buffer (pH = 7.4) at T = 298.15 K. The apparent molar volume values [7,8,9,10,11] obtained from the density measurements taken using a DMA 5000 M density meter (Anton Paar, Graz, Austria) attested the complex formation in these systems. Different pH values are achieved in aqueous solutions when different amino acids/peptides dissolve in water. The use of a buffer solvent prevents shifts in the equilibrium of the ionic forms and tautomers of the studied solutes and ensures the correct analysis of the behavior of amino acids/peptides or nucleic bases under conditions of a constant pH = 7.4, in contrast to aqueous solutions that are characterized by varying pH values.
3. Results and Discussion
3.1. Characterization of Ionic State of Amino Acids and Peptides in Solution
Amino acids and peptides exist in aqueous solution in ionized forms due to hydrolysis and acid dissociation processes. These solutes contain sites capable of dissociation and protonation. These include carboxyl and amino groups, imidazole fragments, and hydroxyl groups, which can be located in the main backbone or in the side chains of the molecules. The dissolution of these solutes is accompanied by a significant change in the acidity of the medium. Moreover, varying the concentration of the solution from 0 to 0.1 mol kg−1 can cause a change in the pH value of up to 1.0 unit and redistribute the ionic forms of the amino acid/peptide. Therefore, the interpretation of the molar partial thermodynamic properties of such solutions becomes uncertain.
The aqueous solutions of different amino acids/peptides have different pH indices. To standardize data, studies of the amino acid/peptide interactions with other molecules should carried out in an aqueous buffer solution at a fixed pH value, usually at pH = 7.4.
In the works [1,2,3,4,12,13,14,15,16], the distribution of amino acid/peptide ionic forms coexisting in water at different pH values was calculated. Table 1 summarizes the data obtained for the studied substances in aqueous solutions at pH = 7.4. Some details of the calculations of the data in Table 1 are included in the Supplementary Materials (Supplemental Information). As can be seen, the zwitterion +HL− is the dominant form of most amino acids/peptides, except for the compounds whose molecules contain the acid-active side groups, such as the carboxyl group in the Glu residue and the imidazole fragment in the His residue. It can be noted that the fraction of zwitterions decreases when going from monomeric amino acids to peptides.

Table 1.
Mole fractions of ion forms of amino acids and peptides in an aqueous solution at pH = 7.4 and T = 298.15 K.
Two important conclusions follow from the above. First, the experiments with amino acids/peptides must be performed in a buffered medium, and the buffer solution is considered an aqueous solvent. Secondarily, the interactions of the dominant ionic forms of amino acids/peptides and the nucleobases molecules should be considered primarily among other solute–co-solute interactions in the buffer solution.
3.2. Thermochemical Quantities of Amino Acids and Peptides in Water and Aqueous Buffers
The dependence of the ionic state of amino acids/peptides on the medium acidity leads to the differences in the enthalpies of dissolution of the solutes in water, ΔsolHmw, and in aqueous buffer solution at a fixed pH value, ΔsolHmbuffer. A comparison of ΔsolHmw and ΔsolHmbuffer values has been made in a number of studies [12,14,17]. It is known that amino acids and peptides exist in crystals as zwitterions [18], and zwitterions, anions, and cations can coexist in a water medium, as shown above. The balance of several contributions determines the value of the enthalpy of dissolution of the crystalline substances ΔsolHm:
- in the pure waterin an aqueous buffer mediumwhere ΔsolvHw is the enthalpy of the zwitterionic form solvation in water; Σ(α·ΔintH1) is the sum of the enthalpies of protonation–deprotonation of acid-active groups with the formation of other ionic forms of the amino acid/peptide, and α is the fraction of the forms, which depends on the pH of the solution; ΔintH2 is the enthalpy of amino acid/peptide–electrolyte ion interaction; and ΔsubH is the enthalpy of lattice destruction (sublimation enthalpy). If the measurements are carried out in the same buffer with a constant pH and the ionic strength of the solution, the contribution Σ(α·ΔintH1) remains constant for each amino acid/peptide.
The dissolution enthalpy of a solute in a buffer contains the additional contributions of Σ(α·ΔintH1) and ΔintH2 compared to the dissolution enthalpy in pure water. The process of the zwitterions deprotonation was found to make the greatest contribution to change in the dissolution enthalpy of the solute in the buffer. As shown in Table 1, a significant fraction of the anionic form of the peptides is present in the buffer at a fixed pH = 7.4, whereas this form is absent in aqueous solution, where only the zwitterionic species are present. The contribution of Σ(α × ΔintH1) to the dissolution enthalpy of peptides in the buffer was estimated using the enthalpies of acid dissociation of the NH3+ group of peptides, ΔdisH2, taken from [19,20,21,22], and the values of the fraction of the formed anionic form of peptides, α2 (Table 1), according to the ratio:
For example, the following contributions have been calculated for GlyGly
(α·ΔintH1) = α2·ΔdisH2 = 0.11·44.3 = 4.9 kJ mol−1;
Σ(α·ΔintH1) = α2·ΔdisH2 = 0.16·42.9 = 6.9 kJ mol−1;
Σ(α·ΔintH1) = α2·ΔdisH2 = 0.05·40.76 = 2.03 kJ mol−1.
The calculated contributions Σ(α·ΔintH1) satisfactorily describe the differences between the dissolution enthalpies of a solute in water and buffer solution: (11.84 and 16.5) kJ mol−1 for GlyGly; (21.9 and 27.88) kJ mol−1 for GlyTyr [12]; (21.2 and 22.71) kJ mol−1 for Asn [17].
Thus, in most cases, the dissolution of peptide/amino acids in an aqueous buffer is accompanied by a greater endothermic effect than in water due to the significant contribution of the acid dissociation of the NH3+ group of solutes in a buffer with pH = 7.4. The electric forces of interactions between the peptide/amino acid ionic forms and the Na+, K+, Cl−, H2PO4−, and HPO42− ions of buffer give a small exothermic contribution to ΔsolHmbuffer and lead to a decrease in the endothermic effect. This trend results from the data on the enthalpic coefficients of the pairwise interaction of individual amino acids with electrolytes [23].
When the nucleic base (NB), as a co-solute, is added to the buffer solution, the dissolution enthalpy of an amino acid/peptide in the solvent (NB + buffer) can be expressed as
ΔintH3 is the enthalpy of the amino acid/peptide–NB interaction.
In the expression for the enthalpy of the transfer of an amino acid/peptide, defined as the difference in the values of ΔsolHmbuffer and ΔsolHmbuffer+NB, the contributions Σ(α∙ΔintH1), ΔintH2 and ΔsubH disappear. Thus, the enthalpy of transfer is a thermochemical characteristic of the interaction of a solute with a co-solute
But the contribution ΔintH3 takes different values in water and buffer media due to the change in the proportion of zwitterionic and anionic forms of the solute. The transfer enthalpy is proportional to the enthalpy of the complex formation (ΔrH), and Equation (4) can be rewritten as
where αr is the degree of amino acid/peptide conversion (i.e., the fraction of the bound amino acid/peptide in complex), which depends on the complexation constant (log Kr) [24,25]. As shown in works [1,2,3,4,5,6], the concentration dependences of ΔtrHm values displayed a non-linear character in (amino acid/peptide–NB–buffer) systems. Apparently, the observed regularity of changes in ΔtrHm vs. m plots for ternary systems can be associated with the effect of complex formation in the solutions studied. The HEAT program package for any models of binding stoichiometry [24] was used to find the thermodynamic parameters of the complex formation.
3.3. Structural Approach to Complex Formation of Amino Acids and Peptides with Nucleic Bases
The complex formation of amino acids and peptides with nucleic bases has been confirmed by the computer simulation methods in a number of studies, in which the structure of the resulting complexes has been analyzed. The structures of the pyrimidine nucleic bases with the numbering of reaction centers in heterocycles are shown in Figure 1.
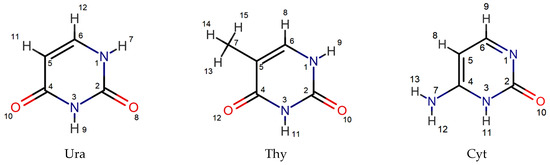
Figure 1.
Structures of pyrimidine nucleic bases: uracil (Ura), thymine (Thy), and cytosine (Cyt).
Hunter K.C. et al. [26] showed the possibility of H-bonding of O2(O4) and HN3 centers of the uracil with OH, S, COOH and amide groups of the monomeric amino acids. In the works of Dąbkowska I. et al. [27,28,29], the carboxyl group of amino acids is indicated as the site of H-bonding with uracil and thymine. Moreover, the hydrogen bonds with the HN1 and O2 centers of the nucleic base are more favorable than with the HN3 and O4 centers. Alkorta I. and Elguero J. [30] studied the interaction of some nucleobases with the short molecule of the formiglycinamide as a model of the protein backbone. It was noted that the CO and HN amide fragments of the model molecule can be involved in H-bonding with the NH2 and N moieties of nucleobases. In the studies reviewed, the amino acids were generally regarded in a neutral molecular form, which is capable of forming two H-bonds with a nucleic acid base.
In the study of [31], the structures of complexes formed by ionized peptides with nucleic bases of the pyrimidine series were studied. The ionized forms of peptides corresponded to their dominant states in a neutral aqueous solution at pH = 7.4. In the peptides, the terminal charged groups move away from each other due to the chain elongation, and, consequently, they may act as polydentate ligands, unlike the amino acids. The charged amino and carboxylate groups at the backbone ends and in the side chains, as well as the polar amide pieces in the middle of the chain, can serve as hydrogen-bonding centers. Thus, all the studies reviewed led to the conclusion that the complexes of amino acids and peptides with nucleic bases are stabilized by intermolecular hydrogen bonds. The hydrogen bond lengths are within 1.573–1.735 Å. As recent research has shown [32], the strongest H-bonds are formed by nucleobases with the carboxylate group of peptides; the energies of hydrogen bonds calculated by using the correlation with the electron density at bond critical points are from −36.22 to −40.91 kJ mol−1. It has been shown that amino and amide groups are capable of forming hydrogen bonds, the energies of which take smaller absolute values: (−30.69 to −21.06 kJ mol−1 for bonds with the NH3+ group, and −25.96 to −17.79 kJ mol−1 for bonds with the amide NH group).
The stacking or π-π interaction can occur between the nucleic base cycles and the amino acids and peptides containing a side aromatic fragment in the structure [33,34,35]. In this case, the stacking competes with the hydrogen-bonding effect, since the favorable orientations of the molecules of the peptide and the nucleic base for these types of interactions are not the same. The simultaneous implementation of both hydrogen bonding and the stacking effect was established in the alanyl–tyrosine complex with cytosine [31].
3.4. Thermodynamics of Complex Formation Between Amino Acids and Nucleic Bases in Aqueous Buffer Solutions
The available thermodynamic parameters [3,4,5] of the complex formation of aromatic amino acids with uracil at pH = 7.4 are summarized in Table 2 at temperature T = 298.15 K. Taking into consideration the low concentrations of the reagents in solutions and the non-electrolyte nature of organic compounds, it is reasonable to assume that such experimental conditions for the complexation reaction are similar to the standard ones at standard temperature T = 298.15 K and pressure P = 0.1 MPa. Under these conditions, the amino acids took the form of a zwitterion. The composition of the amino acid/uracil complexes was found to be 1:2. The complex formation in a buffer medium is the exothermic process in all the above cases. According the data in [36], the comlexation of tryptophan with uracil is accompanied by a smaller exothermic effect in the water (−3.5 kJ mol−1) than in the phosphate buffer (−22.7 kJ mol−1). An increase in the negative ΔrG0 values in the Trp→Phe→His sequence is accompanied by an increase in the exothermic effect (ΔrH0 < 0) and a decrease in the positive entropy. The changes in the enthalpy and entropy compensate each other, as shown in Figure 2.

Table 2.
Thermodynamic parameters of complex formation of amino acids and peptides with nucleic bases in a phosphate buffer medium with pH = 7.4 at 298.15 K and P = 0.1 MPa.
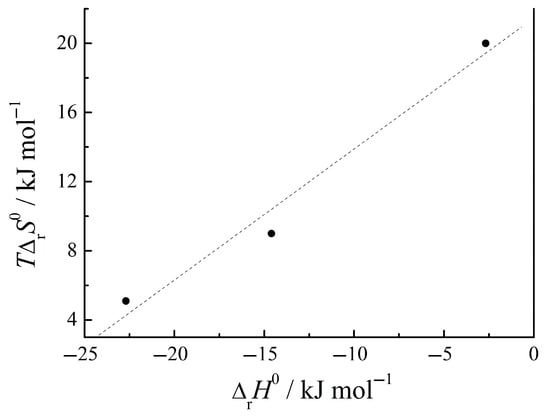
Figure 2.
Enthalpy–entropy compensation in complex formation of Ura with heterocyclic amino acids (Trp, Phe, His) in buffer solution (T = 298.15 K).
The relationship between the thermodynamic parameters of complexation and the acid–base properties of amino acids offers the opportunity to clarify the role of electronic effects or proton-donor properties in the interaction of the uracil with the aromatic amino acids. The dissociation constants K°1 and K°2 (pK = −log K, at 298.15 K and zero ionic strength I = 0) [37] depend on the electron density of O and N atoms in the donor groups of COOH and NH3+ located in the molecules of an amino acid. Increasing the electron density of the O-atom lowers the dissociation constant of the carboxyl group of the amino acid (increase in pK value), thereby promoting the ionized COO- group to act as a hydrogen bond acceptor. At the same time, the ability of the NH3+ group of the amino acid to donate a proton may decrease when the electron density of the N-atom rises. This trend determines changes in the thermodynamic parameters of complexation (stability constants, thermal effects) through the above groups. The manifestation of the regular dependence of changes in the Gibbs energy, enthalpy and entropy in the reaction on the dissociation constants of the COOH group in amino acid molecules, pK°1, is demonstrated in Figure 3.
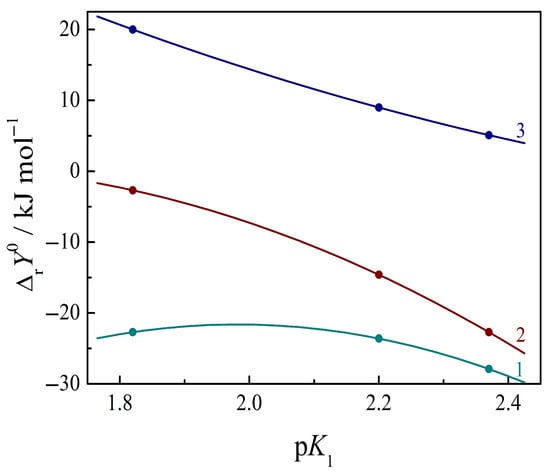
Figure 3.
Relationship between the standard thermodynamic parameters in the reaction of complexation of Ura with heterocyclic amino acids and the dissociation constant of COOH group of the amino acid: 1—Gibbs energy change ΔrG0; 2—enthalpy change ΔrH0; 3—entropy factor change TΔrS0, T = 298.15 K.
Figure 3 shows that the complexation reaction constant (log Kr), change in the negative values of the Gibbs energy (ΔrG°), and the exothermic effect (ΔrH0) of the reaction increase in the series of amino acids from His to Trp with an increase in pK°1 values; however, a decrease in the entropy effect (TΔrS°) is observed in this series. Such trends are favorable for the reaction studied and may be associated with a change in the electron density of the O-atoms in the carboxyl group of amino acids. The manifestation of the monotonic dependence of log Kr, ΔrG0, ΔrH0, and TΔrS0 on pK1 evidences the hydrogen bonding of uracil through the COO− group from the amino acids. On the contrary, the regular dependence of the above thermodynamic properties on the dissociation constants of the amino group of amino acids is absent; therefore, the H-bonding of uracil through the NH3+ group from an amino acid is not evident.
It is known [33] that an amino acid’s ability for stacking interactions with nucleic bases increases in the series Phe < His ≈ Tyr < Trp. Apparently, the stacking interaction between the indole ring of the Trp zwitterion and the pyrimidine ring of the Ura molecule additionally contributes to the complexation process; it is reflected in the greater stability of the Trp:2Ura complex and the greater enthalpy change, compared to the complexes of Phe and His.
3.5. Thermodynamics of Complex Formation Between Peptides and Nucleic Bases in Aqueous Buffer Solutions
Data on the complexation of nucleic bases with peptides are more numerous. The generalization of the available thermodynamic parameters [1,2] is presented in Table 2. Under the condition of a buffered saline medium at pH = 7.4, the dominant ionic form is zwitterion for GlyGly, GlyPhe, AlaAla, AlaTyr, AlaGln; the tripolar anionic forms of GluGlu and GluCysGly dominate in solution. The composition of the formed peptide/uracil complexes was 1:1. The interaction of a number of different structure peptides with pyrimidine nucleic bases in buffered saline at pH = 7.4 was investigated using the calorimetric method in [1,2]. The peptides under study differ from each other in the charge of the dominant ionic form in solution, the hydrophobicity, and the backbone length. Peptides toward the nucleobases behave differently compared to monomeric amino acids due to the structural features of the resulting complexes. Peptides, as polydentate ligands, are capable of forming a greater number of hydrogen bonds with nucleic acid bases. As noted above, not only the carboxylate but also the protonated amino group, as well as the polar amide fragment of a peptide, can be simultaneously involved in the formation of hydrogen bonds. The lengthening of the backbone, its flexibility and the removal of positively and negatively charged groups from each other in the structure of the peptide ion favor such a capability to appear. Therefore, the dependence of the thermodynamic parameters of complexation on the ability of only the peptide carboxyl group to acid dissociation is not clearly expressed, as in the case of monomeric amino acids. One can note the manifestation of such dependence for the enthalpies of complexation, as shown in Figure 4, but the course of the dependences turns out to be the opposite for peptide complexation with uracil and cytosine. It is likely that the additional contribution of the amino group and the amide fragments of peptides to H-bonding with nucleic bases is individual for each pair of reagents and varies for different peptides and different nucleic bases. The constant of acid dissociation of the side carboxyl group of the GlyGlu peptide was used in the correlation in Figure 4, since it is this group that coordinates to the uracil and cytosine molecules according to quantum chemical modeling [31]. The H-bond acceptor ability of the ionized COO- group strengthens when the dissociation constant of the COOH group of peptides decreases (pK value increases). This trend can be observed in the case of the complexation of peptides with cytosine, Figure 4. Cytosine/peptide complexes are probably stabilized by H-bonding via the COO− groups of peptides. The recent quantum chemical data [32] confirm the strongest hydrogen bonds are formed by the nucleic bases with the carboxylate group of the peptide, and the energies of hydrogen bonds with amino and amide groups take smaller absolute values.
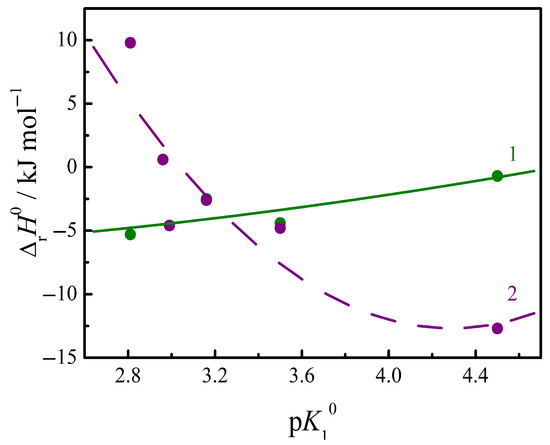
Figure 4.
Relationship between the enthalpy of complexation of peptides with pyrimidine nucleic bases at T = 298.15 K: 1—with uracil; 2—with cytosine. Values of ΔrH0 are from Refs. [1,2].
The influence of the peptide structure on the binding patterns with nucleic bases is manifested in the fine balance of enthalpy and entropy factors. Preference in the interaction of peptides of different structures is not a consequence of the complementarity of the reagents structures but is determined by the optimal ratio of the enthalpy and entropy factors of the reaction in solution. In most cases, the formation of peptide complexes with uracil and cytosine is due to the dominance of the entropy factor.
The hydrogen-bonding ability of the active sites of thymine differs from that of uracil due to the introduction of a methyl substituent at position 5, which causes a redistribution of electron density in the heterocycle. Thus, it was found [31,32] that the coordination of the anion of glutathione with the HN(1) and O(8) moieties of uracil is energetically more favorable than with the HN(3) and O(8) sites. But the coordination of the peptide with different pairs of thymine sites, the HN(1) and O(10) or HN(3) and O(12), leads to almost identical values of changes in the Gibbs energy. In a structureless polarizable medium, the peptide complexes with thymine show a slight preference compared to uracil, and the values of ΔrG are −10.89 and −7.96 kJ mol−1, respectively. Full consideration of the solvation effects in the obtained experimental data shows a preference for the peptides forming complexes with thymine in the enthalpy effect and a significant loss in the entropy of the reaction (Table 2).
It is interesting to test the compensation relationships between the Gibbs energies or entropies and enthalpies of the complex formation. Formally, the ternary systems (aqueous buffer + nucleic base + dipeptides) can be considered as a series of similar systems, in which only the dipeptides differ. The complexation process in these systems exhibits some features compared to the relationships between the Gibbs energies and enthalpies of complexation found for the non-electrolyte systems in the non-associated solvents, in which hydrogen bonding and charge–transfer complex formation occur [38]. The data in Figure 5 show that an increase in negative values of ΔrG0, indicating the favorability of peptide complexation with nucleic bases, is accompanied by a decrease in the enthalpy (an increase in the exothermic effect) and an increase in the entropy. For the peptide complexation with the cytosine, the ratio of changes Δ (ΔrG0)/Δ(ΔrH0) or the slope of the dependence of ΔrG0 vs. ΔrH0 is 0.5 in magnitude approaches the coefficient of 0.66 found in the study of non-aqueous solutions [38]. But the slope of the dependence of ΔrG0 vs. ΔrH0 is 1.8 for the peptide complexation with the uracil that is significantly higher. The intercept in the relationships between ΔrG0 and ΔrH0 is negative in both cases considered, in contrast to the results from [38], where it is equal to +2.5 kJ mol−1.
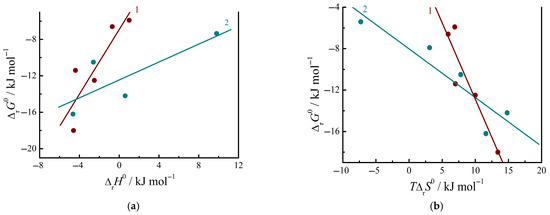
Figure 5.
Relationships (a) ΔrG0 vs. ΔrH0 and (b) ΔrG0 vs. TΔrS0 for the complexation process of peptides with nucleic bases: 1—with Ura; 2—with Cyt. Data from Refs. [1,2].
In the series of peptide–uracil complexes, the available data do not show the effect of compensation between TΔrS0 and ΔrH0 values, Figure 6a. The scattering of data may be due to the variation in the mode of coordination of different peptides with uracil in the forming complexes. When the peptide complexes with cytosine are formed, the changes in the enthalpy and entropy of the process compensate each other satisfactorily, Figure 6b.
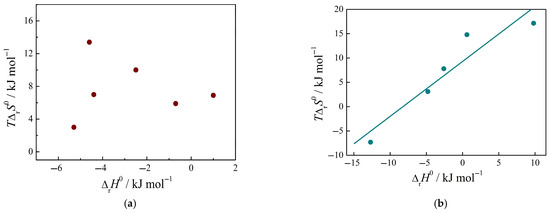
Figure 6.
Enthalpy–entropy compensation in the process of complexation of peptides with nucleic bases: with uracil (a); with cytosine (b). Data from Refs. [1,2].
The correlation between the values of ΔrG0 and TΔrS0 appears more clearly, Figure 5, as compared with the ΔrG0 and TΔrS0 relationship. Evidently, the entropy factor in the complexation reaction of each nucleic base with peptides in the series considered is not constant, and the change in entropy turns out to be the dominant effect determining the patterns of the complexation process in the aqueous medium.
The entropy change during the peptide–nucleobase complex formation exhibits dependence on the hydrophobicity of the peptides. We used the partition coefficients of peptides in the 1-octanol/aqueous buffer (pH = 7.4) system, log P′, as known hydrophobicity indicators, which were calculated on the bases of the correlation equation [1,39]. Figure 7 demonstrates that the positive values of entropy change increase with the increasing hydrophobicity of peptides log P’ in the series GluCysGly < GlyGlu < GlyGly < GlyPhe for complexation with the uracil, and in the series GluCysGly < GlyGlu < GlyPhe < AlaGln < AlaTyr for complexation with the cytosine. The relationship between the entropy of complexation and the peptide hydrophobicity can be interpreted within the framework of the overlapping hydration sphere model. The stability of the hydration shells formed about the peptides increases with increasing hydrophobicity. The destruction of these hydration shells during overlapping with hydration spheres of the co-solutes (NB) leads to greater disorder, i.e., to a more favorable entropic effect for the complex formation.
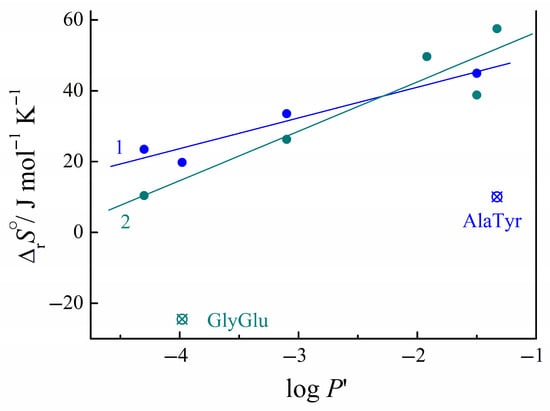
Figure 7.
Dependences of the change in entropy upon complexation with uracil (1) and cytosine (2) on the hydrophobicity of the peptide log P′. Data are calculated from Refs. [1,2].
Falling out of the pattern is observed in the case of the complexes (AlaTyr + uracil) and (GlyGlu + cytosine). The structural features of these complexes are responsible for the observed deviations. As shown by quantum chemical studies [31], stacking interactions are possible between the side aromatic fragment of the AlaTyr peptide and the uracil heterocycle. In complex (GlyGlu + cytosine), the H-bonds with a long side fragment (CH2)3COO− are preferable compared to the α-COO− group. Both effects can lead to a decrease in the mobility of the side fragments of the peptide in the complexes and be reflected in a decrease in the entropy of complex formation.
J.M. Sturtevant in 1977 [40] formulated several regularities for the entropy of protein reactions, according to which the exposure of non-polar and charged groups, as well as H-bonding, makes a negative contribution. This regularity was repeated in a review by C. Hélène and G. Lancelot [41]. The new data considered allow us to refine the thermodynamic model using the concept of overlapping hydrated spheres. Strengthening the hydrophobic interactions of the nucleic bases with the peptides in an aqueous solution makes a positive contribution to the entropy of the reaction. Blocking the polar groups of the nucleic base and the charged groups of the peptide due to H-bonding between them, breaking H-bonds with water and reducing the electrostriction of the solvent molecules around the charged groups, also contribute positively to the entropy.
3.6. Change of Volumetric Properties of Uracil Under Addition of Amino Acids and Peptides
The process of complexation between uracil molecules and amino acid/peptide ions leads to a change in the physicochemical properties of the uracil solutions with the amino acids and the peptides. The volumetric properties of solutes turn out to be very sensitive to the occurrence of complexation in a multicomponent solution; the volumetric characteristics and especially their temperature derivatives provide information on the subtle rearrangement of the solvation shells of molecules involved in the complex. The apparent molar volumes of nucleic acid bases, ΦV2, in an aqueous solutions were the object of a number studies [7,8,9,10,42,43,44,45,46,47]. The concentration dependences of ΦV2 for many solutes in water, including the uracil, are often interpreted as a linear trend [7,48,49]. The behavior of the solutes in an aqueous buffer medium is more complicated. It was shown earlier [9,10] that for the uracil in a buffered saline solution at temperatures from 288.15 to 313.15 K, a linear trend appears only in the dilute solution region, m < 0.015 mol kg−1. A further increase in concentration produces more significant deviation from the linearity of the ΦV2 vs. m function, especially in the low-temperature region, T ≤ 298 K, where the effect of the uracil association can be the strongest.
The shape of the concentration dependence ΦV2 = f(m) for the uracil in buffered saline (lines 1 and 3 in Figure 8) changes significantly when a peptide is added to the solution (lines 2 and 4 in Figure 8). The non-linear trend of ΦV2 = f(m) dependences and the appearance of a maximum in Figure 8 are induced by the process of the complex formation between the uracil and the peptide. The ratio of the reagents determines the fraction of the complex formed. The maximum point on the dependences equal to ~0.015 mol kg−1 indicates the ~1:1 stoichiometry of the uracil/peptide complex. The complex formation of the uracil with the amino acids (Phe, Trp, His) [50] and several peptides (GlyGly, GlyGlu, GlyPhe, GlyTyr) [9,10] in a buffer solution at pH = 7.4 was detected through the volume properties. The analogous results of the volumetric studies are known for different solutes with the addition of a co-solute [43,44,45]. The complexation of uracil and other nucleic bases with amino acids and peptides of various structures has also been proven using computer simulations and the thermochemical data, as shown above.
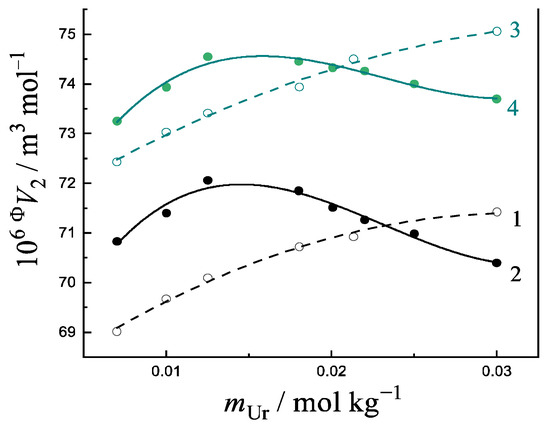
Figure 8.
Concentration dependence of the apparent molar volume of uracil in phosphate-buffered saline: 1—(Ura + buffer) at 288.15 K; 2—(Ura + buffer + GlyGlu) at 288.15 K; 3—(Ura + buffer) at 313.15 K; 4—(Ura + buffer + GlyGlu) at 313.15 K. Data are calculated from Refs. [9,10].
The available volumetric properties from [7,8,9,10,42,44,51] are summarized in Table 3. We analyzed the data and concluded that the additions of various amino acids and peptides arouse noticeable changes in the standard apparent molar volume of Ura in a buffer solution. These changes are characterized as the standard molar volumes of transfer ΔtrV°2. The variation in the volume reflects the structural rearrangement during complexation between hydrated particles. The penetration of an ionized amino acid or peptide into the hydration shell of neutral uracil is accompanied by the partial desolvation effect, the formation of hydrogen bonds with its molecule, the blocking of the hydrophilic centers of uracil, the change in the packing density of uracil solvation shells, and the displacement of water molecules from the hydration shell into the bulk.

Table 3.
Standard apparent molar volumes ΦV°2 of uracil in water and aqueous buffer solution and changes of standard apparent molar volume (ΔtrV°2) with additions of various amino acids and peptides at different temperatures and pH = 7.4.
The data in Table 4 confirm that the standard (at infinite dilution) apparent molar volume of the uracil in water solvent and in a buffer solution increases with temperature. The manifestation of this trend is due to the thermal disruption in the structure of water. The variation in the standard apparent molar volume can be expressed as a polynomial function of temperature
where a, b, and c are empirical constants. The limiting molar expansibilities at infinite dilution, ΦE°, can be obtained by differentiating Equation (4) with respect to temperature:

Table 4.
Limiting molar expansibilities of uracil (Ura), ΦE° = (∂ΦV°2/∂T)P, in buffered saline and in buffered saline with additive of the peptides (m = 0.0125 mol·kg−1) at different temperatures.
The ΦE° values of Ura in the peptide buffer saline at different temperatures are recorded in Table 4. The values of ΦE° are positive and decrease under the influence of the hydrophilic peptides GlyGlu and GlyTyr added to the solution; this trend is especially noticeable at low temperatures. The additions of more hydrophobic peptides GlyGly and GlyPhe lead to an increase in the limiting molar expandability of the uracil in a solution.
The standard molar volumes of the transfer of Ura, (ΔtrV°2), from buffer to buffer solutions with the addition of amino acid and peptides exhibit more complicated dependences on temperature. Figure 9 demonstrates that the ΔtrV°2 values increase non-monotonically with temperature when an amino acid is added to the Ura buffer, and, conversely, they decrease with temperature when a peptide is added to the same solution. The course of the temperature dependences of ΔtrV°2 is influenced not only by the thermal destruction of the water structure but the values of ΔtrV°2 are strongly influenced by the penetration of hydrophilic and hydrophobic fragments of the amino acids/peptides into the hydration shells of the Ura molecule. It can be noted that the temperature dependence of the standard apparent molar volumes is sharper for the uracil involved in the amino acid complexes than for free uracil. But in the composition of Ura/peptide complexes, the standard apparent molar volume of the uracil changes with temperature to a lesser extent, and the values of ΔtrV°2 fall as the temperature rises. The reason for the different effects of amino acids and peptides is the multisite mode of H-bonding of the peptides to the uracil (as discussed in Section 3.3). The effect of the thermal destruction of the solvent, inherent in the uracil solution, is excluded from the transfer volume values. That is why the ΔtrV°2 values, unlike ΦV°2 quantities, may decrease with increasing temperature. Such dependences reflect the influence of different groups of the peptide penetrating into the hydration shell of the uracil.
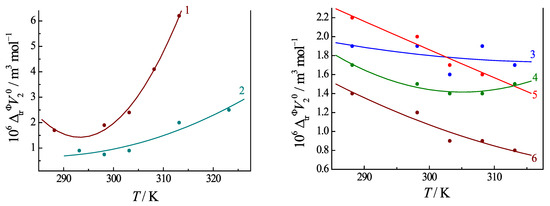
Figure 9.
The standard apparent molar volume of Ura transfer (ΔtrV°2) from buffer to buffer solution with the addition of histidine (1), phenylalanine (2), glycyl-glycine (3), glycyl-L-tyrosine (4), glycyl-L-phenylalanine (5), glycyl-L-glutamic acid (6) at different temperatures. Values of (ΔtrV°2) are calculated from Refs. [7,8,9,10].
Naturally, there are relationships between the change in the volume parameters of the uracil and the hydrophobicity of the added amino acids and peptides. We used the scale proposed by Kyte-Doolittle [52] to estimate the degree of hydrophobicity (f) of the second amino acid residuals in glycyl dipeptides. As can be seen from Figure 10, at low temperature (288 K), the ΔtrV°2 values of the uracil increase almost linearly with increasing peptide hydrophobicity, regardless of their ionic state. As a result of the decrease in the stability of the hydration shells of non-polar groups and the weakening of the hydrophobic effect at higher temperatures, a noticeable deviation from the linear trend appears on the ΔtrV°2 vs. f dependences in the range of 298–313 K. In some cases, the values of ΔtrV°2 can slightly decrease with increasing peptide hydrophobicity. Such behavior of the volumetric properties is typical for the case of interactions between hydrophobic moieties [53,54,55,56]. Peptides contribute to an increase in the ΦV°2 and ΔtrV°2 values of Ura when the hydrophobic interaction is significant (as in the case of GlyPhe). An increase in the above volumes of Ura is less telling when the hydrophilic effect dominates, as in the case of GlyGlu. Thus, the clear dependence of the change in volume, arising from the uracil–peptide interactions, on the hydrophobicity of the peptides proves the significant contribution from the hydrophobic effect to the formation of the complexes between the reagents.
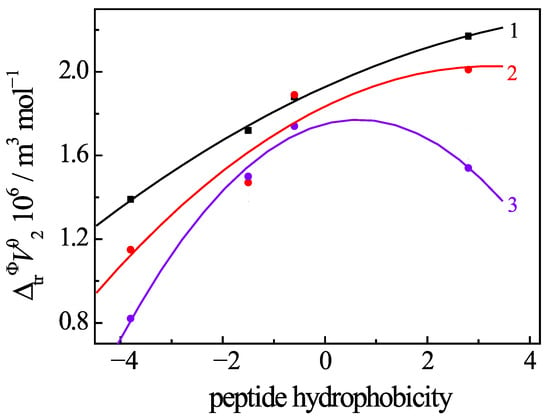
Figure 10.
Dependence of changes in the standard molar volume (ΔtrV°2) of Ura in buffer saline with the addition of peptides on the hydrophobicity of second amino acid residue in the glycyl peptide at 288.15 K (1); 298.15 K (2); 313 K (3). Values of (ΔtrV°2) are calculated from Refs. [9,10].
Small zwitterions of the amino acids interact with the uracil only through the carboxylate group, as described in Section 3.3. Hydrophobic fragments of the amino acids are located at a remote distance from the uracil cycle, and, therefore, the hydrophobic interaction is not dominant in the complexation. In this case, the dependence of volumetric parameters on the hydrophpbicity of added amino acids differs from the effect of added peptides. As shown in Figure 11, the addition of Phe, which has the highest hydrophobicity index, causes the lowest change in the standard apparent molar volume of the uracil. Conversely, the addition of His, which has the lowest hydrophobicity index due to a hydrophilic side chain in its structure, sees the maximal rise in the standard apparent molar volume of Ura.
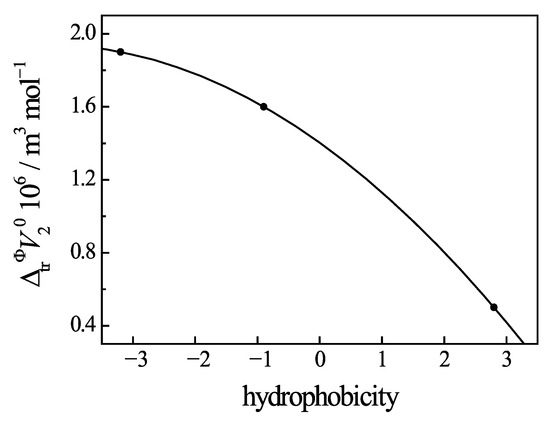
Figure 11.
Dependence of changes in the standard molar volume (ΔtrV°2) of uracil in buffer saline with the addition of amino acids on their hydrophobicity at 298.15 K. Values of (ΔtrV°2) are calculated from Refs. [7,8].
Since the reagents under study consist of both hydrophilic and hydrophobic groups, there is competition among different types of interactions between the solute and the co-solute in the solutions. Hydrophilic–ionic interactions between polar groups of the nucleic acid base and charged groups of zwitterions of the co-solute (amino acid/peptide) as well as hydrophilic–hydrophilic interactions between polar groups of Ura and amino acid/peptide will contribute positively to ΔtrV°2 values. Hydrophobic–ionic interactions of the non-polar parts of Ura with the zwitterions of the amino acid/peptide and hydrophobic–hydrophobic interactions will contribute negatively to ΔtrV°2 values [57]. The studied systems indicate that hydrophilic–ionic and hydrophilic–hydrophilic interactions dominate over hydrophobic–ionic and hydrophobic–hydrophobic interactions for the forming complexes of Ura with the amino acids and peptides. But changes in the temperature derivative of the standard apparent molar volume (limiting molar expansibility) of the uracil show a maximum increase in the thermal stability of the hydration shell of the uracil upon the complexation with the hydrophobic peptides and, conversely, a decrease in its thermal stability upon complexation with more hydrophilic peptides. Thus, the hydrophobic interaction in the course of the complex formation of the uracil with the peptides makes a significant contribution to the volumetric parameters of the solutions studied.
4. Conclusions
Data on the acid dissociation constants and the distribution of coexisting ionic forms of the solutes are required to correctly interpret the thermodynamic parameters of the biological compounds in an aqueous solution.
The modes of coordination of the amino acid and the peptide ions to the nucleic acid base molecules differ. Amino acids are coordinated, as a rule, through the carboxyl group and can form 2:1 complexes with nucleobases. Peptides as polydentate ligands can form several H-bonds with the nucleic acid base molecule through the carboxyl, amino, and amide groups. The differences in the coordination modes are reflected in the thermodynamic parameters that describe the behavior of these reagents under the formation of complexes with nucleic bases.
The interaction of the peptides with the pyrimidine nucleic bases in buffered saline results in the formation of complexes of low to moderate stability. Hydrogen bonding and hydrophobic interaction determine the patterns in the thermodynamic parameters of the complexation. The charge of the peptide ion has no significant effect on the complexation with nucleic bases.
A subtle balance of enthalpy and entropy effects governs the preference for binding the different structures of peptides with the nucleic bases. The values of the entropy of the complexation reaction and their dependence on the hydrophobicity of the peptides indicate a significant evolution of the hydration shells of nucleic bases and peptides during interactions between them.
Changes in the volumetric characteristics (apparent molar volumes, standard molar volumes, transfer volume and molar expansibilities) of the nucleic bases under the influence of amino acids and peptides also confirm a significant evolution of the hydration shells of the reagents upon complexation. It was possible to identify the principal patterns of the influence of the amino acid and peptide additions on the volumetric properties of the uracil.
- -
- The manifestation of a maximum in the non-linear concentration dependences of the apparent molar volumes of Ura in a buffer saline with the additives of an amino acid/peptide shows the formation of ion–molecular complexes between a solute and co-solute (NB). The ratio of the reagent concentrations at the maximum point indicates the stoichiometry of the resulting complex.
- -
- The regular relationship between the volume changes, induced by the uracil–peptide interaction, and the hydrophobicity of the peptides evidences the major role the hydrophobic effect plays in the complexation process in solutions.
- -
- The effect of temperature on the volumetric properties of Ura in the solution is determined by the thermal disruption of the water structure and by the influence of hydrophilic and hydrophobic groups of the peptides that penetrate into the hydration shell of uracil. This is most clearly manifested in the values of the standard apparent molar transfer volumes and the limiting molar expansibilities.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/liquids5030019/s1, Supplementary Material S1: Structures of L for some solutes; Supplementary Material S2: Acid-base equilibria in amino acid/peptide solutions.
Author Contributions
Conceptualization, V.P.B.; validation, V.P.B., E.Y.T. and I.N.M.; investigation, E.Y.T. and I.N.M.; writing—review and editing, E.Y.T. and V.P.B.; supervision, V.P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by a grant from the Russian Science Foundation No. 22-23-01118.
Data Availability Statement
All new data obtained in this work are contained in the tables and graphs presented in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Barannikov, V.P.; Smirnov, V.I.; Mezhevoi, I.N.; Koltyshev, D.R. Patterns of interaction between peptides of various structures and pyrimidine nucleic bases in a buffered saline medium according to the analysis of thermodynamic parameters. J. Mol. Liq. 2024, 415, 126340. [Google Scholar] [CrossRef]
- Barannikov, V.P.; Smirnov, V.I.; Mezhevoi, I.N.; Koltyshev, D.R. Thermochemical study of the interaction of cytosine and uracil with peptides in a buffered saline: Complex formation with beta-endorphin 30-31 (human), L-glutathion (reduced) and α-L-alanyl-L-tyrosine. Int. J. Mol. Sci. 2023, 24, 9764. [Google Scholar] [CrossRef] [PubMed]
- Badelin, V.G.; Tyunina, E.Y.; Mezhevoi, I.N.; Tarasova, G.N. Thermodynamic characteristics of molecular interactions between L-tryptophan and nicotinic acid and uracyl in aqueous buffer solutions at 298.15 K. Russ. J. Phys. Chem. A 2015, 89, 2229–2233. [Google Scholar] [CrossRef]
- Tyunina, E.Y.; Badelin, V.G.; Mezhevoi, I.N.; Tarasova, G.N. Thermodynamics of aromatic amino acid interactions with heterocyclic ligands. J. Mol. Liq. 2015, 211, 494–497. [Google Scholar] [CrossRef]
- Tyunina, E.Y.; Badelin, V.G.; Mezhevoi, I.N. Observation of complex formation between L-histidine and heterocyclic compounds in water and aqueous buffer solution using calorimetric and spectroscopic methods. J. Mol. Liq. 2019, 278, 505–511. [Google Scholar] [CrossRef]
- Badelin, V.G.; Tarasova, G.N.; Tyunina, E.Y.; Bichkova, S.A. Investigation of interaction between L-histidine and heterocyclic substances in aqueous solutions by UV spectroscopy. Izv. Vyssh. Uchebn. Zaved. Khim. Khim. Tekhnol. 2018, 61, 11–18. [Google Scholar] [CrossRef]
- Tyunina, E.Y.; Badelin, V.G.; Mezhevoi, I.N. Volumetric and heat capacity studies of heterocyclic compounds in aqueous amino acids buffer solutions at 298.15 K. J. Chem. Thermodyn. 2019, 131, 40–48. [Google Scholar] [CrossRef]
- Tyunina, E.Y. Interaction between uracil and L-histidine in an aqueous buffer solution in the 288.15–313.15 K range of temperature. Russ. J. Phys. Chem. A 2021, 95, 2254–2262. [Google Scholar] [CrossRef]
- Barannikov, V.P.; Tyunina, E.Y.; Tarasova, G.N. Characterization of complexation of uracil with peptides through its volumetric properties in buffer saline solution at different temperatures. J. Chem. Thermodyn. 2025, 201, 107402. [Google Scholar] [CrossRef]
- Barannikov, V.P.; Tyunina, E.Y.; Tarasova, G.N. Changes in the volumetric properties of uracil in a buffered saline upon interaction with peptides: The effect of glycyl-L-tyrosine and glycyl-L-glutamic acid. J. Chem. Thermodyn. 2023, 185, 107113. [Google Scholar] [CrossRef]
- Kulikov, O.V.; Lapshev, P.V.; Parfenyuk, E.V. The role of weak and specific forces in the interaction of amino acids with cytosine, uracil and caffeine. Mendeleev Commun. 1995, 5, 72–74. [Google Scholar] [CrossRef]
- Smirnov, V.I.; Barannikov, V.P. Thermochemical characteristics of some glycylpeptides interaction with anionic micelles in a phosphate-buffered saline solution of sodium dodecyl sulfate. J. Chem. Thermodyn. 2022, 174, 106853. [Google Scholar] [CrossRef]
- Barannikov, V.P.; Kurbatova, M.S.; Mezhevoi, I.N. The influence of structure of isomolecular dipeptides of α-L-alanyl-α-Lalanine and β-alanyl-β-alanine on their behavior in aqueous micellar solution of SDS. Thermochim. Acta 2020, 689, 178647. [Google Scholar] [CrossRef]
- Barannikov, V.P.; Smirnov, V.I.; Kurbatova, M.S. The thermochemical behavior of glycyl-L-histidine and β-alanyl-L-histidine peptides in (SDS + phosphate-buffered saline) micellar solution at pH = 7.4. J. Mol. Liq. 2021, 331, 115766. [Google Scholar] [CrossRef]
- Lytkin, A.I.; Barannikov, V.P.; Badelin, V.G.; Krutova, O.N. Enthalpies of acid dissociation of L-carnosine in aqueous solution. J. Therm. Anal. Calorim. 2020, 139, 3683–3689. [Google Scholar] [CrossRef]
- Tyunina, E.Y.; Mezhevoi, I.N.; Stavnova, A.A. Molecular complexes of polar basic amino acids (L-lysine, L-histidine) with nicotinic acid in water and buffer solution: A thermodynamic aspects. J. Chem. Thermodyn. 2021, 161, 106552. [Google Scholar] [CrossRef]
- Tyunina, E.Y.; Smirnov, V.I.; Mezhevoi, I.N.; Barannikov, V.P. Thermochemical and volumetric studies of pyridine-3-carboxylic acid (vitamin B3) in a phosphate buffered saline solution with L-asparagine: Manifestation of molecular interactions. J. Mol. Liq. 2025, 423, 126902. [Google Scholar] [CrossRef]
- The Cambridge Crystallographic Data Centre, Leibniz Institute for Information Infrastructure. Available online: https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=1105666&DatabaseToSearch=Published (accessed on 1 November 2022).
- Badelin, V.G.; Barannikov, V.P.; Tarasova, G.N.; Chernyavskaya, N.V.; Katrovtseva, A.V.; Fam, T.L. Thermodynamical characteristics of acid-base equilibria in GlycylGlycylGlycine aqueous solutions at 298 K. Russ. J. Phys. Chem. A 2012, 86, 40–44. [Google Scholar] [CrossRef]
- Gorboletova, G.G.; Gridchin, S.N.; Sazonova, E.S. Heat effects of acid-base interactions in aqueous solutions of glycylglycine. Russ. J. Phys. Chem. A 2005, 79, 1222–1226. [Google Scholar]
- Lytkin, A.I.; Chernikov, V.V.; Krutova, O.N.; Damrina, K.V.; Skvortsov, I.A. Thermochemical study of acid—Base reactions in a glycyl-tyrosine aqueous solution. Russ. J. Phys. Chem. A 2016, 90, 735–738. [Google Scholar] [CrossRef]
- Lytkin, A.I.; Krutova, O.N.; Golubev, A.A.; Badelin, V.G.; Tyunina, E.Y. Effect of the nature of background electrolyte on the thermodynamic characteristics of the acid-base reactions of L-asparagine in aqueous solutions. Russ. J. Phys. Chem. A 2019, 93, 1729–1732. [Google Scholar] [CrossRef]
- Piekarski, H.; Nowicka, B. Calorimetric studies of interactions of some peptides with electrolytes, urea and ethanol in water at 298.15 K. J. Therm. Anal. Calorim. 2010, 102, 31–36. [Google Scholar] [CrossRef]
- Vasil’ev, V.P.; Borodin, V.A.; Kozlovsky, E.V. Application of PC in Chemical Analytical Calculations; High School: Moscow, Russia, 1993. (In Russian) [Google Scholar]
- Barannikov, V.P.; Badelin, V.G.; Venediktov, E.V.; Mezhevoi, I.N.; Guseinov, S.S. Thermodynamical characteristics of the reaction of pyridoxal-5′-phosphate with L-amino acids in aqueous buffer solution. Russ. J. Phys. Chem. A 2011, 85, 16–20. [Google Scholar] [CrossRef]
- Hunter, K.C.; Millen, A.L.; Wetmore, S.D. Effects of hydrogen-bonding and stacking interactions with amino acids on the acidity of uracil. J. Phys. Chem. B 2007, 111, 1858–1871. [Google Scholar] [CrossRef] [PubMed]
- Gutowski, M.; Dąbkowska, I.; Rak, J.; Xu, S.; Nilles, J.M.; Radisic, D.; Bowen, K.H., Jr. Barrier-free intermolecular proton transfer in the uracil-glycine complex induced by excess electron attachment. Eur. Phys. J. D 2002, 20, 431. [Google Scholar] [CrossRef]
- Dąbkowska, I.; Rak, J.; Gutowski, M.; Nilles, J.M.; Stokes, S.T.; Bowen, K.H., Jr. Barrier-free intermolecular proton transfer induced by excess electron attachment to the complex of alanine with uracil. J. Chem. Phys. 2004, 120, 6064–6071. [Google Scholar] [CrossRef] [PubMed]
- Dąbkowska, I.; Rak, J.; Gutowski, M.; Nilles, J.M.; Stokes, S.T.; Radisic, D.; Bowen, K.H., Jr. Barrier-free proton transfer in anionic complex of thymine with glycine. Phys. Chem. Chem. Phys. 2004, 6, 4351–4357. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J. Interaction of protein backbone with nucleic acid bases. J. Phys. Chem. B 2003, 107, 5306–5310. [Google Scholar] [CrossRef]
- Kurbatova, M.S.; Barannikov, V.P. Complexes of ionized dipeptides of glycyl-L-glutamic acid and alanyl-L-tyrosine with nucleic bases of the pyrimidine series. J. Struct. Chem. 2023, 64, 2213–2225. [Google Scholar] [CrossRef]
- Kurbatova, M.S.; Barannikov, V.P. DFT-calculations and RDG analysis (topology) of complexes between glutathione and nucleic bases of pyrimidine series pyrimidine series. J. Mol. Model. 2025, 3, 98. [Google Scholar] [CrossRef]
- Rutledge, L.R.; Campbell-Verduyn, L.S.; Wetmore, S.D. Characterization of the stacking interactions between DNA or RNA nucleobases and the aromatic amino acids. Chem. Phys. Lett. 2007, 444, 167–175. [Google Scholar] [CrossRef]
- Saito, I.; Sugiyama, H.; Matsuura, T.; Fukuyama, K. Stacking interaction between tryptophan and uracil in a synthetic model compound. Tetrahedron Lett. 1985, 26, 4467–4470. [Google Scholar] [CrossRef]
- Troitiňo, D.; Bailey, L.; Peral, F. Formation of hydrogen-bonded dimers of uracil and amino acids: Cysteine, lysine and phenylalanine. A density functional theory study. J. Mol. Struct. Theochem. 2006, 767, 131–138. [Google Scholar] [CrossRef]
- Lapschov, P.V.; Kulikov, O.V. Thermodynamics and mechanism of interaction of uracil with amino acids in water. Russ. Chem. Bull. 1977, 46, 892–894. [Google Scholar] [CrossRef]
- Nagai, H.; Kuwabara, K.; Carta, G. Temperature Dependence of the Dissociation Constants of Several Amino Acids. J. Chem. Eng. Data 2008, 53, 619–627. [Google Scholar] [CrossRef]
- Solomonov, B.N.; Yagofarov, M.I. The relationship between the Gibbs energies and enthalpies of hydrogen bonding and charge-transfer complex formation in non-electrolytes solutions. Is it a rule? J. Mol. Liq. 2025, 424, 127053. [Google Scholar] [CrossRef]
- Palekar, D.; Shiue, M.; Lien, E.J. Correlation of Physicochemical Parameters to the Hydrophobic Contribution Constants of Amino Acids Residues in Small Peptides. Pharm. Res. 1996, 13, 1191–1195. [Google Scholar] [CrossRef] [PubMed]
- Sturtevant, J.M. Heat capacity and entropy changes in processes involving proteins. Prog. Natl. Acad. Sci. USA 1977, 74, 2236–2240. [Google Scholar] [CrossRef] [PubMed]
- Hélène, C.; Lancelot, G. Interactions between functional groups in protein-nucleic acid associations. Prog. Biophys. Mol. Biol. 1982, 39, 1–68. [Google Scholar] [CrossRef] [PubMed]
- Banipal, T.S.; Kaur, N.; Banipal, P.K. Volumetric studies on nucleic acids bases and nucleosides in aqueous guanidine hydrochloride solutions at T= (288.15 to 318.15) K and at atmospheric pressure. J. Chem. Thermodyn. 2015, 82, 12–24. [Google Scholar] [CrossRef]
- Kaur, N.; Banipal, P.K.; Banipal, T.S. Physico-chemical effects of caffeine on aqueous solutions of pyrimidine based model compounds of nucleic acids. J. Mol. Liq. 2016, 221, 721–732. [Google Scholar] [CrossRef]
- Zielenkiewicz, W.; Poznański, J.; Zielenkiewicz, A. Partial molar volumes of aqueous solutions of some halo and amino derivatives of uracil. J. Solut. Chem. 2000, 29, 757–769. [Google Scholar] [CrossRef]
- Kishore, N.; Ahluwalia, J.C. Partial molar heat capacities and volumes of transfer of nucleic acid bases, nucleosides and nucleotides from water to aqueous solutions of sodium and calcium chloride at 25 °C. J. Solut. Chem. 1990, 19, 51–64. [Google Scholar] [CrossRef]
- Patel, S.G.; Kishore, N. Thermodynamics of nucleic acid bases and nucleosides in water from 25 to 55 °C. J. Solut. Chem. 1995, 24, 25–38. [Google Scholar] [CrossRef]
- Fucaloro, A.F.; Dewey, K.; Fan, G.; Imuta, K.; Jensen, D.; Muranaka, M. Partial molar volumes of uracil, thymine, adenine in water and of adenine in aqueous solutions of uracil and thymine. J. Solut. Chem. 2008, 37, 1289–1304. [Google Scholar] [CrossRef]
- Tyunina, E.Y.; Mezhevoi, I.N.; Dunaeva, V.V. Thermodynamic properties of crystalline L-carnosine and its aqueous solutions. J. Chem. Thermodyn. 2020, 150, 106206. [Google Scholar] [CrossRef]
- Rani, R.; Rajput, S.; Sharma, K.; Baboria, V. Volumetric and viscometric properties od amino acids in aqueous solutions of various drugs at different temperatures: A review. Mol. Phys. 2022, 120, e19920259. [Google Scholar] [CrossRef]
- Barannikov, V.P.; Tyunina, E.Y. Regularities of changes in thermodynamic parameters induced by the complexes formation of uracil with some aromatic amino acids in a buffer solution at pH 7.4. Izv. Vyssh. Uchebn. Zaved. Khim. Khim. Tekhnol. ChemChemTech. 2022, 65, 38–46. [Google Scholar] [CrossRef]
- Rajput, P.; Richu; Sharma, T.; Kumar, A. Temperature dependent physicochemical investigations of some nucleic acid bases (uracil, thymine and adenine) in aqueous inositol solutions. J. Mol. Liq. 2021, 326, 115210. [Google Scholar] [CrossRef]
- Kyte, J.; Doolittle, R.F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982, 157, 105–132. [Google Scholar] [CrossRef] [PubMed]
- Lee, B. Analyzing solvent reorganization and hydrophobicity. Methods Enzymol. 1995, 259, 555–576. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.J.; Chaudhry, M.A. Thermodynamic study of the three pharmacologically significant drugs: Density, viscosity, and refractive index measurements at different temperatures. J. Chem. Thermodyn. 2009, 41, 221–226. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J.; Zheng, H.; Liu, D. Volumetric properties of some α-amino acids in aqueous guanidine hydrochloride at 5, 15, 25, and 35 °C. J. Solut. Chem. 1998, 27, 473–483. [Google Scholar] [CrossRef]
- Krumgalz, B.S. Ionic limiting partial molar volumes in various solvents. J. Chem. Soc. Faraday Trans. I 1980, 76, 1887–1904. [Google Scholar] [CrossRef]
- Gurney, R.W. Ionic Processes in Solution; McGraw Hill: New York, NY, USA, 1953. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).