Compensation Relationships in the Solvation Thermodynamics of Proton Acceptors in Aliphatic Alcohols

Abstract

Solvent association and solute–solvent complexation are known to influence the relationship between the thermodynamic functions of solvation, known as the compensation relationship. Here, we accomplish a series of works devoted to the analysis of Gibbs energy–enthalpy relations in the systems with different capabilities of hydrogen bonding. The data on proton acceptors solvated in alcohols were collected, and the quantitative regularities in their solvation thermodynamics were established, depending on the binding degree in solution. The equations connecting the Gibbs energies and enthalpies of solvation in the systems with competition for hydrogen bonding sites were derived from the previously found correlation between the thermodynamic functions of complexation and solvation in simpler solutions. These equations enabled the successful prediction of the solvation enthalpies of 56 proton acceptors in alcohols (RMSD = 1.8 kJ·mol⁻¹). Together with the results of the previous works, the general linear equation connecting the Gibbs energies and enthalpies of solvation in various solute–solvent systems has been obtained. This finding led us to reshaping common understanding of the compensation relationship phenomenon.

1. Introduction

The phenomenon of compensation between the enthalpy (ΔH) and entropy (ΔS) changes is observed in numerous physicochemical and biochemical processes [1]. Its studies have a long history (nearly 90 years [2,3,4,5,6]), indicating the significance, on the one hand, and incompleteness, on the other hand. Great efforts have been made to establish the limitations and origins of compensation relationships, their similarities and differences in various phenomena (conformational equilibrium [7], weak bimolecular association [8,9], molecular recognition [10], protein binding [11,12,13], and many others), and exclude the effects of experimental artifacts [14,15,16]. Particular attention was paid to the processes in solutions [1,17,18], accompanied by various intermolecular interactions. Common understanding of the enthalpy–entropy compensation at the molecular level implies that it should hold as long as the same type of intermolecular force operates throughout [19,20]. At the same time, rigorous statistical mechanics-based treatment shows that there is an entropy–enthalpy cancellation upon solvent reorganization, regardless of the solvent and solute nature [21,22]. Its role in the compensation phenomenon was repeatedly highlighted [17,23]. Although certain cases of enthalpy–entropy compensation are predicted by fundamental laws of thermodynamics, our understanding of this phenomenon is still limited and requires further experimental and theoretical studies.

We studied the compensation phenomenon in a series of works [24,25,26] devoted to the relationship between the Gibbs energies (Δ_solvG) and enthalpies of solvation (Δ_solvH). We chose these parameters, as Δ_solvG, Δ_solvS, and Δ_solvH are connected via the Gibbs’s formula:

Δ_solvG = Δ_solvH − T Δ_solvS

(1)

Δ_solvG and Δ_solvH are typically determined in independent experiments, while Δ_solvS is found from their difference by Equation (1).

Our investigations of ΔH vs. ΔG relationships are intended to facilitate the prediction of one of these quantities through another, as well as gain fundamental knowledge of the regularities causing the enthalpy–entropy compensation in the infinitely diluted solutions, important yet simple systems. In Refs. [24,25], the quantitative ΔH vs. ΔG relationships were established for four clue types of solute–solvent systems exhibiting different capabilities of hydrogen bonding:

• No A-S and S-S hydrogen bonding is present.
• A undergoes hydrogen bonding with non-associated solvent S.
• Solute A incapable of hydrogen bonding in associated solvent S.
• Both A-S and S-S hydrogen bonds are present in solution.

In case 4, we previously [25] considered the data on proton donors in alcohols but did not cover proton acceptors solvation. In this work, the relationship between the Gibbs energies and enthalpies of proton acceptors in aliphatic alcohols is analyzed.

2. Methodology

2.1. Definitions and the Framework

The same definitions and framework hold as in our previous papers [24,25]. The thermodynamic functions of solvation (Δ_solvf^A/S) correspond to the transfer of one mole of an ideal gas phase solute A at p⁰ = 1 bar to the infinitely diluted solution in a solvent S. In associated solvents that can form A-S hydrogen bonds, Δ_solvf^A/S is represented as a sum of three contributions (Equation (2)):

$${\Delta }_{\mathrm{solv}}{f}^{\mathrm{A}/\mathrm{S}}={\Delta }_{\mathrm{solv}\left(\mathrm{nonsp}\right)}{f}^{\mathrm{A}/\mathrm{S}}+{\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{f}^{\mathrm{A}/\mathrm{S}}+{\Delta }_{\mathrm{s}.\mathrm{e}.}{f}^{\mathrm{A}/\mathrm{S}}$$

(2)

Δ_solv(nonsp)f^A/S corresponds to thermodynamic function of nonspecific solvation (due to van der Waals forces) and Δ_int(sp)f^A/S is associated with specific interactions (hydrogen bonding or charge-transfer complex formation). Δ_s.e.f^A/S is the solvophobic effect contribution [27].

In case A and S undergo hydrogen bonding (HB) according to Equation (3):

$${\mathrm{A}}_{(\mathrm{S})}+{\mathrm{S}}_{(\mathrm{S})}\rightleftarrows \mathrm{A}\cdots {\mathrm{S}}_{(\mathrm{S})}$$

(3)

The Gibbs energy of HB can be found from the equilibrium constant of the corresponding process (Equation (4)):

$${\Delta }_{\mathrm{HB}}G=-RT\ln K_{\mathrm{HB}}$$

(4)

On the other hand, the Gibbs energy of specific interaction is found from the binding degree of A in S, α^A/S (in this work, mole fraction scale is adopted for both equilibrium constants and binding degrees; K_HB = α^A/S/(1 − α^A/S)) (Equation (5)):

$${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{G}^{\mathrm{A}/\mathrm{S}}=RT\ln (1-{\alpha }^{\mathrm{A}/\mathrm{S}})$$

(5)

Then, Δ_int(sp)f^A/S and Δ_HBf^A/S are connected by Equations (6) and (7):

$${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{G}^{\mathrm{A}/\mathrm{S}}=-RT\ln \left[\exp \left(-{\displaystyle \frac{{\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}/\mathrm{S}}}{RT}}\right)+1\right]$$

(6)

$${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{H}^{\mathrm{A}/\mathrm{S}}={\alpha }^{\mathrm{A}/\mathrm{S}}·{\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}\text{-}\mathrm{S}}={\displaystyle \frac{{\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}/\mathrm{S}}}{\exp \left(\frac{{\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}/\mathrm{S}}}{RT}\right)+1}}$$

(7)

The solvophobic effect primarily contributes to the Gibbs energies of solvation in associated solvents. In works [27,28], a simple method for calculating Δ_s.e.G^A/S was proposed (Equation (8)):

$${\Delta }_{\mathrm{s}.\mathrm{e}.}{G}^{\mathrm{A}/\mathrm{S}}=k_{\mathrm{S}}\cdot V_{\mathrm{x}}^{\mathrm{A}}+b_{\mathrm{S}}$$

(8)

where V_x^A is the McGowan volume of solute [29] and k_S and b_S are solvent-defined empiric parameters; b_S is close to 0 and k_S depends on hydrogen bonding network density [27]. The V_x, k_S, and b_S values used in this work for evaluating Δ_s.e.G^A/S are presented in Tables S1 and S2. k_S and b_S values for octanol, initially derived in Ref. [27], were updated. The previous estimates were based on the solvation enthalpies and Gibbs energies of octane in a set of organic solvents, whose uncertainty, due to the small solvophobic effect, notably influences Δ_s.e.G^A/S vs. V_x^A fitting quality. k_S = 1.4·10⁻² kJ·cm⁻³ was found from the correlation with hydrogen bond concentration in the neat liquid [27] and b_S was set to zero (see Table S1).

In this work, we did not consider the solvation processes in water and formamide. These solvents surprisingly also exhibit an enthalpic solvophobic effect [27].

Thus, the above framework enables the detailed analysis of the compensation relationship between the enthalpies and Gibbs energies of specific and nonspecific interactions after excluding the contribution of the solvophobic effects using Equation (8).

2.2. Compensation Relationships Between Δ_solvG and Δ_solvH of Organic Non-Electrolytes

In Ref. [24], we showed that, in the absence of A-S and S-S HB, for aromatic/heteroaromatic, short-chained aliphatic compounds, and inert gases, Equation (9) held for Δ_solvG^A/S and Δ_solvH^A/S:

Δ_solvG^A/S/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0

(9)

N = 586, RMSD (the root-mean-square deviation) = 1.0 kJ·mol⁻¹.

When A forms strong HB (α ≈ 1) with a non-associated solvent S, Equation (10) is valid:

Δ_solvG^A/S/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0 + 2.5n

(10)

where 2.5n is the enthalpy-independent contribution to the Gibbs energy of solvation due to HB. n is the number of HB formed by a molecule A with a solvent. Equation (10) held for 62 solutes exhibiting HB with non-associated solvents within 1 kJ·mol⁻¹ [24].

Since Equation (9) covers the systems exhibiting van der Waals interactions only, one can write Equation (11):

Δ_solv(nonsp)G^A/S/(kJ·mol⁻¹) = 0.660·Δ_solv(nonsp)H^A/S/(kJ·mol⁻¹) + 17.0

(11)

As long as Equation (2) holds and no solvent association (and Δ_s.e.f^A/S) is present, subtraction of Equation (11) from Equation (10) leads to Equation (12):

Δ_int(sp)G^A/S/(kJ·mol⁻¹) = 0.660·Δ_int(sp)H^A/S/(kJ·mol⁻¹) + 2.5n

(12)

At α ≈ 1 (strong hydrogen bonding), Δ_int(sp)f^A/S ≈ Δ_HBf^A/S. Further, Δ_HBf^A/S in pure S base media was repeatedly shown to match Δ_HBf^A·S in tetrachloromethane. Therefore, in our recent works [30,31,32,33], we checked the validity of Equation (13) connecting Δ_HBG^A···S and Δ_HBH^A·S in inert solvents:

Δ_HBG^A···S/(kJ·mol⁻¹) = 0.660·Δ_HBG^A···S/(kJ·mol⁻¹) + 2.5

(13)

Moreover, its validity for charge-transfer complexes was confirmed. The binding enthalpies of more than 866 acid-base pairs could be calculated from the Gibbs energies at 298.15 K with an RMSD of 1.5 kJ·mol⁻¹.

Association of the solvent influences Equations (9)–(12). For the solvation of a non-hydrogen-bonding solute A in an associated S, Equation (11) holds [24]:

(Δ_solvG^A/S − Δ_s.e.G^A/S)/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0

(14)

Thermodynamics of proton-donating solutes A solvation in associated solvents S is described by Equation (12) [24]:

(Δ_solvG^A/S − Δ_s.e.G^A/S)/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0 + 2.5n

(15)

The goal of the present work is find a quantitative relationship between Δ_solvG^A/S and Δ_solvH^A/S of proton acceptors in associated solvents, namely alcohols. There is a clue difference in the mechanism and possibly thermodynamics of solvation of proton acceptors and proton donors in alcohols. Monohydric alcohols bear two lone pairs and a single acidic proton, i.e., there is an excess of lone pairs in solution. Thus, proton donors do not interfere in alcohol self-association, at least as long as there are no significant steric hindrances between the proton donor and another alcohol molecule bound to the OH group. However, proton acceptors would compete with alcohol molecules for the acidic protons, which are a minority.

The quality of the established relationship was tested against the available literature data on Δ_solvG^A/S and Δ_solvH^A/S, using RMSD and average deviation (AD) as metrics (Equations (13) and (14)):

$$RMSD=\sqrt{{\displaystyle \frac{\Sigma {[{\Delta }_{\mathrm{solv}}H(\mathrm{calc})-{\Delta }_{\mathrm{solv}}H(\mathrm{lit})]}^2}{N-1}}}$$

(16)

$$AD={\displaystyle \frac{\Sigma [{\Delta }_{\mathrm{solv}}H(\mathrm{calc})-{\Delta }_{\mathrm{solv}}H(\mathrm{lit})]}{N}}$$

(17)

3. Results

The data on Δ_solvH^A/S and Δ_solvG^A/S were taken from Refs. [34,35,36,37,38,39,40,41,42,43,44,45]. The values are listed in

Table 1. The Gibbs energies and enthalpies of solvation of proton acceptors in aliphatic alcohols at 298.15 K, solvophobic effect Gibbs energies calculated according to Equation (8), and the differences between the Gibbs energies of solvation corrected for solvophobic effects and found according to Equation (9).

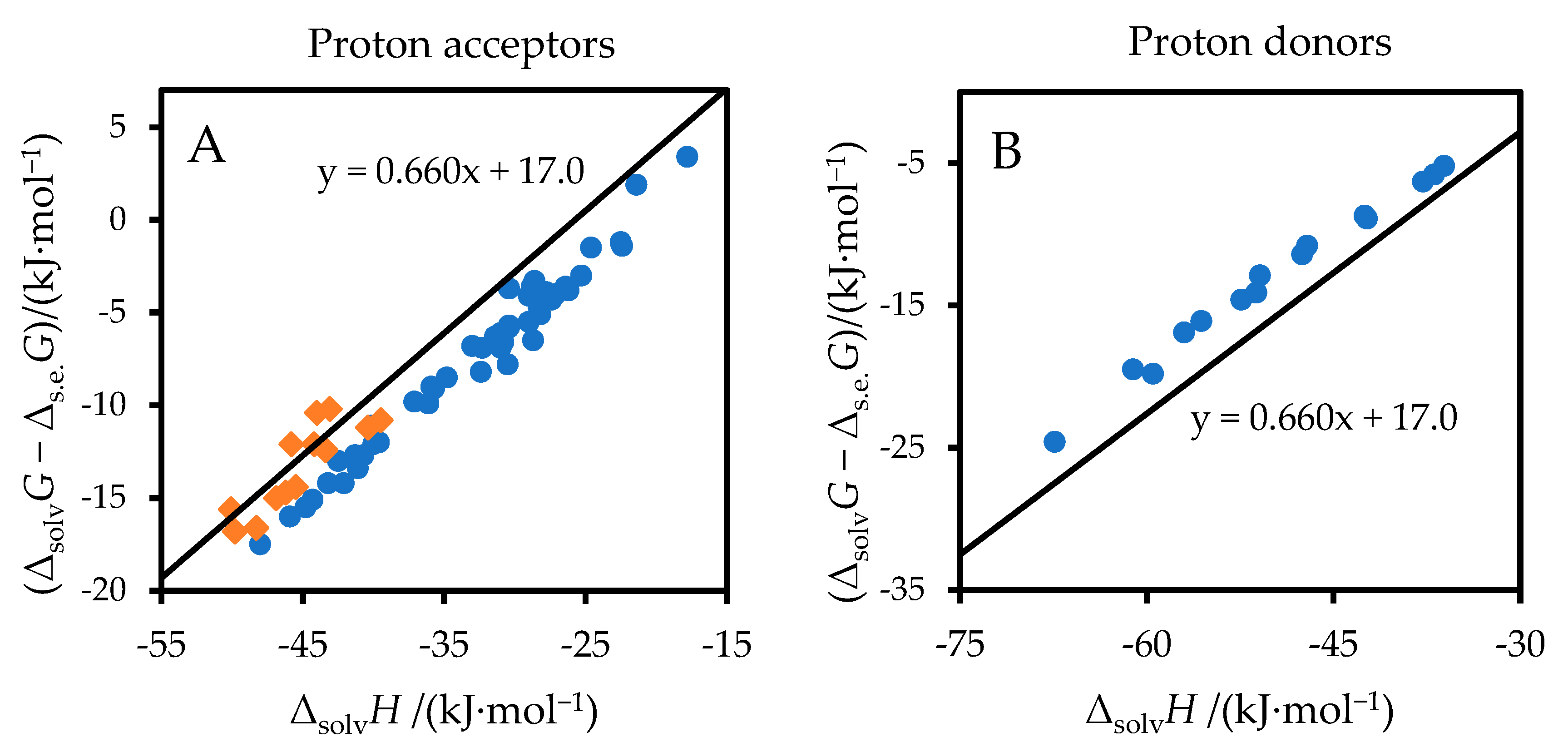
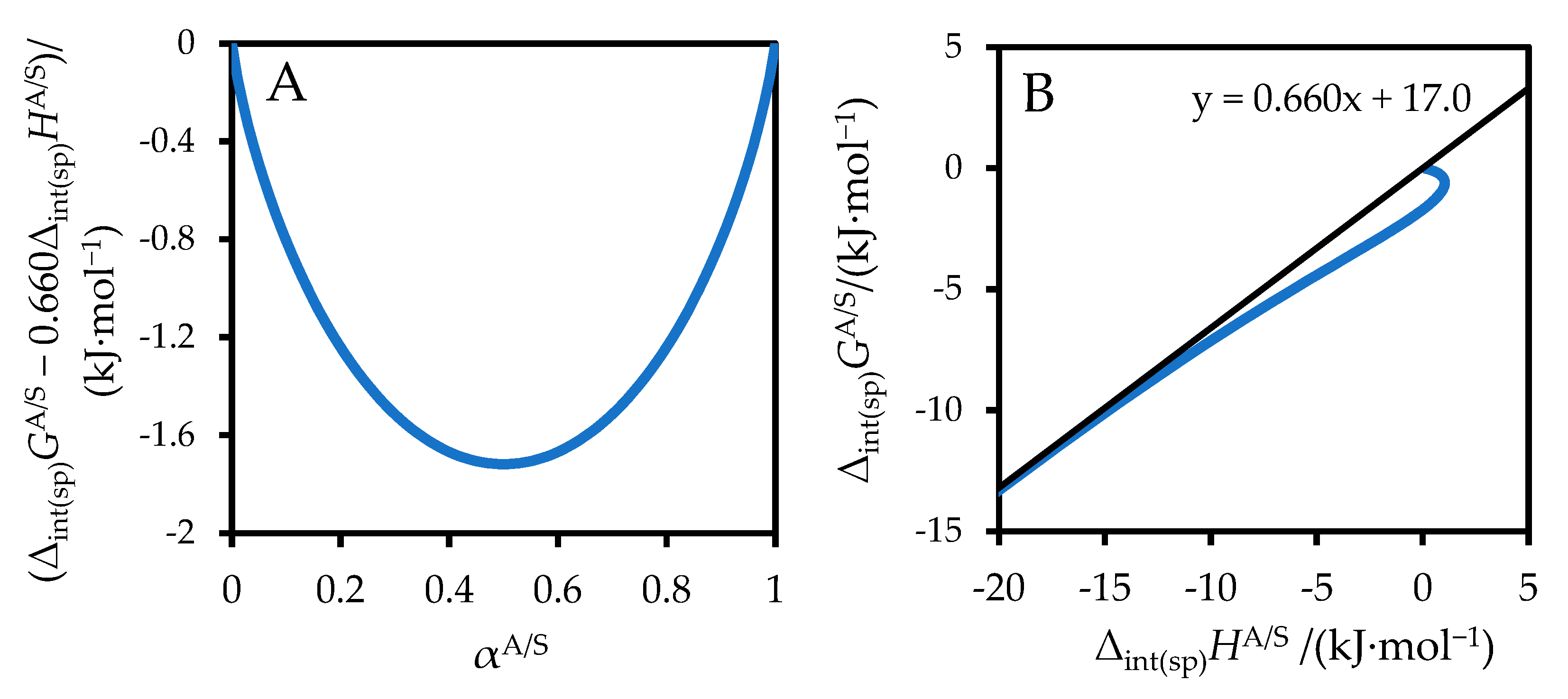
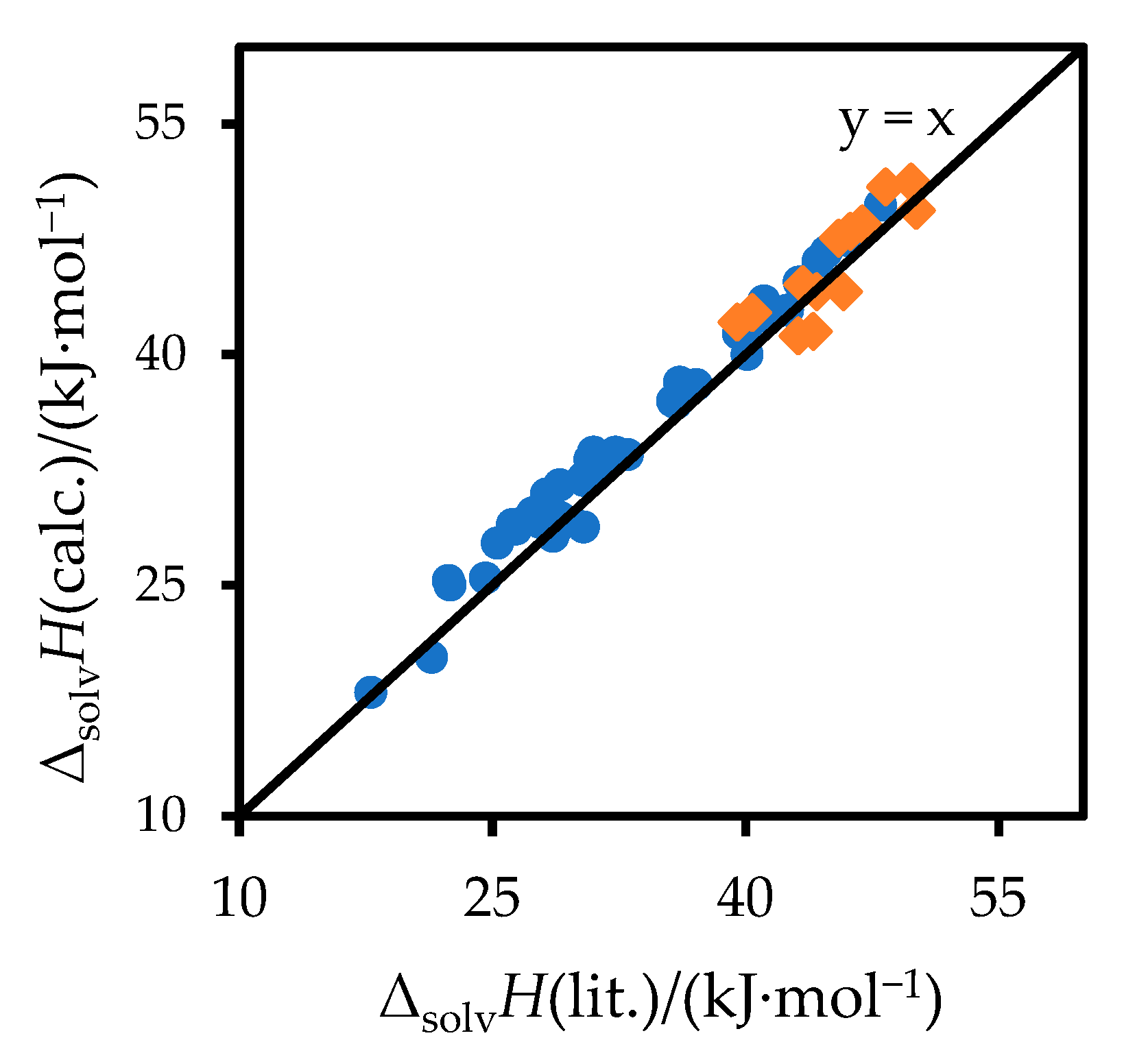
Solute	Solvent	−ΔsolvG (Lit)	Δs.e.G (Equation (8))	Δs.e.G − ΔsolvGA/S(Lit)	−ΔsolvH (Lit)	Δs.e.G − ΔsolvGA/S (Equation (14))	Δ a	Ref. ΔsolvH	Ref. ΔsolvG
		kJ·mol−1
Pyridine	Methanol	8.4	3.7	12.1	44.2	12.2	−0.1	[42,46], this work	[39]
2-Methylpyridine	Methanol	11.2	4.4	15.6	50.1	16.1	−0.4	[40,41]	[39]
3-Methylpyridine	Methanol	12.4	4.4	16.8	49.8	15.9	1.0	[37]	[39]
2-Hexanone	Methanol	5.9	5.2	11.1	40.1	9.5	1.7	[42]	[35]
2-Heptanone	Methanol	9.1	6.0	15.1	44.3	12.2	2.8	[42]	[35]
2-Pentanone	Methanol	4.5	4.5	9.0	35.9	6.7	2.4	[42]	[43]
4-Heptanone	Methanol	8.2	6.0	14.2	43.2	11.5	2.7	[42]	[43]
Acetone	Methanol	0.6	3.1	3.6	28.8	2.0	1.6	[42]	[35]
Butanone	Methanol	3.2	3.8	6.9	32.3	4.3	2.7	[42]	[35]
Butyl acetate	Methanol	6.5	5.5	12.1	40.0	9.4	2.7	[37]	[35]
N,N-Dimethylformamide	Methanol	13.9	3.6	17.5	48.0	14.7	2.9	[36]	[43]
Methyl acetate	Methanol	0.8	3.4	4.1	29.0	2.1	2.0	[42]	[35]
Methyl pentanoate	Methanol	6.4	5.5	12.0	39.6	9.1	2.8	[37]	[35]
Propyl acetate	Methanol	4.2	4.8	9.1	35.7	6.6	2.5	[37]	[35]
Tetrahydrofuran	Methanol	2.6	3.4	6.1	31.0	3.5	2.7	[42]	[35]
Acetonitrile	Methanol	1.0	2.3	3.3	28.6	1.9	1.4	[42]	[35]
1,4-Dioxane	Methanol	4.8	3.8	8.5	34.8	6.0	2.5	[42]	[35]
Pyridine	Ethanol	8.9	3.5	12.4	43.4	11.6	0.7	[42]	[35]
2-Methylpyridine	Ethanol	10.9	4.1	15.0	46.9	14.0	1.0	[37]	[39]
3-Methylpyridine	Ethanol	12.5	4.1	16.6	48.3	14.9	1.7	[37]	[39]
Triethylamine	Ethanol	5.4	5.0	10.4	44.0	12.0	−1.6	[42]	[35]
Acetone	Ethanol	0.8	3.0	3.8	26.2	0.3	3.5	[42]	[35]
Butanone	Ethanol	3.0	3.6	6.6	30.8	3.3	3.3	[42]	[35]
Acetonitrile	Ethanol	1.6	2.4	4.0	27.1	0.9	3.1	[42]	[35]
N,N-Dimethylformamide	Ethanol	12.1	3.4	15.5	44.8	12.6	3.0	[42]	[43]
Tetrahydrofuran	Ethanol	2.4	3.3	5.7	30.4	3.1	2.6	[42]	[43]
Ethyl acetate	Ethanol	2.0	3.8	5.8	30.4	3.1	2.7	[42]	[35]
1,4-Dioxane	Ethanol	4.6	3.5	8.2	32.4	4.4	3.8	[44]	[35]
Pyridine	1-Butanol	8.7	2.6	11.2	40.4	9.7	1.6	[42]	[35]
2-Methylpyridine	1-Butanol	11.7	3.0	14.7	46.2	13.5	1.2	[40,41]	[39]
Triethylamine	1-Butanol	6.4	3.7	10.2	43.1	11.4	−1.3	[42]	[35]
Butylamine	1-Butanol	9.2	2.9	12.1	45.8	13.2	−1.1	[42]	[38]
Acetone	1-Butanol	0.8	2.2	3.0	25.3	−0.3	3.2	[42]	[35]
Butyl ether	1-Butanol	8.5	4.5	13.0	42.5	11.1	1.9	[42]	[35]
Ethyl acetate	1-Butanol	2.7	2.8	5.5	29.0	2.1	3.4	[42]	[35]
Methyl ether	1-Butanol	−5.3	1.9	−3.4	17.8	−5.3	1.8	[42]	[35]
Propionitrile	1-Butanol	2.9	2.2	5.1	28.2	1.6	3.5	[44], this work	[43]
1,4-Dioxane	1-Butanol	5.2	2.6	7.8	30.5	3.1	4.7	[44], this work	[35]
Pyridine	1-Octanol	9.8	1.0	10.8	39.5	9.1	1.7	[36]	[39]
2-Methylpyridine	1-Octanol	13.2	1.2	14.4	45.5	13.0	1.3	[40,41]	[39]
Acetone	1-Octanol	0.7	0.8	1.4	22.4	−2.2	3.7	[34]	[35]
Butanone	1-Octanol	3.3	1.0	4.3	27.4	1.1	3.2	[34]	[35]
2-Pentanone	1-Octanol	5.7	1.2	6.9	31.0	3.5	3.4	[34]	[35]
2-Hexanone	1-Octanol	8.5	1.4	9.9	36.1	6.8	3.0	[34]	[35]
2-Heptanone	1-Octanol	11.2	1.6	12.7	40.7	9.9	2.9	[36]	[35]
Acetonitrile	1-Octanol	0.7	0.6	1.2	22.5	−2.2	3.4	[37]	[35]
Propionitrile	1-Octanol	2.8	0.8	3.6	26.4	0.4	3.2	[37]	[35]
2-Octanone	1-Octanol	14.2	1.8	16.0	45.9	13.3	2.7	[37]	[38]
Methyl acetate	1-Octanol	0.7	0.9	1.5	24.6	−0.8	2.3	[34]	[35]
Propyl acetate	1-Octanol	5.6	1.3	6.8	33.0	4.8	2.0	[34]	[35]
Butyl acetate	1-Octanol	8.3	1.5	9.8	37.1	7.5	2.3	[34]	[35]
Butyronitrile	1-Octanol	5.3	1.0	6.3	31.4	3.7	2.5	[34]	[35]
Ethyl acetate	1-Octanol	2.9	1.1	3.9	27.8	1.3	2.6	[34]	[35]
Pentyl acetate	1-Octanol	11.0	1.7	12.7	41.3	10.3	2.4	[34]	[35]
Propyl formate	1-Octanol	2.6	1.1	3.7	30.4	3.1	0.7	[34]	[35]
Methyl formate	1-Octanol	−2.6	0.7	−1.9	21.4	−2.9	1.0	[34]	[35]
Tetrahydrofuran	1-Octanol	3.8	0.9	4.7	28.3	1.7	3.0	[34]	[35]
N,N-Dimethylformamide	1-Octanol	12.5	0.9	13.4	41.1	10.1	3.3	[37]	[35]
Benzonitrile	1-Octanol	12.9	1.3	14.2	42.1	10.8	3.4	[37]	[35]
1,4-Dioxane	1-Octanol	5.6	1.0	6.5	28.7	1.9	4.6	[34]	[35]

^a The difference between columns 7 and 5.

(columns 3 and 5). In addition, the data obtained in this work are included in Table 1. For several systems, Δ_solvH^A/S were taken not directly from the literature but calculated from vaporization and solution enthalpies (see Table S3).

Δ_s.e.G calculated according to Equation (8) are listed in column 4. In column 6, the differences Δ_solvG^A/S(lit) − Δ_s.e.G are provided. In column 7, the deviations between the latter differences and the values calculated from Δ_solvH(lit) using Equation (9) are shown.

The data on 60 solute–solvent pairs were collected in total. In Figure 1A, the Δ_solvG^A/S(lit) − Δ_s.e.G values are plotted against Δ_solvH^A/S(lit). The solid line corresponds to Equation (14). In Figure 1B, an analogous comparison is made for proton donors solvated in alcohols with the data taken from Ref. [25].

In contrast with proton donors, obeying Equation (15), for most proton acceptors, the Δ_solvG^A/S(lit) − Δ_s.e.G values are either nearly on or below the line given by Equation (14): Δ_solvG^A/S − Δ_s.e.G = 0.660·Δ_solvH^A/S + 17.0 kJ·mol⁻¹. It is reflected in the magnitudes of the deviation Δ = − [(Δ_solvG^A/S(lit) − Δ_s.e.G) − (0.66·Δ_solvH + 17 kJ·mol⁻¹)] (column 8).

The Δ values are closer to 0 for strong proton acceptors. Average deviation for 13 solute–solvent systems containing pyridine, 2-methylpyridine, 3-methylpyridine, triethylamine, and n-butylamine as solutes is 0.4 kJ·mol⁻¹. The quantitative measure of proton accepting ability of amines and pyridines in alcohol medium is α > 0.8 (i.e., Δ_int(sp)G < −4 kJ·mol⁻¹) [47].

For 47 other solutes (α < 0.8), the Δ values are positive (corresponding to negative deviations from Equation (14)). The most positive deviations (2.5–4.5 kJ·mol⁻¹) are seen for 1,4-dioxane, carrying the two distant proton-accepting atoms. For other 43 solutes, including ketones, esters, ethers, amides, and nitriles, the average deviation is 2.6 kJ·mol⁻¹. The model predicting such behavior based on the framework given in Section 2 is proposed below.

4. Discussion

Since there two lone pairs and single acidic proton in an alkanol molecule, solvation of a proton acceptor A in an alcohol S can result in breaking some of S_n associates into smaller counterparts S_m and S_n-m (Equation (18)):

$${\mathrm{A}}_{(\mathrm{S})}+{\mathrm{S}}_{\mathrm{n}(\mathrm{S})}\rightleftarrows \mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}(\mathrm{S})}+{\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}(\mathrm{S})}$$

(18)

Otherwise, no A-S hydrogen bonds are formed.

Reaction (18) can be represented as a sum of two hydrogen bonding equilibria:

$${\mathrm{S}}_{\mathrm{m}}\cdots {\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}(\mathrm{S})}\rightleftarrows {\mathrm{S}}_{\mathrm{m}(\mathrm{S})}+{\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}(\mathrm{S})}$$

(19)

$${\mathrm{A}}_{(\mathrm{S})}+{\mathrm{S}}_{\mathrm{m}(\mathrm{S})}\rightleftarrows \mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}(\mathrm{S})}$$

(20)

Then, the Gibbs energy of reaction (18) (Δ_HBG^A/S) can be represented as the difference between ${\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}}}$ and ${\Delta }_{\mathrm{HB}}{G}^{{\mathrm{S}}_{\mathrm{m}}\cdots {\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}}}$:

$${\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}/\mathrm{S}}={\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}}}-{\Delta }_{\mathrm{HB}}{G}^{{\mathrm{S}}_{\mathrm{m}}\cdots {\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}}}$$

(21)

The same applies to the enthalpies:

$${\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}/\mathrm{S}}={\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}}}-{\Delta }_{\mathrm{HB}}{H}^{{\mathrm{S}}_{\mathrm{m}}\cdots {\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}}}$$

(22)

For each process (19) and (20), the compensation relationships given by the general Equation (13) are expected to hold:

$${\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}}}/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})=0.660 \cdot {\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}\cdots {\mathrm{S}}_{\mathrm{m}}}/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})+2.5$$

(23)

$${\Delta }_{\mathrm{HB}}{G}^{{\mathrm{S}}_{\mathrm{m}}\cdots {\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}}}/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})=0.660 \cdot {\Delta }_{\mathrm{HB}}{H}^{{\mathrm{S}}_{\mathrm{m}}\cdots {\mathrm{S}}_{\mathrm{n}\text{-}\mathrm{m}}}/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})+2.5$$

(24)

Their subtraction leads to Equation (25):

$${\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}/\mathrm{S}}=0.660\cdot {\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}/\mathrm{S}}$$

(25)

Considering Equations (6) and (7), at α ≈ 1, Equation (25) can be transformed as follows:

$${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{G}^{\mathrm{A}/\mathrm{S}}=0.660\cdot {\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{H}^{\mathrm{A}/\mathrm{S}}$$

(26)

Then, the total solvation enthalpies of strong proton acceptors in alcohols are expected to obey Equation (14): (Δ_solvG^A/S − Δ_s.e.G^A/S)/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0. This is indeed correct for pyridine, 2-methylpyridine, 3-methylpyridine, triethylamine, and n-butylamine solvated in alkanols, as seen from Table 1 and Figure 1A. In this case, an additional term of 2.5 kJ·mol⁻¹ is cancelled due to alcohol-alcohol HB disruption and alcohol-proton acceptor HB formation.

In the general case (0 < α < 1), ${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{H}^{\mathrm{A}/\mathrm{S}}$ can be expressed through α, using Equations (4), (7) and (25):

$${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{H}^{\mathrm{A}/\mathrm{S}}=\alpha \cdot {\Delta }_{\mathrm{HB}}{H}^{\mathrm{A}/\mathrm{S}}={\displaystyle \frac{\alpha \cdot {\Delta }_{\mathrm{HB}}{G}^{\mathrm{A}/\mathrm{S}}}{0.660}}={\displaystyle \frac{\alpha RT}{0.660}}\ln ({\displaystyle \frac{\alpha }{1-\alpha }})$$

(27)

while ${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{G}^{\mathrm{A}/\mathrm{S}}=RT\ln (1-{\alpha }^{\mathrm{A}/\mathrm{S}})$ (Equation (5)).

Thus, both ${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{H}^{\mathrm{A}/\mathrm{S}}$ and ${\Delta }_{\mathrm{int}\left(\mathrm{sp}\right)}{G}^{\mathrm{A}/\mathrm{S}}$ are represented as a function of α. In Figure 2A, the differences of Δ_int(sp)G^A/S (Equation (5)) − 0.66 · Δ_int(sp)H^A/S (Equation (27)) are plotted vs. α^A/S. In Figure 2B, Δ_int(sp)G^A/S (Equation (5)) vs. Δ_int(sp)H^A/S (Equation (27)).

The differences are 0 at α^A/S = 0 and α^A/S = 1. In these cases, the total solvation Gibbs energies and enthalpies should obey Equation (14), as observed experimentally (α^A/S = 0 means that there are no specific interactions between solute and solvent; α^A/S = 1 corresponds to strong proton acceptors discussed above).

At the intermediate α^A/S values, negative deviations arise between Δ_int(sp)G^A/S (Equation (5)) and 0.660 · Δ_int(sp)H^A/S (Equation (27)). They reach −1.7 kJ·mol⁻¹ and are pronounced at 0.1 < α^A/S < 0.9, i.e., −5.7 kJ·mol⁻¹ < Δ_int(sp)G^A/S < −0.3 kJ·mol⁻¹. In this case, Equation (28) would describe the dependence between total solvation enthalpies and Gibbs energies:

(Δ_solvG^A/S − Δ_s.e.G^A/S)/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0 − 1.7

(28)

The negative deviations from the line given by Equation (14) qualitatively and quantitatively agree with the observations for the weaker proton acceptors in Table 1. The slightly greater deviations in the case of 1,4-dioxane may be caused by partial binding of its second oxygen atom.

It is important to highlight that the deviations from Equation (14) predicted by Equations (27) and (28) are not directly connected to the enthalpy of hydrogen bonding. Equation (28) is a straightforward consequence of Equation (25), arising when the competition for hydrogen bonding sites is present in solution.

Equations (14) and (28) may be rearranged to enable the calculation of Δ_solvH^A/S of proton acceptors in alcohols from Δ_solvG^A/S measured at 298.15 K.

Strong proton acceptors (binding degree > 0.9):

$${\Delta }_{\mathrm{solv}}{H}^{\mathrm{A}/\mathrm{S}}/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})={\displaystyle \frac{({\Delta }_{\mathrm{solv}}{G}^{\mathrm{A}/\mathrm{S}}-{\Delta }_{\mathrm{s}.\mathrm{e}.}{G}^{\mathrm{A}/\mathrm{S}})/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})-17.0}{0.660}}$$

(29)

Weaker proton acceptors (binding degree 0.1–0.9):

$${\Delta }_{\mathrm{solv}}{H}^{\mathrm{A}/\mathrm{S}}/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})={\displaystyle \frac{({\Delta }_{\mathrm{solv}}{G}^{\mathrm{A}/\mathrm{S}}-{\Delta }_{\mathrm{s}.\mathrm{e}.}{G}^{\mathrm{A}/\mathrm{S}})/(\mathrm{kJ}\cdot {\mathrm{mol}}^{-1})-15.3}{0.660}}$$

(30)

The results of application of Equations (29) and (30) to 56 solute–solvent systems from Table 1 (excluding 1,4-dioxane) are presented in Figure 3.

RMSD between the calculated and literature values is 1.8 kJ·mol⁻¹ and AD is 1.2 kJ·mol⁻¹. Equation (30) slightly overestimates Δ_solvH^A/S of weak proton acceptors. However, its excellent predictive capability stems from the complete independence from the initial experimental data.

We expect that the methodology used for derivation of Equations (27)–(30) should apply to other associated solvents, such as carboxylic acids and primary/secondary amines. Unfortunately, only scarce data are available for such systems at the moment [43,48]. The analysis of the relationships between Δ_solvG and Δ_solvH of various molecular compounds, including proton acceptors, can be a tool for studying enthalpic manifestations of the solvophobic effect in water and formamide.

5. Conclusions

In this work, we completed a series of studies of the relationships between Δ_solvG and Δ_solvH of organic non-electrolytes. The general relationship is obtained between the thermodynamic functions of solvation of organic non-electrolytes (Equation (31)):

(Δ_solvG^A/S − Δ_s.e.G^A/S)/(kJ·mol⁻¹) = 0.660·Δ_solvH^A/S/(kJ·mol⁻¹) + 17.0 + Δ

(31)

where the residual term Δ arises in hydrogen-bonded systems and does not depend on the enthalpy of solvation or specific interaction. Equation (31) enables the calculation of Δ_solvG from Δ_solvH and vice versa.

The Δ_solvG^A/S vs. Δ_solvH^A/S relationship has the same slope for non-hydrogen-bonded systems, solutes bound with non-associated solvents, and proton acceptors/donors solvated in associated liquids. Furthermore, a combination of the results obtained in our works [24,25,26,30,31,32,33] enables the conclusion that there is a common compensation relationship in the thermodynamics of solvation and complex formation in solution. The intercepts of the relationships may change due to complex formation, but the variation is not directly connected with the enthalpies of these processes. They have a purely entropic origin (solvophobic effect, loss of freedom degrees upon complexation) or arise from incomplete complexation in the systems exhibiting competition for free protons or lone pairs.

It enables reshaping the common understanding of the compensation phenomena in thermodynamics of intermolecular interactions, which is reflected in definitions given earlier in Refs. [49]: “This compensation is perhaps more easily understood in the language of statistical mechanics, where we associate decreases in enthalpy (exothermic changes) with ‘tighter’ binding and consequently with less entropy (freedom of motion)” and [1]: “The compensation relationship should be attributed to the phenomenon in which a change in enthalpy is compensated by a corresponding change in entropy, leading to a decrease in free energy.” We believe that the compensation necessarily means an unambiguous connection between the enthalpy and the certain fraction of the Gibbs energy (or entropy, TΔS(comp.)) in a series of processes, with the remaining fraction of ΔG and ΔS being enthalpy-independent, i.e., non-compensated, TΔS(noncomp.). The latter may be contributed by the association, structural transformations processes, solvophobic effects, and the standard state choice. Notoriously, for solvation and complex formation processes we studied in Refs. [24,25,33], the slope of ΔG vs. ΔH relation did not depend on the intermolecular interaction type:

ΔG = ΔH − TΔS = ΔH − TΔS(comp.) − TΔS(noncomp.) =
0.660·ΔH − TΔS(noncomp.)

(32)

The wide applicability of such ΔG vs. ΔH relationships established in our recent works calls for deeper theoretical investigations of the compensation phenomenon.

6. Experimental

6.1. Materials

Pyridine (CAS № 110-86-1, C₅H₅N, Thermo Fisher Scientific, Waltham, MA, USA), 1,4-dioxane (CAS № 123-91-1, C₄H₈O₂, Acros), propionitrile (CAS № 107-12-0, C₃H₅N, Aldrich, St. Louis, MO, USA), methanol (CAS № 67-56-1, CH₄O, Ekos-1), and 1-butanol (CAS № 71-36-3, C₄H₁₀O, Ekos-1) were of commercial origin with a purity more than 0.99 (mole fraction). Each sample was distilled before the measurements to remove water traces and other impurities, following the standard procedures [50]. After distillation, water contents were determined by Fischer titration and did not exceed 0.05% (mole fraction). The impurity mass fraction determined by Agilent 7890 B gas chromatograph equipped with a flame ionization detector was below 0.001.

6.2. Solution Calorimetry

The solution enthalpies of proton acceptors in linear alcohols were measured at 298.15 K using a TAM III precision solution calorimeter (TA Instruments, New Castle, DE, USA). Glass ampules containing 20–60 mg of the sample were broken in the pre-thermostated glass cell filled with 100 mL of solvent (methanol or 1-butanol). There was no dependence observed between values obtained experimentally and molality of solute, which confirms achievement of infinite dilution conditions. Verification of calorimetric system was performed by measurement of the solution enthalpy of 1-propanol and potassium chloride in bidistilled water in the previous work [51]. The obtained values of the solution enthalpies in alcohols are shown in Table S4 of the Supplementary Material.