Abstract
Concentrated suspensions exhibit intriguing behaviors under external forces, including vibration and shear. While previous studies have focused primarily on cornstarch suspensions, this paper reports a novel observation that colloidal silica suspensions also exhibit dancing, bouncing, solidification, and melting under vertical vibration. Unlike cornstarch, silica particles offer high stability, controlled size distribution, and tunable surface properties, making them an ideal system for investigating these phenomena. The 70 wt.% aqueous suspensions of spherical silica particles with a diameter of 0.55 μm were subjected to controlled vertical vibration (60–100 Hz, 100–500 m/s2). High-speed video analysis revealed dynamic transitions, including melting, fingering, squirming, fragmentation, and jumping. The solidified suspension retained its shape after vibration ceased but melted upon weak vibration. This study demonstrates that such dynamic state transitions are not exclusive to starch-based suspensions but can also occur in well-defined colloidal suspensions. Our findings provide a new platform for investigating shear-thickening, jamming, and vibrational solidification in suspensions with controllable parameters. Further work is required to elucidate the underlying mechanisms.
1. Introduction
Concentrated colloidal and granular suspensions—mixtures of densely packed solid particles in a liquid—are ubiquitous in industrial and environmental processes [1,2,3] and are found in materials such as cement paste, paints, and food products [3,4]. At high particle concentrations, these systems exhibit complex rheological responses, including yield stress, shear thinning, shear thickening, and jamming, arising from particle-particle interactions, internal structure, and confinement effects [5,6,7,8,9]. Understanding and controlling such behaviors are essential for both fundamental science [10,11] and practical applications [12,13].
A well-known example is the starch suspension. It undergoes dramatic, stress-dependent transitions between fluid-like and solid-like states, including transient solidification upon impact [6,14]. Rheological studies have revealed a transition from shear-thinning at low stress to shear-thickening and eventual jamming, driven by frictional contacts and dilatancy [6,11,14,15].
Beyond rheology, cornstarch–water suspensions exhibit striking macroscopic dynamics under vertical vibration. Merkt et al. [16] reported the formation of stable surface holes that persist for thousands of vibration cycles. Von Kann et al. [17] further demonstrated that, among various dense suspensions, only cornstarch suspensions display a remarkably diverse set of dynamic phenomena—such as stable holes, rivers, fingering, and jumping motions—not observed in Newtonian or dilute systems. Climbing behavior of cornstarch–water suspensions has also been reported [18,19]. However, the biological origin and polydispersity of cornstarch pose limitations for mechanistic studies: the particles are irregular in shape, heterogeneous in size, and sensitive to environmental conditions, making them unsuitable as clean, reproducible model systems.
James et al. [20] demonstrated that interparticle hydrogen bonding is essential for the emergence of shear jamming in dense suspensions. Since cornstarch particles carry abundant hydroxyl groups, such bonding likely plays a key role in their unusual behaviors under vibration. This insight suggests that similar dynamics may arise in other hydrogen-bonding systems, such as colloidal and non-colloidal silica suspensions. In fact, granular suspension of silica and glass showed jamming and granulation at high shear stress and melting at weak vibration [21,22].
Colloidal silica suspensions offer a well-defined model system: silica particles are rigid, monodisperse, chemically stable, and possess tunable surface properties [23,24,25]. They have been successfully used for elucidating the formation of hydroclusters at the onset of shear thickening [26]. Shah et al. [27] investigated the behavior of dense colloidal silica suspensions by observing falling drops impacting onto a glass slide. Their high-speed imaging revealed a flow-to-solid transition induced by the sudden mechanical impact, providing insight into impact-induced solidification in dense suspensions. These characteristics make colloidal silica suspensions ideal for uncovering fundamental mechanisms in systems subjected to external forcing [28,29,30].
Until recently, however, it remained unclear whether colloidal silica-based systems could reproduce the intriguing dynamic behaviors observed in cornstarch–water mixtures under vibration. This question was addressed by Kobayashi et al. [31], who discovered that concentrated colloidal silica suspensions can exhibit wall-climbing motion when the container is tapped vertically. Their findings suggest that such dynamic behaviors are not exclusive to starch-based materials but can also emerge in well-characterized colloidal systems.
In this study, we build upon previous work by systematically investigating the dynamic behaviors of highly concentrated colloidal silica suspensions under vertical vibration. Through direct observation and high-speed imaging, we identify a diverse range of phenomena—including melting, fingering, squirming, fragmentation, and bouncing—depending on the vibration parameters and particle concentration. In certain regimes, the suspensions transiently solidify into structures that retain their shape after the vibration ceases, yet melt again under weak vibration. These observations suggest the presence of vibration-induced, phase-like transitions in a well-defined colloidal model system.
The results of this study demonstrate that the diverse dynamic responses previously considered unique to cornstarch–water suspensions can also be reproduced in silica-based systems. This opens the way for more precise investigations in the future, enabling deeper understanding of phenomena such as vibrational jamming, dynamic solidification, and the coupling between microstructure and flow.
2. Materials and Methods
2.1. Sample Preparation
Colloidal silica suspensions were prepared using monodisperse spherical silica particles (diameter: 0.55 μm; KE-P 50, Nippon Shokubai, Osaka, Japan) and deionized water produced by pure water production equipment (ELIX 5 Advantage 5, Millipore, Tokyo, Japan). The KE-P silica particles have been used when preparing suspensions of monodisperse spherical particles [23,25,29]. The silica powder and deionized water were added to polypropylene containers (A-6 ointment type; inner diameter: 48 mm; height: 66 mm; MI Chemical, Itami, Japan), sealed, and mixed thoroughly for at least 5 min using a planetary centrifugal mixer (AR-100, Thinky, Tokyo, Japan). This process yielded silica–water suspensions with silica concentrations of 68, 70, and 72 wt.%, each prepared at 5 g. Assuming the densities of silica and water to be 1.9 g/mL and 1.0 g/mL, respectively, the resulting volume fractions (total volumes) are 0.53 (3.4 mL), 0.55 (3.3 mL), and 0.58 (3.3 mL), respectively.
Prior to experiments, the suspensions were further homogenized using a test tube mixer (Delta mixer Se-04, Taitec, Tokyo, Japan). The pH of similarly prepared suspensions was approximately 6, as measured with a compact pH meter (Laqua Twin pH-22B, Horiba, Kyoto, Japan). At this pH and lower salt level, without adding electrolytes, silica particles in water are negatively charged, and electric double-layer repulsion contributes to the stability and suspension rheology [23,25,32].
2.2. Experiments
The prepared suspensions were subjected to controlled vertical vibration using a commercial vibration system (WaveMaker05, Asahi, Tokyo, Japan). Each sample container was affixed to the vibrating platform with double-sided adhesive tape, and an accelerometer was attached to the container lid to monitor acceleration. The vibration frequency was varied at 60, 70, 80, 90, and 100 Hz, and the corresponding acceleration levels were set to approximately 100, 200, 300, 400, and 500 m/s2. The corresponding vibration amplitudes, calculated from the frequency and acceleration settings, ranged from 0.25 mm (at 100 Hz and 100 m/s2) to 3.5 mm (at 60 Hz and 500 m/s2). All vibration experiments were conducted at least one day after sample preparation to allow the suspension to equilibrate.
The dynamic behavior of the suspension within the container was visually observed for approximately one minute under each set of conditions. The suspensions exhibited various dynamic responses, including vigorous surface waves resembling those of water, undulating motions reminiscent of dancing, and bouncing while forming compact, clustered shapes. The bouncing/jumping was most attractive to us. Thus, these behaviors were classified into three categories: “no dance, no jump,” “dance-like,” and “jump”. A state diagram in the acceleration–frequency space was constructed for each particle concentration.
To further analyze the development of the jumping behavior and the accompanying shape transformation—particularly the rounding of the suspension—a high-speed camera (EX-F1, Casio, Tokyo, Japan) operating at 300 fps was used to record videos under the conditions that produced the most pronounced jumping behavior (70 wt.%, 80 Hz, 500 m/s2).
To quantify the shape transformation, we computed the time evolution of solidity, defined as the ratio of the projected area of the suspension to the area of its convex hull. Solidity was calculated frame-by-frame using ImageJ ver. 1.54f. A higher solidity indicates a more compact and rounded shape, whereas a lower value reflects a more irregular or fragmented configuration.
In addition, the steady shear viscosities of the 68 and 70 wt.% suspensions were measured to determine whether they exhibit shear thickening behavior. Viscosity as a function of shear rate was measured using a rheometer equipped with a concentric-cylinder geometry (ONRH-1, Ohna Tech, Tsukuba, Japan). The suspension was placed in the gap between the two cylinders and sheared by rotating the outer glass cylinder. All rheological measurements were performed on the day of sample preparation.
All the experiments were carried out in an air-conditioned room at 293 K.
3. Results and Discussion
3.1. State Diagram and Visocisty
The state diagram is shown in Figure 1. At 68 wt.%, the suspension exhibited surface waves under vertical vibration. These wave patterns probably resembled nonlinear Faraday waves [17]. No squirming or jumping behavior was observed under the applied vibration conditions at this concentration, suggesting that the suspension remained in a fluid-like, unstructured state throughout. It appeared to flow easily and did not exhibit any noticeable yield-stress behavior.
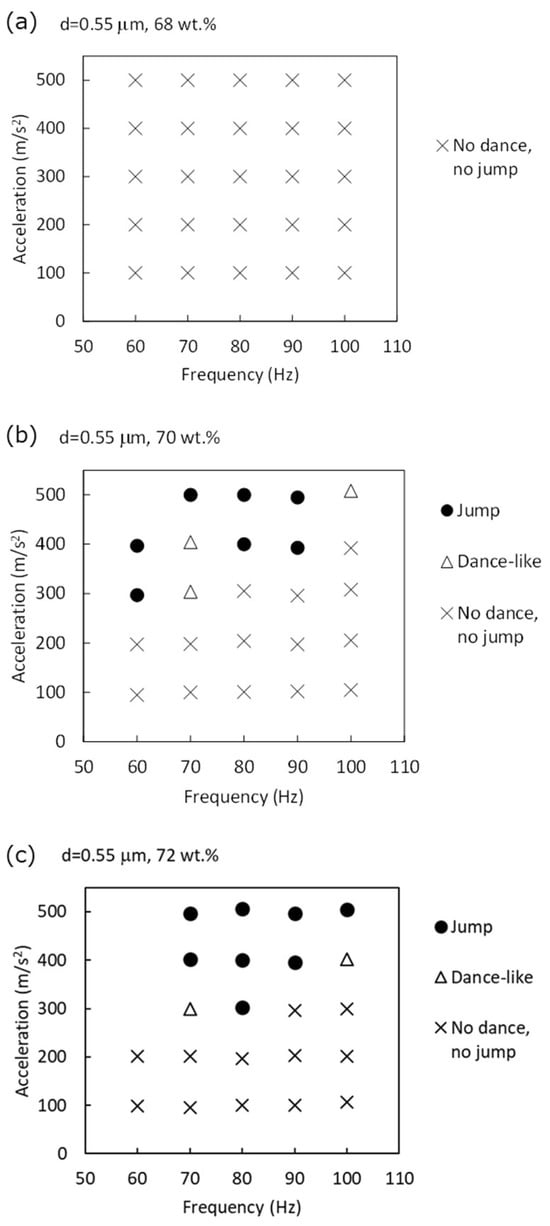
Figure 1.
State diagram of dynamic behaviors exhibited by colloidal silica suspensions under vertical vibration. Behavioral regimes—no dance/no jump, dance-like, and jump—are mapped as a function of acceleration and vibration frequency. Results are shown for suspensions with silica concentrations of (a) 68, (b) 70, and (c) 72 wt.%.
In contrast, at silica concentrations of 70 and 72 wt.%, the suspensions exhibited distinct dynamic behaviors not seen at 68 wt.%. At vibration accelerations above approximately 300 m/s2, dance-like squirming emerged. When the acceleration was further increased to 400–500 m/s2, portions of the suspension detached from the main body and began jumping in the container. These fragments eventually coalesced into a bouncing mass that became progressively more compact and rounded over time, indicative of a transition toward a dynamically solidified state. This aspect will be addressed in the following section.
The steady shear viscosities of the 68 wt.% and 70 wt.% suspensions are plotted in Figure 2. The plot confirms that the viscosity data of the 68 wt.% suspension exhibits shear-thinning behavior only. Meanwhile, the 70 wt.% suspension exhibits shear thickening behavior, consistent with expectations for dense colloidal systems. Data points corresponding to the highest shear rates were excluded, as flow cessation likely due to jamming was observed under these conditions. After the high-shear measurements, separation of suspension was observed. The absence of shear thickening and jumping behavior in the 68 wt.% sample supports the idea that shear thickening is necessary for the onset of jumping. However, in our preliminary experiments using silica particles with a diameter of 1.0 μm, we observed shear thickening but no significant jumping behavior (e.g., the suspension did not reach the lid). This result suggests that shear thickening alone is not sufficient for higher jumping, and other factors such as particle size may also play an important role.
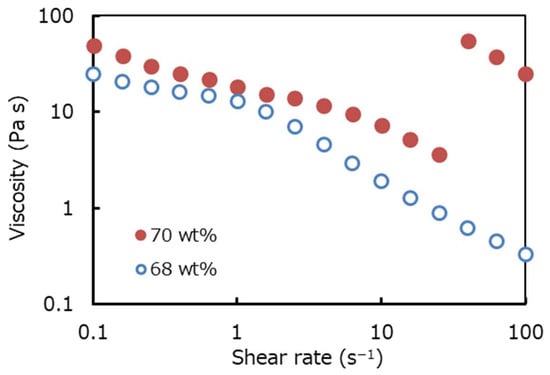
Figure 2.
Steady shear viscosities of the 68 wt.% and 70 wt.% silica suspensions as a function of shear rate. The suspension exhibits non-Newtonian rheology, showing shear thinning at low shear rates and shear thickening at higher shear rates for 70 wt.% suspension.
3.2. Dynamic Behavior Under Vertical Vibration
The behavior of the 70 wt.% silica suspension under vertical vibration at 80 Hz and 500 m/s2 is presented in Movies S1 and S2 (Supplementary Information), with representative snapshots shown in Figure 3. The dynamic sequence is described below.

Figure 3.
Snapshots at different times showing vibration-induced dynamic transitions in a 70 wt.% silica suspension. Under vertical vibration at 80 Hz and 500 m/s2, the suspension undergoes melting, fingering, squirming, fragmentation, jumping, and eventual spheroidization. Time is indicated in each frame. See also Movie S1.
At the initial state (0 s), the suspension behaved like a yield-stress fluid, resisting gravitational flow and maintaining a tilted suspension–air interface within the container. Upon applying vertical vibration, the suspension began to flow (~2 s), indicating a transition from a solid-like to a liquid-like state.
As the vibration continued, finger-like protrusions began to grow upward from the suspension surface (~13.4 s), accompanied by writhing, undulating motion. Eventually, fragments of the suspension detached from the main body and began bouncing within the container (~17–20 s). These fragments gradually coalesced, forming a compact mass that repeatedly jumped (~20 s onward). Interestingly, this compact mass retained its shape even after the vibration ceased, but it melted and flowed down under weak vibration, as shown in Movie S2.
Over time, the compact mass became increasingly rounded, suggesting a self-organized spheroidization process. The time evolution of solidity is shown in Figure 4. Due to the irregular and extended shapes associated with finger formation and writhing motion, the solidity decreased to ~0.5 by 15 s. As the fragments coalesced during repeated jumping, the solidity steadily increased, reaching ~0.9, indicating the emergence of a more compact, spheroidal structure.
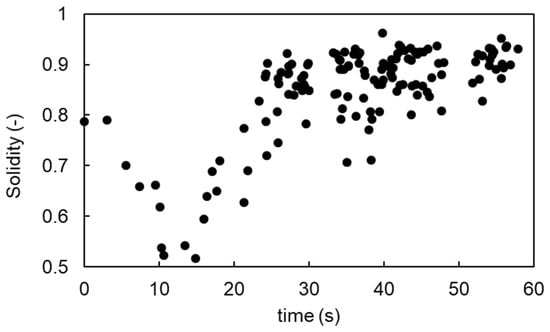
Figure 4.
Time evolution of solidity during vibration-induced shape transformation. Solidity is defined as the ratio of the projected area to the convex hull area of the suspension. An initial decrease reflects irregular fingering and squirming, while a subsequent increase indicates compaction and spheroidization of the jumping mass. See also Figure 3 for the corresponding snapshots.
This sequence of behaviors—yield-stress-like immobility, vibration-induced flow, finger formation, fragmentation, jumping, and spheroidization—has not been reported previously in simple colloidal silica suspensions and may represent a new class of vibration-induced phase-transition-like phenomena.
Finger-like protrusions consistently appeared prior to the onset of jumping, suggesting localized stress concentration and deformation within the suspension. These features may be associated with transient jamming and internal force redistribution under vibration. Although no stable surface holes were observed, the progression from finger formation to fragmentation and jumping bears intriguing similarities to the behavior previously reported for vibrated cornstarch in water suspensions [17].
In particular, Merkt et al. [16] reported the formation of persistent surface holes and finger-like instabilities in granular glass sphere or cornstarch suspensions under vertical vibration. Although hole formation was not reproduced in our system, the underlying physical mechanisms—such as shear-induced jamming, nonlinear surface responses, and localized pattern formation—may be shared. The absence of holes in our observations may be due to the differences in the volume of suspensions.
The emergence of dynamic structuring—such as finger formation and jumping—in colloidal silica suspensions composed of hard, spherical, and inorganic colloidal particles suggests that pattern formation under vertical vibration arises from shear jamming through a complex interplay of general mechanical interactions, such as frictional and adhesive particle constraints, capillary forces, and fluid-mediated interparticle motion. This interpretation is consistent with previous studies on granular suspensions by Hodgson et al. [22], Garat et al. [21], James et al. [20] and Majumdar et al. [15]. Hodgson et al. [22] and Garat et al. [21] demonstrated that shear jamming at high stress induces the formation of granules, which can subsequently melt under weak vibration. James et al. [20] showed that shear jamming in dense suspensions is promoted by interparticle hydrogen bonding. Majumdar et al. [15] reported that shear jamming transitions are often accompanied by the inward fluid motion and the occurrence of capillary force constraining particles. Although silica is an inorganic material, its surface silanol groups (Si–OH) can form hydrogen bonds, potentially contributing to transient interparticle adhesion. Furthermore, in colloidal-scale systems, the narrow interparticle gaps can impede fluid flow, thereby stabilizing and prolonging the jammed state, which is melted by weak vibration.
In summary, the vibration-induced dynamic transitions observed in silica suspensions at 70 and 72 wt.%—including finger formation, fragmentation, jumping, and spheroidization—demonstrate that such behaviors are not exclusive to granular starch–water suspensions but can also emerge in inorganic colloidal suspensions. Although not all phenomena previously reported in starch-based suspensions were reproduced, our findings suggest that the fundamental physical principles driving dynamic structure formation under vibration may be broadly applicable to a wide range of dense particulate suspensions.
In the present setup, the influence of vertical container walls cannot be completely eliminated. While this may be viewed as a limitation, we note that in many practical and industrial applications, colloidal suspensions are also confined within vessels where such boundary effects are unavoidable. Therefore, the presence of vertical walls in our system reflects realistic conditions and does not necessarily detract from the relevance of the observed dynamics. For future studies, more controlled geometries—such as droplet impacts on flat substrates as demonstrated by Shah et al. [27]—may be combined with vertical vibration to further isolate and investigate the underlying mechanisms of transition and pattern formation.
4. Conclusions
In this study, we investigated the vibrationally induced dynamic behaviors of highly concentrated colloidal silica suspensions and identified a sequence of transitions, including melting, fingering, squirming, fragmentation, jumping, and bouncing. Our findings demonstrate that such dynamic transitions are not unique to cornstarch suspensions but can also emerge in aqueous colloidal silica suspensions.
The observed behaviors are likely driven by a combination of vibrational shear jamming, capillary effects, and interparticle interactions—including fluid motion, electrostatic forces, frictional contacts, and hydrogen bonding. Further studies are needed to clarify how particle size, suspension viscosity, and surface chemical properties of particles and solvents influence the onset and evolution of these vibration-induced transitions.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/liquids5030018/s1. Instructions for viewing Movies S1 and S2. The supplementary PowerPoint file contains embedded videos illustrating key dynamic behaviors. Please open the file in Microsoft PowerPoint and enter presentation mode. To play a video, click directly on the image shown in the corresponding slide.
Author Contributions
Conceptualization, M.K. and T.S.; methodology, M.K., T.S., R.I. and S.S.; validation, M.K.; formal analysis, M.K.; investigation, M.K., T.S., R.I. and S.S.; resources, M.K.; data curation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, M.K., T.S., R.I. and S.S.; visualization, M.K. and R.I.; supervision, M.K. and T.S.; project administration, M.K. and T.S.; funding acquisition, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Innovative Science and Technology Initiative for Security, ATLA, Japan (Grant Number JPJ004596) and the JSPS KAKENHI (24K01875, 24K17982, 25K01164) and the Kurita Water and Environment Foundation (24A024).
Data Availability Statement
Data is available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wagner, N.J.; Mewis, J. Theory and Applications of Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Coussot, P. Mudflow Rheology and Dynamics; Routledge: London, UK, 2017; ISBN 9781351429894. [Google Scholar]
- Ohshima, H.; Furusawa, K. Electrical Phenomena at Interfaces Fundamentals: Measurements, and Applications, 2nd ed.; Taylor & Francis: Oxfordshire, UK, 1998; ISBN 9780824790394. [Google Scholar]
- Blanco, E.; Hodgson, D.J.M.; Hermes, M.; Besseling, R.; Hunter, G.L.; Chaikin, P.M.; Cates, M.E.; Van Damme, I.; Poon, W.C.K. Conching chocolate is a prototypical transition from frictionally jammed solid to flowable suspension with maximal solid content. Proc. Natl. Acad. Sci. USA 2019, 116, 10303–10308. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, M.; Adachi, Y.; Ooi, S. On the Steady Shear Viscosity of Coagulated Suspensions. Nihon Reoroji Gakkaishi 2000, 28, 143–144. [Google Scholar] [CrossRef]
- Brown, E.; Jaeger, H.M. Shear thickening in concentrated suspensions: Phenomenology, mechanisms and relations to jamming. Rep. Prog. Phys. 2014, 77, 046602. [Google Scholar] [CrossRef] [PubMed]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Cambridge Monographs on Mechanics. In Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 2012; ISBN 9780511608810. [Google Scholar]
- Johnson, S.B.; Franks, G.V.; Scales, P.J.; Boger, D.V.; Healy, T.W. Surface chemistry–rheology relationships in concentrated mineral suspensions. Int. J. Miner. Process 2000, 58, 267–304. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Kobayashi, M.; Adachi, Y. Yield stress of mixed suspension of silica particles and lysozymes: The effect of zeta potential and adsorbed amount. Colloids Surfaces A Physicochem. Eng. Asp. 2019, 578, 123575. [Google Scholar] [CrossRef]
- Mari, R.; Seto, R.; Morris, J.F.; Denn, M.M. Discontinuous shear thickening in Brownian suspensions by dynamic simulation. Proc. Natl. Acad. Sci. USA 2015, 112, 15326–15330. [Google Scholar] [CrossRef]
- Singh, A.; Ness, C.; Seto, R.; de Pablo, J.J.; Jaeger, H.M. Shear Thickening and Jamming of Dense Suspensions: The “Roll” of Friction. Phys. Rev. Lett. 2020, 124, 248005. [Google Scholar] [CrossRef]
- Nakamura, H.; Kusano, T.; Hiruta, O.; Tani, M.; Ishii, M. Physical property control for innovative powder processes—Rheological control of concentrated slurry and wet granules. Adv. Powder Technol. 2020, 31, 1784–1788. [Google Scholar] [CrossRef]
- Komoda, Y.; Ishibashi, K.; Kuratani, K.; Hidema, R.; Suzuki, H.; Kobayashi, H. Rheological interpretation of the structural change of LiB cathode slurry during the preparation process. J. Comput. Inf. Syst. Open 2022, 5, 100038. [Google Scholar] [CrossRef]
- Samitsu, S.; Tamate, R.; Ueki, T. Rheological Properties of Dense Particle Suspensions of Starches: Shear Thickening, Shear Jamming, and Shock Absorption Properties. Langmuir 2024, 40, 26852–26863. [Google Scholar] [CrossRef]
- Majumdar, S.; Peters, I.R.; Han, E.; Jaeger, H.M. Dynamic shear jamming in dense granular suspensions under extension. Phys. Rev. E 2017, 95, 012603. [Google Scholar] [CrossRef] [PubMed]
- Merkt, F.S.; Deegan, R.D.; Goldman, D.I.; Rericha, E.C.; Swinney, H.L. Persistent Holes in a Fluid. Phys. Rev. Lett. 2004, 92, 184501. [Google Scholar] [CrossRef] [PubMed]
- von Kann, S.; Snoeijer, J.H.; van der Meer, D. Phase Diagram of Vertically Vibrated Dense Suspensions. Phys. Fluids 2014, 26, 113302. [Google Scholar] [CrossRef]
- Shinbrot, T.; Rutala, M.; Montessori, A.; Prestininzi, P.; Succi, S. Paradoxical ratcheting in cornstarch. Phys. Fluids 2015, 27, 103101. [Google Scholar] [CrossRef]
- Hou, X.; Peterson, J.D. A study of dense suspensions climbing against gravity. J. Non-Newtonian Fluid Mech. 2022, 307, 104868. [Google Scholar] [CrossRef]
- James, N.M.; Han, E.; de la Cruz, R.A.L.; Jureller, J.; Jaeger, H.M. Interparticle hydrogen bonding can elicit shear jamming in dense suspensions. Nat. Mater. 2018, 17, 965–970. [Google Scholar] [CrossRef]
- Garat, C.; de Richter, S.K.; Lidon, P.; Colin, A.; Ovarlez, G. Using good vibrations: Melting and controlled shear jamming of dense granular suspensions. J. Rheol. 2022, 66, 237–256. [Google Scholar] [CrossRef]
- Hodgson, D.J.M.; Hermes, M.; Blanco, E.; Poon, W.C.K. Granulation and suspension rheology: A unified treatment. J. Rheol. 2022, 66, 853–858. [Google Scholar] [CrossRef]
- Nakamura, H.; Makino, S.; Ishii, M. Effects of electrostatic interaction on rheological behavior and microstructure of concentrated colloidal suspensions. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 623, 126576. [Google Scholar] [CrossRef]
- Fujita, Y.; Kobayashi, M. Transport of colloidal silica in unsaturated sand: Effect of charging properties of sand and silica particles. Chemosphere 2016, 154, 179–186. [Google Scholar] [CrossRef]
- Kobayashi, M.; Skarba, M.; Galletto, P.; Cakara, D.; Borkovec, M. Effects of heat treatment on the aggregation and charging of Stöber-type silica. J. Colloid Interface Sci. 2005, 292, 139–147. [Google Scholar] [CrossRef]
- Cheng, X.; McCoy, J.H.; Israelachvili, J.N.; Cohen, I. Imaging the Microscopic Structure of Shear Thinning and Thickening Colloidal Suspensions. Science 2011, 333, 1276–1279. [Google Scholar] [CrossRef]
- Shah, P.; Arora, S.; Driscoll, M.M. Coexistence of solid and liquid phases in shear jammed colloidal drops. Commun. Phys. 2022, 5, 222. [Google Scholar] [CrossRef]
- Shikata, T.; Pearson, D.S. Viscoelastic behavior of concentrated spherical suspensions. J. Rheol. 1994, 38, 601–616. [Google Scholar] [CrossRef]
- Lee, Y.-F.; Luo, Y.; Bai, T.; Velez, C.; Brown, S.C.; Wagner, N.J. Microstructure and rheology of shear-thickening colloidal suspensions with varying interparticle friction: Comparison of experiment with theory and simulation models. Phys. Fluids 2021, 33, 033316. [Google Scholar] [CrossRef]
- Ong, B.; Leong, Y.; Chen, S. Interparticle forces in spherical monodispersed silica dispersions: Effects of branched polyethylenimine and molecular weight. J. Colloid Interface Sci. 2009, 337, 24–31. [Google Scholar] [CrossRef]
- Kobayashi, M.; Sugimoto, T.; Sato, S.; Ishibashi, R. Climbing Colloidal Suspension. Liquids 2023, 3, 40–47. [Google Scholar] [CrossRef]
- Moteki, A.; Kobayashi, M. Rheological Behavior of an Aqueous Suspension of Oxidized Carbon Nanohorn (CNHox). Nanomaterials 2024, 14, 1247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).