Ab Initio Investigation of the Hydration of the Tetrahedral d⁰ Transition Metal Oxoanions NbO₄³⁻, TaO₄³⁻, CrO₄²⁻, MoO₄²⁻, WO₄²⁻, MnO₄⁻, TcO₄⁻, ReO₄⁻, and of FeO₄, RuO₄, and OsO₄

Abstract

The geometries and vibrational frequencies of various configurations of XO₄^m−(H₂O)_n, X = Fe, Ru, Os, m = 0; X = Mn, Tc, Re, m = 1; X = Cr, Mo, W, m = 2; and X = Nb, Ta, m = 3; n = 0–6 are calculated at various levels up to MP2/6-31+G* and B3LYP/6-31+G*. These properties are studied as a function of increasing cluster size. The experimental and theoretical bond distances and vibrational spectra are compared where available, and predictions are made where they are not.

1. Introduction

The hydration of ions is crucial to understanding the properties of electrolyte solutions. Solution diffraction data using either X-rays or neutrons has established that water molecules arrange themselves in hydration shells around ions [1]. For metal cations, the existence and nature of an aqua ion can often be proven by Raman spectroscopy and/or ab initio calculations [2,3,4,5,6,7]. For oxoanions, the influence of the first hydration shell of water molecules is much smaller. One of the authors has examined the effect of the first hydration sphere on the main-group tetraoxo anions [8], some of their protonated forms [9,10,11,12,13,14], as well as several borate species [15,16,17,18] by ab initio computational methods. Therein, we have demonstrated that ab initio modeling using restricted Hartree-Fock (HF) theory with modest basis sets gives reasonable structural and vibrational properties, even if a full hydration sphere or an implicit solvation model is not employed. In this paper, we present our studies of naked and explicitly hydrated niobate, tantalate, chromate, molybdate, tungstate, permanganate, pertechnetate, perrhenate; and of iron, ruthenium, and osmium tetroxide, including optimization and frequency calculation up to the MP2/6-31+G* level and with up to twelve water molecules [19].

2. Materials and Methods

Calculations were carried out using Gaussian 03 [20], using the standard 6-31G* and 6-31+G* basis sets in conjunction with the standard HF, MP2, and B3LYP levels of theory. For the atoms of the second and third transition metal series, the standard SDD effective core potential and associated basis set was used in conjunction with the 6-31G(d) and 6-31+G(d) basis sets (O,H). The second-order Moller-Plesset (MP2) calculations use the frozen core approximation. A stepping stone approach was used, where the geometries and molecular orbital coefficients at the levels HF/6-31G*, HF/6-31+G*, MP2/6-31G*, MP2/6-31+G*, B3LYP/6-31G*, and B3LYP/6-31+G* were sequentially optimized (geom = allcheck guess = read). Default optimization specifications were normally used. After each level, a frequency calculation was performed at the same level, and the resulting force constants were used in the following optimization. Z-matrix coordinates constrained to the appropriate symmetry were used to speed up the optimizations and simplify the assignment of vibrational modes (FOpt = z-matrix, ReadFC). The force constants were evaluated at the first geometry as well (FOpt = CalcFC). The quadratic convergence method was applied automatically if the SCF failed to converge (SCF = XQC). Additional options were specified individually or in combination, as needed, to converge the geometry and energy (SCF: NoDIIS and/or IntRep and/or CDIIS; FOpt = CalcAll and/or GDIIS). Additional calculations with Gaussian 16 [21] were carried out to explore the BLYP and PBE functionals, often used for ab initio MD simulations and the effect of an implicit solvation model (CPCM).

3. Results

The XO₄^m− ion, or molecule, of T_d symmetry has nine modes of internal vibration spanning the vibrational representation ${\Gamma }_{vib}=A_1+E+2T_2$. All modes are Raman active, whereas only the T₂ modes are IR active. The structures are analogous to those reported previously for perchlorate [8]. In the following subsections, we review the geometries and vibrational frequencies of each molecule or ion, followed by our results.

3.1. Permanganate

The crystal structures of permanganate salts have been examined for several decades. For potassium permanganate (Pnma), Mooney determined the average Mn-O distance to be 1.59(9) Å [22]. Refinements include those of Ramaseshan et al. (1.55(1) Å) [23], Palenik (1.629(8) Å) [24], Hoppe (1.60(1)) [25], and Marabello et al. (1.615(1) Å) [26]. Other anhydrous alkali permanganate structure determinations include those of Fischer et al. (Li: neutron diffraction, 1.623(17) Å) [27], Bauchert et al. (Na: 1.610(13) Å) [28], and Hoppe et al. (Rb: 1.603(5) Å; Cs: 1.604(3) Å) [25]. Lithium permanganate can also exist as the trihydrate (1.615(8) Å) [29,30]. The more modern determinations squarely place the Mn-O distance in the range 1.60–1.63 Å.

The resonance Raman spectrum of KMnO₄(aq) was measured with the 514.5 and 488 nm argon laser lines by Kiefer and Bernstein [31,32]. The Mn-O stretching bands at 837.5 (ν₁-A₁) and 906.5 cm⁻¹ (ν₃-T₂), as well as several overtones nν₁ and combinations nν₁ + ν₃, were observed in light and heavy water. Weinstock, Schulze, and Muller observed, using a He-Ne laser at 633 nm, the normal Raman spectrum of KMnO₄(aq) [33] and found bands at 839 ± 1 (ν₁-A₁), 914 ± 5 (ν₃-T₂), 360 ± 5 (ν₂-E), and 430 ± 5 (ν₄-T₂) cm⁻¹. In an argon matrix, the ν₃ mode appears at 896.9 cm⁻¹ [34].

The calculated bond lengths and vibrational frequencies for MnO₄⁻ are given in

Table 1. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of permanganate, MnO₄⁻.

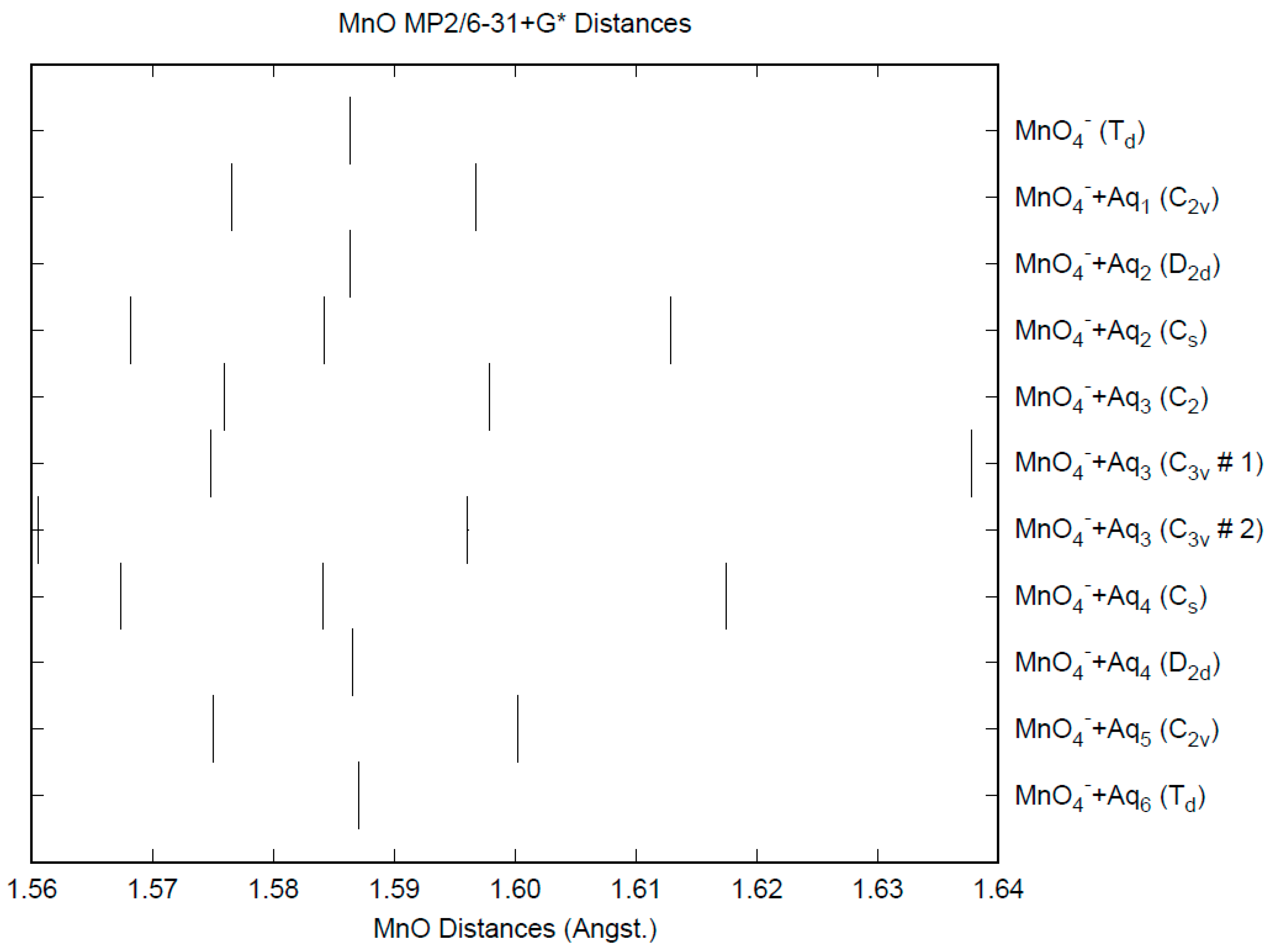
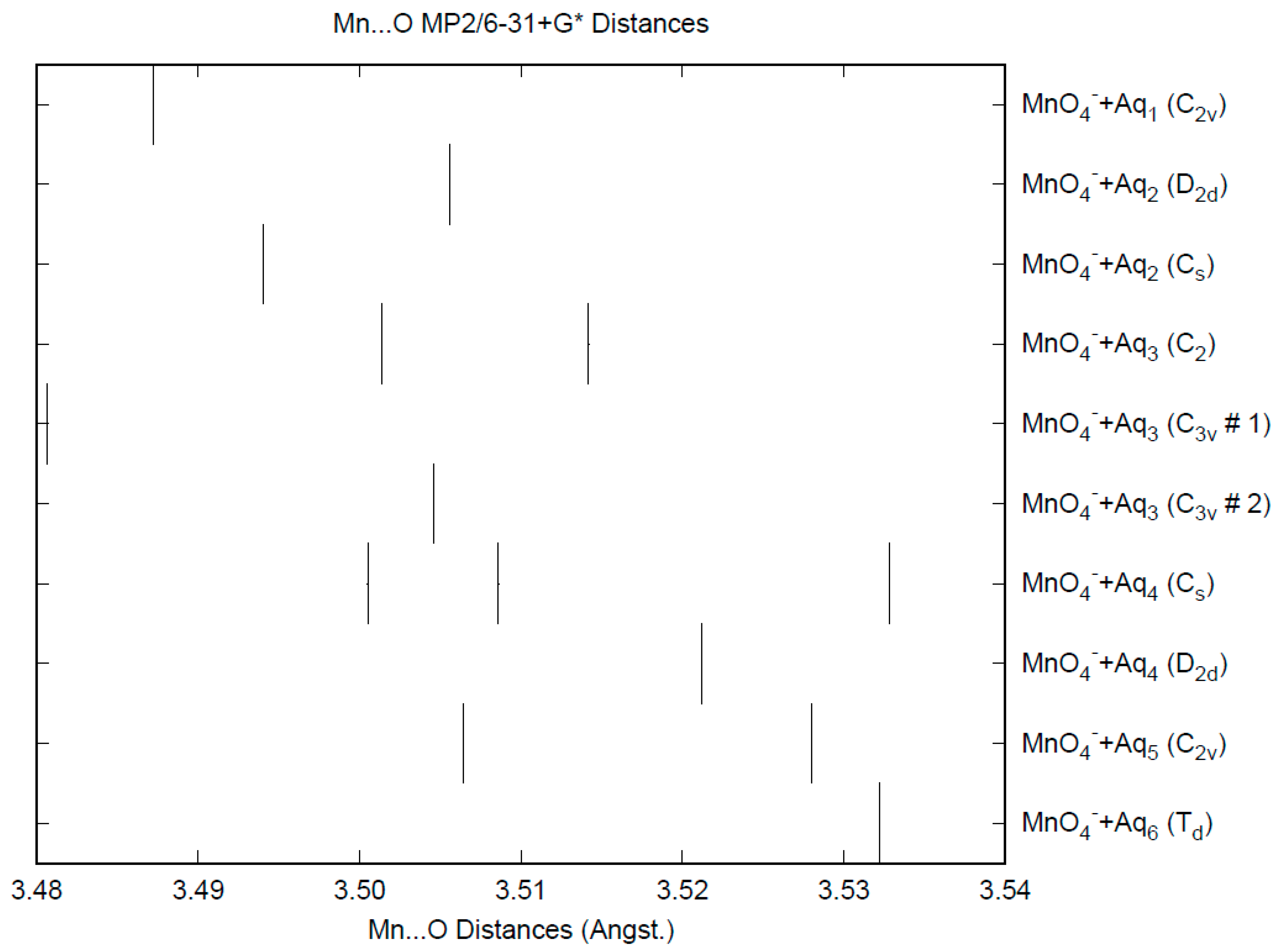
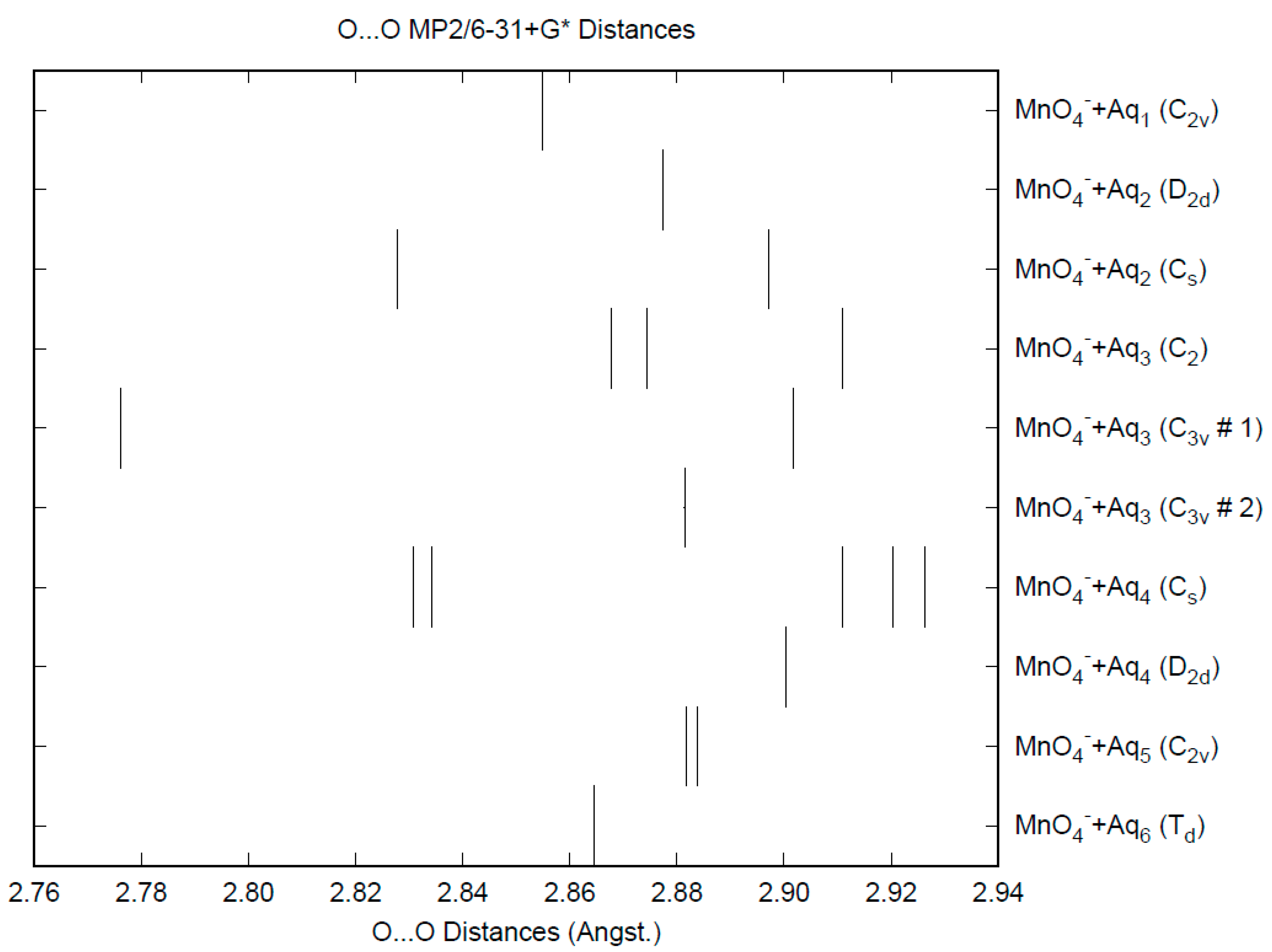
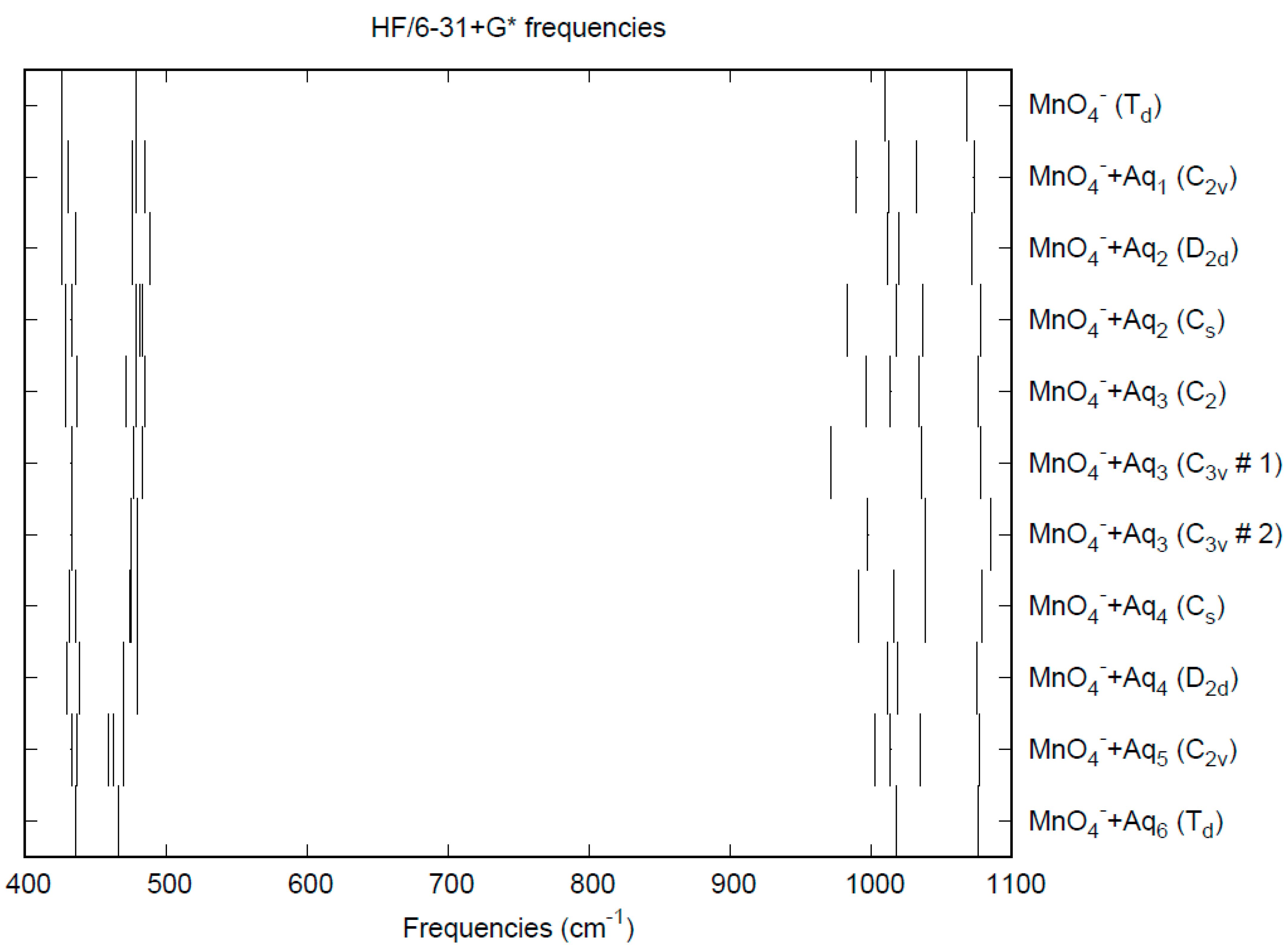
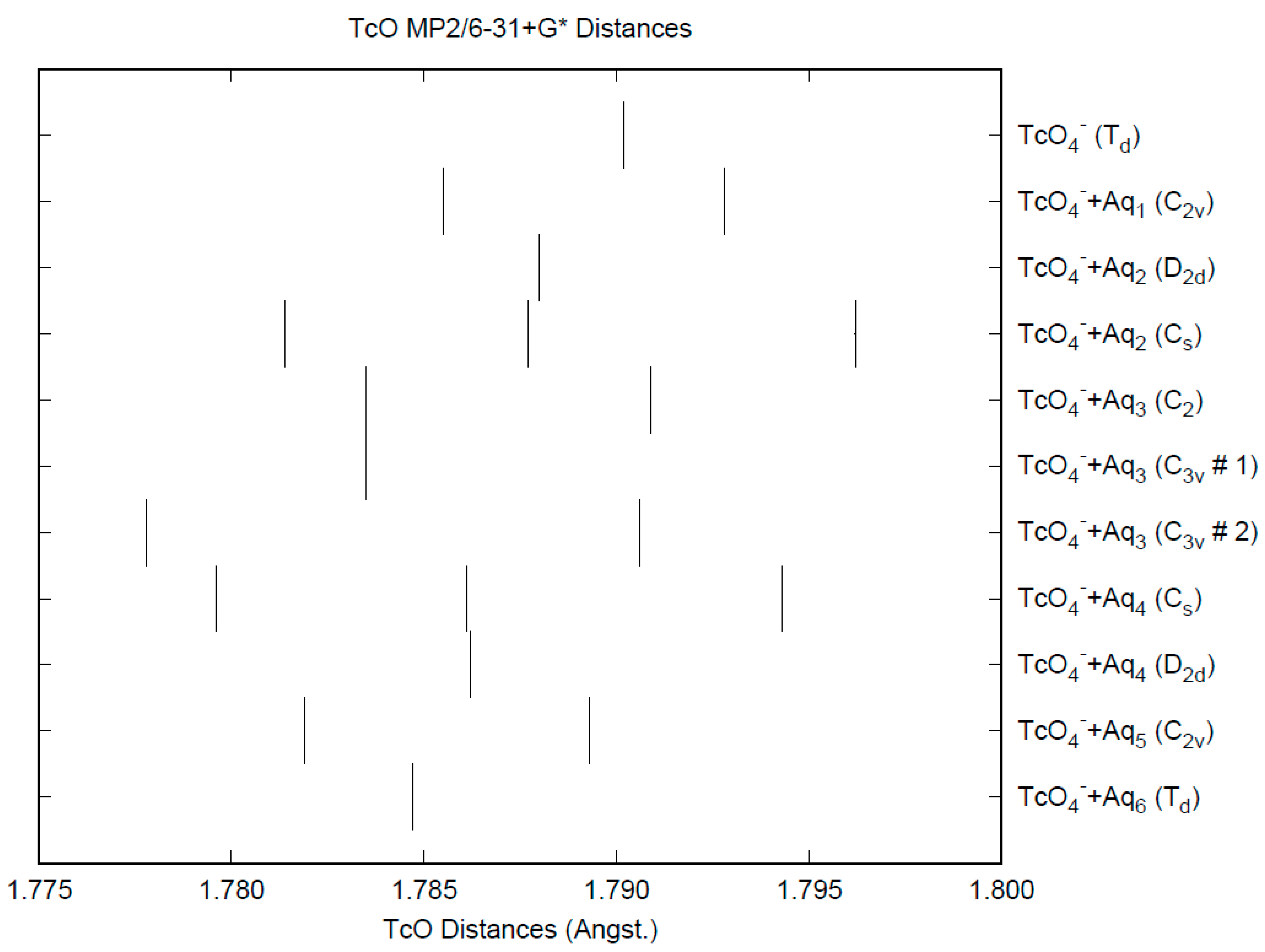
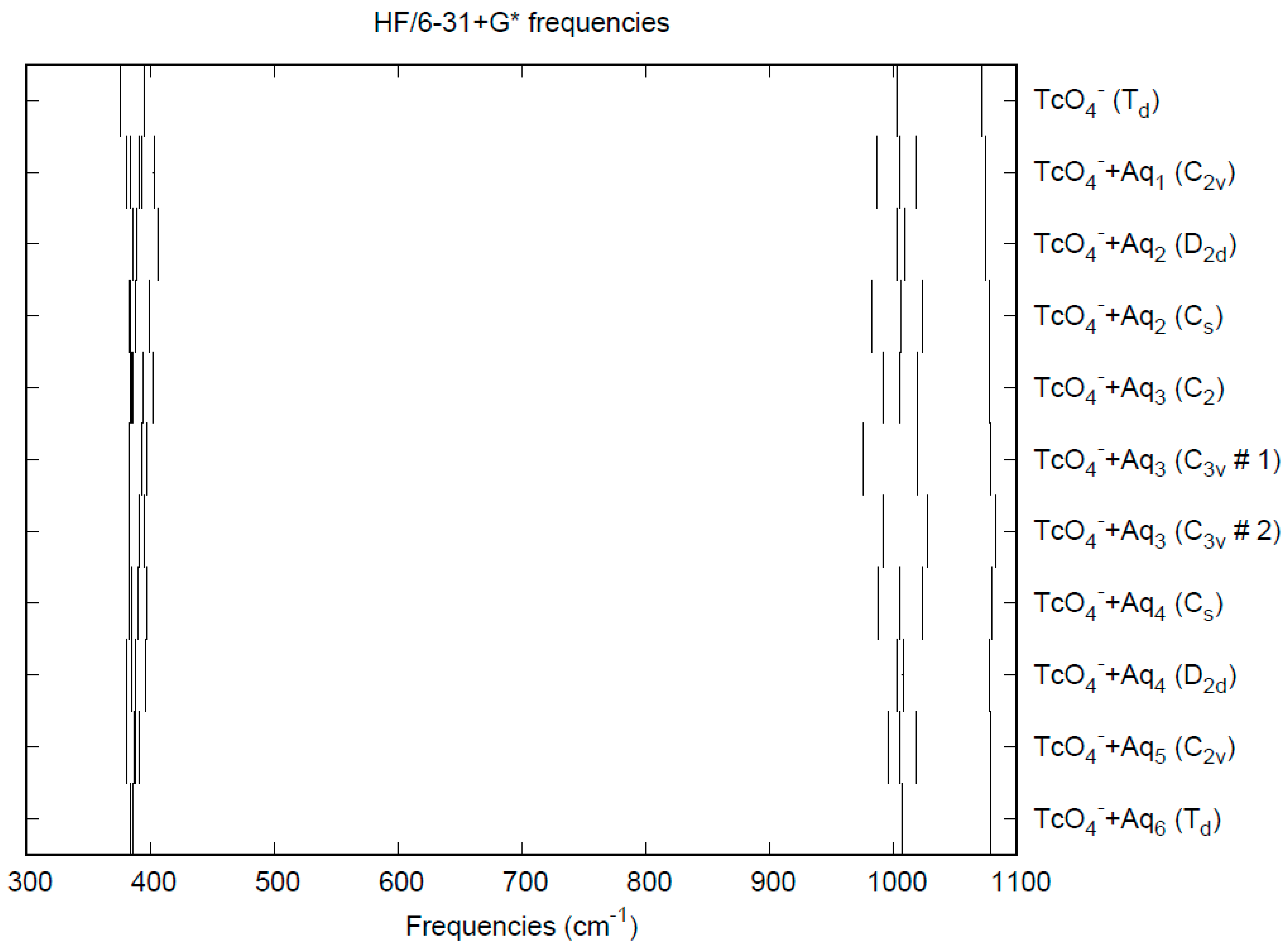
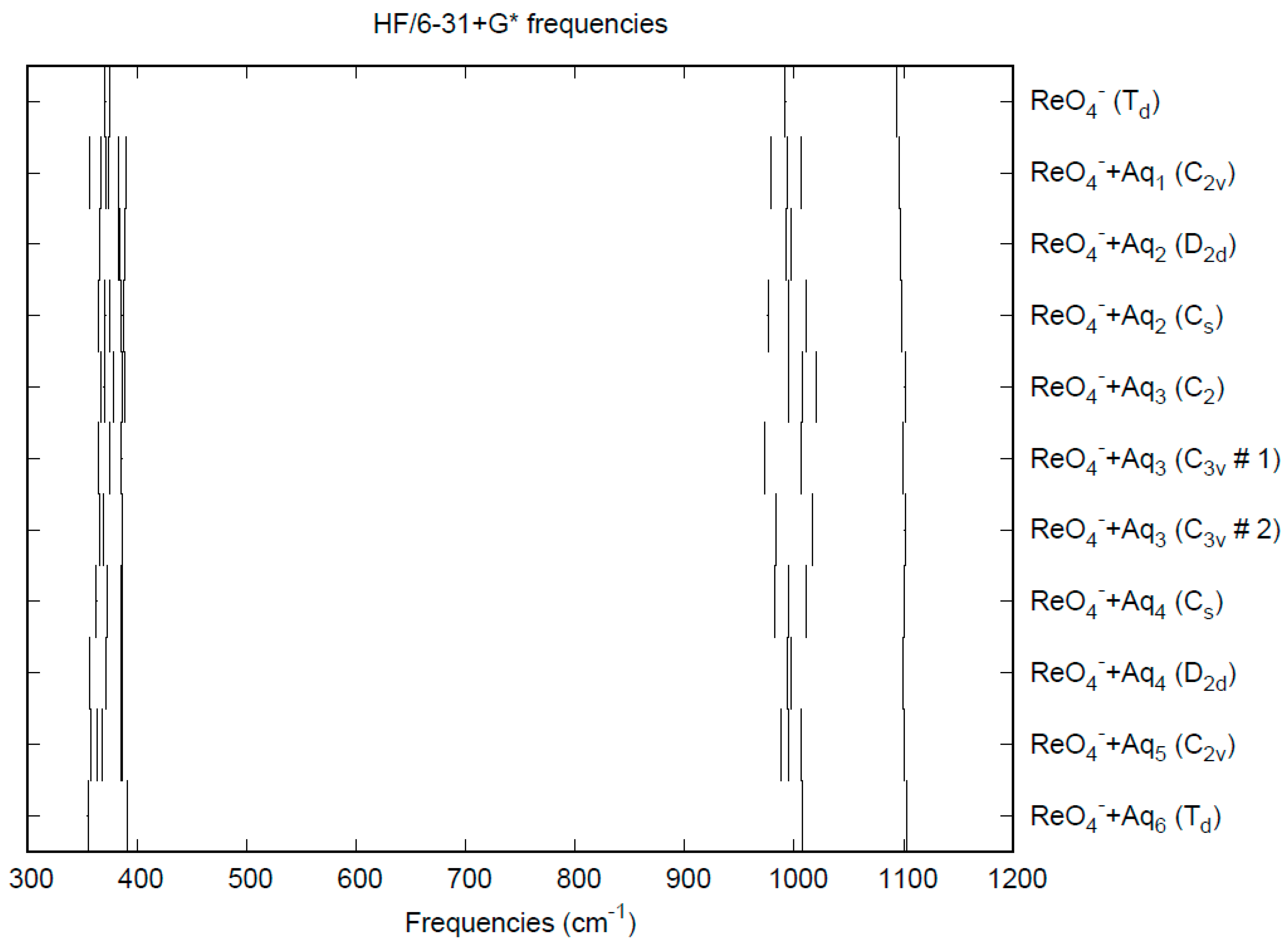
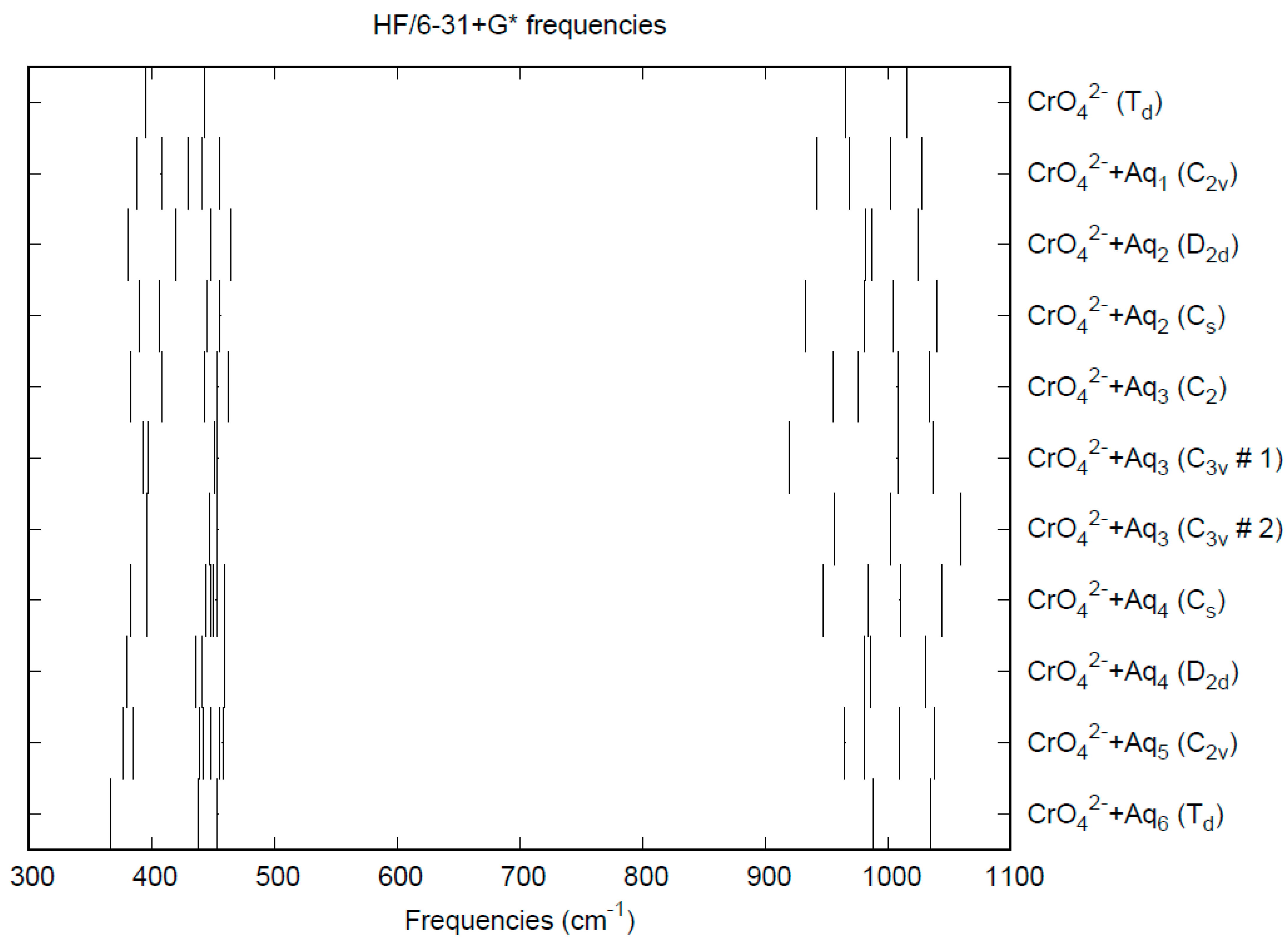
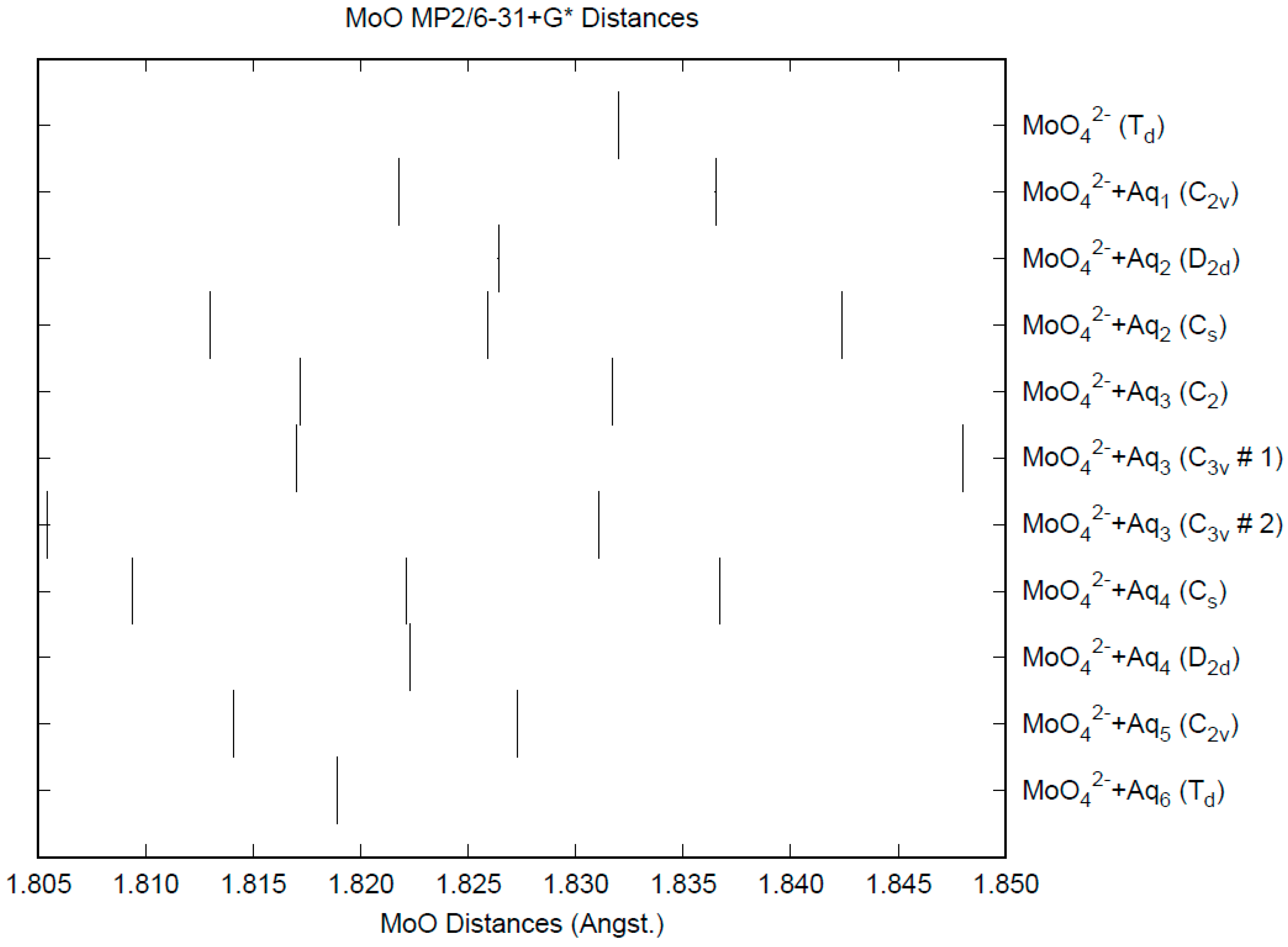
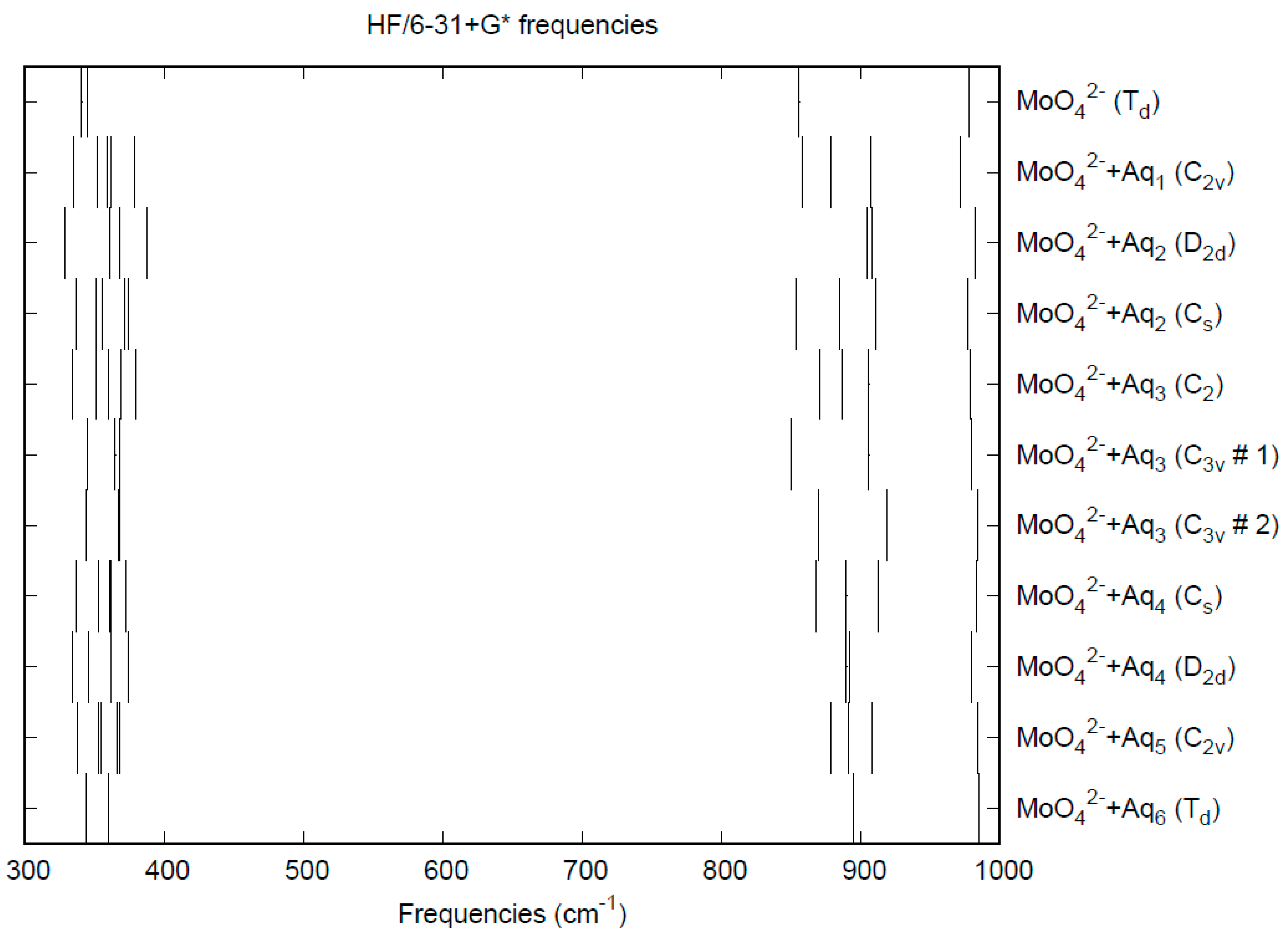
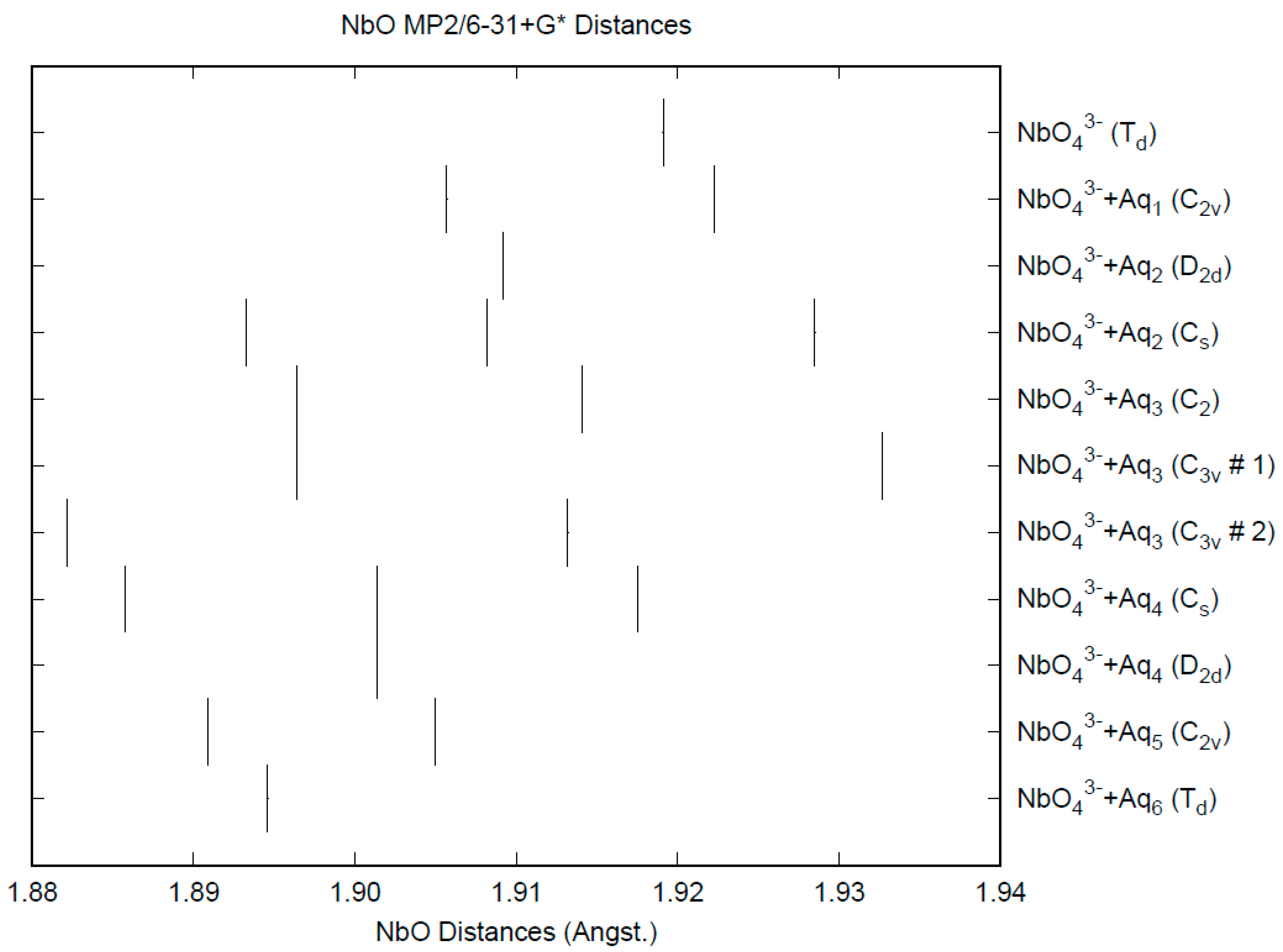
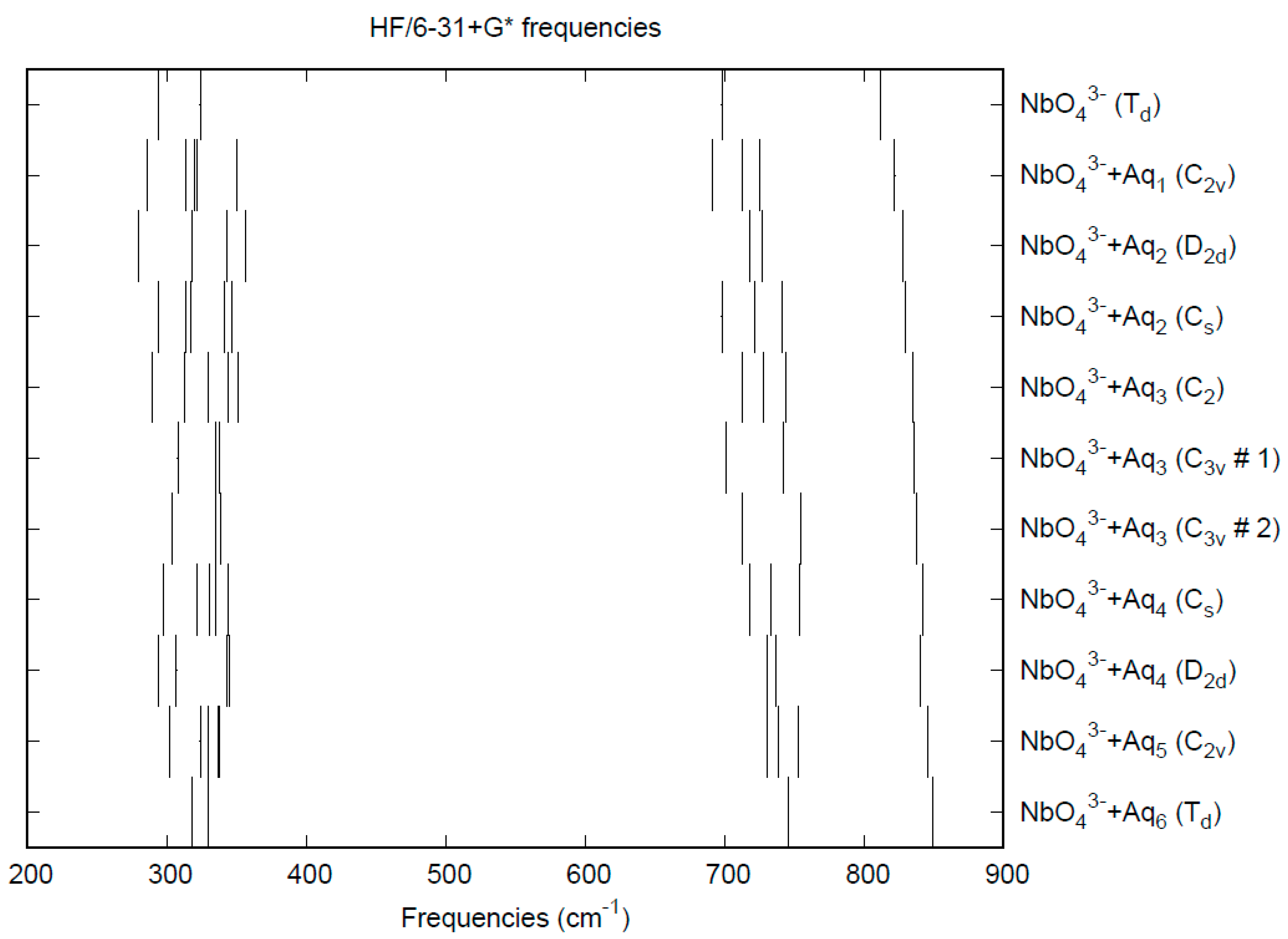
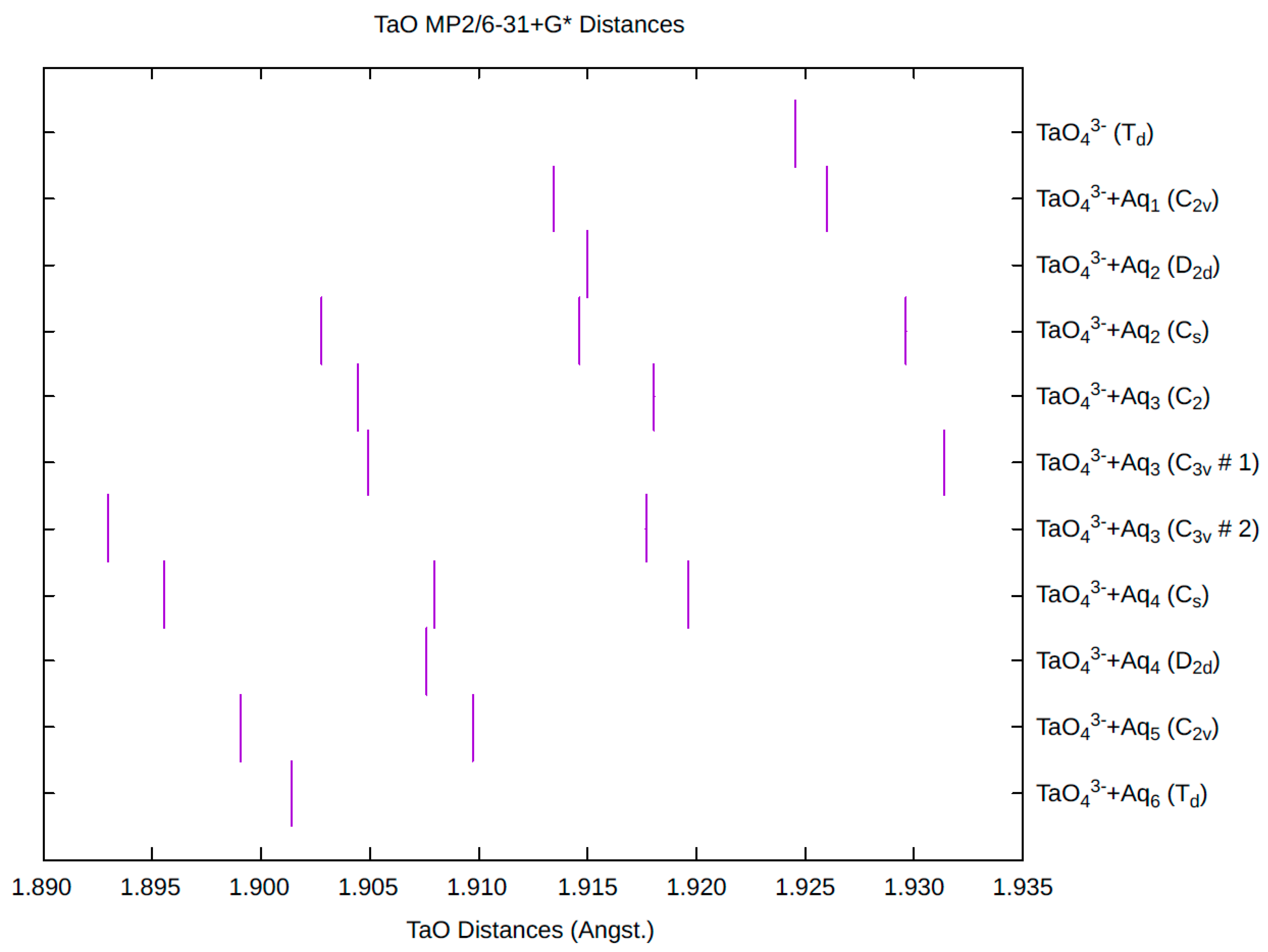
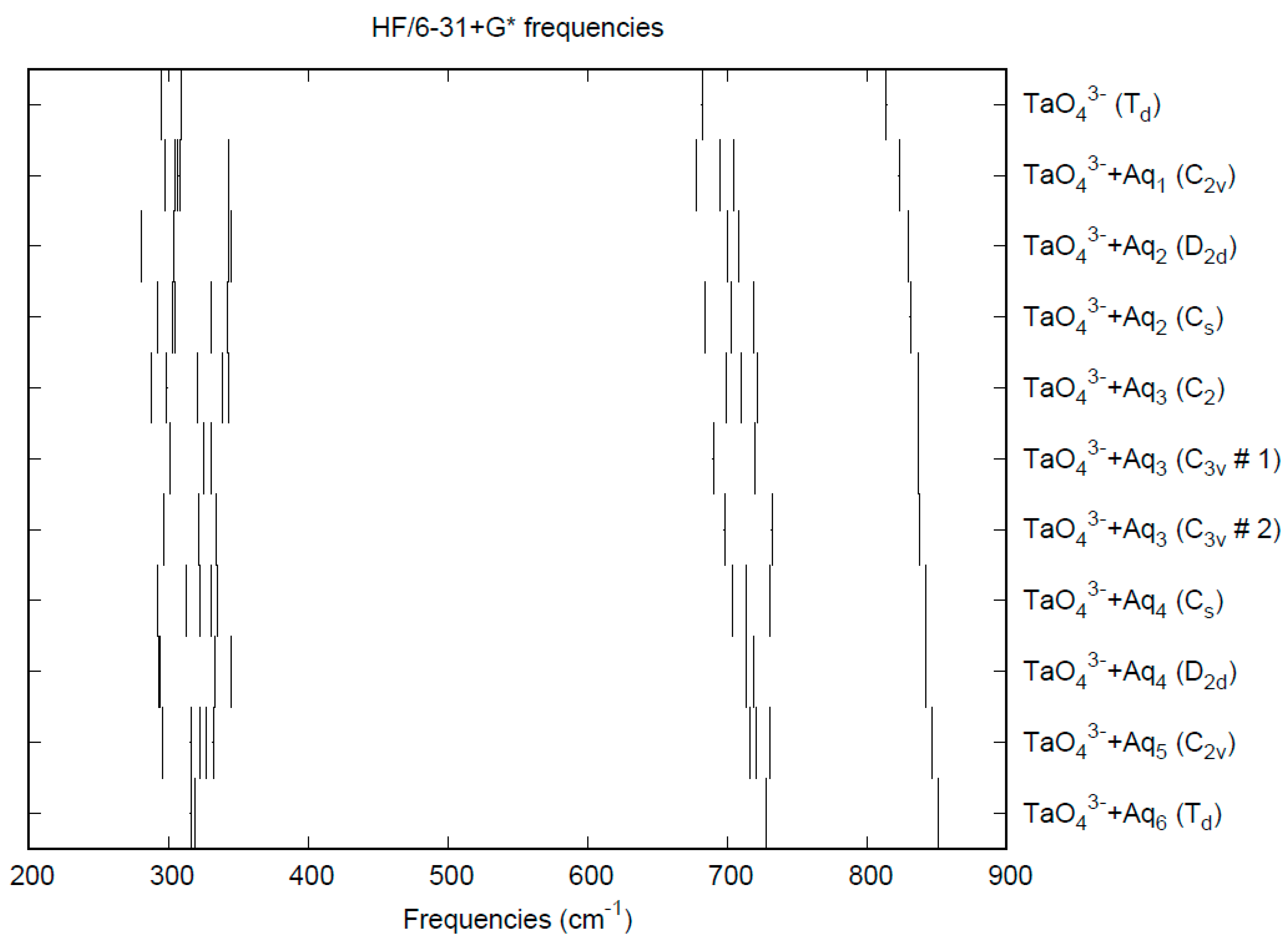
	d(Mn-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.5399	1082	438	1039	490
HF/6-31+G(d)	1.5449	1068	426	1011	480
MP2/6-31G(d)	1.5797	1695	438	1761	446
MP2/6-31+G(d)	1.5864	1694	438	1710	447
B3LYP/6-31G(d)	1.5947	957	379	1018	426
B3LYP/6-31+G(d)	1.6018	936	368	986	417
BLYP/6-31G(d)	1.6232	888	354	959	401
BLYP/6-31+G(d)	1.6315	865	344	927	392
PBE/6-31G(d)	1.6116	909	360	982	406
PBE/6-31+G(d)	1.6194	886	350	949	396
CPCM-HF/6-31G(d)	1.5386	1084	437	1008	480
CPCM-HF/6-31+G(d)	1.5438	1070	426	972	469
CPCM-MP2/6-31G(d)	1.5780	1691	439	1644	454
CPCM-MP2/6-31+G(d)	1.5847	1688	438	1562	453
CPCM-B3LYP/6-31G(d)	1.5927	962	377	1006	419
CPCM-B3LYP/6-31+G(d)	1.5998	941	366	967	409
CPCM-BLYP/6-31G(d)	1.6210	890	352	952	392
CPCM-BLYP/6-31+G(d)	1.6294	866	342	914	382
CPCM-PBE/6-31G(d)	1.6094	912	358	975	398
CPCM-PBE/6-31+G(d)	1.6173	889	348	936	389

. The Hartree-Fock distances are too short compared to the experiment, but the MP2 and especially the DFT distances are in much better agreement. The Hartree-Fock frequencies are overestimated, which is a well-known problem with the theory and can be corrected by an empirical scaling factor. The DFT frequencies are reasonably close to the experiment, with the deformation modes being quite close, although the stretching frequencies are overestimated by up to 100 cm⁻¹. The MP2 stretching frequencies, on the other hand, are nearly twice the experimental values, and this must be regarded as an abysmal failure of the MP2 method. The difficulty that permanganate can present to computational chemistry, especially with regard to electronic transitions, is well known [35,36,37,38,39,40,41,42,43,44,45,46,47]. The CPCM solvation model gives rise to slightly smaller Mn-O distances and T₂ frequencies.

The effect of water upon the Mn-O distances (MP2/6-31+G(d)) in MnO₄⁻•nH₂O (n = 0–6) is similar to that of the Cl-O distances in the analogous perchlorate [8] (Figure 1). However, the net effect is a very slight lengthening of the Mn-O distance by 0.0007 Å (n = 6), compared with the shortening observed in perchlorate. However, the individual Mn-O distances can vary by up to 0.05 Å (in perchlorate, the variation was only 0.02 Å). This might be reflected in larger bandwidths in the vibrational spectra. Although the Mn-O distances are approximately 0.1 Å longer than the corresponding Cl-O distances, the Mn…O distances are actually about 0.1 Å shorter than the corresponding Cl…O distances (Figure 2). The O…O distances are about 0.2 Å shorter (Figure 3) than the corresponding distances in perchlorate, suggesting that the hydrogen bonding is stronger in permanganate than in perchlorate. This is also seen in the O…H distances (Figure 4). Unlike perchlorate, there is only a slight increase of the hydrogen bonding indicators (O…O, O…H) on the number of water molecules, but the ranges are much larger. This also indicates that the permanganate ion has an unusual solvation dependence. In an aqueous solution, the Mn-O distance is 1.630(5) Å by LAXS, and the Mn…O distance is 4.095(8) Å [48]. While the Mn-O distance is well-reproduced by the hexahydrate calculations, the Mn…O distance is too short because the double-donor water molecules are too close to the central metal. This is rectified in the dodecahydrate model, in which the Mn…O distance lies in the range 3.83–4.09 Å, depending on the level of theory.

The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 5. The deformation frequencies are lower than in perchlorate and are also much closer together. In addition, the HF/6-31+G* level predicts that the asymmetric stretching mode is lower than the symmetric stretching mode for permanganate, whereas the opposite is true in the experiment and also for both the calculated and experimental perchlorate spectrum [8].

3.2. Pertechnetate

The determination of the properties of pertechnetate salts requires special care because of the radioactivity of technetium. The crystal structure of potassium pertechnetate gives a Tc-O distance of 1.711(3) Å (1.724 Å corrected) [49]. Other anhydrous pertechnetate crystal structure determinations include those of German et al. (Na: 100 K, 1.7208(3) Å; 296 K, 1.7183(6) Å) [50], Weaver et al. (neutron diffraction: Na, 1.737(4) Å; K, 1.739(14) Å; Rb, 1.723(3) Å; Cs, 1.67(3) Å) [51], and Meyer et al. (Cs: 1.715(50) Å) [52]. The lithium salt crystallizes as the trihydrate (1.717(7) Å) [53]. The average Tc-O distances fall mostly in the high end of the range 1.67–1.74 Å.

Busey and Keller [54] observed Raman bands at 912 and 325 cm⁻¹ for 2 mol/L NH₄TcO₄(aq). Weinstock, Schulze, and Muller observed the normal Raman spectrum of KTcO₄(aq) [33] and found bands at 912 ± 1 (ν₁-A₁), 912 ± 4 (ν₃-T₂), 325 ± 2 (ν₂-E), and 336 ± 10 (ν₄-T₂) cm⁻¹. An infrared band was found at 334 ± 10 (ν₄-T₂) cm⁻¹.

The calculated bond lengths and vibrational frequencies for TcO₄⁻ are given in

Table 2. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of pertechnetate, TcO₄⁻.

	d(Tc-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.6822	1077	376	1021	400
HF/6-31+G(d)	1.6835	1072	377	1003	396
MP2/6-31G(d)	1.7847	824	291	978	304
MP2/6-31+G(d)	1.7902	813	295	962	304
B3LYP/6-31G(d)	1.7305	935	322	935	342
B3LYP/6-31+G(d)	1.7333	927	325	917	340
BLYP/6-31G(d)	1.7558	875	304	886	325
BLYP/6-31+G(d)	1.7593	865	308	867	324
PBE/6-31G(d)	1.7442	895	310	904	329
PBE/6-31+G(d)	1.7470	886	313	887	328
CPCM-HF/6-31G(d)	1.6831	1068	370	981	345
CPCM-HF/6-31+G(d)	1.6845	1062	371	955	339
CPCM-MP2/6-31G(d)	1.7863	833	291	964	289
CPCM-MP2/6-31+G(d)	1.7929	823	297	941	290
CPCM-B3LYP/6-31G(d)	1.7315	912	284	910	297
CPCM-B3LYP/6-31+G(d)	1.7346	900	280	885	290
CPCM-BLYP/6-31G(d)	1.7575	858	274	869	285
CPCM-BLYP/6-31+G(d)	1.7615	846	276	845	281
CPCM-PBE/6-31G(d)	1.7451	877	277	885	288
CPCM-PBE/6-31+G(d)	1.7484	865	277	863	283

. The Hartree-Fock distances are too short compared to the experiment, but the MP2 distances are too long. The DFT distances are in much better agreement. In accordance with the inverse relationship between distance and vibrational frequency, the Hartree-Fock frequencies are overestimated, and the MP2 frequencies are underestimated. In addition, HF places the ν₁-A₁ band above the ν₃-T₂ band by 50–70 cm⁻¹, whereas MP2 reverses this order by 150 cm⁻¹. Only the DFT frequencies are reasonably close to the experiment, predicting the near degeneracy of the two modes. The CPCM solvation model gives rise to slightly larger Tc-O distances and smaller frequencies.

The effect of water upon the Tc-O distances (MP2/6-31+G(d)) in TcO₄⁻•nH₂O (n = 0–6) is similar to that of the Cl-O distances in the analogous perchlorate (Figure 6) [8]. The net effect is a slight shortening of the Tc-O distance by 0.005 Å (n = 6), unlike permanganate. The individual Tc-O distances vary by up to 0.01 Å (in perchlorate, the variation was larger at 0.02 Å). The Tc-O distances are approximately 0.3 Å longer than the corresponding Cl-O distances, although the Tc…O distances are about the same as the corresponding Cl…O distances (Figure S1). The O…O (Figure S2) and O…H (Figure S3) distances are about the same as in perchlorate.

The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 7. The deformation frequencies are lower than in perchlorate and are also much closer together. In addition, the HF/6-31+G* level predicts that the asymmetric stretching mode is lower than the symmetric stretching mode for pertechnetate, whereas experimentally, the modes are degenerate. The effect of hydration is similar to that in perchlorate.

3.3. Perrhenate

The crystal structure of potassium perrhenate was determined by Morrow [55] to give Re-O distances of 1.77(3) Å. The structure was further refined by Lock and Turner [56] (Re-O = 1.723(4) Å), Krebs and Hasse [49] (Re-O = 1.719(5) Å), and Brown, Powell, and Stuart [57] (neutron diffraction, Re-O = 1.739(1) Å, 15 K; 1.736(2), 150 K; 1.731(2) Å, 298 K). Other anhydrous perrhenate determinations include those of sodium perrhenate [58], (Re-O = 1.728(2) Å), rubidium perrhenate [59,60] (Re-O = 1.722(6) Å, 297 K; 1.729(2) Å, 159 K), two forms of cesium perrhenate [61,62,63] (Pnma, Re-O = 1.714(4) Å, 297 K; I4₁/amd, 1.683(7) Å, 468 K), and lithium perrhenate [64] (Re-O = 1.715(26) Å). In addition, the crystal structure of some hydrated lithium perrhenate forms are known: LiReO₄•H₂O [65] (Re-O = 1.720(12) Å) and LiReO₄•1.5H₂O [66] (Re-O = 1.72(1) Å). The more modern determinations squarely place the Re-O distance in the range of 1.683–1.739 Å. A comparison with the nearly identical Tc-O distances is evidence for the well-known lanthanide contraction. Weinstock, Schulze, and Muller observed the normal Raman spectrum of KReO₄(aq) [33] and found bands at 971 ± 1 (ν₁-A₁), 920 ± 4 (ν₃-T₂), and 331 ± 2 (ν₂-E) cm⁻¹. An infrared band was found at 322 ± 10 (ν₄-T₂) cm⁻¹.

The calculated bond lengths and vibrational frequencies for ReO₄⁻ are given in

Table 3. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of perrhenate, ReO₄⁻.

	d(Re-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.7089	1098	375	1009	374
HF/6-31+G(d)	1.7101	1094	275	993	372
MP2/6-31G(d)	1.7885	844	304	906	297
MP2/6-31+G(d)	1.7927	833	308	887	299
B3LYP/6-31G(d)	1.7511	963	325	922	321
B3LYP/6-31+G(d)	1.7535	956	327	905	321
BLYP/6-31G(d)	1.7740	905	308	875	306
BLYP/6-31+G(d)	1.7770	896	312	858	306
PBE/6-31G(d)	1.7635	924	314	892	309
PBE/6-31+G(d)	1.7659	916	317	876	309
CPCM-HF/6-31G(d)	1.7117	1057	322	964	284
CPCM-HF/6-31+G(d)	1.7132	1049	314	940	276
CPCM-MP2/6-31G(d)	1.7890	852	299	907	264
CPCM-MP2/6-31+G(d)	1.7939	841	306	884	268
CPCM-B3LYP/6-31G(d)	1.7548	933	277	899	260
CPCM-B3LYP/6-31+G(d)	1.7578	923	277	876	256
CPCM-BLYP/6-31G(d)	1.7780	889	284	864	257
CPCM-BLYP/6-31+G(d)	1.7817	879	288	843	256
CPCM-PBE/6-31G(d)	1.7667	904	282	878	256
CPCM-PBE/6-31+G(d)	1.7697	894	284	857	254

. The Hartree-Fock distances are slightly too short compared to the experiment, but the MP2 distances are too long. The B3LYP distances are slightly too long. In accordance with the inverse relationship between distance and vibrational frequency, the Hartree-Fock frequencies are overestimated, and the MP2 frequencies are underestimated. In addition, HF places the ν₁-A₁ band above the ν₃-T₂ band by 90–100 cm⁻¹, whereas MP2 reverses this order by 50–60 cm⁻¹. Only the B3LYP frequencies are reasonably close to the experiment. The CPCM solvation model gives rise to slightly larger Re-O distances and usually smaller frequencies.

The effect of water upon the Re-O distances (MP2/6-31+G(d)) in ReO₄⁻•nH₂O (n = 0–6) is similar to that of the Tc-O distances in the analogous pertechnetate (Figure S4). The net effect is a slight shortening of the Re-O distance by 0.005 Å (n = 6). The individual Re-O distances vary by up to 0.01 Å (in perchlorate, the variation was larger at 0.02 Å). The Re…O, O…O, and O…H distances are about the same as the corresponding distances in the hydrated pertechnetate (Figures S5–S7). The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 8. The deformation frequencies are lower than in perchlorate and are also much closer together. In addition, the HF/6-31+G* level correctly predicts that the asymmetric stretching mode is lower than the symmetric stretching mode for perrhenate. The effect of hydration is similar to that in perchlorate. In an aqueous solution, the Re-O distance is 1.735(2) Å by LAXS, and the Re…O distance is 4.197(7) Å [48]. While the Re-O distance is well-reproduced by the calculations, the Re…O distance is too short in the hexahydrate. This is mostly rectified in the dodecahydrate model, in which the Re…O distance lies in the range 3.87–4.08 Å, depending on the level of theory.

3.4. Iron, Ruthenium, and Osmium Tetroxide

Iron(VIII) oxide remains unknown. Ruthenium(VIII) oxide occurs in at least two modifications: a cubic form [67] and a monoclinic form [67,68]. The Ru-O distances are 1.696(1) and 1.699(2) Å, respectively. Osmium(VIII) oxide has been studied by both X-ray [69] and (gas phase) electron [70] diffraction. The distances obtained were 1.74(2) and 1.711(3) Å, respectively. The vibrational spectra of these two molecules have been measured by several authors (

Table 4. Vibrational Frequencies (cm⁻¹) of RuO₄ and OsO₄.

ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)	Type	Ref.
RuO4
		920		IR, gas	[71]
(880) 1		914		IR, CCl4 sol.	[71]
(879)		913	330	IR, liquid	[72]
882	323	914	334	R, liquid	[73]
883	318	921	332	R, sat. aq.	[73]
881	obscured	916	obscured	R, CCl4 sol.	[73]
OsO4
965	335	954	335	R, liquid	[74]
		953	325	IR, solid	[74]
(968) 2		960		IR, gas	[71]
(967) 3		954		IR, CCl4 sol.	[71]
964	338	953	334	R, liquid	[73]
962	333	952	333	R, sat. aq.	[73]
965.5	333.1	960.1	322.7	R, gas	[75]
964.5	335.2	954		R, CCl4 sol.	[76]
		960.5	329.0	IR, gas	[76]
		955.0	326.0	IR, CCl4 sol.	[76]

¹ For RuO₄(CCl₄), combination and overtone bands were observed at 1794 cm⁻¹ (ν₁ + ν₃), 1831 cm⁻¹ (2ν₃). ² For OsO₄(g), combination and overtone bands were observed at 1919 cm⁻¹ (ν₁ + ν₃), 1928 cm⁻¹ (2ν₃). ³ For OsO₄(CCl₄), combination and overtone bands were observed at 1910 cm⁻¹ (ν₁ + ν₃), 1921 cm⁻¹ (2ν₃).

). Both molecules contain a tetrahedral MO₄ moiety in the gas and solution phase, consistent with the crystal structure of the solids.

The calculated bond lengths and vibrational frequencies for FeO₄, RuO₄, and OsO₄ are given in

Table 5. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of iron tetroxide, FeO₄; ruthenium tetroxide, RuO₄; and osmium tetroxide, OsO₄.

	d(Fe-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.5199	927	426	513	446
HF/6-31+G(d)	1.5222	932	419	508	456
MP2/6-31G(d)	1.5023	2493	578	3136	524
MP2/6-31+G(d)	1.5069	2514	575	3143	528
B3LYP/6-31G(d)	1.5711	968	386	1038	437
B3LYP/6-31+G(d)	1.5768	950	377	1015	439
BLYP/6-31G(d)	1.6009	895	361	978	411
BLYP/6-31+G(d)	1.6078	875	352	953	402
PBE/6-31G(d)	1.5891	917	368	1003	418
PBE/6-31+G(d)	1.5955	898	359	978	409
CPCM-HF/6-31G(d)	1.5206	913	413	481	397
CPCM-HF/6-31+G(d)	1.5229	917	408	472	407
CPCM-MP2/6-31G(d)	1.5026	2510	572	3032	517
CPCM-MP2/6-31+G(d)	1.5070	2531	570	3012	522
CPCM-B3LYP/6-31G(d)	1.5722	966	380	1023	422
CPCM-B3LYP/6-31+G(d)	1.5776	951	371	999	414
CPCM-BLYP/6-31G(d)	1.6020	892	347	966	395
CPCM-BLYP/6-31+G(d)	1.6087	869	335	939	385
CPCM-PBE/6-31G(d)	1.5901	918	360	992	404
CPCM-PBE/6-31+G(d)	1.5963	898	349	966	395
	d(Ru-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.6394	1116	393	1060	405
HF/6-31+G(d)	1.6396	1115	392	1052	403
MP2/6-31G(d)	1.7631	1080	312	1683	350
MP2/6-31+G(d)	1.7654	1082	315	1698	352
B3LYP/6-31G(d)	1.6977	951	333	974	350
B3LYP/6-31+G(d)	1.6989	947	334	964	348
BLYP/6-31G(d)	1.7259	883	313	916	332
BLYP/6-31+G(d)	1.7277	877	314	905	331
PBE/6-31G(d)	1.7132	907	320	940	338
PBE/6-31+G(d)	1.7145	903	321	930	337
CPCM-HF/6-31G(d)	1.6422	1089	348	1014	334
CPCM-HF/6-31+G(d)	1.6425	1087	348	1001	331
CPCM-MP2/6-31G(d)	1.7674	1085	286	1660	322
CPCM-MP2/6-31+G(d)	1.7705	1090	291	1675	324
CPCM-B3LYP/6-31G(d)	1.7010	935	328	952	295
CPCM-B3LYP/6-31+G(d)	1.7026	926	319	937	289
CPCM-BLYP/6-31G(d)	1.7308	842	227	891	266
CPCM-BLYP/6-31+G(d)	1.7333	833	224	875	262
CPCM-PBE/6-31G(d)	1.7168	873	257	916	274
CPCM-PBE/6-31+G(d)	1.7186	865	251	902	270
	d(Os-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.6672	1152	391	1075	383
HF/6-31+G(d)	1.6668	1154	390	1070	382
MP2/6-31G(d)	1.7863	861	310	1126	311
MP2/6-31+G(d)	1.7867	859	314	1124	314
B3LYP/6-31G(d)	1.7192	991	335	975	330
B3LYP/6-31+G(d)	1.7197	988	335	966	329
BLYP/6-31G(d)	1.7449	925	317	921	313
BLYP/6-31+G(d)	1.7459	920	317	910	313
PBE/6-31G(d)	1.7334	947	324	942	319
PBE/6-31+G(d)	1.7340	944	324	933	318
CPCM-HF/6-31G(d)	1.6715	1131	359	1039	302
CPCM-HF/6-31+G(d)	1.6712	1132	358	1029	299
CPCM-MP2/6-31G(d)	1.7873	870	295	1120	320
CPCM-MP2/6-31+G(d)	1.7885	867	299	1117	324
CPCM-B3LYP/6-31G(d)	1.7228	965	282	957	280
CPCM-B3LYP/6-31+G(d)	1.7238	959	278	943	277
CPCM-BLYP/6-31G(d)	1.7494	896	264	903	292
CPCM-BLYP/6-31+G(d)	1.7511	889	264	888	292
CPCM-PBE/6-31G(d)	1.7370	920	269	925	282
CPCM-PBE/6-31+G(d)	1.7380	914	267	913	281

. In all cases, the DFT distances are greater than the HF distances. For RuO₄ and OsO₄, the MP2 distances are longer still, whereas for the hypothetical FeO₄, the MP2 distance is slightly shorter than HF. The DFT levels give the best agreement with the M-O distance and vibrational frequencies for RuO₄ and OsO₄. The MP2 vibrational frequencies are poor in all cases. The CPCM solvation model gives rise to slightly larger M-O distances and usually smaller frequencies.

All attempts to optimize structures of hydrated iron, ruthenium, or osmium(VIII) oxide in which the water was hydrogen-bonded to the oxygen atoms of the metal tetroxide resulted in optimized structures with imaginary modes corresponding to water wagging or partially optimized structures where the water reorients in a wagging motion to approach the metal atom more closely. In the case of iron tetroxide, other structures can form, such as peroxides or ozonides. This is consistent with the supposition that Fe^VIIIO₄ is not the most stable form of iron tetroxide but rather Fe^VIO₂(µ₂-O₂) [77].

3.5. Chromate

The crystal structures of alkali metal chromate salts are known. Early determinations of the anhydrous salts placed the average Cr-O distance as 1.60 Å (Na [78], K [79], Rb [80], Cs [81]). The redetermination of anhydrous potassium chromate (Pnam) [82] gave a Cr-O distance of 1.644 Å (1.670 Å corrected) or 1.646 Å [83]. Other (re)determinations give Li (R$\overline{3}$) [84], 1.653 Å (1.660 Å corr.); Na (Cmcm) [85], neutron diffraction 1.645 Å; Rb (Pnam) [86], 1.632 Å; and Cs (Pnma) [87], neutron diffraction, 1.650(5) Å. Several hydrates of sodium chromate can form, including the tetrahydrate (P2₁/c) with a Cr-O distance of 1.64(4) Å [88], decahydrate (P2₁/c) and sesquihydrate (F2dd) with Cr-O distances of 1.646(7) and 1.652(5) Å, respectively [89]. The crystal structure of the hexahydrate remains unknown, presumably because of its narrow stability range (19.525–25.90 °C) [90,91].

The resonance Raman spectrum of aqueous chromate ion was measured with the 514.5 and 363.8 nm argon laser lines by Kiefer and Bernstein [32]. The Cr-O stretching bands at 848 (ν₁-A₁), 887 (ν₃-T₂), 350 (ν₂-E), and 369 cm⁻¹ (ν₄-T₂) were observed with the 514.5 nm line. For the 363.8 nm line, only the stretching modes at 848 (ν₁-A₁) and 890 (ν₃-T₂) were observed, as well as several overtones nν₁ and combination ν₁+ ν₃, were observed in light and heavy water. Early Raman work by Venkateswaran [92] gave bands at 840–860 (ν₁-A₁), 874–879 (ν₃-T₂), 481–486 (ν₂-E), and 503–513 (ν₄-T₂) cm⁻¹. Stammreich et al. observed aqueous solutions of sodium, potassium, and ammonium chromate using the He 587.56 nm line [93], and found Raman shifts of 847 (ν₁-A₁), 884 (ν₃-T₂), 348 (ν₂-E), and 368 (ν₄-T₂) cm⁻¹. Weinstock et al. observed, using a He-Ne laser at 633 nm, the normal Raman spectrum of K₂CrO₄(aq) [33] and found bands at 846 ± 1 (ν₁-A₁), 890 ± 4 (ν₃-T₂), 349 ± 2 (ν₂-E), and 368 ± 2 (ν₄-T₂) cm⁻¹. In their study of the chromate—dichromate--hydrogen chromate equilibria, the values obtained by Michel and Machiroux [94] were 846, 887, 348, and 371 cm⁻¹. The aqueous IR and EXAFS spectrum were measured by Hoffmann and coworkers [95], who observed the chromate band at 880 ± 1 cm⁻¹ at pH 8.5. The EXAFS analyses (pH = 13) gave a Cr-O distance of 1.660(3) and 1.656(3) Å using two models.

The calculated bond lengths and vibrational frequencies for CrO₄²⁻ are given in

Table 6. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of chromate, CrO₄²⁻.

	d(Cr-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.5968	1043	410	1010	455
HF/6-31+G(d)	1.6056	1017	395	967	443
MP2/6-31G(d)	1.6868	1029	327	1100	377
MP2/6-31+G(d)	1.6996	998	319	1018	369
B3LYP/6-31G(d)	1.6479	897	348	925	391
B3LYP/6-31+G(d)	1.6572	872	338	887	384
BLYP/6-31G(d)	1.6756	830	323	865	364
BLYP/6-31+G(d)	1.6859	804	316	832	361
PBE/6-31G(d)	1.6642	849	328	885	368
PBE/6-31+G(d)	1.6737	823	321	851	364
CPCM-HF/6-31G(d)	1.5896	1065	410	993	452
CPCM-HF/6-31+G(d)	1.5984	1035	391	934	434
CPCM-MP2/6-31G(d)	1.6802	1023	322	1028	380
CPCM-MP2/6-31+G(d)	1.6920	993	319	916	375
CPCM-B3LYP/6-31G(d)	1.6397	902	334	924	378
CPCM-B3LYP/6-31+G(d)	1.6488	881	328	873	372
CPCM-BLYP/6-31G(d)	1.6672	842	317	874	359
CPCM-BLYP/6-31+G(d)	1.6769	822	316	828	356
CPCM-PBE/6-31G(d)	1.6558	856	315	892	358
CPCM-PBE/6-31+G(d)	1.6650	837	315	845	357

. The Hartree-Fock distances are about 0.05 Å too short compared to the experiment, but the MP2 distances are about 0.05 Å too long. The B3LYP distances are very close. The Hartree-Fock frequencies are overestimated. The MP2 stretching frequencies are also overestimated, which is somewhat unusual. In addition, HF places the ν₁-A₁ band above the ν₃-T₂ band by 30–50 cm⁻¹, whereas MP2 reverses this order by 20–70 cm⁻¹. Only the DFT frequencies (and MP2 deformation frequencies) are reasonably close to the experiment. The CPCM solvation model gives rise to smaller Cr-O distances.

The effect of water upon the Cr-O distances (MP2/6-31+G(d)) in CrO₄²⁻•nH₂O (n = 0–6) is given in Figure 9. The net effect is a moderate shortening of the Cr-O distance by 0.01 Å (n = 6). The individual Cr-O distances vary by up to 0.05 Å (in perchlorate, the variation was smaller at 0.02 Å). The Cr…O distance is about the same as the corresponding distance in the hydrated permanganate (Figure S8), although there is less variation within a particular species. For the O…H and O…O distances, the increase of about 0.1 Å upon going from mono to hexahydrate is much more pronounced than permanganate, although the spread within a species is about half (O…H) to the same (O…O) (Figures S9 and S10). The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 10. The frequencies are lower than in permanganate. In addition, the HF/6-31+G* level predicts that the asymmetric stretching mode is lower than the symmetric stretching mode for chromate, whereas experimentally, the modes are reversed. The effect of hydration is similar to that in permanganate, except that the splitting within degenerate modes is about twice as large, which makes it more difficult to correlate the two stretching modes because of the overlap. In an aqueous solution, the Cr-O distance is 1.660(3) Å by LAXS, and the Cr…O distance is 3.955(5) Å [48]. While the Cr-O distance is well-reproduced by the calculations, the Cr…O distance is too short in the hexahydrate. This is rectified in the dodecahydrate model, in which the Cr…O distance lies in the range of 3.78–3.88 Å, depending on the level of theory.

3.6. Molybdate

Numerous authors have investigated the crystal structures of alkali metal molybdate salts. The space group of anhydrous lithium molybdate was determined to be P3₂ by Barinova et al. [96]. The average Mo-O distance was 1.768 Å. However, Yip et al. argued [97] that the correct space group was $R\overline{3}$, as shown previously by Kolitsch [98] between 103 and 293 K (1.764 Å), whereas Zachariasen [99] suggested that $P\overline{3}$ was correct. Anhydrous sodium molybdate was shown to exist in four modifications [100] between 623 and 923 K: α (Fd-3m), β (unknown), γ (Fddd), and δ (P6₃/mmc) by powder diffraction. The low-temperature α-form was confirmed and refined by Fortes [101] using neutron powder diffraction (Mo-O = 1.7716 Å). Anhydrous potassium molybdate was found [102] to crystallize in the space group C2/m, with Mo-O distance of 1.76(1) Å. A powder diffraction study of anhydrous potassium, rubidium, and cesium molybdate [103] provided cell constants and fractional coordinates of the metal atoms, but the oxygen atoms were not located. Later, annealed anhydrous rubidium molybdate (Pnam) was found [104] to have an Mo-O distance of 1.75(2) Å. Anhydrous cesium molybdate was found [105] to crystallize in the space group Pcmn, with a Mo-O distance of 1.773 Å (corrected 1.792 Å). In addition to anhydrous salts, sodium molybdate dihydrate is also known. Mitra and Verma found [106] a space group Pcba with an average Mo-O distance of 1.82(3) Å (octahedrally coordinated). Other authors found tetrahedral coordination. Atovmyan et al. found [107] a space group of Pcab with an average Mo-O distance of 1.76(6) Å. A (re)determination by Matsumoto et al. gave [108] space group Pbca, Mo-O distance of 1.772(14) Å. Another redetermination by Capitelli (Pbca) gave Mo-O distances of 1.767(10) Å and also located the hydrogen atoms [109]. Neutron powder diffraction was used by Fortes [110] (Pbca) to give Mo-O distances of 1.766(10) Å. The consensus for a Mo-O distance of 1.77 Å is clear.

Early Raman work by Venkateswaran [92] gave the molybdate frequencies of 897–944 (ν₁-A₁), 841–896 (ν₃-T₂), 218–241 (ν₂-E), and 317–361 cm⁻¹ (ν₄-T₂). Busey and Keller [54] found Raman bands at 897 (ν₁-A₁), 841 (ν₃-T₂), and 318 cm⁻¹ (either ν₂-E or ν₄-T₂) for sodium molybdate. Weinstock et al. [33] measured sodium molybdate at 897 (ν₁-A₁), 837 (ν₃-T₂), 317 (ν₂-E, R), and 325 cm⁻¹ (ν₄-T₂, IR). Dean and Wilkinson [111] gave an accurate value of 986.1 cm⁻¹ for the value of ν₁-A₁ extrapolated to infinite dilution.

The calculated bond lengths and vibrational frequencies for MoO₄²⁻ are given in

Table 7. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of molybdate, MoO₄²⁻.

	d(Mo-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.7569	977	341	901	370
HF/6-31+G(d)	1.7601	966	342	874	365
MP2/6-31G(d)	1.8241	784	280	803	295
MP2/6-31+G(d)	1.8320	766	286	775	296
B3LYP/6-31G(d)	1.7951	863	291	825	314
B3LYP/6-31+G(d)	1.8005	849	298	801	314
BLYP/6-31G(d)	1.8182	812	276	782	298
BLYP/6-31+G(d)	1.8248	797	285	760	300
PBE/6-31G(d)	1.8070	828	280	798	301
PBE/6-31+G(d)	1.8126	814	288	776	302
CPCM-HF/6-31G(d)	1.7534	968	315	876	318
CPCM-HF/6-31+G(d)	1.7569	953	313	838	310
CPCM-MP2/6-31G(d)	1.8188	810	291	808	297
CPCM-MP2/6-31+G(d)	1.8271	787	295	764	291
CPCM-B3LYP/6-31G(d)	1.7898	881	298	829	309
CPCM-B3LYP/6-31+G(d)	1.7950	867	303	795	308
CPCM-BLYP/6-31G(d)	1.8117	835	286	794	297
CPCM-BLYP/6-31+G(d)	1.8178	819	292	762	295
CPCM-PBE/6-31G(d)	1.8007	850	289	807	299
CPCM-PBE/6-31+G(d)	1.8059	836	295	776	298

. The Hartree-Fock distances are slightly too short (0.01 Å) compared to the experiment, but the MP2 distances are about 0.06 Å too long. The B3LYP distances are slightly too long (0.03 Å). It seems that this example is unusual compared to the others in that the Hartree-Fock distances are closest to X-ray diffraction results. The Hartree-Fock frequencies overestimate the experiment, whereas the MP2 and B3LYP frequencies underestimate it. In addition, HF and B3LYP place the ν₁-A₁ band above the ν₃-T₂ band, whereas MP2 reverses this order. The B3LYP frequencies are closest to the experiment. The CPCM solvation model gives rise to smaller Mo-O distances and larger A₁ frequencies.

The effect of water upon the Mo-O distances (MP2/6-31+G(d)) in MoO₄²⁻•nH₂O (n = 0–6) is given in Figure 11. The net effect is a moderate shortening of the Mo-O distance by 0.013 Å (n = 6). The individual Mo-O distances vary by up to 0.025 Å (in chromate, the variation was larger at 0.05 Å). The Mo…O distance is about 0.1 Å larger/smaller than the corresponding distance in the hydrated chromate/pertechnetate (Figure S11), although there is less variation within a particular species. For the O…H and O…O distances, the increase of about 0.1 Å upon going from mono to hexahydrate is much similar to chromate, although the spread within a species is about half (Figures S12 and S13). In 2M sodium molybdate solution, the Mo-O (Mo…O) distance was found to be 1.786(8) (4.06(2)) Å by LAXS [112]. The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 12. The frequencies are lower than in pertechnetate and chromate. The effect of hydration is similar to that in chromate, except that the splitting within degenerate modes is somewhat smaller. The splitting is still large enough to obfuscate the correlation between the two deformation modes because of the overlap. In an aqueous solution, the Mo-O distance is 1.775(4) Å by LAXS, and the Mo…O distance is 4.010(3) Å [48]. While the Mo-O distance is well-reproduced by the calculations, the Mo…O distance is too short in the hexahydrate. This is rectified in the dodecahydrate model, in which the Mo…O distance lies in the range of 3.82–3.94 Å, depending on the level of theory.

3.7. Tungstate

The crystal structures of alkali metal tungstates have been investigated. Zachariasen and Plettinger showed [113] that anhydrous lithium tungstate has space group $R\overline{3}$, with W-O bonds of 1.79(2) Å. Okada et al. showed [114] that anhydrous sodium tungstate has space group Fd3m, with W-O bonds of 1.819(8) Å. This was revisited by Fortes [101] ($Fd\overline{3}m$), who found a somewhat shorter length of 1.7830(2) Å using neutron diffraction. Anhydrous potassium tungstate crystallizes [115] in the space group C2/m, with a W-O distance of 1.79(2) Å. Powder diffraction on anhydrous potassium, rubidium, and cesium tungstate [103] provided cell constants and fractional coordinates of the metal atoms, but as with the molybdates, the oxygen atoms were not located. By neutron powder diffraction [104], it was found that rubidium tungstate crystallizes in the space group C2/m, W-O = 1.775(9) Å. To the best of our knowledge, the crystal structure of cesium tungstate remains unknown.

Early Raman work by Venkateswaran [92] gave the tungstate frequencies at 934 (ν₁-A₁), 840 (ν₃-T₂), 325 (ν₂-E), and 452 cm⁻¹ (ν₄-T₂). Busey and Keller [54] found IR and Raman bands at 928–931 (ν₁-A₁), 813–855 (ν₃-T₂), 335 cm⁻¹ (either or both ν₂-E, ν₄-T₂) for sodium tungstate powder (anhydrous and dihydrate). Weinstock et al. [33] measured the Raman spectrum of sodium tungstate and found bands at 931 (ν₁-A₁), 838 (ν₃-T₂), and 325 cm⁻¹ (either or both ν₂-E, ν₄-T₂). Dean and Wilkinson [111] gave an accurate value of 931.1 cm⁻¹ for the value of ν₁-A₁ extrapolated to infinite dilution.

The calculated bond lengths and vibrational frequencies for WO₄^2× are given in

Table 8. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of tungstate, WO₄²⁻.

	d(W-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.7781	989	341	881	349
HF/6-31+G(d)	1.7806	979	341	857	345
MP2/6-31G(d)	1.8305	828	293	791	289
MP2/6-31+G(d)	1.8349	815	298	769	290
B3LYP/6-31G(d)	1.8107	883	297	807	298
B3LYP/6-31+G(d)	1.8150	870	301	786	297
BLYP/6-31G(d)	1.8315	835	282	768	283
BLYP/6-31+G(d)	1.8367	821	288	748	284
PBE/6-31G(d)	1.8212	849	287	782	284
PBE/6-31+G(d)	1.8255	837	292	763	286
CPCM-HF/6-31G(d)	1.7762	985	324	868	315
CPCM-HF/6-31+G(d)	1.7792	974	323	834	313
CPCM-MP2/6-31G(d)	1.8221	859	305	805	288
CPCM-MP2/6-31+G(d)	1.8267	843	309	771	287
CPCM-B3LYP/6-31G(d)	1.8060	903	306	816	296
CPCM-B3LYP/6-31+G(d)	1.8105	889	308	785	294
CPCM-BLYP/6-31G(d)	1.8257	854	290	779	274
CPCM-BLYP/6-31+G(d)	1.8309	838	293	749	271
CPCM-PBE/6-31G(d)	1.8156	870	295	793	281
CPCM-PBE/6-31+G(d)	1.8199	856	298	765	278

. With the experimental distances spanning the range from 1.775–1.819 Å, the Hartree-Fock distances are at the low end of this range, and the B3LYP distances are at the high end. The MP2 distances are somewhat too long. The Hartree-Fock frequencies overestimate the experiment, whereas the B3LYP frequencies underestimate it by about the same amount. The MP2 frequencies underestimate the experiment a bit more, which matches the inverse trend expected with bond length. All methods correctly place the ν₁ band higher than ν₃ and predict the near degeneracy of the ν₂ and ν₄ bands. The CPCM solvation model gives rise to slightly smaller W-O distances and larger stretching frequencies.

The effect of water upon the W-O distances (MP2/6-31+G(d)) in WO₄²⁻•nH₂O (n = 0–6) is given in Figure S14. The net effect is a moderate shortening of the W-O distance by 0.012 Å (n = 6). The individual W-O distances vary by up to 0.015 Å, which is smaller than in chromate and molybdate. The W…O distance is about the same as the corresponding distance in the hydrated molybdate (Figure S15), although there is less variation within a particular species. For the O…H and O…O distances, the increase of about 0.1 Å upon going from mono to hexahydrate is much similar to molybdate, as are the actual values, although the spread within a species is about half (Figures S16 and S17). In 2M sodium tungstate solution, the W-O (W…O) distance was found to be 1.786(8) (4.06(2)) Å by LAXS [112]. The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 13. The frequencies are slightly lower than in molybdate, except for ν₁. The effect of hydration is similar to that in molybdate, except that the splitting within degenerate modes is somewhat smaller. As with molybdate, the splitting is still large enough to obfuscate the correlation with the two deformation modes because of the overlap. In an aqueous solution, the W-O distance is 1.797(4) Å by LAXS, and the W…O distance is 4.024(4) Å [48]. While the W-O distance is well-reproduced by the calculations, the W…O distance is too short in the hexahydrate. This is rectified in the dodecahydrate model, in which the W…O distance lies in the range 3.82–3.94 Å, depending on the level of theory.

3.8. Niobates

Unlike the previously mentioned anions, the experimental evidence for the existence of orthoniobate (NbO₄³⁻), especially in aqueous solution, is scant. We therefore review some of the literature on the complex chemistry of the Nb₂O₅·M₂O·H₂O (M = Li, Na, K, Rb, Cs) phase diagrams and the compounds therein.

Studies of niobium oxide [116,117] and the phase equilibria with lithium [118], sodium [119], potassium [120], rubidium [121], and cesium [122] carbonate/oxide were carried out by Reisman and coworkers. Amorphous niobium oxide, upon heating, converts to the γ-phase at 435 °C, which then converts to the α-phase at 830 °C before melting at 1491 °C. The existence of the previously identified β and δ phases as equilibrium phases was ruled out [116]. A metastable ε-phase was observed between 1300–1500 °C [117]. Lithium niobates form with a niobium to lithium ratio of 14:1 (Li₂Nb₂₈O₇₁), 4:1 (Li₂Nb₈O₂₁), 1:1 (LiNbO₃), and 1:3 (Li₃NbO₄) [118]. Only LiNbO₃ could be readily indexed from powder X-ray diffraction. Sodium niobates form at the same ratios, and all could be indexed [119]. Potassium niobates form at ratios of 22:3 (K₆Nb₄₄O₁₁₃), 3:1 (KNb₃O₈), 3:2 (K₄Nb₆O₁₇), 1:1 (KNbO₃), and 1:3 (K₃NbO₄) [120]. The metastable 7:6 and 6:7 compounds may also form [123]. Rubidium niobates form at ratios of 15:2 (Rb₄Nb₃₀O₇₇), 4:1 (Rb₂Nb₈O₂₁), 11:4 (Rb₈Nb₂₂O₅₉), 2:1 (Rb₂Nb₄O₁₁), 3:2 (Rb₄Nb₆O₁₇), 1:1 (RbNbO₃), 3:4 (Rb₈Nb₆O₁₉), and 1:4 (Rb₈Nb₂O₉) [121]. Cesium niobates form at ratios of 15:2 (Cs₄Nb₃₀O₇₇), 13:5 (Cs₅Nb₁₃O₃₅), 2:1 (Cs₂Nb₄O₁₁), 3:2 (Cs₄Nb₆O₁₇), and 1:1 (CsNbO₃) [122]. From these results, it appears that compounds of stoichiometry M₃NbO₄ only exist for M = Li, Na, and K.

The structures of these compounds have proven difficult to elucidate. Powder diffraction gives the intensity of the scattered waves (X-ray, neutron, electron) as a function of scattering angle 2θ, which generally uniquely characterizes the compound. If this can be indexed, then the unit cell parameters and sometimes the space group can be identified. In favorable cases, a single crystal can be grown, and the related technique of X-ray crystallography may be applied.

3.8.1. Niobium Oxides

Early work on the oxides of niobium suggested the existence of three polymorphs of Nb₂O₅, the low (T), medium (M), and high (H)-temperature forms, and the powder diffraction patterns were measured (copper-K_α) [124]. The H-form of Brauer appears to be equivalent to the α-form of Reisman [116], who was able to index to a monoclinic cell, a = 21.34 Å, b = 3.816 Å, c = 19.47 Å, β = 120.33°. A crystal structure of this form was determined by Gatehouse and coworkers (P₂, a = 21.16 Å, b = 3.822 Å, c = 19.35 Å, β = 119.83°) [125]. The structure consists of three types of building blocks: a slab consisting of edge-shared 3 × 5 NbO₆ octahedra, a slab of edge-shared 3 × 4 NbO₆ octahedra, and two tetrahedral holes, one of which consisted of NbO₄ tetrahedra. The tetrahedra contain Nb-O distances of 1.65(5) and 1.68(5) Å. The structure was refined by Kato (P2/m, a = 21.153 Å, b = 3.8233 Å, c = 19.356 Å, β = 119.80°) [126], who altered the space group by delocalizing the tetrahedra over both holes. The Nb-O distance in the tetrahedra was altered to 1.826 Å. Hahn’s niobium(V) oxide appears to be the low-temperature T-form [127], as do the forms examined by Frevel [128] and Nolander [129] (Pba2 or Pbam, a = 6.170 Å, b = 29.25 Å, c = 3.928 Å). Single-crystal X-ray diffraction was carried out by Kato and Tamura [130] (Pbam, a = 6.175 Å, b = 29.175 Å, c = 3.930 Å). The structure consists of sheets of 6- (octahedral) or 7-coordinated (pentagonal bipyramidal) niobium atoms, along with some nine-coordinate interstitial niobium atoms. A single-crystal X-ray diffraction study of the M-form was carried out by Mertin and coworkers [131] (I4/mmm, a = 20.44 Å, b= 3.832 Å), who found sheets of 4 × 4 corner linked niobium octahedra that are edge-linked to other 4x4 sheets. The crystal structure of ζ-Nb₂O₅ was solved by Laves et al. [132] (B2/b, a = 12.73 Å, b = 5.56 Å, c = 4.88 Å, γ = 105.08°) and consists of a dense network of NbO₆ octahedra. The crystal structure of another form, N-Nb₂O₅, was solved by Andersson [133] (C2/m, a = 28.51 Å, b = 3.830 Å, c = 17.48 Å, β = 120.80°). The structure is composed of 4 × 4 blocks of NbO₆ octahedra. Powder diffraction gives slightly different values [134] (C2/m, a = 28.53 Å, b = 3.827 Å, c = 17.58 Å, β = 125.10°). We speculate that it may be possible to make in situ small amounts of transient NbO₄³⁻ or its protonated forms by partial dissolution of the H-form, which already contains some tetrahedral niobium(V).

3.8.2. Lithium Niobates

There are several known structures for lithium niobates. Lithium orthoniobate, Li₃NbO₄, was studied by Blasse [135], who determined a cubic form from powder X-ray diffraction with a = 8.433 Å and also located the niobium atoms. It was also studied by Grenier et al. [136], who found cubic forms for both the low (Fm3m, a = 4.212 Å) and high (I23, a = 8.429 Å) temperature modifications using powder X-ray diffraction. In the low-temperature form (I), the cations were randomly distributed, whereas, in the high-temperature form (II), powder neutron diffraction gives a tetrahedral grouping of niobium octahedra, with lithium octahedra completing the 3D network. The structure might be viewed as a Nb₄O₄ core bound to 12 additional oxygens to form Nb₄O₁₆¹²⁻, held together by Li⁺ ions. The positions were further refined by Grenier and Bassi [137]. The unit cell was confirmed by Whiston and Smith [138] (cubic, a = 8.4300 ± 0.0008). Ukei et al. revised the space group of the high-temperature form to I-43m, a = 8.412 Å [139].

Lithium metaniobate, LiNbO₃, is the most studied by far because of its ferroelectric properties. Bailey [140] found that LiNbO₃ crystallizes in the space group R3c with a rhombohedral unit cell (a = 5.4920 Å, α = 55.88°). The corresponding hexagonal unit cell has a_H = 5.147 Å c_H = 13.856 Å. Two possible models were considered for the atomic positions. Megaw discussed the relationship of this structure to its ferroelectricity [141]. Powder neutron diffraction was carried out by Shiozaki and Mitsui [142], suggesting a disordered distribution of lithium ions. Abrahams et al. carried out a single crystal X-ray diffraction study at ambient temperature (R3c, a_H = 5.14829(2) Å, c_H = 13.8631(4) Å; a_R = 5.4944, α = 55.87°) [143]. They found that the unit cell consists of 6 planar sheets of oxygen atoms perpendicular to c, with the octahedral interstices filled by Nb, Li, and X, where X indicates a vacancy. Isotropic thermal parameters were sufficient. The following single-crystal neutron diffraction study [144] confirmed the results and cast doubt on the accuracy of the atomic positions found from powder neutron diffraction determined previously [142]. The powder X-ray diffraction method was then applied at 24, 250, 500, 750, 1000, and 1200 °C [145], where the atomic arrangement essentially remains unchanged. Absorption and extinction effects gave unphysical values for the isotropic B at some temperatures. The shifts in atomic positions led Abrahams to propose that at the Curie point (1210 °C), the space group changes to the paraelectric R-3. Stoichiometric LiNbO₃ melts incongruently, and the congruently melting compound corresponds to a stoichiometry of Li_0.946NbO_2.973 (Li_0.955Nb_1.009O₃). A small amount of Li₂O has been lost. This form crystallizes (R3c, a_H = 5.15052(6) Å, c_H = 13.86496(3) Å) nearly identically to the stoichiometric compound (R3c, a_H = 5.14739(8) Å, c_H = 13.85614(9) Å) [146]. In the congruent form, 4.2% of the niobium ions have migrated to the vacated lithium sites. It was found that the thermal vibrations of the congruent form were anharmonic. A single crystal study on the congruent form was carried out by Ohgaki et al. (R3c, a_H = 5.15020(6) Å, c_H = 13.8653(4) Å), who also incorporated anharmonic corrections for vibration [147]. There also exists an ilmenite-type polymorph of LiNbO₃, characterized by Kumada et al. using powder diffraction (R3, a = 5.212 Å, c = 14.356 Å) [148]. Neutron powder diffraction both below (R3c) and above (R-3c) the Curie point demonstrated that the high-temperature paraelectric phase of LiNbO₃ had disordered lithium on both sides of a LiO₃ pyramid [149]. Synchrotron X-ray studies have also been carried out [150,151].

It was argued by Whiston and Smith that the Li₂Nb₈O₂₁ (1:4) compound observed by Reisman and Holtzberg [118] was actually LiNb₃O₈ (monoclinic, a = 7.435 Å, b = 5.618 Å, c = 7.079 Å, β = 101.0°) [138]. Powder and single-crystal X-ray diffraction was used to solve the structure of LiNb₃O₈ by Lundberg (P21/a, a = 15.262(2) Å, b = 5.033(1) Å, c = 7.457(1) Å, β = 107.34(1)°) [152]. It is comprised of chains of edge-shared metal octahedra. The structure was also solved by Gatehouse and Leverett (P2₁/c, a = 7.459(4) Å, b = 5.034(4) Å, c = 15.270(7) Å, β = 107.33(3)°) [153].

The structure of Li₇NbO₆ [154] was solved by Muhle using powder X-ray diffraction (P-1, a = 5.37932(9) Å, b = 5.91942(11) Å, c = 5.37922(9) Å, α = 117.0033(9)°, β = 119.6023(7)°, γ = 63.2570(9)°) [155]. This structure is interesting in that it consists of isolated NbO₆⁷⁻ octahedra held together by octahedrally and tetrahedrally-coordinated lithium ions. Because of the structure of Li₇NbO₆, it may be possible to generate in situ protonated forms of NbO₆⁷⁻ from it before subsequent condensation.

The crystal structure of Li₈Nb₂O₉ was solved by Braun and Hoppe (P-1, a = 15.210 Å, b = 8.815 Å, c = 5.858 Å, α = 109.8°, β = 101.4°, γ = 87.0°) [156] It consists of a network of edge and vertex fused NbO₆ octahedra.

The compound Li₂Nb₂₈O₇₁ of Reisman and Holtzberg [118] was argued by Whiston and Smith to actually be Li₂Nb₂₄O₆₁ (monoclinic, a = 44.79 Å, b = 3.807 Å, c = 28.38 Å, β = 106.5°) [138]. Norin and Nolander argued that extensive twinning of crystals occurred and obtained a powder pattern consistent with the space group being either C2, Cm, or C2/m (a = 28.52(2) Å, b = 3.828(2) Å, c = 17.55(1) Å, β = 124.98(4)°) [134]. There were many similarities to N-N₂O₅.

3.8.3. Sodium Niobates

Sodium orthoniobate, Na₃NbO₄, was studied by Whiston and Smith (C2 or Cm or C2/m, a = 12.23 Å, b = 12.85 Å, c = 5.782 Å, β = 121.5°) [138]. Bouillaud found two forms, a cubic form (a = 4.606 Å) [157] with random Li⁺ and Nb⁵⁺ arrangement and a monoclinic form (a = 11.095(5) Å, b = 12.993(5) Å, c = 5.730(5) Å, β = 108.9(5)°) which was believed to be the form observed by Whiston and Smith, in spite of the differences in lattice constants. These lattice constants were confirmed by Barker and Wood, who also observed a third orthorhombic phase (a = 13.806 Å, b = 13.411 Å, c = 9.579 Å) [158]. Meyer and Hoppe determined the crystal structure of the monoclinic form (C2/m, a = 11.068 Å, b = 13.032 Å, c = 5.733 Å, β = 109.13°) and found it to consist of discrete Nb₄O₁₆¹²⁻ ions [159].

Sodium metaniobate, NaNbO₃, has been investigated by numerous groups. It was found to be pseudocubic at ambient temperature by Barth (a = 3.890 Å) [160]. Wood found reversible polymorphism: 25 °C, orthorhombic (a₀ = 5.512 Å, b₀ = 5.577 Å, c₀ = 4 × 3.885 Å; also can be described as pseudotetragonal a₀ = 2 × 3.921 Å, c₀ = 4 × 3.885 Å; monoclinic axes a₀ = 2 × 3.921 Å, b₀ = 4 × 3.885 Å, c₀ = 2 × 3.921 Å, β = 90.67°); 300 °C, orthorhombic pseudotetragonal (a₀ = 2 × 3.91 Å, c₀ = 4 × 3.94 Å); 425 °C, tetragonal pseudocubic (a₀ = 2 × 3.928, c₀ = 4 × 3.928 Å); 490 °C, tetragonal pseudocubic (a₀ = 2 × 3.93, c₀ = 4 × 3.93 Å) [161]. Vousden found an orthorhombic phase at ambient temperature (a = 5.5682 Å, b = 3.8795 Å, c = 5.5052 Å) [162]. Upon heating, phase changes to tetragonal (300 °C) and cubic (600 °C) forms were noted. Reisman noted the existence of four phases (α, β, γ, δ) with phase transitions at 640, 562, and 354 °C. Single crystal diffraction of the room-temperature form (δ) gave (P22₁2, a = 5.5682 Å, b = 15.5180 Å, c = 5.5052 Å) [163], which was inconsistent with its ferroelectric nature [164,165]. Shirane et al. undertook optical, dielectric, and X-ray measurements from 20–670 °C [166]. In addition, Francombe examined the diffraction lines from 20–640 °C [167]. Solovev studied polycrystalline NaNbO₃ with X-rays between −200–700 °C [168]. The subcell lattice parameters ranged between 3.87–3.95 Å, giving six regions: pseudomonoclinic (−200–360 °C), pseudomonoclinic (360–430 °C), pseudocubic (430–470 °C), pseudocubic (470–520 °C), tetragonal (520–640 °C), and cubic (640–700 °C). Bouillaud found in a study of solid solutions that the monoclinic end member NaNbO₃ was pseudocubic with a = c = 3.9150(8) Å, b =3.8800(8) Å, 90.72(5)° with superstructure 2a.2b.2c [169]. A single crystal study at room temperature by Sakowski-Cowley et al. gave an orthorhombic structure (Pbma, a = 5.566 Å, b = 15.520 Å, c = 5.506 Å) [170]. The results of Hewat [171] using neutron diffraction matched those of Sakowski-Cowley. A study of the room temperature (P-antiferromagnetic) and a new low-temperature ferromagnetic N phase by Darlington and Megaw [172] showed that the transition occurred at about -110 °C. This structure was further refined by Seidel and Hoffmann at 20 K [173]. Further high-precision study of the high-temperature transitions up to 800 °C in a single crystal by Glazer and Megaw [174] demonstrated the existence of six high-temperature phases: P (<373 °C), R (373–480 °C), S (480–520 °C), T₁ (520–575 °C), T₂ (575–640 °C), and the cubic phase (>640 °C). The crystal structure of the tetragonal T₂ form at 600 °C was solved by Glazer and Megaw (P4/mbm, a = 5.5639(8), b = 5.5639(8), c = 3.9428(8)) [175] and can be described as slight tilting of the NbO₆ octahedra from the cubic perovskite structure. Essentially, the same structure was proposed by Ishida and Honjo [176]. The structure was further refined by Darlington and Knight by synchrotron powder diffraction at 615 °C [177]. The crystal structures of the orthorhombic S (500 °C) and T₁ (530 °C) phases were solved by Ahtee et al. [178]. The lattice parameters are: for T₁, Ccmm, a = 7.8642 Å, b = 7.8550 Å, c = 7.8696 Å; for S, Pnmm, a = 7.8608 Å, b = 7.8556 Å, c = 7.8606 Å. The structures can be described as successively more tilted regular NbO₆ octahedra. The T₁ structure was further refined by Darlington and Knight by synchrotron powder diffraction at 540 °C [177]. Nanoparticles 20 nm in size refined best to Pmc2₁, a = 7.8636(7) Å, b = 5.6306(9) Å, c = 5.5483(9) Å, according to Shanker et al. [179] This appears to be similar to the room-temperature polar phase described by Johnston et al. (P2₁ma, a = 5.571(1) Å, b = 7.766(1) Å, c = 5.513(1) Å) [180]. Using neutron diffraction, Darlington and Knight [181] confirmed the structures of the T₁ and T₂ phases and, based on the superlattice reflections, suggested that Phase S was a 2 × 4 × 6 multiplicity instead of the 2 × 2 × 2 reported by Ahtee et al. [178] Phase R had the same multiplicity. In addition, Phase P was suggested to be monoclinic (a₀ = 5.5101 Å, b₀ = 5.5717 Å, c₀ = 15.5181 Å, β = 89.94°). Koruza et al. used powder X-ray diffraction [182] and found: R, 420 °C, Pmmn, a = 7.8440(12) Å, b = 7.8459(13) Å, c = 7.8567(3) Å; 300 °C, Pbcm, a = 5.5327(2) Å, b = 5.5630(2) Å, c = 15.6450(5) Å; 250 °C, Pmc2₁, a = 7.8066(2) Å, b = 5.5279(2) Å, c = 5.5637(2) Å; and 25 °C, Pmc2₁, a = 7.7633(3) Å, b = 5.5143(2) Å, c = 5.5655(2) Å. Mishra et al. carried out a neutron powder diffraction study over a wide range of temperature [183] and found: 1075 K, U, cubic, Pm-3m, a = 3.9507(2) Å; 900 K, T₂, tetragonal, P4/mbm; 850 K, T₁, orthorhombic, Cmcm; 770 K, S, orthorhombic, Pbnm, a = 5.5555(2) Å, b = 5.5556(2) Å, c = 47.1489(9) Å; 680 K, R, orthorhombic, Pbnm; a = 5.5459(1) Å, b = 5.5505(1) Å; c = 23.5229(3) Å; 300 K, P, orthorhombic, Pbma. Peel and coworkers used both neutron and X-ray powder diffraction between 360 and 520 °C [184] and found that phase S (500 °C) was a 2 × 2 × 4 structure, Pmmn, a = 7.85684(4) Å, b = 7.86748(7) Å, c = 15.72795(13) Å, and that phase R (440 °C) was a 2x2x6 structure, Pmmn, a = 7.85371(6) Å, b = 23.54619(19) Å, c = 7.85677(7) Å (a 2 × 6 × 2 Pnma model was also close). An ilmenite form also exists (R3, a = 5.333(1) Å, b = 15.611(4) Å) [148].

Another sodium-rich structure, Na₅NbO₅, was found by Darriet et al. [185]. This structure is unique in that it has discrete square pyramidal NbO₅⁵⁻ coordinated to sodium atoms with oxygen voids.

The crystal structure of Na₂Nb₄O₁₁ was determined by Jahnberg (C2/c, a = 10.840 Å, b = 6.162 Å, c = 12.745 Å, β = 106.22°) [186], confirming the stoichiometry of Andersson [187]. It consists of sheets of edge-shared pentagonal bipyramidal NbO₇. These sheets are connected to each other by NbO₆ octahedra and NaO₇ polyhedra. The presence of ferroelectricity suggested that a noncentrosymmetric space group might be more appropriate, and the refinement of powder diffraction data was conducted by Maso and West (Cc, a = 10.8427(1) Å, b = 6.1664(6) Å, c = 12.7524(1) Å, β = 106.176(1)°) [188].

The structure of NaNb₃O₈ was examined using powder X-ray diffraction, and an orthorhombic cell was found: Andersson, Pbam or Pba2, a = 12.372 Å, b = 37.10 Å, c = 3.954 Å [187]; Bouillaud, a = 12.344(4) Å, b = 37.121(6) Å, b = 3.950(2) Å [189]; Nedjar, Pmnm or Pmn2₁, a = 8.771(14) Å, b = 10.16(2) Å, c = 3.784(3) Å [190]. The layers can be described as edge-shared NbO₆ octahedra, sharing their corners with NbO₄ tetrahedra. A high-pressure form, synthesized by Range et al., consists of both NbO₇ and NbO₈ polyhedra (Ibam, a = 7.3244(4) Å, b = 10.3100(5) Å, c = 7.0426(4) Å) [191].

Using single crystal X-ray diffraction, Andersson solved the structure of NaNb₁₃O₃₃ (C2/m, a = 22.40 Å, b = 3.834 Å, c = 15.37 Å, β = 91.47°) [192]. It consists of a 3D network of octahedral NbO₆ along with square-planar NaO₄. The powder diffraction pattern was also published [187].

3.8.4. Potassium Niobates

The potassium niobates are described next. Potassium orthoniobate, K₃NbO₄, was confirmed to exist by Guerchais, who gave the d-spacings [193]. It was also studied by Addison, who identified that there were two different powder patterns corresponding to two phases of the purported compound, depending on the synthesis temperature [194], in agreement with one of two scenarios suggested by the observations of Reisman [120]. Stecura et al. found that a = 12.05(4) Å, b = 14.34(5) Å, c = 10.50(3) Å [195]. Meyer and Hoppe found a cubic γ structure with a = 8.605 Å, and a tetragonal β structure with a = 6.14 Å, c = 8.37 Å [196].

Potassium pyroniobate, K₄Nb₂O₇, was proposed by Guerchais, who provided the d-spacings [193].

Potassium metaniobate, KNbO₃, was found by Vousden to be orthorhombic by X-ray powder diffraction (a = 5.7203 Å, b = 3.9714 Å, c = 5.6946 Å) [162]. Wood found reversible polymorphism: 25 °C, orthorhombic (a₀ = 5.702(10) Å, b₀ = 5.739(10) Å, c₀ = 3.984(10) Å; also can be described as pseudotetragonal a₀ = 4.045 Å, c₀ = 3.984 Å; monoclinic axes a₀ = 4.045 Å, b₀ = 3.984 Å, c₀ = 4.045 Å, β = 90.35°); 260 °C, tetragonal (a₀ = 4.00(2) Å, c₀ = 4.07(2) Å); 500 °C, cubic (a₀ = 4.024(1) Å) [161]. The phase changes occur between 200–225 and 420–435 °C. These are in good agreement with the later temperature-dependent study of Shirane et al. from 25–510 °C [166]. Reisman inferred the existence of this compound from the phase diagram [120] and refined procedures for its preparation [197]. Guerchais also found a pseudocubic structure (a = 4.029 Å) [193]. A single crystal X-ray diffraction by Katz and Megaw at room temperature also gave excellent agreement (Bmm2, a = 5.697 Å, b = 3.971 Å, c = 5.721 Å) with the expected distorted perovskite structure [198]. The tetragonal phase was refined by Hewat at 270 °C using single crystal neutron diffraction (P4mm) [199]. Hewat also refined the structure using powder neutron diffraction [200] for the tetragonal (P4mm, a = 3.996 Å, c = 4.063 Å), orthorhombic (Amm2, a = 3.973 Å, b = 5.695 Å, c = 5.721 Å) and rhombohedral (−43 °C, R3m, a = 4.016 Å, α = 89.817°) phases. Sugimoto confirmed the structure of the room temperature form (Amm2, a = 3.9807(7) Å, b = 5.688(1) Å, c = 5.711(1) Å) [201]. Nanowires were synthesized by Kim et al. in a monoclinic phase, as determined by X-ray and neutron powder diffraction (P1m1, a = 4.04976(6) Å, b = 3.99218(6) Å, c = 4.02076 Å, β = 90.1012(27)°) [202].

A metastable orthorhombic phase, K₁₂Nb₁₄O₄₁, was found by Whiston and Smith (a = 8.81 Å, b = 21.55 Å, c = 3.76 Å) [138].

The compound K₄Nb₆O₁₇ was identified by Reisman and Holtzberg [120] and confirmed by Guerchais, who gave the d-spacings [193]. The lattice parameters of this tetragonal cell were given by Whiston and Smith as a = 12.575(2) Å, c = 3.763(1) Å [138]. However, Gasperin and Le Bihan found a lamellar structure consisting of sheets of NbO₆ octahedra (P2₁nb, a = 7.83 Å, b = 33.21 Å, c = 6.46 Å) [203].

The tetragonal compound K₆Nb_10.8O₃₀ was made by Becker and Hold, whose crystal structure was solved (P4/mbm, a = 12.537(2) Å, c =3.9730(1) Å) [204]. The tungsten-bronze-type structure contains NbO₆ octahedra vertex shared with two others to form an Nb₃O₁₅ unit, and these are vertex-connected to form a sheet. Above and below these units is a site 20% occupied by tricapped trigonal prism Nb⁵⁺, together with planes of potassium and oxygen ions.

The triclinic compound K₃Nb₇O₁₉ was synthesized by Fallon et al., and single-crystal XRD was carried out (P-1, a = 14.143(3), b = 9.948(2), c = 6.463(2) Å, α = 106.45(2), β = 95.82(1), γ = 97.29(1)°) [205]. It consists of double strings of seven edge-shared NbO₆ octahedra.

The tetragonal compound KNb₃O₈ was reported by Reisman et al. [120] and by Whiston and Smith (a = 37.71(3) Å, c = 3.939(5) Å) [138]. Gasperin solved the crystal structure of an orthorhombic form (Amam, a = 8.903(3), b = 21.16(2), c = 3.799(2) Å) [206]. It has a lamellar structure consisting of two edge-shared octahedral units connected by a vertex-shared octahedra.

The compound K₂Nb₈O₂₁ was found by Guerchais, who gave the d-spacings [193]. It was also indexed by Whiston and Smith [138] to be primitive tetragonal, a = 27.41, c = 3.955 Å, but they expressed doubts about stoichiometry.

The compound KNb₅O₁₃ was prepared by Kwak et al. and characterized by single crystal X-ray diffraction (Pbcm, a = 5.672(2), b = 10.737(5), c = 16.742(6) Å) [207]. It consists of slabs of NbO₆ octahedra connected by oxygen atoms, with potassium ions occupying the tunnels produced.

The compound KNb₇O₁₈ was studied by electron microscopy and electron diffraction by Hu et al., who found that it was tetragonal, with a = 27.5, c = 3.94 Å [208]. The x and y positions were located, but not the z positions.

The compound K₆Nb₄₄O₁₁₃, proposed by Reisman et al. [120], was indexed as monoclinic by Whiston and Smith (a = 19.83, b = 3.899, c = 19.03 Å, β = 115.0°) [138].

3.8.5. Rubidium Niobates

The rubidium niobates are described next. Rb₈Nb₂O₉ was identified by Reisman and Holtzberg [121].

Rb₃NbO₄ was found by Meyer and Hoppe [196]. At least three polymorphs exist. Two cubic forms were identified by powder diffraction: α, a = 4.45 Å and γ, a = 8.90 Å, the latter of which was isotypic with the potassium analog. In addition, there exists a tetragonal form, a = 6.30 Å, c = 8.81 Å. Annealing of the reactant mixtures at constant temperature gives the tetragonal form first, followed by the α form (2 weeks) and γ form (3 months).

Rb₈Nb₆O₁₉ was identified by Reisman and Holtzberg [121].

RbNbO₃ was identified by Reisman and Holtzberg [121]. The “pyrgom” (Greek for piled-up) structure was solved by Serafin and Hoppe as triclinic (a = 8.87 Å; b = 8.39 Å; c = 5.11 Å; α = 94.6°; β = 93.5°; γ = 113.9° [209] and P-1, a = 8.882(3) Å, b = 8.395(3) Å, c = 5.109(2) Å, α = 94.60(3)°, β = 93.53(3)°, γ = 113.83(3)°) [210]. Each niobium possesses a tetragonal pyramid of oxygen atoms connected by edges to others in chains. The chains are connected by rubidium atoms. A high-pressure orthorhombic perovskite form is also known (a = 3.9965 Å, b = 5.8360 Å, c = 5.8698 Å) [211].

Rb₄Nb₆O₁₇ was identified by Reisman and Holtzberg [121]. Iyer and Smith identified it as orthorhombic (a = 6.42 Å, b = 7.68 Å, c = 38.55 Å) [212] but suggested a slightly different composition Rb₈Nb₁₄O₃₉. The crystal structure of a hydrated version of this salt, Rb₄Nb₆O₁₇·3H₂O, was solved by Gasperin and Le Bihan (Pmnb, a = 7.83(1) Å, b = 39.06(5) Å, c = 6.57 (1) Å) [213].

Rb₂Nb₄O₁₁ was identified by Reisman and Holtzberg [121]. Iyer and Smith identified it as monoclinic (Cm, C2, or C2/m, a = 12.95 Å, b = 7.48 Å, c = 14.92 Å, β = 106.4°) [212] but suggested Rb₁₂Nb₂₂O₆₁ as the stoichiometry.

Rb₈Nb₂₂O₅₉ was identified by Reisman and Holtzberg [121]. Iyer and Smith suggested hexagonal symmetry (P6₃22, a = 7.45 Å, c = 7.66 Å) [212] but reformulated it as RbNb₃O₈. The structure was solved by Fallon and Gatehouse (R-3m, a = 7.527(6) Å, c = 43.17(2) Å) [214]. Dewan and coworkers also solved the structure (R-3m, a = 7.53(1) Å, c = 43.39(6) Å) [215], as did Jones and Robertson (R-3m, a_h = 7.52 Å, c_h = 43.17 Å; rhombohedral a_r = 15.03 Å, α_r = 29.0°) [216] and Voronkova et al. (R-3m, a = 7.502(1), c = 43.12(2)) [217]. This structure was referred to as 11-L (a = 7.7224(7) Å, c = 43.180(5) Å) by Minor et al. [218] Two other structures of similar composition, 16-L (a = 7.5138(5) Å, c = 65.115(9) Å) and 9-L (a = 7.5179(2) Å, c = 36.353(1) Å) were noted.

A structure identified as “RbNb₃O₉” was solved (hexagonal, P6/mmm, a = 7.39 Å, c = 3.89 Å; orthorhombic Cmmm, a = 13.038 Å, b = 7.502 Å, c = 3.89 Å) and described as being similar to the hexagonal tungsten bronzes [219]. The c-axis is about half of that reported by Iyer and Smith for RbNb₃O₈ [212]. It appears similar to the hexagonal-type bronze of Minor et al. (a = 12.991(4) Å, b = 7.550(1) Å, c = 3.8978(8) Å) [218].

Rb₂Nb₈O₂₁ was identified by Reisman and Holtzberg [121]. Iyer and Smith suggested tetragonal symmetry (a = 26.55 Å, c = 3.85 Å) [212]. Jones and Robertson suggested orthorhombic symmetry (Cmcm (more likely) or Cmc2, a = 7.55(1) Å, b = 13.00(2) Å, c = 7.78(1) Å) [216].

Rb₄Nb₃₀O₇₇ was identified by Reisman and Holtzberg [121]. Iyer and Smith suggested monoclinic symmetry (Pm, P2, or P2/m, a = 20.17 Å, b = 3.83 Å, c = 20.75 Å, β = 123.5°) [212]. It was suggested that this may have been a solid solution for the composition Rb₂Nb₂₆O₆₆ because of its similarity to the high-temperature form of Nb₂O₅. One phase present in Reisman’s sample, called “Rb₃Nb₅₄O₁₄₆”, was indexed as tetragonal (P42₁2 or P-42₁m, a = 27.69 Å, c = 3.98 Å) [219]. It consists of octahedra surrounding a heptagonal tunnel. This appears similar to the Gatehouse tetragonal bronze (a = 27.484(3) Å, c = 3.9656(4) Å) [218].

3.8.6. Cesium Niobates

The cesium niobates are described next. Cs₃NbO₄ was synthesized by Meyer and Hoppe [196]. They found a face-centered cubic structure (a = 9.19 Å).

CsNbO₃ was identified by Reisman and Mineo [122]. Iyer and Smith found that it crystallized at 870 °C with orthorhombic symmetry (a = 7.24 Å, b = 15.13 Å, c = 9.77 Å) [212]. Meyer and Hoppe solved the crystal structure and found it to be monoclinic (P2₁/c, a = 5.148 Å, b = 15.89 Å, c = 9.143 Å, β = 93.3°) with discrete Nb₄O₁₂⁴⁻ ions [220].

Cs₄Nb₆O₁₇ was identified by Reisman and Mineo [122].

Cs₂Nb₄O₁₁ was identified by Reisman and Mineo [122]. Iyer and Smith found that it crystallized at 1170 °C with orthorhombic symmetry (a = 13.03 Å, b = 7.60 Å, c = 14.36 Å) [212]. Gasperin also found orthorhombic symmetry (P2nn, a = 10.484 (2) Å, b = 28.898 (4) Å, c = 7.464 Å) [221]. A different high-temperature phase was found by Smith et al. at 450 K (Imma, a = 7.4729 (5) Å, b = 28.9520 (18) Å, c = 10.5080 (6) Å) [222].

Cs₁₀Nb₂₆O₇₀ was identified by Reisman and Mineo [122].

Cs₈Nb₂₂O₅₉, after reformulating as CsNb₃O₈, was found to be isomorphous to the rubidium compound by Dewan et al. [215]. They found the following space group and unit cell (R-3m, a = 7.53(1) Å, c = 43.02(6) Å), as did Voronkova and coworkers (R-3m, a = 7.53(2) Å, c = 42.83(4) Å) [217], and Jones and Robertson (R-3m, a_r = 15.02 Å, α_r = 28.9°; a_h = 7.50 Å, c_h = 43.15 Å) [216].

Cs₄Nb₃₀O₇₇ was identified by Reisman and Mineo [122].

3.8.7. Calculations on Orthoniobate

The calculated bond lengths and vibrational frequencies for NbO₄³⁻ are given in

Table 9. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of orthoniobate, NbO₄³⁻.

	d(Nb-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.8669	832	289	726	328
HF/6-31+G(d)	1.8754	812	294	699	325
MP2/6-31G(d)	1.9054	716	237	614	257
MP2/6-31+G(d)	1.9191	694	253	610	266
B3LYP/6-31G(d)	1.8796	736	248	642	278
B3LYP/6-31+G(d)	1.8966	699	256	624	278
BLYP/6-31G(d)	1.8956	739	246–257	556–605	208–237
BLYP/6-31+G(d)	1.9044	719	235–252	568–573	223–229
PBE/6-31G(d)	1.8851	752	212–235	593–602	184
PBE/6-31+G(d)	1.8929	730	241–262	547–592	217–240
CPCM-HF/6-31G(d)	1.8490	859	285	757	292
CPCM-HF/6-31+G(d)	1.8570	834	287	705	284
CPCM-MP2/6-31G(d)	1.8911	764	258	694	266
CPCM-MP2/6-31+G(d)	1.9030	735	263	641	258
CPCM-B3LYP/6-31G(d)	1.8736	786	254	708	262
CPCM-B3LYP/6-31+G(d)	1.8830	766	265	667	261
CPCM-BLYP/6-31G(d)	1.8934	752	244	678	253
CPCM-BLYP/6-31+G(d)	1.9035	729	250	641	253
CPCM-PBE/6-31G(d)	1.8830	760	245	687	253
CPCM-PBE/6-31+G(d)	1.8916	742	257	652	253

. The only structures containing discrete orthoniobate are the salts of potassium, rubidium, and cesium, whose structures contain a lot of disorder [196]. However, with fractional coordinates for Nb (0, 0, 0) and O ± (0, 0.211, 0.01) and ±(0.211, 0, 0.01), and cubic unit cell of dimensions 8.90 Å, K₃NbO₄ would have an Nb-O distance of 1.88 Å. The Hartree-Fock distances are slightly less than this, the B3LYP distances are slightly higher, and the MP2 distances are too long. To the best of our knowledge, the vibrational frequencies of orthoniobate have not been measured. We expect a clear separation of the symmetric and antisymmetric stretching frequencies, but it is possible that there may be an accidental degeneracy of the deformation frequencies, which are mostly predicted to be within 30 cm⁻¹ of each other. The CPCM solvation model gives rise to smaller Nb-O distances and larger stretching frequencies.

The effect of water upon the Nb-O distances (MP2/6-31+G(d)) in NbO₄³⁻•nH₂O (n = 0–6) is given in Figure 14. The net effect is a moderate shortening of the Nb-O distance by 0.025 Å (n = 6). The individual Nb-O distances vary by up to 0.04 Å. These changes are a little more pronounced than for the divalent ions. The Nb…O distance exhibits an odd behavior, decreasing from n = 1 to n = 3 and then leveling off or even increasing slightly. (Figure S18). For the O…H and O…O distances, the increase of about 0.1 Å upon going from mono to hexahydrate is consistent with the divalent ions (Figures S19 and S20). The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 15. The effect of hydration is to increase the stretching frequencies by about 40 cm⁻¹ going from n = 0 to n = 6, whereas the deformation frequencies only slightly increase. The splitting is large enough to obfuscate the correlation between the two deformation modes because of the overlap, and these might not be able to be observed separately in aqueous solution.

3.9. Tantalates

Like orthoniobate, the experimental evidence for the existence of orthotantalate (TaO₄³⁻), especially in aqueous solution, is scarce. We therefore review some of the literature on the complex chemistry of the Ta₂O₅·M₂O·H₂O (M = Li, Na, K, Rb, Cs) phase diagrams and the compounds therein.

The phases Na₃TaO₄, NaTaO₃, and a compound intermediate in composition between Na₂Ta₄O₁₁ and NaTa₃O₈ were identified by King et al. [223]. Reisman studied the phase diagrams of Li₂O·Ta₂O₅, Na₂O·Ta₂O₅ [224], and K₂O·Ta₂O₅ [225]. Minor and coworkers studied the tantalum-rich portion of the Rb₂O·Ta₂O₅ phase diagram [218]. Tantalum oxide, upon heating, slowly converts from the room-temperature β-phase to the α-phase at 1360 °C before melting at 1872 °C. The melting point of the β-phase is 1785 °C [225]. Lithium tantalates form with a tantalum to lithium ratio of 3:1 (LiTa₃O₈), 1:1 (LiTaO₃), and 1:3 (Li₃TaO₄), whereas sodium tantalates form with a tantalum to lithium ratio of 3:1 (NaTa₃O₈), 2:1 (Na₂Ta₄O₁₁) and 1:1 (NaTaO₃) [224]. Potassium tantalates form with a tantalum-to-potassium ratio of 5:1 (KTa₅O₁₃), 2:1 (K₂Ta₄O₁₁), 1:1 (KTaO₃), and 1:3 (K₃TaO₄) [225].

3.9.1. Tantalum Oxide

For Ta₂O₅, Brauer found only a single structure that was isomorphic to the low-temperature form of Nb₂O₅ by powder diffraction [124]. However, Lagergren and Magneli found an additional high-temperature phase with a transition temperature at 1320 ± 20 °C [226], which was confirmed by Reisman et al. at 1360 ± 5 °C [224]. They could not index the lines but suggested a monoclinic or possibly triclinic system with only a small deviation from an orthorhombic system. Frevel and Rinn found a unit cell (a = 7.32 Å, b = 15.55 Å, c = 10.79 Å, β = 120.6°) and a pseudohexagonal modification (a = 3.60(2) Å, c = 3.88(1) Å) [128]. King and coworkers reported an orthorhombic (sub?)cell (a = 6.18 Å, b = 3.66 Å, c = 3.89 Å) with pseudohexagonal subcell a′ = 3.54–3.66 Å, c′ = 3.89 Å [223].

3.9.2. Lithium Tantalates

For Li₃TaO₄, Reisman was unable to index the powder diffraction patterns [224]. Blasse, however, found that it could be assigned a pseudo-tetragonal unit cell with a = 6.01 Å, c = 16.67 Å [227]. Zocchi and coworkers used X-ray and neutron diffraction to find the structures of the low-temperature β (C2/c, a = b = 8.500(3) Å, c = 9.344(3) Å, β = 117.05(2)°) and high-temperature α (P2/n, a = 6.018(1) Å, b = 5.995(1) Å, c = 12.865 Å, β = 103.53(2)°) phases [228]. Du Boulay reinvestigated the low-temperature form (C2/c, a = 8.508(1) Å, b = 8.516(1) Å, c = 9.338(1) Å, β = 116.869(10)°) [229].

For LiTaO₃, Lapitskii and Simanov indexed this salt on the basis of a rhombohedral cell [230]. Abrahams and Bernstein also found it to be rhombohedral by single-crystal X-ray diffraction (R3c, a_H = 5.15428(1) Å, c_H = 13.78351(2) Å) and found the atomic coordinates to be analogous to the niobate [231]. They repeated the measurements with neutron diffraction to confirm the positions of the lithium atoms between one of the two models [232]. As the temperature increases, it transforms from the ferroelectric phase (R3c) to a paraelectric phase (940 K, R-3c, a_T = 5.2203 Å, c_T = 13.7631 Å) at the Curie temperature T_c = 907 K, as followed by neutron diffraction at 298K, 760 K, 820 K, 885 K, and 940 K [233]. Hsu and coworkers found the following unit cell parameters: R3c, rhombohedral, a = 5.471(2) Å, α = 56.16(3)° [150].

For LiTa₃O₈, Reisman was unable to index the powder diffraction patterns [224]. Whiston proposed that this might actually have been Li₂Ta₈O₂₁ [138]. Gatehouse and Leverett showed that LiTa₃O₈ was isomorphous to the niobate (P2₁/c, a = 7.41(5), b = 5.10(4), c = 15.12(10), β = 107.2(1)°) [153]. Roth and coworkers found that there were three crystalline forms, a low-temperature form L-LiTa₃O₈ (monoclinic, P2₁/c, a = 7.41 Å, b = 5.10 Å, c = 15.12 Å, β = 107.2°) stable below 800 °C and isomorphic to LiNa₃O₈, an intermediate temperature form M-LiTa₃O₈ (monoclinic, Cc or C2/c, a = 9.420 Å, b = 11.536 Å, c = 5.055 Å, β = 91.53°) stable between 800–1100 °C, and a high-temperature form H-LiTa₃O₈ (orthorhombic, Pmma, P2₁ma, or Pm2a, a = 16.716 Å, b = 8.941 Å, c = 3.840 Å) stable between 1100°C and the melting temperature of 1600 °C [234]. Gatehouse et al. found by XRD that M-LiTa₃O₈ was monoclinic (C2/c, a = 9.413(5) Å, b = 11.522(6) Å, c = 5.050(3) Å, β = 91.05(10)°) and similar to the mineral wodginite Mn₄B₄Ta₈O₃₂ [235]. This was confirmed by Santoro et al. using neutron diffraction (C2/c, a = 9.410(2) Å, b = 11.522(2) Å, c = 5.0506(5) Å, β = 91.108(5)°) [236]. Nord and Thomas found by powder and crystal X-ray diffraction that H-LiTa₃O₈ was orthorhombic (Pmma, a = 16.705(2) Å, b = 3.836(1) Å, c = 8.928(1) Å) but could only locate the lithium atoms by powder neutron diffraction [237]. Werner et al. found by powder X-ray diffraction approximate lithium positions in a series of solid solutions of Li_1−xTa₃O_8−xF_x, including x = 0 (a = 16.702(1) Å, b = 3.8485(5) Å, c = 8.9340(5) Å) [238]. Fallon et al. found by single-crystal XRD the space group Pmma, a = 16.702(8) Å, b = 3.840(4) Å, c = 8.929(5) Å [239]. Hodeau et al. revised the space group by electron and neutron diffraction (Pmmn, a = 16.718(2) Å, b = 7.696(1) Å, c = 8.931(1) Å) [240].

3.9.3. Sodium Tantalates

For Na₃TaO₄, King and coworkers found a hexagonal unit cell (a = 16.40 Å, c = 16.81 Å) [223]. Whiston found a = 12.23 Å, b = 12.85 Å, c = 5.732 Å, β = 121.5° [138].

For NaTaO₃, Vousden found an orthorhombic phase at ambient temperature (a = 5.5239 Å, b = 3.8831 Å, c = 5.4778 Å) [162]. King and coworkers found a larger tetragonal (or orthorhombic and pseudotetragonal) unit cell (a = 10.99 Å, b = 10.99 Å, c = 7.64 Å) [223]. Kay and Miles found the orthorhombic distorted perovskite structure from single crystal X-ray diffraction (Pc2₁n, a = 5.4941 Å, b = 7.7508 Å, c = 5.5130 Å) [241]. Reisman also used an orthorhombic cell (a = 5.5237 Å, b = 2(3.8961) Å, c = 5.4781 Å) [224]. Ismailzade showed that it underwent phase transitions from pseudomonoclinic (296 K, a = c = 3.8895 Å, b = 3.8859 Å, β = 90.37°) to another pseudomonoclinic (753 K, a = c = 3.918 Å, b = 3.8859 Å, β = 90.03°), to tetragonal (823 K, a = b = c = 3.923 Å, β = 90.02°), and then to cubic (903 K, a = b = c= 3.929 Å) [242]. Ahtee used powder diffraction difference reflection intensities to refine the structure to allow tilting of the TaO₆ octahedra (Pcmn) [243]. Later, Ahtee used neutron diffraction to reexamine the room-temperature phase (Pcmn, a = 5.4842(2) Å, b = 7.7952(2) Å, c = 5.5213(2) Å), and two high-temperature phases: at 803 K (Bmmb, a = 7.8453(5) Å, b = 7.8541(8) Å, c = 7.8633 (5) Å) and 873 K (Bmmb, a = 7.8560(10) Å, b = 7.8724(7) Å, c = 7.8604 (9) Å); and at 893 K (P4/mbm, a_T = 5.5552(3) Å; c_T = 3.9338(4) Å) [244]. Darlington re-examined these high-temperature phases using neutron diffraction every 5 K and suggested that the low-temperature structure determined previously was incorrect [177]. Shanker found unit cell parameters: Pbnm, a = 5.5883(4) Å, b = 5.6584(3) Å, c = 7.9309(7) Å [179]. Kennedy and coworkers used powder neutron diffraction to study the phase transitions from 298 K to 933 K [245]. The orthorhombic structure (300 K, Pbnm, a = 5.4768(1) Å, b = 5.5212(1) Å, c = 7.7890(2) Å) transforms to orthorhombic (773 K, Cmcm, a = 7.8337(2), b = 7.8485(3), c = 7.8552(3)) at ~700 K, then to tetragonal (843 K, P4/mbm, a = 5.5503(1) Å, c = 3.9335 (1) Å) at 835 K, and finally to cubic (893 K, Pm-3m, a = 3.9313(1)) above 890 K.

For Na₂Ta₄O₁₁, King and coworkers found a tetragonal unit cell (a = 11.00 Å, b = 11.00 Å, c = 14.6 Å) [223]. Reisman found an orthorhombic unit cell (a = 6.00 Å, b = 2(3.83) Å, c = 5.08 Å) [224]. Whiston found a tetragonal unit cell (a = 7.860(1) Å, c = 7.152(3) Å) [138]. Chaminade et al. were able to index it in the monoclinic lattice (a = 10.760 Å, b = 6.200 Å, c = 12.720 Å, β = 106.35°) and a hexagonal lattice (a = 6.208 ± 0.003 Å, c = 36.659 ± 0.010 Å) [246]. Similarities were found between this compound and the subsequently discovered mineral natrotantite, which was synthesized by Ercit and coworkers, who found the unit cell parameters (R-3c, a = 6.2092(1) Å, c = 36.619(1) Å) [247]. Mattes and Schaper found a very similar structure (R-3c, a = 6.198(3) Å, c = 36.56(2) Å) and also located the atoms [248].

For NaTa₃O₈, Reisman assumed an orthorhombic unit cell (a = 2(3.87) Å, b = 2(5.97) Å, c = 5.97 Å) [224]. Whiston claimed that this was actually Na₂Ta₈O₂₁ with a tetragonal unit cell (a = 12.5 Å, c = 3.92 Å) [138]. Chaminade indexed the latter in an orthorhombic unit cell (a = 12.430 ± 0.005 Å, b = 37.290 ± 0.015 Å, c = 3.900 ± 0.002 Å) [246].

3.9.4. Potassium Tantalates

For K₃TaO₄, the interplanar spacings were reported but not indexed by Reisman et al. [225]. Whiston also failed to index them [138]. This was identified as a corrosion product of tantalum metal upon the action of potassium by comparison of the powder patterns [249]. Stecura was finally able to index the pattern of the hygroscopic corrosion product and found a body-centered orthorhombic system with a = 14.19(5) Å, b = 17.04(5) Å, and c = 12.41(4) Å [195].

For KTaO₃, Vousden found a cubic phase at ambient temperature (a = 3.9885 Å) [162]. The X-ray line spacings of Reisman et al. agreed with those of Vousden [225]. Zhurova et al. also found a cubic system (Pm-3m, a = 3.9883(2)) [250].

For K₂Ta₄O₁₁, the interplanar spacings were reported but not indexed by Reisman et al. [225]. Sawaguchi observed its formation from KTaO₃ by slowly cooling the melt. This tetragonal bronze structure has a = 12.574 Å, c = 3.969 Å [251]. Whiston observed a tripling of one of the axes (a = 37.29 Å, c = 3.878 Å) [138].

For KTa₅O₁₃, the interplanar spacings were reported but not indexed by Reisman et al. [222]. Whiston also failed to index these [138]. Awadalla and Gatehouse were successful at determining the unit cell (Pbcm, a = 5.653(3), b = 10.708(5), c = 16.799(7)) and atomic positions [252].

3.9.5. Rubidium Tantalates

Rb₃TaO₄ was synthesized by Meyer and Hoppe [196]. They found a face-centered cubic structure (a = 8.90 Å).

Rb₈Ta₆O₁₉·nH₂O, n = 4,14 was synthesized by Hartl et al. who found the unit cell parameters (n = 4, C2/c, a = 12.169(4) Å, b = 14.592(5) Å, c = 14.147(4) Å, β = 90.734(6)° and n = 14, P2₁/n, a = 10.3130(6) Å, b = 15.9072(9) Å, c = 11.5043(6) Å, β = 100.060(1)°) [253]. These compounds consist of discrete [Ta₆O₁₉]⁸⁻ ions.

RbTaO₃ was found to be monoclinic by Serafin and Hoppe (C2/m, a = 9.589 Å, b = 8.503 Å, c = 8.135 Å, β = 94.87°) [254].

Du Boulay and coworkers identified orthorhombic Rb₃Ta₅O₁₄ from synchrotron X-ray data (Pnma, a = 7.3677(3) Å, 14.7904(19) Å, c = 25.379(3) Å) [255].

Iyer and Smith found that RbTa₃O₈ crystallized with orthorhombic symmetry (space group C222, Cmm2, Cm2m, or Cmmm, a = 13.07 Å, b = 7.26 Å, c = 3.85 Å, β = 105°) [212], whereas Voronkova found a different space group and unit cell (R-3m, a = 7.486(9) Å, c = 43.02(3) Å) [217]. Minor and coworkers found this as well (9-L, hexagonal, a = 7.508 Å, c = 36.41 Å) [218] and also identified a compound Rb₈Ta₂₂O₅₉ (11-L) along with some bronzes (labeled GTB—Gatehouse tetragonal bronze and HTB—hexagonal tungsten bronze). They found a hexagonal unit cell (a = 7.5065(7) Å, c = 43.194(5) Å) [218].

3.9.6. Cesium Tantalates

Cs₃TaO₄ was synthesized by Meyer and Hoppe [196]. They found a face-centered cubic structure (a = 9.29 Å).

Cs₈Ta₆O₁₉·nH₂O, n = 0,14 was synthesized by Hartl et al. who found the unit cell parameters (n = 0, I4/m, a = 9.859(1) Å, c = 14.033(1) Å and n = 14, P2₁/n, a = 10.554(1) Å, b = 16.149(6) Å, c = 11.714(1) Å, β = 99.97(2)°) [253]. These compounds consist of discrete [Ta₆O₁₉]⁸⁻ ions.

Iyer and Smith found that CsTaO₃ crystallized at 1400 °C with monoclinic symmetry (a = 12.90 Å, b = 7.51 Å, c = 14.81 Å, β = 105°) [212].

Serafin and Hoppe investigated the structure of Cs₃Ta₅O₁₄ (Pbam, a = 26.235(2) Å, b = 7.429(1) Å, c = 7.388 (1) Å) [256]. A reinvestigation by Du Boulay et al. only marginally changed the parameters (Pbam, a = 26.219(6) Å, b = 7.4283(10) Å, c = 7.3914 (10) Å) [257].

Voronkova found for CsTa₃O₈ the following unit cell (R-3m, a = 7.473(2), c = 42.78(2)) [217].

3.9.7. Calculations on Orthotantalate

The calculated bond lengths and vibrational frequencies for TaO₄³⁻ are given in

Table 10. Bond lengths (Å) and vibrational frequencies (unscaled, cm⁻¹) of orthotantalate, TaO₄³⁻.

	d(Ta-O)	ν1 (A1)	ν2 (E)	ν3 (T2)	ν4 (T2)
HF/6-31G(d)	1.8807	835	292	709	313
HF/6-31+G(d)	1.8894	814	296	682	309
MP2/6-31G(d)	1.9118	737	245	611	250
MP2/6-31+G(d)	1.9245	714	258	604	257
B3LYP/6-31G(d)	1.8870	784	208	575–612	235–244
B3LYP/6-31+G(d)	1.8960	766	218–220	551–589	243–252
BLYP/6-31G(d)	1.9030	753	209	597–599	220–232
BLYP/6-31+G(d)	1.9117	730	258	548–583	213–229
PBE/6-31G(d)	1.8933	762	208	604–607	221–233
PBE/6-31+G(d)	1.9009	741	259–261	559–593	212–228
CPCM-HF/6-31G(d)	1.8634	858	288	744	2872
CPCM-HF/6-31+G(d)	1.8721	833	288	698	264
CPCM-MP2/6-31G(d)	1.8907	789	266	697	252
CPCM-MP2/6-31+G(d)	1.9012	762	269	650	247
CPCM-B3LYP/6-31G(d)	1.8831	798	261	696	248
CPCM-B3LYP/6-31+G(d)	1.8925	775	269	659	246
CPCM-BLYP/6-31G(d)	1.9009	765	248	667	236
CPCM-BLYP/6-31+G(d)	1.9109	740	255	632	234
CPCM-PBE/6-31G(d)	1.8912	773	252	675	238
CPCM-PBE/6-31+G(d)	1.8998	752	261	642	237

. It is believed that the only structures containing discrete orthotantalate are the salts of rubidium and cesium [193]. To the best of our knowledge, the oxygen positions have not been precisely determined. Our predictions are quite similar for orthotantalate as for orthoniobate, with bond lengths following the trend HF < B3LYP < MP2. To the best of our knowledge, the vibrational frequencies of orthotantalate have not been measured. Like orthoniobate, we expect a clear separation of the symmetric and antisymmetric stretching frequencies but an accidental degeneracy of the deformation frequencies, which are mostly predicted to be within 30 cm⁻¹ of each other. For the B3LYP frequencies, the degeneracy was not strictly maintained, most likely because the density matrix did not maintain full symmetry. The CPCM solvation model gives rise to smaller Ta-O distances and larger stretching frequencies.

The effect of water upon the Ta-O distances (MP2/6-31+G(d)) in TaO₄³⁻•nH₂O (n = 0–6) is given in Figure 16. The net effect is a moderate shortening of the Ta-O distance by 0.022 Å (n = 6). The individual Ta-O distances vary by up to 0.04 Å. These changes are similar to orthoniobate. The Ta…O distance exhibits an odd behavior similar to orthoniobate, decreasing from n = 1 to n = 3 and then leveling off or even increasing slightly. (Figure S21). For the O…H and O…O distances, the increase of about 0.1 Å upon going from mono to hexahydrate is consistent with orthoniobate (Figures S22 and S23). The vibrational frequencies (HF/6-31+G*) as a function of hydration number are shown in Figure 17. The effect of hydration is to increase the stretching frequencies by about 40 cm⁻¹ going from n = 0 to n = 6, whereas the deformation frequencies only slightly increase. The splitting is large enough to obfuscate the correlation between the two deformation modes because of the overlap, and these might not be able to be observed separately in aqueous solution. This behavior is similar to orthoniobate.

4. Discussion

For most of the tetrahedral species discussed above, the B3LYP/6-31+G* level of theory gives excellent values of the metal-oxygen bond distance and the vibrational frequencies. This result is encouraging, given the small basis set size and the lack of a solvation model. The overall trends for the anions upon hydration are, for the most part, consistent with our previous work on similar anions [8]. In some cases, the MP2-FC level severely overestimates the vibrational frequencies. Our standard assumption of the structures of the hydrated anions, based on our prior calculations, can sometimes give small imaginary frequencies, usually at the MP2/6-31G* and B3LYP/6-31G* levels, which may be due to the lack of diffuse functions on these basis sets. These assumptions were shown to be incorrect for the neutral species RuO₄ and OsO₄. For the highly charged orthoniobate and orthotantalate anions, convergence difficulties were observed for some structures for the B3LYP levels.

Based on these calculations, we predict that it will be difficult or impossible to prepare FeO₄, especially in aqueous solution, as attempts to hydrate this molecule often led to hydrated forms of FeO₂(μ₂-O₂), FeO(μ₃-O₃), O + FeO₃, or even O + FeO₂(OH)₂. The extremely basic nature of NbO₄³⁻ and TaO₄³⁻ suggests that these could only exist in extremely basic aqueous solutions. Ions derived from niobium(V) and tantalum(V) tend to be octahedrally coordinated and/or strongly condensed into more complex ions such as NbO₅⁵⁻, NbO₆⁷⁻, Nb₄O₁₂⁴⁻, Nb₄O₁₆¹²⁻, and Ta₆O₁₉⁸⁻. We believe that the best chance to observe the NbO₄³⁻ and TaO₄³⁻ ions in aqueous solution would be by flowing concentrated rubidium or cesium hydroxide over the corresponding orthoniobate or tantalate salt and quickly observing downstream before these coordination expansion/condensation reactions can happen.

5. Conclusions

A series of ab initio and density functional calculations at several levels of theory on several hydrated permanganate, pertechnetate, perrhenate, chromate, molybdate, tungstate, orthoniobate, orthotantalate ions; and of iron(VIII), ruthenium(VIII), and osmium(VIII) oxide have been carried out and structural and vibrational characteristics determined. Based on a careful comparison of the experimental X-ray diffraction and solution vibrational spectra of known species to our calculations, the B3LYP/6-31+G* level of theory can reproduce experiment fairly well and allows us to make predictions for the as yet unknown FeO₄, NbO₄³⁻, and TaO₄³⁻ species.