An Ab Initio Investigation of the Hydration of Antimony(III)

Abstract

The energies, structures, and vibrational frequencies of [Sb(H₂O)_n]³⁺, n = 0–9, 18 have been calculated at the Hartree–Fock and second-order Møller–Plesset levels of theory using the CEP, LANL2, and SDD effective core potentials in combination with their associated basis sets, or with the 6-31G* and 6-31+G* basis sets. The metal–oxygen distances and totally symmetric stretching frequency of the aqua ions were compared with each other and with related crystal structure measurements where available.

1. Introduction

Although the structure of many metal ions in solution is known, some remain elusive [1]. Many are known to be toxic to man, but this is dependent on the oxidation state and speciation, which often depends on pH and the presence of counterions that solubilize the metal by complex formation. While computational chemistry can assist in supporting and rationalizing proposed speciation models, one drawback is that there are typically few all-electron basis sets that can be used. For elements with a high atomic number, relativistic effects can play an important role. Effective core potentials (ECPs) replace the explicit description of core electrons by a potential, and are paired with basis sets describing the outermost electrons. The ECPs represent the scalar relativistic effects only, but the spin–orbital relativistic effects should be small. In a previous work, we benchmarked some common ECPs for the aqua complexes of the heavy metals mercury(II) and thallium(III), both of which have valence electron configuration 5d¹⁰ [2]. It was shown that the ECPs reproduce the known hexacoordination of thallium(III), and supported a hexacoordinate model for mercury(II) over a heptacoordinate model. We also extended this work to lead(II), with valence electron configuration 6s²5d¹⁰ [3]. The presence of an ns² subshell can give rise to either hemidirected structures (which tend to be favored at lower coordination numbers) with ligands that are not symmetrically distributed around the central ion, or holodirected structures with a symmetrical distribution. No consensus exists on the coordination number of lead(II), with predictions ranging from 4 to 9, but our results were most consistent with a hemidirected hexaaqualead(II) species. For the smaller aquatin(II) ion (5s²4d¹⁰), we found that the preferred hydration mode was a tricoordinate trigonal pyramidal triaquatin(II), agreeing with recent experiments [4]. We extend our work now to antimony(III), which has the same valence electron configuration as tin(II) but a higher charge. The structure of aquaantimony(III) is unknown, so one of our aims is to predict its structure. The presence of the ns² subshell, as with lead(II) and tin(II), will be shown to have a pronounced effect on the structures compared to those without it.

The literature on the solution chemistry of antimony(III) is sparse. The solubility of rhombic Sb₂O₃ was examined by Gayer and Garrett over half a century ago, and they proposed that dissolved antimony(III) exists as SbO⁺, Sb(OH)₃, and SbO₂⁻ as the pH is increased [5]. This was confirmed spectrophotometrically by Mishra and Gupta, who suggested that the neutral species could be either Sb(OH)₃ or SbO(OH) [6]. Potentiometrically, SbO⁺ is equivalent to Sb(OH)₂⁺, SbO₂⁻ is equivalent to Sb(OH)₄⁻, and Sb³⁺ is proposed to exist only in strongly acidic solutions [7]. Ahrland and Bovin examined the solution chemistry of antimony(III) oxide in perchloric and nitric acid [8]. At an ionic strength of 5.0 mol/L, maintained by sodium perchlorate or nitrate, the two modifications of Sb₂O₃(s) are only metastable above a perchloric acid concentration of 0.3 mol/L (orthorhombic) or 0.7 mol/L (cubic), and the equilibrium solid phase is Sb₄O₅(OH)ClO₄·1/2H₂O. Other solid phases exist at higher acid concentrations. In nitric acid at a nitrate concentration of 5.0 mol/L, the equilibrium solid phase is Sb₄O₄(OH)₂(NO₃)₂. Analysis suggests that the aqueous speciation at a low pH consists of Sb(OH)₂⁺, and possibly Sb₂(OH)₂⁴⁺. Zakaznova-Herzog and Seward used UV/visible spectroscopy to examine the equilibria of antimonous acid and was able to explain their results using the species H₃SbO₃(aq), H₄SbO₃⁺, and H₂SbO₃⁻(aq) from 25–300 °C, pH = 0.8–12.5 at a total antimony concentration of ~10⁻⁴ mol/L [9].

We now consider if insight may be gained by examining the solid-state structures of antimony oxides and their hydrates. Antimony(V) oxide, and its mono and trihydrate, were discussed by Natta and Baccaredda [10]. Well-aged (5 years!) monohydrate Sb₂O₅·H₂O (also known as antimonic acid, HSbO₃) was found to belong to a cubic space group (Schonflies notation, O_h⁷; Hermann–Mauguin notation, $Fd\overline{3}{m}_2$), with a = 10.23 ± 0.02 Å, Z = 8. The compound Sb₂O₄ of the same space group was formulated as the pyroantimonate [Sb^III₂O]⁴⁺[Sb^V₂O₇]^4–. However, Dihlstrom and Westgren suggested that “Sb₂O₄” was actually Sb₃O₆OH, as Sb^IIIOOH·Sb^V₂O₅, with a = 10.28 Å [11]. They found the distances Sb^III-O, 2.48 Å; Sb^III-O(H), 2.23 Å, Sb^V-O, 2.02 Å. Another form of antimonic acid, Sb₂O₅·3H₂O, was found by England et al. to have a pyrochlore (A₂M₂O₆O’, $Fd\overline{3}m$) structure via powder diffraction [12]. Other forms, described by Watelet et al. as [H(H₂O)_n]₁₂Sb₁₂O₃₆, (n = 0.33, 1), space group Im3, a = 9.470(5), and 9.497(3) Å, respectively, have Sb-O distances in the range 1.939–2.006 Å [13]. These solids are proton conductors. Another antimony oxide hydroxide HSb₃O₈ was described by Jager et al. [14] as space group P2/n, with cell constants a = 9.456(2), b = 8.691(2), c = 9.909(2) Å, β = 90.25(2)°, Z = 6. The Sb-O distances fall in the range 1.890–2.140 Å. Riviere et al. obtained an Fd3m space group for H₂Sb₂O₆·H₂O, a = 10.365(2) Å, with Sb-O = 1.971 Å [15]. For antimony(III) oxide, the structure of the cubic α form was refined by Svensson [16], who found a space group Fd3m and a = 11.1519(2) Å. It forms discrete Sb₄O₆ units of symmetry T_d with trigonal pyramidal antimony(III) with an Sb-O distance of 1.977(1) Å and angles of 95.93(8)°. Svensson also examined the orthorhombic β modification of antimony(III) oxide [17], and found a space group Pccn, a = 4.911, b = 12.464, c = 5.412 Å. The structure is composed of double infinite chains, with the antimony lone pair perpendicular to the chains. The antimony is trigonal pyramidal, with Sb-O distances in the range 1.977(7)–2.023(4) Å. A novel γ modification was reported by Orosel et al., with space group P2₁2₁2₁, a = 11.6411(1), b = 7.5666(0), c = 7.4771(0) Å, with Sb-O distances in the range 1.87–2.24 Å [18]. In Sb₄O₄(OH)₂(NO₃)₂, Bovin found sheets of 3-coordinate trigonal pyramidal and 4-coordinate seesaw antimony(III) separated by nitrate ions [19]. The Sb-O distances in the SbO₃ units are in the range 1.942(7)–2.067(6) Å, and in the SbO₄ units, 2.019(6)–2.265(6) Å. In Sb₄O₅(OH)ClO₄·1/2H₂O, Bovin found short chains of SbO_n polyhedra forming layers separated by the perchlorate ions and water molecules [20]. The Sb-O distances in the SbO₃ units are in the range 1.969(11)–2.027(8) Å, and in the SbO₄ units, 1.952(9)–2.378(8) Å. In the antimony oxide sulfate Sb₆O₇(SO₄)₂, Bovin found that the three unique antimony atoms were trigonally pyramidally coordinated to oxygen atoms, with Sb-O distances between 1.994(17) and 2.207(18) Å, but with a fourth oxygen close 2.327(14)–2.382(18) [21]. Mercier et al. found for the oxonium antimony sulfate, (H₃O)₂Sb₂(SO₄)₄, that antimony exists as both a seesaw SbO₄ and square pyramidal SbO₅ polyhedra, with corresponding distances of 2.032(10)–2.359(19) Å and 2.012(15)–2.263(13) Å [22]. The axial distance of SbO₅ is the shortest. To summarize this literature, antimony(V) tends to exist as an octahedrally coordinated moiety in the presence of oxide/hydroxide, whereas antimony(III) can exist as either a trigonal pyramidal SbO₃, seesaw SbO₄, or square pyramidal SbO₅ coordinated moiety in a similar environment.

2. Materials and Methods

Calculations were performed using Gaussian 98 [23]. In this program version, the ability to calculate analytical frequencies of molecules in which core electrons are described by effective core potentials was introduced. Therefore, many variants of these were tried. The MP2 calculations use the frozen core approximation. A stepping-stone approach was used for geometry optimization, in which the geometries at the levels HF/CEP-4G, HF/CEP-31G*, HF/CEP-121G*, HF/LANL2MB, HF/LANL2DZ, and HF/SDD were sequentially optimized. For minimum energy structures, the MP2/CEP-31G* and MP2/CEP-121G* calculations were also performed. Calculations were also carried out using the 6-31G* and 6-31+G* basis sets on the atoms of the water molecules (5d) with an effective core potential and basis set on the metal ion (denoted as ECP+6-31G* or 6-31+G*). For shorthand, we denote the mixed basis sets as follows: CEP-121G* on Sb, 6-31G* on O,H, as basis set A; LANL2DZ on Sb, 6-31G* on O, H, as basis set B; SDD on Sb, 6-31G* on O,H, as basis set C; and the corresponding basis sets with diffuse functions are indicated by adding a “+” to the basis set name. Default optimization specifications were used. After each level, where possible, a frequency calculation was performed at the same level and the resulting Hessian was used in the following optimization. Z-matrix coordinates constrained to the appropriate symmetry were used to speed up the optimizations. Because frequency calculations are carried out at each level, any problems with the Z-matrix coordinates would manifest themselves by giving imaginary frequencies corresponding to modes orthogonal to the spanned Z-matrix space. The Hessian was evaluated at the first geometry (opt = CalcFC) for the first level in a series to aid geometry convergence. We note that, for the heavy elements only, the three different CEP basis sets are equivalent (CEP-121G*) but differ for the oxygen and hydrogen atoms. The choice of core electrons defining the pseudopotential depends on the specific core potential (CEP and LANL2, [Kr]4d¹⁰; SDD, [Ar]3d¹⁰). Gaussian 03 [24] and Gaussian 16 [25] were used to correct errors and omissions.

In many cases to follow, the symmetry of the minimum energy complexes was the same as those previously found for bismuth [26]. To confirm these results, starting with high symmetry structures, systematic desymmetrization along the various irreducible representations was carried out [27,28]. We did not employ an implicit solvation model for reasons described previously [3].

3. Results

3.1. A Survey of Structures

Antimony(III) might be expected to show similar properties to tin(II), although the higher charge would cause stronger interactions with water molecules. The point group symmetry for mono- through octaaquaantimony(III) was initially usually found to be C_2v, C₂, C₃, C_2v or C₂, C_2v, C₃, C_2v [5+2], and S₈, respectively. The diaquaantimony(III) species, like lead and tin, ascended in symmetry to a planar C_2v structure at HF/LANL2MB. Initially, all attempts to generate a stable 7-coordinate antimony resulted in two water molecules moving to the second hydration sphere. We initially did not find a stable D₃ enneaaquaantimony(III) structure.

The results of the systematic desymmetrization procedure [27] for aquaantimony(III) are as follows (see Figure 1 and Figure S1):

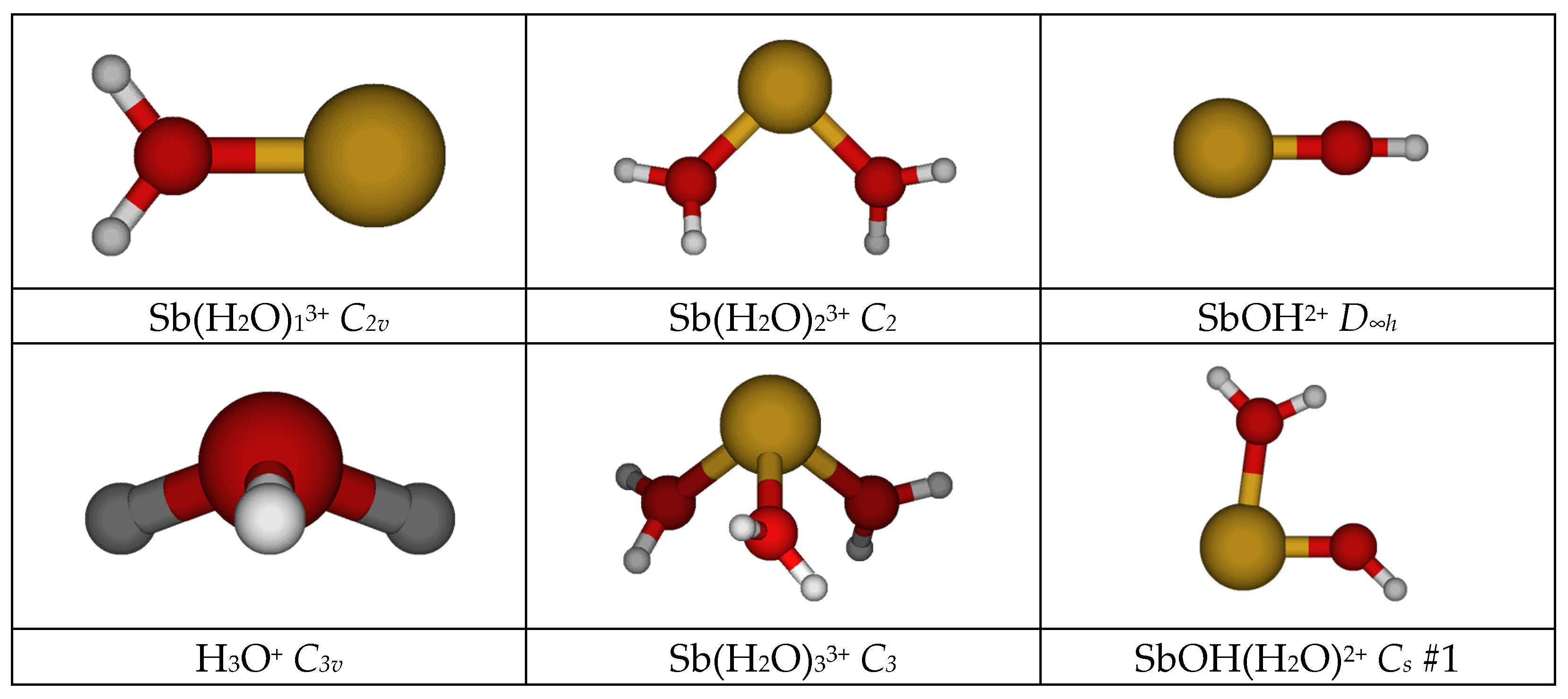
• The monoaquaantimony(III) remains C_2v at all levels.
• The most stable diaquaantimony(III) remains the bent C₂ at all levels except HF/LANL2MB (C_2v planar). The linear holodirected D_2d structure is approximately 50 kJ/mol higher in energy, but the unstable bent C_s structure is only slightly higher in energy (<1 kJ/mol for nonminimal basis sets). All attempts to generate a [1+1] structure instead result either in proton transfer to give SbOH²⁺ + H₃O⁺, which was much lower in energy, or recoordination to give the [2+0] C_s structure.
• The most stable triaquaantimony(III) remains the pyramidal C₃ at all levels. The two pyramidal C_3v structures are 10–30 kJ/mol higher in energy, whereas the planar holodirected D_3h and D₃ structures are 125–150 kJ/mol higher in energy still. The unstable [2+1] C_2v structure was ~90 kJ/mol higher in energy, and upon desymmetrization, underwent proton transfer to give the much-lower-in-energy SbOH(H₂O)²⁺ + H₃O⁺.
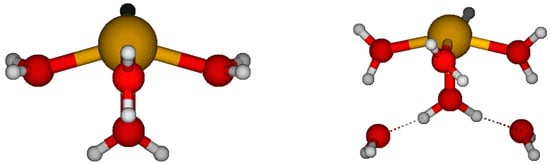
• The most stable tetraaquaantimony(III) is usually the seesaw C_2v #3 (all mixed basis sets, HF/SDD), but it can be C₂ (all CEP, HF/LANL2DZ) or C_s (HF/LANL2MB). The other C_2v structures are higher in energy (10–25 kJ/mol). The holodirected D_2d #1, #2, and S₄ structures are much higher in energy (75–125 kJ/mol). The unstable C_s #2 [3+1] structures are up to 50 kJ/mol higher in energy, and upon desymmetrization, undergo a proton transfer to give the much-lower-in-energy SbOH(H₂O)₂²⁺ + H₃O⁺.
• The most stable pentaaquaantimony(III) is the square pyramidal C_2v #1, with the other three C_2v structures which are 25–50 kJ/mol higher in energy. The usually unstable [4+1] structures are 15–50 kJ/mol higher in energy. To our surprise, the C_2v #1 [4+1] is stable at HF/CEP-121G*, HF/LANL2MB, HF/A, HF/B, HF/C, and HF/A+. At the other levels, there is a B₁ imaginary mode, along which a proton transfer occurs to give SbOH(H₂O)₃²⁺ + H₃O⁺. At the MP2 levels, desymmetrization along an A₂ mode gives rise to a C₂ structure, which is slightly lower in energy.
• The most stable hexaaquaantimony(III) is the distorted octahedral C₃. The octahedral T_h structure is ~18–50 kJ/mol higher in energy. The two C_s [5+1] structures examined often underwent proton transfer to give SbOH(H₂O)₄²⁺ + H₃O⁺. However, if the [5+1] structures were stationary points, they were lower in energy than the [6+0] forms by about 25 kJ/mol. In some cases, they were actually minima (HF/CEP-121G*, all HF mixed basis sets). Given how shallow (or in some cases, nonexistent) the barrier to proton transfer is to give the deprotonated forms, it is reasonable to conclude that the aquaantimony(III) species would only exist in an extremely acidic solution. Combined with the results for the pentaaquaantimony(III), this suggests that antimony(III) is actually pentacoordinate square pyramidal.
• Of the 16 different C_2v heptaaquaantimony(III) structures tried, none were stable, either possessing imaginary modes or dissociating to a [6+1], [5+2], or [4+3] structure. Structures #1, #2, and #4, nearly always dissociated. The remainder usually remained 7-coordinate, except occasionally dissociating at HF/CEP-4G and HF/LANL2MB. In some cases, the [5+2] structures underwent a double proton transfer and possibly a water elimination to give Sb(OH)₂(H₂O)_2/3⁺ + 1/0H₂O + 2H₃O⁺. Of the 7-coordinate C_2v structures, #16 was the lowest in energy, unless #1 was a stationary point, in which case, it was lower in energy. In all cases, the [5+2] structure was 20–80 kJ/mol lower in energy than the 7-coordinate C_2v #16 structure. Upon desymmetrization of the remaining 7-coordinate C_2v structures to C₂, many coalesced to C₂ #16, some dissociated to [5+2], but at some levels, C₂ #5, #6, #11, and #13 also exist, with at least one imaginary B mode. When these were desymmetrized to C₁ #1–5, a stable C₁ #3 or #5 was found at some levels, or ligand dissociation to a [6+1] or [5+2] structure took place. Desymmetrization of the C_2v structures along the B modes gave one of 27 possible C_s structures. Of these, C_s #1, #5, and either #13 or #20 often coalesce (to C_s #5); C_s #2, #7, #14 and #22 often coalesce (to C_s #7); C_s #12 coalesces to C_s #8; C_s #11, #18, and #26 often coalesce (to C_s #26); C_s #19 and C_s #15 ascend in symmetry to either C_2v #10 or #12; C_s #16 and #24 often coalesce to C_s #10 or to each other; C_s #25 coalesces to C_s #21; C_s #27 coalesces to C_s #23; and C_s #17 remains unique. None of these C_s structures are minima, except C_s #13 at HF/A+. The C_s structures desymmetrize to C₁ #6–21. Of these possibilities, for the most part, they coalesced to the previously found C₁ #3 or #5 structures, or underwent ligand dissociation to give [6+1] or [5+2] structures. This exemplifies the power of the systematic desymmetrization procedure in finding minimum energy structures that would otherwise be difficult to locate. In all cases where a seven-coordinate minimum energy structure exists (HF/CEP-31G*, HF/CEP-121G*, MP2/CEP-31G*, MP2/CEP-121G*, HF/C, HF/A+, HF/B+, HF/C+, MP2/A+), it is less stable than a [5+2] or [6+1] structure (or a proton transferred version thereof). The 7-coordinate structures are unlikely to have any significant population in an aqueous solution under ambient conditions.
• For octaaquaantimony(III), two D_4h (square prism) and two D_4d (square antiprism) structures were first examined. Multiple imaginary modes were present.
• For the D_4d #1 and #2 structures, desymmetrization along the A₂ imaginary mode gave the same S₈ #1 structure; along the B₁ imaginary mode, the same D₄ #2 structure; and along the B₂ imaginary mode, the C_4v #1 and #2 structures. For the D_4h #1 and #2 structures, desymmetrization along the A_1u imaginary mode gave the D₄ #2 structure found before; along the A_2g imaginary mode, the same C_4h #1 structure; along the A_2u imaginary mode, the C_4v #3 [4+4] and #4 structures; along the B_2g imaginary mode (D_4h #1), the D_2h #1 structure ascended in symmetry to D_4h #2; along the B_1u mode, D_2d #1 and #3 coalesced; along the B_2u mode, D_2d #2 and #4, respectively. Another D_2d structure (#5) was formed by combining other D_2d structures.
• Desymmetrization of the C_4h #1 structure along the A_u mode usually gives the S₈ #1 structure (via C₄ #1), and along the B_u mode, D_2d #5 (via S₄ #1); the S₈ #1 structure along the B mode at two levels, C₄ #1; the D₄ #1 structure along the A₂ mode, C₄ #1, and along the B₂ mode, D₂ #1; the D_2d #1 structure along the A₂ mode, S₄ #2, the B₁ mode, D₂ #1, and the B₂ mode, [4+4] C_2v #1; the D_2d #2 structure along the A₂ mode, S₄ #2, the B₁ mode, D₂ #1, and the B₂ mode, C_2v #2; the D_2d #4 structure along the A₂ mode, S₄ #2, the B₁ mode, D₂ #1, and the B₂ mode, C_2v #3; the D_2d #5 structure along the B₁ mode, D₂ #1, and the B₂ mode, [6+2] C_2v #4. All of these structures had at least one imaginary frequency.
• Desymmetrization of the S₄ #2 structure along the B mode, C₂ #1 (which was close in structure to the D₂ #1 structure); the D₂ #1 structure along the B₁ mode gave either the [4+4] or [6+2] C₂ #1, or more usually the stable S₈ #1.
• For enneaaquaantimony(III), four D_3h structures were first examined. Desymmetrization along the A₁” mode led to the common D₃ #1 structure (which was only stable at MP2/CEP-31G*); the A₂′ mode led to either the unstable C_3h #1 or #2 structures; and the A₂” mode led to the unstable C_3v #1–4 structures. The C_3v #2 and 3 structures were usually of [6+3] coordination. When these structures were desymmetrized, they nearly always resulted in expulsion of three water molecules to the second hydration sphere to give the (usually) stable C₃ #1 [6+3]. An unstable [6+3] D₃ structure was also found, which desymmetrized to give the even more stable C₃ #2 [6+3].

To summarize these results, it appears that the square pyramidal pentaaquaantimony(III) ion is the most stable aqua ion. There is a strong propensity to react with second-shell water molecules to form hydroxo complexes. While stable structures with coordination numbers between six and nine do exist at some levels of theory, the corresponding structures in which some waters have moved to the second hydration shell are more stable (in some cases, with proton transfer). These higher-coordination aqua complexes might exist at high pressures. The aqua ion, if it exists, would only exist at a very low pH.

3.2. The Sb-O Distance

In Figure 2, a plot of the dependence of the average Sb-O distance as a function of the coordination number n is given for all of the levels investigated. The Sb-O distance lengthened with the increase in coordination number. With the exception of HF/LANL2MB, the results were fairly uniform (for the most part, within 0.05 Å). The HF/LANL2MB level is the only Hartree–Fock level calculation using a minimal basis set on the valence shell of all atoms, and therefore does not have enough flexibility to fully describe the bonding between antimony(III) and oxygen. The pairs HF/CEP-31G* and HF/CEP-121G*, and MP2/CEP-31G* and MP2/CEP-121G*, were nearly coincident with each other, with the latter pair giving slightly longer bond lengths. The variation in the Sb-O distance with the level of theory was smaller than that of Sn-O [4]. Based on our calculations, if the coordination number is indeed 5, then we would expect an average Sb-O distance of around 2.25 Å.

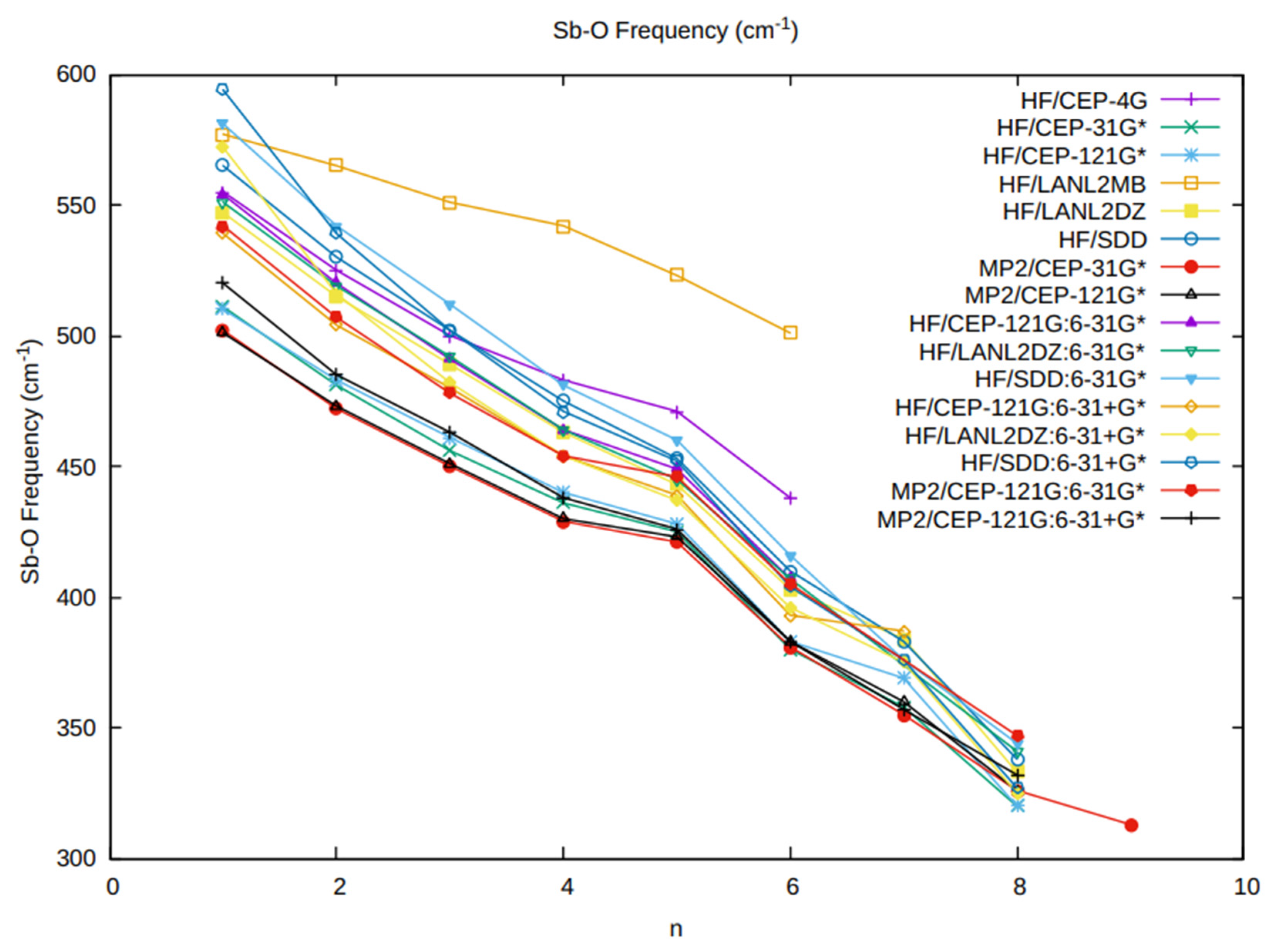
3.3. The Sb-O Vibrational Frequency

In Figure 3, a plot of the dependence of the frequency of the most intense Raman Sb-O stretching mode as a function of the coordination number n is given for all of the levels investigated. As expected, this frequency drops with hydration number n. The minimal basis set levels HF/LANL2MB, and to some extent, HF/CEP-4G, are different than the others, having higher values. The CEP-4G basis set is a minimal basis set on oxygen and hydrogen, but is actually using the triple-zeta valence basis set (CEP-121G) on the antimony atom. There is a levelling off of the frequency, and then a bigger drop at n = 6. For n = 4 and 5, the vibrational mode is somewhat more localized, being due predominantly to either the equatorial oxygen motion (n = 4) or the apical oxygen motion (n = 5). The HF/CEP-31G*, HF/CEP-121G*, MP2/CEP-31G*, MP2/CEP-121G*, and MP2/A+ levels form the group with the lowest vibrational frequencies. The HF calculations using the SDD basis set on Sb form a group with the highest vibrational frequencies. For the levels using split valence basis sets, if the coordination number is indeed 5, then the predictions for the Sb-O symmetric stretching motion center around 450 ± 30 cm⁻¹. In solution, the effect of the second hydration shell would increase this by an estimated 60 cm⁻¹, meaning that our best guess for the Sb-O mode in an aqueous solution would be 510 cm⁻¹.

4. Discussion

To the best of our knowledge, experimental data on the structure and vibrational spectra of antimony(III) aqua complexes are lacking. Our energetic comparisons suggest that the coordination number should be 5. From this, we have made predictions as to the Sb-O distance (2.25 ± 0.05 Å) and vibrational frequency (510 ± 30 cm⁻¹) that might be observed. We may compare the X-ray crystal structures involving Sb³⁺-O^2– (or OH⁻) interactions with the same coordination geometry. Our predictions for trigonal pyramidal (n = 3) lie at around 2.10 Å (cf. 1.977 Å in α-As₄O₆ [16], 1.977–2.023 Å in β-As₄O₆ [16], 1.942–2.067 Å in Sb₄O₄(OH)₂(NO₃)₂ [19], 1.969–2.027 Å in Sb₄O₅(OH)ClO₄·1/2H₂O [20], 1.994–2.207 Å in Sb₆O₇(SO₄)₂ [21]); for seesaw (n = 4), at around 2.17 Å (cf. 2.019–2.265 Å in Sb₄O₄(OH)₂(NO₃)₂ [19], 1.952–2.378 Å in Sb₄O₅(OH)ClO₄·1/2H₂O [20], 2.032–2.359 Å in (H₃O)₂Sb₂(SO₄)₄ [22]); and for square pyramidal (n = 5), at around 2.25 Å (cf. 2.012–2.263 Å in (H₃O)₂Sb₂(SO₄)₄ [22]). The separation by distance between the axial and equatorial sites in the seesaw and square pyramid is reproduced. Our predictions for the Sb³⁺-OH₂ distances are about 0.1 Å longer than the Sb-O distances between the antimony(III) and either the O^2– or OH⁻ moieties in the crystal structures, in which there should be stronger attractive forces.

5. Conclusions

The common CEP, LANL2, and SDD pseudopotentials were paired with various basis sets to study the hydrated antimony(III) ion. Calculations using minimal basis sets (HF/LANL2MB, HF/CEP-4G) performed poorly. The calculated structures of the aqua complexes compared favorably with the crystal structures of the oxides/hydroxides. Symmetry can be used to guide the search for new structures and to rule out structures. For the smaller coordination numbers, the effect of the ns² subshell is clearly to form a hemidirected structure in which the electrons act similarly as a ligand or lone pair would. The factors giving rise to either holodirected or hemidirected structures were thoroughly discussed by Shimony-Livny et al. for Pb(II) and do not need to be repeated here [29]. There is a propensity for the aqua complexes of smaller coordination numbers of type [n + 1] to hydrolyze to form the aquahydroxoantimony(III) complex and a hydronium ion, which is evidence for the strong Lewis acidity of antimony(III). We predict that antimony(III) might exist in extremely acidic solutions with a coordination number of 5, an average Sb-O distance of 2.25 Å, and with a Raman-active Sb-O totally symmetric stretching motion occurring at around 510 cm⁻¹.