Solvation Enthalpies and Free Energies for Organic Solvents through a Dense Neural Network: A Generalized-Born Approach †
Abstract
1. Introduction
2. Methods
- (1) the number of atoms in the solute molecule N;
- (2) the molecular volume Vtot: Vtot= ∑IVI;
- (3) the total surface area Stot composed of atomic surfaces: Stot= ∑ISI;
- (4–12) atomic surface areas summed over all the atoms of a given element L: SL = ∑IϵLSI for L = H, C, N, O, F, S, Cl, Br, and I. The atomic volumes VI and surfaces SI are efficiently calculated by simple formulas based on geometric considerations. The details are given in [38];
- (13–21) the Born-type self-terms, also summed over all the atoms of a given element L:
- (22–51) the Born-type pair terms:
- (52–56) five solvent-related input features: in addition to the dielectric constant, boiling point, and the number of nonhydrogen atoms employed in my previous work [38], in this paper, the molar volume and the number of hydrogen-bond centers (the sum of the donor and acceptor centers) are also used.
3. Results and Discussion
3.1. Database
3.2. Training
3.3. Performance of ESE-ΔH-DNN
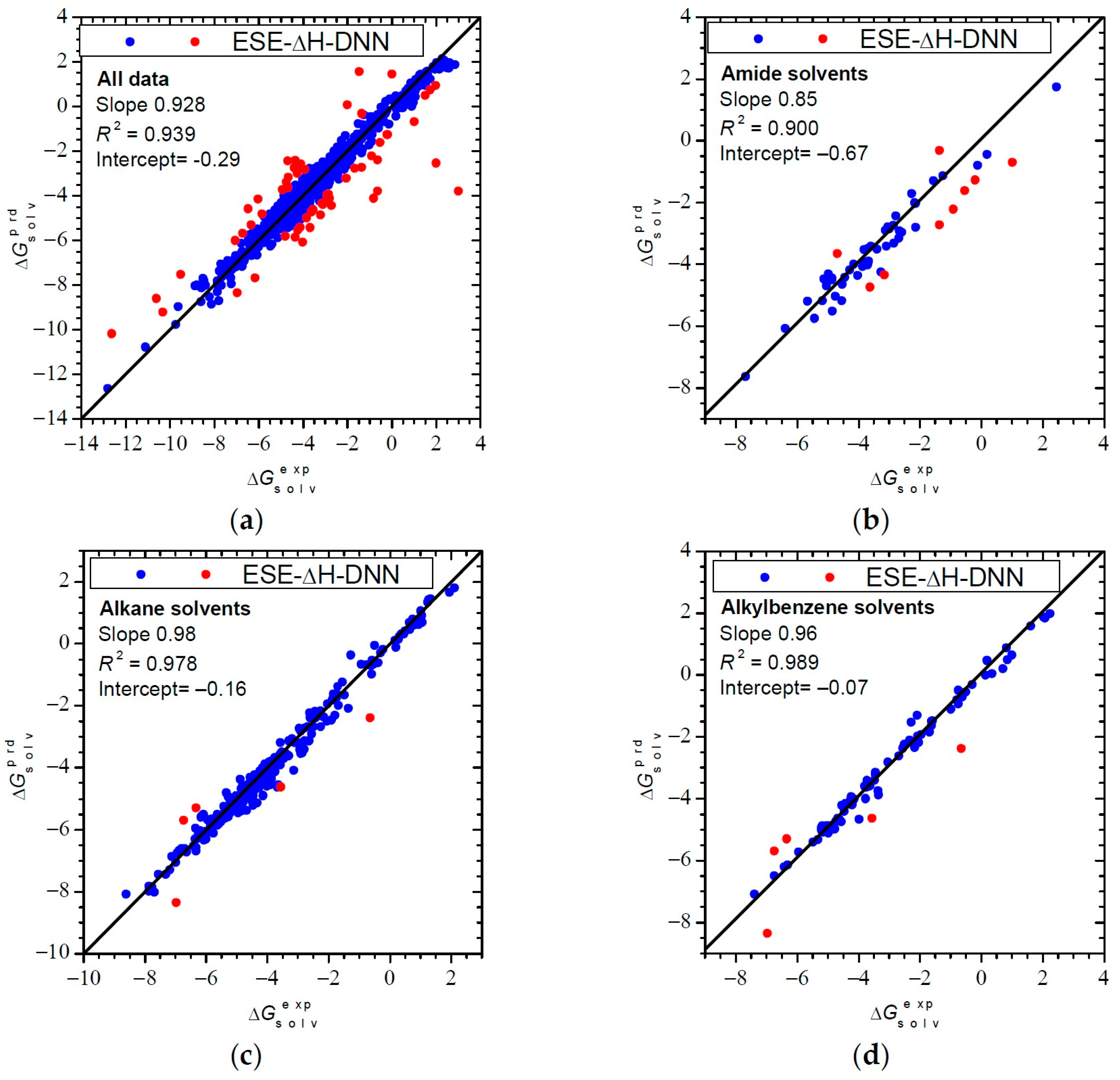
3.3.1. Performance for Solvation Gibbs Free Energies
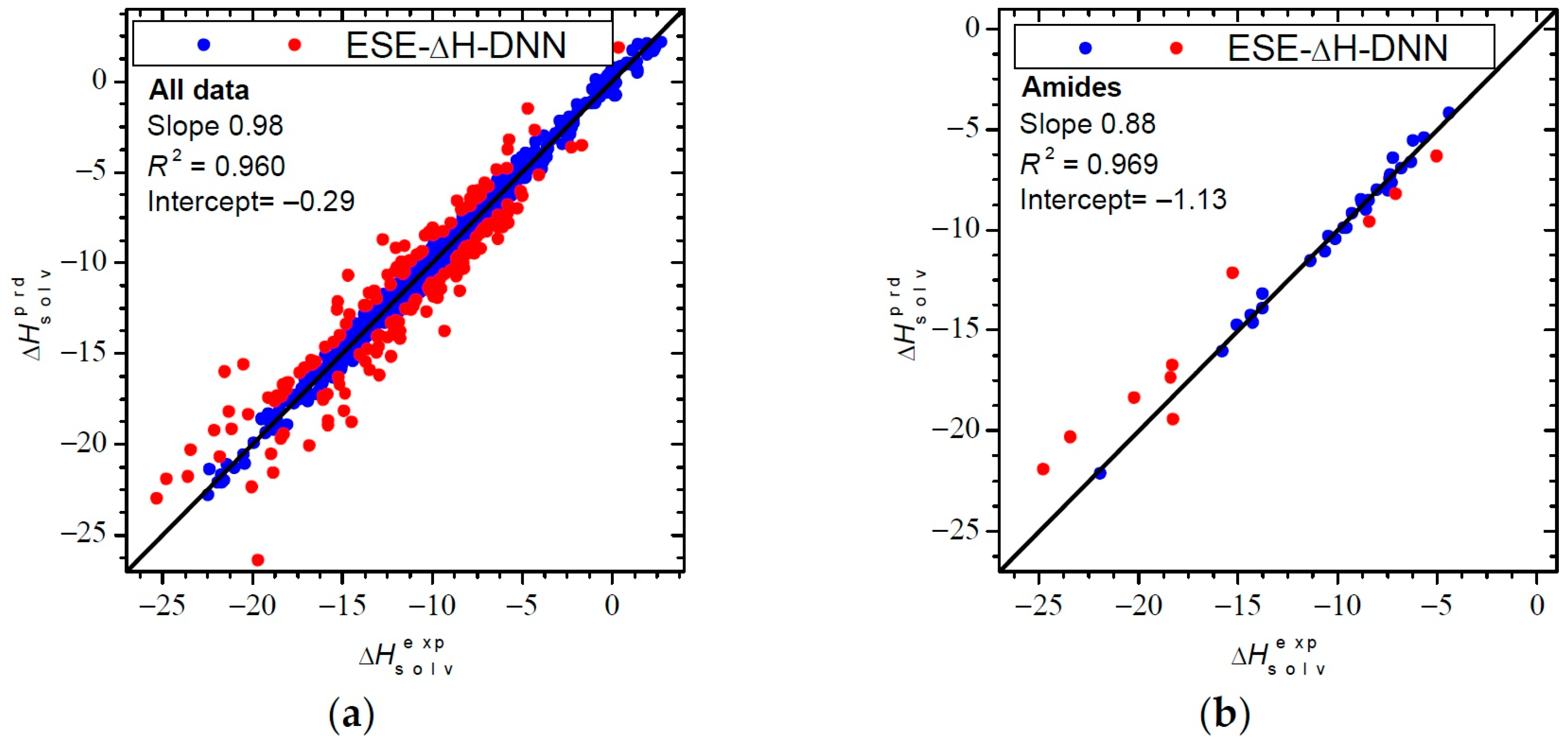
3.3.2. Performance for Solvation Enthalpies
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torrie, G.; Valleau, J. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- You, W.; Tang, Z.; Chang, C.A. Potential mean force from umbrella sampling simulations: What can we learn and what is missed? J. Chem. Theory Comput. 2019, 15, 2433–2443. [Google Scholar] [CrossRef] [PubMed]
- Chipot, C.; Pohorille, A. Calculating free energy differences using perturbation theory. In Free Energy Calculations: Theory and Applications in Chemistry and Biology; Chipot, C., Pohorille, A., Eds.; Springer Series in Chemical Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; Volume 86, p. 33. ISBN 540-38447-2. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourik, T.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M.; Tomasi, J. A new definition of cavities for the computation of solvation free energies by the polarizable continuum model. J. Chem. Phys. 1997, 107, 3210–3221. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anistropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of solvent effects in isotropic and anisotropic dielectrics, and in ionic solutions with a unified integral equation method: Theoretical bases, computational implementation and numerical applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Robb, M.A. A direct procedure for the evaluation of solvent effects in MC-SCF calculations. J. Chem. Phys. 1999, 111, 5295–5302. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. (Theochem) 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Pomogaeva, A.; Chipman, D.M. Hydration energy from a composite method for implicit representation of solvent. J. Chem. Theory Comput. 2014, 10, 211–219. [Google Scholar] [CrossRef]
- Hille, C.; Ringe, S.; Deimel, M.; Kunkel, C.; Acree, W.E.; Reuter, K.; Oberhofer, H. Generalized molecular solvation in non-aqueous solutions by a single parameter implicit solvation scheme. J. Chem. Phys. 2019, 150, 041710. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Klamt, A. The COSMO and COSMO-RS solvation models. WIREs Comput. Mol. Sci. 2011, 1, 699–709. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T.J. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Generalized Born solvation model SM12. J. Chem. Theory Comput. 2013, 9, 609–620. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. General parameterized SCF model for free energies of solvation in aqueous solution. J. Am. Chem. Soc. 1991, 113, 8305–8311. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. An SCF solvation model for the hydrophobic effect and absolute free energies of aqueous solvation. Science 1992, 256, 213–217. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. A universal approach to solvation modeling. Acc. Chem. Res. 2008, 41, 760–768. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Uniform treatment of solute–solvent dispersion in the ground and excited electronic states of the solute based on a solvation model with state-specific polarizability. J. Chem. Theory Comput. 2013, 9, 3649–3659. [Google Scholar] [CrossRef]
- Born, M. Volumen und Hydratationswärme der Ionen. Z. Physik 1920, 1, 45–48. (In German) [Google Scholar] [CrossRef]
- Onufriev, A.V.; Case, D.A. Generalized Born implicit solvent models for biomolecules. Annu. Rev. Biophys. 2019, 48, 275–296. [Google Scholar] [CrossRef] [PubMed]
- Grycuk, T. Deficiency of the Coulomb-field approximation in the generalized Born model: An improved formula for Born radii evaluation. J. Chem. Phys. 2003, 119, 4817–4826. [Google Scholar] [CrossRef]
- Grant, J.; Pickup, B.; Sykes, M.; Kitchen, C.; Nicholls, A. The Gaussian Generalized Born model: Application to small molecules. Phys. Chem. Chem. Phys. 2007, 9, 4913–4922. [Google Scholar] [CrossRef] [PubMed]
- Lange, A.W.; Herbert, J.M. Improving Generalized Born models by exploiting connections to Polarizable Continuum Models. I. An improved effective Coulomb operator. J. Chem. Theory Comput. 2012, 8, 1999–2011. [Google Scholar] [CrossRef] [PubMed]
- Voityuk, A.A.; Vyboishchikov, S.F. A simple COSMO-based method for calculation of hydration energies of neutral molecules. Phys. Chem. Chem. Phys. 2019, 21, 18706–18713. [Google Scholar] [CrossRef] [PubMed]
- Voityuk, A.A.; Vyboishchikov, S.F. Fast and accurate calculation of hydration energies of molecules and ions. Phys. Chem. Chem. Phys. 2020, 22, 14591–14598. [Google Scholar] [CrossRef]
- Vyboishchikov, S.F.; Voityuk, A.A. Fast non-iterative calculation of solvation energies for water and nonaqueous solvents. J. Comput. Chem. 2021, 42, 1184–1194. [Google Scholar] [CrossRef] [PubMed]
- Vyboishchikov, S.F.; Voityuk, A.A. Solvation free energies for aqueous and nonaqueous solutions computed using PM7 atomic charges. J. Chem. Inf. Model. 2021, 61, 4544–4553. [Google Scholar] [CrossRef]
- Vyboishchikov, S.F. A quick solvation energy estimator based on electronegativity equalization. J. Comput. Chem. 2023, 44, 307–318. [Google Scholar] [CrossRef]
- Vyboishchikov, S.F.; Voityuk, A.A. Noniterative solvation energy method based on atomic charges. In Chemical Reactivity: Approaches and applications; Kaya, S., von Szentpály, L., Serdaroğlu, G., Guo, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 2, pp. 399–427. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Stasyuk, A.J.; Vyboishchikov, S.F. A simple model for calculating atomic charges in molecules. Phys. Chem. Chem. Phys. 2018, 20, 23328–23337. [Google Scholar] [CrossRef] [PubMed]
- Vyboishchikov, S.F.; Voityuk, A.A. Iterative atomic-charge partitioning of valence electron density. J. Comp. Chem. 2019, 40, 875–884. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Jerome, S.V.; Cramer, C.J.; Truhlar, D.G. Charge Model 5: An extension of Hirshfeld population analysis for the accurate description of molecular interactions in gaseous and condensed phases. J. Chem. Theory Comput. 2012, 8, 527–541. [Google Scholar] [CrossRef] [PubMed]
- Kříž, K.; Řezáč, J. Reparametrization of the COSMO solvent model for semiempirical methods PM6 and PM7. J. Chem. Inf. Model. 2019, 59, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Vyboishchikov, S.F. Dense neural network for calculating solvation free energies from electronegativity-equalization atomic charges. J. Chem. Inf. Model. 2023, 63, 6283–6292. [Google Scholar] [CrossRef] [PubMed]
- Vyboishchikov, S.F. Predicting solvation free energies using electronegativity-equalization atomic charges and a dense neural network: A generalized-Born approach. J. Chem. Theory Comput. 2023, 19, 8340–8350. [Google Scholar] [CrossRef]
- The Program Executable Is Available Free of Charge. Available online: https://github.com/vyboishchikov/ESE-EE-DNN (accessed on 3 July 2024).
- The Program Executable Is Available Free of Charge. Available online: https://github.com/vyboishchikov/ESE-GB-DNN (accessed on 3 July 2024).
- Chen, Y.; Krämer, A.; Charron, N.E.; Husic, B.E.; Clementi, C.; Noé, F. Machine learning implicit solvation for molecular dynamics. J. Chem. Phys. 2021, 155, 084101. [Google Scholar] [CrossRef]
- Vermeire, F.H.; Green, W.H. Transfer learning for solvation free energies: From quantum chemistry to experiments. Chem. Engin. J. 2021, 418, 129307. [Google Scholar] [CrossRef]
- Low, K.; Coote, M.L.; Izgorodina, E.I. Explainable solvation free energy prediction combining graph neural networks with chemical intuition. J. Chem. Inf. Model. 2022, 62, 5457–5470. [Google Scholar] [CrossRef]
- Lim, H.; Jung, I. MLSolvA: Solvation free energy prediction from pairwise atomistic interactions by machine learning. J. Cheminform. 2021, 13, 56. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Hartke, B. Improved prediction of solvation free energies by machine-learning polarizable continuum solvation model. Nat. Commun. 2021, 12, 3584. [Google Scholar] [CrossRef] [PubMed]
- Bernazzani, L.; Duce, C.; Micheli, A.; Mollica, V.; Tiné, M.R. Quantitative structure–property relationship (QSPR) prediction of solvation Gibbs energy of bifunctional compounds by recursive neural networks. J. Chem. Eng. Data 2010, 55, 5425–5428. [Google Scholar] [CrossRef]
- Hutchinson, S.T.; Kobayashi, R. Solvent-specific featurization for predicting free energies of solvation through machine learning. J. Chem. Inf. Model. 2019, 59, 1338–1346. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wang, C.; Wu, K.; Wei, G.W. Breaking the polar–non-polar division in solvation free energy prediction. J. Comput. Chem. 2018, 39, 217–233. [Google Scholar] [CrossRef] [PubMed]
- Jaquis, B.J.; Li, A.; Monnier, N.D.; Sisk, R.G.; Acree, W.E.; Lang, A.S.I.D. Using machine learning to predict enthalpy of solvation. J. Solut. Chem. 2019, 48, 564–573. [Google Scholar] [CrossRef]
- Chung, Y.; Vermeire, F.H.; Wu, H.; Walker, P.J.; Abraham, M.H.; Green, W.H. Group contribution and machine learning approaches to predict Abraham solute parameters, solvation free energy, and solvation enthalpy. J. Chem. Inf. Model. 2022, 62, 433–446. [Google Scholar] [CrossRef] [PubMed]
- Svobodová Vařeková, R.; Jiroušková, Z.; Vaněk, J.; Suchomel, Š.; Koča, J. Electronegativity equalization method: Parameterization and validation for large sets of organic, organohalogene and organometal molecule. Int. J. Mol. Sci. 2007, 8, 572–582. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: https://scikit-learn.org/stable (accessed on 1 March 2024).
- Nesterov, Y. A method of solving a convex programming problem with convergence rate O(1/k2). Sov. Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In International Conference on Learning Representations. 2016. Available online: https://openreview.net/pdf/OM0jvwB8jIp57ZJjtNEZ.pdf (accessed on 8 November 2023).
- Martín, A.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: http://tensorflow.org (accessed on 30 April 2023).
- Lu, J.Z.; Acree, W.E.; Abraham, M.H. Updated Abraham model correlations for enthalpies of solvation of organic solutes dissolved in benzene and acetonitrile. Phys. Chem. Liquids 2019, 57, 84–99. [Google Scholar] [CrossRef]
- Acree, W.E., Jr.; (University of North Texas, Denton, TX, USA). Personal communication, 2024.
- Available online: http://cactus.nci.nih.gov/chemical/structure (accessed on 1 March 2024).
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Landrum, G. Rdkit Documentation, Release 1 September 2019. 2019. Available online: https://buildmedia.readthedocs.org/media/pdf/rdkit/latest/rdkit.pdf (accessed on 1 March 2024).
- Available online: https://webbook.nist.gov (accessed on 1 March 2024).
- Available online: https://www.stenutz.eu/chem (accessed on 1 March 2024).
- Marenich, A.V.; Kelly, C.P.; Thompson, J.D.; Hawkins, G.D.; Chambers, C.C.; Giesen, D.J.; Winget, P.; Cramer, C.J.; Truhlar, D.G. Minnesota Solvation Database—Version 2012, University of Minnesota, 26 November 2012. Available online: https://conservancy.umn.edu/bitstream/handle/11299/213300/MNSolDatabase_v2012.zip (accessed on 10 June 2024).
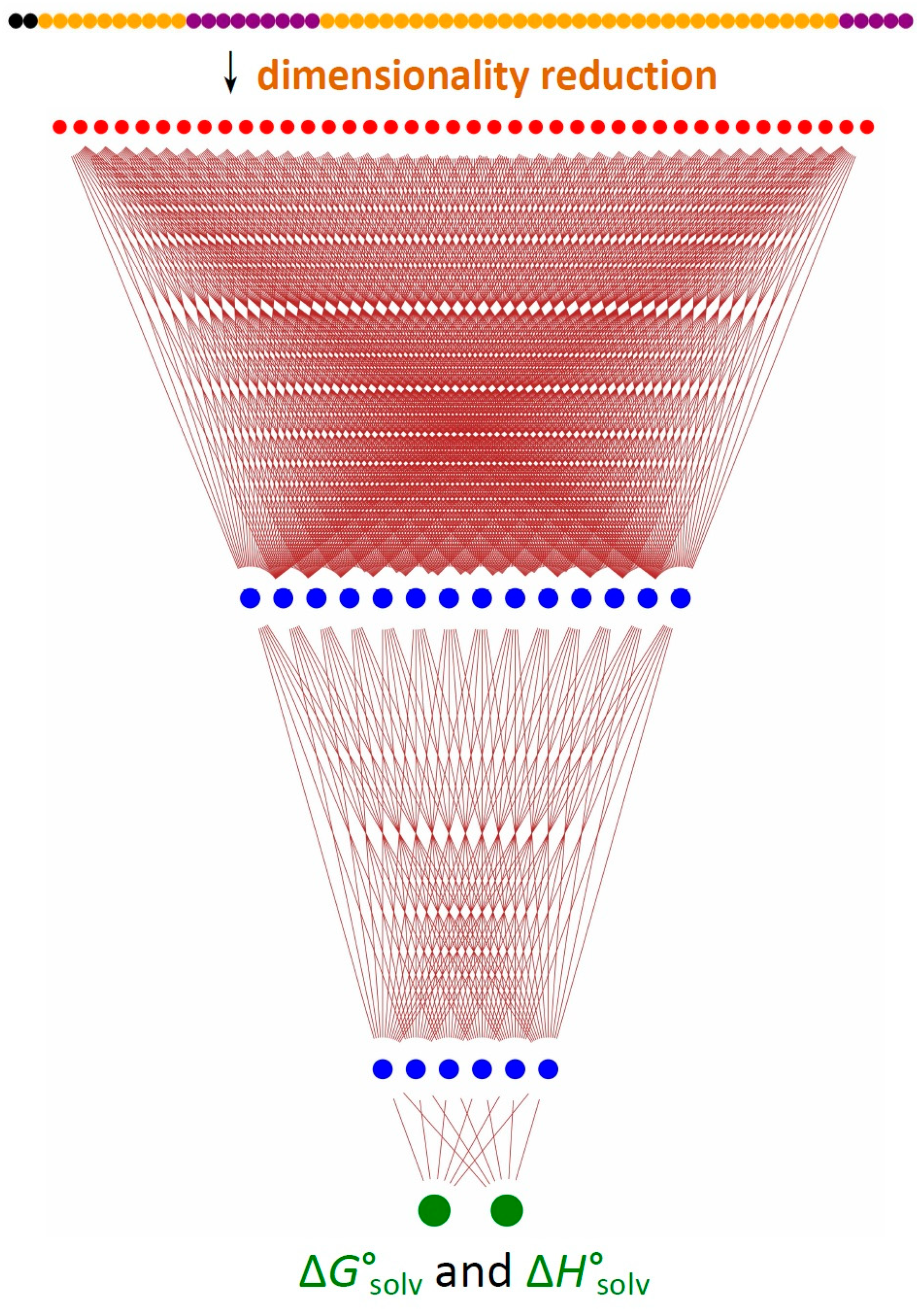
| ΔG°solv, kcal/mol | ΔH°solv, kcal/mol | |||||
|---|---|---|---|---|---|---|
| Solvent Class a | MSE | MAE | RMSE | MSE | MAE | RMSE |
| Alkanes (245/186) | −0.10 | 0.24 | 0.34 | −0.27 | 0.52 | 0.75 |
| Alkoxyalcohols (44/7) | −0.13 | 1.03 | 1.55 | −0.02 | 0.40 | 0.43 |
| Aromatic (81/71) | 0.04 | 0.19 | 0.25 | 0.11 | 0.61 | 0.85 |
| Amides (56/39) | −0.17 | 0.47 | 0.62 | 0.19 | 0.68 | 1.06 |
| Ethers (64/65) | −0.21 | 0.34 | 0.70 | 0.22 | 0.58 | 0.80 |
| Esters (45/8) | 0.02 | 0.25 | 0.33 | −0.54 | 0.59 | 0.80 |
| Haloalkanes (123/85) | 0.18 | 0.41 | 0.55 | 0.16 | 0.60 | 0.80 |
| Haloaromatic (50/38) | −0.17 | 0.48 | 0.69 | −0.31 | 0.65 | 0.93 |
| Ketones (60/41) | 0.05 | 0.26 | 0.36 | 0.41 | 0.73 | 0.90 |
| Miscellaneous (154/472) | 0.01 | 0.39 | 0.57 | −0.09 | 0.63 | 1.00 |
| ALL (922/1036) | −0.03 | 0.36 | 0.59 | −0.04 | 0.62 | 0.96 |
| ΔG°solv | ΔH°solv | |||||
|---|---|---|---|---|---|---|
| Solvent Class a | Slope | Intercept | R2 | Slope | Intercept | R2 |
| Alkanes (245/186) | 0.98 | −0.16 | 0.978 | 0.99 | −0.33 | 0.972 |
| Alkoxyalcohols (44/7) | 0.55 | −1.61 | 0.384 | 1.21 | 1.85 | 0.972 |
| Aromatic (81/71) | 0.96 | −0.07 | 0.989 | 0.91 | 0.03 | 0.965 |
| Amides (56/39) | 0.84 | −0.67 | 0.900 | 0.88 | −1.13 | 0.969 |
| Ethers (64/65) | 0.94 | −0.42 | 0.933 | 0.97 | −0.09 | 0.976 |
| Esters (45/8) | 0.92 | −0.27 | 0.976 | 0.81 | −2.33 | 0.853 |
| Haloalkanes (123/85) | 0.92 | −0.24 | 0.956 | 0.97 | −0.13 | 0.962 |
| Haloaromatic (50/38) | 1.02 | −0.11 | 0.944 | 1.08 | 0.46 | 0.949 |
| Ketones (60/41) | 0.94 | −0.13 | 0.978 | 0.96 | 0.07 | 0.979 |
| Miscellaneous (154/472) | 0.89 | −0.36 | 0.926 | 0.99 | −0.23 | 0.953 |
| ALL (922/1036) | 0.93 | −0.29 | 0.939 | 0.98 | −0.29 | 0.960 |
| ΔG°solv, kcal/mol | ΔH°solv, kcal/mol | |||||
|---|---|---|---|---|---|---|
| Solvent a | MSE | MAE | RMSE | MSE | MAE | RMSE |
| Alkane solvents: | ||||||
| Pentane (6/3) | −0.03 | 0.13 | 0.20 | −0.04 | 0.41 | 0.43 |
| Hexane (27/32) | −0.15 | 0.33 | 0.49 | −0.08 | 0.49 | 0.61 |
| Heptane (27/49) | −0.02 | 0.27 | 0.36 | −0.31 | 0.54 | 0.80 |
| Octane (27/12) | −0.08 | 0.16 | 0.23 | 0.01 | 0.31 | 0.38 |
| Nonane (14/2) | −0.08 | 0.20 | 0.25 | −0.36 | 0.36 | 0.46 |
| Decane (15/11) | 0.08 | 0.17 | 0.22 | −0.28 | 0.50 | 0.71 |
| Undecane (10/2) | −0.20 | 0.32 | 0.42 | −0.33 | 0.34 | 0.48 |
| Dodecane (11/8) | −0.07 | 0.17 | 0.19 | −0.29 | 0.41 | 0.57 |
| Hexadecane (65/17) | −0.06 | 0.22 | 0.31 | −0.25 | 0.35 | 0.42 |
| Tetradecane (2/3) | −0.12 | 0.24 | 0.27 | 0.50 | 0.68 | 0.87 |
| Pentadecane (1/0) | −0.32 | 0.32 | 0.32 | |||
| Methylcyclohexane (5/0) | −0.29 | 0.29 | 0.50 | |||
| Cyclohexane (33/51) | −0.23 | 0.32 | 0.42 | −0.48 | 0.67 | 0.96 |
| Cyclooctane (2/0) | −0.10 | 0.10 | 0.11 | |||
| Alkoxyalcohol solvents: | ||||||
| 2-methoxyethanol (6/7) | 0.23 | 0.27 | 0.36 | −0.02 | 0.40 | 0.43 |
| 2-ethoxyethanol (4/0) | 0.55 | 0.55 | 0.59 | |||
| 2-butoxyethanol (6/0) | −1.16 | 1.39 | 2.79 | |||
| diethylene glycol (17/0) | −0.42 | 0.99 | 1.16 | |||
| triethylene glycol (11/0) | 0.43 | 1.49 | 1.74 | |||
| Aromatic solvents: | ||||||
| Benzene (13/46) | −0.09 | 0.17 | 0.23 | −0.14 | 0.59 | 0.84 |
| Toluene (25/25) | −0.03 | 0.21 | 0.29 | 0.56 | 0.65 | 0.86 |
| Ethylbenzene (12/0) | 0.09 | 0.19 | 0.20 | |||
| o-xylene (8/0) | 0.08 | 0.12 | 0.15 | |||
| m-xylene (11/0) | 0.14 | 0.18 | 0.20 | |||
| p-xylene (12/0) | 0.17 | 0.24 | 0.31 | |||
| Amide solvents: | ||||||
| Formamide (15/18) | −0.53 | 0.63 | 0.73 | 0.39 | 0.91 | 2.33 |
| Methylformamide (7/8) | −0.40 | 0.60 | 0.81 | 0.36 | 1.10 | 1.42 |
| N-methylacetamide (15/0) | −0.24 | 0.42 | 0.56 | |||
| N-methyl-2-pyrrolidone (19/14) | 0.25 | 0.35 | 0.46 | 0.53 | 0.80 | 1.30 |
| Ether solvents: | ||||||
| diethyl ether (7/7) | −0.28 | 0.30 | 0.51 | 0.09 | 0.22 | 0.29 |
| dipropyl ether (5/0) | −0.14 | 0.18 | 0.28 | |||
| diisopropyl ether (4/0) | −0.23 | 0.44 | 0.47 | |||
| dibutyl ether (6/20) | −0.17 | 0.24 | 0.41 | 0.22 | 0.53 | 0.72 |
| methyl tert-butyl ether (5/0) | −0.24 | 0.39 | 0.45 | |||
| bis(2-ethoxyethyl) ether (1/0) | 0.51 | 0.51 | 0.51 | |||
| Tetrahydrofuran (17/32) | −0.02 | 0.25 | 0.43 | 0.19 | 0.69 | 0.93 |
| Tetrahydropyran (4/0) | −0.04 | 0.16 | 0.18 | |||
| anisole(15/0) | −0.52 | 0.56 | 1.22 | |||
| Ester solvents: | ||||||
| methyl acetate (10/8) | −0.04 | 0.37 | 0.47 | −0.54 | 0.58 | 0.80 |
| ethyl acetate (13/24) | 0.00 | 0.27 | 0.36 | −0.15 | 0.56 | 0.74 |
| propyl acetate (6/0) | 0.11 | 0.16 | 0.17 | |||
| butyl acetate (8/0) | 0.09 | 0.17 | 0.21 | |||
| pentyl acetate (7/0) | −0.02 | 0.23 | 0.26 | |||
| hexyl acetate (1/0) | −0.08 | 0.08 | 0.08 | |||
| Haloalkane solvents: | ||||||
| Dichloromethane (9/24) | 0.02 | 0.26 | 0.29 | −0.59 | 0.68 | 0.87 |
| Chloroform (48/21) | 0.34 | 0.51 | 0.67 | 0.77 | 0.86 | 1.08 |
| carbon tetrachloride (45/40) | 0.21 | 0.30 | 0.40 | 0.29 | 0.42 | 0.54 |
| 1-chlorobutane (8/0) | 0.02 | 0.35 | 0.39 | |||
| Dibromomethane (2/0) | 0.32 | 0.42 | 0.52 | |||
| Bromoethane (2/0) | 0.13 | 0.39 | 0.41 | |||
| methylene iodide (9/0) | −0.57 | 0.63 | 0.71 | |||
| Haloaromatic solvents: | ||||||
| Fluorobenzene (3/0) | −0.54 | 0.54 | 0.58 | |||
| Chlorobenzene (21/30) | −0.30 | 0.41 | 0.53 | −0.28 | 0.64 | 0.96 |
| Bromobenzene (14/0) | −0.35 | 0.44 | 0.53 | |||
| Iodobenzene (8/0) | −0.08 | 0.30 | 0.45 | |||
| Hexafluorobenzene (4/0) | 1.24 | 1.24 | 1.69 | |||
| Ketone solvents: | ||||||
| Acetone (20/27) | 0.01 | 0.35 | 0.50 | 0.32 | 0.78 | 0.95 |
| 2-butanone (10/7) | 0.18 | 0.21 | 0.28 | 0.35 | 0.41 | 0.52 |
| 3-pentanone (1/0) | 0.21 | 0.21 | 0.21 | |||
| 2-hexanone (2/0) | 0.23 | 0.23 | 0.24 | |||
| 4-methyl-2-pentanone (1/0) | 0.29 | 0.29 | 0.29 | |||
| Cyclohexanone (13/7) | 0.05 | 0.20 | 0.25 | 0.78 | 0.85 | 1.00 |
| Acetophenone (8/0) | 0.10 | 0.19 | 0.23 | |||
| Cyclopentanone (1/0) | −0.06 | 0.06 | 0.06 | |||
| 2-methylcyclohexanone (4/0) | −0.36 | 0.36 | 0.39 | |||
| Miscellaneous solvents: | ||||||
| Benzonitrile (9/0) | 0.08 | 0.21 | 0.27 | |||
| tributyl phosphate (16/0) | −0.14 | 0.57 | 1.01 | |||
| propylene carbonate (12/17) | 0.04 | 0.20 | 0.30 | −0.19 | 0.61 | 0.74 |
| carbon disulfide (5/0) | −0.36 | 0.43 | 0.51 | |||
| Triethylamine (4/10) | 0.18 | 0.19 | 0.35 | 0.65 | 0.93 | 1.58 |
| Ethoxybenzene (3/0) | −0.14 | 0.66 | 0.77 | |||
| 2-methylpyridine (4/0) | 0.40 | 0.41 | 0.47 | |||
| benzyl ether (1/0) | −0.57 | 0.57 | 0.57 | |||
| 3-methylphenol (1/0) | 1.87 | 1.87 | 1.87 | |||
| acetic acid (10/14) | −0.08 | 0.48 | 0.60 | 0.12 | 0.66 | 0.94 |
| Nitroethane (1/0) | 0.60 | 0.60 | 0.60 | |||
| benzyl alcohol (2/0) | −0.30 | 0.30 | 0.35 | |||
| Butyronitrile (9/0) | −0.11 | 0.16 | 0.20 | |||
| Aniline (11/0) | −0.44 | 0.61 | 0.69 | |||
| Nitromethane (4/9) | 0.09 | 0.21 | 0.31 | −0.49 | 0.55 | 0.66 |
| Nitrobenzene (3/0) | 0.68 | 0.68 | 0.76 | |||
| dimethyl sulfoxide (11/37) | 0.22 | 0.65 | 0.79 | −0.58 | 0.75 | 1.08 |
| Propionitrile (4/0) | −0.03 | 0.34 | 0.39 | |||
| Acetonitrile (6/41) | 0.15 | 0.25 | 0.33 | −0.23 | 0.89 | 1.23 |
| ethyl benzoate (3/0) | −0.03 | 0.24 | 0.26 | |||
| Sulfolane (18/0) | 0.24 | 0.36 | 0.43 | |||
| Pyridine (12/14) | 0.05 | 0.22 | 0.29 | 0.21 | 1.37 | 1.97 |
| diethyl carbonate (5/15) | −0.12 | 0.33 | 0.51 | 0.10 | 0.29 | 0.33 |
| Solvent a | ΔG°solv, kcal/mol | Solvent a | ΔG°solv, kcal/mol | ||||
|---|---|---|---|---|---|---|---|
| MSE | MAE | RMSE | MSE | MAE | RMSE | ||
| acetic acid (7) | 0.43 | 0.78 | 0.87 | fluoroctane (6) | −0.11 | 0.16 | 0.19 |
| aniline (9) | 0.00 | 0.53 | 0.63 | heptane (69) | −0.08 | 0.36 | 0.59 |
| anisole (8) | −0.06 | 0.22 | 0.28 | hexadecane (198) | −0.12 | 0.29 | 0.56 |
| benzene (74) | −0.04 | 0.42 | 0.75 | hexadecyl iodide (9) | 0.44 | 0.44 | 0.51 |
| bromobenzene (27) | −0.47 | 0.50 | 0.61 | hexane (59) | −0.23 | 0.36 | 0.56 |
| bromoform (12) | 0.10 | 0.26 | 0.32 | iodobenzene (20) | −0.31 | 0.41 | 0.54 |
| bromooctane (5) | 0.25 | 0.25 | 0.28 | isooctane (32) | −0.37 | 0.38 | 0.46 |
| butyl acetate (21) | 0.10 | 0.38 | 0.50 | isopropylbenzene (19) | 0.03 | 0.22 | 0.26 |
| butylbenzene (10) | 0.42 | 0.42 | 0.47 | isopropyltoluene (6) | 0.25 | 0.25 | 0.30 |
| carbon disulfide (14) | −0.51 | 0.58 | 0.67 | mesitylene (7) | 0.31 | 0.31 | 0.37 |
| carbon tetrachloride (78) | 0.01 | 0.25 | 0.41 | nonane (26) | −0.11 | 0.20 | 0.25 |
| chlorobenzene (38) | −0.59 | 0.60 | 0.72 | nonanol (10) | 0.27 | 0.42 | 0.50 |
| chloroform (108) | 0.09 | 0.65 | 0.98 | octane (38) | −0.23 | 0.28 | 0.37 |
| chlorohexane (11) | −0.07 | 0.17 | 0.20 | pentadecane (9) | 0.12 | 0.16 | 0.20 |
| cyclohexane (92) | −0.49 | 0.53 | 0.81 | pentane (26) | −0.41 | 0.43 | 0.47 |
| decalin (27) | −0.26 | 0.36 | 0.56 | perfluorobenzene (15) | 0.94 | 0.94 | 1.02 |
| decane (39) | −0.11 | 0.23 | 0.34 | phenyl ether (6) | −0.55 | 0.55 | 0.62 |
| decanol (11) | 0.38 | 0.50 | 0.58 | sec–butylbenzene (5) | 0.31 | 0.31 | 0.35 |
| dibromoethane (10) | −0.17 | 0.26 | 0.31 | tert–butylbenzene (14) | 0.12 | 0.18 | 0.21 |
| dibutyl ether (14) | −0.22 | 0.47 | 0.65 | tetrachloroethene (10) | 0.04 | 0.23 | 0.30 |
| dichloromethane (11) | −0.26 | 0.39 | 0.55 | tetrahydrofuran (7) | 0.18 | 0.27 | 0.30 |
| diethyl ether (71) | −0.03 | 0.74 | 1.30 | tetralin (9) | −0.92 | 0.92 | 1.15 |
| diisopropyl ether (21) | −0.10 | 0.45 | 0.66 | toluene (50) | 0.01 | 0.20 | 0.31 |
| dimethylpyridine (6) | −0.16 | 0.34 | 0.54 | tributyl phosphate (16) | 1.43 | 1.49 | 1.79 |
| dodecane (8) | −0.29 | 0.35 | 0.45 | triethylamine (7) | 0.25 | 0.26 | 0.38 |
| ethoxybenzene (7) | −0.08 | 0.22 | 0.30 | trimethylbenzene (11) | 0.27 | 0.27 | 0.29 |
| ethyl acetate (23) | 0.72 | 0.95 | 1.99 | undecane (13) | −0.09 | 0.29 | 0.40 |
| ethylbenzene (29) | −0.06 | 0.24 | 0.33 | xylene (48) | 0.08 | 0.25 | 0.34 |
| fluorobenzene (7) | −0.66 | 0.66 | 0.79 | ALL (1543) | −0.08 | 0.42 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vyboishchikov, S.F. Solvation Enthalpies and Free Energies for Organic Solvents through a Dense Neural Network: A Generalized-Born Approach. Liquids 2024, 4, 525-538. https://doi.org/10.3390/liquids4030030
Vyboishchikov SF. Solvation Enthalpies and Free Energies for Organic Solvents through a Dense Neural Network: A Generalized-Born Approach. Liquids. 2024; 4(3):525-538. https://doi.org/10.3390/liquids4030030
Chicago/Turabian StyleVyboishchikov, Sergei F. 2024. "Solvation Enthalpies and Free Energies for Organic Solvents through a Dense Neural Network: A Generalized-Born Approach" Liquids 4, no. 3: 525-538. https://doi.org/10.3390/liquids4030030
APA StyleVyboishchikov, S. F. (2024). Solvation Enthalpies and Free Energies for Organic Solvents through a Dense Neural Network: A Generalized-Born Approach. Liquids, 4(3), 525-538. https://doi.org/10.3390/liquids4030030








