Effect of Ligand Binding on Polymer Diffusiophoresis
Abstract
1. Introduction
2. Discussion
2.1. Theoretical Background
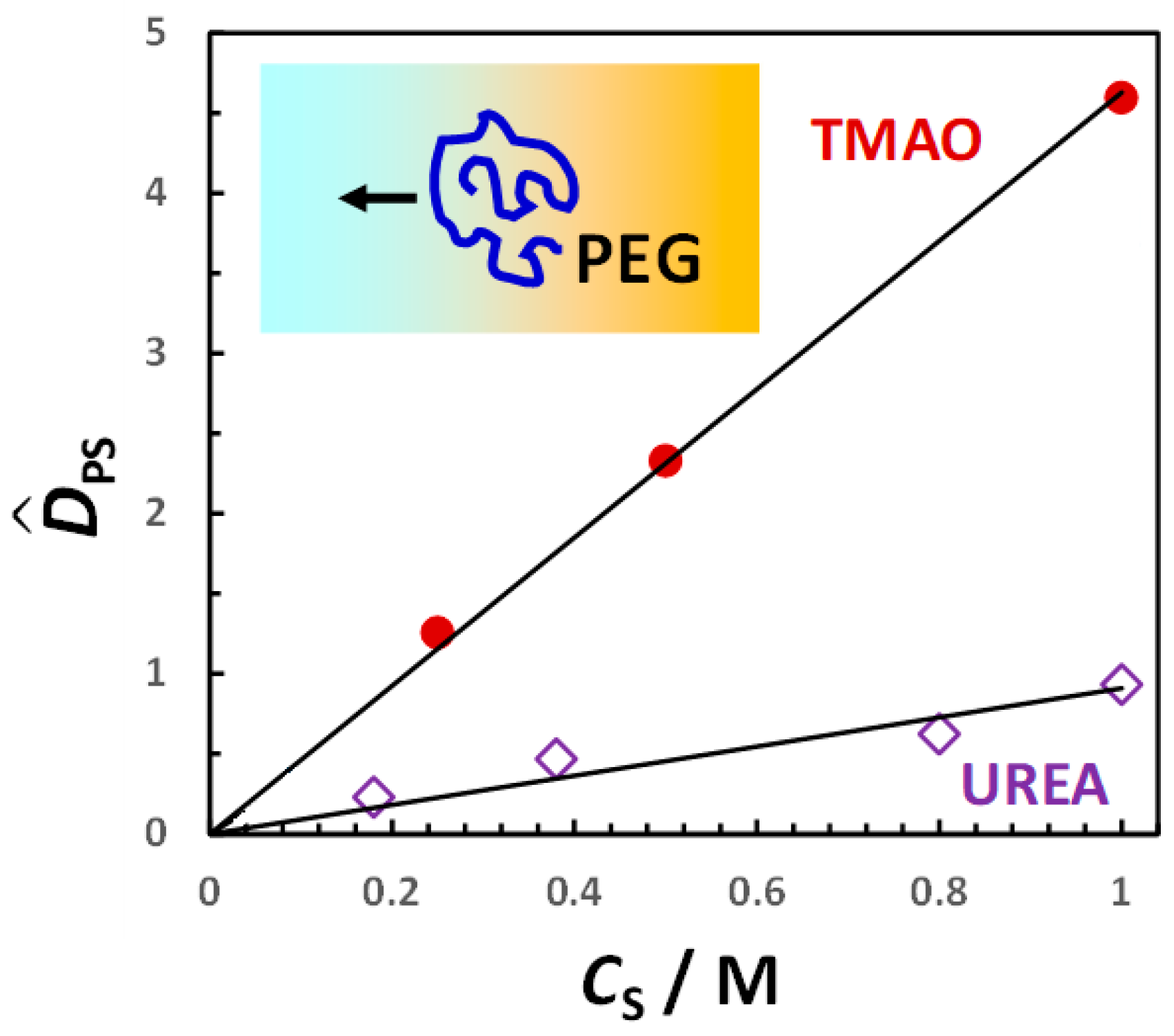
2.2. Analysis of Experimental Data
2.3. Ligand-Binding Model for Polymer Diffusiophoresis
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bekdemir, A.; Stellacci, F. A centrifugation-based physicochemical characterization method for the interaction between proteins and nanoparticles. Nat. Commun. 2016, 7, 13121. [Google Scholar] [CrossRef] [PubMed]
- Keurentjes, J.T.F.; Janssen, A.E.M.; Broek, A.P.; Van der Padt, A.; Wesselingh, J.A.; Van ‘T Riet, K. Multicomponent diffusion in dialysis membranes. Chem. Eng. Sci. 1992, 47, 1963–1971. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Wong, T.I.; Liu, X.; Zhou, X.; Liedberg, B. Electrofocusing-enhanced localized surface plasmon resonance biosensors. Nanoscale 2015, 7, 17244–17248. [Google Scholar] [CrossRef] [PubMed]
- Chayen, N.E.; Saridakis, E. Protein crystallization: From purified protein to diffraction-quality crystal. Nat. Methods 2008, 5, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Dey, K.K.; Das, S.; Poyton, M.F.; Sengupta, S.; Butler, P.J.; Cremer, P.S.; Sen, A. Chemotactic separation of enzymes. ACS Nano 2014, 8, 11941–11949. [Google Scholar] [CrossRef]
- Sochacki, K.A.; Shkel, I.A.; Record, M.T.; Weisshaar, J.C. Protein diffusion in the periplasm of E. coli under osmotic stress. Biophys. J. 2011, 100, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Vagias, A.; Sergelen, K.; Koynov, K.; Košovan, P.; Dostalek, J.; Jonas, U.; Knoll, W.; Fytas, G. Diffusion and Permeation of Labeled IgG in Grafted Hydrogels. Macromolecules 2017, 50, 4770–4779. [Google Scholar] [CrossRef]
- Kar, A.; Chiang, T.Y.; Rivera, I.O.; Sen, A.; Velegol, D. Enhanced Transport into and out of Dead-End Pores. ACS Nano 2015, 9, 746–753. [Google Scholar] [CrossRef]
- Wesselingh, J.A. Controlling diffusion. J. Control Release 1993, 24, 47–60. [Google Scholar] [CrossRef]
- Miguez, D.G.; Vanag, V.K.; Epstein, I.R. Fronts and pulses in an enzymatic reaction catalyzed by glucose oxidase. Proc. Natl. Acad. Sci. USA 2007, 104, 6992–6997. [Google Scholar] [CrossRef]
- Semenov, S.N.; Markvoort, A.J.; de Greef, T.F.A.; Huck, W.T.S. Threshold Sensing through a Synthetic Enzymatic Reaction-Diffusion Network. Angew. Chem.-Int. Edit. 2014, 53, 8066–8069. [Google Scholar] [CrossRef] [PubMed]
- Velegol, D.; Garg, A.; Guha, R.; Kar, A.; Kumar, M. Origins of concentration gradients for diffusiophoresis. Soft Matter 2016, 12, 4686–4703. [Google Scholar] [CrossRef]
- Shim, S. Diffusiophoresis, Diffusioosmosis, and Microfluidics: Surface-Flow-Driven Phenomena in the Presence of Flow. Chem. Rev. 2022, 122, 6986–7009. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.L. Colloid Transport by Interfacial Forces. Annu. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Prieve, D.C. Migration of a colloidal particle in a gradient of electrolyte concentration. Adv. Colloid Interface Sci. 1982, 16, 321–335. [Google Scholar] [CrossRef]
- Peter, Q.A.E.; Jacquat, R.P.B.; Herling, T.W.; Challa, P.K.; Kartanas, T.; Knowles, T.P.J. Microscale Diffusiophoresis of Proteins. J. Phys. Chem. B 2022, 126, 8913–8920. [Google Scholar] [CrossRef]
- Abecassis, B.; Cottin-Bizonne, C.; Ybert, C.; Ajdari, A.; Bocquet, L. Boosting migration of large particles by solute contrasts. Nat. Mater. 2008, 7, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Prieve, D.C.; Roman, R. Diffusiophoresis of a rigid sphere through a viscous electrolyte solution. J. Chem. Soc. Faraday Trans. 2 1987, 83, 1287–1306. [Google Scholar] [CrossRef]
- Guha, R.; Shang, X.; Zydney, A.L.; Velegol, D.; Kumar, M. Diffusiophoresis contributes significantly to colloidal fouling in low salinity reverse osmosis systems. J. Membr. Sci. 2015, 479, 67–76. [Google Scholar] [CrossRef]
- Shin, S.; Shardt, O.; Warren, P.B.; Stone, H.A. Membraneless water filtration using CO2. Nat. Commun. 2017, 8, 15181. [Google Scholar] [CrossRef]
- Barrios, E.C.; Krause, T.C.; Annunziata, O. Salt-induced diffusiophoresis of a nonionic micelle: Roles of salting out and proximity to surfactant cloud point. J. Mol. Liq. 2022, 359, 119271. [Google Scholar] [CrossRef]
- Lechlitner, L.R.; Annunziata, O. Macromolecule Diffusiophoresis Induced by Concentration Gradients of Aqueous Osmolytes. Langmuir 2018, 34, 9525–9531. [Google Scholar] [CrossRef] [PubMed]
- McAfee, M.S.; Zhang, H.; Annunziata, O. Amplification of salt-induced polymer diffusiophoresis by increasing salting-out strength. Langmuir 2014, 30, 12210–12219. [Google Scholar] [CrossRef] [PubMed]
- Kadajji, V.G.; Betageri, G.V. Water Soluble Polymers for Pharmaceutical Applications. Polymers 2011, 3, 1972–2009. [Google Scholar] [CrossRef]
- Liu, Z.; Robinson, J.T.; Sun, X.M.; Dai, H.J. PEGylated nanographene oxide for delivery of water-insoluble cancer drugs. J. Am. Chem. Soc. 2008, 130, 10876–10877. [Google Scholar] [CrossRef]
- Doane, T.L.; Cheng, Y.; Babar, A.; Hill, R.J.; Burda, C. Electrophoretic Mobilities of PEGylated Gold NPs. J. Am. Chem. Soc. 2010, 132, 15624–15631. [Google Scholar] [CrossRef]
- Kolate, A.; Baradia, D.; Patil, S.; Vhora, I.; Kore, G.; Misra, A. PEG—A versatile conjugating ligand for drugs and drug delivery systems. J. Control Release 2014, 192, 67–81. [Google Scholar] [CrossRef]
- Patist, A.; Kanicky, J.R.; Shukla, P.K.; Shah, D.O. Importance of micellar kinetics in relation to technological processes. J. Colloid Interface Sci. 2002, 245, 1–15. [Google Scholar] [CrossRef]
- Kulkarni, J.A.; Thomson, S.B.; Zaifman, J.; Leung, J.; Wagner, P.K.; Hill, A.; Tam, Y.Y.C.; Cullis, P.R.; Petkau, T.L.; Leavitt, B.R. Spontaneous, solvent-free entrapment of siRNA within lipid nanoparticles. Nanoscale 2020, 12, 23959–23966. [Google Scholar] [CrossRef]
- Uchegbu, I.F.; Vyas, S.P. Non-ionic surfactant based vesicles (niosomes) in drug delivery. Int. J. Pharm. 1998, 172, 33–70. [Google Scholar] [CrossRef]
- Record, M.T.; Anderson, C.F. Interpretation of preferential interaction coefficients of nonelectrolytes and of electrolyte ions in terms of a two-domain model. Biophys. J. 1995, 68, 786–794. [Google Scholar] [CrossRef] [PubMed]
- Timasheff, S.N. Protein-solvent preferential interactions, protein hydration, and the modulation of biochemical reactions by solvent components. Proc. Natl. Acad. Sci. USA 2002, 99, 9721–9726. [Google Scholar] [CrossRef] [PubMed]
- Schurr, J.M.; Rangel, D.P.; Aragon, S.R. A contribution to the theory of preferential interaction coefficients. Biophys. J. 2005, 89, 2258–2276. [Google Scholar] [CrossRef] [PubMed]
- Barrios, E.C.; Penino, K.V.; Annunziata, O. Diffusiophoresis of a Nonionic Micelle in Salt Gradients; Roles of Preferential Hydration and Salt-Induced Surfactant Aggregation. Int. J. Mol. Sci. 2022, 23, 13710. [Google Scholar] [CrossRef] [PubMed]
- Annunziata, O.; Buzatu, D.; Albright, J.G. Protein diffusiophoresis and salt osmotic diffusion in aqueous solutions. J. Phys. Chem. B 2012, 116, 12694–12705. [Google Scholar] [CrossRef]
- Annunziata, O.; Fahim, A. A unified description of macroion diffusiophoresis, salt osmotic diffusion and collective diffusion coefficient. Int. J. Heat Mass Transf. 2020, 163, 120436. [Google Scholar] [CrossRef]
- Vergara, A.; Capuano, F.; Paduano, L.; Sartorio, R. Lysozyme Mutual Diffusion in Solutions Crowded by Poly(ethylene glycol). Macromolecules 2006, 39, 4500–4506. [Google Scholar] [CrossRef]
- Annunziata, O. On the role of solute solvation and excluded-volume interactions in coupled diffusion. J. Phys. Chem. B 2008, 112, 11968–11975. [Google Scholar] [CrossRef][Green Version]
- McAfee, M.S.; Annunziata, O. Effects of Salting-In Interactions on Macromolecule Diffusiophoresis and Salt Osmotic Diffusion. Langmuir 2015, 31, 1353–1361. [Google Scholar] [CrossRef]
- Fahim, A.; Annunziata, O. Amplification of Salt-Induced Protein Diffusiophoresis by Varying Salt from Potassium to Sodium to Magnesium Chloride in Water. Langmuir 2020, 36, 2635–2643. [Google Scholar] [CrossRef]
- Anderson, C.F.; Courtenay, E.S.; Record, M.T. Thermodynamic Expressions Relating Different Types of Preferential Interaction Coefficients in Solutions Containing Two Solute Components. J. Phys. Chem. B 2002, 106, 418–433. [Google Scholar] [CrossRef]
- Zhang, H.X.; Annunziata, O. Macromolecular hydration compared with preferential hydration and their role on macromolecule-osmolyte coupled diffusion. Phys. Chem. Chem. Phys. 2009, 11, 8923–8932. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, T.; Timasheff, S.N. Preferential interactions of proteins with salts in concentrated solutions. Biochemistry 1982, 21, 6545–6552. [Google Scholar] [CrossRef]
- van Holde, K.E.; Johnson, W.C.; Ho, P.S. Principles of Physical Biochemistry, 2nd ed.; Pearson, Prentice Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- Miller, D.G. Thermodynamics of irreversible processes—The experimental verification of the onsager reciprocal relations. Chem. Rev. 1960, 60, 15–37. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Musilova, L.; Mracek, A.; Cabral, A.; Santos, M.A.; Cabral, I.; Esteso, M.A.; Valente, A.J.M.; Leaist, D. Host-guest paracetamol/cyclodextrin complex formation evaluated from coupled diffusion measurements. J. Chem. Thermodyn. 2021, 161, 106551. [Google Scholar] [CrossRef]
- Paduano, L.; Sartorio, R.; Vitagliano, V.; Costantino, L. Diffusion coefficients of the system alpha-cyclodextrin-n-butylurea-water at 25 degrees C. J. Solut. Chem. 1995, 24, 1143–1153. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Annunziata, O. Effect of Ligand Binding on Polymer Diffusiophoresis. Liquids 2023, 3, 414-425. https://doi.org/10.3390/liquids3040026
Annunziata O. Effect of Ligand Binding on Polymer Diffusiophoresis. Liquids. 2023; 3(4):414-425. https://doi.org/10.3390/liquids3040026
Chicago/Turabian StyleAnnunziata, Onofrio. 2023. "Effect of Ligand Binding on Polymer Diffusiophoresis" Liquids 3, no. 4: 414-425. https://doi.org/10.3390/liquids3040026
APA StyleAnnunziata, O. (2023). Effect of Ligand Binding on Polymer Diffusiophoresis. Liquids, 3(4), 414-425. https://doi.org/10.3390/liquids3040026





