Next Article in Journal
Prediction of the Structural Color of Liquid Crystals via Machine Learning
Previous Article in Journal
Effect of Ligand Binding on Polymer Diffusiophoresis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Liquids
Volume 3
Issue 4
10.3390/liquids3040027
liquids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-Guest Binding: IV. The QM Treatment, GB Models and the Multi-Trajectory Extension

by
Xiaohui Wang
1,2,
Mao Wang
3 and
Zhaoxi Sun
2,*
1
Beijing Leto Laboratories Co., Ltd., Beijing 100094, China
2
College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China
3
NCS Testing Technology Co., Ltd., No. 13, Gaoliangqiao Xiejie, Beijing 100081, China
*
Author to whom correspondence should be addressed.
Liquids 2023, 3(4), 426-439; https://doi.org/10.3390/liquids3040027
Submission received: 22 August 2023 / Revised: 19 October 2023 / Accepted: 23 October 2023 / Published: 24 October 2023
Browse Figures
Review Reports Versions Notes

Abstract

:
Due to the similarity of host–guest complexes and protein–ligand and protein–protein assemblies, computational tools for protein–drug complexes are commonly applied in host–guest binding. One of the methods with the highest popularity is the end-point free energy technique, which estimates the binding affinity with gas-phase and solvation contributions extracted from simplified end-point sampling. Our series papers on a set of carboxylated-pillararene host–guest complexes have proven with solid numerical evidence that standard end-point techniques are practically useless in host–guest binding, but alterations, such as slightly increasing interior dielectric constant in post-processing calculation and shifting to the multi-trajectory realization in conformational sampling, could better the situation and pull the end-point method back to the pool of usable tools. Also, the force-field selection plays a critical role, as it determines the sampled region in the conformational space. In the current work, we continue the efforts to explore potentially promising end-point modifications in host–guest binding and further extend the sampling time to an unprecedent length. Specifically, we comprehensively benchmarked the shift from the original MM description to QM Hamiltonians in post-processing the popular single-trajectory sampling. Two critical settings in the multi-scale QM/GBSA regime are the selections of the QM Hamiltonian and the implicit-solvent model, and a scan of combinations of popular semi-empirical QM Hamiltonians and GB models is performed. The multi-scale QM/GBSA treatment is further combined with the three-trajectory sampling protocol, introducing a further advanced modification. The sampling lengths in the host–guest complex, solvated guest and solvated host ensembles are extended to 500 ns, 500 ns and 12,000 ns. As a result, the sampling quality in end-point calculations is unprecedently high, enabling us to draw conclusive pictures of investigated forms of modified end-point free energy methods. Numerical results suggest that the shift to the QM Hamiltonian does not better the situation in the popular single-trajectory regime, but noticeable improvements are observed in the three-trajectory sampling regime, especially for the DFTB/GBSA parameter combination (either DFTB2 or its third-order extension), the quality metrics of which reach an unprecedently high level and surpass existing predictions (including costly alchemical transformations) on this dataset, hinting on the applicability of the advanced three-trajectory QM/GBSA end-point modification for host–guest complexes.

1. Introduction

Fixed-charge force fields are widely applied in end-point free energy calculations as an efficient tool for configurational sampling [1,2,3]. The extracted equilibrium snapshots of the systems of interest are then fed to some selected Hamiltonians (often also the force field description in conjunction with implicit solvent) to extract the free energy of binding. However, the accuracy level of this workflow is often criticized due to the lack of explicit polarization and a proper treatment of charge transfer [4,5,6]. To alleviate this issue, there is a tendency to upgrade the description to some QM levels (ab initio or some semi-empirical Hamiltonians) in free energy estimation [7,8,9,10,11]. Specifically, the method samples the configurational space with fixed-charge force fields but re-computes the energetics at some QM levels. The multi-scale QM/GBSA treatment has been claimed to improve the prediction quality of binding affinities in a number of publications [12,13,14,15,16,17]. For instance, the QM/GBSA regime exhibits astonishingly satisfactory performance in several protein–ligand complexes, especially for the PM6 derivatives and DFTB selections as the QM level [18]. Further, there are scientific reports about extremely accurate reproduction of experimental affinities of host–guest complexes [19,20]. However, such improvements of description accuracy only deal with one aspect of the problem, while other remaining influencing factors such as sampling quality could still introduce systematic errors that are difficult to quantify. As the costly nature of the multiscale treatment limits the exhaustiveness of conformational sampling, it lacks a solid foundation of approximating ensemble average with the time-series data and the QM-augmented free energy outcomes are severely configuration-dependent [21]. For instance, only ~150 sampled configurations are considered in a previous work [20], which obviously involves convergence problems in the end-point statistics. Further, multi-modal binding behaviors are often observed in many host–guest complexes [22,23,24,25]. A more critical problem is that shifting from the force-field description to QM levels in free energy estimation, if treated rigorously, should involve a reweighting factor. As the original force-field treatment MM/GBSA already incorporates a similar approximation, i.e., sampling in explicit solvent but calculating free energy estimates in implicit solvent, practitioners always neglect this reweighting procedure in the QM treatment. All these defects, influencing factors and intrinsic approximations of the end-point workflow make the net merits of the QM treatment questionable, and a viewpoint based on extensive conformational sampling seems necessary to draw any concluding remarks.
Water-soluble pillar[n]arenes have grown to be a crucial macrocycle family with wide applications in drug delivery and material research [26,27,28,29]. The host–guest dataset involving the 6-unit carboxylated pillararene (WP6) from the SAMPL9 challenge, as a good testing bed for free energy techniques, has been extensively investigated in our end-point series [30,31,32], as well as many others [33,34]. Standard end-point applications seem useless in predictions of both absolute affinities and their relative ranks and are even worse than docking scores [31], while modified regimes, especially the three-trajectory realization, perform quite well in rank predictions [30,32]. As end-point methods (both standard and modified) exhibit behaviors somehow different from existing experiences accumulated in biomacromolecular complexes (e.g., protein–ligand systems) [31,32], practical hands-on experiments are necessary to validate the applicability of advanced end-point modifications. In this paper, we continue the efforts to explore potentially promising modified end-point regimes, specifically, the QM treatment in end-point calculations, still based on the WP6 host-guest testing bed. The QM/GBSA regime in the popular single-trajectory realization is thoroughly benchmarked. The combinations of six popular semi-empirical QM Hamiltonians and four popular GB models are explored and the best-performing QM/GBSA setup is identified. Further, the QM treatment is combined with the relatively unpopular yet promising three-trajectory realization, producing a further advanced three-trajectory QM/GBSA end-point regime that has never been explored in existing publications. Based on the extensive sampling and parameter scan, some concluding remarks and recommendations of applying the QM/GBSA modification in both the single- and three-trajectory realizations are provided.

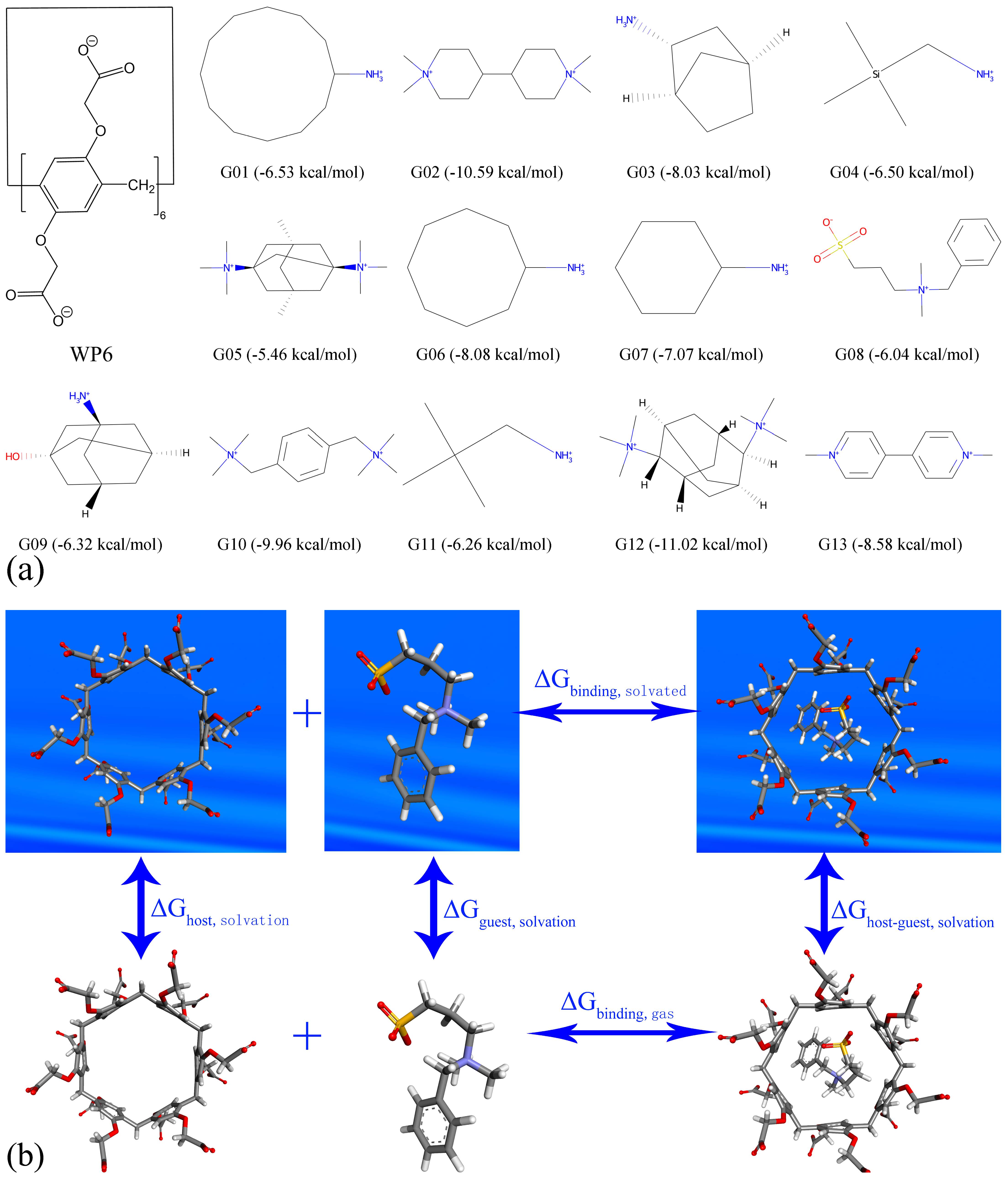
2. Model Construction and Configurational Sampling

The 2D chemical structures of all molecules involved in this work are presented in Figure 1a. The parameter files of the WP6 host and 13 guests (from G1 to G13) are downloaded from the GitHub repository of our WP6 end-point series https://github.com/proszxppp/WP6-host-guest-binding (accessed on 7 April 2023). The RESP-1 charge set (RESP [35] charges fitted with the HF [36,37,38]/6-31G* ESP) is picked due to its proven performance in our previous validations [30,31,32]. The GAFF2 parameter set is used to describe the other terms in the fixed-charge force field.
The 3D structures of host, guest and host–guest complexes are also extracted from the GitHub repository. The docked poses with the Autodock4 scoring function [39] are used. The host-only, guest-only and host–guest systems are then solvated with TIP3P water [40,41] with the 12 Å solute-edge distance and neutralized with monovalent spherical counter ions Na+ or Cl− [42,43]. Each simulation cell is treated with periodic boundary conditions. Molecular dynamics simulation is then initiated using the hybrid-precision GPU engine in AMBER [44], with the SHAKE constraints [45,46] on bonds involving hydrogen, a 2 fs time step, Langevin dynamics [47] for temperature regulation at 300 K, isotropic scaling and Monte Carlo barostat for pressure regulation at 1 atm, the AMBER default 8 Å real-space cutoff for non-bonded interactions and the PME method to treat long-range electrostatics. For relaxation, the constructed box is energy-minimized for 5000 cycles, constant-volume heating in 120 ps, NPT equilibration for 1 ns.
The single- and three-trajectory realizations require different sampling procedures, which deserve to be discussed in more details. For the popular single-trajectory realization, the only ensemble to sample is the bound state (i.e., solvated host–guest complex), while the three-trajectory realization requires the sampling in both the bound and unbound states. The former bound-state trajectory could be shared by both single- and three-trajectory protocols, while the latter unbound states are unique in three-trajectory sampling and contain two ensembles, including the solvated host and the solvated guest. In our previous work [30], it has been observed that the bound host–guest and the unbound guest-only systems are easier to sample, while the sampling of the solvated host is much more difficult, mainly due to the rotational dynamics of the -CH2-COO− rims and its impacts on implicit-solvent energetics. The lengths of the production run in our previous work are 300 ns for all of the three ensembles (i.e., host, guest and host–guest systems), with which the host-only system has statistical errors much larger than the other. Considering these facts, in the current work, the sampling lengths are adjusted to distribute the sampling time (and computational resources) in a smarter manner, in order to better the overall statistics in the three-trajectory estimates. Further, the overall sampling time in each ensemble is lengthened to make the outcome statistically more reliable. Consequently, the relatively easy-to-sample guest-only and host–guest systems are sampled for 500 ns, while the simulation time in the difficult-to-sample host-only system is lengthened to 12,000 ns. The resulting quality/reliability of end-point statistics is unprecedently high. The sampling interval of host–guest configurations is set to 10 ps. All free energy results obtained in this work are summarized in Tables S1–S8.

3. Results and Discussion

An illustration of the thermodynamic cycle used in end-point free energy calculation is depicted in Figure 1b. In both the single- and three-trajectory realizations, the target observable, the binding affinity ΔGbinding,sovlated, is computed indirectly according to the cycle closure condition. The solvation contributions of individual molecules and the gas-phase binding thermodynamics are computed with the trajectory time series, and then combined to obtain the final estimate. In the single-trajectory realization, only the solvated host–guest ensemble (top-right) is sampled, and configurations used in energy evaluations in the other states are approximately extracted from the single complex trajectory. This treatment neglects the binding-induced conformational rearrangements, but exactly cancels internal energetics. By contrast, the three-trajectory realization samples all three solvated states, which incorporates the conformational change upon binding/unbinding and is believed to be a more realistic solution.

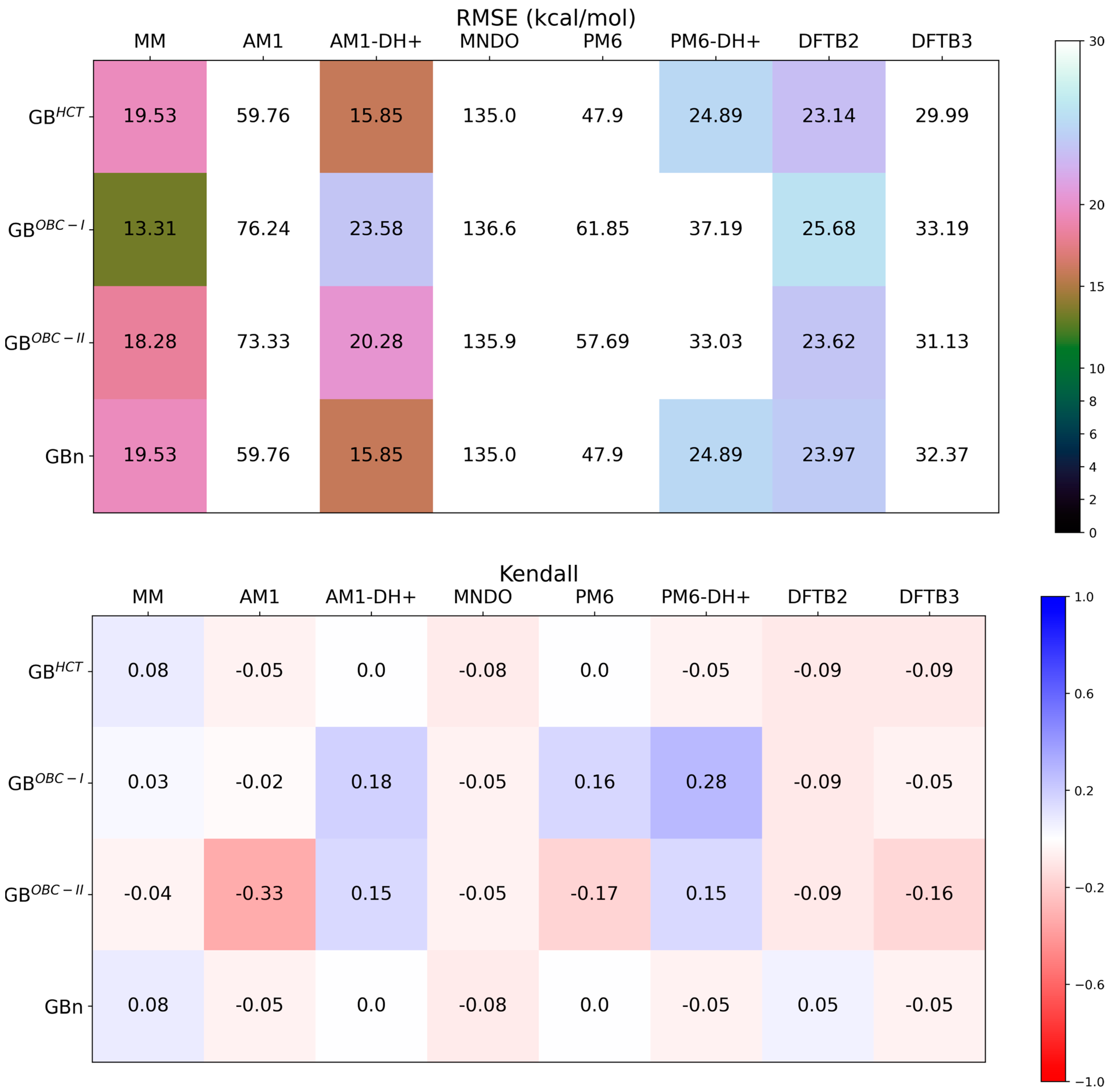
3.1. The QM Treatment

We first consider the shift from the force-field description to the QM treatment in the popular single-trajectory realization, in order to accumulate experience of the brute-force application of this end-point modification. The single-trajectory realization only samples the bound host–guest complex. According to the sampling length and interval mentioned in the previous section, 500 ns unbiased simulation is performed and 50,000 snapshots are extracted. For MM post-processing analyses (i.e., MM/GBSA), all these snapshots are considered. As such costs seem slightly high for the QM/GBSA treatment, we subsample the trajectory by a factor of 10, leading to an equivalent sampling interval of 100 ps. The subsampled snapshots are fed to a series of commonly applied QM/GBSA Hamiltonians. Specifically, the QM part could be described with AM1 [48], the hydrogen-bond- and dispersion-corrected version AM1-DH+, MNDO [49], PM6 [50], its hydrogen-bond- and dispersion-corrected form PM6-DH+, DFTB2 with the mio parameter set [51,52], and DFTB3 with the 3ob parameter set [53,54], while the GB model considered includes GBHCT [55,56], GBOBC-I, GBOBC-II [57,58] and GBn [59]. The two GBOBC models correspond to the two sets of parameters published in the same paper [57]. The concentration of mobile counter ions for Debye–Hückel screening is set to 0.1 M. The nonpolar solvation contribution is treated with the solvent-accessible surface area method [60]. The entropic contribution is estimated with the popular normal mode approximation. As the calculation of the costly Hessian matrix is required in this framework and its estimates are relatively insensitive to configurations, the 5000-snapshot trajectory set is further subsampled by a factor of 10 for entropy calculations.
The computed single-trajectory MM/GBSA and QM/GBSA estimates are presented in Tables S1–S4, along with quality metrics including the root-mean-squared error (RMSE), the mean signed error (MSE), Kendall τ rank coefficient [61], the Pearlman’s predictive index (PI) [62] and the Pearson correlation coefficient. Kendall’s ranking coefficient estimates the consistency of the reference rank and the predicted one, and PI achieves a similar goal but involves a weighting factor derived from the magnitude of the reference data. Pearson r measures the linear correlation between the reference and the prediction. All three correlation metrics have values between −1 and 1, and a high-quality prediction is expected to have large values (e.g., close to 1). Before checking the performance statistics of these systematic calculations, we first perform further sanity checks on two factors. First, in Figure S1, we added some benchmark test on the salt concentration parameter used in GB models. The MM/GBSA treatment with all four GB models and three QM/GBSA Hamiltonians (AM1, MNDO and PM6) with the GBOBC-II model in the single-trajectory realization are considered. Obviously, the computational results with the 0.1 M concentration are in perfect agreement with the 0.15 M results, suggesting negligible influences of the salt-concentration variable when its value is picked in a reasonable range. Other issues in QM/GBSA calculations are the convergence problem in SCF iterations and unsupported elements for specific systems (G4 and G13) under some Hamiltonians (specifically DFTB). In Table S9, the impact of inclusion/exclusion of the two guests with problems in DFTB calculations (i.e., G4 and G13) is presented. Still, no obvious variation is observed. Therefore, the numerical data presented in Tables S1–S4 could be considered solid.
We compare the performance statistics between different parameter combinations in the single-trajectory realization in Figure 2. The error metric RMSE is selected to evaluate the deviations of absolute affinities. It can be clearly seen that the MM/GBSA treatment with the GBOBC-I model performs best, but the smallest RMSE is still as large as ~13 kcal/mol. The shift to QM descriptions does not lead to improved accuracy, which indicates that the QM/GBSA treatment is unhelpful for the reproduction of absolute affinities. For rank predictions, the Kendall τ and PI with the MM/GBSA description are both close to zero, regardless of the selected GB model, which indicates that the MM/GBSA methods predict ranks similar to random experiments. Some QM/GBSA selections lead to bettered performance for ranking predictions, e.g., PM6 and its derivative with corrections (τ ~0.3 and PI ~0.3), but the prediction quality is still far from satisfactory. Finally, for linear correlation, the PM6 and PM6-DH+ predictions exhibit weak positive correlation with the experimental reference, while at the other levels no linear correlation or weak negative correlation is observed. Aside from these overall trends, some insights on specific models could be observed. For example, comparing the performance statistics with and without the -DH+ correction (i.e., AM1 vs. AM1-DH+, PM6 vs. PM6-DH+), the corrected Hamiltonians often produce better accuracies for absolute affinities, ranking and linear correlations. As for the comparison between DFTB2 and DFTB3, the former achieves smaller RMSE compared with the latter, but for correlation metrics their statistics are very similar. Another trend concerns the implicit solvent models. For all three correlation coefficients, the quality metrics with the GBOBC-I implicit solvent model are better than the other three solvent models, regardless of the employed Hamiltonian for the solutes. However, the opposite is observed for the absolute affinities (RMSE). Overall, shifting to the QM treatment minorly betters the rank predictions but deteriorates absolute values in the popular single-trajectory end-point sampling regime.
Comparing the best-performing QM/GBSA results with other modifications considered in our previous works [30,32], the current ranking coefficients are comparable to or slightly worse than PBSA_E/GBSA_E, the dielectric-constant variation and its three-trajectory extension. The underperformance of the QM/GBSA treatments in the main-stream single-trajectory realization is in stark contrast to many existing reports on satisfactory correlation in protein–ligand complexes [18,21] and almost perfect prediction of binding affinities in host–guest complexes [19,20], which hints on the dissimilarity of protein–ligand and host–guest situations and the potential bias in previous computational experiments due to limited sampling or potential bias in the dataset (lucky shots). Our data with unprecedented statistical quality provide conclusive evidence of the practical performance of the QM/GBSA treatment. Further considering the significant increase in computational costs due to the incorporation of QM calculations in QM/GBSA formulism, we generally do not recommend applying QM/GBSA in the popular single-trajectory end-point free energy calculation.

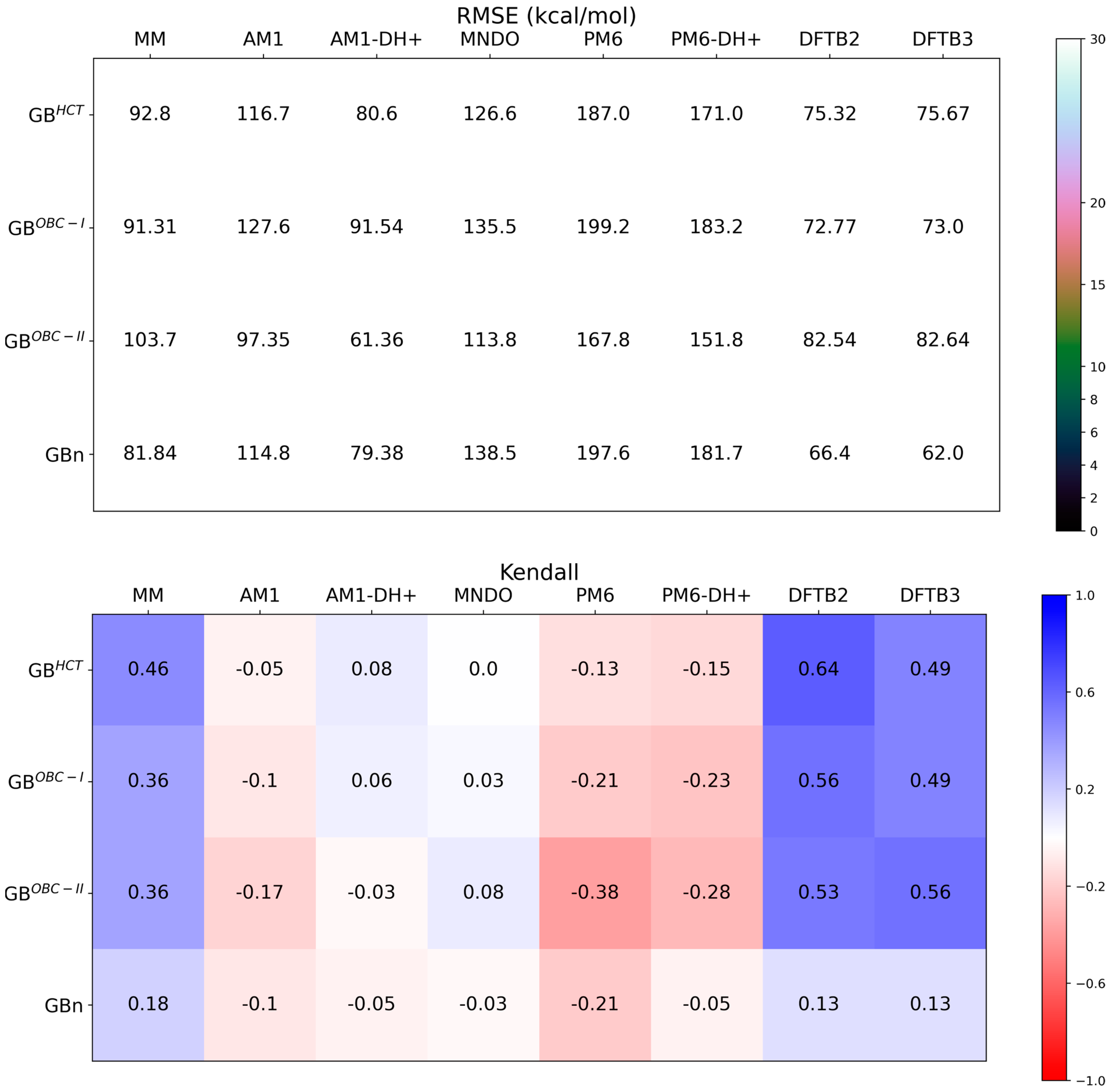
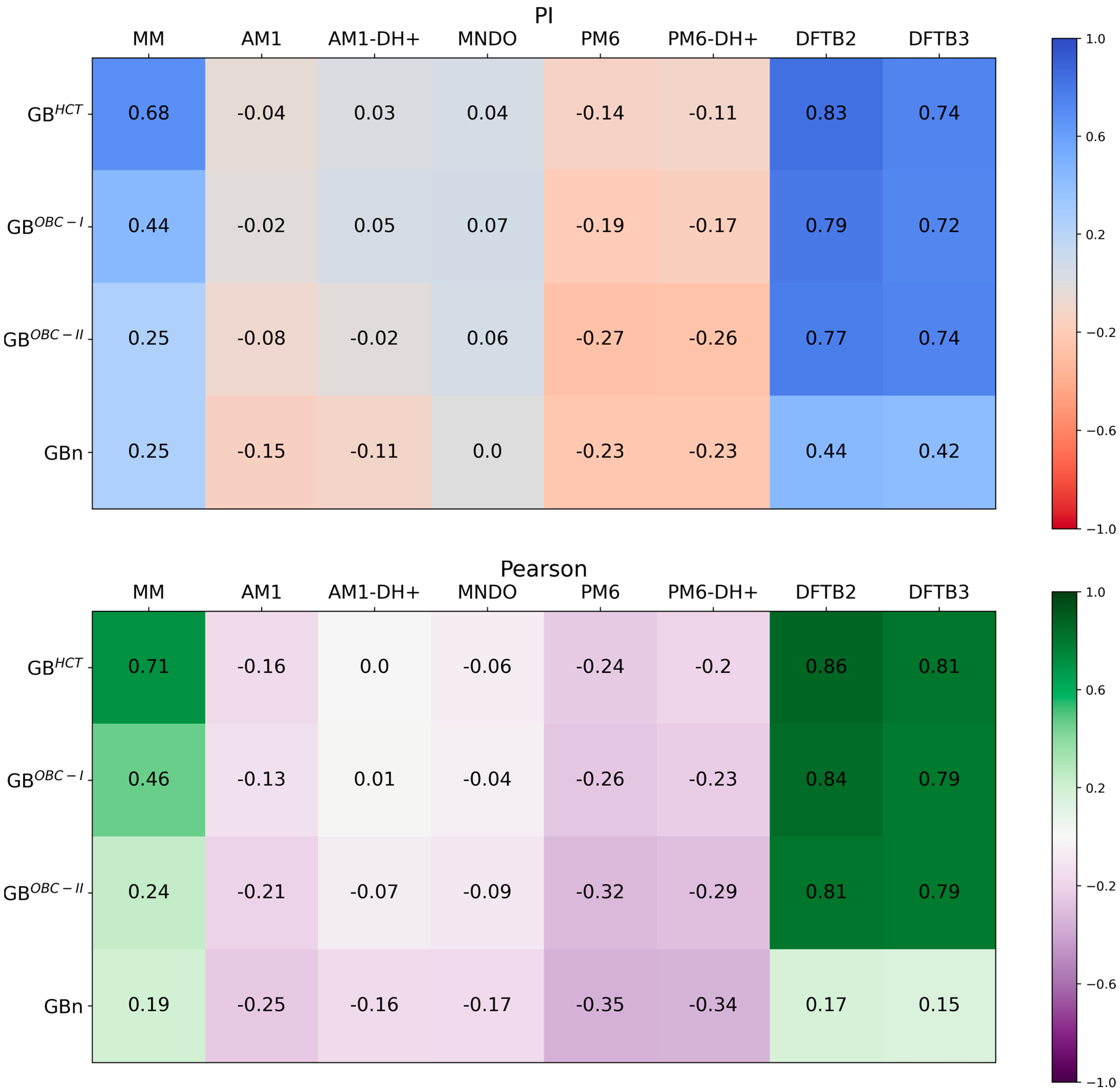
3.2. Three-Trajectory QM/GBSA

After checking the performance of the QM/GBSA treatment in the popular single-trajectory realization, we then turn to a more advanced three-trajectory QM/GBSA end-point regime. This modification has never been explored in existing literatures, due to both the overwhelming energetic fluctuation in the three-trajectory realization and the high computational cost of the QM treatment. Fortunately, the small sizes of individual molecules in host–guest complexes minimize both aspects and make the combined three-trajectory QM/GBSA treatment feasible.
The three-trajectory realization of end-point free energy calculations samples both the bound host–guest and unbound host-only and guest-only systems. As observed in our previous work, the host-only system is rather difficult to sample due to the conformational fluctuations in the -CH2-COO− rims [30]. The sampling length of this system is thus extended to an unprecedent length of 12,000 ns. The host–guest and guest-only systems are also sampled extensively for 500 ns. Overall, the current sampling protocol produces the longest trajectory and the highest-level end-point sampling statistics for this dataset. Based on the sampled configurations, the enthalpic parts of individual ensembles (ΔHi, i = host, guest or host–guest) are extracted with the implicit-solvent Hamiltonians (MM/GBSA and QM/GBSA), while the normal mode approximation [63] with the MM/GBSA Hamiltonian is still used to represent the entropic contribution TΔSi. Similar to the single-trajectory realization, the extracted snapshots are subsampled with the 1/10 ratio to decrease the computational cost, leading to an equivalent sampling interval of 100 ps. Consequently, the numbers of snapshots used in QM/GBSA enthalpy calculations are 5000 for each host–guest complex, 5000 for each solvated guest and 120,000 for the solvated host, and those in the normal mode analysis are 500 for host–guest complex, 500 for solvated guest and 12,000 for solvated host. Still, two critical components of the QM/GBSA Hamiltonian (the QM level and the GB model) are benchmarked, in a fashion similar to the previous single-trajectory realization. Further, we check the inclusion/exclusion of the two guests with convergence problems with the DFTB Hamiltonians in the three-trajectory realization in Table S9, where still no obvious influence is observed.
The performance statistics of different free energy extraction regimes are compared in Figure 3. For the absolute values, the huge deviations (huge RMSE) suggest that the three-trajectory QM/GBSA regime is practically useless when the absolute values of binding affinities are pursued. The similar applies to the MM/GBSA Hamiltonian, which reflects that this could be a general problem for the three-trajectory sampling protocol. In stark contrast, the Kendall τ and PI of the DFTB/GBSA Hamiltonian (either DFTB2 or the full third-order calculation) are satisfactorily large (τ ≥ 0.5 and PI > 0.7) especially for the GBHCT, GBOCB-I and GBOBC-II models, and are obviously improved compared with its MM/GBSA counterpart. Such prediction quality of affinity ranks (ranking power) is better than all fixed-charge predictions reported up to now [30,31,32,33], including costly alchemical methods (τ ~0.5 and PI ~0.7) and many other modified end-point regimes investigated in our previous works. As for the Pearson r (scoring power), their large values (>0.8) suggest strong positive correlations between the experimental reference and the three-trajectory QM/GBSA predictions. Compared with the DFTB/GBSA descriptions, the other QM selections seem rather unsuccessful in reproducing absolute values and ranking predictions and even perform worse than the MM description, which is not unexpected considering their inaccurate energetics and less successful error cancellations. Therefore, the selection of the QM level matters, and a sufficiently high-quality option should be applied. As for more detailed comparison between different parameter sets, the improvements given by the -DH+ correction are observed for AM1 and PM6, similar to the single-trajectory situation. Unlike the previous GBOCB-I-best behavior of the single-trajectory QM/GBSA treatment, in the current three-trajectory case, the best implicit solvent model is GBHCT. Comparing the DFTB2 and DFTB3 statistics, we observe that the former DFTB2 level outperforms the updated parameter set in most cases. Overall, according to our systematic benchmark on a series of QM/GBSA descriptions, the DFTB/GBSA description with one of the three popular GB models (GBHCT, GBOCB-I and GBOBC-II) serves as a usable selection to be combined with the three-trajectory end-point sampling protocol in host–guest binding.

4. Concluding Remarks

In this work, in order to provide a solid assessment of the predictive power of the QM/GBSA modification, we thoroughly benchmarked the workflow on a series of WP6 host–guest complexes. The computational cost of QM calculations in host–guest systems is relatively low, making the QM/GBSA Hamiltonian affordable. Extensive fixed-charge sampling is conducted in each ensemble, after which MM/GBSA and QM/GBSA postprocessing is conducted to extract the end-point free energy estimates. Under the popular single-trajectory sampling protocol, the QM/GBSA method slightly betters the rank predictions, but the reproduction of absolute affinities is deteriorated significantly. The best-performing QM/GBSA selection is PM6-DH+ with the GBOBC-I model. The correlation coefficients computed with this parameter combination is comparable to or slightly worse than the other modifications considered in our previous works, including PBSA_E/GBSA_E, the dielectric-constant-variable regime and its three-trajectory extension. Due to the significant increase in computational costs in QM/GBSA calculations, we generally do not recommend its usage in the popular single-trajectory end-point free energy calculations. However, a caution that we would add is that the underperformance of the single-trajectory QM/GBSA regime could be limited to systems similar to the current testing bed, e.g., highly-charged pillararenes, as the accuracy level of end-point workflows often exhibits a severe system-dependent behaviors. Thus, further numerical experiences on other systems would still be pursued, in order to secure a more general conclusive picture.
The three-trajectory realization is seldom applied due to the huge energetic fluctuations in biomolecules. Fortunately, the small sizes of host–guest complexes lead to smaller magnitudes of energy fluctuations, thus making the three-trajectory realization practically usable. The high cost of QM/GBSA descriptions hinders the applicability in biomacromolecules, but is made computationally feasible for smaller receptor–ligand cases such as host–guest complexes. Jointly, the unprecedently explored three-trajectory QM/GBSA method could be applied in host–guest binding with numerical statistics of sufficiently high quality. The numerical results suggest that the QM/GBSA description with the DFTB selection (either DFTB2 or the third-order extension) and many GB models (GBHCT, GBOBC-I or GBOBC-II) performs best, surpassing all fixed-charge predictions on this dataset, including alchemical transformations, the three-trajectory MM/GBSA regime (its base model) and many other modified end-point free energy techniques explored in our previous works. The predictions exhibit strong positive linear correlation with experiment, and the affinity rank can be accurately computed. The selection of the QM level seems important, and many crude semi-empirical QM levels (e.g., AM1, PM6 and MNDO) should be avoided, while more accurate options such as DFTB and even higher-level selections could be considered. For the GB models, all popular options could be considered, but the three models GBHCT, GBOCB-I or GBOBC-II seem the most successful ones in terms of error cancellation.
Finally, considering the observed numerical performance of the advanced three-trajectory QM/GBSA treatment in the current pillararene host–guest dataset, a straightforward expectation and step further is to extend the method to other species, e.g., cucurbiturils and cyclodextrins. While, technically, such an extension is straightforward, we would add a caution that the performance metrics cannot be guaranteed to be as good as the current case, due to many influencing factors involved in the end-point framework. Specifically, the accuracy level of end-point calculations relies heavily on error cancellation. It is well known that the error cancellation exhibits a system-dependent behavior. The errors of individual terms (e.g., solvation with implicit solvent models, QM Hamiltonian, force-field sampling) need to be in a balanced form to enable successful predictions. Despite the success of the advanced three-trajectory QM/GBSA regime, numerical experience with it is still limited. Therefore, further systematic benchmarks are required and scheduled in the future to provide more insights into the practical screening power of the purposed regime.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/liquids3040027/s1. Figure S1: Comparison between free energy estimates obtained with two salt-concentration conditions (0.1 M and 0.15 M) with (a) MM/GBSA and (b) QM/GBSA Hamiltonians in the single-trajectory realization. While for MM/GBSA estimates four GB models are employed, in QM/GBSA calculations only the GBOBC-II model is considered. Table S1: Single-trajectory end-point estimates of WP6 host-guest binding affinities with the GBHCT model (kcal/mol). Table S2: Single-trajectory end-point estimates of WP6 host-guest binding affinities with the GBOBC-I model (kcal/mol). Table S3: Single-trajectory end-point estimates of WP6 host-guest binding affinities with the GBOBC-II model (kcal/mol). Table S4: Single-trajectory end-point estimates of WP6 host-guest binding affinities with the GBn model (kcal/mol). Table S5: Three-trajectory end-point estimates of WP6 host-guest binding affinities with the GBHCT model (kcal/mol). Table S6: Three-trajectory end-point estimates of WP6 host-guest binding affinities with the GBOBC-I model (kcal/mol). Table S7: Three-trajectory end-point estimates of WP6 host-guest binding affinities with the GBOBC-II model (kcal/mol). Table S8: Three-trajectory end-point estimates of WP6 host-guest binding affinities with the GBn model (kcal/mol). Table S9: Comparison between quality metrics computed with all guest molecules and without G4 and G13 (the two guests with convergence problems or with elements unsupported for DFTB Hamiltonians) in the single- and three-trajectory realizations for all post-processing Hamiltonians except DFTB. The GBOBC-II implicit solvent model is used here. The inclusion/exclusion of G4 and G13 perturbs the results in a Hamiltonian-dependent manner, but the magnitudes of variations of the quality metrics are generally insignificant.

Author Contributions

X.W.: Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing—review & editing. M.W.: Investigation, Resources, Software, Validation, Visualization, Writing—review & editing. Z.S.: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing—original draft, Writing—review & editing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Beijing Natural Science Foundation (Grant No. 7224357).

Data Availability Statement

The atomic-charge files for host and guest molecules and the docking-produced bound structures of all host–guest pairs can be accessed online at https://github.com/proszxppp/WP6-host-guest-binding. All free energy estimates obtained in this work are given in the supporting information. For readers interested in more detailed energy components (e.g., detailed enthalpic and entropic contributions in the three-trajectory realization), please contact the corresponding author to access the data.

Acknowledgments

We thank the anonymous reviewers for valuable comments and critical reading.

Conflicts of Interest

There are no conflict of interest to declare.

References

  1. Wang, X.; Huai, Z.; Sun, Z. Host Dynamics under General-Purpose Force Fields. Molecules 2023, 28, 5940. [Google Scholar] [CrossRef] [PubMed]
  2. Alexov, E.; Mehler, E.L.; Baker, N.; Baptista, A.M.; Huang, Y.; Milletti, F.; Erik Nielsen, J.; Farrell, D.; Carstensen, T.; Olsson, M.H.M.; et al. Progress in the prediction of pKa values in proteins. Proteins Struct. Funct. Bioinform. 2011, 79, 3260–3275. [Google Scholar] [CrossRef]
  3. Li, C.; Zhang, A.; Wang, L.; Zuo, J.; Zhu, C.; Xu, J.; Wang, M.; Zhang, J.Z.H. Development of a polynomial scoring function P3-Score for improved scoring and ranking powers. Chem. Phys. Lett. 2023, 824, 140547. [Google Scholar] [CrossRef]
  4. Su, P.C.; Tsai, C.C.; Mehboob, S.; Hevener, K.E.; Johnson, M.E. Comparison of radii sets, entropy, QM methods, and sampling on MM-PBSA, MM-GBSA, and QM/MM-GBSA ligand binding energies of F. tularensis enoyl-ACP reductase (F abI). J. Comput. Chem. 2015, 36, 1859–1873. [Google Scholar] [CrossRef]
  5. Sangpheak, W.; Khuntawee, W.; Wolschann, P.; Pongsawasdi, P.; Rungrotmongkol, T. Enhanced stability of a naringenin/2, 6-dimethyl β-cyclodextrin inclusion complex: Molecular dynamics and free energy calculations based on MM-and QM-PBSA/GBSA. J. Mol. Graph. Model. 2014, 50, 10–15. [Google Scholar] [CrossRef] [PubMed]
  6. Tsitsanou, K.E.; Hayes, J.M.; Keramioti, M.; Mamais, M.; Oikonomakos, N.G.; Kato, A.; Leonidas, D.D.; Zographos, S.E. Sourcing the affinity of flavonoids for the glycogen phosphorylase inhibitor site via crystallography, kinetics and QM/MM-PBSA binding studies: Comparison of chrysin and flavopiridol. Food Chem. Toxicol. 2013, 61, 14–27. [Google Scholar] [CrossRef] [PubMed]
  7. Gundelach, L.; Fox, T.; Tautermann, C.S.; Skylaris, C.-K. BRD4: Quantum mechanical protein–ligand binding free energies using the full-protein DFT-based QM-PBSA method. Phys. Chem. Chem. Phys. 2022, 24, 25240–25249. [Google Scholar] [CrossRef]
  8. Nutho, B.; Pengthaisong, S.; Tankrathok, A.; Lee, V.S.; Ketudat Cairns, J.R.; Rungrotmongkol, T.; Hannongbua, S. Structural basis of specific glucoimidazole and mannoimidazole binding by Os3BGlu7. Biomolecules 2020, 10, 907. [Google Scholar] [CrossRef]
  9. Li, J.; Huang, Y.; Wu, M.; Wu, C.; Li, X.; Bao, J. Structure and energy based quantitative missense variant effect analysis provides insights into drug resistance mechanisms of anaplastic lymphoma kinase mutations. Sci. Rep. 2018, 8, 10664. [Google Scholar] [CrossRef]
  10. Chetter, B.A.; Kyriakis, E.; Barr, D.; Karra, A.G.; Katsidou, E.; Koulas, S.M.; Skamnaki, V.T.; Snape, T.J.; Psarra, A.-M.G.; Leonidas, D.D.; et al. Synthetic flavonoid derivatives targeting the glycogen phosphorylase inhibitor site: QM/MM-PBSA motivated synthesis of substituted 5,7-dihydroxyflavones, crystallography, in vitro kinetics and ex-vivo cellular experiments reveal novel potent inhibitors. Bioorg. Chem. 2020, 102, 104003. [Google Scholar] [CrossRef]
  11. Dutkiewicz, Z. Computational methods for calculation of protein-ligand binding affinities in structure-based drug design. In Theoretical and Computational Chemistry; Iwona, G., Bartosz, T., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2021; pp. 1–40. [Google Scholar]
  12. Maier, S.; Thapa, B.; Erickson, J.; Raghavachari, K. Comparative assessment of QM-based and MM-based models for prediction of protein–ligand binding affinity trends. Phys. Chem. Chem. Phys. 2022, 24, 14525–14537. [Google Scholar] [CrossRef] [PubMed]
  13. Wang, Y.; Liu, J.; Li, J.; He, X. Fragment-based quantum mechanical calculation of protein–protein binding affinities. J. Comput. Chem. 2018, 39, 1617–1628. [Google Scholar] [CrossRef] [PubMed]
  14. Liu, J.; Wang, X.; Zhang, J.Z.H.; He, X. Calculation of protein–ligand binding affinities based on a fragment quantum mechanical method. RSC Adv. 2015, 5, 107020–107030. [Google Scholar] [CrossRef]
  15. Lukac, I.; Abdelhakim, H.; Ward, R.A.; St-Gallay, S.A.; Madden, J.C.; Leach, A.G. Predicting protein–ligand binding affinity and correcting crystal structures with quantum mechanical calculations: Lactate dehydrogenase A. Chem. Sci. 2019, 10, 2218–2227. [Google Scholar] [CrossRef]
  16. Thapa, B.; Beckett, D.; Erickson, J.; Raghavachari, K. Theoretical Study of Protein–Ligand Interactions Using the Molecules-in-Molecules Fragmentation-Based Method. J. Chem. Theory Comput. 2018, 14, 5143–5155. [Google Scholar] [CrossRef]
  17. Okimoto, N.; Otsuka, T.; Hirano, Y.; Taiji, M. Use of the Multilayer Fragment Molecular Orbital Method to Predict the Rank Order of Protein–Ligand Binding Affinities: A Case Study Using Tankyrase 2 Inhibitors. ACS Omega 2018, 3, 4475–4485. [Google Scholar] [CrossRef] [PubMed]
  18. Mishra, S.K.; Koča, J. Assessing the Performance of MM/PBSA, MM/GBSA, and QM–MM/GBSA Approaches on Protein/Carbohydrate Complexes: Effect of Implicit Solvent Models, QM Methods, and Entropic Contributions. J. Phys. Chem. B 2018, 122, 8113–8121. [Google Scholar] [CrossRef]
  19. Nutho, B.; Khuntawee, W.; Rungnim, C.; Pongsawasdi, P.; Wolschann, P.; Karpfen, A.; Kungwan, N.; Rungrotmongkol, T. Binding mode and free energy prediction of fisetin/β-cyclodextrin inclusion complexes. Beilstein J. Org. Chem. 2014, 10, 2789–2799. [Google Scholar] [CrossRef] [PubMed]
  20. Rungrotmongkol, T.; Chakcharoensap, T.; Pongsawasdi, P.; Kungwan, N.; Wolschann, P. The inclusion complexation of daidzein with β-cyclodextrin and 2,6-dimethyl-β-cyclodextrin: A theoretical and experimental study. Monatshefte Chem.-Chem. Mon. 2018, 149, 1739–1747. [Google Scholar] [CrossRef]
  21. Ciancetta, A.; Genheden, S.; Ryde, U. A QM/MM study of the binding of RAPTA ligands to cathepsin B. J. Comput.-Aided Mol. Des. 2011, 25, 729–742. [Google Scholar] [CrossRef]
  22. Sun, Z.; He, Q.; Gong, Z.; Kalhor, P.; Huai, Z.; Liu, Z. A General Picture of Cucurbit[8]uril Host-Guest Binding: Recalibrating Bonded Interactions. Molecules 2023, 28, 3124. [Google Scholar] [CrossRef]
  23. Sun, Z.; Zheng, L.; Kai, W.; Huai, Z.; Liu, Z. Primary vs. Secondary: Directionalized Guest Coordination in β-Cyclodextrin Derivatives. Carbohydr. Polym. 2022, 297, 120050. [Google Scholar] [CrossRef] [PubMed]
  24. Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit[8]uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef]
  25. Sun, Z. SAMPL7 TrimerTrip Host-Guest Binding Poses and Binding Affinities from Spherical-Coordinates-Biased Simulations. J. Comput.-Aided Mol. Des. 2021, 35, 105–115. [Google Scholar] [CrossRef] [PubMed]
  26. Hao, Q.; Kang, Y.; Xu, J.-F.; Zhang, X. pH/ROS Dual-Responsive Supramolecular Vesicles Fabricated by Carboxylated Pillar[6]arene-Based Host–Guest Recognition and Phenylboronic Acid Pinacol Ester Derivative. Langmuir 2020, 36, 4080–4087. [Google Scholar] [CrossRef]
  27. Zhang, X.; Cheng, Q.; Li, L.; Shangguan, L.; Li, C.; Li, S.; Huang, F.; Zhang, J.; Wang, R. Supramolecular therapeutics to treat the side effects induced by a depolarizing neuromuscular blocking agent. Theranostics 2019, 9, 3107. [Google Scholar] [CrossRef] [PubMed]
  28. Hua, B.; Shao, L.; Zhang, Z.; Sun, J.; Yang, J. Pillar [6] arene/acridine orange host–guest complexes as colorimetric and fluorescence sensors for choline compounds and further application in monitoring enzymatic reactions. Sens. Actuators B Chem. 2018, 255, 1430–1435. [Google Scholar] [CrossRef]
  29. Liu, Y.; Chen, X.; Ding, J.; Yu, L.; Ma, D.; Ding, J. Improved solubility and bioactivity of camptothecin family antitumor drugs with supramolecular encapsulation by water-soluble pillar [6] arene. ACS Omega 2017, 2, 5283–5288. [Google Scholar] [CrossRef]
  30. Liu, X.; Zheng, L.; Qin, C.; Yalong, C.; Zhang, J.Z.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-Guest Binding: III. Force-Field Comparison, Three-Trajectory Realization and Further Dielectric Augmentation. Molecules 2023, 28, 2767. [Google Scholar] [CrossRef]
  31. Liu, X.; Zheng, L.; Qin, C.; Zhang, J.Z.H.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-guest Binding: I. Standard Procedure. J. Comput.-Aided Mol. Des. 2022, 36, 735–752. [Google Scholar] [CrossRef]
  32. Liu, X.; Zheng, L.; Cong, Y.; Gong, Z.; Yin, Z.; Zhang, J.Z.; Liu, Z.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-guest Binding: II. Regression and Dielectric Constant. J. Comput.-Aided Mol. Des. 2022, 36, 879–894. [Google Scholar] [CrossRef] [PubMed]
  33. Procacci, P.; Guarnieri, G. SAMPL9 blind predictions using nonequilibrium alchemical approaches. J. Chem. Phys. 2022, 156, 164104. [Google Scholar] [CrossRef] [PubMed]
  34. Macchiagodena, M.; Pagliai, M.; Procacci, P. NE-RDFE: A protocol and toolkit for computing relative dissociation free energies with GROMACS between dissimilar molecules using bidirectional nonequilibrium dual topology schemes. J. Comput. Chem. 2023, 44, 1221–1230. [Google Scholar] [CrossRef] [PubMed]
  35. Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1992, 97, 10269–10280. [Google Scholar] [CrossRef]
  36. Mcweeny, R.; Diercksen, G. Self-Consistent Perturbation Theory. II. Extension to Open Shells. J. Chem. Phys. 1968, 49, 4852–4856. [Google Scholar] [CrossRef]
  37. Pople, J.A.; Nesbet, R.K. Self-Consistent Orbitals for Radicals. J. Chem. Phys. 1954, 22, 571–572. [Google Scholar] [CrossRef]
  38. Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
  39. Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef]
  40. Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
  41. Price, D.J.; Brooks, C.L., III. A Modified TIP3P Water Potential for Simulation with Ewald Summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef]
  42. Joung, I.S.; Cheatham, T.E., III. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
  43. Joung, I.S.; Cheatham, T.E. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef]
  44. Case, D.A.; Cheatham, T.E.; Tom, D.; Holger, G.; Luo, R.; Merz, K.M.; Alexey, O.; Carlos, S.; Bing, W.; Woods, R.J. The Amber Biomolecular Simulation Programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
  45. Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical Integration of The Cartesian Equations of Motion of A System with Constraints: Molecular Dynamics of n -alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
  46. Miyamoto, S.; Kollman, P.A. Settle: An Analytical Version of The SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
  47. Pastor, R.W.; Brooks, B.R.; Szabo, A. An analysis of the accuracy of Langevin and molecular dynamics algorithms. Mol. Phys. 1988, 65, 1409–1419. [Google Scholar] [CrossRef]
  48. Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
  49. Dewar, M.J.S.; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc. 1977, 99, 4899–4907. [Google Scholar] [CrossRef]
  50. Stewart, J.J. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef]
  51. Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
  52. Niehaus, T.A.; Elstner, M.; Frauenheim, T.; Suhai, S. Application of an approximate density-functional method to sulfur containing compounds. J. Mol. Struct. THEOCHEM 2001, 541, 185–194. [Google Scholar] [CrossRef]
  53. Gaus, M.; Goez, A.; Elstner, M. Parametrization and benchmark of DFTB3 for organic molecules. J. Chem. Theory Comput. 2013, 9, 338–354. [Google Scholar] [CrossRef]
  54. Gaus, M.; Cui, Q.; Elstner, M. DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [Google Scholar] [CrossRef] [PubMed]
  55. Hawkins, G.D.; Cramer, C.J.; Truhlar, D.G. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 1996, 100, 19824–19839. [Google Scholar] [CrossRef]
  56. Hawkins, G.D.; Cramer, C.J.; Truhlar, D.G. Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett. 1995, 246, 122–129. [Google Scholar] [CrossRef]
  57. Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef]
  58. Feig, M.; Onufriev, A.; Lee, M.S.; Im, W.; Case, D.A. Performance comparison of generalized born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. J. Comput. Chem. 2004, 25, 265–284. [Google Scholar] [CrossRef]
  59. Hai, N.; Pérez, A.; Bermeo, S.; Simmerling, C. Refinement of Generalized Born Implicit Solvation Parameters for Nucleic Acids and their Complexes with Proteins. J. Chem. Theory Comput. 2015, 11, 3714. [Google Scholar]
  60. Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
  61. Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
  62. Pearlman, D.A.; Charifson, P.S. Are Free Energy Calculations Useful in Practice? A Comparison with Rapid Scoring Functions for the p38 MAP Kinase Protein System. J. Med. Chem. 2001, 44, 3417–3423. [Google Scholar] [CrossRef] [PubMed]
  63. Case, D.A. Normal mode analysis of protein dynamics. Curr. Opin. Struct. Biol. 2010, 4, 285–290. [Google Scholar] [CrossRef]
Liquids 03 00027 g001
Figure 1. (a) The 2D chemical structures of WP6 host–guest pairs and the corresponding binding affinities and (b) the thermodynamic cycle used in end-point free energy estimation.
Figure 1. (a) The 2D chemical structures of WP6 host–guest pairs and the corresponding binding affinities and (b) the thermodynamic cycle used in end-point free energy estimation.
Liquids 03 00027 g001
Liquids 03 00027 g002aLiquids 03 00027 g002b
Figure 2. Quality metrics for the single-trajectory MM/GBSA and QM/GBSA estimates.
Figure 2. Quality metrics for the single-trajectory MM/GBSA and QM/GBSA estimates.
Liquids 03 00027 g002aLiquids 03 00027 g002b
Liquids 03 00027 g003aLiquids 03 00027 g003b
Figure 3. Quality metrics for the three-trajectory MM/GBSA and QM/GBSA estimates.
Figure 3. Quality metrics for the three-trajectory MM/GBSA and QM/GBSA estimates.
Liquids 03 00027 g003aLiquids 03 00027 g003b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, X.; Wang, M.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-Guest Binding: IV. The QM Treatment, GB Models and the Multi-Trajectory Extension. Liquids 2023, 3, 426-439. https://doi.org/10.3390/liquids3040027

AMA Style

Wang X, Wang M, Sun Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-Guest Binding: IV. The QM Treatment, GB Models and the Multi-Trajectory Extension. Liquids. 2023; 3(4):426-439. https://doi.org/10.3390/liquids3040027

Chicago/Turabian Style

Wang, Xiaohui, Mao Wang, and Zhaoxi Sun. 2023. "Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-Guest Binding: IV. The QM Treatment, GB Models and the Multi-Trajectory Extension" Liquids 3, no. 4: 426-439. https://doi.org/10.3390/liquids3040027

APA Style

Wang, X., Wang, M., & Sun, Z. (2023). Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene Host-Guest Binding: IV. The QM Treatment, GB Models and the Multi-Trajectory Extension. Liquids, 3(4), 426-439. https://doi.org/10.3390/liquids3040027

Article Metrics

Back to TopTop